Effects of Ionic Strength on Lateral Particle Migration in Shear-Thinning Xanthan Gum Solutions
Abstract
1. Introduction
2. Experimental
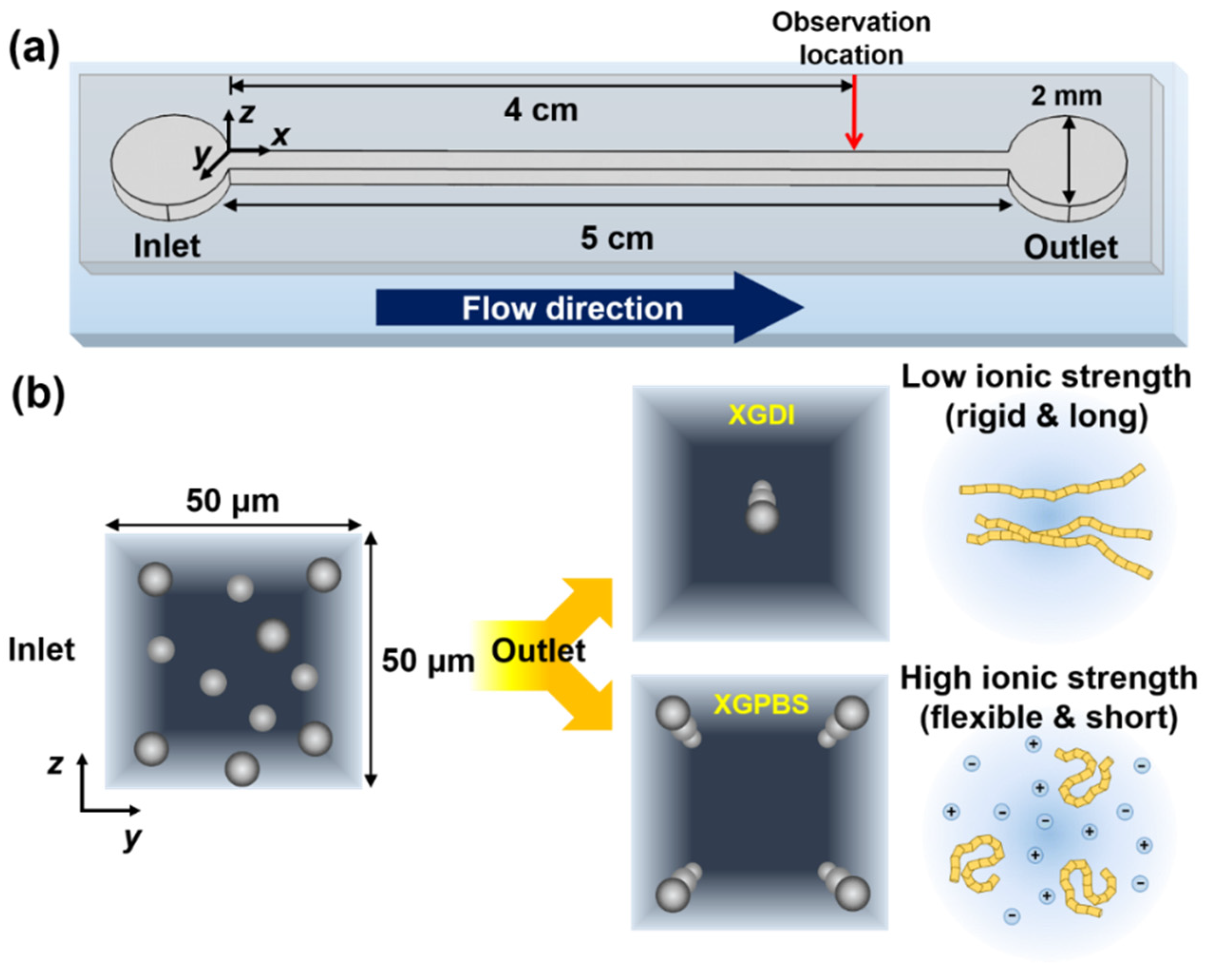
2.1. Microchannel and Materials
2.2. Microfluidics, Imaging, and Flow Characterization
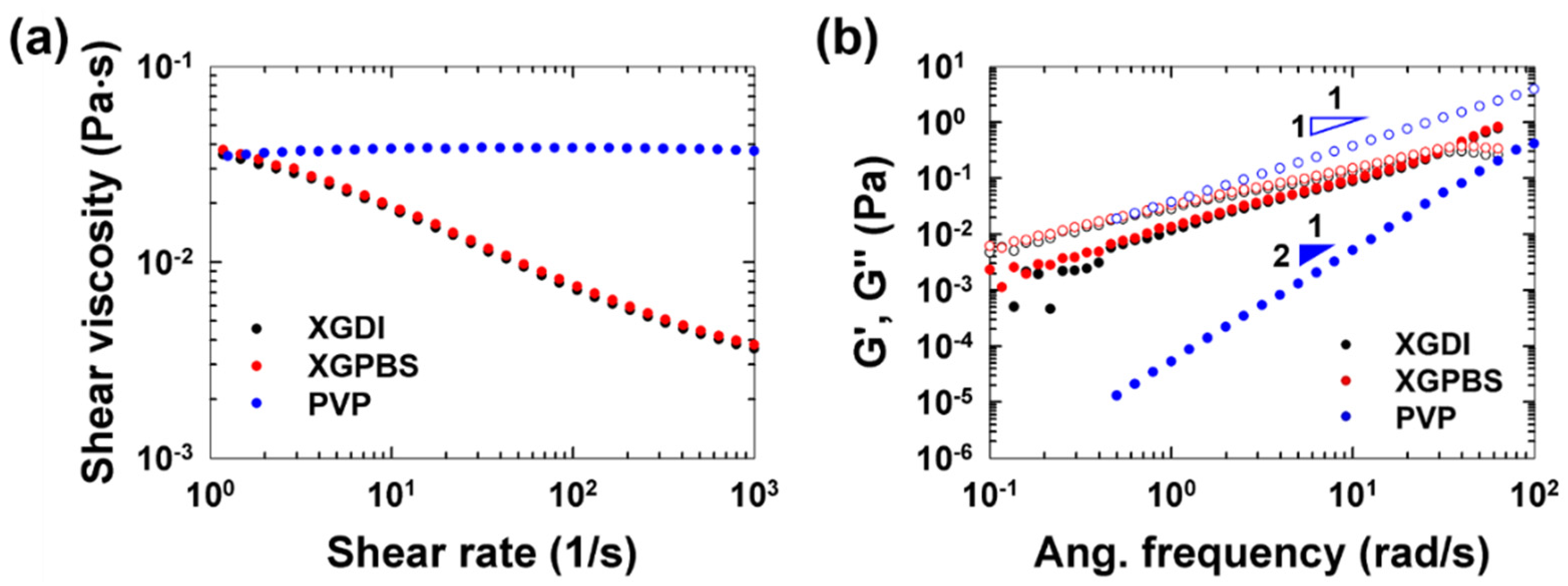
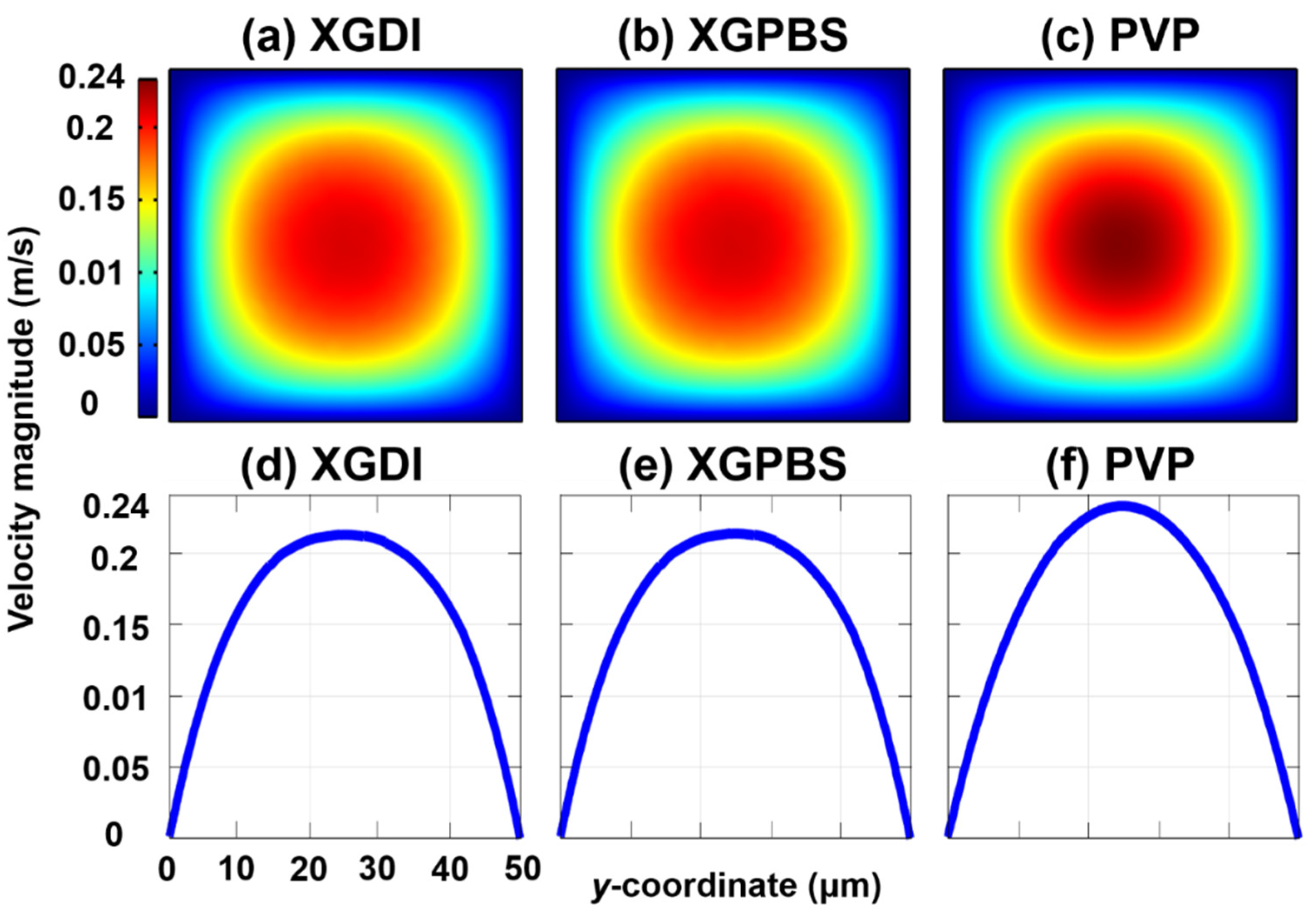
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tabeling, P. Introduction to Microfluidics; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Ligler, F.S.; Kim, J.S. The Microflow Cytometer; Pan Stanford Publishing: Danvers, MA, USA, 2010. [Google Scholar]
- Xuan, X.; Zhu, J.; Church, C. Particle focusing in microfluidic devices. Microfluid. Nanofluid. 2010, 9, 1–16. [Google Scholar] [CrossRef]
- Amini, H.; Lee, W.; Di Carlo, D. Inertial microfluidic physics. Lab Chip 2014, 14, 2739. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, D. Inertial microfluidics. Lab Chip 2009, 9, 3038. [Google Scholar] [CrossRef] [PubMed]
- D’Avino, G.; Greco, F.; Maffettone, P.L. Particle migration due to viscoelasticity of the suspending liquid and its relevance in microfluidic devices. Annu. Rev. Fluid Mech. 2017, 49, 341–360. [Google Scholar] [CrossRef]
- Lu, X.; Liu, C.; Hu, G.; Xuan, X. Particle manipulations in non-Newtonian microfluidics: A review. J. Colloid Interface Sci. 2017, 500, 182–201. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Kim, J.Y.; Lee, S.J.; Lee, S.S.; Kim, J.M. Sheathless elasto-inertial particle focusing and continuous separation in a straight rectangular microchannel. Lab Chip 2011, 11, 266–273. [Google Scholar] [CrossRef]
- Kim, J.Y.; Ahn, S.W.; Lee, S.S.; Kim, J.M. Lateral migration and focusing of colloidal particles and DNA molecules under viscoelastic flow. Lab Chip 2012, 12, 2807–2814. [Google Scholar] [PubMed]
- Kang, K.; Lee, S.S.; Hyun, K.; Lee, S.J.; Kim, J.M. DNA-based highly tunable particle focuser. Nat. Commun. 2013, 4, 2567. [Google Scholar] [CrossRef]
- Cha, S.; Shin, T.; Lee, S.S.; Shim, W.; Lee, G.; Lee, S.J.; Kim, Y.; Kim, J.M. Cell stretching measurement utilizing viscoelastic particle focusing. Anal. Chem. 2012, 84, 10471–10477. [Google Scholar] [CrossRef]
- D’Avino, G.; Romeo, G.; Villone, M.M.; Greco, F.; Netti, P.A.; Maffettone, P.L. Single line particle focusing induced by viscoelasticity of the suspending liquid: Theory, experiments and simulations to design a micropipe flow-focuser. Lab Chip 2012, 12, 1638. [Google Scholar] [CrossRef]
- Leshansky, A.M.; Bransky, A.; Korin, N.; Dinnar, U.; Leshansky, A. Tunable nonlinear viscoelastic “focusing” in a microfluidic device. Phys. Rev. Lett. 2007, 98, 234501. [Google Scholar] [CrossRef] [PubMed]
- Del Giudice, F.; Sathish, S.; D’Avino, G.; Shen, A.Q. “From the Edge to the Center”: Viscoelastic migration of particles and cells in a strongly shear-thinning liquid flowing in a microchannel. Anal. Chem. 2017, 89, 13146–13159. [Google Scholar] [CrossRef] [PubMed]
- Seo, K.W.; Kang, Y.J.; Lee, S.J. Lateral migration and focusing of microspheres in a microchannel flow of viscoelastic fluids. Phys. Fluids 2014, 26, 63301. [Google Scholar] [CrossRef]
- Gauthier, F.; Goldsmith, H.L.; Mason, S.G. Particle motions in non-Newtonian media. Rheol. Acta 1971, 10, 344–364. [Google Scholar] [CrossRef]
- Villone, M.; D’Avino, G.; Hulsen, M.; Greco, F.; Maffettone, P.L. Particle motion in square channel flow of a viscoelastic liquid: Migration vs. secondary flows. J. Non-Newton. Fluid Mech. 2013, 195, 1–8. [Google Scholar] [CrossRef]
- Huang, P.; Joseph, D. Effects of shear thinning on migration of neutrally buoyant particles in pressure driven flow of Newtonian and viscoelastic fluids. J. Non-Newton. Fluid Mech. 2000, 90, 159–185. [Google Scholar] [CrossRef]
- Li, D.; Xuan, X. The motion of rigid particles in the Poiseuille flow of pseudoplastic fluids through straight rectangular microchannels. Microfluid. Nanofluid. 2019, 23, 54. [Google Scholar] [CrossRef]
- Li, D.; Xuan, X. Fluid rheological effects on particle migration in a straight rectangular microchannel. Microfluid. Nanofluid. 2018, 22, 49. [Google Scholar] [CrossRef]
- Whitcomb, P.J.; Macosko, C.W. Rheology of xanthan gum. J. Rheol. 1978, 22, 493–505; [Google Scholar] [CrossRef]
- Song, K.W.; Kim, Y.S.; Chang, G.S. Rheology of concentrated xanthan gum solutions: Steady shear flow behavior. Fiber Polym. 2006, 7, 129–138. [Google Scholar] [CrossRef]
- Zirnsak, M.A.; Boger, D.V.; Tirtaatmadja, V. Steady shear and dynamic rheological properties of xanthan gum solutions in viscous solvents. J. Rheol. 1999, 43, 627–650. [Google Scholar] [CrossRef]
- Khagram, M. Extensional Flow of Xanthan Gum Solutions. J. Rheol. 1985, 29, 191–207. [Google Scholar] [CrossRef]
- Sousa, P.C.; Pinho, F.T.; Oliveira, M.S.N.; Alves, M.A. Extensional flow of blood analog solutions in microfluidic devices. Biomicrofluidics 2011, 5, 14108. [Google Scholar] [CrossRef] [PubMed]
- Calejo, J.; Pinho, D.; Galindo-Rosales, F.; Lima, R.; Campo-Deaño, L. Particulate blood analogues reproducing the erythrocytes cell-free layer in a microfluidic device containing a hyperbolic contraction. Micromachines 2016, 7, 4. [Google Scholar] [CrossRef] [PubMed]
- Pinho, D.; Campo-Deaño, L.; Lima, R.; Pinho, F.T. In vitro particulate analogue fluids for experimental studies of rheological and hemorheological behavior of glucose-rich RBC suspensions. Biomicrofluidics 2017, 11, 054105. [Google Scholar] [CrossRef] [PubMed]
- Campo-Deaño, L.; Dullens, R.P.A.; Aarts, D.G.A.L.; Pinho, F.T.; Oliveira, M.S.N. Viscoelasticity of blood and viscoelastic blood analogues for use in polydymethylsiloxane in vitro models of the circulatory system. Biomicrofluidics 2013, 7, 034102. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Norisuye, T.; Fujita, H. Double-stranded helix of xanthan in dilute solution: Evidence from light scattering. Polym. J. 1984, 16, 341–350. [Google Scholar] [CrossRef]
- Camesano, T.A.; Wilkinson, K.J. Single molecule study of xanthan conformation using atomic force microscopy. Biomacromolecules 2001, 2, 1184–1191. [Google Scholar] [CrossRef]
- Xia, Y.; Whitesides, G.M. Soft lithography. Angew. Chem. 1998, 37, 550–575. [Google Scholar] [CrossRef]
- Cho, K.S.; Hyun, K.; Ahn, K.H.; Lee, S.J. A geometrical interpretation of large amplitude oscillatory shear response. J. Rheol. 2005, 49, 747. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Morris, C.J.; Forster, F.K. Oscillatory flow in microchannels. Exp. Fluids 2004, 36, 928–937. [Google Scholar] [CrossRef]
- Fuerstman, M.J.; Lai, A.; Thurlow, M.E.; Shevkoplyas, S.S.; Stone, H.A.; Whitesides, G.M. The pressure drop along rectangular microchannels containing bubbles. Lab Chip 2007, 7, 1479–1489. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Lee, S.S.; Ahn, S.W.; Kang, K.; Shim, W.; Lee, G.; Hyun, K.; Kim, J.M. Deformability-selective particle entrainment and separation in a rectangular microchannel using medium viscoelasticity. Soft Matter 2012, 18, 5011. [Google Scholar] [CrossRef]
- Japper-Jaafar, A.; Escudier, M.; Poole, R. Laminar, transitional and turbulent annular flow of drag-reducing polymer solutions. J. Non-Newton. Fluid Mech. 2010, 165, 1357–1372. [Google Scholar] [CrossRef]
- Li, G.; McKinley, G.H.; Ardekani, A.M. Dynamics of particle migration in channel flow of viscoelastic fluids. J. Fluid Mech. 2015, 785, 486–505. [Google Scholar] [CrossRef]
- Ho, B.P.; Leal, L.G. Migration of rigid spheres in a 2-dimensional unidirectional shear-flow of a 2nd-order fluid. J. Fluid Mech. 1976, 76, 783–799. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Jendrejack, R.M.; Schwartz, D.C.; De Pablo, J.J.; Graham, M. Shear-induced migration in flowing polymer solutions: Simulation of long-chain DNA in microchannels. J. Chem. Phys. 2004, 120, 2513–2529. [Google Scholar] [CrossRef]
- Jo, K.; Chen, Y.L.; De Pablo, J.J.; Schwartz, D.C. Elongation and migration of single DNA molecules in microchannels using oscillatory shear flows. Lab Chip 2009, 9, 2348–2355. [Google Scholar] [CrossRef]
- Losserand, S.; Coupier, G.; Podgorski, T. Migration velocity of red blood cells in microchannels. Microvasc. Res. 2019, 124, 30–36. [Google Scholar] [CrossRef]
- Kumar, A.; Graham, M. Margination and segregation in confined flows of blood and other multicomponent suspensions. Soft Matter 2012, 8, 10536. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Gompper, G. White blood cell margination in microcirculation. Soft Matter 2014, 10, 2961–2970. [Google Scholar] [CrossRef] [PubMed]
- Del Giudice, F.; D’Avino, G.; Greco, F.; Netti, P.A.; Maffettone, P.L. Effect of fluid rheology on particle migration in a square-shaped microchannel. Microfluid. Nanofluid. 2015, 19, 95–104. [Google Scholar] [CrossRef]


| Property | XGDI | XGPBS | PVP | |
|---|---|---|---|---|
| Zero-shear viscosity (cP) | μ0 | 38.9 | 45.6 | 38.1 |
| Infinite-shear viscosity (cP) | μinf | 1.3 | 1.7 | |
| Power-law index | n | 0.56 | 0.58 | |
| Relaxation time (ms) | λ | 34.2 | 29.3 | 1.4 |
| Q (mL·h−1) | XGDI | XGPBS | PVP | |||
|---|---|---|---|---|---|---|
| Re | Wi | Re | Wi | Re | Wi | |
| 0.2 | - | - | 0.0292 | 1.2 | ||
| 0.36 | 0.0514 | 54.6 | 0.0439 | 46.9 | 0.0525 | 2.2 |
| 0.64 | 0.0914 | 97.1 | 0.0780 | 83.3 | 0.0933 | 3.9 |
| 1.3 | 0.1857 | 197.3 | 0.1584 | 169.2 | - | |
| 2 | 0.2856 | 303.6 | 0.2437 | 260.4 | ||
| 4 | 0.5713 | 607.1 | 0.4873 | 520.7 | ||
| 6 | 0.8569 | 910.7 | 0.7310 | 781.1 | ||
| 8 | 1.1425 | 1214.2 | 0.9747 | 1041.4 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, M.; Hong, S.O.; Lee, S.H.; Hyun, K.; Kim, J.M. Effects of Ionic Strength on Lateral Particle Migration in Shear-Thinning Xanthan Gum Solutions. Micromachines 2019, 10, 535. https://doi.org/10.3390/mi10080535
Cho M, Hong SO, Lee SH, Hyun K, Kim JM. Effects of Ionic Strength on Lateral Particle Migration in Shear-Thinning Xanthan Gum Solutions. Micromachines. 2019; 10(8):535. https://doi.org/10.3390/mi10080535
Chicago/Turabian StyleCho, Mira, Sun Ok Hong, Seung Hak Lee, Kyu Hyun, and Ju Min Kim. 2019. "Effects of Ionic Strength on Lateral Particle Migration in Shear-Thinning Xanthan Gum Solutions" Micromachines 10, no. 8: 535. https://doi.org/10.3390/mi10080535
APA StyleCho, M., Hong, S. O., Lee, S. H., Hyun, K., & Kim, J. M. (2019). Effects of Ionic Strength on Lateral Particle Migration in Shear-Thinning Xanthan Gum Solutions. Micromachines, 10(8), 535. https://doi.org/10.3390/mi10080535




