Design of Rigidity and Breaking Strain for a Kirigami Structure with Non-Uniform Deformed Regions
Abstract
1. Introduction
2. Theory and Methods
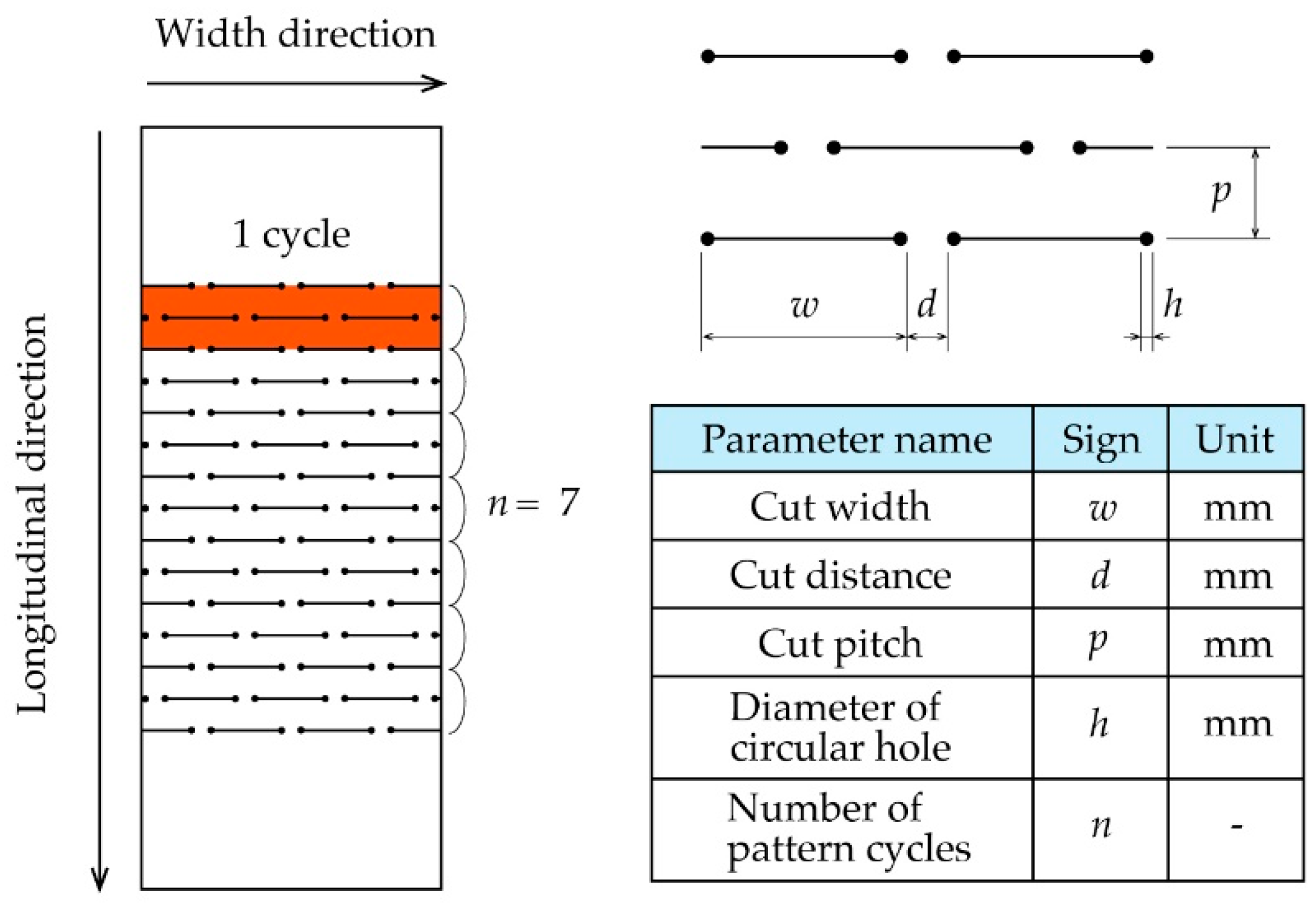
2.1. Definition of a Kirigami Structure
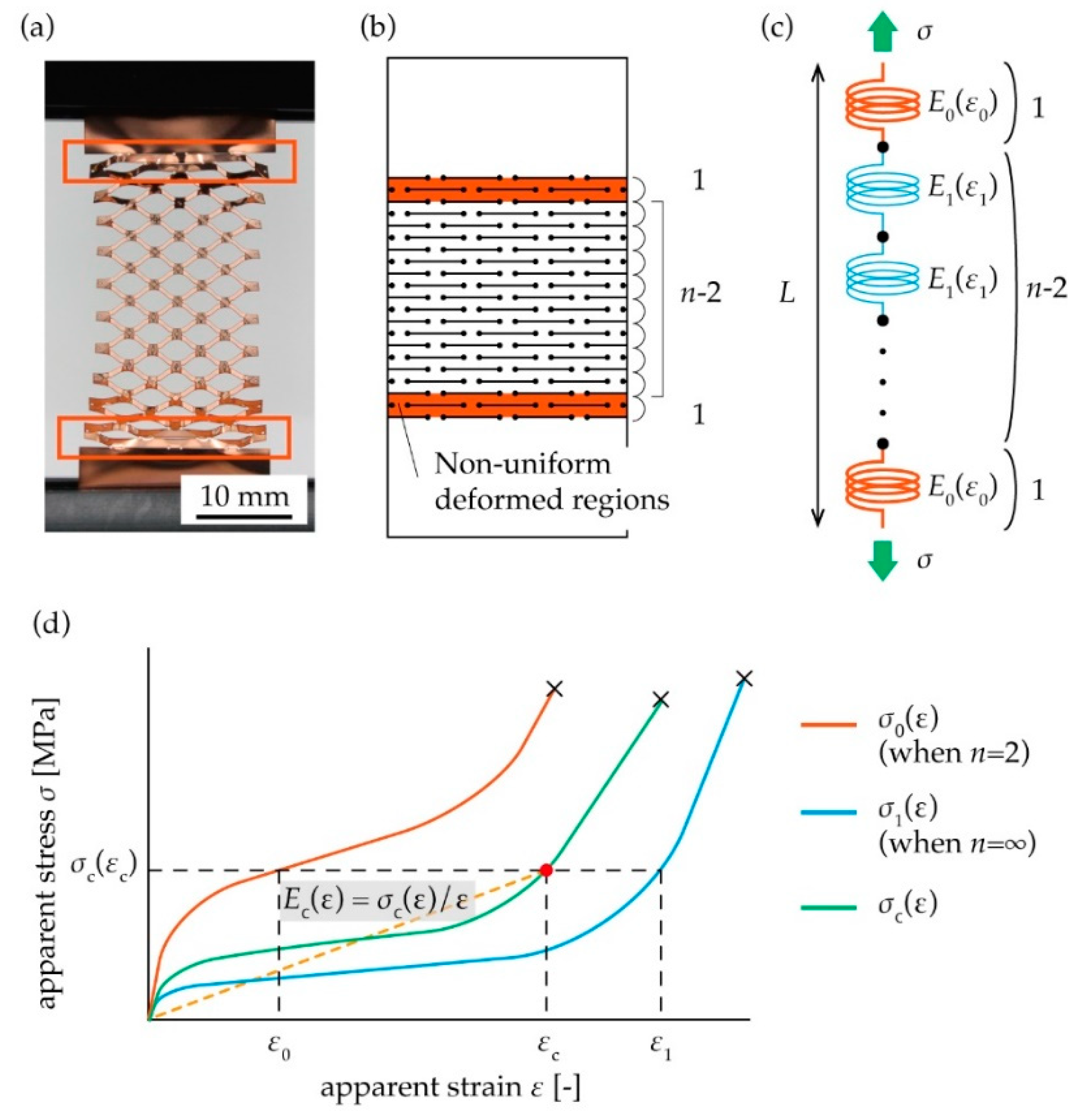
2.2. Theory of the Spring Model Proposed in This Study
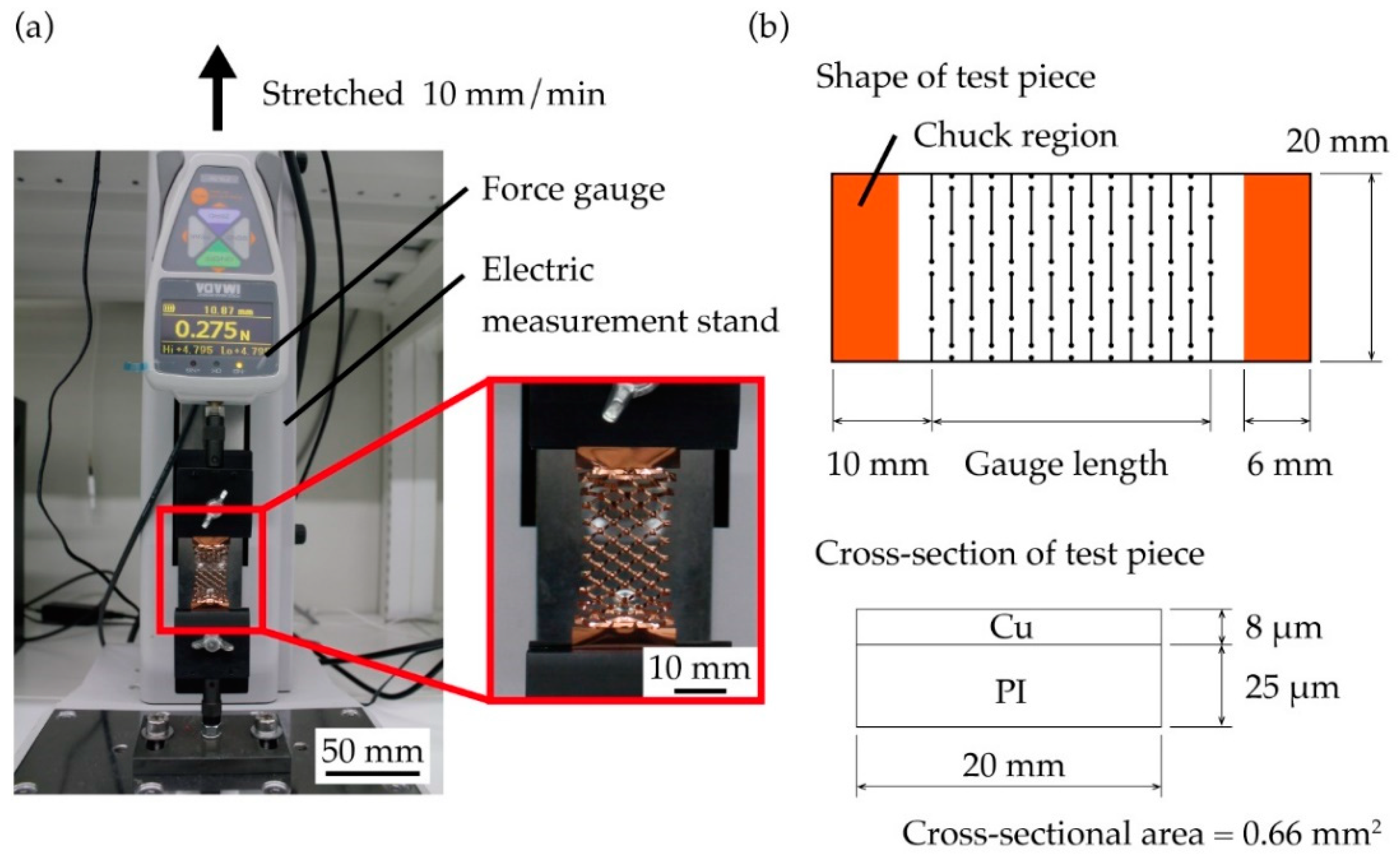
2.3. Tensile Testing Method
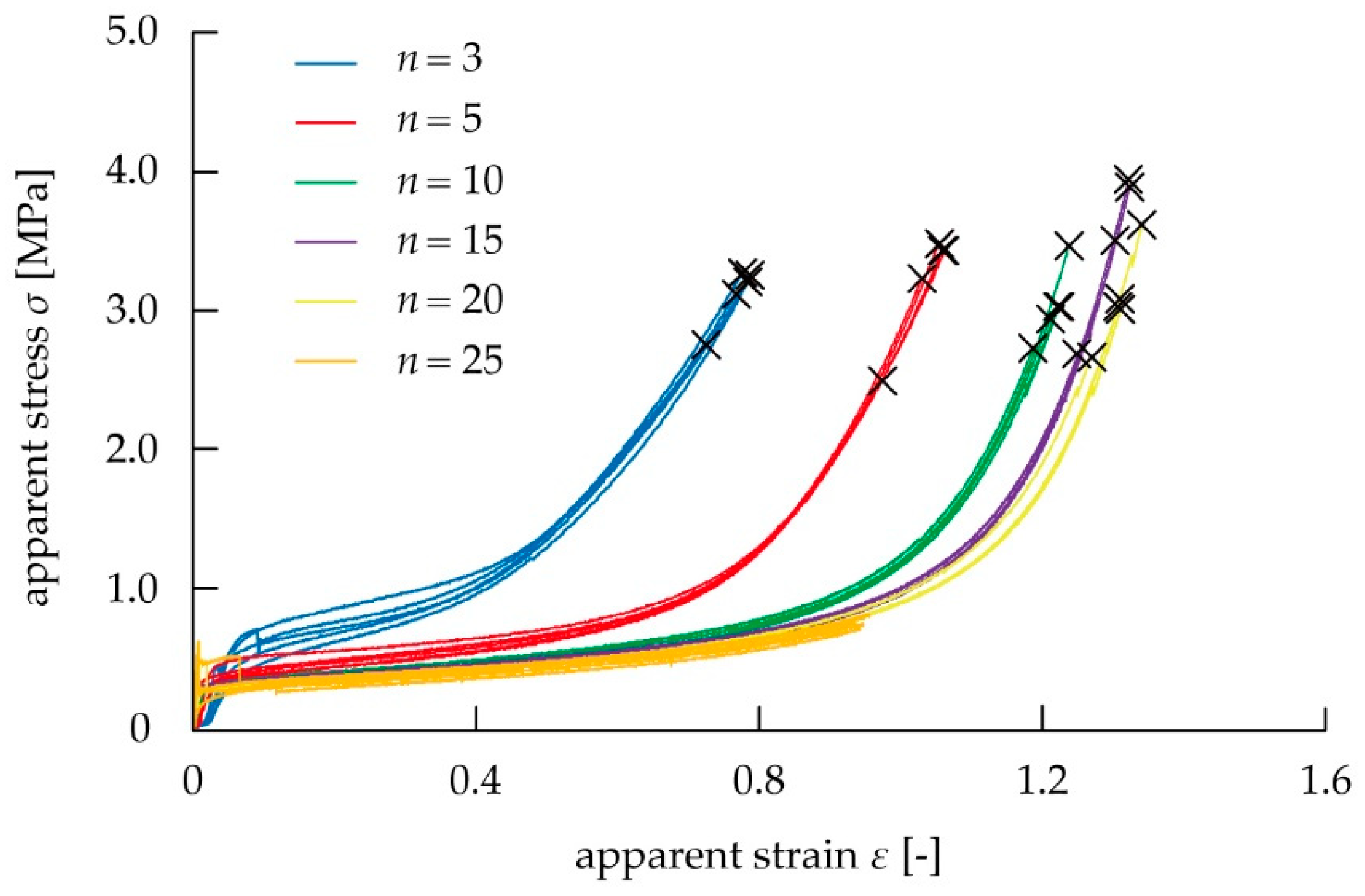
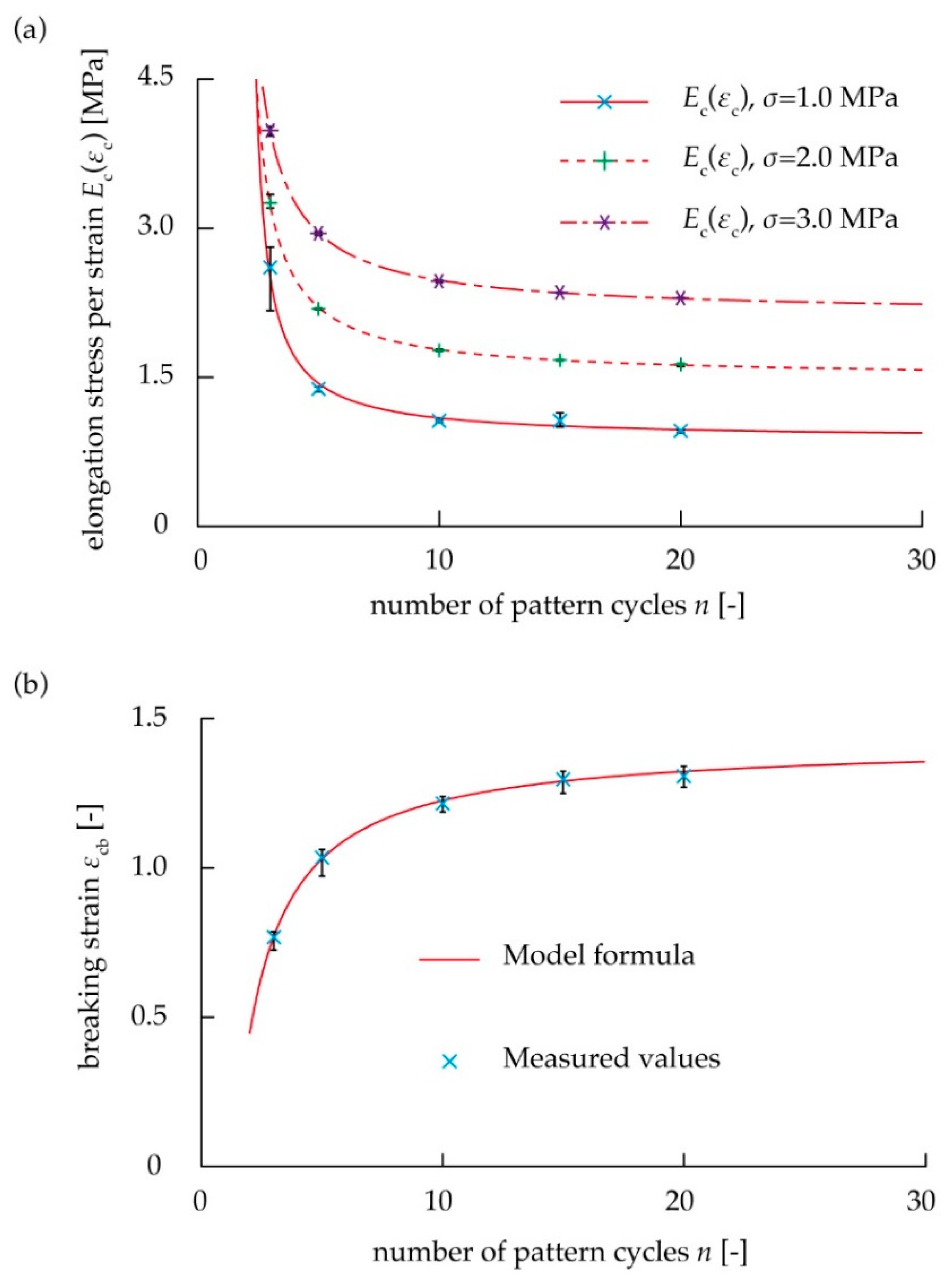
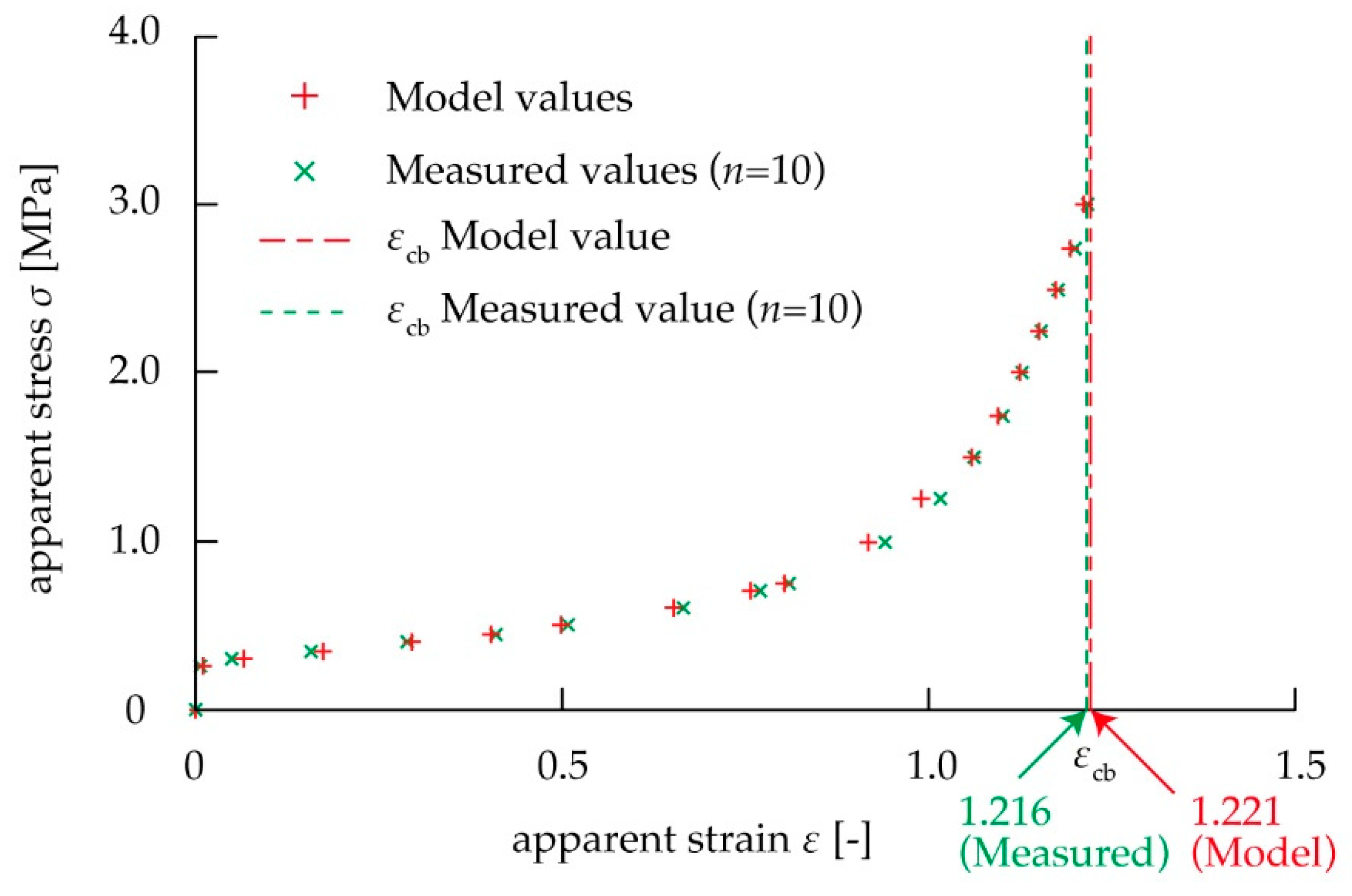
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shyu, T.C.; Damasceno, P.F.; Dodd, P.M.; Lamoureux, A.; Xu, L.; Shlian, M.; Shtein, M.; Glotzer, S.C.; Kotov, N.A. A kirigami approach to engineering elasticity in nanocomposites through patterned defects. Nat. Mater. 2015, 14, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Isobe, M.; Okumura, K. Initial rigid response and softening transition of highly stretchable kirigami sheet materials. Sci. Rep. 2016, 6, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Hwang, D.G.; Bartlett, M.D. Tunable mechanical metamaterials through hybrid kirigami structures. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, L.; Duan, S.; Jiang, H.; Shen, J.; Li, C. Kirigami-patterned highly stretchable conductors from flexible carbon nanotube-embedded polymer films. J. Mater. Chem. C 2017, 5, 8714–8722. [Google Scholar] [CrossRef]
- Tang, Y.; Lin, G.; Yang, S.; Yi, Y.K.; Kamien, R.D.; Yin, J. Programmable kiri-kirigami metamaterials. Adv. Mater. 2017, 29, 1–9. [Google Scholar] [CrossRef]
- Lei, X.-W.; Nakatani, A.; Doi, Y.; Matsunaga, S. Bifurcation analysis of periodic kirigami structure with out-plane deformation. J. Soc. Mater. Sci. Jpn. 2018, 67, 202–207. [Google Scholar] [CrossRef][Green Version]
- Rafsanjani, A.; Bertoldi, K. Buckling-induced kirigami. Phys. Rev. Lett. 2017, 118, 1–5. [Google Scholar] [CrossRef]
- Tang, Y.; Yin, J. Design of cut unit geometry in hierarchical kirigami-based auxetic metamaterials for high stretchability and compressibility. Extrem. Mech. Lett. 2017, 12, 77–85. [Google Scholar] [CrossRef]
- Moshe, M.; Esposito, E.; Shankar, S.; Bircan, B.; Cohen, I.; Nelson, D.R.; Bowick, M.J. Kirigami mechanics as stress relief by elastic charges. Phys. Rev. Lett. 2019, 122, 048001. [Google Scholar] [CrossRef]
- Dias, M.A.; McCarron, M.P.; Rayneau-Kirkhope, D.; Hanakata, P.Z.; Campbell, D.K.; Park, H.S.; Holmes, D.P. Kirigami actuators. Soft Matter. 2017, 13, 9087–9092. [Google Scholar] [CrossRef]
- Zheng, W.; Huang, W.; Gao, F.; Yang, H.; Dai, M.; Liu, G.; Yang, B.; Zhang, J.; Fu, Y.Q.; Chen, X.; et al. Kirigami-inspired highly stretchable nanoscale devices using multidimensional deformation of monolayer MoS2. Chem. Mater. 2018, 30, 6063–6070. [Google Scholar] [CrossRef]
- Sun, R.; Zhang, B.; Yang, L.; Zhang, W.; Farrow, I.; Scarpa, F.; Rossiter, J. Kirigami stretchable strain sensors with enhanced piezoelectricity induced by topological electrodes. Appl. Phys. Lett. 2018, 112, 1–6. [Google Scholar] [CrossRef]
- Gao, B.; Elbaz, A.; He, Z.; Xie, Z.; Xu, H.; Liu, S.; Su, E.; Liu, H.; Gu, Z. Bioinspired kirigami fish-based highly stretched wearable biosensor for human biochemical–physiological hybrid monitoring. Adv. Mater. Technol. 2018, 3, 1–8. [Google Scholar] [CrossRef]
- Baldwin, A.; Meng, E. A kirigami-based Parylene C stretch sensor. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017; pp. 227–230. [Google Scholar] [CrossRef]
- Jang, N.S.; Kim, K.H.; Ha, S.H.; Jung, S.H.; Lee, H.M.; Kim, J.M. Simple approach to high-performance stretchable heaters based on kirigami patterning of conductive paper for wearable thermotherapy applications. ACS Appl. Mater. Interfaces 2017, 9, 19612–19621. [Google Scholar] [CrossRef] [PubMed]
- Lamoureux, A.; Lee, K.; Shlian, M.; Forrest, S.R.; Shtein, M. Dynamic kirigami structures for integrated solar tracking. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef]
- Morikawa, Y.; Yamagiwa, S.; Sawahata, H.; Numano, R.; Koida, K.; Ishida, M.; Kawano, T. Ultrastretchable kirigami bioprobes. Adv. Healthc. Mater. 2018, 7, 1–10. [Google Scholar] [CrossRef]
- Lee, D.; Saito, K.; Umedachi, T.; Ta, T.D.; Kawahara, Y. Origami robots with flexible printed circuit sheets. In Proceedings of the 2018 ACM International Joint Conference and 2018 International Symposium on Pervasive and Ubiquitous Computing and Wearable Computers, Singapore, 8–12 October 2018; pp. 392–395. [Google Scholar] [CrossRef]
- Sareh, S.; Rossiter, J. Kirigami artificial muscles with complex biologically inspired morphologies. Smart Mater. Struct. 2013, 22. [Google Scholar] [CrossRef]
- Wang, W.; Li, C.; Rodrigue, H.; Yuan, F.; Han, M.W.; Cho, M.; Ahn, S.H. Kirigami/origami-based soft deployable reflector for optical beam steering. Adv. Funct. Mater. 2017, 27, 1–9. [Google Scholar] [CrossRef]
- Zhang, Q.; Wommer, J.; O’Rourke, C.; Teitelman, J.; Tang, Y.; Robison, J.; Lin, G.; Yin, J. Origami and kirigami inspired self-folding for programming three-dimensional shape shifting of polymer sheets with light. Extrem. Mech. Lett. 2017, 11, 111–120. [Google Scholar] [CrossRef]
- Kwok, T.-H.; Wang, C.C.L.; Deng, D.; Zhang, Y.; Chen, Y. Four-dimensional printing for freeform surfaces: Design optimization of origami and kirigami structures. J. Mech. Des. 2015, 137, 111413. [Google Scholar] [CrossRef]
- Memoli, G.; Caleap, M.; Asakawa, M.; Sahoo, D.R.; Drinkwater, B.W.; Subramanian, S. Metamaterial bricks and quantization of meta-surfaces. Nat. Commun. 2017, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Hwang, D.G.; Trent, K.; Bartlett, M.D. Kirigami-inspired structures for smart adhesion. ACS Appl. Mater. Interfaces 2018, 10, 6747–6754. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Shyu, T.C.; Kotov, N.A. Origami and kirigami nanocomposites. ACS Nano 2017, 11, 7587–7599. [Google Scholar] [CrossRef] [PubMed]
- Ning, X.; Wang, X.; Zhang, Y.; Yu, X.; Choi, D.; Zheng, N.; Kim, D.S.; Huang, Y.; Zhang, Y.; Rogers, J.A. Assembly of advanced materials into 3D functional structures by methods inspired by origami and kirigami: A review. Adv. Mater. Interfaces 2018, 5, 1–13. [Google Scholar] [CrossRef]
- Chen, S.H.; Chan, K.C.; Yue, T.M.; Wu, F.F. Highly stretchable kirigami metallic glass structures with ultra-small strain energy loss. Scr. Mater. 2018, 142, 83–87. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taniyama, H.; Iwase, E. Design of Rigidity and Breaking Strain for a Kirigami Structure with Non-Uniform Deformed Regions. Micromachines 2019, 10, 395. https://doi.org/10.3390/mi10060395
Taniyama H, Iwase E. Design of Rigidity and Breaking Strain for a Kirigami Structure with Non-Uniform Deformed Regions. Micromachines. 2019; 10(6):395. https://doi.org/10.3390/mi10060395
Chicago/Turabian StyleTaniyama, Hiroki, and Eiji Iwase. 2019. "Design of Rigidity and Breaking Strain for a Kirigami Structure with Non-Uniform Deformed Regions" Micromachines 10, no. 6: 395. https://doi.org/10.3390/mi10060395
APA StyleTaniyama, H., & Iwase, E. (2019). Design of Rigidity and Breaking Strain for a Kirigami Structure with Non-Uniform Deformed Regions. Micromachines, 10(6), 395. https://doi.org/10.3390/mi10060395




