Defining Cell Cluster Size by Dielectrophoretic Capture at an Array of Wireless Electrodes of Several Distinct Lengths
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Cell Culture
2.3. Device Fabrication
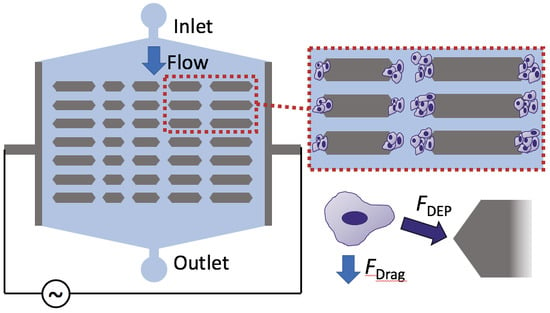
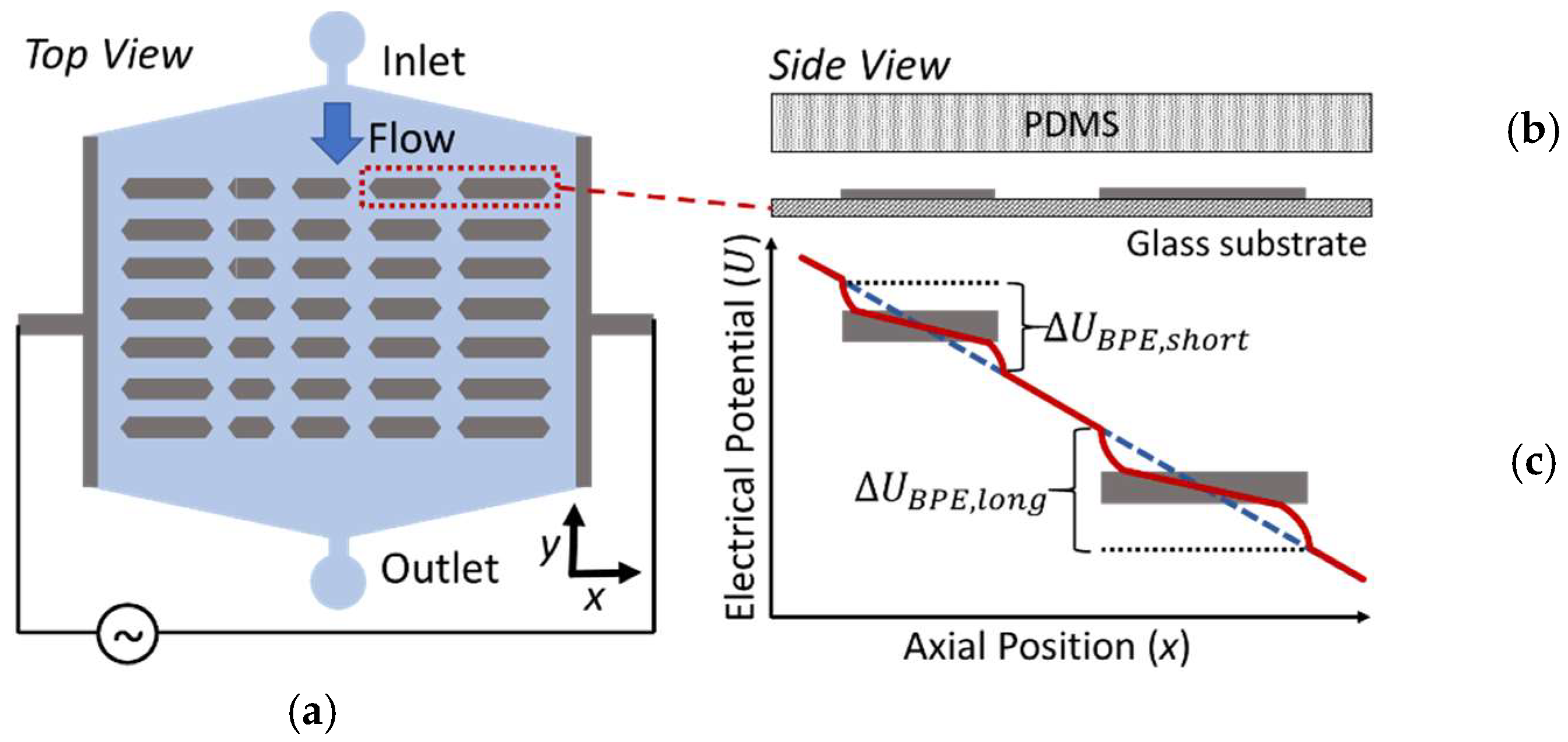
2.4. Device Dimensions
2.5. DEP Capture
3. Results and Discussion
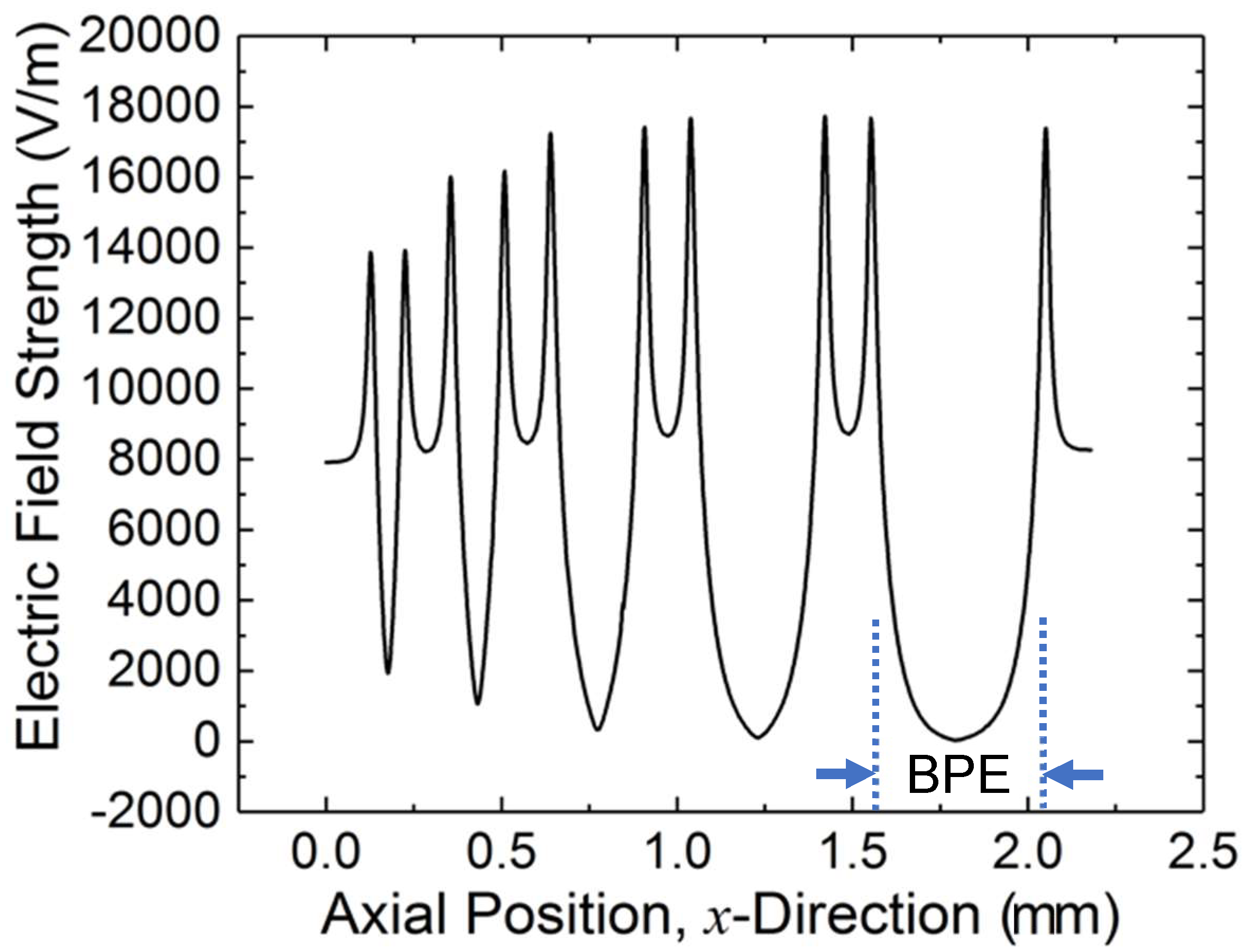
3.1. Theoretical Background
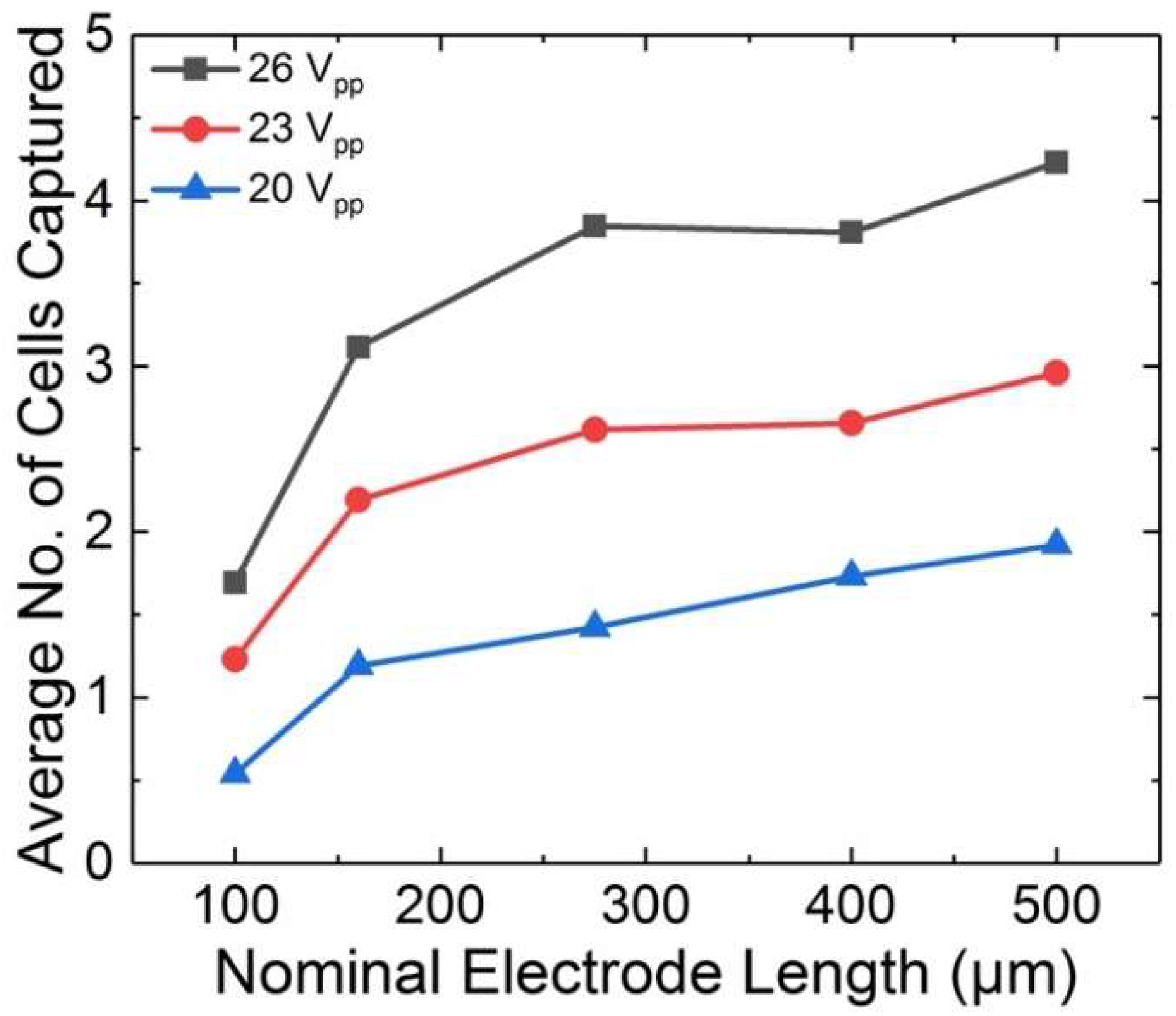
3.2. Correlation of Cell Cluster Size to BPE Length
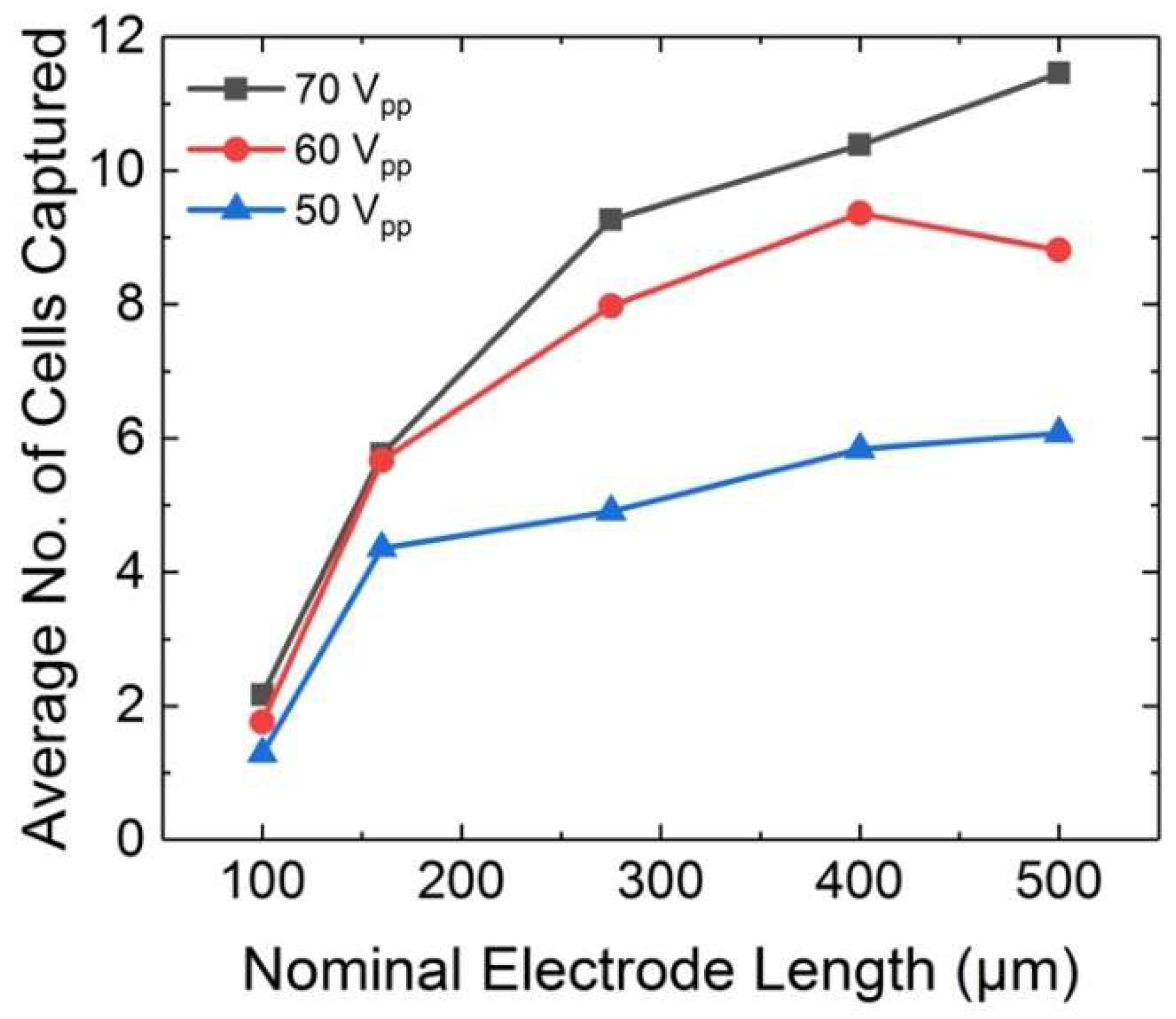
3.3. Cell Cluster Size Controlled by Applied External Voltage at an Array of BPEs of Distinct Lengths
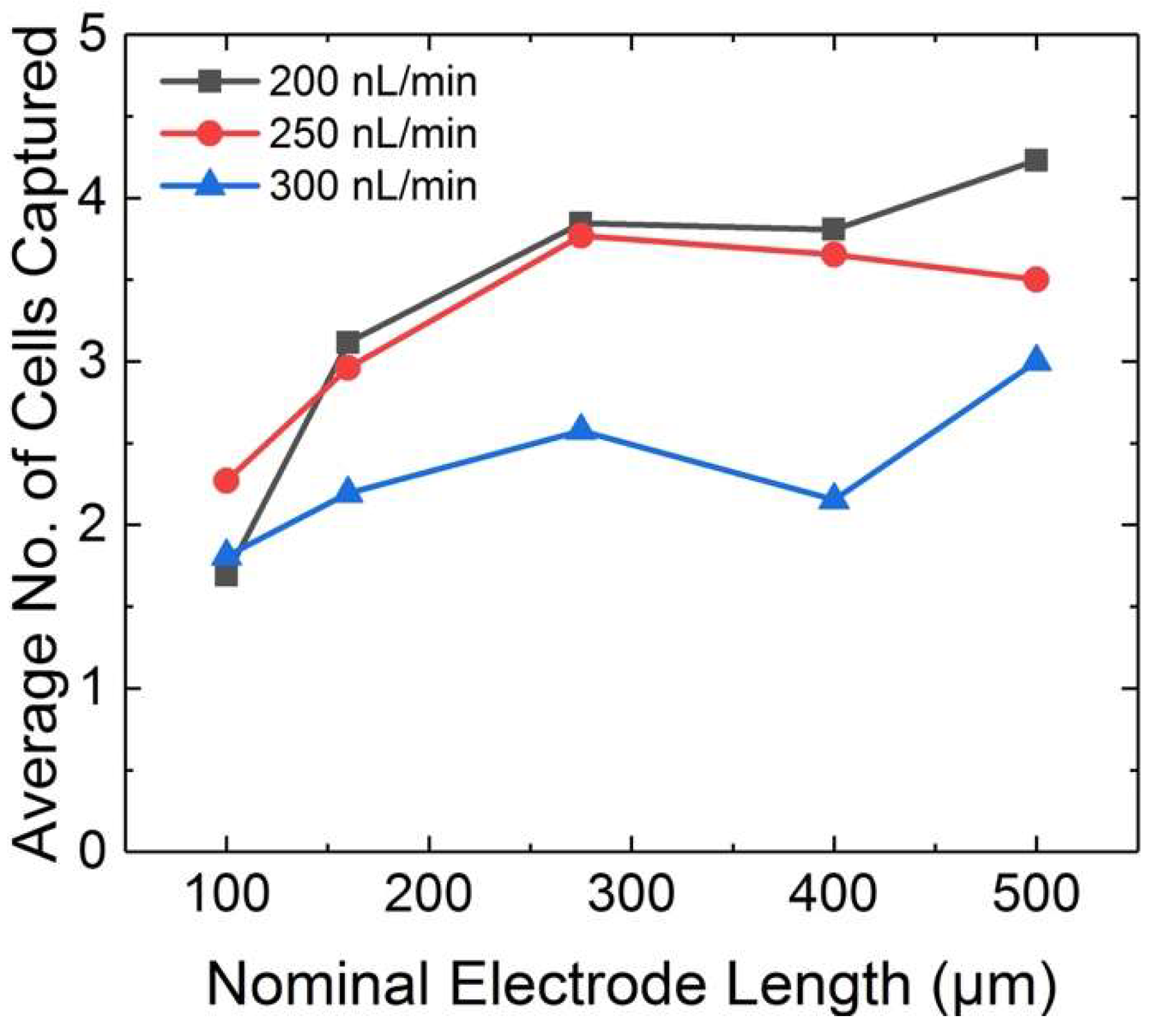
3.4. Cell Cluster Size Controlled by Fluid Flow Rate at Distinct BPE Lengths
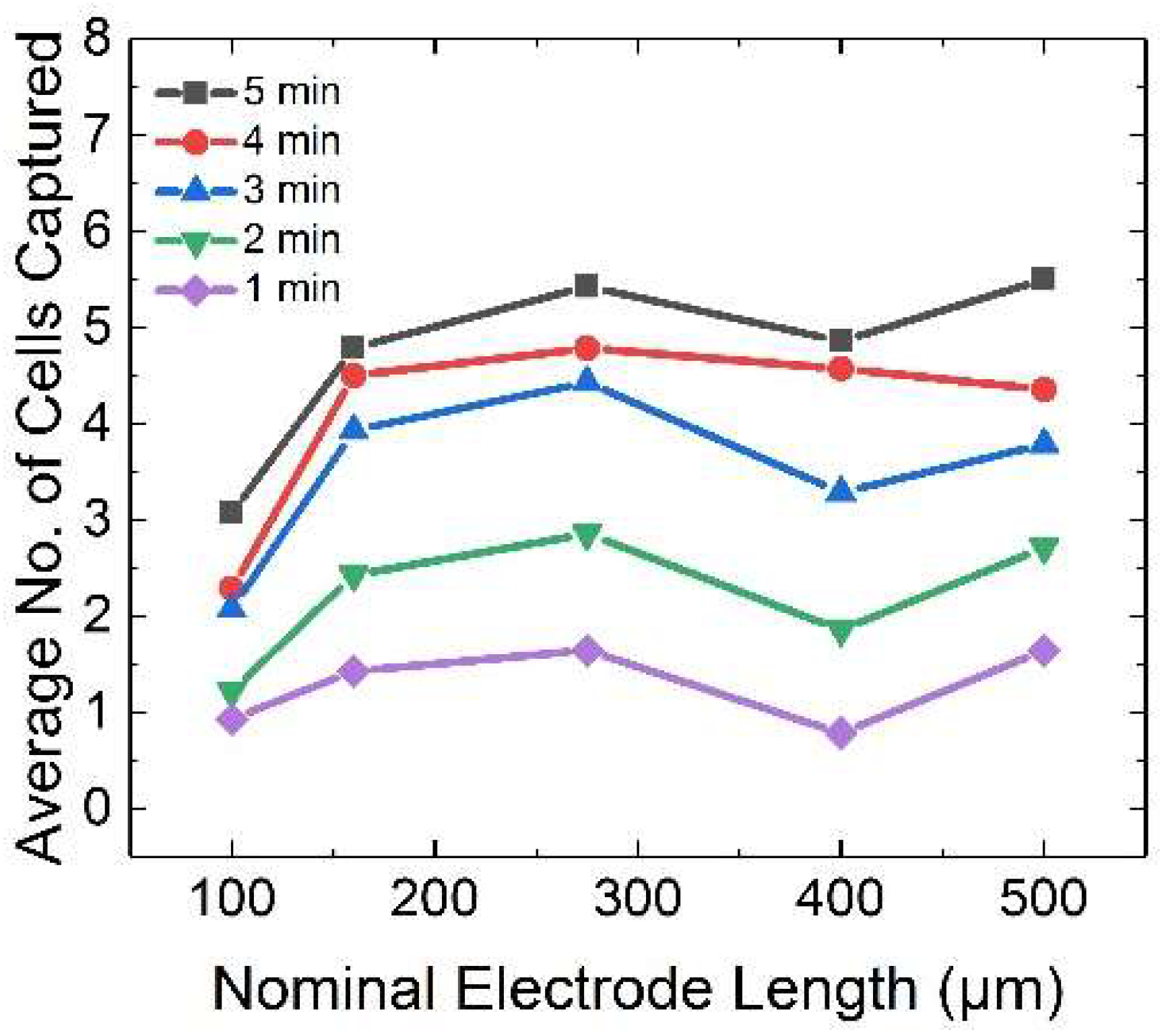
3.5. Time Dependence of Cell Cluster Size
3.6. Control over Cluster Size at Higher Voltage, Flow Rate, and Duration
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hanahan, D.; Weinberg, R.A. The Hallmarks of Cancer. Cell 2000, 100, 57–70. [Google Scholar] [CrossRef]
- Vincent-Salomon, A.; Thiery, J.P. Host microenvironment in breast cancer development: Epithelia-mesenchymal transition in breast cancer development. Breast Cancer Res. 2003, 5, 101–106. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, H.; Dazin, P.; Kapila, Y. Squamous cell carcinoma cell aggregates escape suspension-induced, P53-mediated anoikis: fibronectin and integrin Av mediate survival signals through focal adhesion kinase. J. Biol. Chem. 2004, 279, 48342–48349. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.H.; Yu, Q. Cell aggregation induces phosphorylation of PECAM-1 and Pyk2 and promotes tumor cell anchorage-independent growth. Mol. Cancer 2010, 9, 1–11. [Google Scholar] [CrossRef]
- Hong, Y.; Fang, F.; Zhang, Q. Circulating tumor cell clusters: what we know and what we expect (review). Int. J. Oncol. 2016, 49, 2206–2216. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, F.; Xing, R.; Lin, Y.; Han, Y.; Teng, C.; Wang, Q. Development of large-scale size-controlled adult pancreatic progenitor cell clusters by an inkjet-printing technique. ACS Appl. Mater. Interfaces 2015, 7, 11624–11630. [Google Scholar] [CrossRef]
- Mendelsohn, A.D.; Nyitray, C.; Sena, M.; Desai, T.A. Size-controlled insulin-secreting cell clusters. Acta Biomater. 2012, 8, 4278–4284. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.J.; Bong, K.W.; Reátegui, E.; Irimia, D.; Doyle, P. Porous microwells for geometry-selective, large-scale microparticle arrays. Nat. Mater. 2017, 16, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Dague, E.; Jauvert, E.; Laplatine, L.; Viallet, B.; Thibault, C.; Ressier, L. Assembly of live micro-organisms on microstructured PDMS stamps by convective/capillary deposition for AFM bio-experiments. Nanotechnology 2011, 22, 395102. [Google Scholar] [CrossRef] [PubMed]
- Vedula, S.R.K.; Leong, M.C.; Lai, T.L.; Hersen, P.; Kabla, A.J.; Lim, C.T.; Ladoux, B. Emerging modes of collective cell migration induced by geometrical constraints. Proc. Natl. Acad. Sci. USA 2012, 109, 12974–12979. [Google Scholar] [CrossRef] [PubMed]
- Yusof, A.; Keegan, H.; Spillane, C.D.; Sheils, O.M.; Martin, C.M.; O’Leary, J.J.; Zengerle, R.; Koltay, P. Inkjet-like printing of single-cells. Lab Chip 2011, 11, 2447–2454. [Google Scholar] [CrossRef]
- Ai, Y.; Sanders, C.K.; Marrone, B.L. Separation of escherichia coli bacteria from peripheral blood mononuclear cells using standing surface acoustic waves. Anal. Chem. 2013, 85, 9126–9134. [Google Scholar] [CrossRef]
- Ding, X.; Lin, S.C.S.; Kiraly, B.; Yue, H.; Li, S.; Chiang, I.; Shi, J. On-chip manipulation of single microparticles, cells, and organisms using surface acoustic waves. Proc. Natl. Acad. Sci. USA 2012, 109, 11105–11109. [Google Scholar] [CrossRef]
- Augustsson, P.; Karlsen, J.T.; Su, H.W.; Bruus, H.; Voldman, J. Iso-acoustic focusing of cells for size-insensitive acousto-mechanical phenotyping. Nat. Commun. 2016, 7, 11556–11564. [Google Scholar] [CrossRef]
- Borowiec, J.; Hampl, J.; Singh, S.; Haefner, S.; Friedel, K.; Mai, P.; Brauer, D.; Ruther, F.; Liverani, L.; Boccaccini, A.R.; et al. 3D microcontact printing for combined chemical and topographical patterning on porous cell culture membrane. ACS Appl. Mater. Interfaces 2018, 10, 22857–22865. [Google Scholar] [CrossRef]
- Ho, C.T.; Lin, R.Z.; Chen, R.J.; Chin, C.K.; Gong, S.E.; Chang, H.Y.; Peng, H.L.; Hsu, L.; Yew, T.R.; Chang, S.F.; et al. Liver-cell patterning lab chip: mimicking the morphology of liver lobule tissue. Lab Chip 2013, 13, 3578–3587. [Google Scholar] [CrossRef]
- Kwon, M.; Godinho, S.A.; Chandhok, N.S.; Ganem, N.J.; Azioune, A.; Thery, M.; Pellman, D. Mechanisms to suppress multipolar divisions in cancer cells with extra centrosomes. Genes Dev. 2008, 22, 2189–2203. [Google Scholar] [CrossRef]
- Wei, S.C.; Fattet, L.; Tsai, J.H.; Guo, Y.; Pai, V.H.; Majeski, H.E.; Chen, A.C.; Sah, R.L.; Taylor, S.S.; Engler, A.J.; et al. Matrix stiffness drives epithelial-mesenchymal transition and tumour metastasis through a TWIST1-G3BP2 mechanotransduction pathway. Nat. Cell Biol. 2015, 17, 678–688. [Google Scholar] [CrossRef]
- Ino, K.; Ito, A.; Honda, H. Cell patterning using magnetite nanoparticles and magnetic force. Biotechnol. Bioeng. 2007, 97, 1309–1317. [Google Scholar] [CrossRef]
- Ozkan, M.; Pisanic, T.; Scheel, J.; Barlow, C.; Esener, S.; Bhatia, S.N. Electro-optical platform for the manipulation of live cells. Langmuir 2003, 19, 1532–1538. [Google Scholar] [CrossRef]
- Chiou, P.Y.; Ohta, A.T.; Wu, M.C. Massively parallel manipulation of single cells and microparticles using optical images. Nature 2005, 436, 370–372. [Google Scholar] [CrossRef]
- Jeffries, G.D.M.; Edgar, J.S.; Yiqiong, Z.; Shelby, J.P.; Christine, F.; Chiu, D.T. Using polarization-shaped optical vortex traps for single-cell nanosurgery. Nano Lett. 2007, 7, 415–420. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.C. Optoelectronic tweezers. Nat. Photonics 2011, 5, 322–324. [Google Scholar] [CrossRef]
- Gagnon, Z.R. Cellular dielectrophoresis: Applications to the characterization, manipulation, separation and patterning of cells. Electrophoresis 2011, 32, 2466–2487. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Anand, R.K. Cellular dielectrophoresis coupled with single-cell analysis. Anal. Bioanal. Chem. 2018, 410, 2499–2515. [Google Scholar] [CrossRef] [PubMed]
- Gascoyne, P.R.C.; Shim, S. Isolation of circulating tumor cells by dielectrophoresis. Cancers 2014, 6, 545–579. [Google Scholar] [CrossRef] [PubMed]
- Yale, A.R.; Nourse, J.L.; Lee, K.R.; Ahmed, S.N.; Arulmoli, J.; Jiang, A.Y.L.; McDonnell, L.P.; Botten, G.A.; Lee, A.P.; Monuki, E.S.; et al. Cell surface N-glycans influence electrophysiological properties and fate potential of neural stem cells. Stem Cell Rep. 2018, 11, 869–882. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Lee, I.K.; Taylor, K.; Richters, K.; Baek, D.H.; Ryu, J.H.; Cho, S.J.; Jung, Y.H.; Park, D.W.; Novello, J.; et al. Single-neuronal cell culture and monitoring platform using a fully transparent microfluidic DEP device. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Albrecht, D.R.; Tsang, V.L.; Sah, R.L.; Bhatia, S.N. Photo- and electropatterning of hydrogel-encapsulated living cell arrays. Lab Chip 2005, 5, 111–118. [Google Scholar] [CrossRef]
- Chu, H.K.; Huan, Z.; Mills, J.K.; Yang, J.; Sun, D. Three-dimensional cell manipulation and patterning using dielectrophoresis via a multi-layer scaffold structure. Lab Chip 2015, 15, 920–930. [Google Scholar] [CrossRef]
- Nestor, B.A.; Samiei, E.; Samanipour, R.; Gupta, A.; Van den Berg, A.; Diaz de Leon Derby, M.; Wang, Z.; Rezaei Nejad, H.; Kim, K.; Hoorfar, M. Digital microfluidic platform for dielectrophoretic patterning of cells encapsulated in hydrogel droplets. RSC Adv. 2016, 6, 57409–57415. [Google Scholar] [CrossRef]
- Menad, S.; Franqueville, L.; Haddour, N.; Buret, F.; Frenea-Robin, M. nDEP-driven cell patterning and bottom-up construction of cell aggregates using a new bioelectronic chip. Acta Biomater. 2015, 17, 107–114. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Anand, R.K. High-throughput selective capture of single circulating tumor cells by dielectrophoresis at a wireless electrode array. J. Am. Chem. Soc. 2017, 139, 8950–8959. [Google Scholar] [CrossRef]
- Li, M.; Anand, R.K. Integration of marker-free selection of single cells at a wireless electrode array with parallel fluidic isolation and electrical lysis. Chem. Sci. 2019, 10, 1506–1513. [Google Scholar] [CrossRef]
- Anand, R.K.; Johnson, E.S.; Chiu, D.T. Negative dielectrophoretic capture and repulsion of single cells at a bipolar electrode: the impact of faradaic ion enrichment and depletion. J. Am. Chem. Soc. 2015, 137, 776–783. [Google Scholar] [CrossRef] [PubMed]
- Chow, K.F.; Mavré, F.; Crooks, R.M. Wireless electrochemical DNA microarray sensor. J. Am. Chem. Soc. 2008, 130, 7544–7545. [Google Scholar] [CrossRef]
- Guerrette, J.P.; Percival, S.J.; Zhang, B. Fluorescence coupling for direct imaging of electrocatalytic heterogeneity. J. Am. Chem. Soc. 2013, 135, 855–861. [Google Scholar] [CrossRef]
- Hasheminejad, M.; Fang, Y.; Li, M.; Jiang, Y.; Wang, W.; Chen, H.-Y. Plasmonic imaging of the interfacial potential distribution on bipolar electrodes. Angew. Chem. Int. Ed. 2017, 56, 1629–1633. [Google Scholar] [CrossRef]
- Wu, Y.; Ren, Y.; Tao, Y.; Hou, L.; Jiang, H. High-throughput separation, trapping, and manipulation of single cells and particles by combined dielectrophoresis at a bipolar electrode array. Anal. Chem. 2018, 90, 11461–11469. [Google Scholar] [CrossRef] [PubMed]
- McDonald, J.C.; Whitesides, G.M. Poly(dimethylsiloxane) as a material for fabricating microfluidic devices. Acc. Chem. Res. 2002, 35, 491–499. [Google Scholar] [CrossRef]
- Chou, C.F.; Tegenfelt, J.O.; Bakajin, O.; Chan, S.S.; Cox, E.C.; Darnton, N.; Duke, T.; Austin, R.H. Electrodeless dielectrophoresis of single- and double-stranded DNA. Biophys. J. 2002, 83, 2170–2179. [Google Scholar] [CrossRef]
- Hamdi, F.S.; Français, O.; Subra, F.; Dufour-Gergam, E.; Le Pioufle, B. Microarray of non-connected gold pads used as high density electric traps for parallelized pairing and fusion of cells. Biomicrofluidics 2013, 7, 44101. [Google Scholar] [CrossRef] [PubMed]
- Crane, J.S.; Pohl, H.A. Theoretical models of cellular dielectrophoresis. J. Theor. Biol. 1972, 37, 15–41. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banovetz, J.T.; Li, M.; Pagariya, D.; Kim, S.; Ganapathysubramanian, B.; Anand, R.K. Defining Cell Cluster Size by Dielectrophoretic Capture at an Array of Wireless Electrodes of Several Distinct Lengths. Micromachines 2019, 10, 271. https://doi.org/10.3390/mi10040271
Banovetz JT, Li M, Pagariya D, Kim S, Ganapathysubramanian B, Anand RK. Defining Cell Cluster Size by Dielectrophoretic Capture at an Array of Wireless Electrodes of Several Distinct Lengths. Micromachines. 2019; 10(4):271. https://doi.org/10.3390/mi10040271
Chicago/Turabian StyleBanovetz, Joseph T., Min Li, Darshna Pagariya, Sungu Kim, Baskar Ganapathysubramanian, and Robbyn K. Anand. 2019. "Defining Cell Cluster Size by Dielectrophoretic Capture at an Array of Wireless Electrodes of Several Distinct Lengths" Micromachines 10, no. 4: 271. https://doi.org/10.3390/mi10040271
APA StyleBanovetz, J. T., Li, M., Pagariya, D., Kim, S., Ganapathysubramanian, B., & Anand, R. K. (2019). Defining Cell Cluster Size by Dielectrophoretic Capture at an Array of Wireless Electrodes of Several Distinct Lengths. Micromachines, 10(4), 271. https://doi.org/10.3390/mi10040271