Nonlinear Hysteresis Modeling of Piezoelectric Actuators Using a Generalized Bouc–Wen Model
Abstract
:1. Introduction
2. Classical Bouc–Wen Model
3. Generalized Bouc–Wen Model
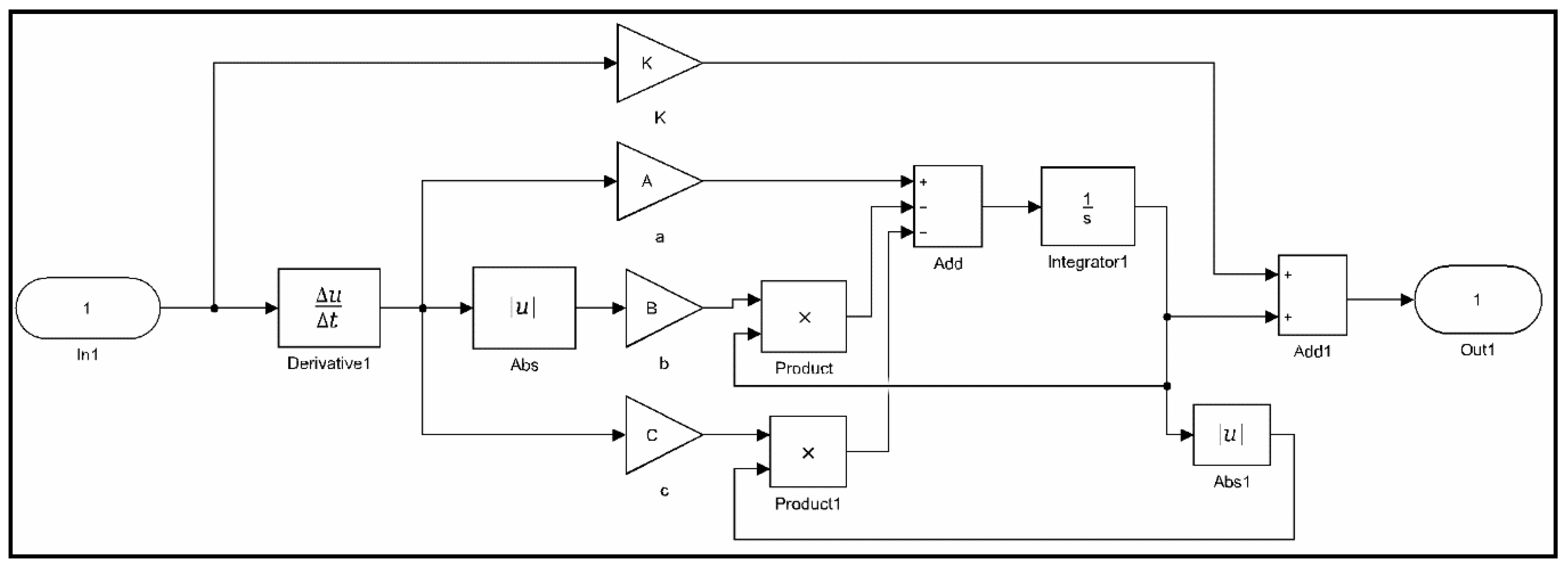
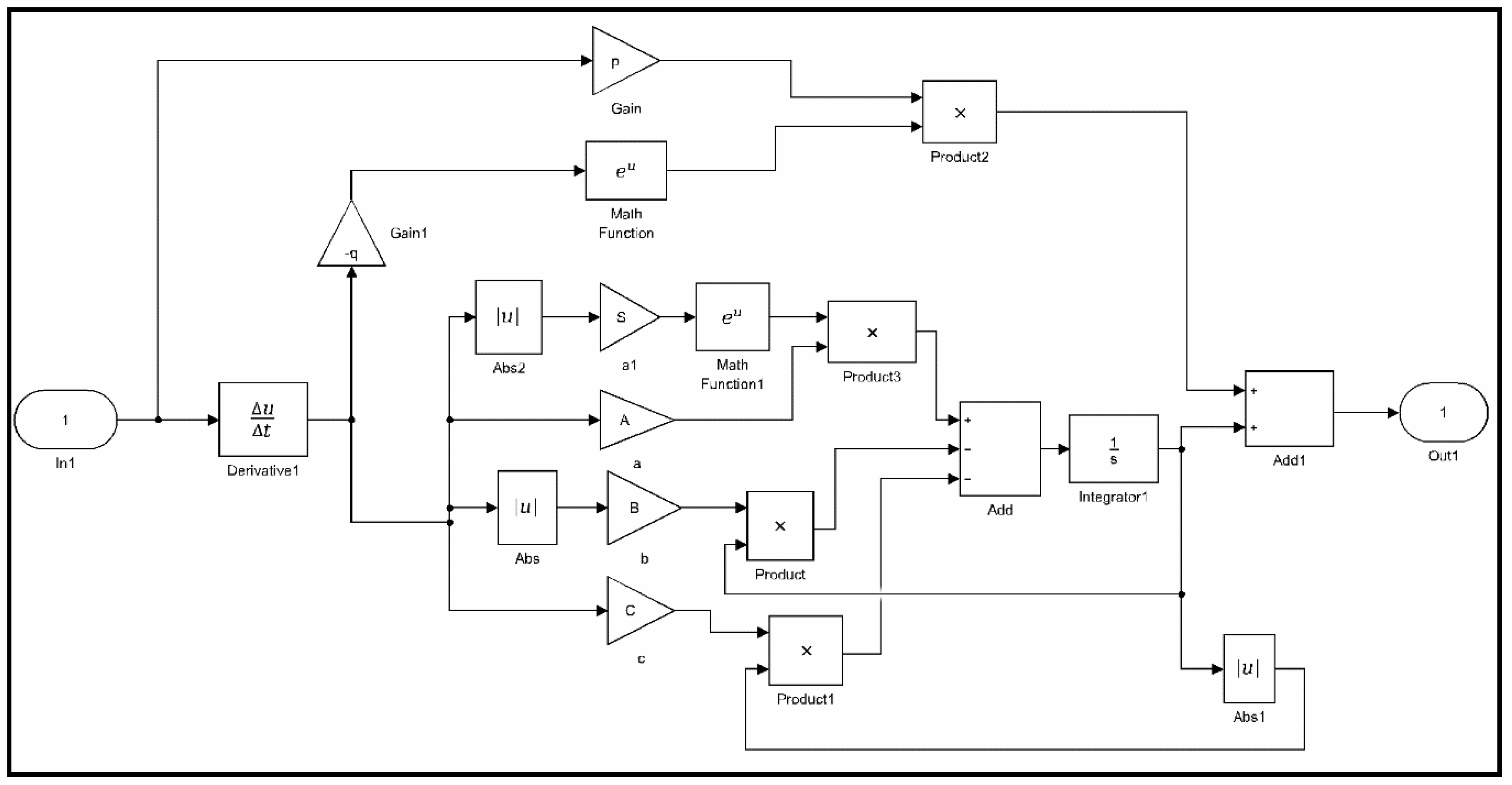
3.1. Formulation of the Generalized Bouc–Wen Model
3.2. Properties of the Generalized Bouc–Wen Model
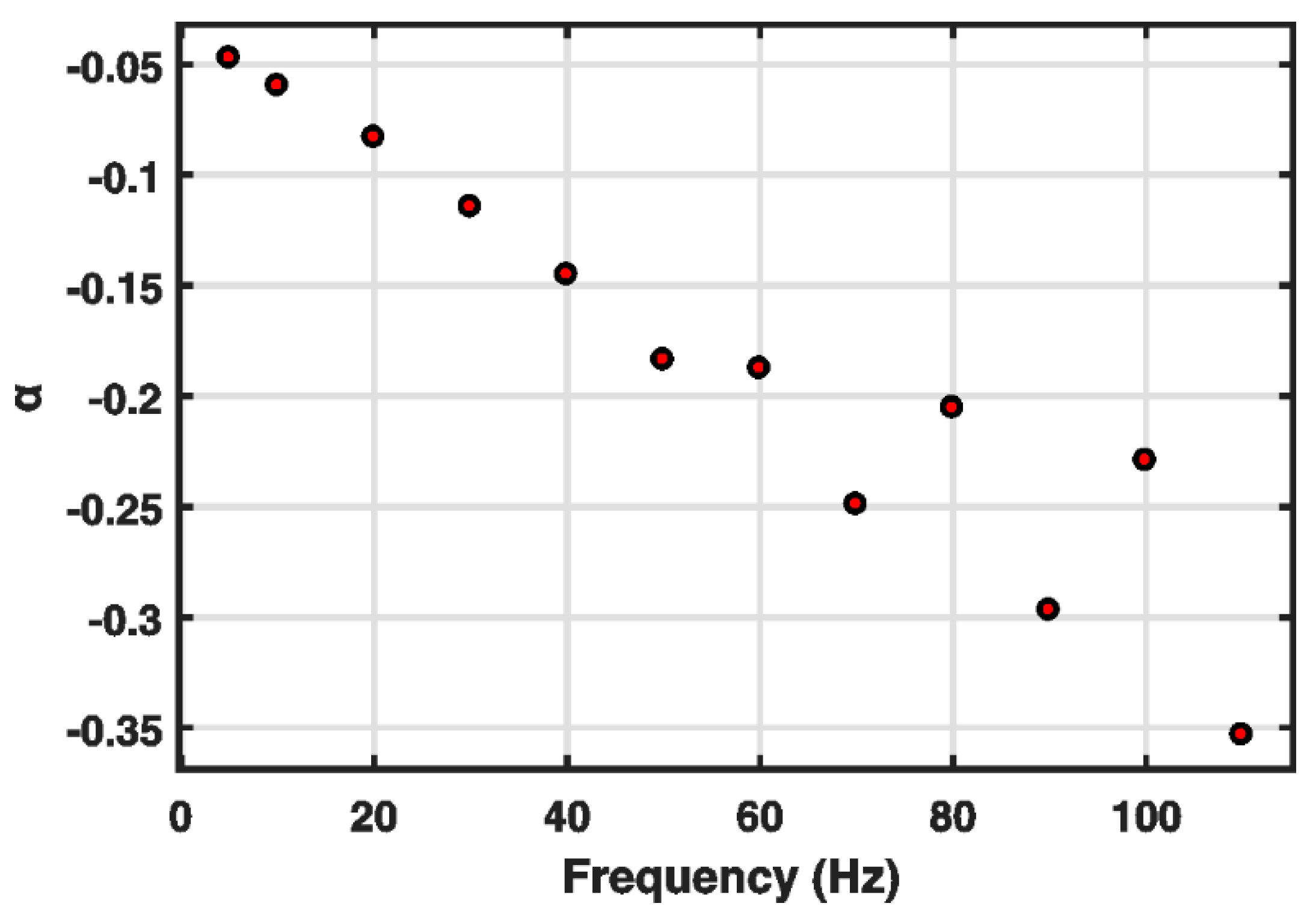
3.3. Parameters Identification
- (1)
- Data collection: Experimental data including output displacements and input voltages for piezoelectric actuators are obtained and recorded.
- (2)
- (3)
- Parameter estimation: The Trust-Region-Reflective algorithm is used to identify the parameters of hysteresis models based on experimental data.
- (4)
- Validation: Comparison of the measured and simulation results predicted by hysteresis models are shown, and the corresponding modeling errors are plotted.
4. Experimental Validation Results and Discussion
4.1. Experimental Setup
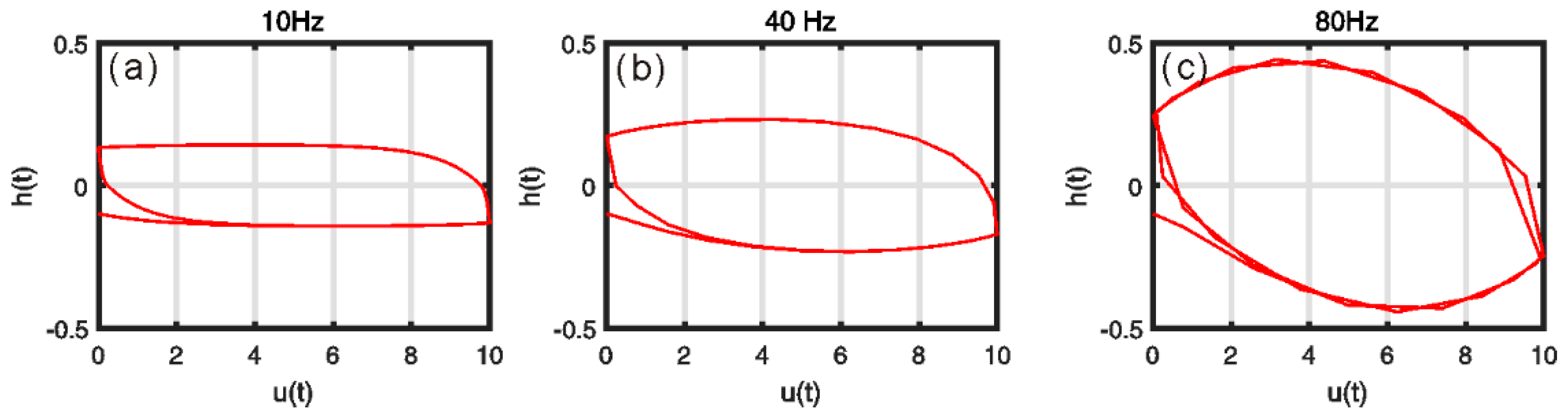
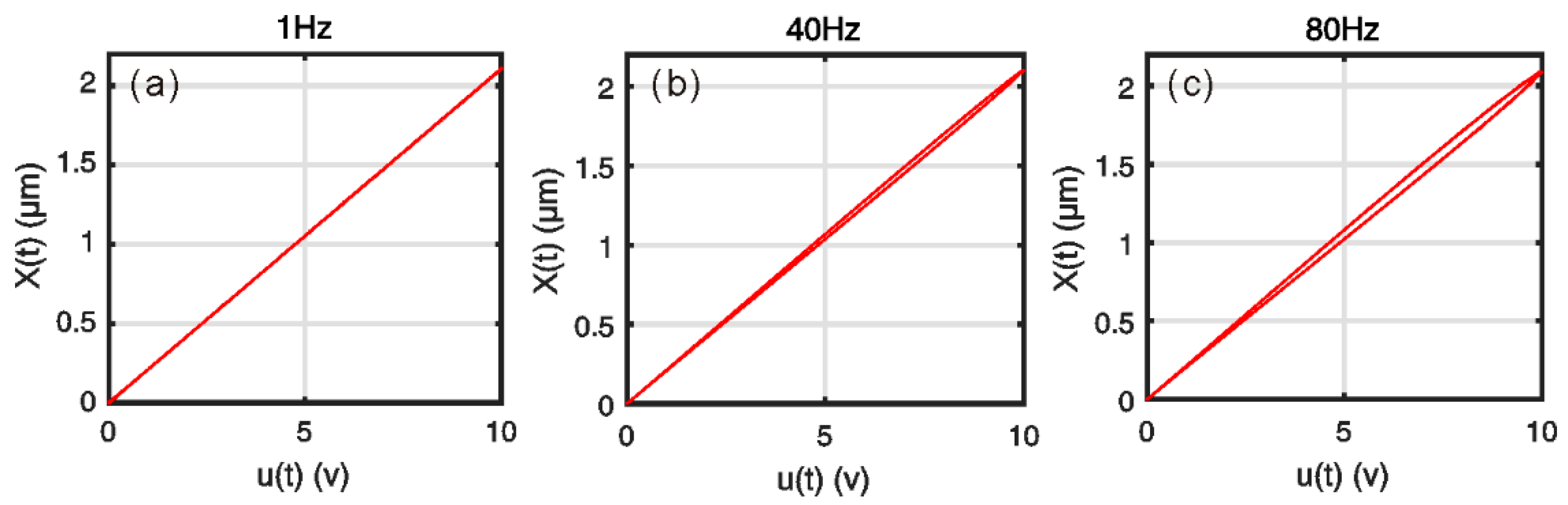
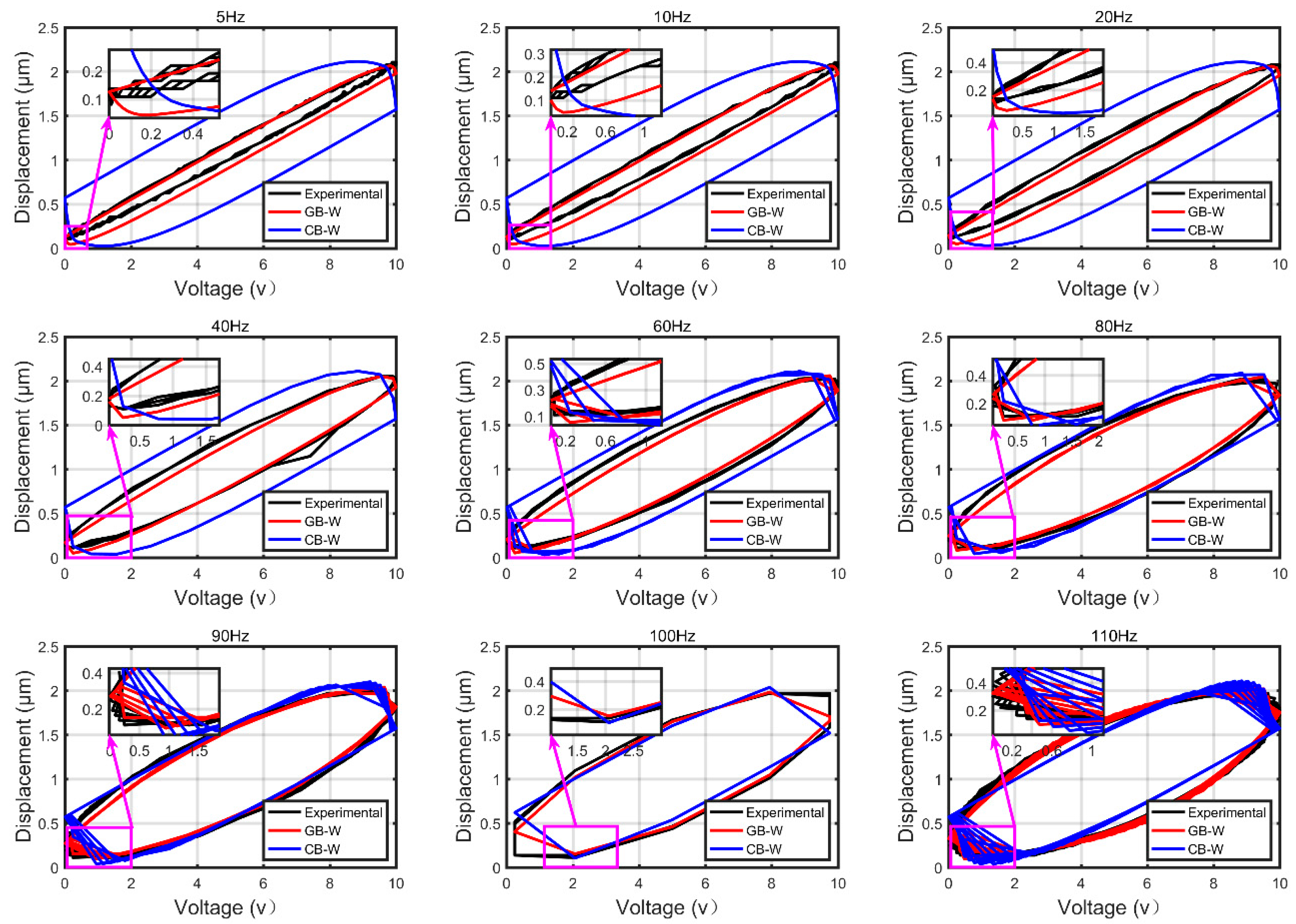
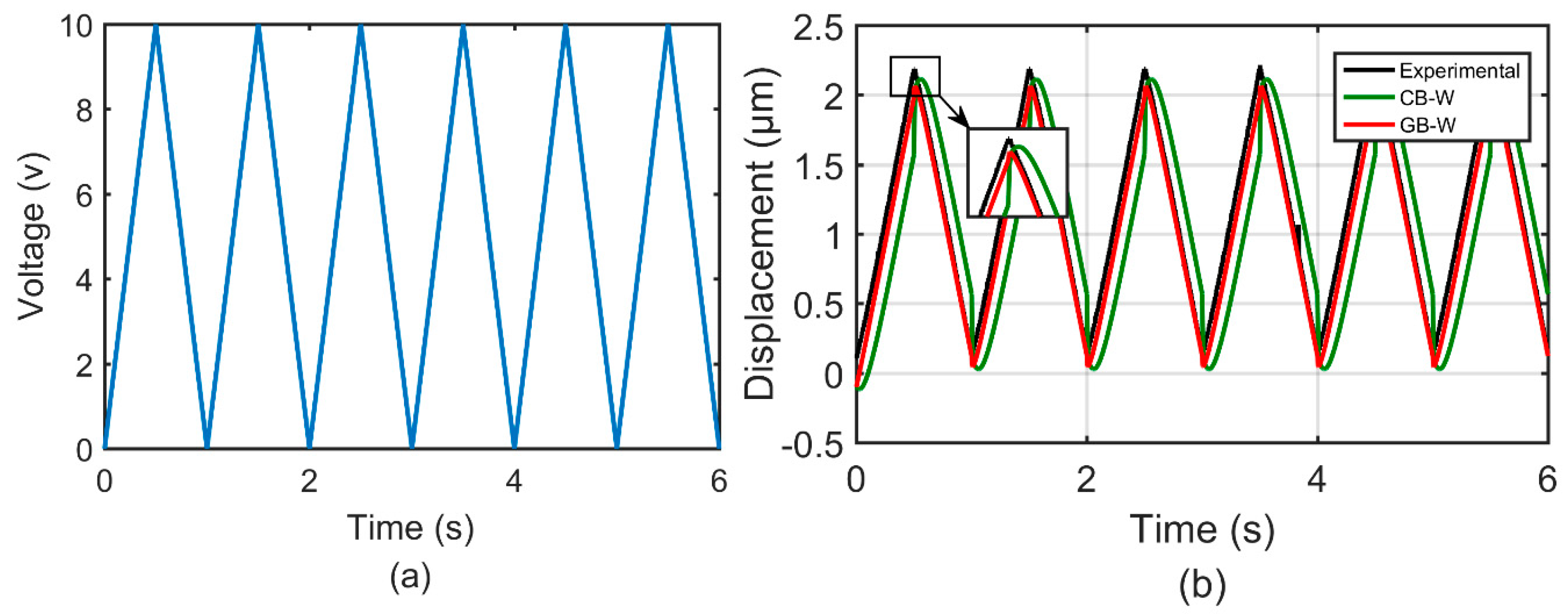
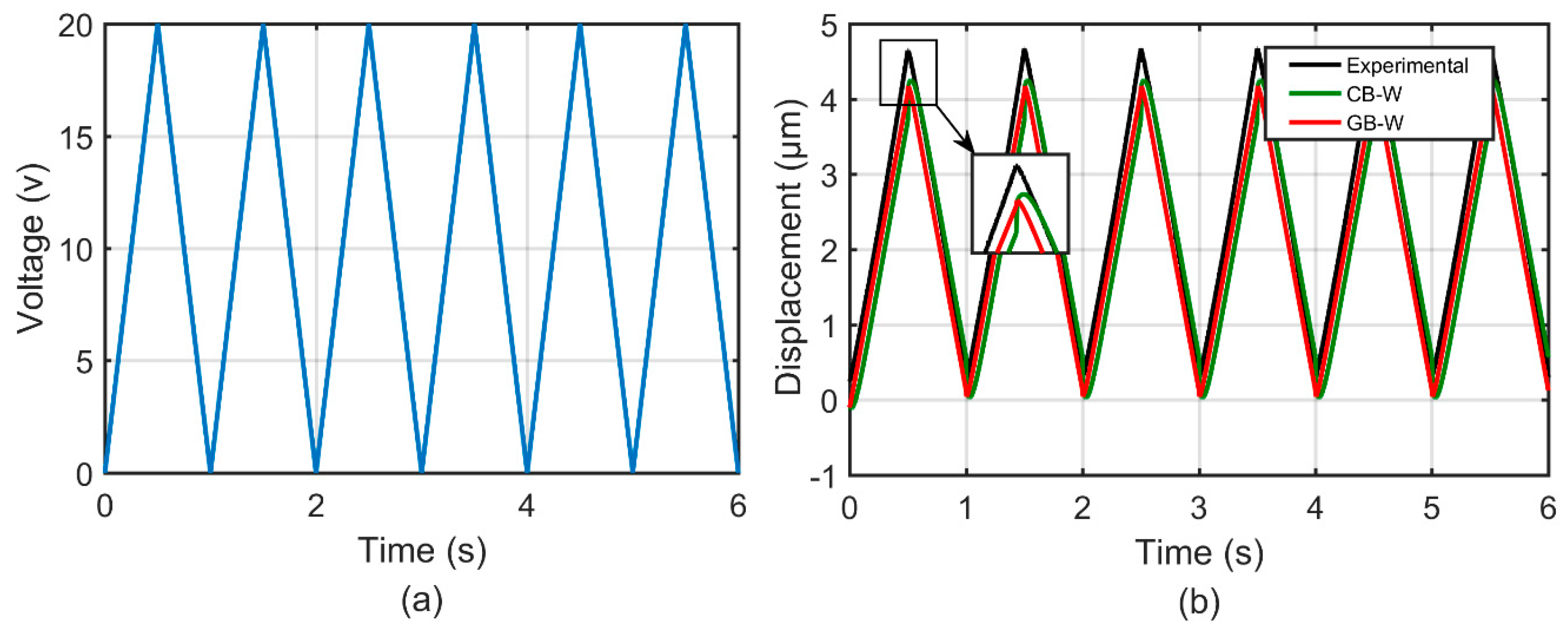
4.2. Results
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dong, R.; Tan, Y.; Chen, H.; Xie, Y. A neural networks based model for rate-dependent hysteresis for piezoceramic actuators. Sens. Actuators A Phys. 2008, 143, 370–376. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Krejčí, P. Prandtl-Ishlinskii hysteresis models for complex time dependent hysteresis nonlinearities. Phys. B Condens. Matter 2012, 407, 1365–1367. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X.; Wu, H. A generalized Prandtl-Ishlinskii model for characterizing the rate-independent and rate-dependent hysteresis of piezoelectric actuators. Rev. Sci. Instrum. 2016, 87, 35002. [Google Scholar] [CrossRef] [PubMed]
- Bernard, Y.; Maalej, A.H.; Lebrun, L.; Ducharne, B. Preisach modelling of ferroelectric behaviour. Int. J. Appl. Electromagn. 2007, 25, 729–733. [Google Scholar] [CrossRef]
- Ge, P.; Jouaneh, M. Generalized Preisach model for hysteresis nonlinearity of piezoceramic actuators. Precis. Eng. J. Am. Soc. Precis. Eng. 1997, 20, 99–111. [Google Scholar] [CrossRef]
- Nguyen, P.; Choi, S.; Song, B. A new approach to hysteresis modelling for a piezoelectric actuator using Preisach model and recursive method with an application to open-loop position tracking control. Sens. Actuators A Phys. 2018, 270, 136–152. [Google Scholar] [CrossRef]
- Tri, V.M.; Tjahjowidodo, T.; Ramon, H.; Van Brussel, H. A new approach to modeling hysteresis in a pneumatic artificial muscle using the Maxwell-slip model. IEEE ASME Trans. Mech. 2011, 16, 177–186. [Google Scholar]
- Goldfarb, M.; Celanovic, N. Modeling piezoelectric stack actuators for control of micromanipulation. Control Syst. IEEE 1997, 17, 69–79. [Google Scholar]
- Oh, J.; Bernstein, D.S. Semilinear Duhem model for rate-independent and rate-dependent hysteresis. IEEE Trans. Automat. Contr. 2005, 50, 631–645. [Google Scholar]
- Oh, J.; Bernstein, D.S. Piecewise linear identification for the rate-independent and rate-dependent DUHEM hysteresis models. IEEE Trans. Automat. Contr. 2007, 52, 576–582. [Google Scholar] [CrossRef]
- Sun, L.N.; Ru, C.H.; Rong, W.B.; Chen, L.G.; Kong, M.X. Tracking control of piezoelectric actuator based on a new mathematical model. J. Micromech. Microeng. 2004, 14, 1439–1444. [Google Scholar]
- Gan, J.; Zhang, X.; Wu, H. Tracking control of piezoelectric actuators using a polynomial-based hysteresis model. AIP ADV 2016, 6, 65204. [Google Scholar] [CrossRef]
- Zhu, W.; Rui, X. Hysteresis modeling and displacement control of piezoelectric actuators with the frequency-dependent behavior using a generalized Bouc Wen model. Precis. Eng. 2016, 43, 299–307. [Google Scholar] [CrossRef]
- Rakotondrabe, M. Bouc–Wen modeling and inverse multiplicative structure to compensate hysteresis nonlinearity in piezoelectric actuators. IEEE Trans. Autom. Sci. Eng. 2011, 8, 428–431. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, D.H. Non-symmetrical Bouc-Wen model for piezoelectric ceramic actuators. Sens. Actuat. A Phys. 2012, 181, 51–60. [Google Scholar] [CrossRef]
- Fujii, F.; Tatebatake, K.I.; Morita, K.; Shiinoki, T. A Bouc–Wen model-based compensation of the frequency-dependent hysteresis of a piezoelectric actuator exhibiting odd harmonic oscillation. Actuators 2018, 7, 37. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q. Adaptive sliding mode control with perturbation estimation and PID sliding surface for motion tracking of a piezo-driven micromanipulator. IEEE Trans. Contr. Syst. Tech. 2010, 18, 798–810. [Google Scholar] [CrossRef]
- Liu, Z.; Lai, G.; Zhang, Y.; Chen, C.L.P. Adaptive neural output feedback control of output-constrained nonlinear systems with unknown output nonlinearity. IEEE Trans. Control Syst. Tech. 2015, 26, 1789–1802. [Google Scholar]
- Lin, C.; Yang, S. Precise positioning of piezo-actuated stages using hysteresis-observer based control. Mechatronics 2006, 16, 417–426. [Google Scholar] [CrossRef]
- Qin, Y.; Zhao, X.; Zhou, L. Modeling and Identification of the rate-dependent hysteresis of piezoelectric actuator using a modified Prandtl-Ishlinskii model. Micromachines 2017, 8, 114. [Google Scholar] [CrossRef]
- Gu, G.; Yang, M.; Zhu, L. Real-time inverse hysteresis compensation of piezoelectric actuators with a modified Prandtl-Ishlinskii model. Rev. Sci. Instrum. 2012, 83, 65106. [Google Scholar] [CrossRef]
- Gan, J.; Zhang, X. An enhanced Bouc-Wen model for characterizing rate-dependent hysteresis of piezoelectric actuators. Rev. Sci. Instrum. 2018, 89, 115002. [Google Scholar] [CrossRef]
- Al Janaideh, M.; Su, C.Y.; Rakheja, S. Development of the rate-dependent Prandtl-Ishlinskii model for smart actuators. Smart Mater. Struct. 2008, 17. [Google Scholar] [CrossRef]
- Mayergoyz, I.D.; Friedman, G. Generalized Preisachmodel of hysteresis. IEEE Trans. Magn. 1988, 24, 212–217. [Google Scholar] [CrossRef]



| Frequency (Hz) | ||||
|---|---|---|---|---|
| 5 | 0.2215 | −0.0473 | 0.0847 | 0.4477 |
| 10 | 0.2209 | −0.0598 | 0.2629 | 0.6506 |
| 20 | 0.2214 | −0.0832 | 0.7183 | 1.1444 |
| 30 | 0.2198 | −0.1146 | 1.5761 | 2.0662 |
| 40 | 0.2181 | −0.1453 | 2.8847 | 3.4124 |
| 50 | 0.2181 | −0.1838 | 2.0272 | 2.6029 |
| 60 | 0.2176 | −0.1877 | 2.4755 | 3.0932 |
| 70 | 0.2153 | −0.2492 | 4.0013 | 4.6221 |
| 80 | 0.2170 | −0.2055 | 2.9687 | 3.5753 |
| 90 | 0.2114 | −0.2970 | 5.9981 | 6.6169 |
| 100 | 0.2166 | −0.2293 | 3.6008 | 4.2298 |
| 110 | 0.2141 | −0.3534 | 3.1034 | 3.7229 |
| Type | PST 150/7/60VS12 |
|---|---|
| Material | PZT |
| Length [mm] ±0.3 | 64 |
| Nominal Thrust/tension [N] | 1800/300 |
| Electrical capacitance [μF] ±20% | 5.4 |
| Resonant frequency [kHz] | 15 |
| Stiffness [N/μm] ±20% | 15 |
| Nominal Stroke [μm] ±15% | 60 |
| Frequency (Hz) | GB–W Model | CB–W Model | ||
|---|---|---|---|---|
| RMSE (μm) | RRMSE (%) | RMSE (μm) | RRMSE (%) | |
| 5 | 0.0742 | 3.52 | 0.4015 | 19.07 |
| 10 | 0.0650 | 3.08 | 0.3959 | 18.81 |
| 20 | 0.0700 | 3.33 | 0.3420 | 16.25 |
| 40 | 0.0316 | 1.50 | 0.2595 | 12.32 |
| 60 | 0.0697 | 3.31 | 0.2110 | 10.02 |
| 80 | 0.0718 | 3.41 | 0.1608 | 7.64 |
| 90 | 0.0679 | 3.23 | 0.1495 | 7.10 |
| 100 | 0.1264 | 6.00 | 0.2183 | 10.37 |
| 110 | 0.0673 | 3.20 | 0.1546 | 7.34 |
| Amplitude | GB–W Model | CB–W Model | ||
|---|---|---|---|---|
| RMSE (μm) | RRMSE (%) | RMSE (μm) | RRMSE (%) | |
| 10 | 0.1315 | 5.94 | 0.4510 | 20.36 |
| 20 | 0.3869 | 8.27 | 0.5441 | 11.63 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gan, J.; Zhang, X. Nonlinear Hysteresis Modeling of Piezoelectric Actuators Using a Generalized Bouc–Wen Model. Micromachines 2019, 10, 183. https://doi.org/10.3390/mi10030183
Gan J, Zhang X. Nonlinear Hysteresis Modeling of Piezoelectric Actuators Using a Generalized Bouc–Wen Model. Micromachines. 2019; 10(3):183. https://doi.org/10.3390/mi10030183
Chicago/Turabian StyleGan, Jinqiang, and Xianmin Zhang. 2019. "Nonlinear Hysteresis Modeling of Piezoelectric Actuators Using a Generalized Bouc–Wen Model" Micromachines 10, no. 3: 183. https://doi.org/10.3390/mi10030183
APA StyleGan, J., & Zhang, X. (2019). Nonlinear Hysteresis Modeling of Piezoelectric Actuators Using a Generalized Bouc–Wen Model. Micromachines, 10(3), 183. https://doi.org/10.3390/mi10030183





