Vertical Field Emission Air-Channel Diodes and Transistors
Abstract
1. Introduction
2. Experiment
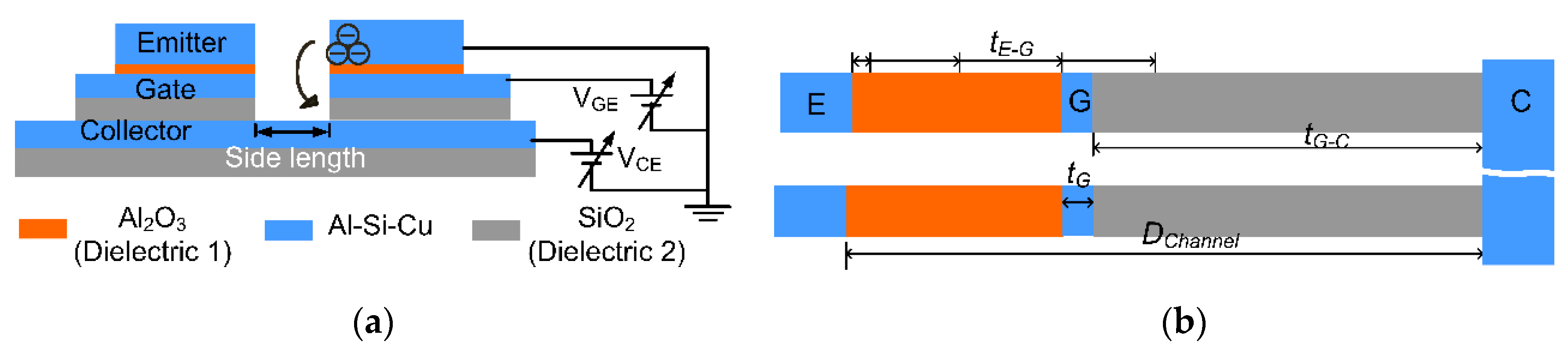
2.1. Modeling of Vertical Vacuum Channel Transistors
2.2. Fabricated Vertical Field Emission Diodes and Experimental Measurement
3. Results and Discussion
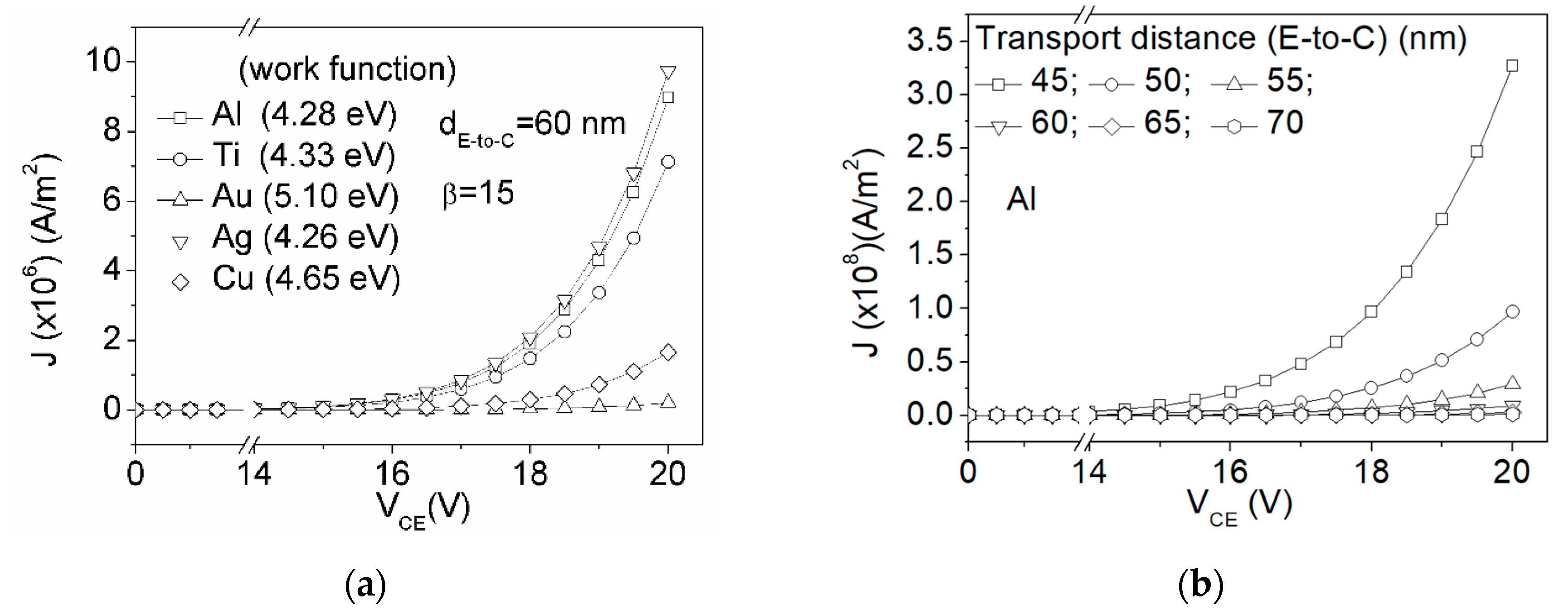
3.1. Current Density Modeling of Field Emission Diodes
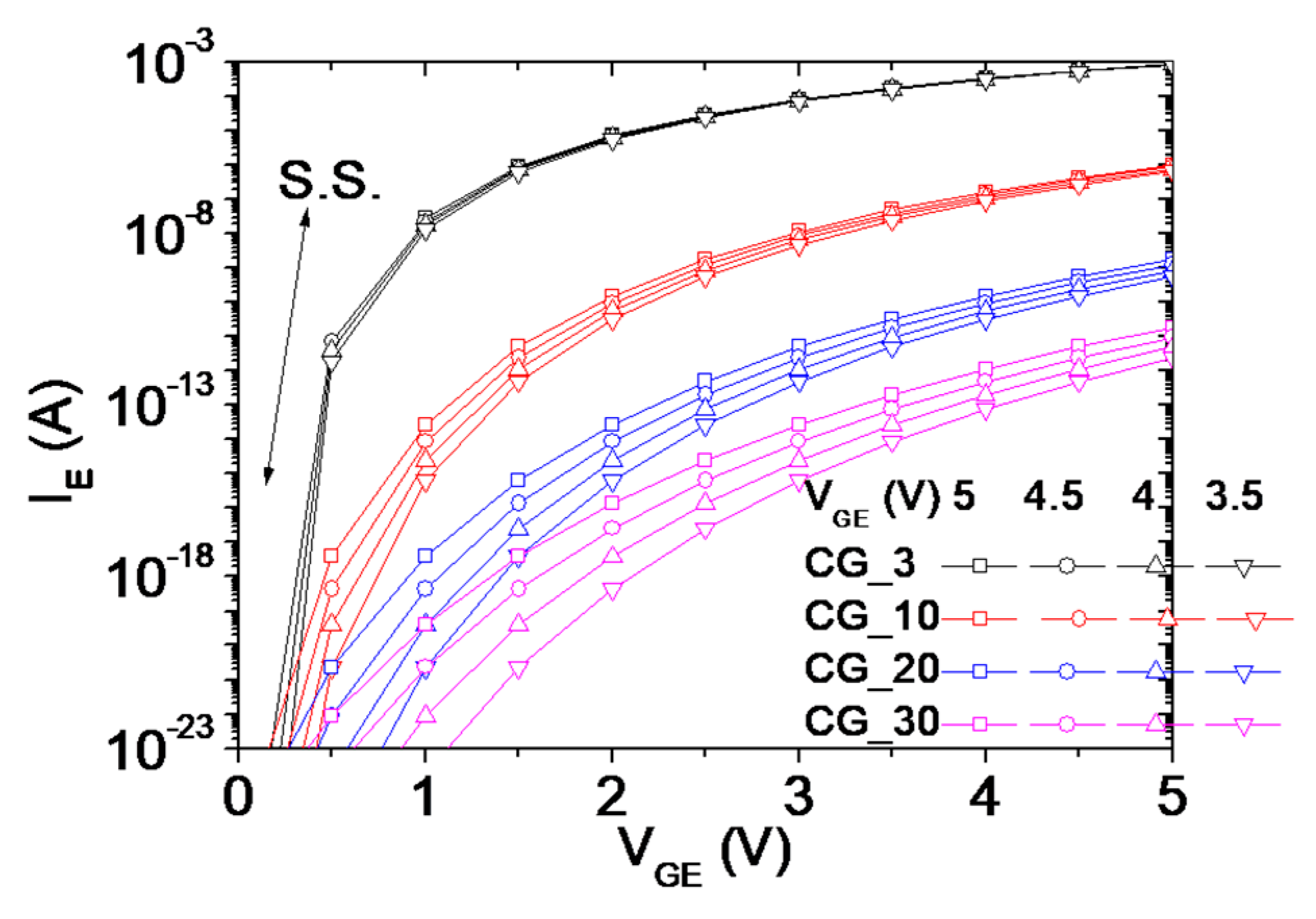
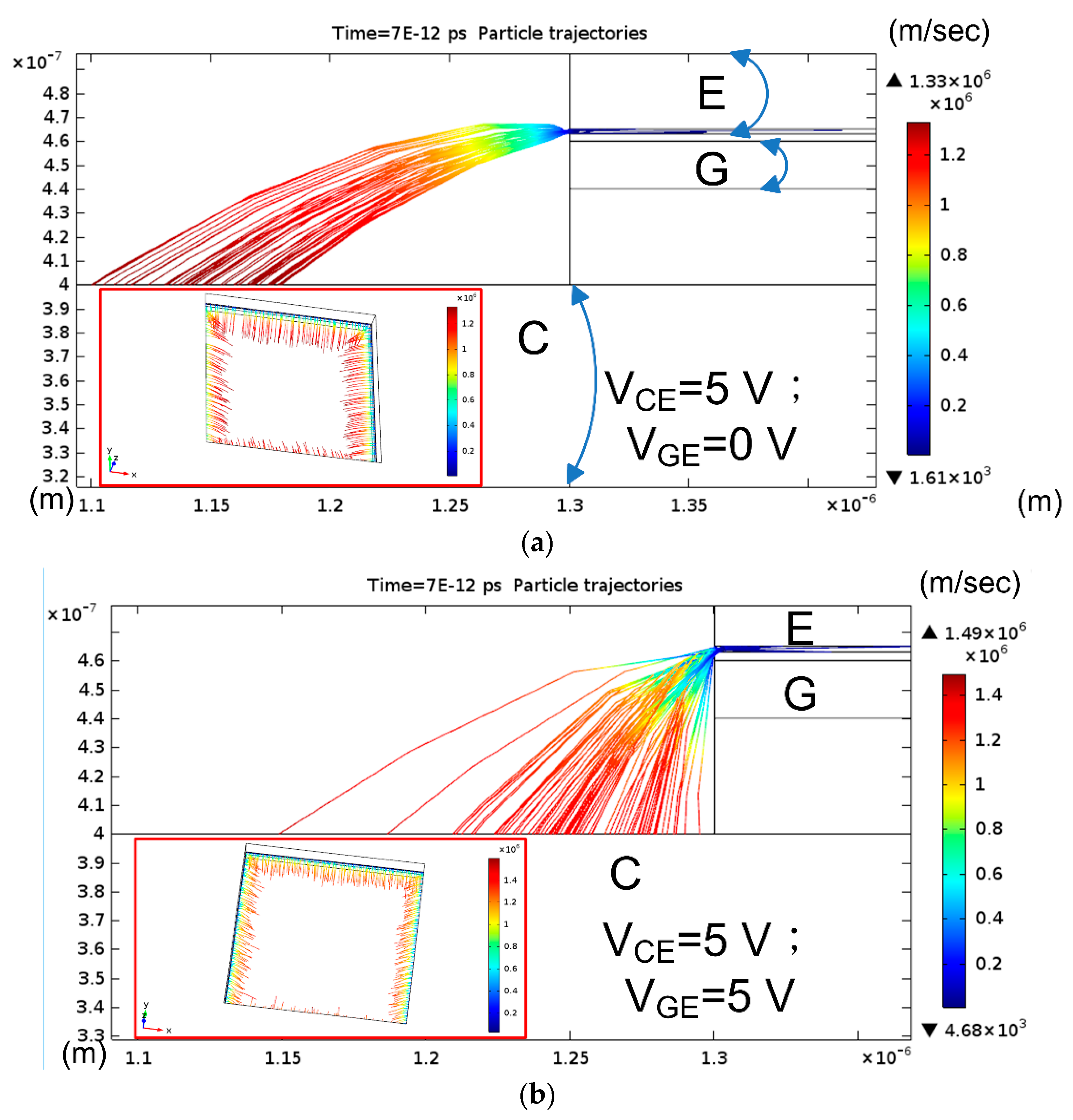
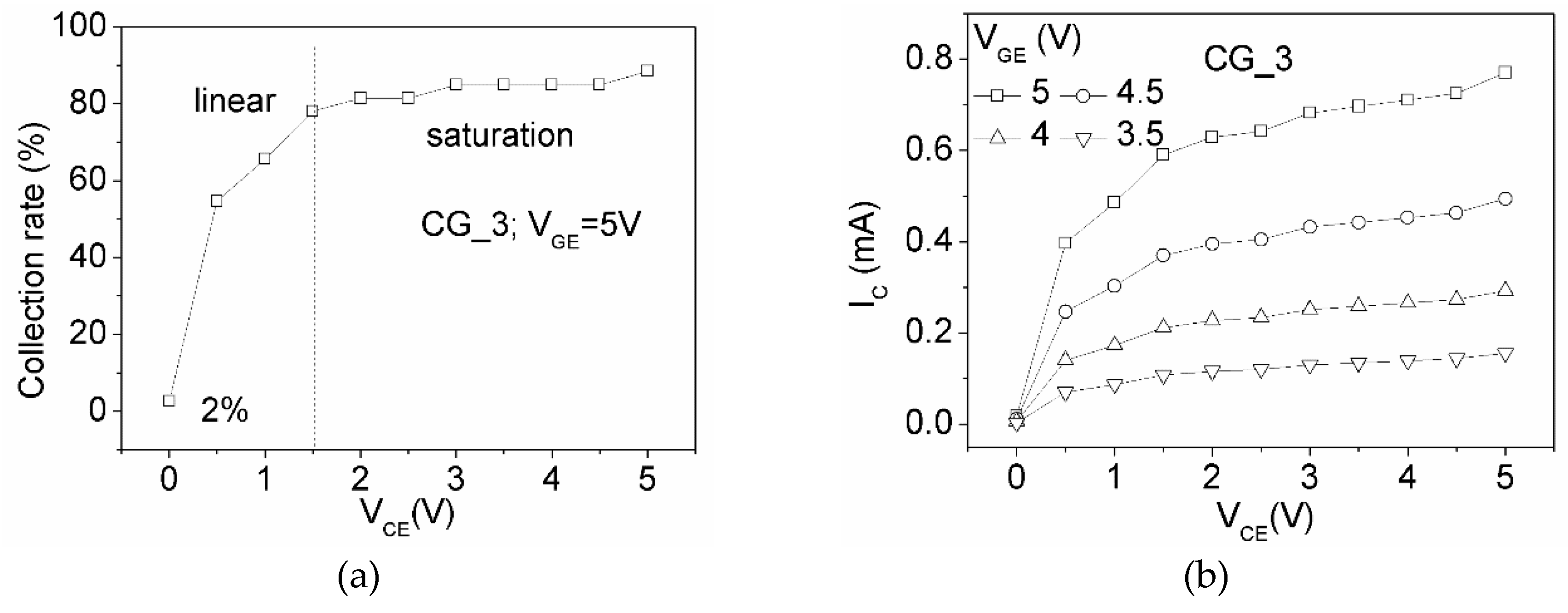
3.2. Finite Element Modeling on Vertical FE Transistors
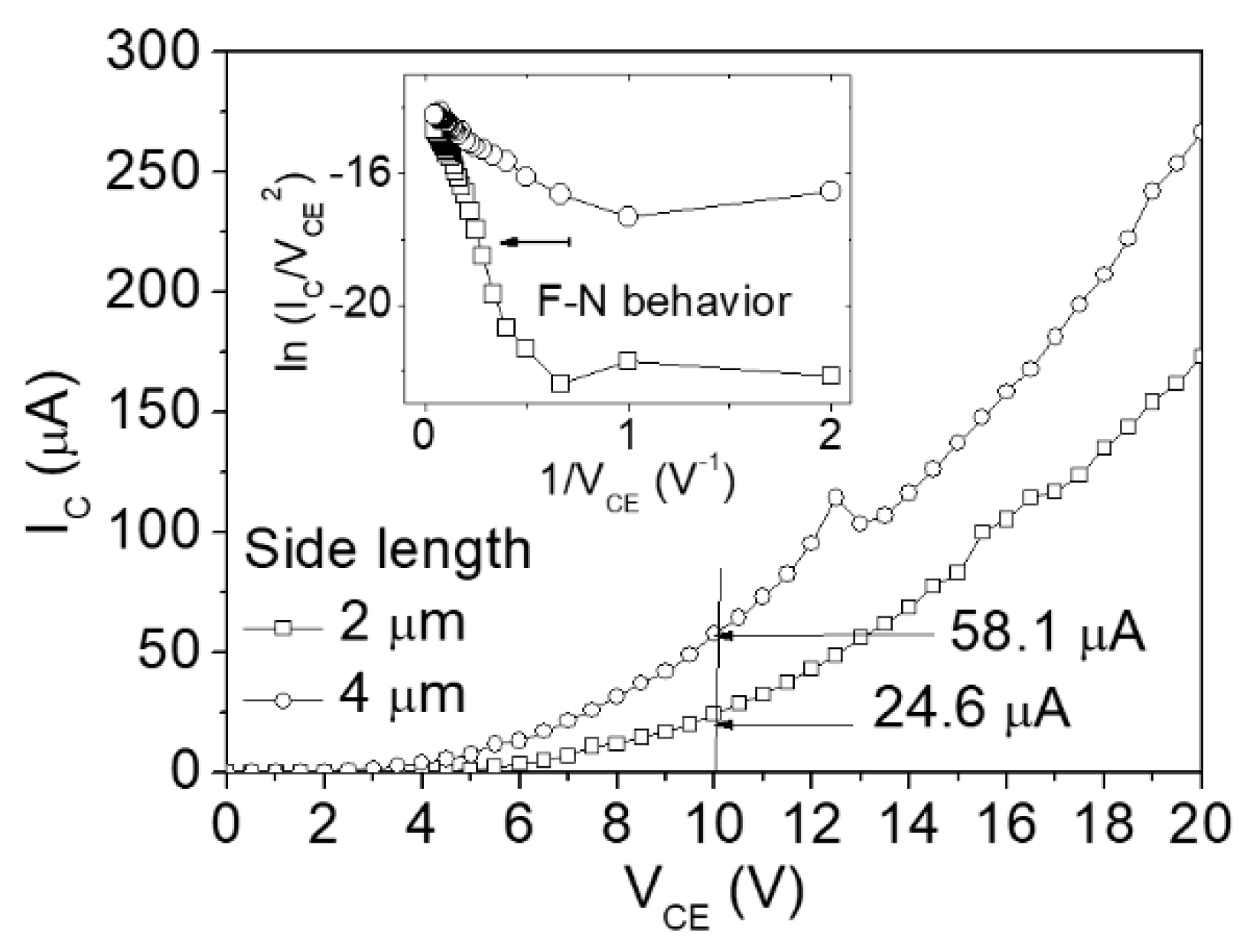
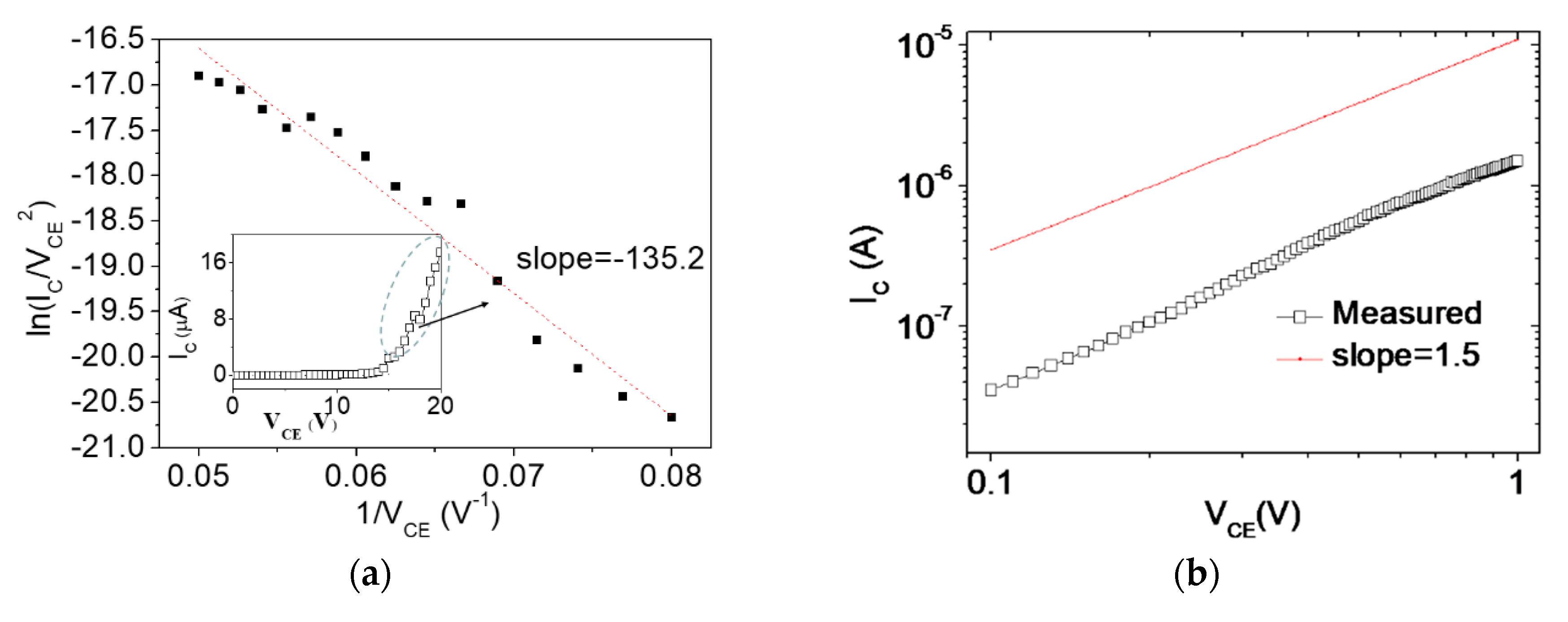
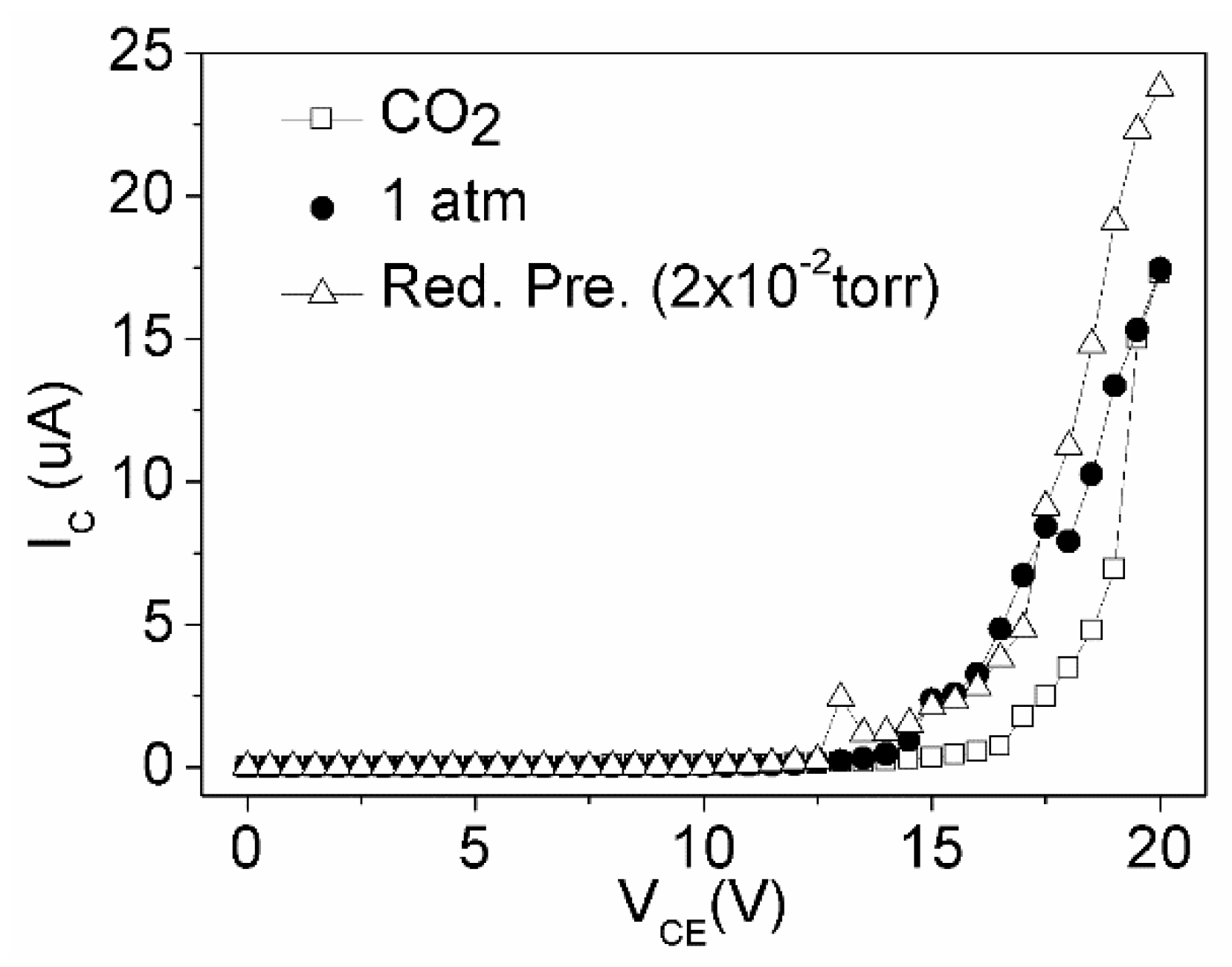
3.3. Measurement of Field Emission Vertical Air Channel Diodes
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Giannazzo, F.; Greco, G.; Roccaforte, F.; Sonde, S.S. Vertical transistors based on 2D materials: status and prospects. Crystals 2018, 8, 70. [Google Scholar] [CrossRef]
- Chavarin, C.A.; Strobel, C.; Kitzmann, J.; Bartolomeo, A.D.; Lukosius, M.; Albert, M.; Wolfgang Bartha, J.; Wenger, C. Current modulation of a heterojunction structure by an ultra-thin graphene base electrode. Materials 2018, 11, 345. [Google Scholar] [CrossRef]
- Bartolomeo, A.D.; Urban, F.; Passacantando, M.; McEvoy, N.; Peters, L.; Iemmo, L.; Luongo, G.; Romeo, F.; Giubileo, F. A WSe2 vertical field emission transistor. Nanoscale 2019, 11, 1538–1548. [Google Scholar] [CrossRef]
- Han, J.W.; Meyyappan, M. The device made of nothing. IEEE Spectr. 2014, 51, 30–35. [Google Scholar] [CrossRef]
- Han, J.W.; Moon, D.I.; Meyyappan, M. Nanoscale vacuum channel transistor. Nano Lett. 2017, 17, 2146–2151. [Google Scholar] [CrossRef]
- Liu, M.; Fu, W.; Yang, Y.; Li, T.; Wang, Y. Excellent field emission properties of VO2(A) nanogap emitters in air. Appl. Phys. Lett. 2018, 112, 093104. [Google Scholar] [CrossRef]
- Srisonphan, S.; Jung, Y.S.; Kim, H.K. Metal–oxide–semiconductor field-effect transistor with a vacuum channel. Nature Nanotech. 2012, 7, 504–508. [Google Scholar] [CrossRef]
- Park, I.J.; Jeon, S.G.; Shin, C. A new slit-type vacuum channel transistor. IEEE Trans. Elect. Devices 2014, 61, 4186–4191. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, X.; Wu, S.; Tian, J. A new kind of vertically aligned field emission transistor with a cylindrical vacuum channel. Vacuum 2017, 137, 163–168. [Google Scholar] [CrossRef]
- Jones, W.M.; Lukin, D.; Scherer, A. Practical nanoscale field emission devices for integrated circuits. Appl. Phys. Lett. 2017, 110, 263101. [Google Scholar] [CrossRef]
- Han, J.-W.; Oh, J.S.; Meyyappan, M. Cofabrication of vacuum field emission transistor (VFET) and MOSFET. IEEE Trans. Nanotechnol. 2014, 13, 464–468. [Google Scholar] [CrossRef]
- Nirantar, S.; Ahmed, T.; Ren, G.; Gutruf, P.; Xu, C.; Bhaskaran, M.; Walia, S.; Sriram, S. Metal–air transistors: semiconductor-free field-emission air-channel nanoelectronics. Nano Lett. 2018, 18, 7478–7484. [Google Scholar] [CrossRef] [PubMed]
- Chang, W.T.; Pao, P.H. Field Electrons Intercepted by Coplanar Gates in Nanoscale Air Channel. IEEE Trans. Electron. Devices 2019, 66, 3961–3966. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.; Oh, H.; Meyyappan, M.; Han, J.W.; Lee, J.S. Design guidelines for nanoscale vacuum field emission transistors. J. Vac. Sci. Technol. B 2016, 34, 042201. [Google Scholar] [CrossRef]
- Gray, H.F.; Campisi, G.J.; Greene, R.F. A vacuum field effect transistor using silicon field emitter arrays. In Proceedings of the 1986 International Electron Devices Meeting, Los Angeles, CA, USA, 7–10 December 1986; pp. 776–779. [Google Scholar] [CrossRef]
- Subramanian, K.; Kang, W.P.; Davidson, J.L.; Ghosh, N.; Galloway, K.F. A review of recent results on diamond vacuum lateral field emission device operation in radiation environments. Microelectron Eng. 2011, 88, 2924–2929. [Google Scholar] [CrossRef]
- Rakhshandehroo, M.R.; Pang, S.W. Field emission from gated Si emitter tips with precise gate–tip spacing, gate diameter, tip sharpness, and tip protrusion. J. Vac. Sci. Technol. B 1997, 15, 2777–2780. [Google Scholar] [CrossRef]
- Hsu, H.; Kang, W.P.; Raina, S.; Huang, J.H. Nanodiamond vacuum field emission device with gate modulated transistor characteristics. Appl. Phys. Lett. 2013, 102, 203105. [Google Scholar] [CrossRef]
- Lan, Y.C.; Lee, C.T.; Chen, S.H.; Lee, C.C.; Tsui, B.Y.; Lin, T.L. Simulation study of carbon nanotube field emission display with under-gate and planar-gate structures. J. Vac. Sci. Technol. B 2004, 22, 1244–1249. [Google Scholar] [CrossRef]
- Kang, W.P.; Davidson, J.L.; Wisitsora, A.; Wonga, Y.M.; Takalkar, R.; Holmes, K.; Kerns, D.V. Diamond vacuum field emission devices. Diam. Relat. Mater. 2004, 13, 1944–1948. [Google Scholar] [CrossRef]
- Lenzlinger, M.; Snow, E.H. Fowler nordheim tunneling into thermally grown SiO2. J. Appl. Phys. 1969, 40, 278–283. [Google Scholar] [CrossRef]
- le Fèbre, A.J.; Abelmann, L.; Lodder, J.C. Field emission at nanometer distances for high-resolution positioning. J. Vac. Sci. Technol. B 2008, 26, 724–729. [Google Scholar] [CrossRef][Green Version]
- Xu, J.; Gu, Z.; Yang, W.; Wang, Q.; Zhang, X. Graphene-based nanoscale vacuum channel transistor. Nanoscale Res. Lett. 2018, 13, 311. [Google Scholar] [CrossRef] [PubMed]
- Talaat, M.; El-Zein, A. A numerical model of streamlines in coplanar electrodes induced by non-uniform electric field. J. Electrostat. 2013, 71, 312–318. [Google Scholar] [CrossRef]
- Schwettman, H.A.; Turneaure, J.P.; Waites, R.F. Evidence for surface-state-enhanced field emission in RF superconducting cavities. J. Appl. Phys. 1974, 45, 914–922. [Google Scholar] [CrossRef]
- Chung, M.S.; Yoon, B.G. Analysis of the slope of the Fowler–Nordheim plot for field emission from n-type semiconductors. J. Vac. Sci. Technol. B 2003, 21, 548–551. [Google Scholar] [CrossRef]
- Child, C.D. Discharge from Hot CaO. Phys. Rev. (Ser. I) 1991, 32, 492–511. [Google Scholar] [CrossRef]
- Butcher, M.; Neuber, A.A.; Cevallos, M.D.; Dickens, J.C.; Krompholz, H. Conduction and breakdown mechanisms in transformer oil. IEEE Trans Plasma Sci. 2006, 34, 467–475. [Google Scholar] [CrossRef]


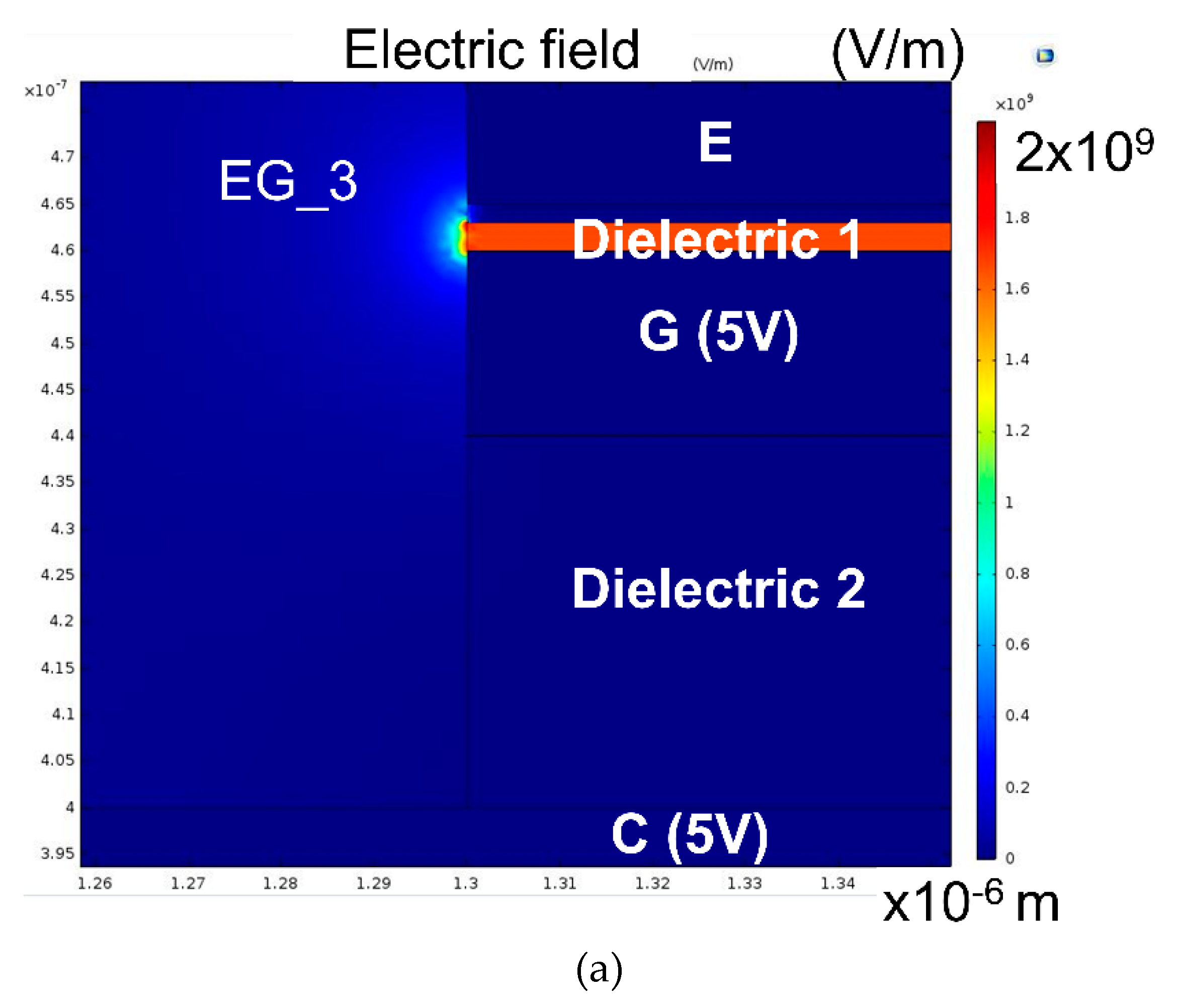
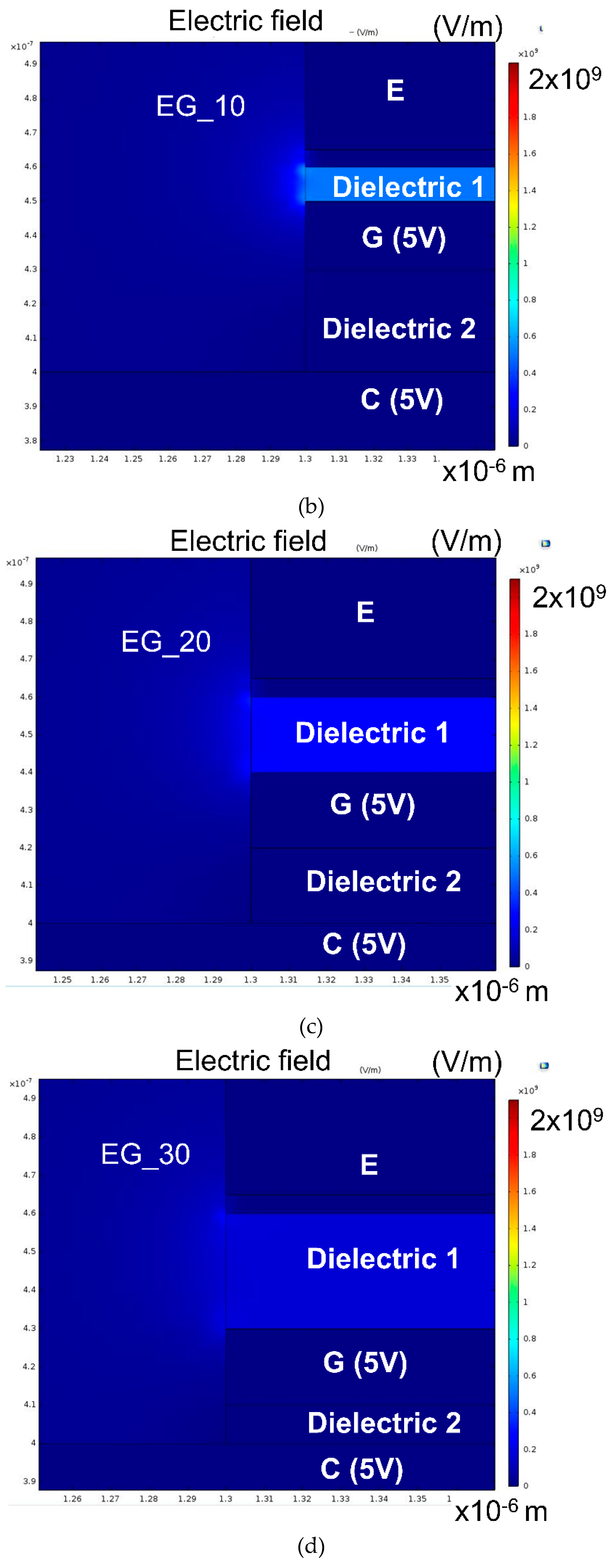
| Dimensions of Transistors | EG_3 | EG_10 | EG_20 | EG_30 |
|---|---|---|---|---|
| DChannel (nm) | 63 | 60 | 60 | 60 |
| tE-G (nm) | 3 | 10 | 20 | 30 |
| tG (nm) | 20 | 20 | 20 | 20 |
| tG-C (nm) | 40 | 30 | 20 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, W.-T.; Hsu, H.-J.; Pao, P.-H. Vertical Field Emission Air-Channel Diodes and Transistors. Micromachines 2019, 10, 858. https://doi.org/10.3390/mi10120858
Chang W-T, Hsu H-J, Pao P-H. Vertical Field Emission Air-Channel Diodes and Transistors. Micromachines. 2019; 10(12):858. https://doi.org/10.3390/mi10120858
Chicago/Turabian StyleChang, Wen-Teng, Hsu-Jung Hsu, and Po-Heng Pao. 2019. "Vertical Field Emission Air-Channel Diodes and Transistors" Micromachines 10, no. 12: 858. https://doi.org/10.3390/mi10120858
APA StyleChang, W.-T., Hsu, H.-J., & Pao, P.-H. (2019). Vertical Field Emission Air-Channel Diodes and Transistors. Micromachines, 10(12), 858. https://doi.org/10.3390/mi10120858





