1. Introduction
Lower limb compression garments are regularly employed in clinical settings [
1] and, more recently, by athletes seeking to improve performance or decrease recovery time [
2,
3]. In medical settings, compression devices including passive compression socks and active intermittent pneumatic compression devices, are used in the treatment of hypertrophic scarring, venous ulcers, deep vein thrombosis and other diseases [
1]. Some examples of physiological testing in [
4,
5] have shown a significant increase in the mean arterial pressure, cardiac output and cardiac stroke volume, with a significant reduction in the heart rate through applying active compression cyclically at frequencies between 1 to 2 Hz and at pressures of approximately 10 mmHg in the knee region. A major challenge for any compression device, regardless of application, is ensuring the consistency and repeatability of the applied pressure throughout its use [
6]. The limited sizing options of most passive compression gear can vary the pressure experienced between subjects due to body shape differences. Further, the consistency of pressure applied by the garment on the same subject can be affected by the donning method [
7]. A further challenge is that the shape, size and tissue compliance of the leg can change during compression application due to fluid redistribution, muscle contraction and movement of the garment/device.
Partsch et al. [
8] made recommendations on the characteristics that an ideal sensor would need in order to measure the interface pressure between a compression garment and the lower leg skin. Specifically, they identify the need for sensors that are low cost, low hysteresis, have minimal creep, high sampling rate, high accuracy, flexibility, durability and small sensor surface area. To date, there has yet to be a sensor developed that meets all these requirements.
Burke et al. [
9] and Ferguson-Pell et al. [
10] examined the use of Tekscan FlexiForce and Interlink Electronics FSR piezoresistive-based sensors for measuring interface pressure in compression garments. Piezoresistive sensors function by measuring the change in resistance under a mechanical load. They are thin and can provide reliable results during dynamic measurements. However, these sensors suffer from significant hysteresis and drift, and thus are not dependable for long time-scale measurements [
8]. Additionally, piezoresistive sensors are dramatically affected by base curvatures under 32 mm in radius [
10] and require relatively large pressures for reliable measurements [
11]. The total error exhibited in the sensors, accounting for errors in repeatability, hysteresis and linearity, is approximately +/− 10 mmHg for a pressure range 0 to 96 mmHg, [
9], which limits the utility of these devices for pressure mapping of compression garments. Note, for the remainder of the document, unless otherwise noted, errors are described for the pressure range of interest between 0 and 100 mmHg.
Similar to piezoresistive sensors, strain gauges also respond to a change in resistance with mechanical strain [
12,
13]. Kraemer et al. [
14] and Ghosh et al. [
15] utilized strain gauges to measure the compression applied by compression garments/bandages on a subject’s thigh and a mannequin leg, respectively. However, since strain gauges exhibit a better sensitivity along their largest dimension, these sensors tend to become thick for measuring interfacial pressures. Additionally, strain gauges tend to exhibit thermal and humidity dependence, and high hysteresis [
12].
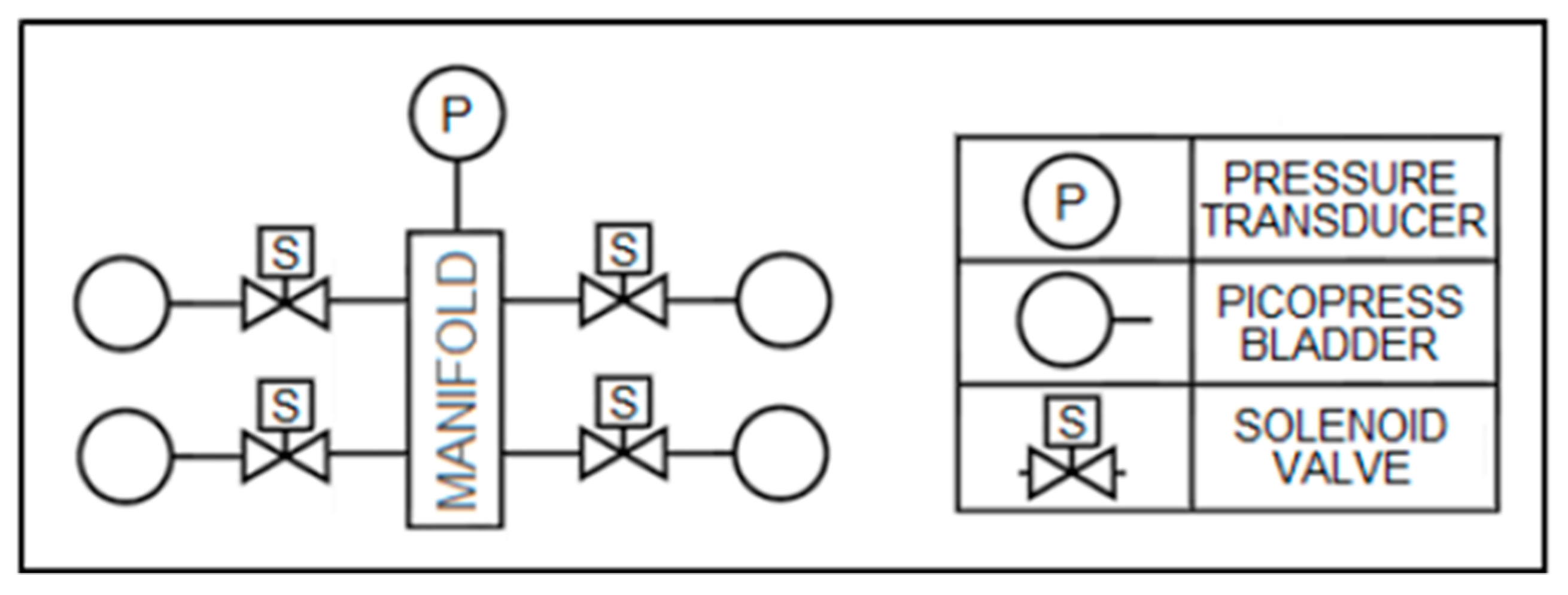
Pneumatic-based sensors are one of the most prevalent designs for measuring compression garment interfacial pressure [
9]. These sensors utilize bladders or compartments that are filled with a small volume of air connected to a pressure transducer through a flexible hose [
16]. As pressure is applied, the volume of the bladder decreases, thus increasing the internal pressure. At a constant temperature, it is assumed that the internal pressure measured by the transducer is equivalent to the external applied pressure [
16]. Commercially available pneumatic sensors, such as the Salzmann MST MKIV [
17], MediGroup Kikuhime [
18] and Microlab PicoPress [
19] are thin and flexible devices that can be used to measure interfacial pressures between the body and compression device. Furthermore, pneumatic pressure transducers have been found to exhibit repeatable results within +/− 3 mmHg of error [
8,
19]. A major shortfall of this technology is its temperature dependence [
8]. Additionally, their high sensitivity to curvature can result in overestimates of pressure by up to 150% [
9]. The sampling rate of the system is affected by the tubing length, which can be important in the evaluation of rapid inflation active compression systems. Additionally, pressure sensing with an array of pneumatic sensors presents multiple inconveniences. The sensors each require a dedicated pressure transducer and have a large surface area (a PicoPress sensor is approximately 50 mm in diameter), resulting in poor spatial resolution. These types of sensors need a great amount of tubing and rely on pressure transducers that are bulky and almost 10 times larger in footprint than the actual sensor, [
19]. Sensor multiplexing can reduce the number of transducers in a system, which uses solenoid valves to isolate each bladder for pressure reading (see
Figure 1). However, the addition of a manifold increases the system volume, lowering the sampling rate and the transducer’s sensitivity to bladder volume change.
Capacitive sensors have also been employed in other textile applications, [
20,
21,
22], such as muscle activity detection, [
20], and pressure mapping for insoles, [
21]. These sensors typically consist of a textile used as a dielectric material with conductive yarn woven as electrodes. They have the benefit of being small (good spatial resolution), flexible, and easily used in arrays for pressure distribution measurements [
23,
24]. Compared to other sensor technologies, they also possess relatively low temperature sensitivities [
23,
24]. Q. Guo et al. [
25] developed a tactile floating electrode capacitive sensor which displayed good linearity up to 350 kPa and improved durability over parallel electrode designs. Capacitive measurements also present their own challenges, often requiring complex circuitry to filter measurement noise [
23]. Signal hysteresis can also affect performance, as the dielectric material is often viscoelastic and exhibits nonlinear behaviour when stressed [
26]. Additionally, the current-pressure relation is nonlinear [
27] which makes it more challenging for proper calibration. Nano-fibers have been employed in the development of pressure sensing technologies for other applications [
27,
28]. However, due to the high temperature sensitivity of materials used, such as gold, they are not suitable for the application of interest.
In this paper, a novel, capacitive-based, dielectric electroactive polymer (DEAP) pressure sensor is developed in collaboration with StretchSense Ltd. for in-situ pressure measurements under textile garments. Specific testing conditions are required when evaluating pressure sensors for compression garments, since the interface is neither flat nor solid. Thus, multiple testing methods are presented in
Section 3, with results in
Section 4. The sensor’s pressure sensitivity, error and durability are characterized. The performance effects due to temperature, humidity, boundary conditions and hysteresis are also examined. This is the first sensor to use DEAP materials measuring low pressure ranges (0 to 100mmHg) for portable and wearable applications, including the fast sampling rate required for many physiological applications. In addition to the sensor fabrication and characterization, the small, portable wireless circuitry for the proposed sensor is one of the novel aspects of this work. The wireless sensing unit communicates data over Bluetooth with the actuation system.
2. Capacitive Sensors
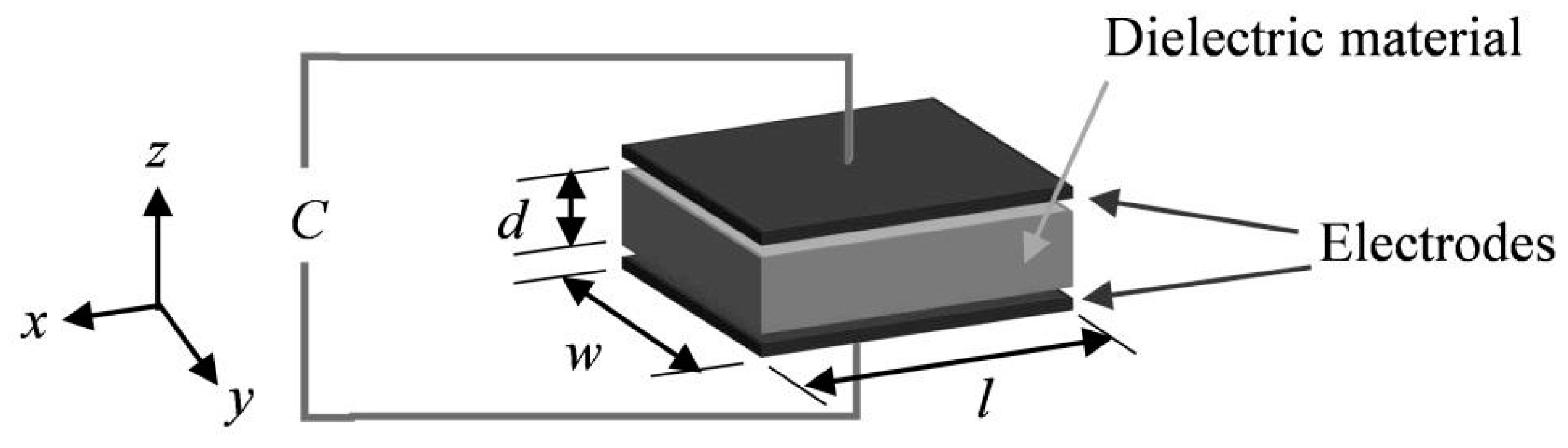
The custom designed sensors developed in collaboration with StretchSense Ltd. for this research are capacitive tactile sensors operating on the principle of a deformable parallel plate capacitor model (shown schematically in
Figure 2). The dielectric layer is made of a silicone-based DEAP. The model consists of two compliant electrode layers of length l and width w separated by a dielectric material of thickness d forming a compliant capacitor [
29].
The capacitance
C, for a parallel plate capacitor is described by:
where
and
are the relative permittivity of the dielectric layer and the vacuum permittivity respectively. Compression of the capacitive sensor along the
z-axis, (see
Figure 2), causes a decrease in the dielectric layer thickness and the distance between the two electrodes,
d. Assuming unconstrained edges and an incompressible material for the dielectric layer, this results in an increase in the area, (
), [
26]. Both changes result in an increase of the capacitance, which can then be correlated to an applied pressure.
A picture of the capacitive sensor used in this study is shown in
Figure 3. This is the third generation of the sensor developed by the authors, which has better sensitivity, increased sampling frequency, wider moving average filter, improved manufacturing procedure and improved noise rejection. The system consists of a battery-powered circuit capable of measuring the capacitance of five sensing elements. There is a trade-off with respect to sensor head size, as the change in capacitance with pressure is directly proportional to the sensor area, while the spatial resolution reduces with increasing size. In order to maintain a small footprint, the outer surface of the sensor is electrically insulated and folded onto itself like an accordion to increase the capacitor area. This folding of the sensor effectively creates a multi-layer sensor, where each layer experiences the same pressure, resulting in a higher initial capacitance and improved pressure sensitivity. As evident in
Figure 3, the sensor head is perforated with a series of holes. These holes decrease the overall stiffness of the sensor, allowing greater deformation during compression.
Figure 4 shows a simplified schematic of the pressure sensor with major dimensions labeled.
Table 1 provides the dimensions and elastic modulus of the StretchSense pressure sensor, as well as specifications of the battery used. The elastic modulus was averaged between two sample tensile tests at a strain rate of 12 mm/minute and is applicable for strains below 10%. In comparison to pneumatic sensors, the sensor design used is only ~25% of the PicoPress bladder surface area. This provides a significant advantage in terms of the design’s spatial resolution.
The capacitance of the sensor is sampled at 660 Hz by a measurement circuit made by StretchSense. The circuit then applies a moving average of 20 data points to generate a final output at 285 Hz. A merit of using capacitive sensing is the stability of sampling rates that are largely independent from experimental setup conditions. Conversely, pneumatic sensor sampling rates are more susceptible to setup conditions as discussed in
Section 1. This high sampling rate is particularly useful for the physiological applications where more dynamic pressure applications, such as pulsations tuned at a person’s heart rate, are used to increase the cardiac performance [
4,
5]. The control circuitry used is designed to minimize noise while maximizing the output data rate.
Comparison to Alternative Capacitive Sensors
The unique DEAP construction presents multiple advantages compared to many parallel plate and floating electrode constructions. Since the electrodes are made of a compliant material with similar stiffness to the silicone dielectric layer, interlayer stresses during bending and stretching are minimized. This construction avoids using thin traces that are common for many parallel plate structures, which may break under repeated bending loads, as also noted by M-Y Cheng et al. [
30]. Additionally, a major advantage of the DEAP parallel plate construction used is its simplicity and resistance to fail under many cycles of loading. The fabrication of the floating electrode and parallel plate sensors is often more complex, requiring multi-step micromachining processes to create air gaps and metal layers [
25,
31]. Conversely, the sensor presented avoids such process steps during fabrication. This greatly improves manufacturing scalability and reduces design complexity.
When compared to the DEAP parallel electrode construction used, Q. Guo et al. [
25] presented a floating electrode design using a robust construction and good linearity over a wider pressure sensing range (up to 350 kPa, or 2625 mmHg). However, the target application of medical compression garments where pulsations are used requires much lower pressure ranges, (0–100 mmHg). Within the scope of these smaller signals, sensor noise and error reduction becomes increasingly critical for the target design. M-Y Cheng et al. [
30] showed that while theoretical sensitivities of parallel plate and floating electrode constructions are the same, parallel plate constructions are predicted to have a better signal-to-noise ratio (SNR). Thus, for the application’s low-pressure operating range, the parallel plate construction used is more advantageous to maximize SNR.
3. Experimental Methods
In this section, the test procedures assessing sensor performance in representative configurations are outlined. One of the challenges in assessing in-situ pressure sensor performance is the difficulty in applying a realistic and measurable (known) boundary (loading) condition. Research that includes the measurement of pressures applied to the leg often neglects the measurement errors introduced when moving from laboratory testing facilities to in-situ measurements. For example, sensor calibration is typically performed on a flat, solid surface; the effect of curvature and compliance of the leg are not examined [
16]. Therefore, one of the objectives of this section is to study the errors that are introduced when taking in-situ pressure measurements on a leg. For this purpose, a series of representative tests were formulated to examine the behaviour of these capacitance-based sensors in different modes.
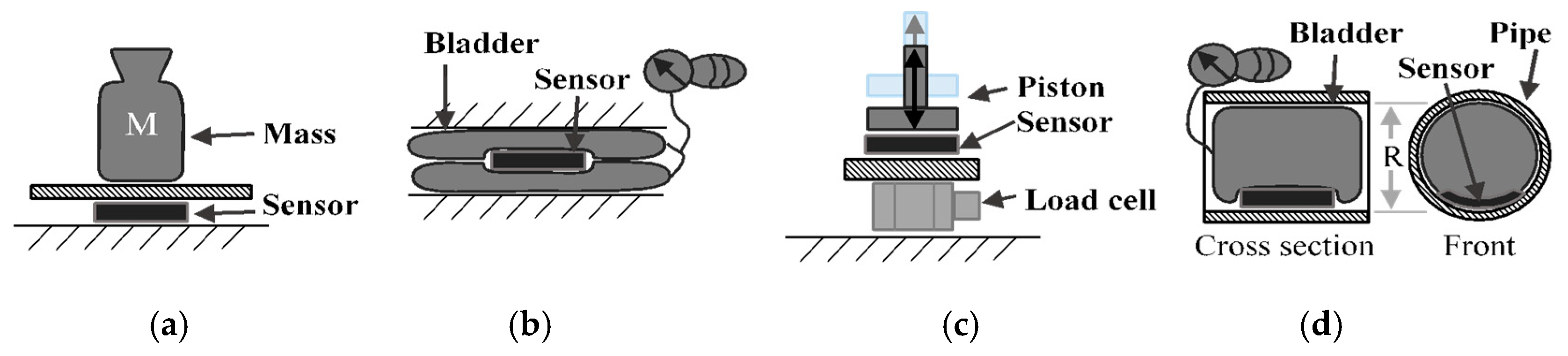
Figure 5 depicts four test setups used to validate the sensor. The tests in all configurations were repeated several times to gather relevant statistics.
The mass test (
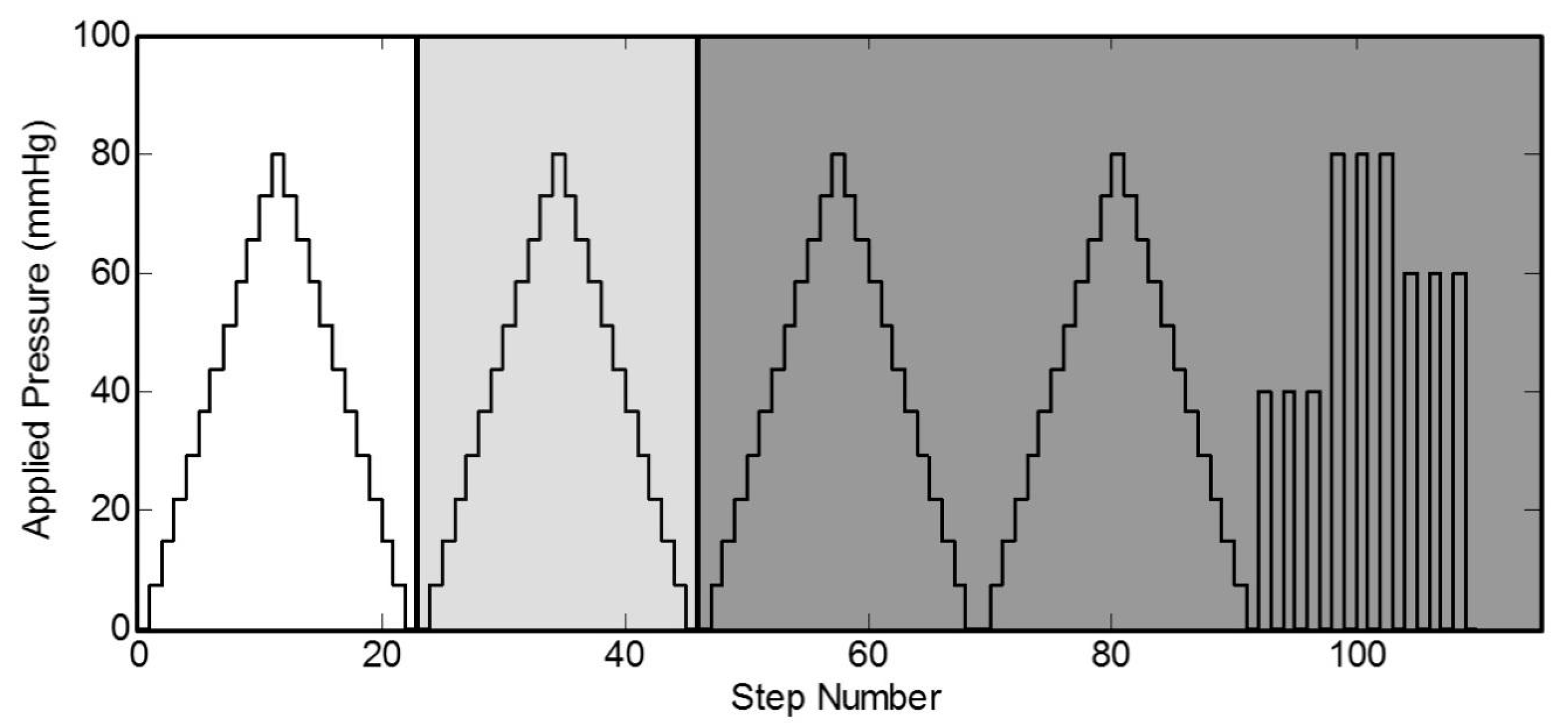
Figure 5a) is performed on a flat surface where the sensor sits with masses stacked on top of it. The mass applied increases in 50 g increments from 0 g up to 550 g. The applied pressure to the sensor is determined by measuring the total weight placed on the sensor over the area of the sensor. The sensor is subjected to static loads at increments of approximately 7 mmHg that are held for 30 s at a time, up to a maximum pressure of 80 mmHg. The average and standard deviation of the capacitance for a 10 s period is collected for each increment. The 10 s period is taken after the load has been applied and the measurement reading has settled. The loading profile (shown in
Figure 6) has four incremental loading and unloading cycles and nine direct loading and unloading cycles. The incremental cycles are used to measure the hysteresis inherent in the sensor. Meanwhile, the direct loading cycles closely match the use-case for these sensors when applied under, for example, intermittent pneumatic compression devices. The results from the first incremental loading and unloading cycle (white section in
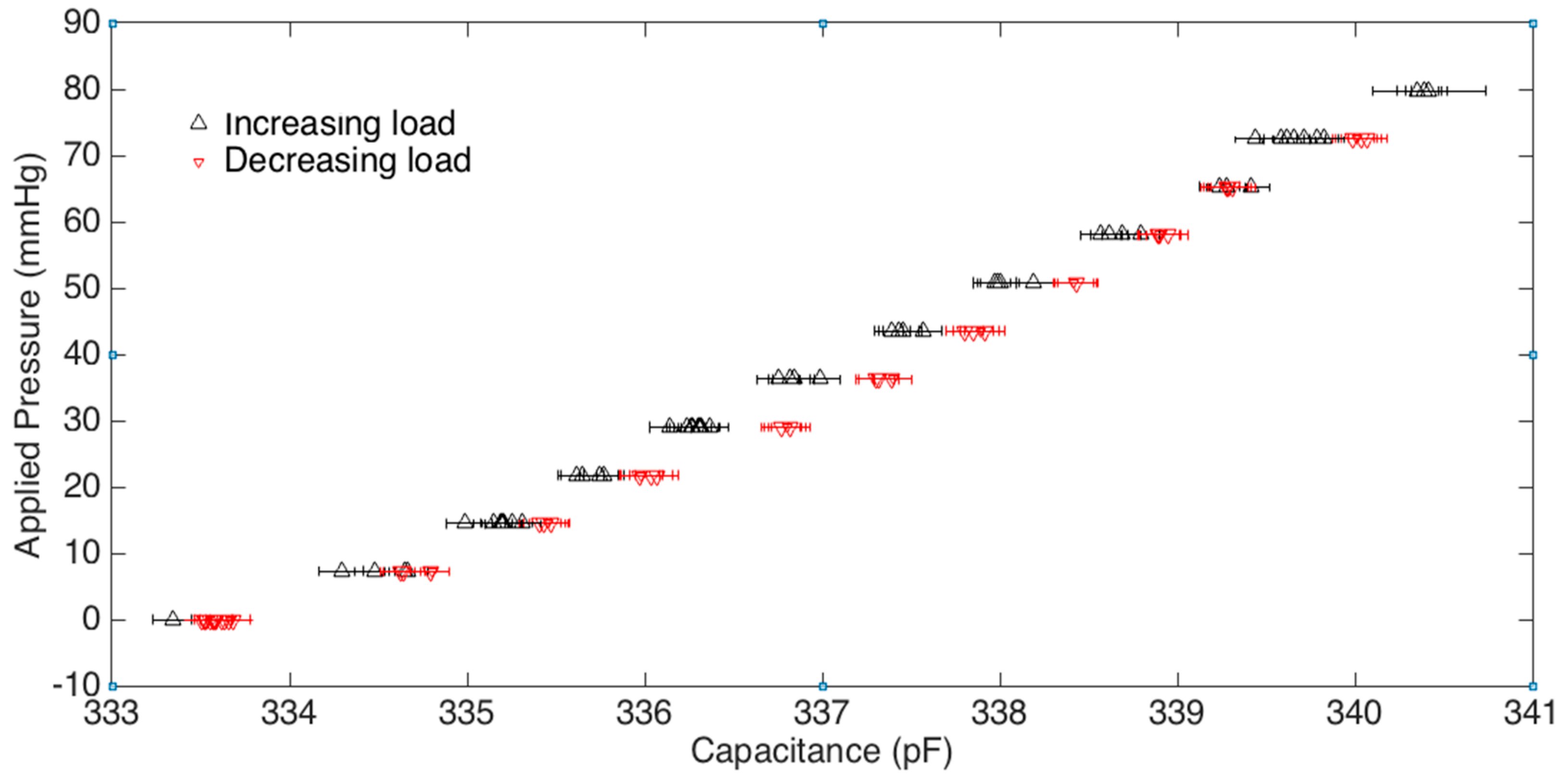
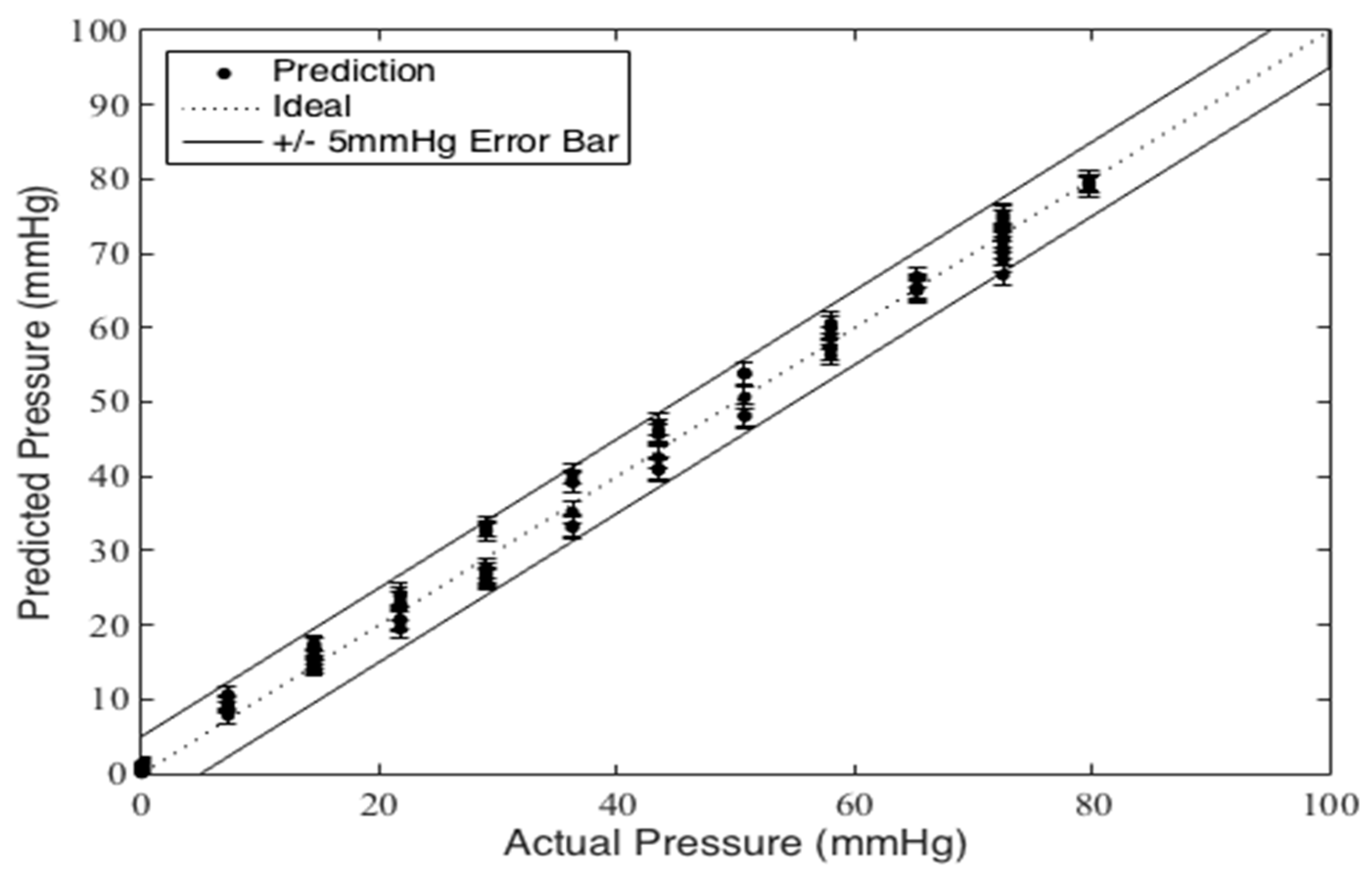
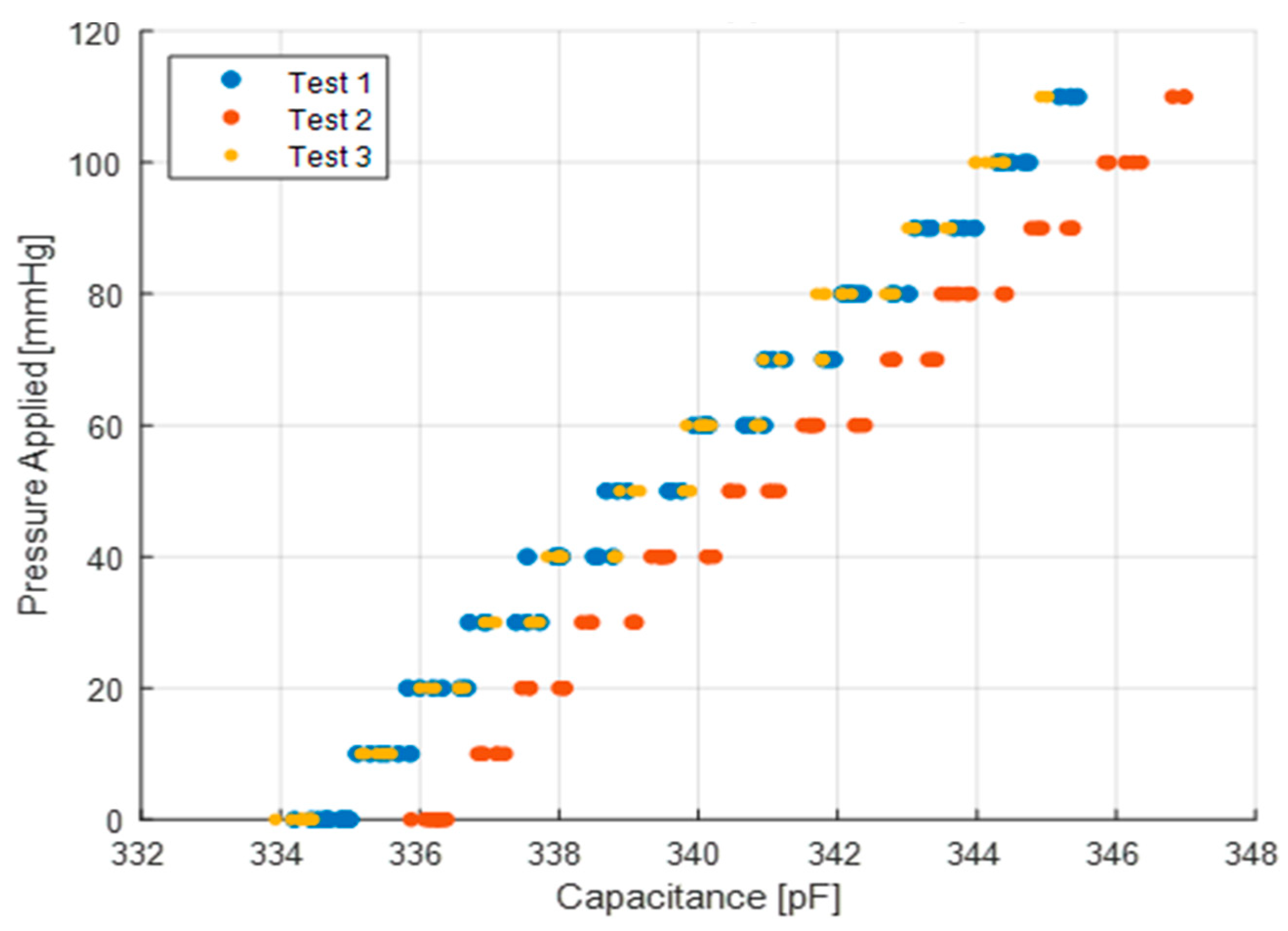
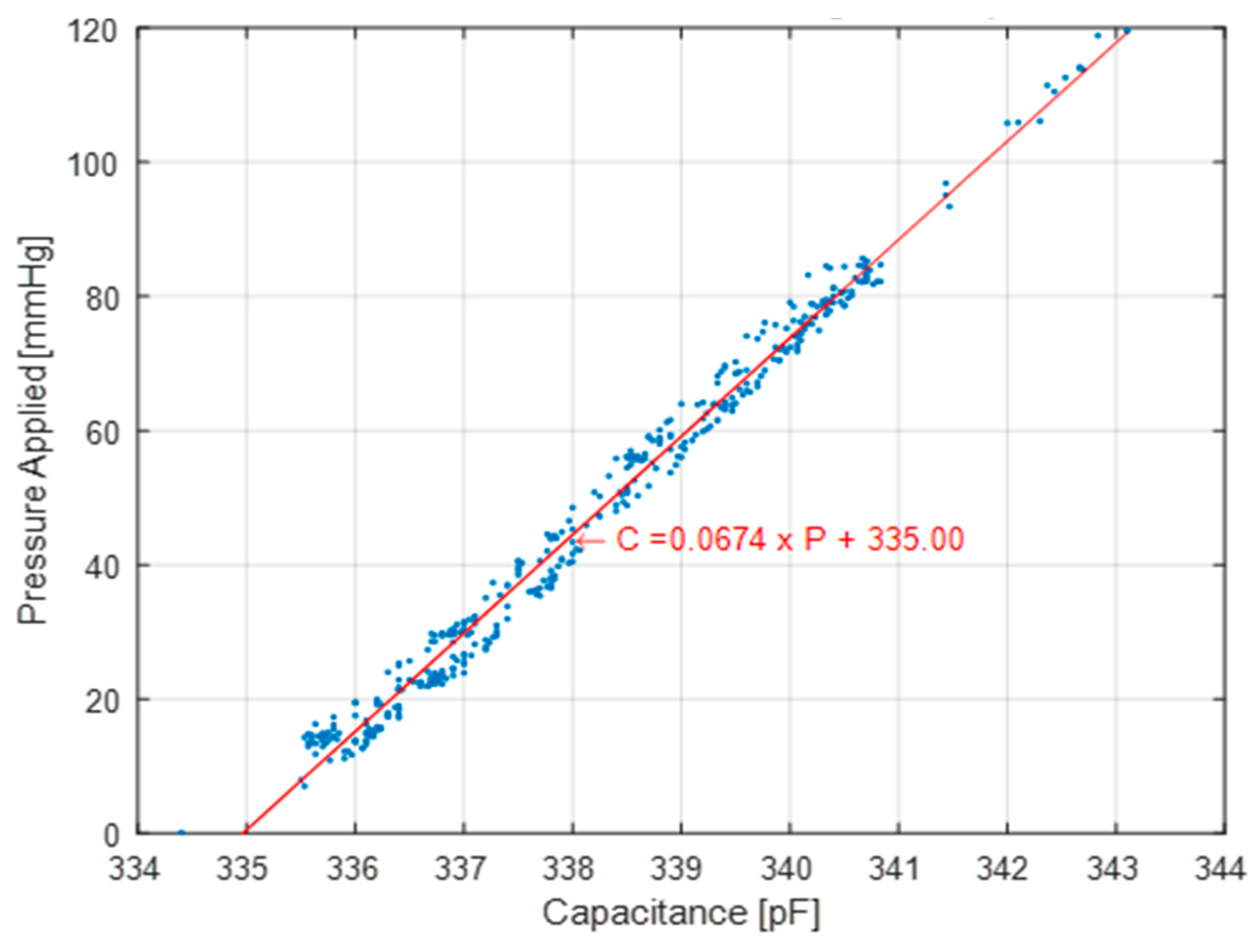
Figure 5) are discarded as a “bedding-in” cycle, as recommended by StretchSense, to allow the sensor to acclimate to a stable position. The second incremental loading and unloading cycle (light grey section) is then used to calibrate the sensor. A fit is applied to the calibration data and this curve fit is then used to convert the capacitance measurements of the remaining validation data (dark grey section) to pressure estimates. This test is meant to examine repeatability, linearity and hysteresis of the sensor in static conditions.
Figure 5b depicts the bladder test, whereby the sensor is placed between two inflatable (18 cm × 38 cm) bladders. The bladders are inflated by a hand pump up to a pressure of 110 mmHg following the same timing procedure as used in the mass test, while the air pressure is measured using a manometer. The assumption is that the internal pressure of the bladder is transmitted to the pressure on the sensor. The main purpose of this test is to mimic a condition where the sensor rests on a soft surface and is used as additional verification for the previous test. It should be noted that the sensor is extremely lightweight, weighing only 1.28 g, as stated in
Section 2. As such, the weight of the sensor per area is negligible compared to the pressures of interest.
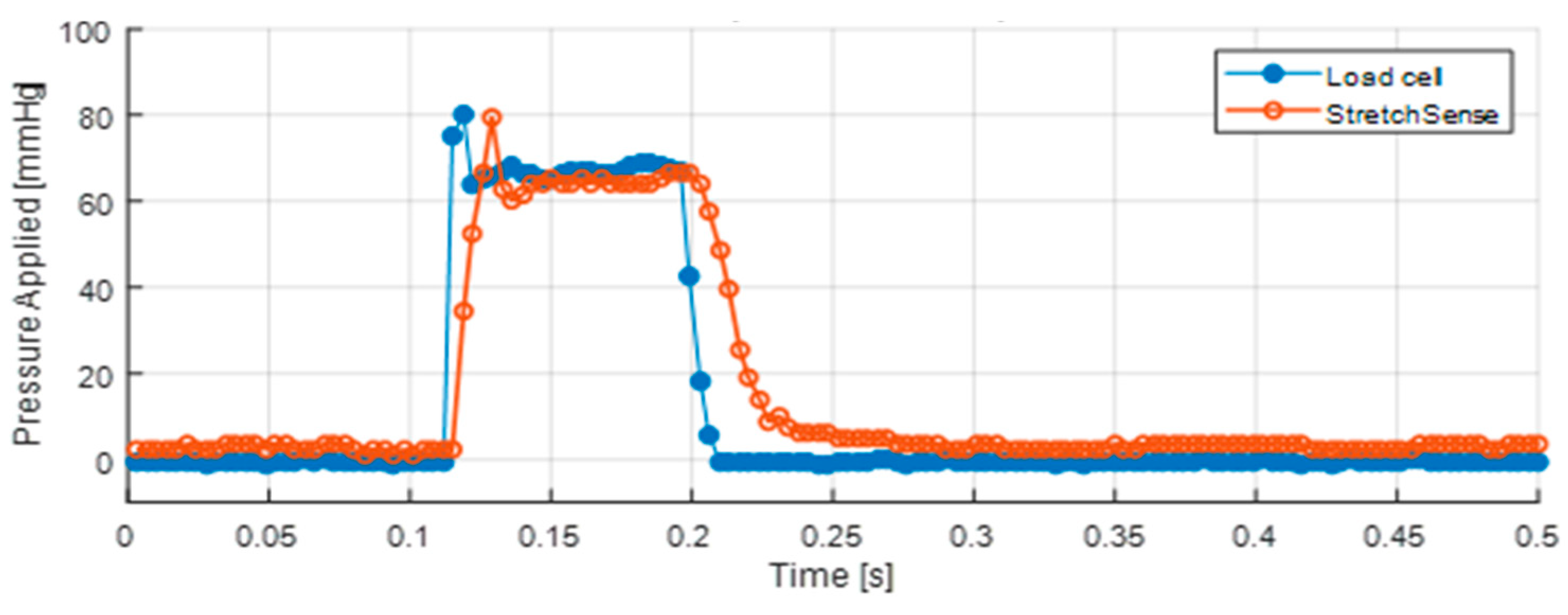
In the piston test (
Figure 5c), the sensor is placed on top of a dynamic load cell (PCB Piezotronics 208C01, Depew, NY, USA) and an impulse is applied to the unit by a pneumatic cylinder. The pneumatic cylinder is controlled with a pressure regulator and flow restrictor valve to enable dynamic pressure application at 1–2 Hz. In this test, the peak values from the load cell and the sensor measurements in each cycle of the pneumatic cylinder were compared. Similar to the mass test, the pressure being applied to the sensor is simply the force measured by the load cell over the area of the sensor. With this test, the dynamic response and repeatability over 400 loading cycles was tested at peak pressures ranging from 0 to 120 mmHg.
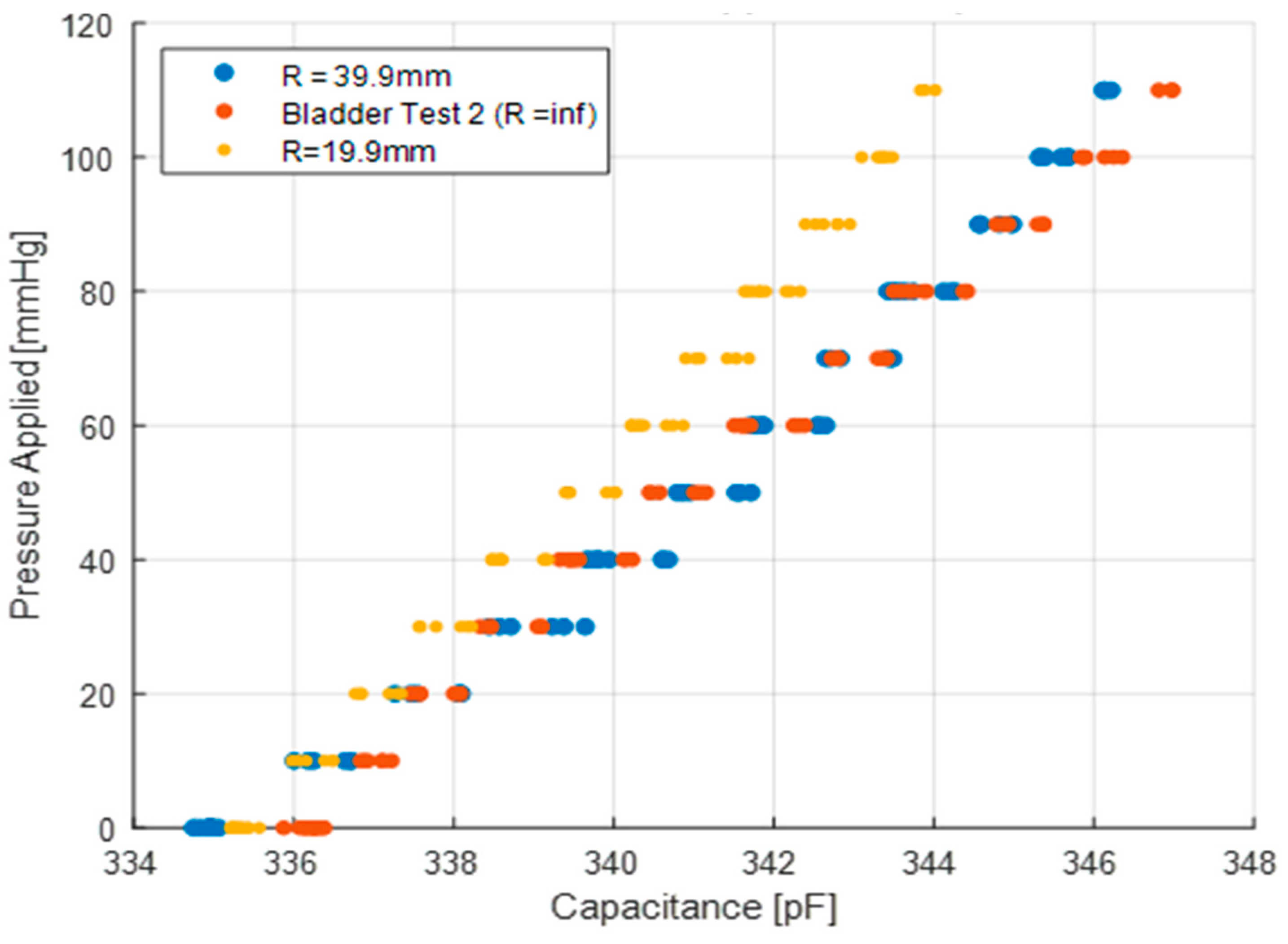
The fourth test (
Figure 5d) is used to determine the change in behaviour due to the curvature of the sensor. The curvature is expected to change the response of the sensor since it deforms when it conforms to a curved surface and, therefore, the capacitance changes. In the curvature test, the sensor is placed inside pipes of 19.9 mm and 39.9 mm radii, and a balloon is inserted and inflated to apply pressure in the range of 0 to 110 mmHg. The static pressure of the balloon is compared to the sensor reading, similar to the bladder test. It is noted that the curvature in this test remains constant and one of the surfaces is rigid, which is not the actual use case. However, this configuration was selected to isolate the effect of sensor curvature.
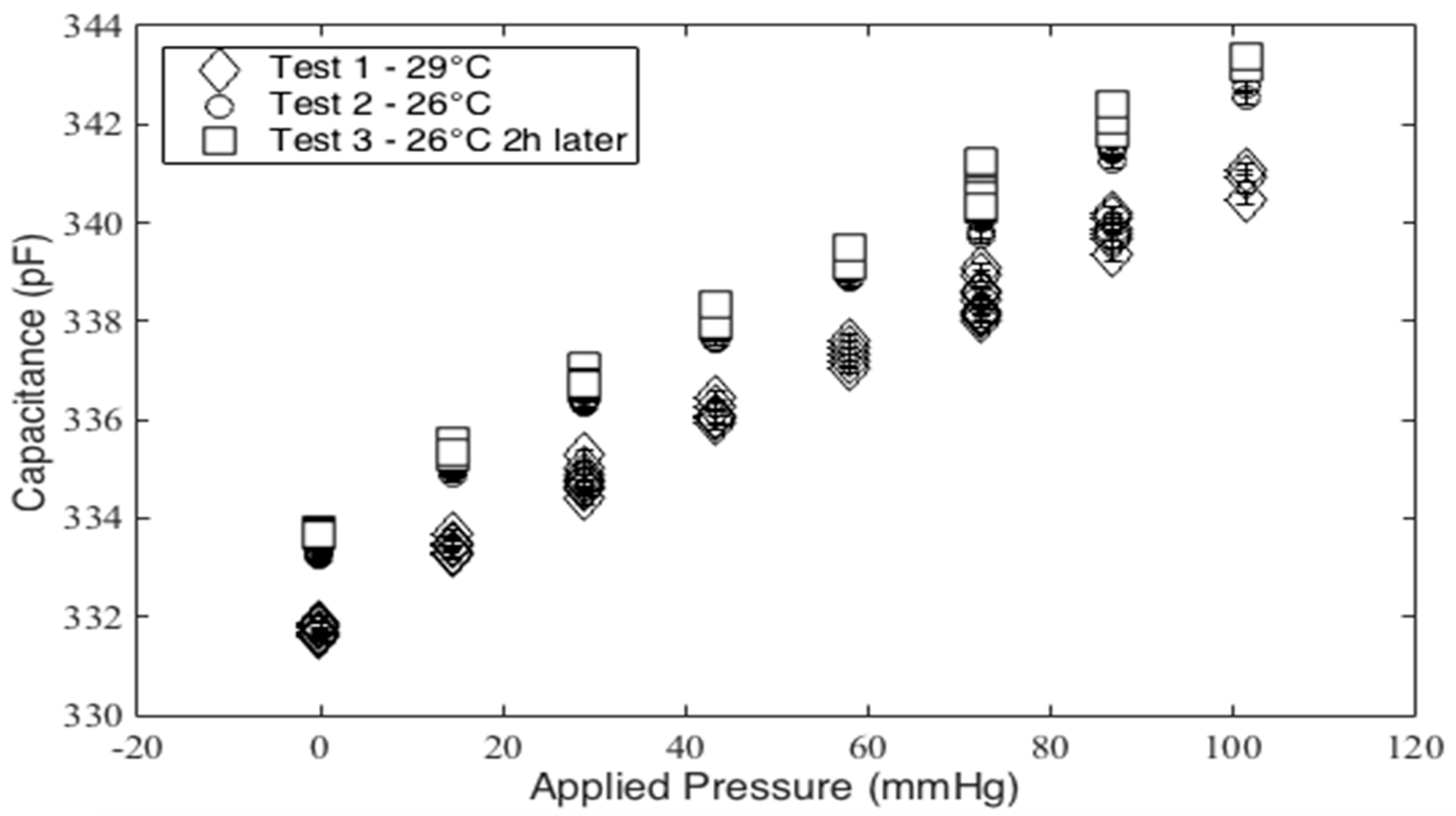
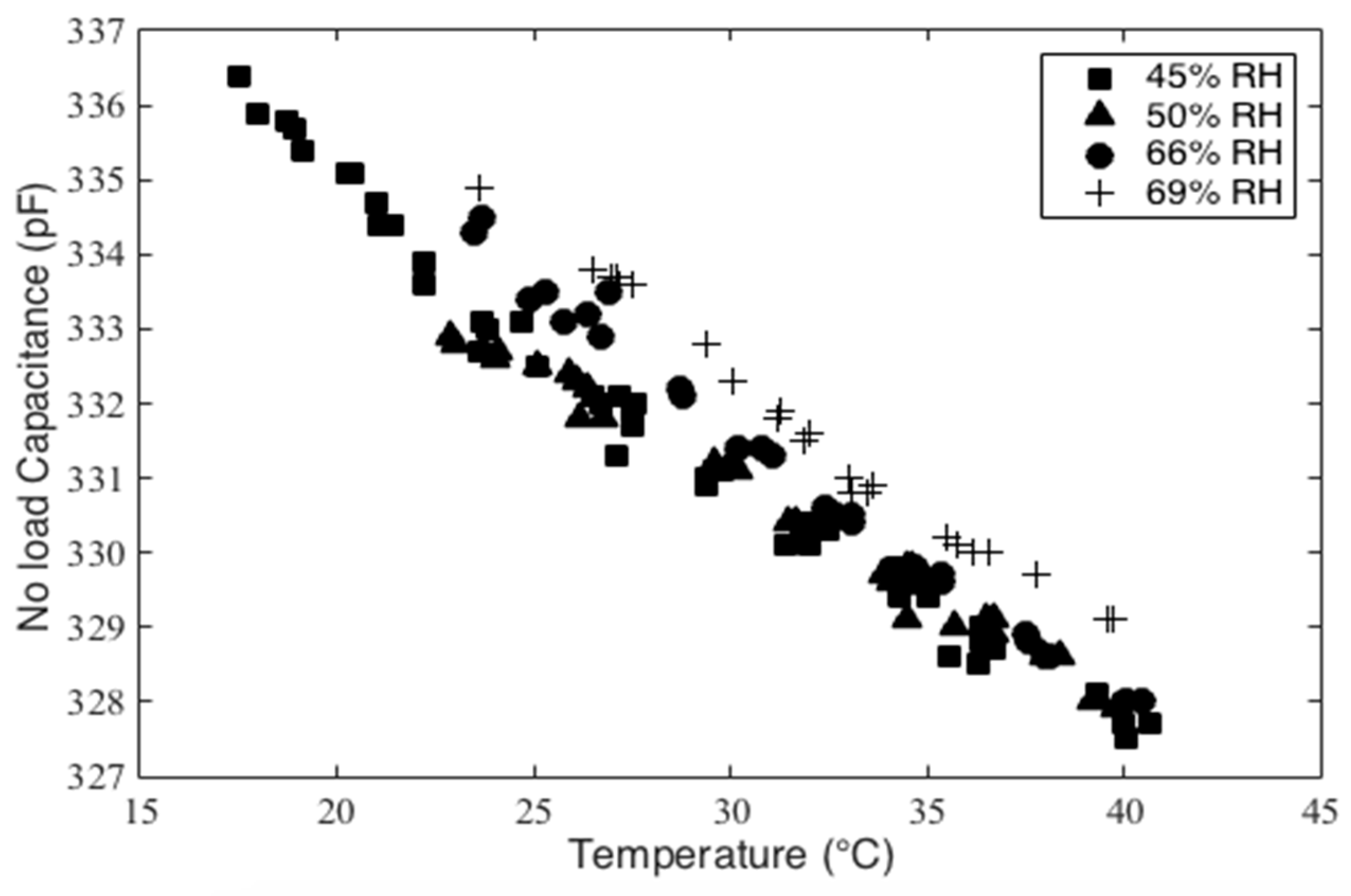
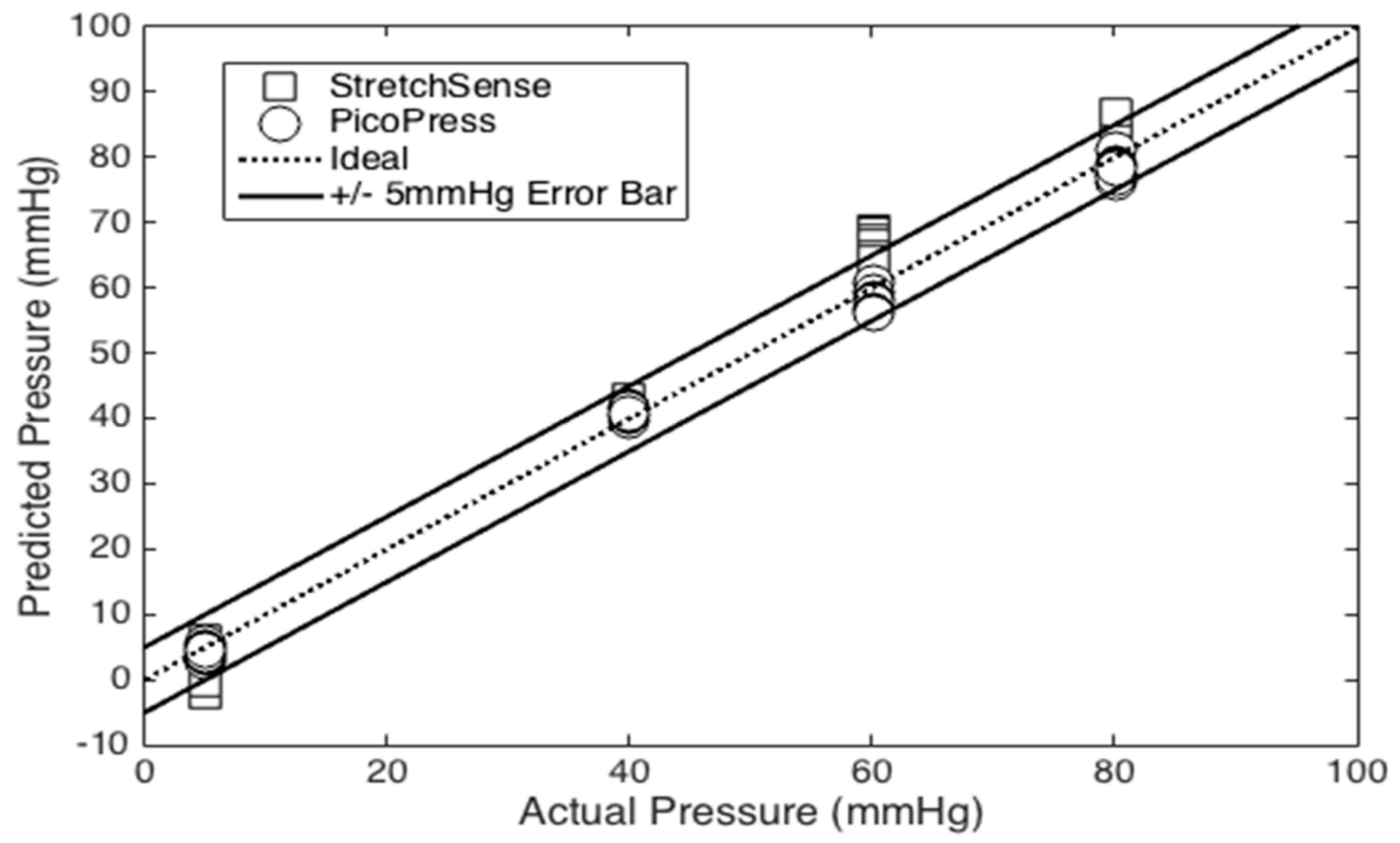
Finally, two additional testing configurations not shown in
Figure 5 are employed. First, the effect of temperature and humidity on the no-load capacitance of the sensor was examined. This is done by repeating the mass test at 26 °C and then comparing it to the data from the 29 °C mass test. In addition, the variance in capacitance of the sensor is observed for a range of 17 to 42 °C and 45 to 69 %RH. Second, a curvature test compares the response of the capacitive sensor to that of the PicoPress pneumatic sensor. This test involved a 3D printed cylinder with a radius of 60 mm to serve as a rigid dummy leg (see
Figure 7). The two sensors are placed on the cylinder with the StretchSense sensor against the cylinder and the PicoPress directly on top of it. Since the PicoPress sensor is considerably larger in size than the StretchSense sensor, the entirety of the StretchSense sensor contacts the PicoPress bladder. A sphygmomanometer is then wrapped around the cylinder and sensors to apply a known pressure. The pressure in the sphygmomanometer is manually controlled with the hand pump. The test involves a series of 10 inflations and deflations of the sphygmomanometer at three different pressures. The applied pressures are 40 mmHg, 60 mmHg, and 80 mmHg, respectively. During deflation, a minimum pressure of 5 mmHg is kept in the sphygmomanometer to prevent the cuff from moving and/or slipping. In this test, the sensor responses were both compared to the sphygmomanometer pressure and each sensor error were calculated.