Fiber Taper-Based Mach–Zehnder Interferometer for Ethanol Concentration Measurement
Abstract
:1. Introduction
2. Methods
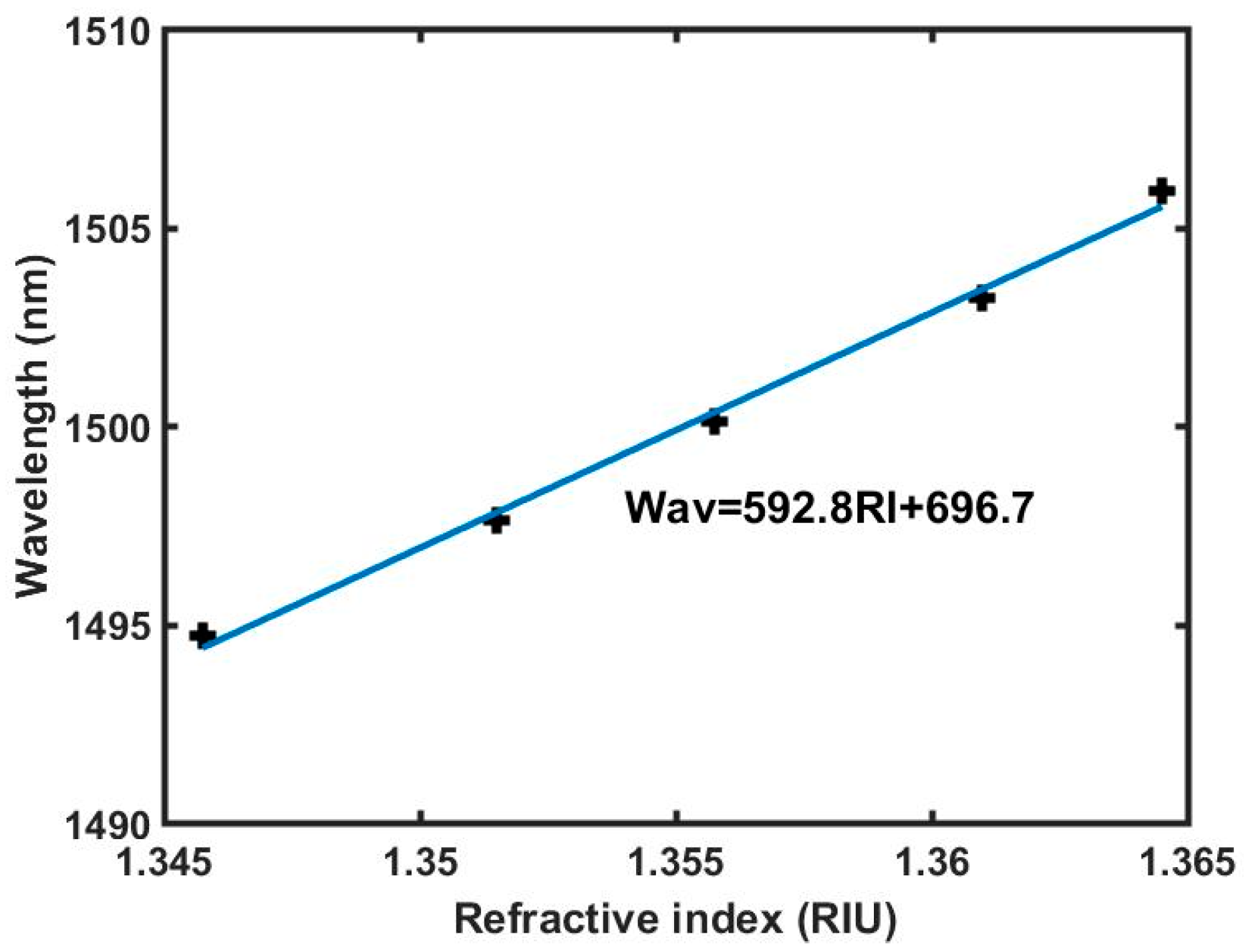
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhou, Y.; Zhou, W.; Chan, C.C.; Wong, W.C.; Shao, L.; Cheng, J.; Dong, X. Simultaneous measurement of curvature and temperature based on pcf-based interferometer and fiber bragg grating. Opt. Commun. 2011, 284, 5669–5672. [Google Scholar] [CrossRef]
- Deng, M.; Tang, C.; Zhu, T.; Rao, Y.-J. Highly sensitive bend sensor based on mach–zehnder interferometer using photonic crystal fiber. Opt. Commun. 2011, 284, 2849–2853. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, J.; Weng, Y.; Rong, Q.; Ma, Y.; Feng, Z.; Hu, M.; Qiao, X. Highly sensitive curvature sensor using an in-fiber mach–zehnder interferometer. IEEE Sens. J. 2013, 13, 1766–1770. [Google Scholar] [CrossRef]
- Frazão, O.; Viegas, J.; Caldas, P.; Santos, J.L.; Araújo, F.M.; Ferreira, L.A.; Farahi, F. All-fiber mach-zehnder curvature sensor based on multimode interference combined with a long-period grating. Opt. Lett. 2007, 32, 3074–3076. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, L.; Wang, S.; Li, B.; Wang, M.; Xiao, H.; Tsai, H. High sensitivity of taper-based mach–zehnder interferometer embedded in a thinned optical fiber for refractive index sensing. Appl. Opt. 2011, 50, 5502–5507. [Google Scholar] [CrossRef]
- Dass, S.; Jha, R. Micrometer wire assisted inline mach–zehnder interferometric curvature sensor. IEEE Photonics Technol. Lett. 2016, 28, 31–34. [Google Scholar] [CrossRef]
- Li, Z.; Liao, C.; Wang, Y.; Dong, X.; Liu, S.; Yang, K.; Wang, Q.; Zhou, J. Ultrasensitive refractive index sensor based on a mach-zehnder interferometer created in twin-core fiber. Opt. Lett. 2014, 39, 4982–4985. [Google Scholar] [CrossRef]
- Liao, C.; Wang, D.N.; Wang, Y. Microfiber in-line mach–zehnder interferometer for strain sensing. Opt. Lett. 2013, 38, 757–759. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, Y.G.; Wang, Z.; Han, T.; Li, S.; Jiang, M.; Ping, S.P.; Quyen, D.X. In-line mach-zehnder interferometer composed of microtaper and long-period grating in all-solid photonic bandgap fiber. Appl. Phys. Lett. 2012, 101, 141106. [Google Scholar] [CrossRef]
- Gong, H.; Wang, D.N.; Xiong, M.; Zhao, C.; Ni, K. Optical fiber hollow ellipsoid for directional bend sensing with a large bending range. Opt. Mater. Express 2017, 7, 1767–1776. [Google Scholar] [CrossRef]
- Xu, L.; Li, Y.; Li, B. Nonadiabatic fiber taper-based Mach-Zehnder interferometer for refractive index sensing. Appl. Phys. Lett. 2012, 101, 153510. [Google Scholar] [CrossRef]
- Li, Z.; Liao, C.; Chen, D.; Song, J.; Jin, W.; Peng, G.; Zhu, F.; Wang, Y.; He, J.; Wang, Y. label-free detection of bovine serum albumin based on an in-fiber mach-zehnder interferometric biosensor. Opt. Express 2017, 25, 17105–17113. [Google Scholar] [CrossRef]
- ShinnFwu, W.; RongSeng, C. D-type fiber biosensor based on surface-plasmon resonance technology and heterodyne interferometry. Opt. Lett. 2005, 30, 233–235. [Google Scholar]
- Liang, W.; Huang, Y.; Xu, Y.; Lee, R.K.; Yariv, A. Highly sensitive fiber bragg grating refractive index sensors. Appl. Phys. Lett. 2005, 86, 151122. [Google Scholar] [CrossRef]
- Morisawa, M.; Muto, S. Plastic optical fiber sensing of alcohol concentration in liquors. J. Sens. 2012, 2012, 1–5. [Google Scholar] [CrossRef]
- Dash, J.N.; Jha, R. Fabry–perot cavity on demand for hysteresis free interferometric sensors. J. Light. Technol. 2016, 34, 3188–3193. [Google Scholar] [CrossRef]
- Chen, H.F.; Wang, D.N.; Hong, W. Slightly tapered optical fiber with inner air-cavity as a miniature and versatile sensing device. J. Light. Technol. 2015, 33, 62–68. [Google Scholar] [CrossRef]
- Liao, C.R.; Hu, T.Y.; Wang, D.N. Optical fiber fabry-perot interferometer cavity fabricated by femtosecond laser micromachining and fusion splicing for refractive index sensing. Opt. Express 2012, 20, 22813–22818. [Google Scholar] [CrossRef]
- Zhou, A.; Qin, B.; Zhu, Z.; Zhang, Y.; Liu, Z.; Yang, J.; Yuan, L. Hybrid structured fiber-optic fabry-perot interferometer for simultaneous measurement of strain and temperature. Opt. Lett. 2014, 39, 5267–5270. [Google Scholar] [CrossRef]
- Liao, C.R.; Xu, L.; Wang, C.; Wang, D.N.; Wang, Y.; Wang, Q.; Yang, K.; Li, Z.; Zhong, X.; Zhou, J.; et al. Tunable phase-shifted fiber bragg grating based on femtosecond laser fabricated in-grating bubble. Opt. Lett. 2013, 38, 4473–4476. [Google Scholar] [CrossRef]
- Hu, T.Y.; Wang, Y.; Liao, C.; Wang, D.N. Miniaturized fiber in-line mach–zehnder interferometer based on inner air cavity for high-temperature sensing. Opt. Lett. 2012, 37, 5082–5084. [Google Scholar] [CrossRef] [PubMed]
- Chin, S.L.; Hosseini, S.A.; Liu, W.; Luo, Q.; Théberge, F.; Aközbek, N.; Becker, A.; Kandidov, V.P.; Kosareva, O.G.; Schroeder, H. The propagation of powerful femtosecond laser pulses in opticalmedia: Physics, applications, and new challenges. Can. J. Phys. 2005, 83, 863–905. [Google Scholar] [CrossRef]
- Wataru, W.; Kazuyoshi, I. Motion of bubble in solid by femtosecond laser pulses. Opt. Express 2002, 10, 603–608. [Google Scholar]
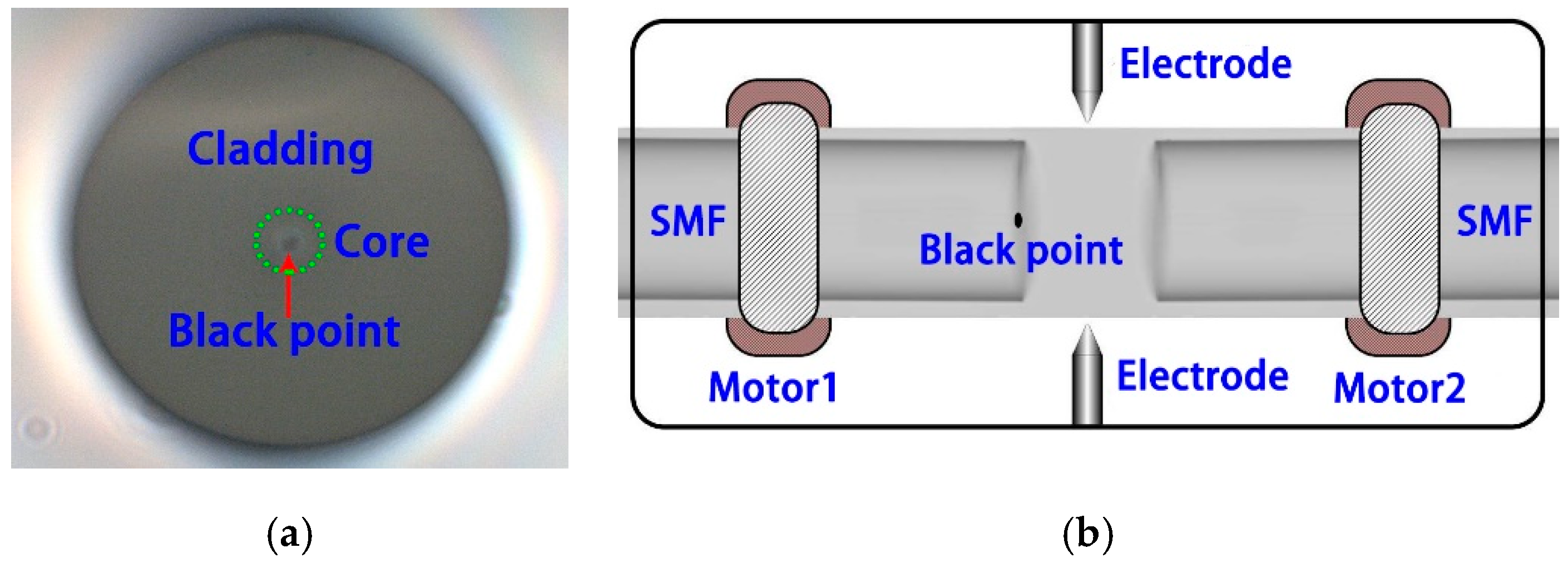

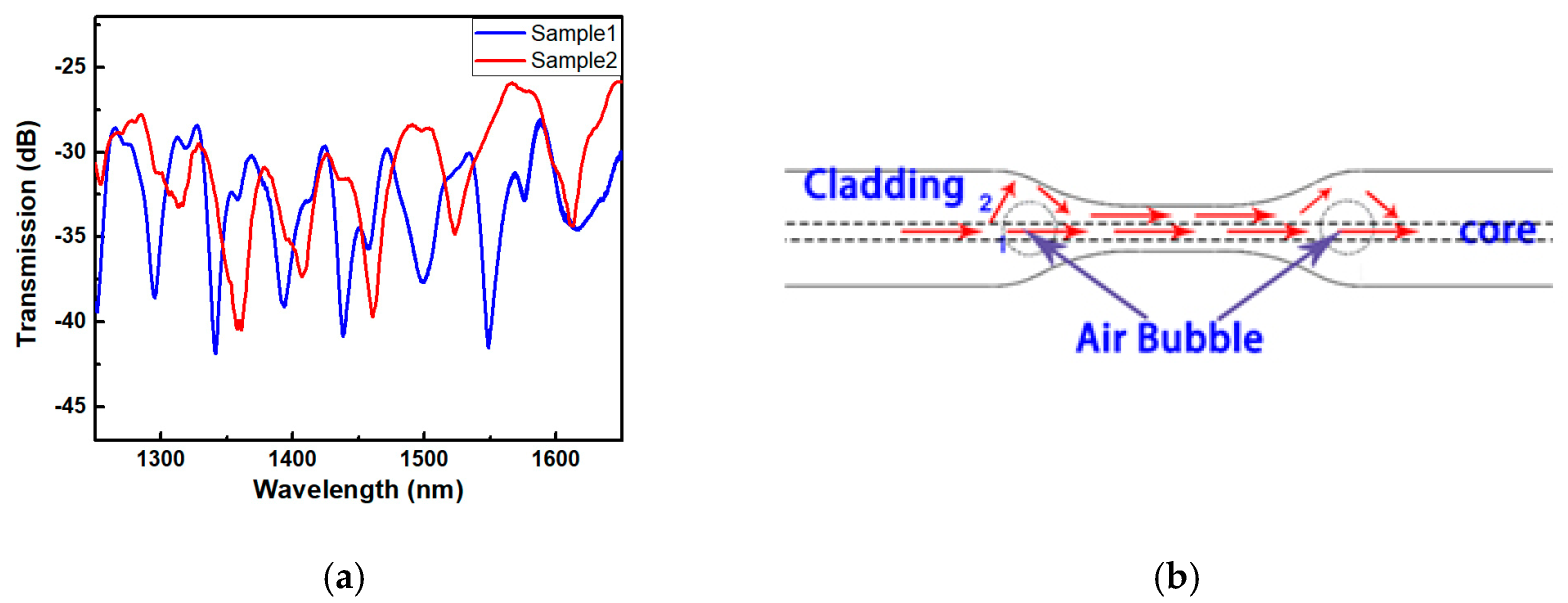
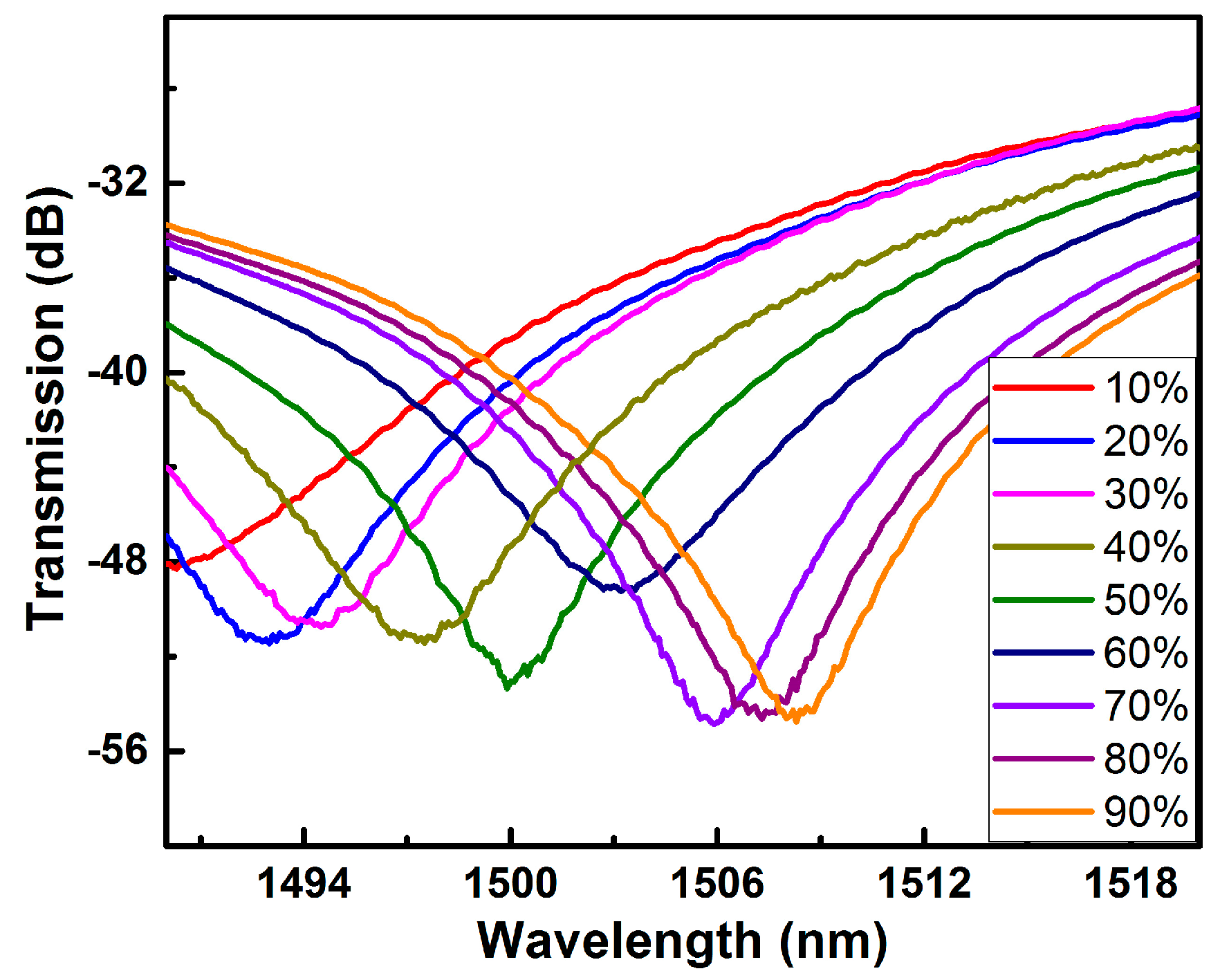
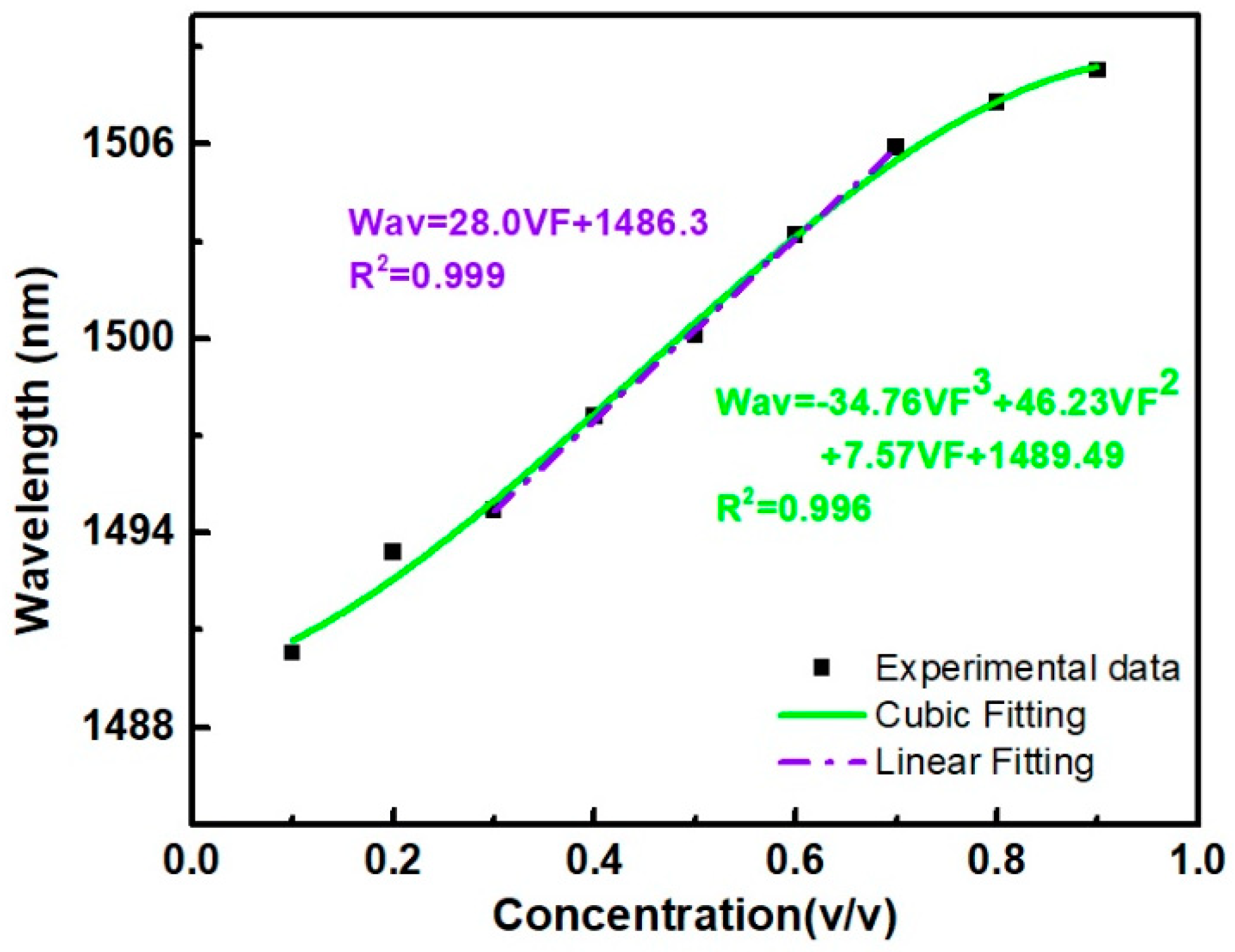
| Device Parameters | Sample 1 | Sample 2 |
|---|---|---|
| Taper length (μm) | 200 | 350 |
| Diameter of Bubble 1 (μm) | 69 | 41 |
| Diameter of Bubble 2 (μm) | 29 | 45 |
| Total bubble diameters (μm) | 98 | 86 |
| Concentration | RI1 | RI2 | RI3 | RI4 | Average RI |
|---|---|---|---|---|---|
| 30% | 1.3462 | 1.3457 | 1.3456 | 1.3455 | 1.3458 |
| 40% | 1.3515 | 1.3518 | 1.3514 | 1.3513 | 1.3515 |
| 50% | 1.3558 | 1.3559 | 1.3560 | 1.3555 | 1.3558 |
| 60% | 1.3608 | 1.3611 | 1.3611 | 1.3610 | 1.3610 |
| 70% | 1.3646 | 1.3645 | 1.3645 | 1.3644 | 1.3645 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, C.; Zhu, F.; Zhou, P.; Wang, Y. Fiber Taper-Based Mach–Zehnder Interferometer for Ethanol Concentration Measurement. Micromachines 2019, 10, 741. https://doi.org/10.3390/mi10110741
Liao C, Zhu F, Zhou P, Wang Y. Fiber Taper-Based Mach–Zehnder Interferometer for Ethanol Concentration Measurement. Micromachines. 2019; 10(11):741. https://doi.org/10.3390/mi10110741
Chicago/Turabian StyleLiao, Changrui, Feng Zhu, Peng Zhou, and Ying Wang. 2019. "Fiber Taper-Based Mach–Zehnder Interferometer for Ethanol Concentration Measurement" Micromachines 10, no. 11: 741. https://doi.org/10.3390/mi10110741
APA StyleLiao, C., Zhu, F., Zhou, P., & Wang, Y. (2019). Fiber Taper-Based Mach–Zehnder Interferometer for Ethanol Concentration Measurement. Micromachines, 10(11), 741. https://doi.org/10.3390/mi10110741





