Tele–Robotic Platform for Dexterous Optical Single-Cell Manipulation
Abstract
:1. Introduction
2. Materials and Methods
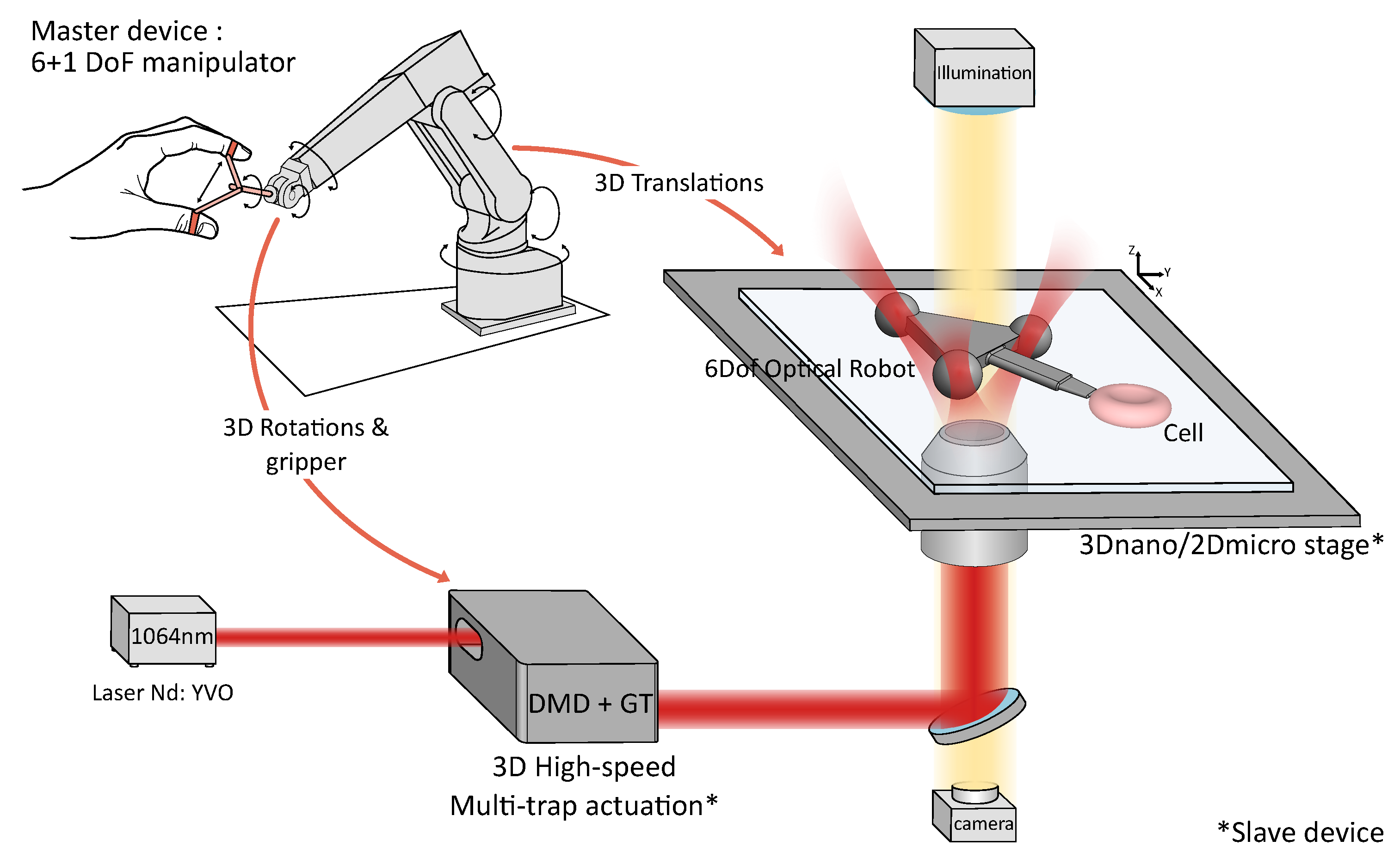
2.1. Teleoperation System Design
2.1.1. Optical System
2.1.2. Slave Robot: Robot-Assisted Stages and High-Speed 3D Multi-Trap Actuation
2.1.3. Master–Slave Coupling
- Position Control: This first mode mirrors the master device’s position and orientation to the slave robot, with an appropriate scaling factor. This factor can be chosen according to the task’s dimensions and the operator’s comfort. This method is suitable to execute precise tasks.
- Velocity Control: This second mode enables control of the slave robot’s velocity. The motion’s direction and amplitude are computed according to the vector made by the center of the master device’s workspace and the position of the handle. A scaling factor can also be chosen according to the task’s requirements. A maximal handling velocity is also defined according to the number of traps, in order to assist the user and help the trapped objects’ retention. The velocity control mode can be enabled independently for translations and rotations, and is suitable for long displacements like sample chamber exploration or for continuous rotation of an object like micro-pump [27] or cell rotation for tomographic imaging [28].
2.2. Evaluation of Teleoperation Performances
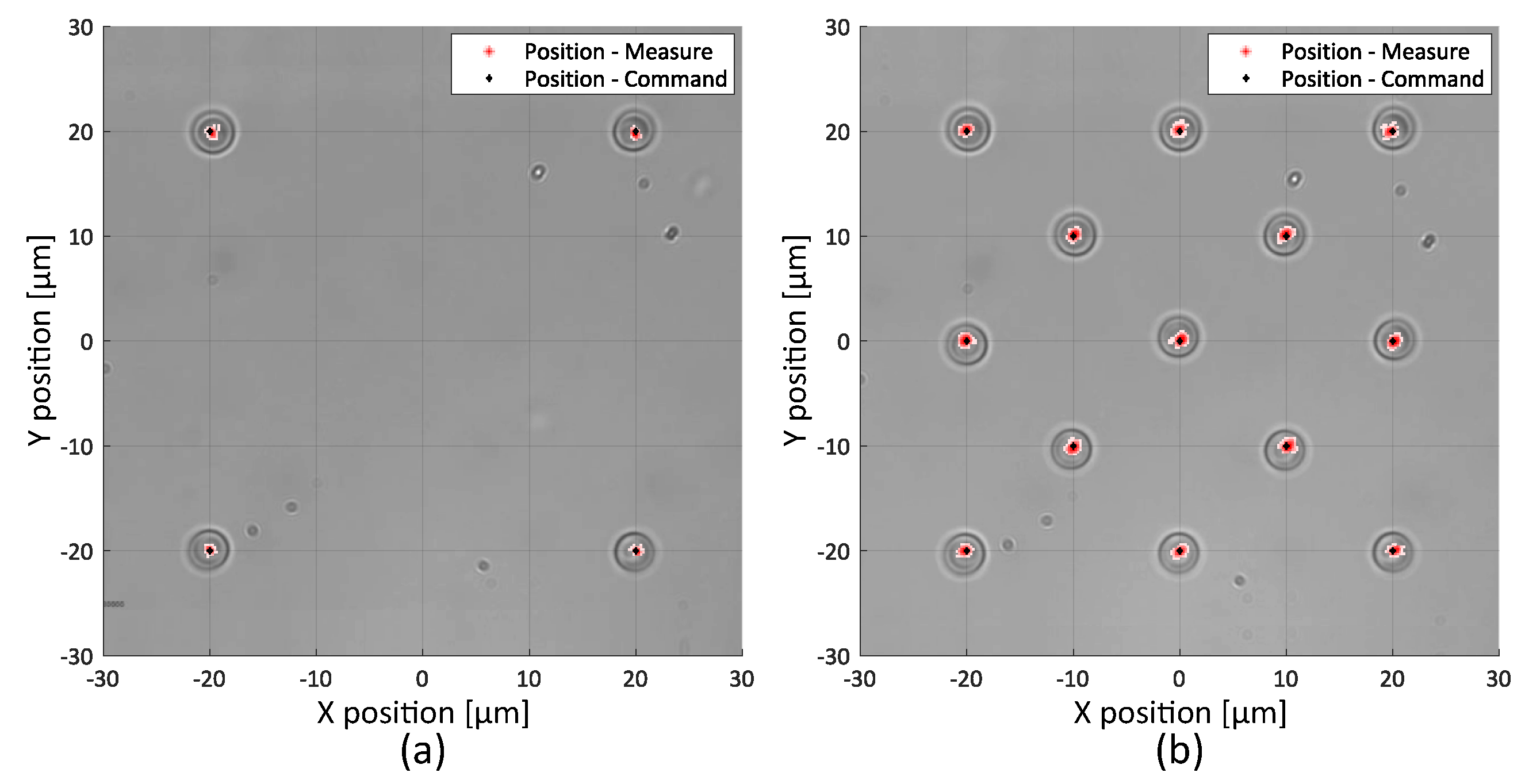
2.2.1. Static Precision
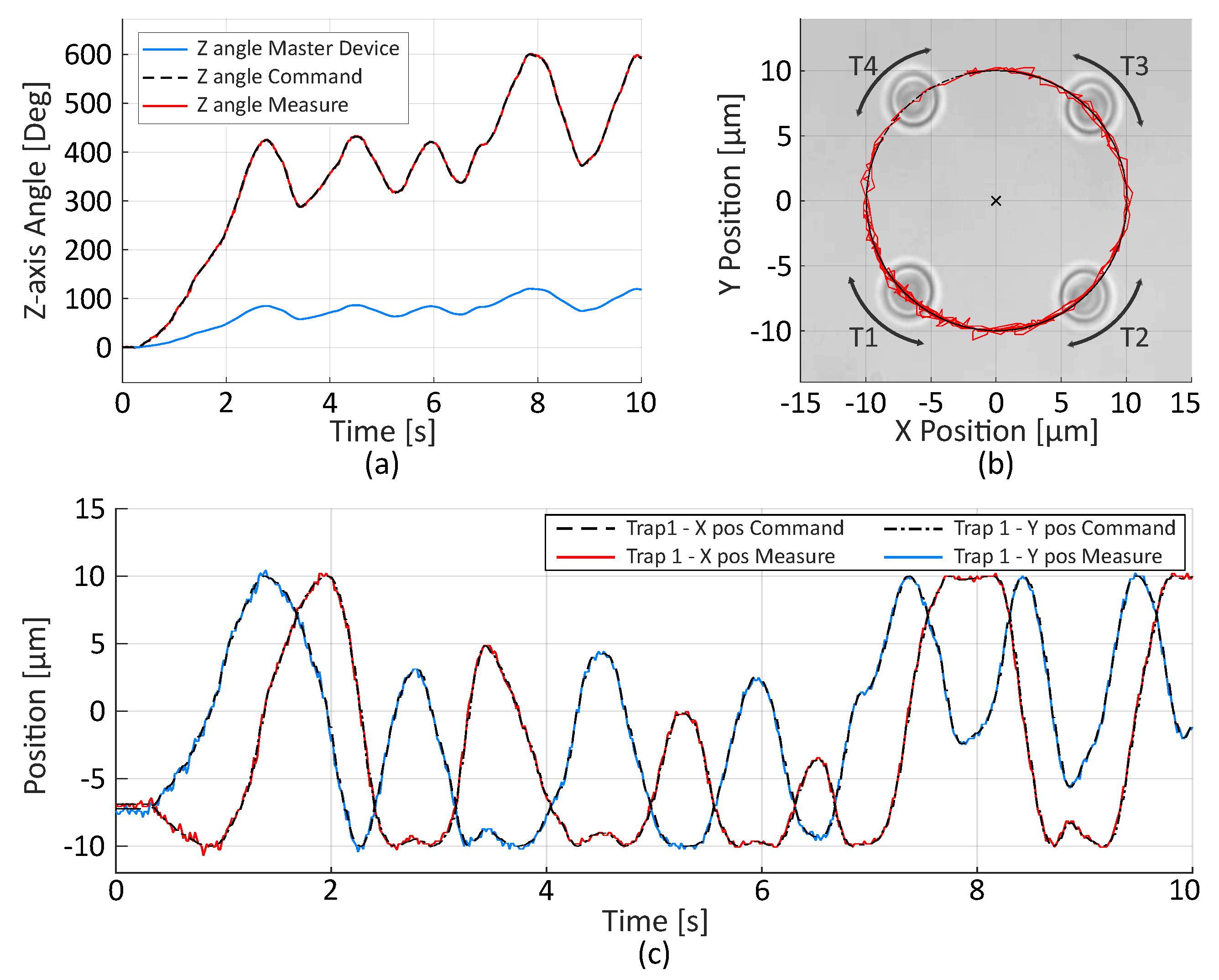
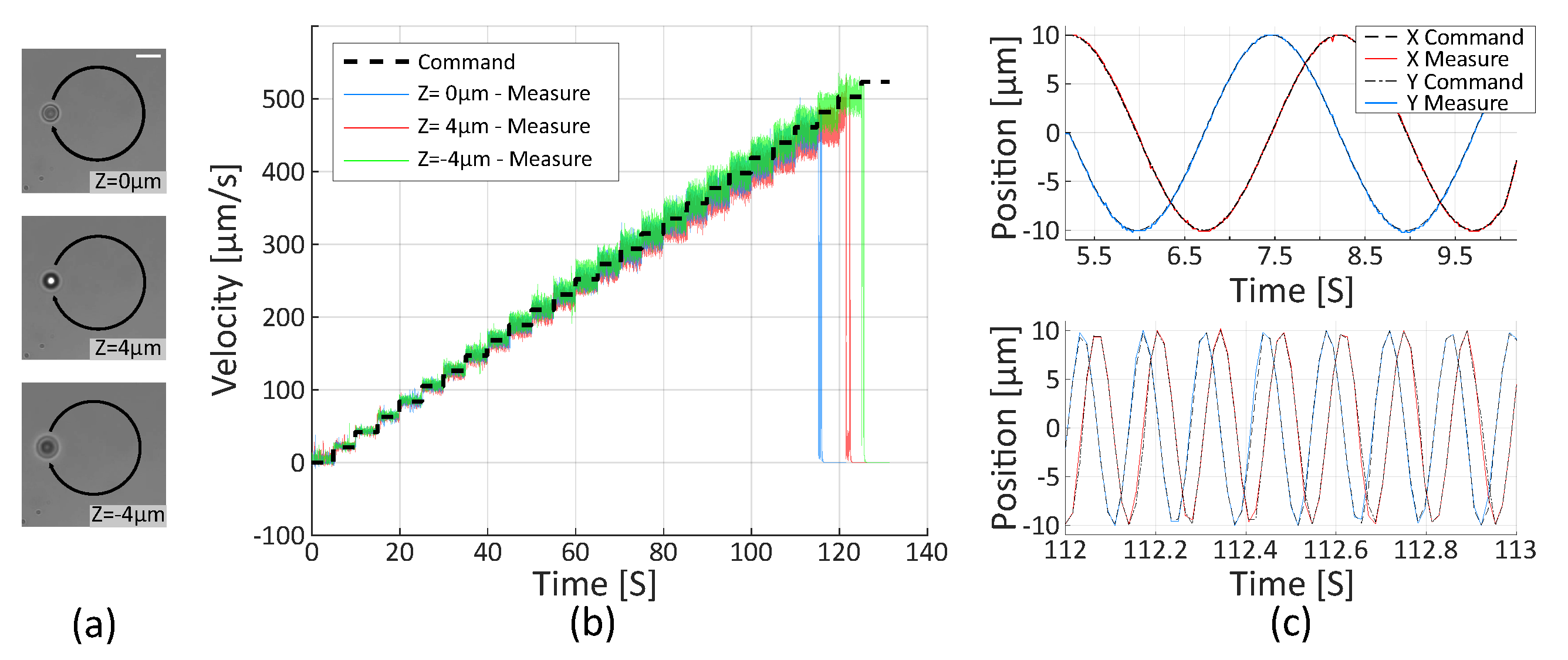
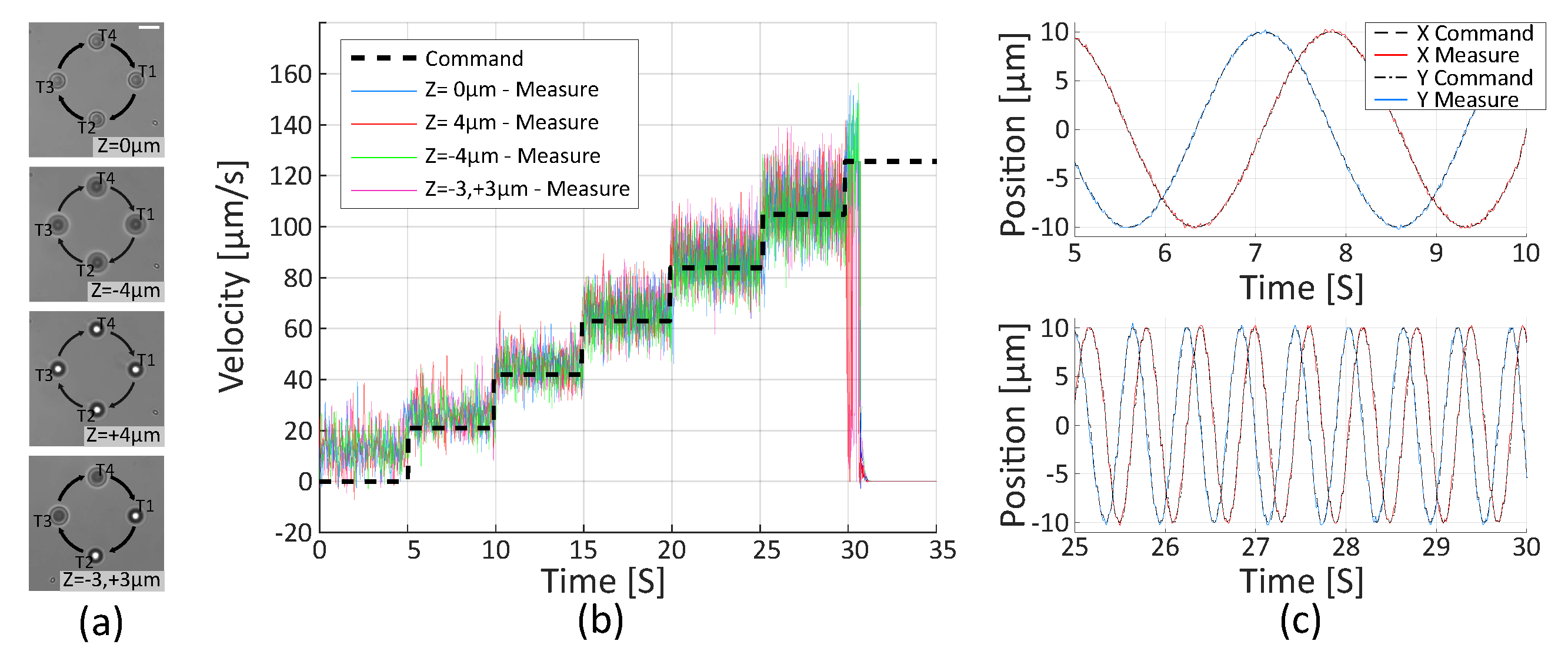
2.2.2. Trajectory Control
2.2.3. Velocity Limitation
3. Results and Discussion
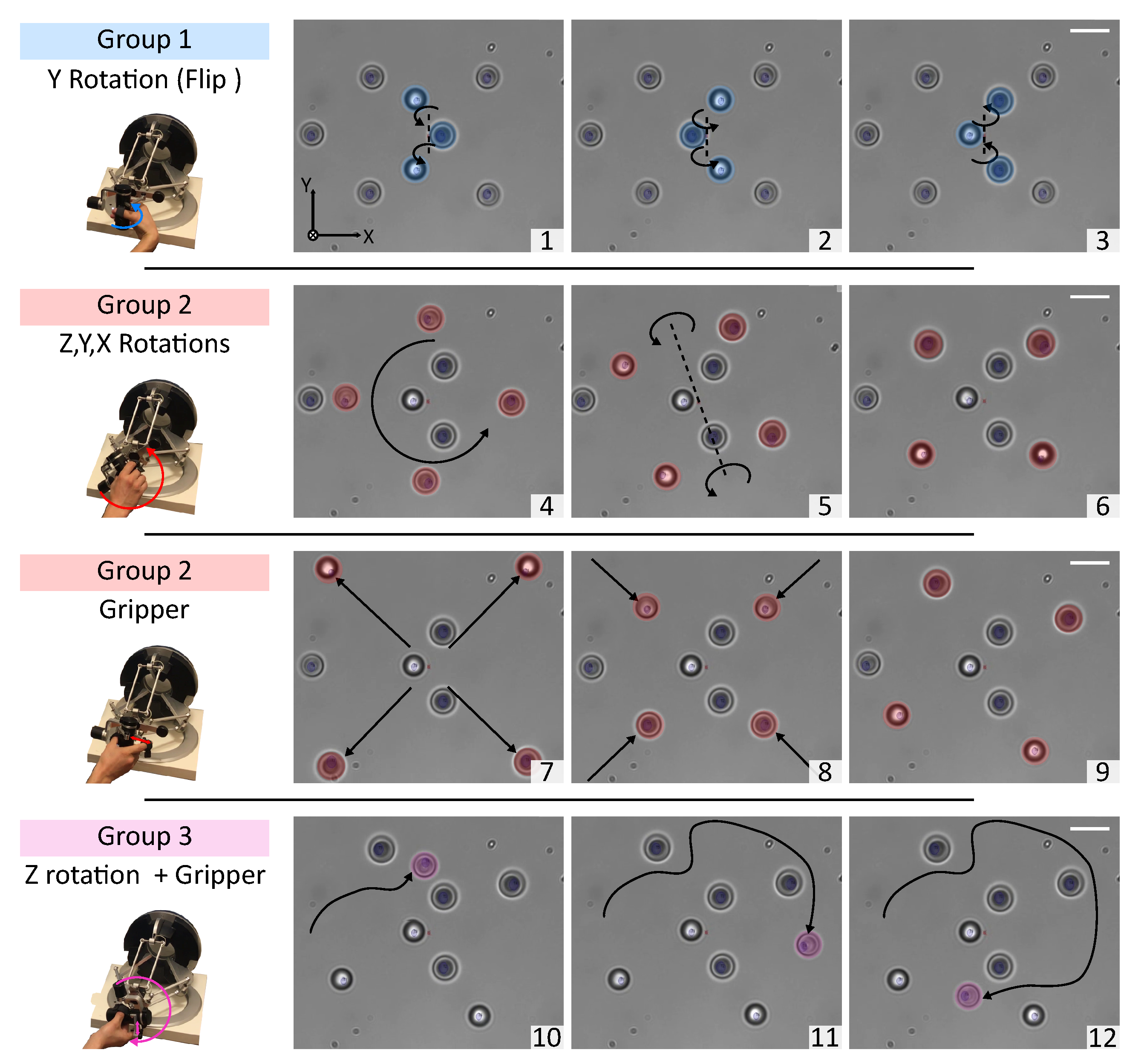
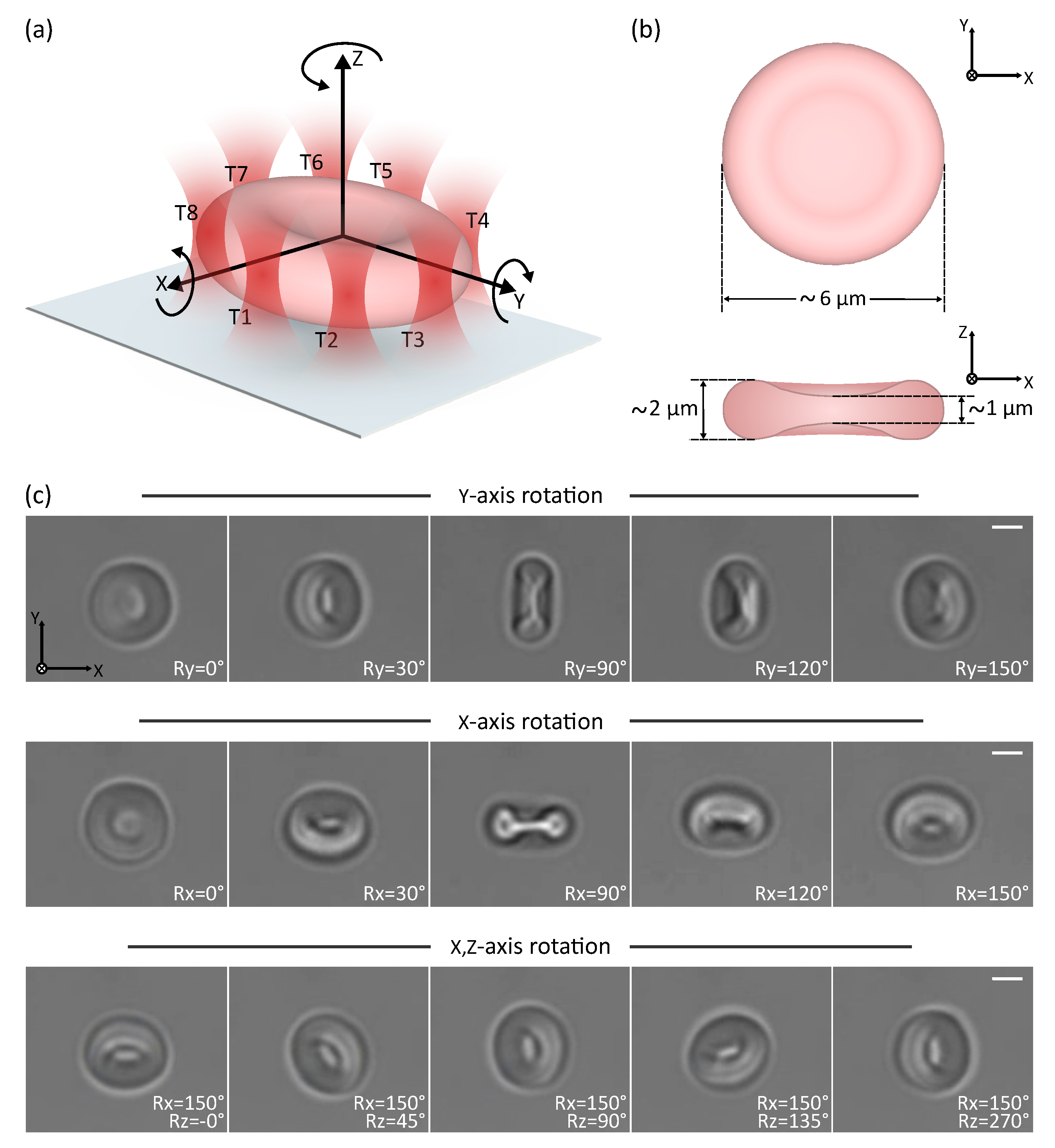
3.1. Direct Manipulation: 3D Rotation of a Cell
3.2. Indirect Manipulation: Six-DoF Teleoperated Optical Robot for Cell Manipulation
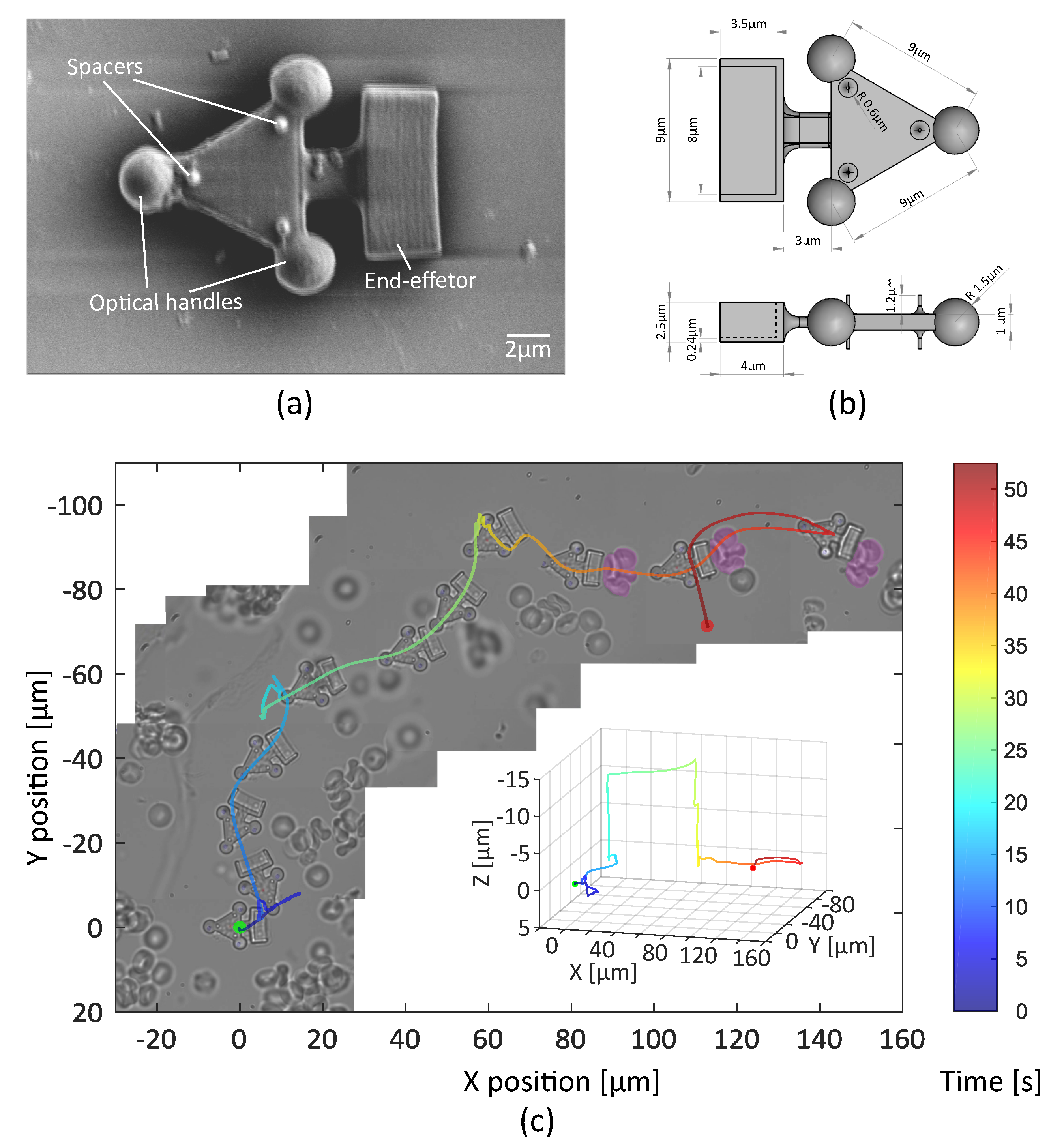
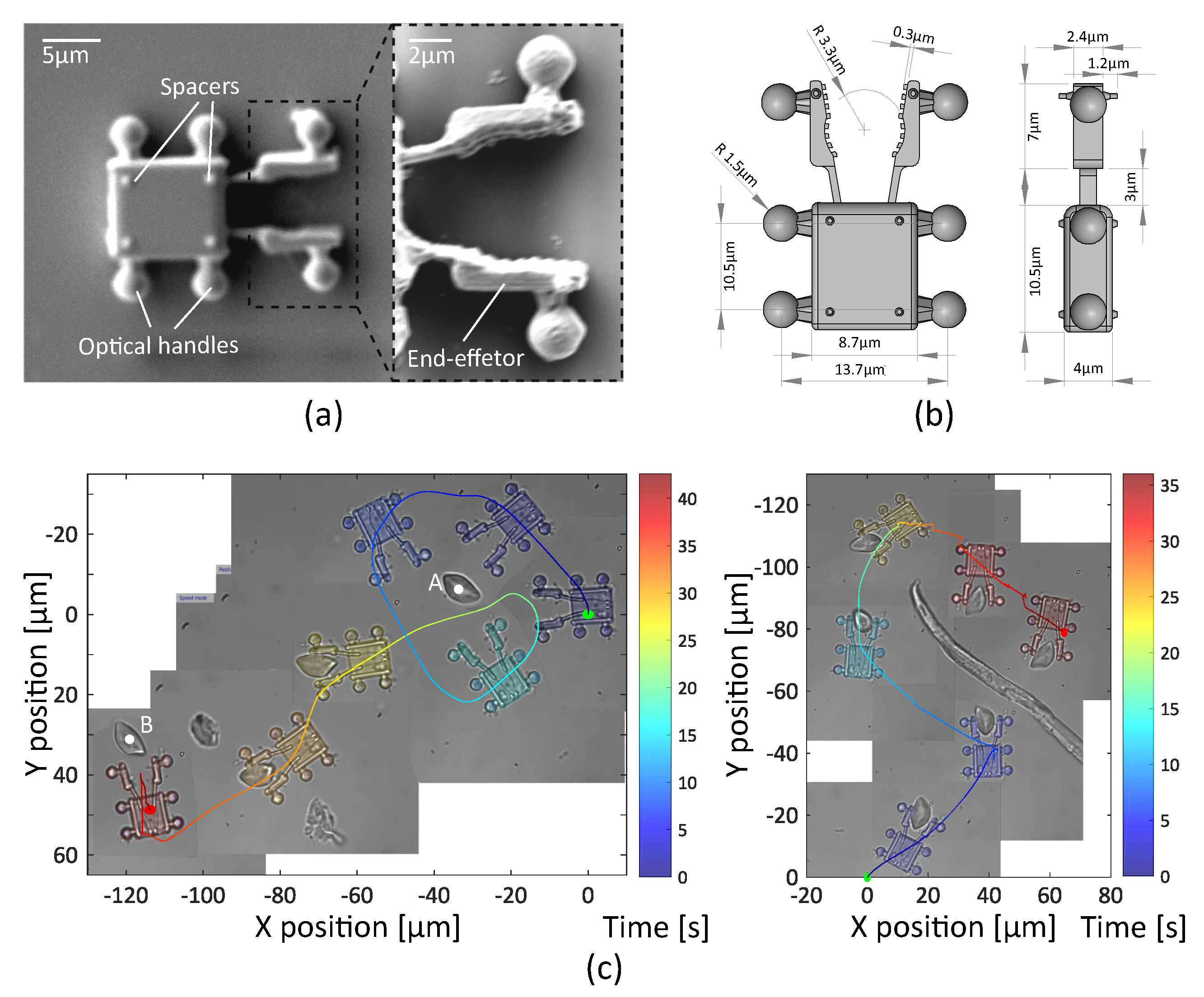
3.2.1. Fabrication and Collection of the Robots
3.2.2. Teleoperated Optical Robot for Cells Transportation
3.2.3. Teleoperated Optical Robot for Dexterous Single-Cell Manipulation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, J.; de Ávila, B.E.F.; Gao, W.; Zhang, L.; Wang, J. Micro/nanorobots for biomedicine: Delivery, surgery, sensing, and detoxification. Sci. Robot. 2017, 2. [Google Scholar] [CrossRef] [PubMed]
- Medina-Sánchez, M.; Magdanz, V.; Guix, M.; Fomin, V.M.; Schmidt, O.G. Swimming microrobots: Soft, reconfigurable, and smart. Adv. Funct. Mater. 2018, 28, 1707228. [Google Scholar] [CrossRef]
- Ceylan, H.; Giltinan, J.; Kozielski, K.; Sitti, M. Mobile microrobots for bioengineering applications. Lab Chip 2017, 17, 1705–1724. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashkin, A.; Dziedzic, J.; Yamane, T. Optical trapping and manipulation of single cells using infrared laser beams. Nature 1987, 330, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, A.; Chowdhury, S.; Gupta, S.K. Optical tweezers: Autonomous robots for the manipulation of biological cells. IEEE Robot. Autom. Mag. 2014, 21, 81–88. [Google Scholar] [CrossRef]
- Curtis, J.E.; Koss, B.A.; Grier, D.G. Dynamic holographic optical tweezers. Opt. Commun. 2002, 207, 169–175. [Google Scholar] [CrossRef]
- Gerena, E.; Regnier, S.; Haliyo, D.S. High-bandwidth 3D Multi-Trap Actuation Technique for 6-DoF Real-Time Control of Optical Robots. IEEE Robot. Autom. Lett. 2019, 4, 647–654. [Google Scholar] [CrossRef]
- Maruyama, H.; Fukuda, T.; Arai, F. Functional gel-microbead manipulated by optical tweezers for local environment measurement in microchip. Microfluid. Nanofluid. 2009, 6, 383. [Google Scholar] [CrossRef]
- Fukada, S.; Onda, K.; Maruyama, H.; Masuda, T.; Arai, F. 3D fabrication and manipulation of hybrid nanorobots by laser. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 2594–2599. [Google Scholar]
- Hayakawa, T.; Fukada, S.; Arai, F. Fabrication of an on-chip nanorobot integrating functional nanomaterials for single-cell punctures. IEEE Trans. Robot. 2014, 30, 59–67. [Google Scholar] [CrossRef]
- Villangca, M.J.; Palima, D.; Bañas, A.R.; Glückstad, J. Light-driven micro-tool equipped with a syringe function. Light Sci. Appl. 2016, 5, e16148. [Google Scholar] [CrossRef]
- Xie, M.; Shakoor, A.; Shen, Y.; Mills, J.K.; Sun, D. Out-of-plane rotation control of biological cells with a robot-tweezers manipulation system for orientation-based cell surgery. IEEE Trans. Biomed. Eng. 2018, 66, 199–207. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Xie, H.; Wei, T.; Chen, S.; Sun, D. Automated Indirect Transportation of Biological Cells with Optical Tweezers and a 3D Printed Microtool. Appl. Sci. 2019, 9, 2883. [Google Scholar] [CrossRef]
- Gibson, G.; Barron, L.; Beck, F.; Whyte, G.; Padgett, M. Optically controlled grippers for manipulating micron-sized particles. New J. Phys. 2007, 9, 14. [Google Scholar] [CrossRef]
- McDonald, C.; McPherson, M.; McDougall, C.; McGloin, D. HoloHands: Games console interface for controlling holographic optical manipulation. J. Opt. 2013, 15, 035708. [Google Scholar] [CrossRef]
- Muhiddin, C.; Phillips, D.; Miles, M.; Picco, L.; Carberry, D. Kinect 4: Holographic optical tweezers. J. Opt. 2013, 15, 075302. [Google Scholar] [CrossRef]
- Shaw, L.; Preece, D.; Rubinsztein-Dunlop, H. Kinect the dots: 3D control of optical tweezers. J. Opt. 2013, 15, 075303. [Google Scholar] [CrossRef]
- Bowman, R.; Gibson, G.; Carberry, D.; Picco, L.; Miles, M.; Padgett, M. iTweezers: Optical micromanipulation controlled by an Apple iPad. J. Opt. 2011, 13, 044002. [Google Scholar] [CrossRef]
- Onda, K.; Arai, F. Parallel teleoperation of holographic optical tweezers using multi-touch user interface. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 1069–1074. [Google Scholar]
- Onda, K.; Arai, F. Robotic approach to multi-beam optical tweezers with computer generated hologram. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1825–1830. [Google Scholar]
- Pacoret, C.; Régnier, S. Invited article: A review of haptic optical tweezers for an interactive microworld exploration. Rev. Sci. Instrum. 2013, 84, 081301. [Google Scholar] [CrossRef] [PubMed]
- Yin, M.; Gerena, E.; Pacoret, C.; Haliyo, S.; Régnier, S. High-bandwidth 3D force feedback optical tweezers for interactive bio-manipulation. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1889–1894. [Google Scholar]
- Tomori, Z.; Keša, P.; Nikorovič, M.; Kaňka, J.; Jákl, P.; Šerỳ, M.; Bernatová, S.; Valušová, E.; Antalík, M.; Zemánek, P. Holographic Raman tweezers controlled by multi-modal natural user interface. J. Opt. 2015, 18, 015602. [Google Scholar] [CrossRef]
- Grammatikopoulou, M.; Yang, G.Z. Gaze contingent control for optical micromanipulation. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5989–5995. [Google Scholar]
- Gerena, E.; Legendre, F.; Régnier, S.; Haliyo, S. Robotic optical-micromanipulation platform for teleoperated single-cell manipulation. In Proceedings of the MARSS 2019–International Conference on Manipulation Automation and Robotics at Small Scales, Helsinki, Finland, 1 July–5 July 2019; p. 60. [Google Scholar]
- Neuman, K.C.; Block, S.M. Optical trapping. Rev. Sci. Instrum. 2004, 75, 2787–2809. [Google Scholar] [CrossRef]
- Maruo, S.; Inoue, H. Optically driven micropump produced by three-dimensional two-photon microfabrication. Appl. Phys. Lett. 2006, 89, 144101. [Google Scholar] [CrossRef]
- Vinoth, B.; Lai, X.J.; Lin, Y.C.; Tu, H.Y.; Cheng, C.J. Integrated dual-tomography for refractive index analysis of free-floating single living cell with isotropic superresolution. Sci. Rep. 2018, 8, 5943. [Google Scholar]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Visscher, K.; Gross, S.P.; Block, S.M. Construction of multiple-beam optical traps with nanometer-resolution position sensing. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 1066–1076. [Google Scholar] [CrossRef] [Green Version]
- Cao, B.; Kelbauskas, L.; Chan, S.; Shetty, R.M.; Smith, D.; Meldrum, D.R. Rotation of single live mammalian cells using dynamic holographic optical tweezers. Opt. Lasers Eng. 2017, 92, 70–75. [Google Scholar]
- Lin, Y.c.; Chen, H.C.; Tu, H.Y.; Liu, C.Y.; Cheng, C.J. Optically driven full-angle sample rotation for tomographic imaging in digital holographic microscopy. Opt. Lett. 2017, 42, 1321–1324. [Google Scholar] [CrossRef]
- Kim, K.; Park, Y. Tomographic active optical trapping of arbitrarily shaped objects by exploiting 3D refractive index maps. Nat. Commun. 2017, 8, 15340. [Google Scholar] [CrossRef]
- Rasmussen, M.B.; Oddershede, L.B.; Siegumfeldt, H. Optical tweezers cause physiological damage to Escherichia coli and Listeria bacteria. Appl. Environ. Microbiol. 2008, 74, 2441–2446. [Google Scholar] [CrossRef]
- Blázquez-Castro, A. Optical Tweezers: Phototoxicity and Thermal Stress in Cells and Biomolecules. Micromachines 2019, 10, 507. [Google Scholar] [CrossRef]
- Banerjee, A.G.; Chowdhury, S.; Gupta, S.K.; Losert, W. Survey on indirect optical manipulation of cells, nucleic acids, and motor proteins. J. Biomed. Opt. 2011, 16, 051302. [Google Scholar] [CrossRef]
- Aekbote, B.L.; Fekete, T.; Jacak, J.; Vizsnyiczai, G.; Ormos, P.; Kelemen, L. Surface-modified complex SU-8 microstructures for indirect optical manipulation of single cells. Biomed. Opt. Express 2016, 7, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Xie, M.; Shakoor, A.; Wu, C. Manipulation of biological cells using a robot-aided optical tweezers system. Micromachines 2018, 9, 245. [Google Scholar] [CrossRef] [PubMed]
- Shakoor, A.; Xie, M.; Luo, T.; Hou, J.; Shen, Y.; Mills, J.K.; Sun, D. Achieve automated organelle biopsy on small single cells using a cell surgery robotic system. IEEE Trans. Biomed. Eng. 2018. [Google Scholar] [CrossRef]
- Wong, C.Y.; Mills, J.K. Cell extraction automation in single cell surgery using the displacement method. Biomed. Microdevices 2019, 21, 52. [Google Scholar] [CrossRef] [PubMed]
- Köhler, J.; Ksouri, S.I.; Esen, C.; Ostendorf, A. Optical screw-wrench for microassembly. Microsyst. Nanoeng. 2017, 3, 16083. [Google Scholar] [CrossRef] [PubMed]
| Parameter | Value |
|---|---|
| Teleoperation loop | 200 Hz |
| Simultaneous optical traps | >15 |
| Translation range | 200 × 200 × 200 |
| Rotation range | 70 × 50 × 9 |
| Trans Max velocity (1T,4T) * | 1500, 110 ** |
| Rot Max velocity (1T,4T) * | 462, 105 ** |
| Static error (1T,4T) * | <200 nm, 400 nm ** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerena, E.; Legendre, F.; Molawade, A.; Vitry, Y.; Régnier, S.; Haliyo, S. Tele–Robotic Platform for Dexterous Optical Single-Cell Manipulation. Micromachines 2019, 10, 677. https://doi.org/10.3390/mi10100677
Gerena E, Legendre F, Molawade A, Vitry Y, Régnier S, Haliyo S. Tele–Robotic Platform for Dexterous Optical Single-Cell Manipulation. Micromachines. 2019; 10(10):677. https://doi.org/10.3390/mi10100677
Chicago/Turabian StyleGerena, Edison, Florent Legendre, Akshay Molawade, Youen Vitry, Stéphane Régnier, and Sinan Haliyo. 2019. "Tele–Robotic Platform for Dexterous Optical Single-Cell Manipulation" Micromachines 10, no. 10: 677. https://doi.org/10.3390/mi10100677





