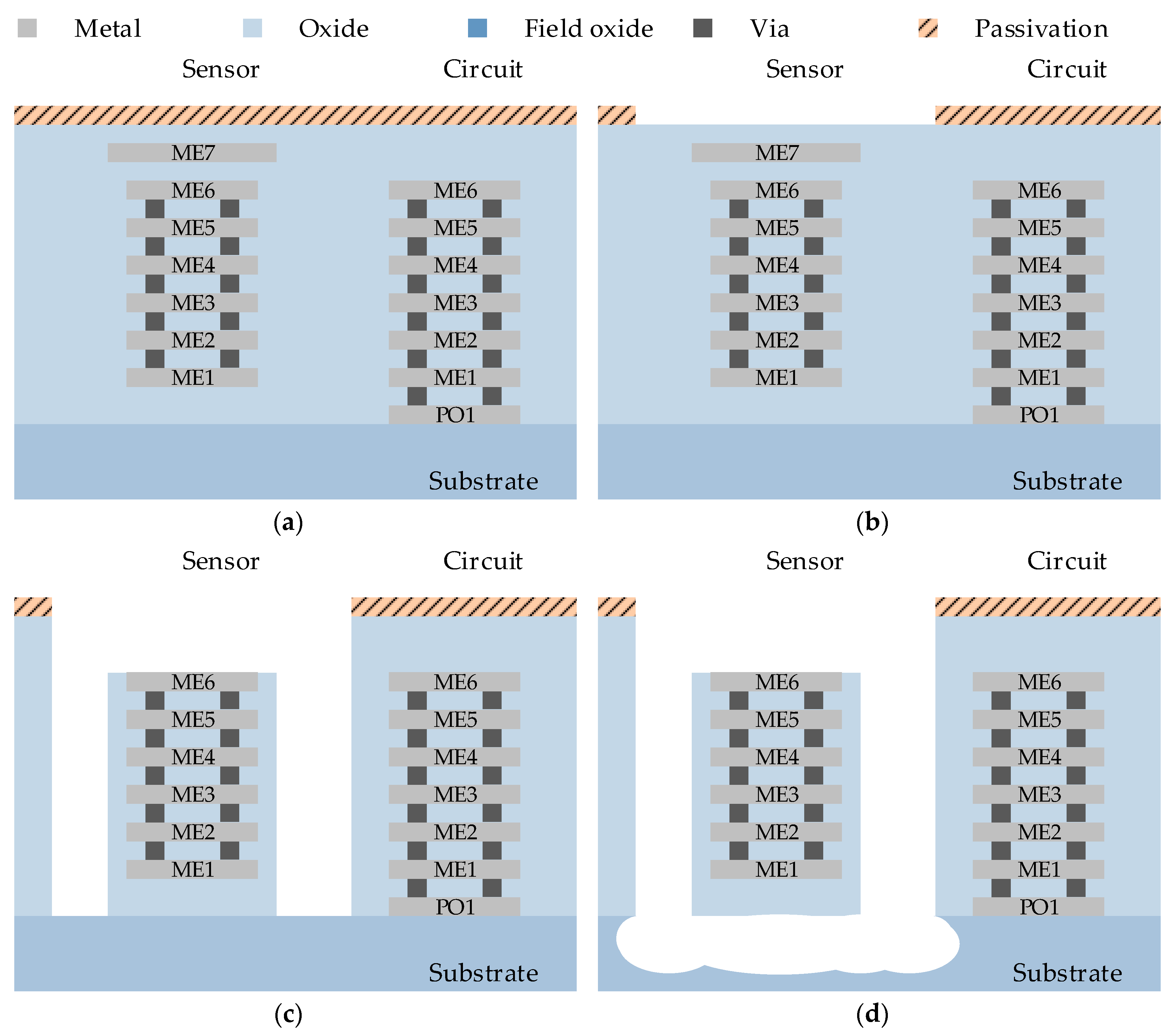
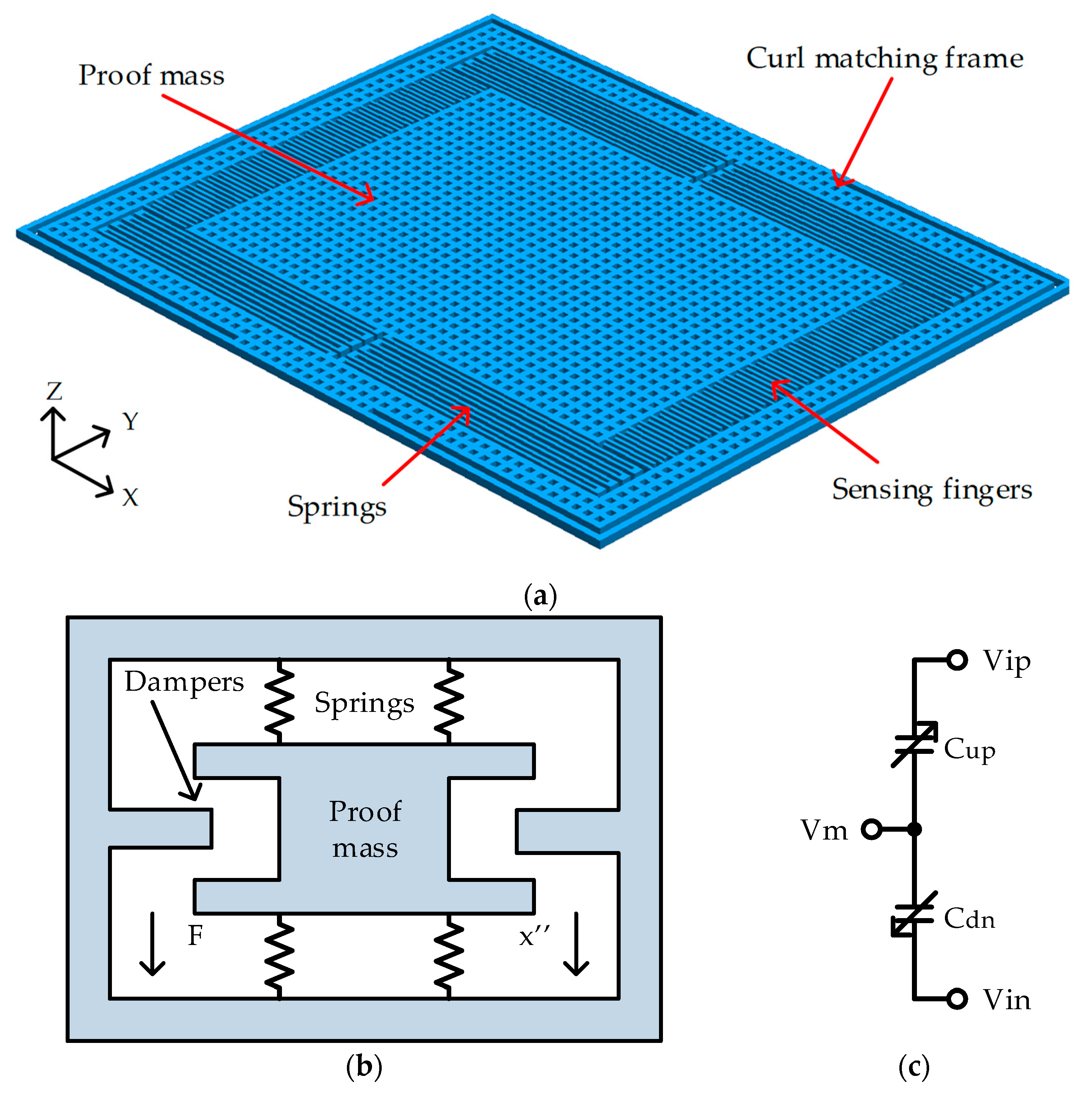
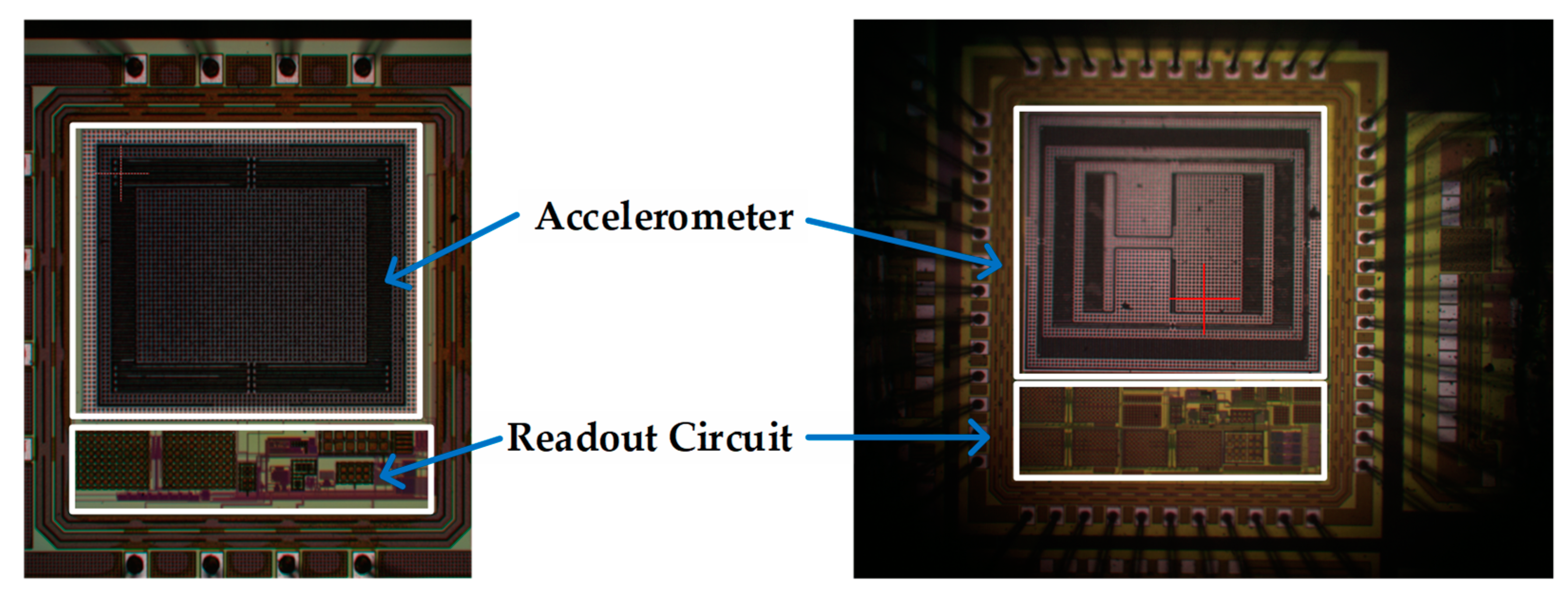
The single axis accelerometer was first implemented and the tri-axis accelerometer was later developed. The proposed CMOS/MEMS accelerometer consisted of a proof mass, sensing fingers, springs, and a curl matching frame.
2.2.1. Single Axis Accelerometer
Figure 2a is the top view of the proposed single axis accelerometer. The proof mass was suspended above the substrate by four sets of springs. The proof mass was a perforated structure that can be undercut etched to release the suspended structures. The density and size of the etching holes was limited by the etching condition of the undercut process. The design used a 6 μm × 6 μm etching hole and 6 μm spacing to form the proof mass based on the MEMS design rules from the manufacturers.
The micro-accelerometer was equivalent to the mechanical model in
Figure 2b. It is a second-order mass-spring-damper system modeled by the force balance equation, where
F is applied force,
m is the mass of suspended proof mass,
x is the displacement,
b is the damping coefficient and
k is the spring constant:
The displacement (
x) was transformed into capacitance (
ΔC) by sensing fingers. The capacitance-to-voltage readout circuit transformed the capacitance to voltage. The circuit model in
Figure 2c was simulated with a readout circuit. The circuit was simulated with Cadence Spectre simulator (Cadence Design Systems, Inc., San Jose, CA, USA).
The stiffness of the spring plays an important role in sensor design. Softer springs have less stiffness, and this means the device will have larger displacement, and hence larger capacitance (ΔC). The stiffness of the spring was decided by the width, length and turns of the springs.
Detailed models can be used to obtain more accurate results at the expense of speed of analysis. By developing a simplified analytical model, we gained insight regarding the mechanical behavior. Accurate results using elaborate models can be obtained using a finite element method (FEM) simulation. Simulations were carried out in CoventorWare 10 (Coventor, Inc., Cary, NC, USA).
MemMech is the FEM mechanical solver of CoventorWare, which is capable of computing displacement, reaction force and modal displacement. The material database provided contains characterized material properties for mechanical simulation. For a linear analysis, the displacement was calculated with the assumption that the stiffness is constant. For the nonlinear structural analysis in MemMech, the structure’s stiffness changed as it deformed. The stiffness matrix of the structure was much more complicated to solve than a linear analysis. The nonlinearity caused by material nonlinearity, boundary nonlinearity and geometric nonlinearity were considered in the FEM simulations.
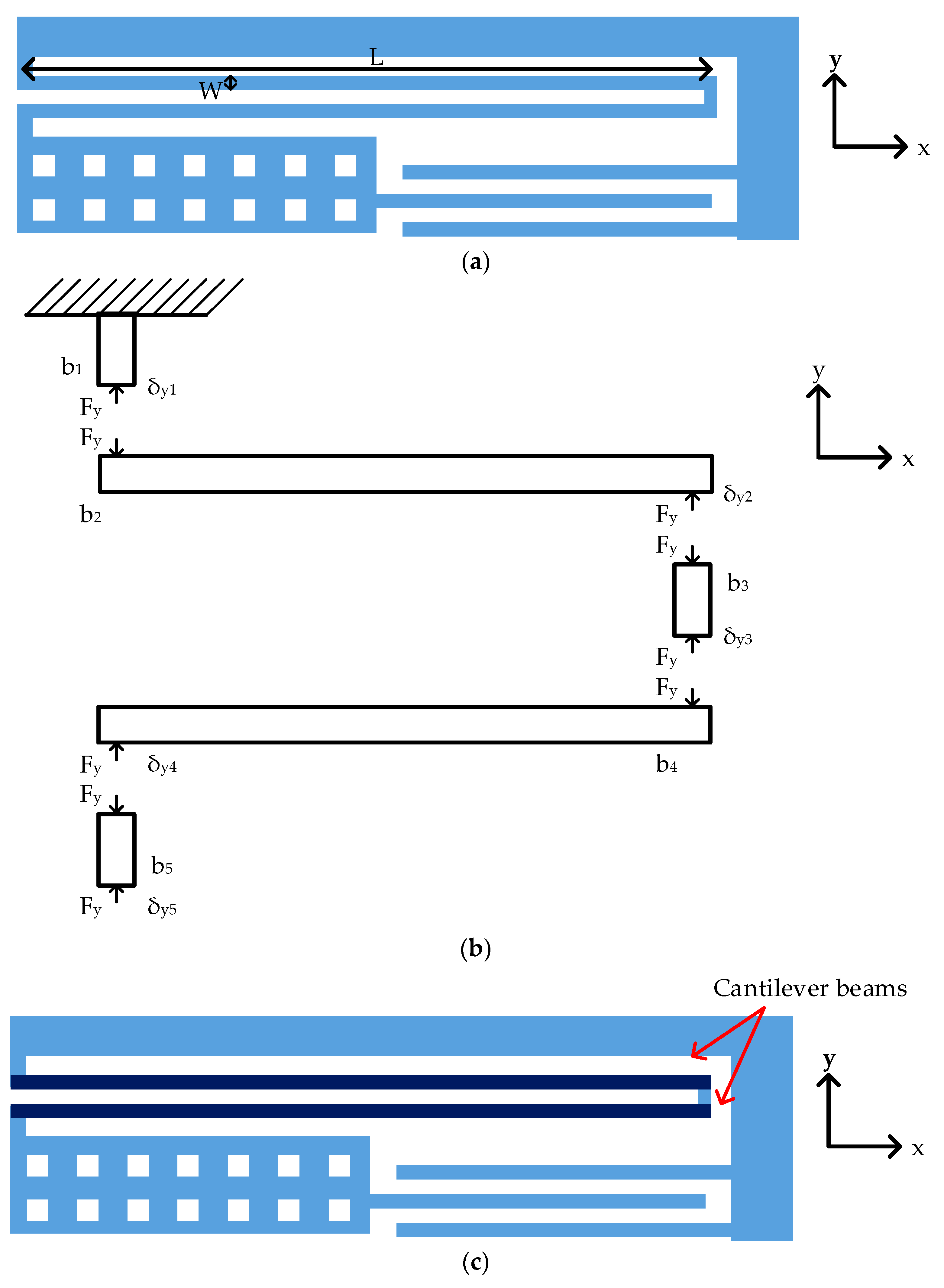
In this paper, serpentine springs are adopted for structure design, as in
Figure 3a. By analyzing the structure, an approximate analytical model for the spring design is presented.
The schematic of proposed serpentine structure is shown in
Figure 3a.
Figure 3b shows the free body diagram of a serpentine spring. The beam segments were indexed from
b1 to
b5. The spring constant was found by applying a force balance to each beam segment. According to Hooke’s law, the relation between applied force (
Fy), spring constant along
y-axis (
ky) and displacement along
y-axis (
δy) is formulated below:
As in
Figure 3b, a lateral force along the
y-axis (
Fy) was applied at the end of the spring. The displacement along
y-axis for each beam segment was given by:
where
i is the index of beam segment from 1 to 5,
δyi is the corresponding displacement along
y-axis, and
kyi is spring constant of the segment along
y-axis.
The spring constant was obtained by summing the displacement of each segment and then divided by the applied force
Fy.
Beam segment
b2 and
b4 were clamped-guided cantilever beams, hence spring constants
ky2 and
ky4 are listed below, where
kc is spring constant along the
y-axis,
E was Young’s modulus of elasticity,
t was the thickness of structure,
W is the width of spring,
n was the number of cantilever beam segments in series and
L was the length of spring [
23].
Beam segments
b1,
b3 and
b5 were rectangular beams hence spring constants
ky1,
ky3 and
ky5 are given by
ks [
23]. The beam segments
b1,
b3 and
b5 were very stiff along the
y-axis. There was almost no displacement along the
y-axis. The width of the segment was deliberately selected two times larger than the cantilever beam to minimize the displacement of segments
b1,
b3 and
b5. The resulting spring constant was about 10
5 times larger than
ky2 and
ky4.
By ignoring the displacement of beam segments
b1,
b3 and
b5, the serpentine spring only consisted of cantilever beams in series as in
Figure 3c.
The spring constant of
n cantilever beam segments in the
y-axis was given by:
The whole structure consisted of four sets of serpentine structures. Therefore, the spring constant of whole structure in the
y-axis was four times that of a single serpentine structure.
Table 1 summarizes the spring design parameters of proposed single axis accelerometer.
The displacement along the
y-axis (
δy) can be obtained by the following equation where
m is mass of the proof mass and
ay was the acceleration along
y-axis. The 1 g acceleration
ay was around 9.81 m/s
2. The dimension of proof mass was 606 μm × 462 μm × 10.14 μm and
m was around 4.32 μg.
With mass and spring constant, the resonant frequency was given by:
Table 2 compares the results predicted by FEM simulations and the proposed simplified analytical model. The predicted spring constant was slightly higher than the FEM results since the displacement was underestimated. From the simplified analytical model above, the
y-axis spring constant was proportional to
W3, therefore the width of the spring (
W), must be kept small to get higher sensitivity. The spring width (
W), was limited to 4 μm by the CMOS/MEMS process. Increasing the spring length (
L), or the number of cantilever beam segments in series
n in a limited size can produce higher sensitivity. The proposed accelerometer had the displacement of 104.99 nm at 1 g. The FEM simulation results are listed in
Table 3.
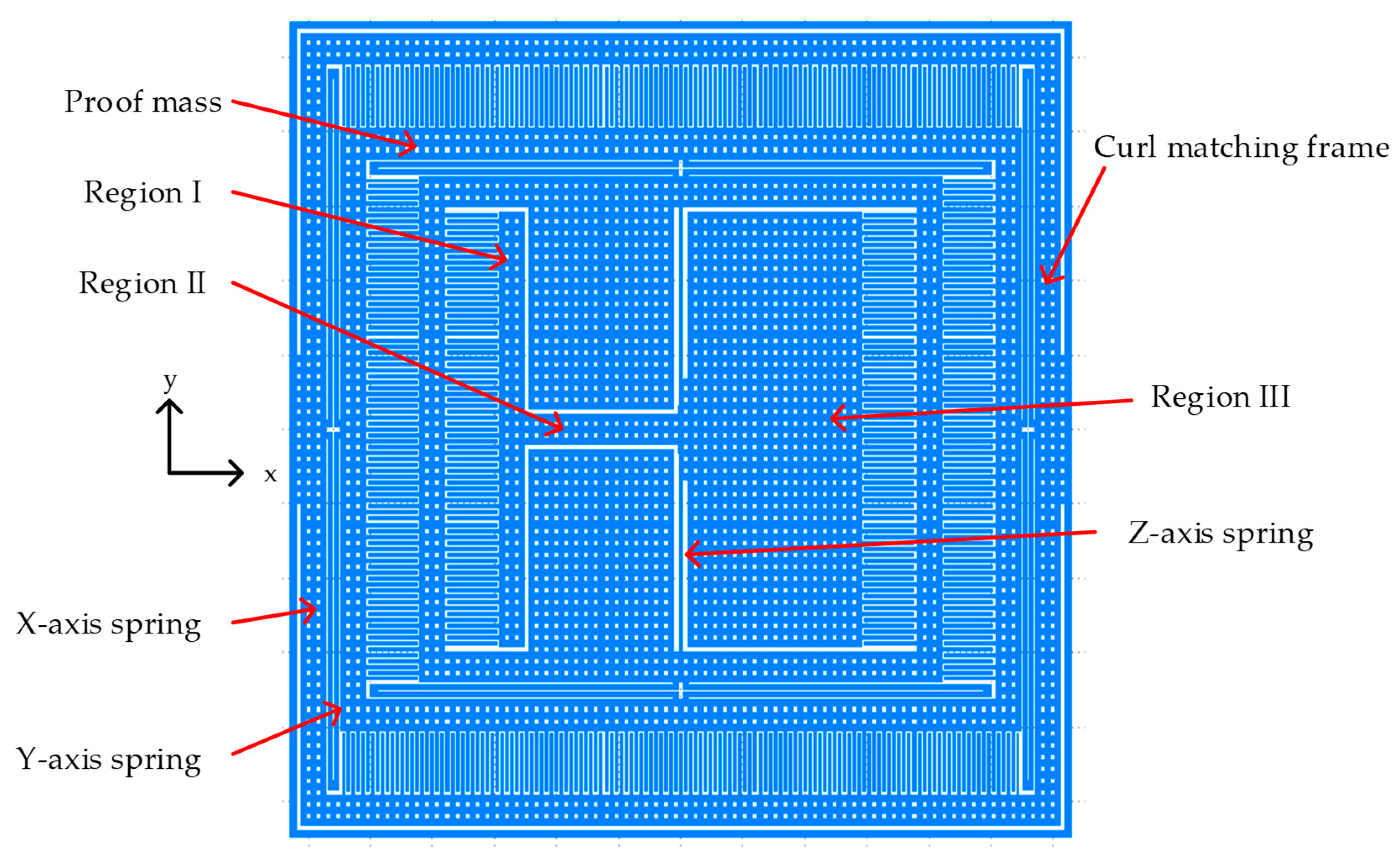
2.2.2. Tri-Axis Accelerometer
Figure 4 shows the proposed tri-axis single proof mass accelerometer. The tri-axis single proof mass accelerometer had an area of 1096 μm × 1256 μm. In order to suppress the structure curving effect, a curl matching frame was presented to achieve the same structure curling at the proof mass and the frame. The perforated structure and the layer combination were same for the proof mass and the frame to match the curling of the two parts. The layer combination ME1 and ME6 was chosen based on our previous work [
9]. The
z-axis sensor was embedded in the proof mass of the
y-axis and the
y-axis sensor was embedded in the proof mass of
x-axis sensor. The springs of the
x and
y-axis were similar to a single axis design.
Table 4 summarizes the in-plane (
x-axis and
y-axis) spring design parameters.
Table 5 shows the results predicted by the FEM simulations and the proposed simplified analytical model.
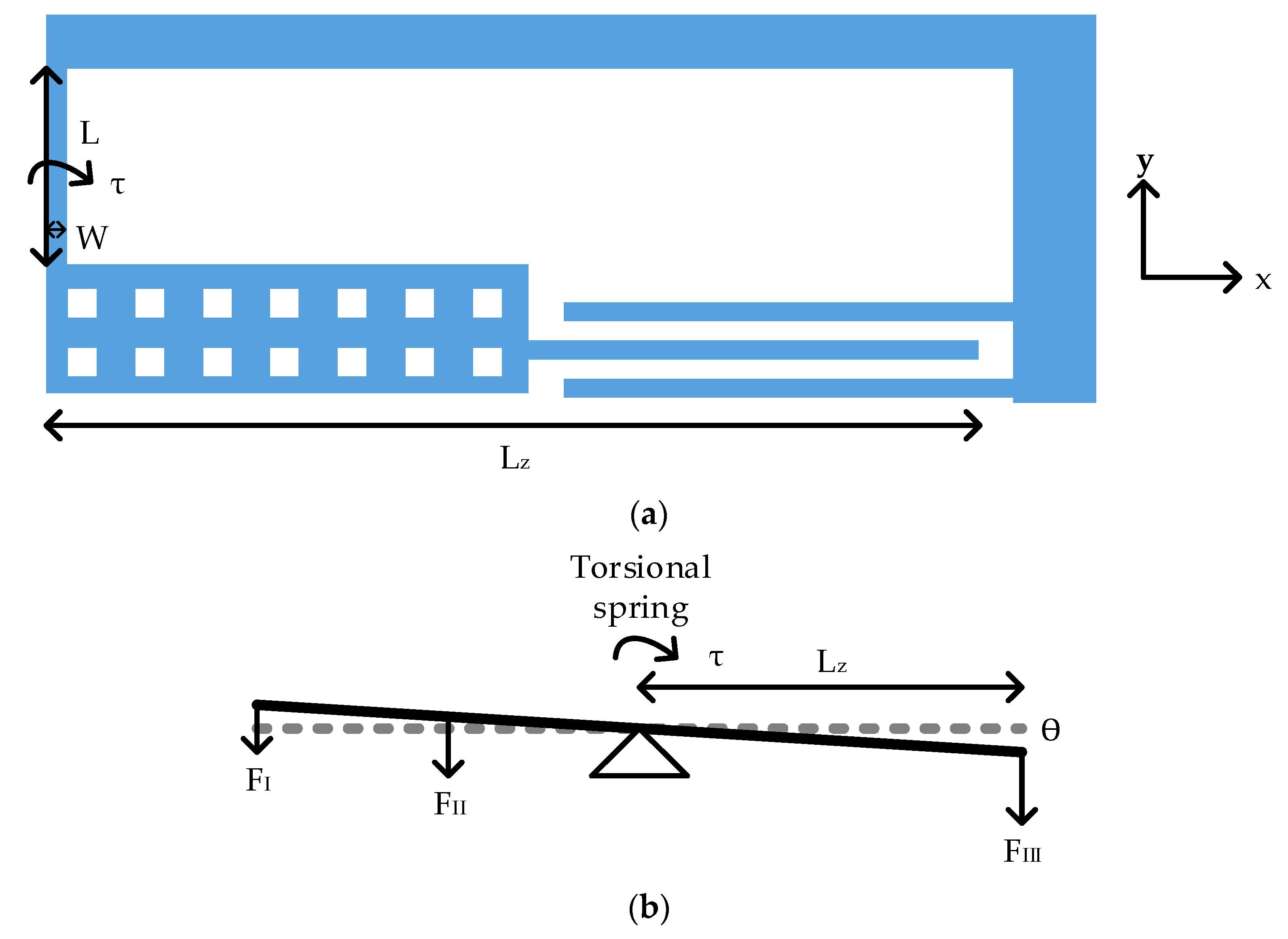
The torsion spring in
Figure 5a was adopted for out-plane sensing. The imbalanced torsional
z-axis sensing element was embedded in the in-plane proof mass. The design equation of the torsion spring was given by [
23,
24]:
where
G is shear modulus,
W is the width of the torsion beam,
L is the length of the torsion beam,
t is structure thickness.
Table 6 summarizes the spring design parameters.
The whole structure consisted of two sets of torsional structures. Therefore, the spring constant of whole structure was two times that of a single torsional structure.
The imbalanced sensing element consisted of three regions as in
Figure 4. The design parameters are specified in
Table 7.
Figure 5b shows the free body diagram of a torsion spring.
FI to
FIII are force from these three parts. According to Hooke’s law in angular form, the relation between applied torque (
τ), torsion spring constant (
kθ) and rotation angle (
θ) is formulated below:
The displacement along
z-axis (
δz) was obtained by the following equation where
Lz is the distance from the torsion spring to the sensing finger as in
Figure 5. For 1 g acceleration
τ was around 2.77 × 10
−12 N·m, rotation angle was 3.23 × 10
−5 rad and
δz was around 16.24 nm. The displacement of FEM simulation was 20.08 nm. The FEM simulation results are listed in
Table 8.