Numerical Study and Optimization of a Novel Piezoelectric Transducer for a Round-Window Stimulating Type Middle-Ear Implant
Abstract
1. Introduction
2. Materials and Methods
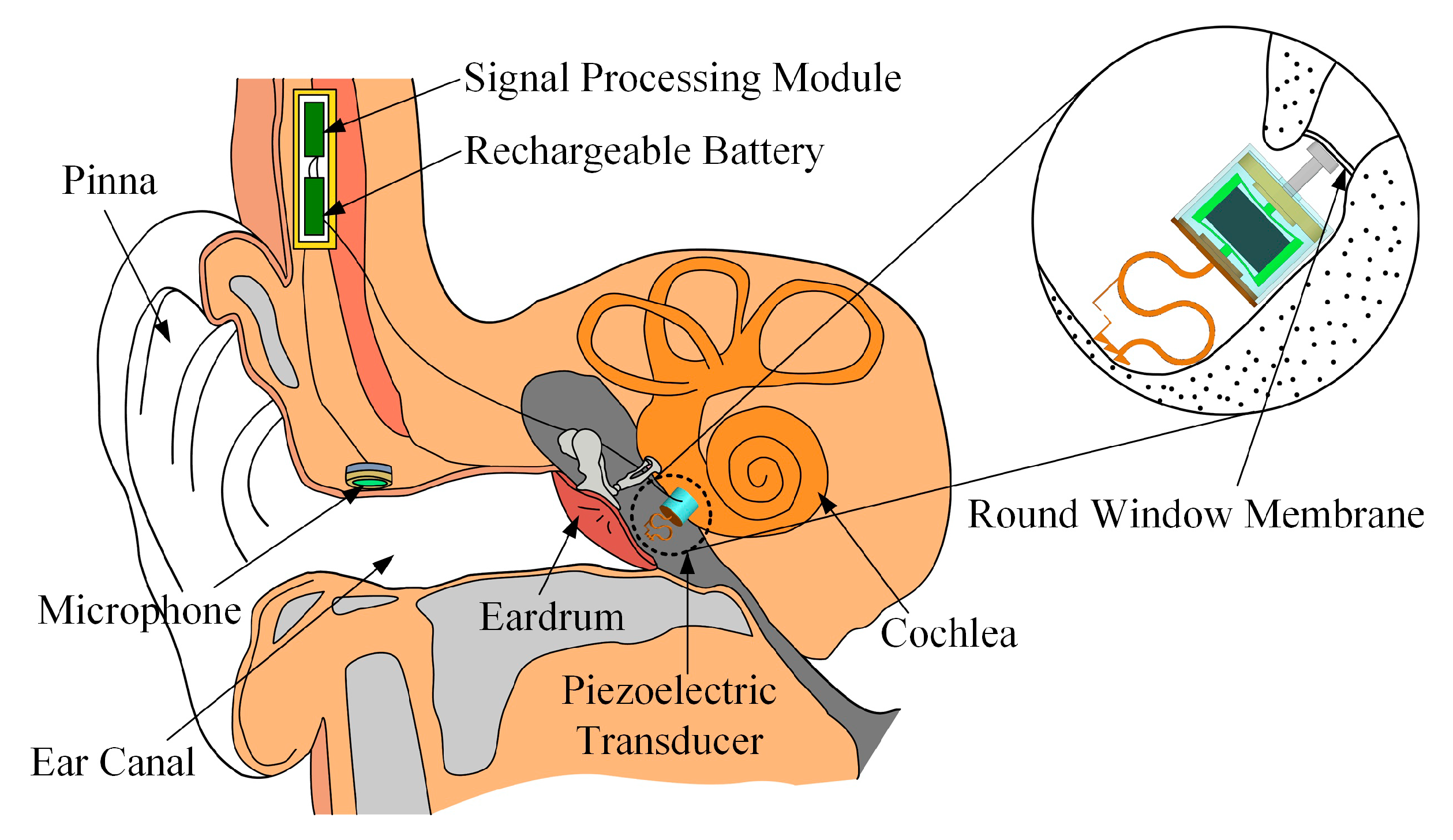
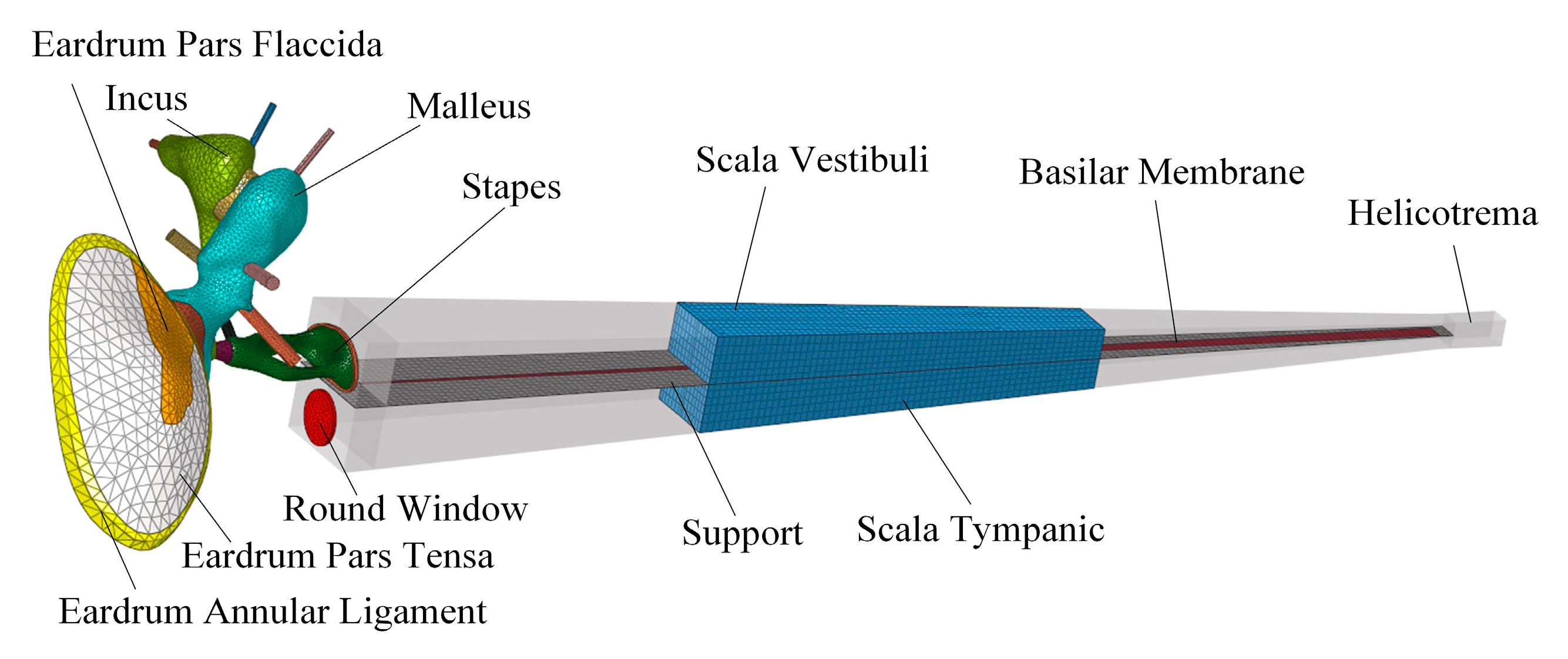
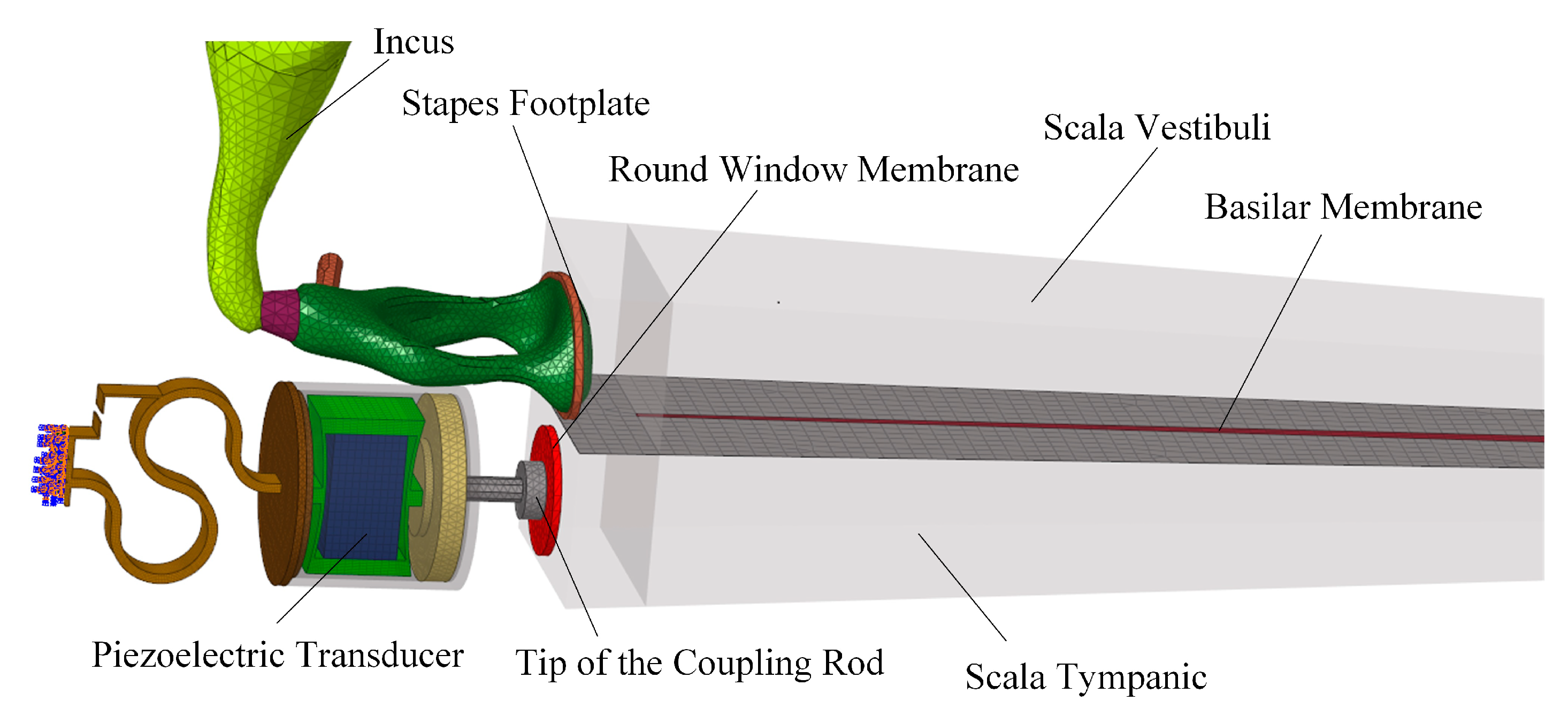
2.1. Concept and Structure of the Piezoelectric Transducer
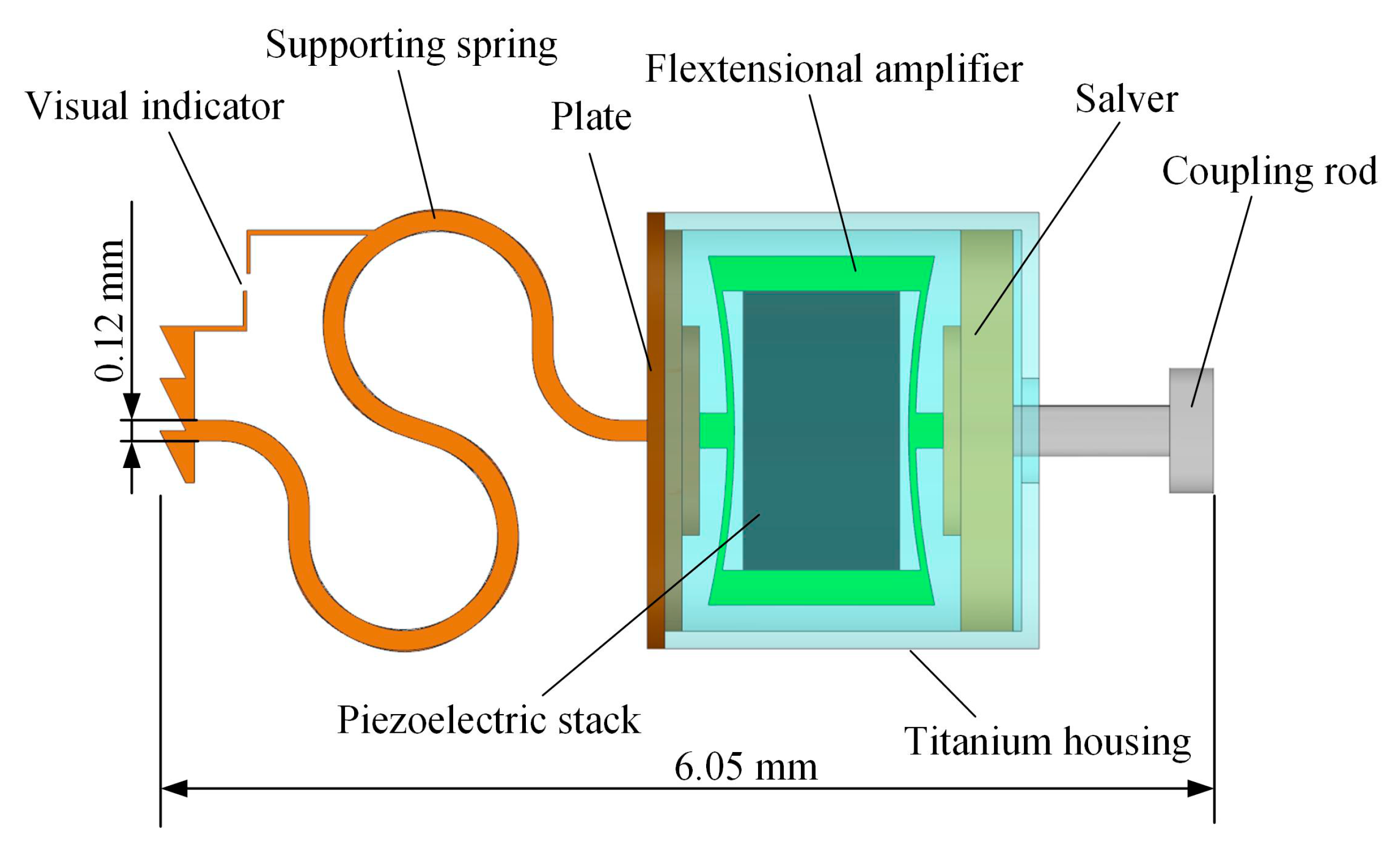
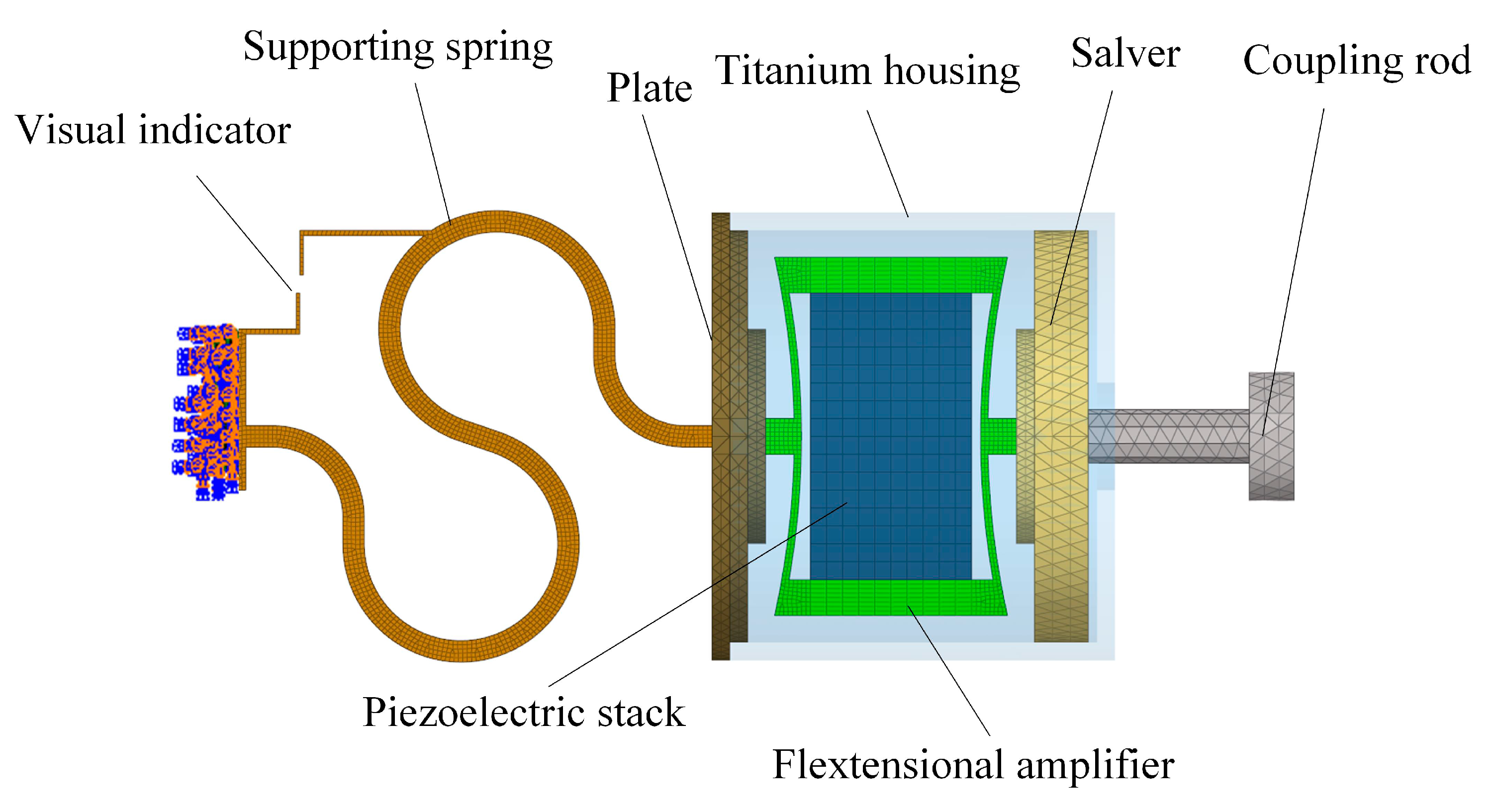
2.2. Design of the Piezoelectric Transducer
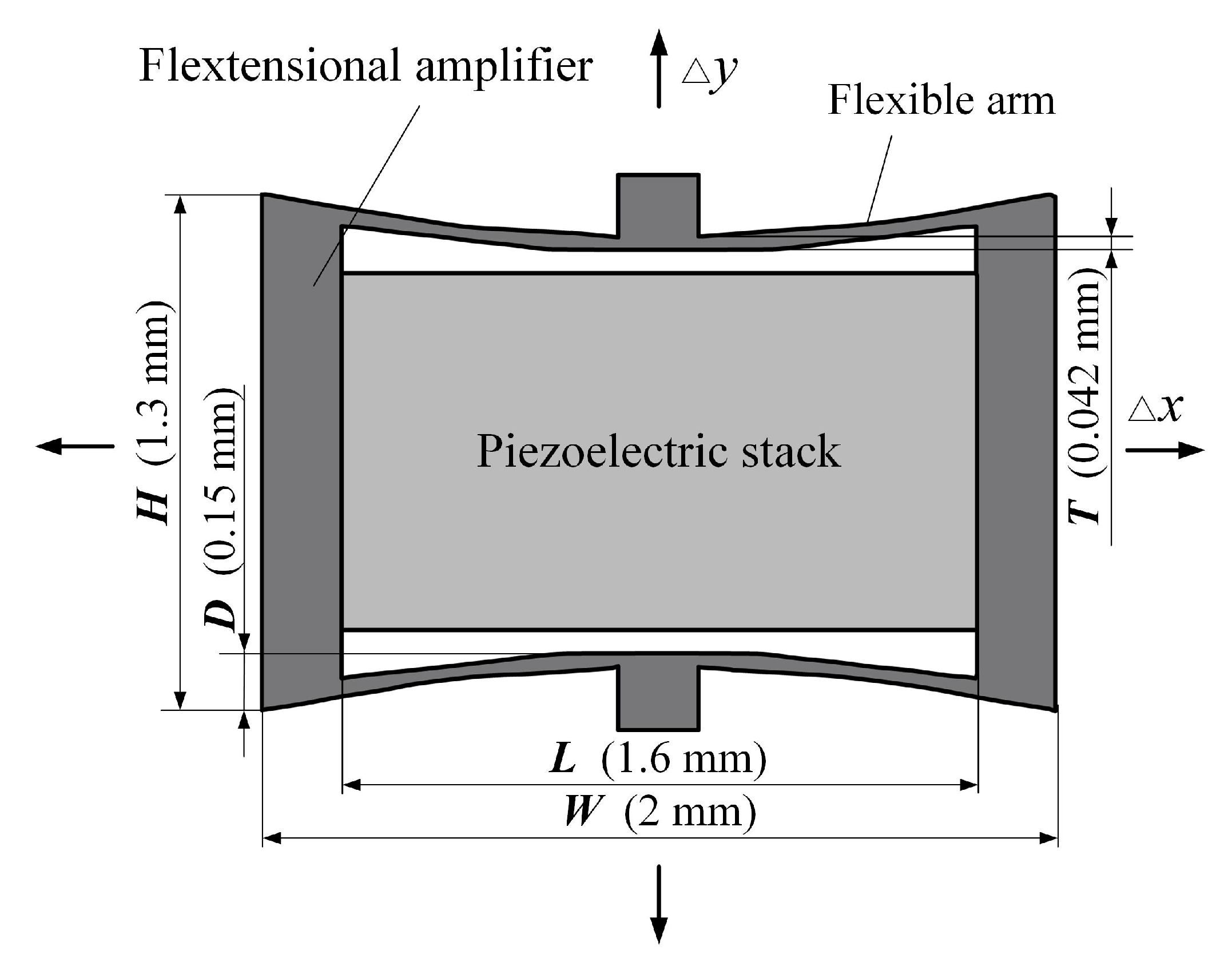
2.2.1. Design of the Piezoelectric Component
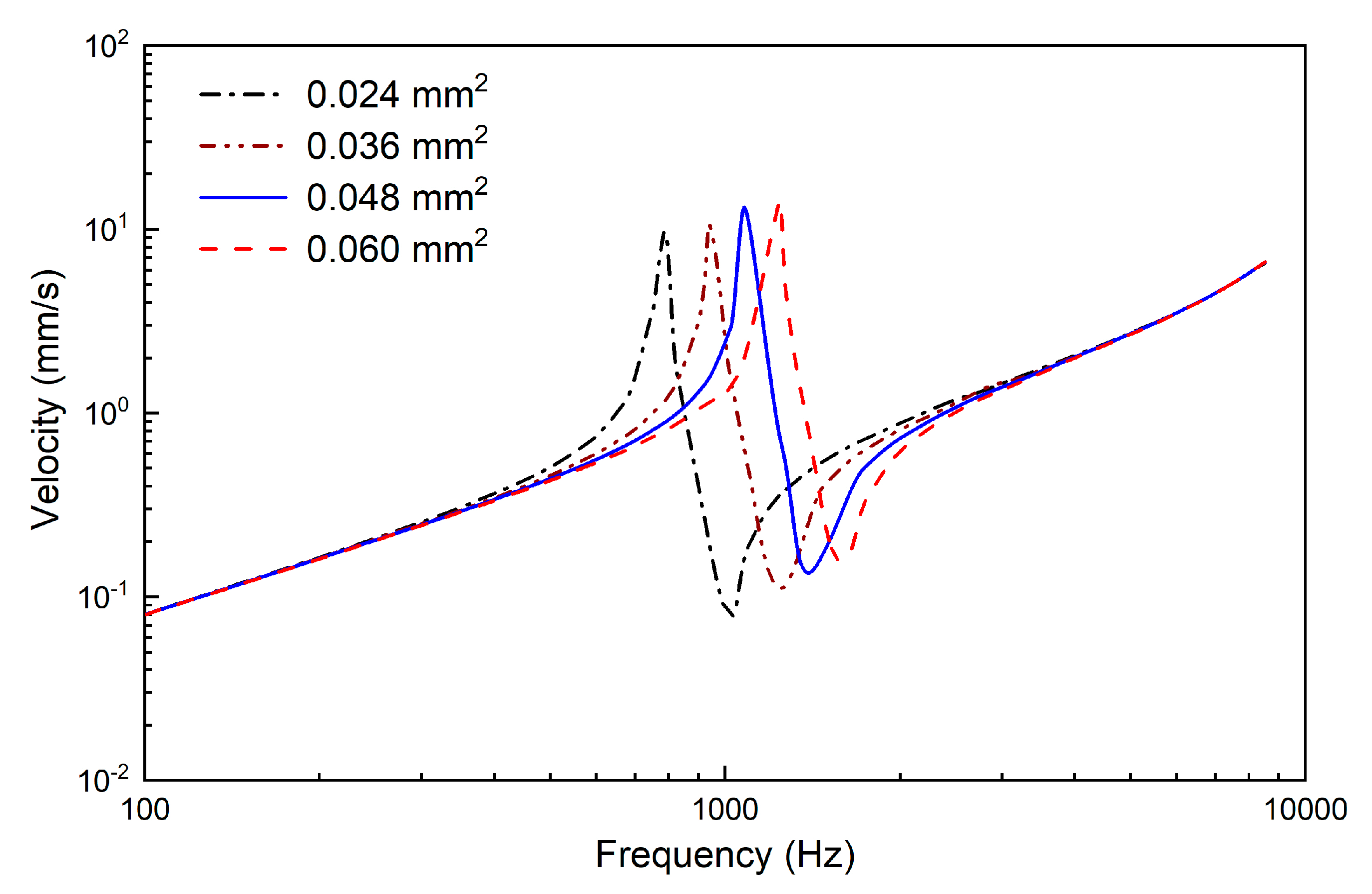
2.2.2. Design of the Supporting Spring
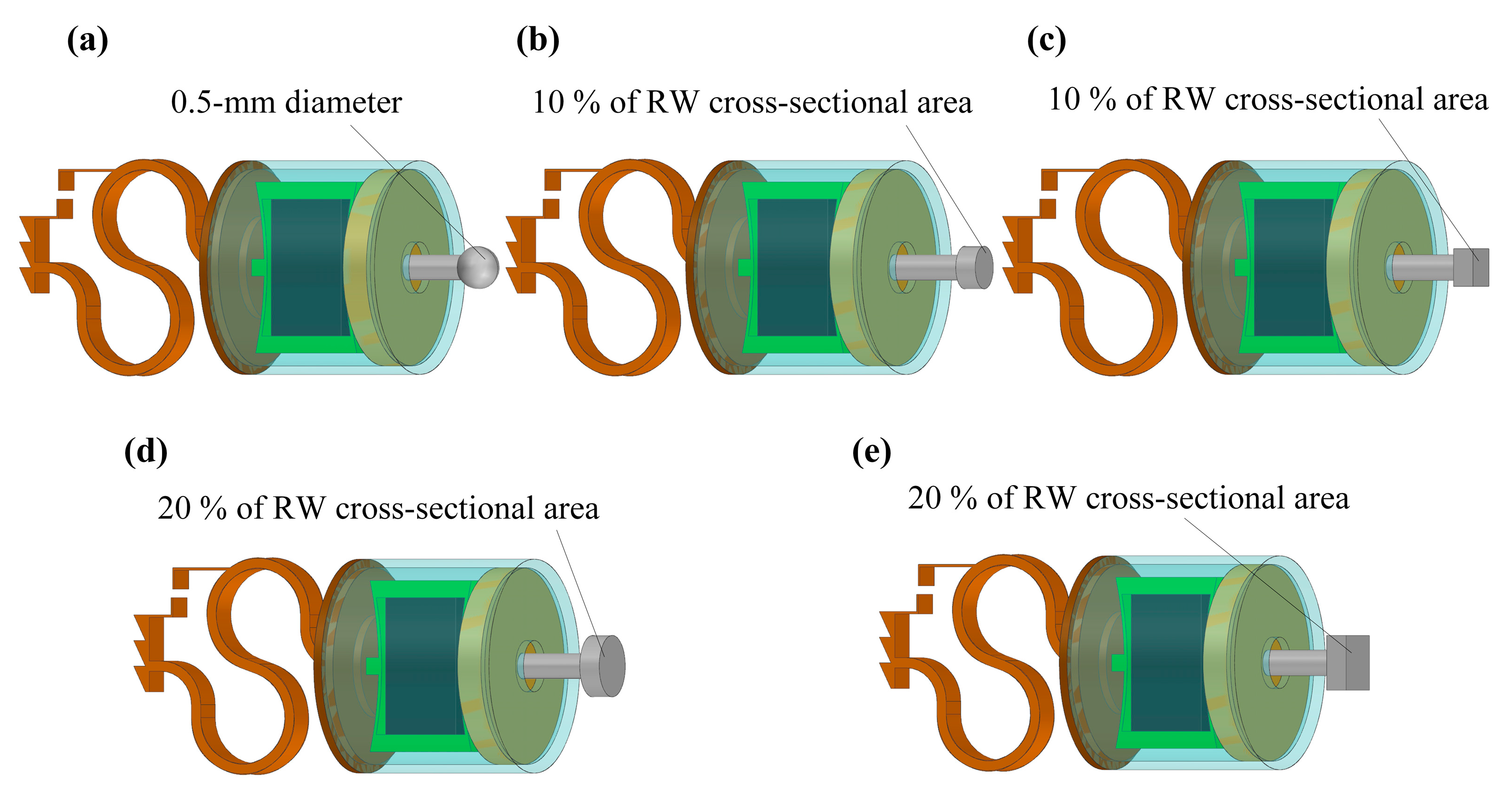
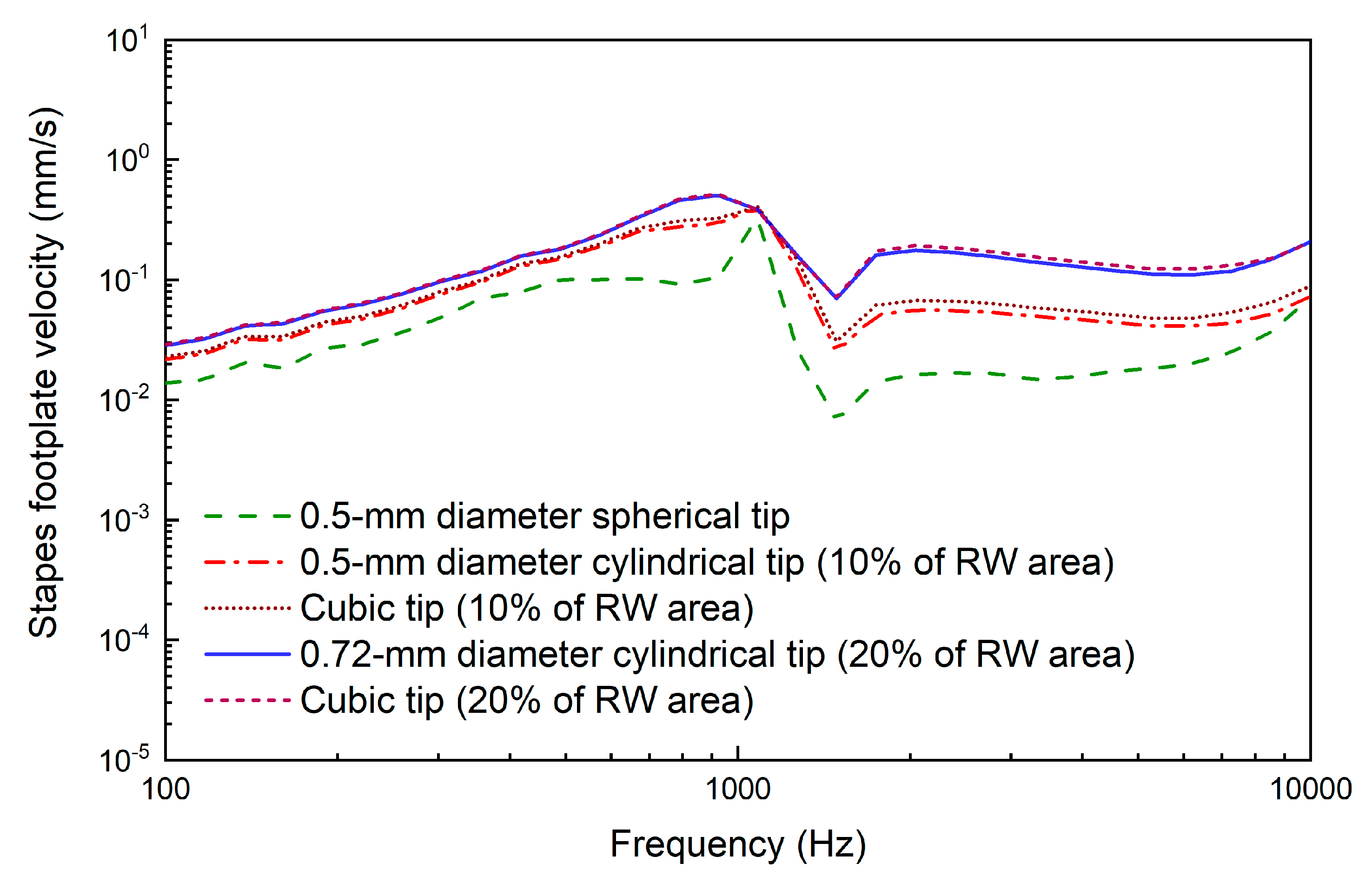
2.2.3. Design of the Coupling Rod Tip
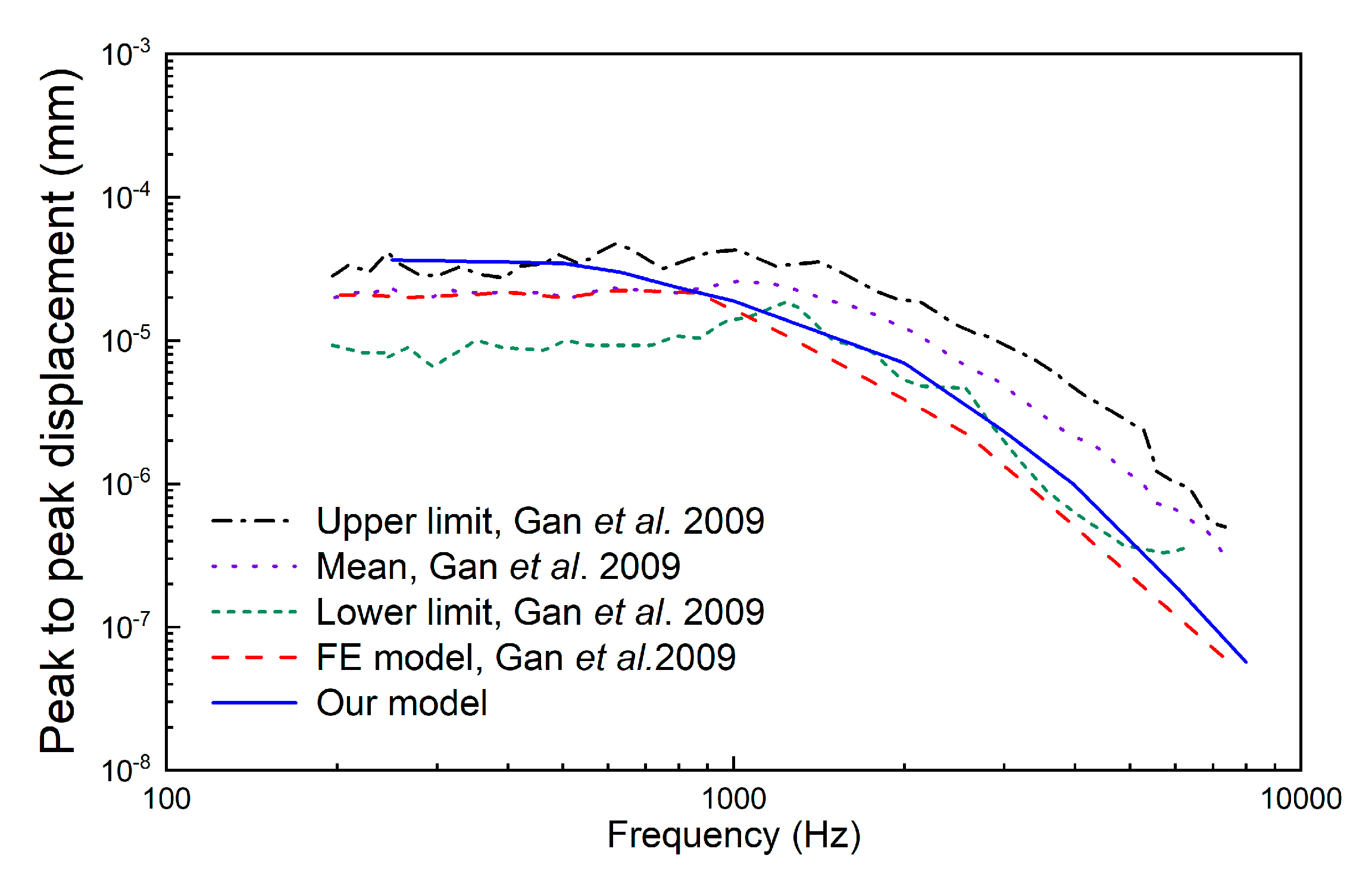
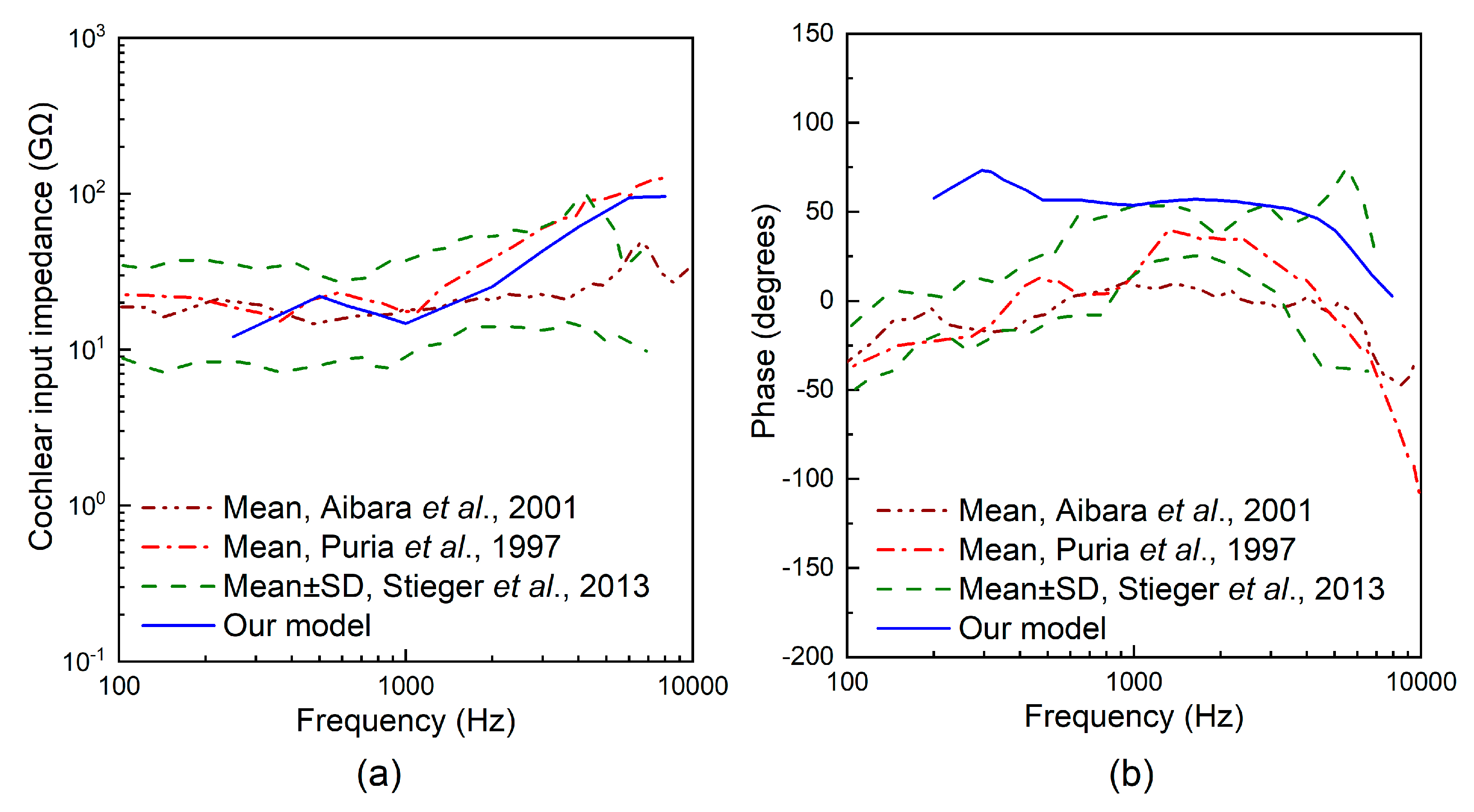
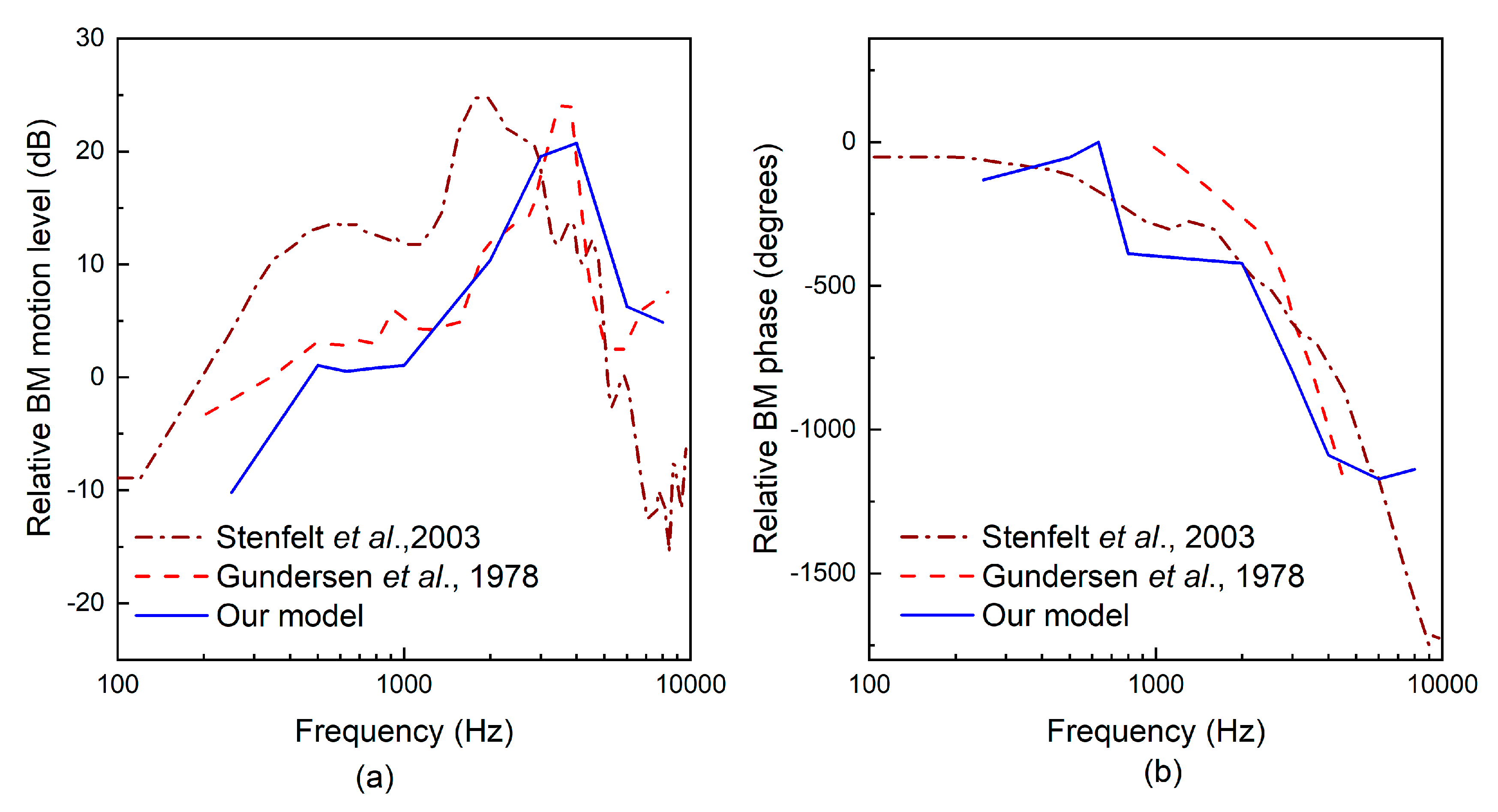
2.3. Evaluation of the Transducer’s Performance
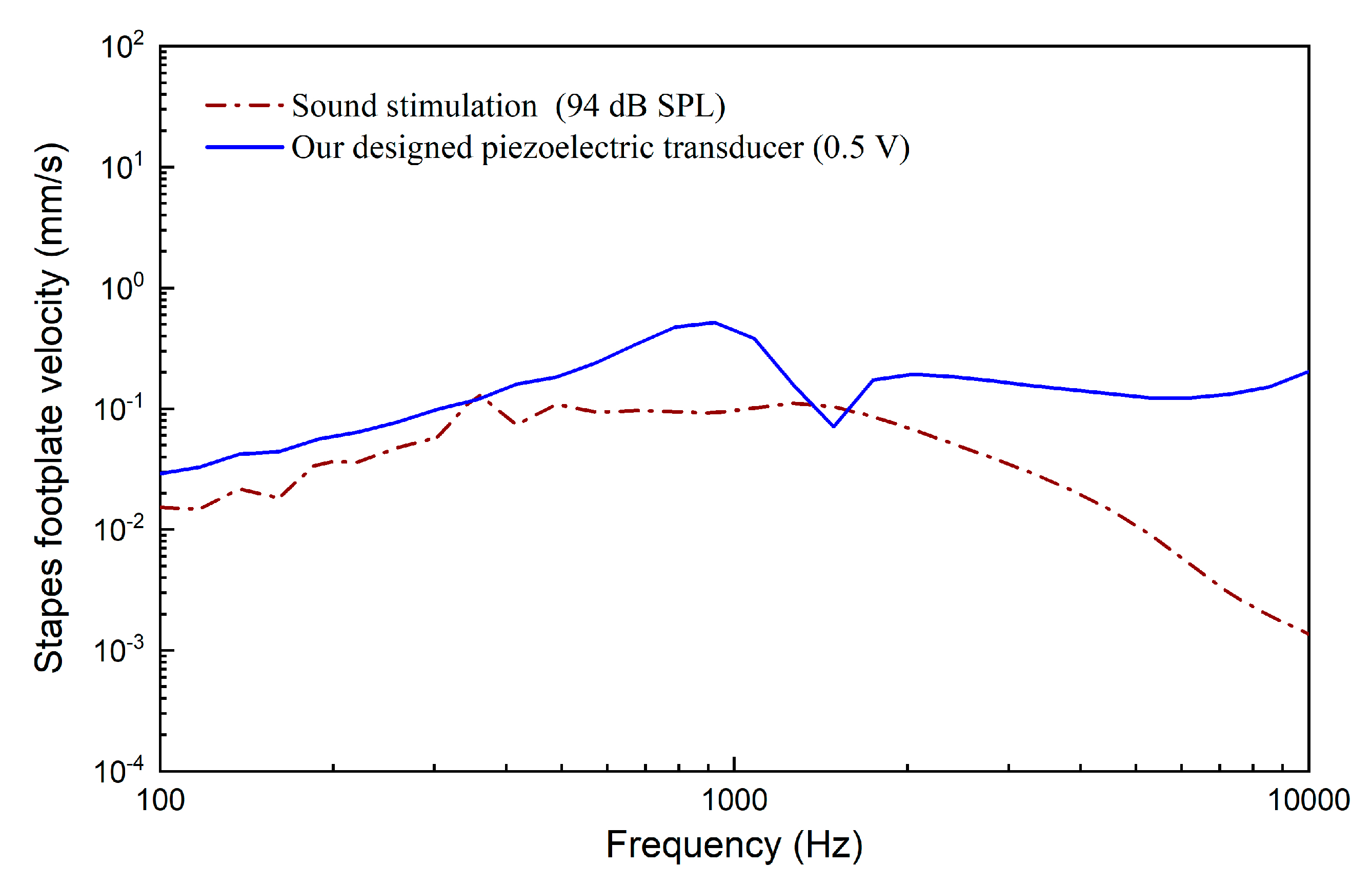
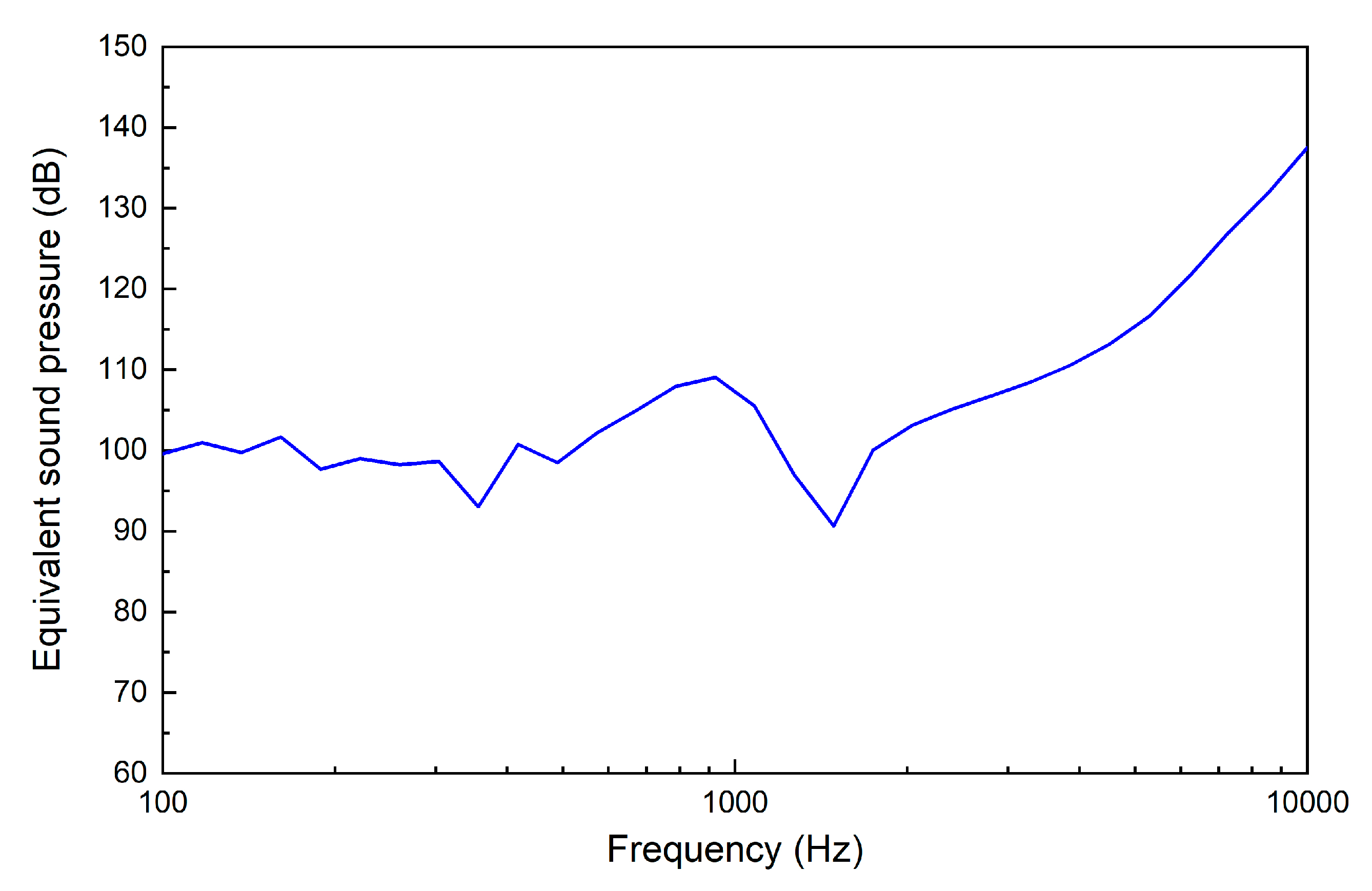
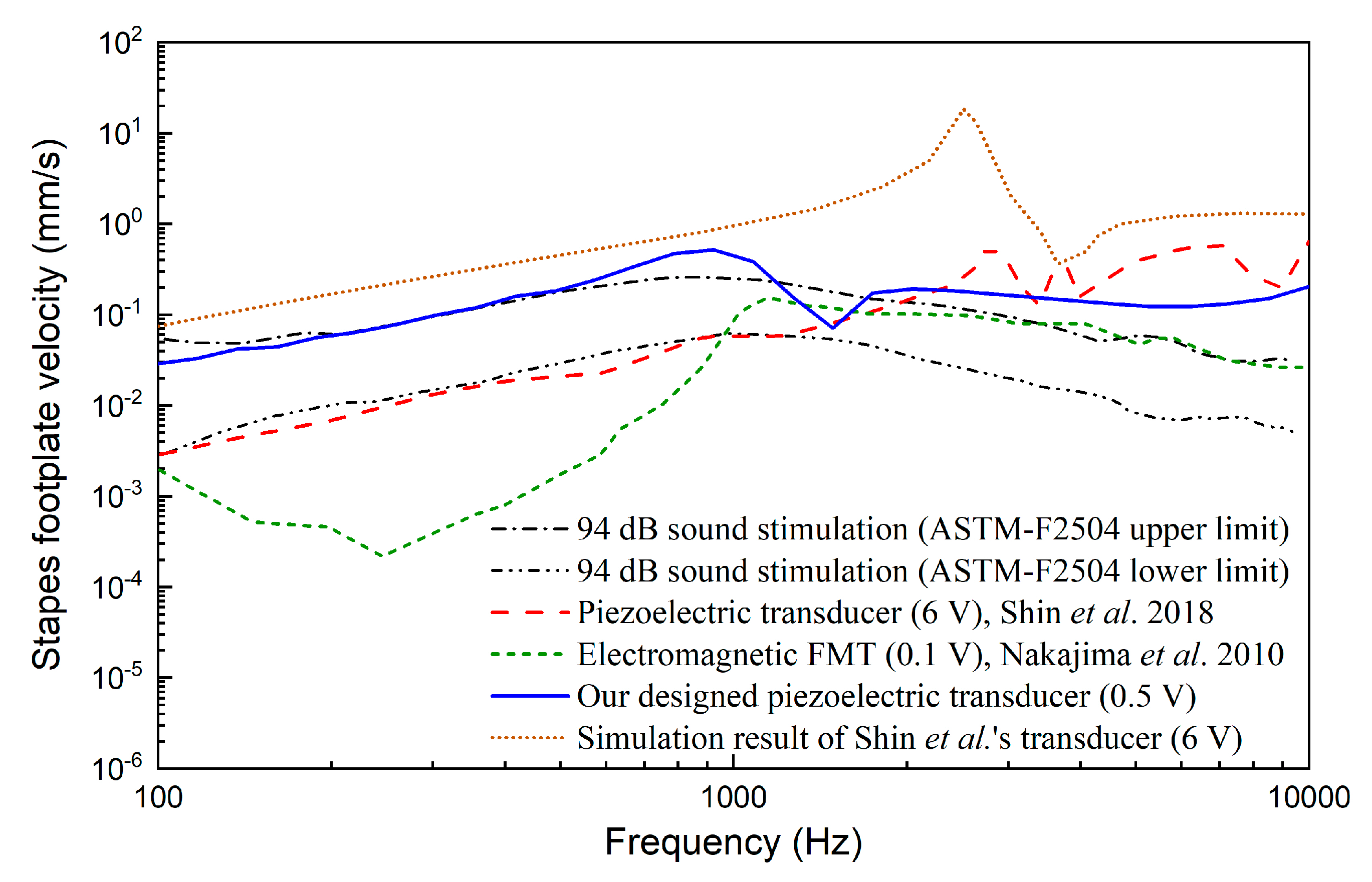
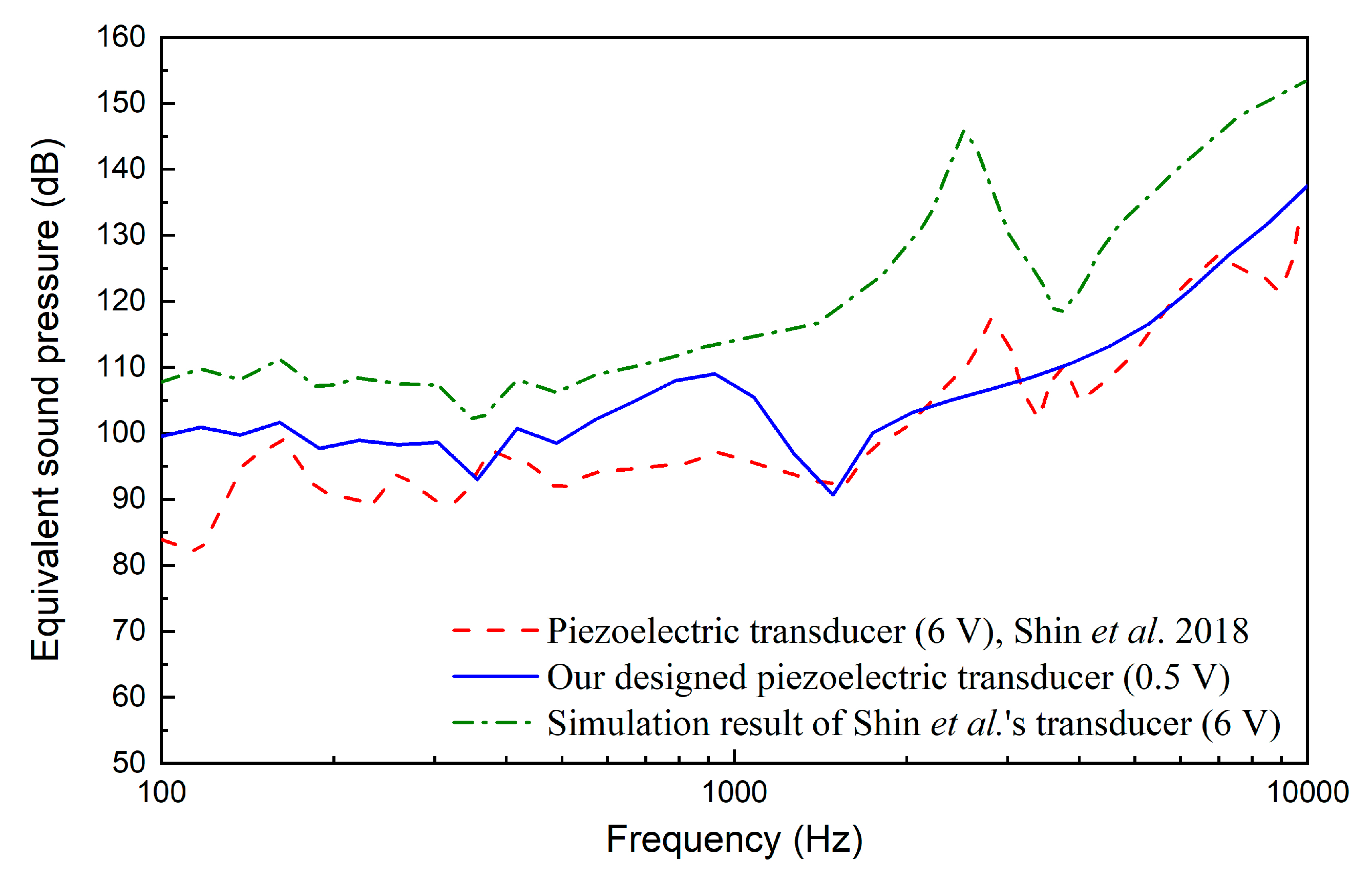
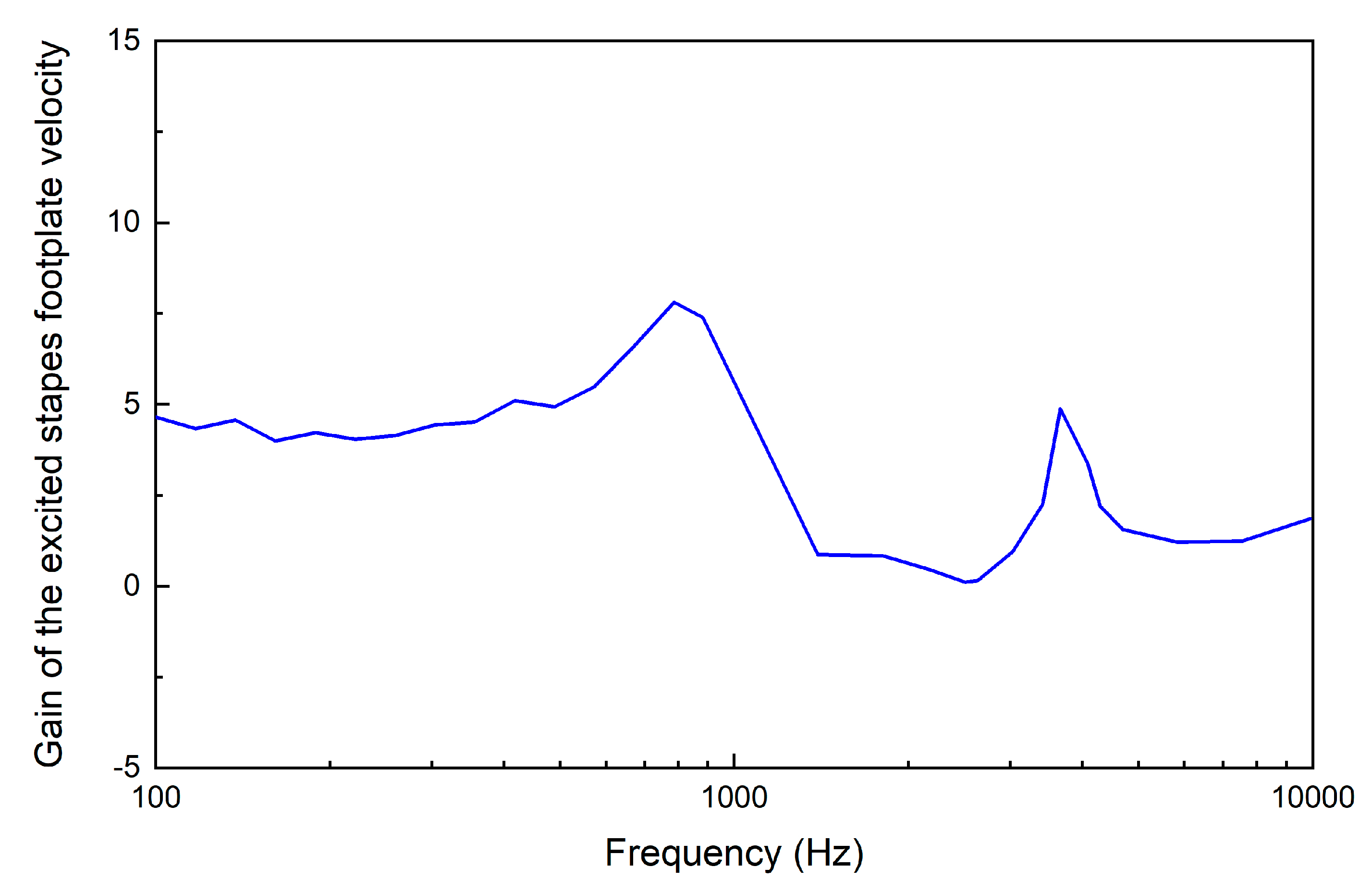
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stevens, G.; Flaxman, S.; Brunskill, E.; Mascarenhas, M.; Mathers, C.D.; Finucane, M. Global Burden of Disease Hearing Loss Expert Group. Global and regional hearing impairment prevalence: An analysis of 42 studies in 29 countries. Eur. J. Public Health 2013, 23, 146–152. [Google Scholar] [CrossRef] [PubMed]
- Moore, B.C.J.; ebrary Inc. Cochlear Hearing Loss Physiological, Psychological and Technical Issues, 2nd ed.; John Wiley & Sons: Chichester, UK; Hoboken, NJ, USA, 2007. [Google Scholar]
- McCormack, A.; Fortnum, H. Why do people fitted with hearing aids not wear them? Int. J. Audiol. 2013, 52, 360–368. [Google Scholar] [CrossRef] [PubMed]
- Hamanishi, S.; Koike, T.; Matsuki, H.; Wada, H. A new electromagnetic hearing aid using lightweight coils to vibrate the ossicles. IEEE Trans. Magn. 2004, 40, 3387–3393. [Google Scholar] [CrossRef]
- Hong, E.-P.; Park, I.-Y.; Seong, K.-W.; Cho, J.-H. Evaluation of an implantable piezoelectric floating mass transducer for sensorineural hearing loss. Mechatronics 2009, 19, 965–971. [Google Scholar] [CrossRef]
- Liu, H.; Cheng, J.; Yang, J.; Rao, Z.; Cheng, G.; Yang, S.; Huang, X.; Wang, M. Concept and evaluation of a new piezoelectric transducer for an implantable middle ear hearing device. Sensors (Basel) 2017, 17, 2515. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.-L.; Jian, J.-T.; Chen, W.-Z.; Shih, C.-H.; Chou, Y.-F.; Liu, T.-C.; Lee, C.-F. The development of a non-surgical direct drive hearing device with a wireless actuator coupled to the tympanic membrane. Appl. Acoust. 2013, 74, 1511–1518. [Google Scholar] [CrossRef]
- Koch, M.; Essinger, T.M.; Bornitz, M.; Zahnert, T. Examination of a mechanical amplifier in the incudostapedial joint gap: Fem simulation and physical model. Sensors (Basel) 2014, 14, 14356–14374. [Google Scholar] [CrossRef]
- Colletti, V.; Soli, S.D.; Carner, M.; Colletti, L. Treatment of mixed hearing losses via implantation of a vibratory transducer on the round window. Int. J. Audiol. 2006, 45, 600–608. [Google Scholar] [CrossRef]
- Zhao, S.; Gong, S.; Han, D.; Zhang, H.; Ma, X.; Li, Y.; Chen, X.; Ren, R.; Li, Y. Round window application of an active middle ear implant (amei) system in congenital oval window atresia. Acta Otolaryngol. 2016, 136, 23–33. [Google Scholar] [CrossRef]
- Colletti, L.; Mandala, M.; Colletti, V. Long-term outcome of round window vibrant soundbridge implantation in extensive ossicular chain defects. Otolaryngol. Head Neck Surg. 2013, 149, 134–141. [Google Scholar] [CrossRef]
- Nakajima, H.H.; Dong, W.; Olson, E.S.; Rosowski, J.J.; Ravicz, M.E.; Merchant, S.N. Evaluation of round window stimulation using the floating mass transducer by intracochlear sound pressure measurements in human temporal bones. Otol. Neurotol. 2010, 31, 506–511. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Xu, D.; Yang, J.; Yang, S.; Cheng, G.; Huang, X. Analysis of the influence of the transducer and its coupling layer on round window stimulation. Acta Bioeng. Biomech. 2017, 19, 103–111. [Google Scholar] [PubMed]
- Schraven, S.P.; Hirt, B.; Gummer, A.W.; Zenner, H.P.; Dalhoff, E. Controlled round-window stimulation in human temporal bones yielding reproducible and functionally relevant stapedial responses. Hear Res. 2011, 282, 272–282. [Google Scholar] [CrossRef] [PubMed]
- Maier, H.; Salcher, R.; Schwab, B.; Lenarz, T. The effect of static force on round window stimulation with the direct acoustic cochlea stimulator. Hear Res. 2013, 301, 115–124. [Google Scholar] [CrossRef] [PubMed]
- Muller, M.; Salcher, R.; Lenarz, T.; Maier, H. The hannover coupler: Controlled static prestress in round window stimulation with the floating mass transducer. Otol. Neurotol. 2017, 38, 1186–1192. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, H.H.; Merchant, S.N.; Rosowski, J.J. Performance considerations of prosthetic actuators for round-window stimulation. Hear. Res. 2009, 263, 114–119. [Google Scholar] [CrossRef] [PubMed]
- Salcher, R.; Schwab, B.; Lenarz, T.; Maier, H. Round window stimulation with the floating mass transducer at constant pretension. Hear. Res. 2014, 314, 1–9. [Google Scholar] [CrossRef]
- Shin, D.H.; Cho, J.H. Piezoelectric actuator with frequency characteristics for a middle-ear implant. Sensors (Basel) 2018, 18, 1694. [Google Scholar] [CrossRef]
- Arnold, A.; Ccandreia, S. Factors improving the vibration transfer of the floating mass transducer at the round window. Otol. Neurotol. 2010, 31, 122–128. [Google Scholar] [CrossRef]
- Homma, K.; Du, Y.; Shimizu, Y.; Puria, S. Ossicular resonance modes of the human middle ear for bone and air conduction. J. Acoust. Soc. Am. 2009, 125, 968–979. [Google Scholar] [CrossRef]
- Lerch, R. Simulation of piezoelectric devices by two- and three-dimensional finite elements. IEEE Trans. Ultrason. Ferroelectr. Frequency Control 1990, 37, 233–247. [Google Scholar] [CrossRef] [PubMed]
- Schraven, S.P.; Hirt, B.; Goll, E.; Heyd, A.; Gummer, A.W.; Zenner, H.P.; Dalhoff, E. Conditions for highly efficient and reproducible round-window stimulation in humans. Audiol. Neurootol. 2012, 17, 133–138. [Google Scholar] [CrossRef]
- Gan, R.Z.; Cheng, T.; Dai, C.; Yang, F.; Wood, M.W. Finite element modeling of sound transmission with perforations of tympanic membrane. J. Acoust. Soc. Am. 2009, 126, 243–253. [Google Scholar] [CrossRef]
- Puria, S.; Peake, W.T.; Rosowski, J.J. Sound-pressure measurements in the cochlear vestibule of human-cadaver ears. J. Acoust. Soc. Am. 1997, 101, 2754–2770. [Google Scholar] [CrossRef] [PubMed]
- Aibara, R.; Welsh, J.T.; Puria, S.; Goode, R.L. Human middle-ear sound transfer function and cochlear input impedance. Hear. Res. 2001, 152, 100–109. [Google Scholar] [CrossRef]
- Stieger, C.; Rosowski, J.J.; Nakajima, H.H. Comparison of forward (ear-canal) and reverse (round-window) sound stimulation of the cochlea. Hear. Res. 2013, 301, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Stenfelt, S.; Puria, S.; Hato, N.; Goode, R.L. Basilar membrane and osseous spiral lamina motion in human cadavers with air and bone conduction stimuli. Hear. Res. 2003, 181, 131–143. [Google Scholar] [CrossRef]
- Gundersen, T.; Skarstein, O.; Sikkeland, T. A study of the vibration of the basilar membrane in human temporal bone preparations by the use of the mossbauer effect. Acta Otolaryngol. 1978, 86, 225–232. [Google Scholar] [CrossRef]
- Homma, K.; Shimizu, Y.; Kim, N.; Du, Y.; Puria, S. Effects of ear-canal pressurization on middle-ear bone- and air-conduction responses. Hear. Res. 2010, 263, 204–215. [Google Scholar] [CrossRef]
- Areias, B.; Parente, M.P.L.; Santos, C.; Gentil, F.; Natal Jorge, R.M. The human otitis media with effusion: A numerical-based study. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 958–966. [Google Scholar] [CrossRef]
- Liu, H.; Rao, Z.; Huang, X.; Cheng, G.; Tian, J.; Ta, N. An incus-body driving type piezoelectric middle ear implant design and evaluation in 3d computational model and temporal bone. Sci. World J. 2014, 2014, 121624. [Google Scholar] [CrossRef] [PubMed]
- Gan, R.Z.; Dai, C.; Wang, X.; Nakmali, D.; Wood, M.W. A totally implantable hearing system--design and function characterization in 3d computational model and temporal bones. Hear. Res. 2010, 263, 138–144. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.-F.; Chen, J.-H.; Chou, Y.-F.; Liu, T.-C. The optimal magnetic force for a novel actuator coupled to the tympanic membrane: A finite element analysis. Biomed. Eng. Appl. Basis Commun. 2007, 19, 171–177. [Google Scholar] [CrossRef]
- Atturo, F.; Barbara, M.; Rask-Andersen, H. Is the human round window really round? An anatomic study with surgical implications. Otol. Neurotol. 2014, 35, 1354–1360. [Google Scholar] [CrossRef]
- Ishii, T.; Takayama, M.; Takahashi, Y. Mechanical properties of human round window, basilar and reissner’s membranes. Acta Otolaryngol. Suppl. 1995, 519, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Schwab, B.; Grigoleit, S.; Teschner, M. Do we really need a coupler for the round window application of an amei? Otol. Neurotol. 2013, 34, 1181–1185. [Google Scholar] [CrossRef] [PubMed]
- ASTM F2504-05. Standard Practice for Describing System Output of Implantable Middle Ear Hearing Devices; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Arnold, A.; Kompis, M.; Candreia, C.; Pfiffner, F.; Häusler, R.; Stieger, C. The floating mass transducer at the round window: Direct transmission or bone conduction? Hear. Res. 2010, 263, 120–127. [Google Scholar] [CrossRef]
- Bornitz, M.; Hardtke, H.J.; Zahnert, T. Evaluation of implantable actuators by means of a middle ear simulation model. Hear. Res. 2010, 263, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Maurer, J.; Savvas, E. The esteem system: A totally implantable hearing device. Adv. Otorhinolaryngol. 2010, 69, 59–71. [Google Scholar]
- Wang, Z.; Mills, R.; Luo, H.; Zheng, X.; Hou, W.; Wang, L.; Brown, S.I.; Cuschieri, A. A micropower miniature piezoelectric actuator for implantable middle ear hearing device. IEEE Trans. Biomed. Eng. 2011, 58, 452–458. [Google Scholar] [CrossRef]

| Elastic Stiffness Constant (GN/m2) | Piezoelectric Constant (C/m2) | Permittivity Constant (× 10−10 F/m) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 146.9 | 81.1 | 81.1 | 131.7 | 31.4 | 32.9 | 10.3 | −3.9 | 14.0 | 114.2 | 88.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Wang, H.; Rao, Z.; Yang, J.; Yang, S. Numerical Study and Optimization of a Novel Piezoelectric Transducer for a Round-Window Stimulating Type Middle-Ear Implant. Micromachines 2019, 10, 40. https://doi.org/10.3390/mi10010040
Liu H, Wang H, Rao Z, Yang J, Yang S. Numerical Study and Optimization of a Novel Piezoelectric Transducer for a Round-Window Stimulating Type Middle-Ear Implant. Micromachines. 2019; 10(1):40. https://doi.org/10.3390/mi10010040
Chicago/Turabian StyleLiu, Houguang, Hehe Wang, Zhushi Rao, Jianhua Yang, and Shanguo Yang. 2019. "Numerical Study and Optimization of a Novel Piezoelectric Transducer for a Round-Window Stimulating Type Middle-Ear Implant" Micromachines 10, no. 1: 40. https://doi.org/10.3390/mi10010040
APA StyleLiu, H., Wang, H., Rao, Z., Yang, J., & Yang, S. (2019). Numerical Study and Optimization of a Novel Piezoelectric Transducer for a Round-Window Stimulating Type Middle-Ear Implant. Micromachines, 10(1), 40. https://doi.org/10.3390/mi10010040






