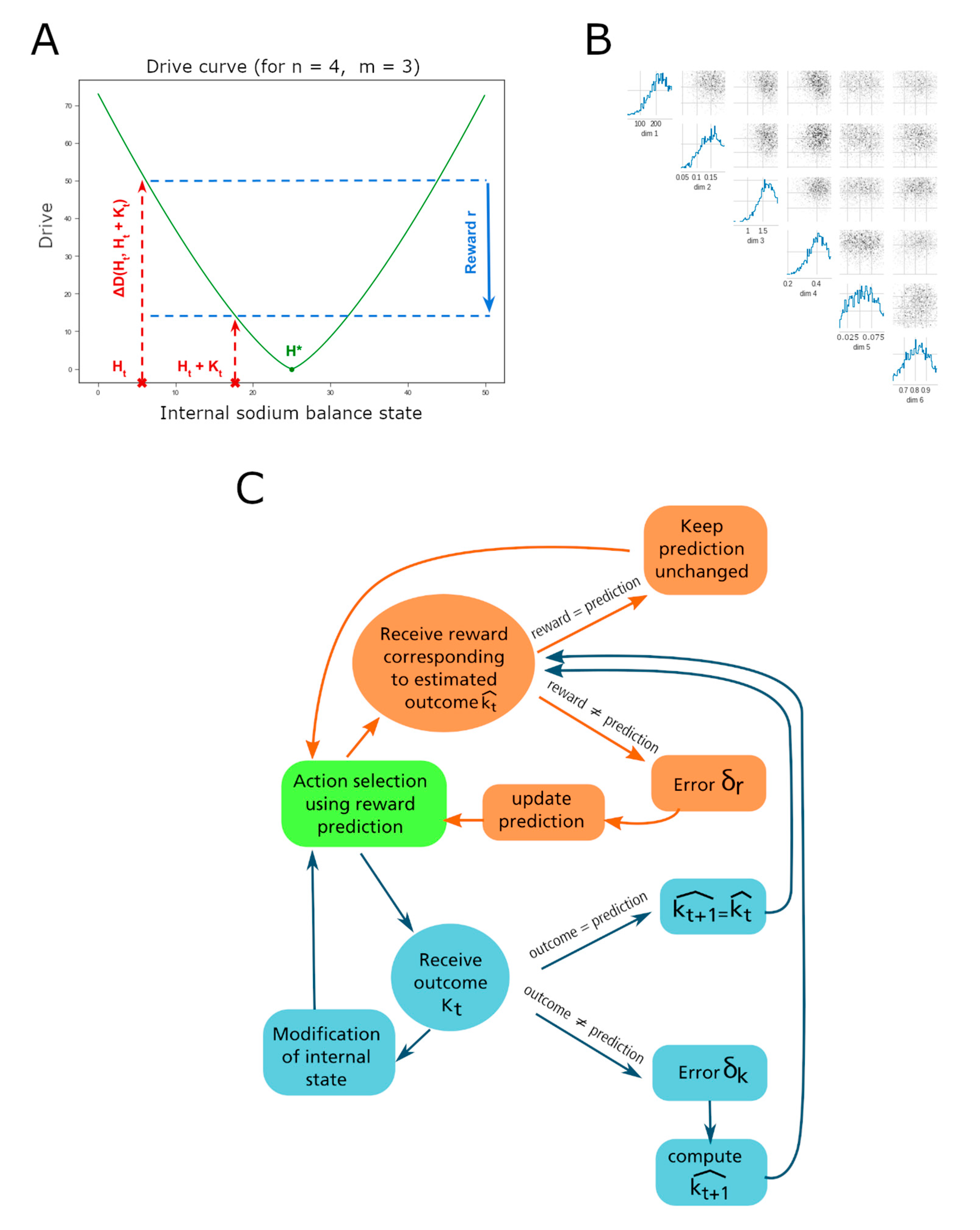
1. Introduction
Seeking and consuming nutrients is essential to survival and the maintenance of life. Animals living in dynamic and volatile environments must develop complex behavioral strategies to obtain the necessary nutritive substances. This has been classically viewed in terms of homeostatic regulation, where complex nutrient-seeking behaviors are triggered by physiological need. Animals also seek nutrients in advance of acute need. How animals acquire nutrient-directed behaviors has most often been examined through the lens of reinforcement learning (RL) theories. In RL, subjects acquire information about signals from the environment that are associated with the receipt of reward [
1]. Importantly, RL signals are distributed throughout the brain [
2,
3]. Similarly, physiological need impacts a wide array of brain circuits that regulate behaviors motivated by nutrient rewards [
4,
5,
6]. Intriguingly, the vast majority of RL theories do not treat the physiological origins of primary reward seeking, nor do they speak to how nutrients and their associated values are modulated by internal state. To maximize survival, physiological needs should augment signals that drive RL to promote learning in environments that offer access to essential nutrients. Thus, the reinforcing value of a nutrient, and consequently the degree to which an RL-based agent can learn from actions that acquire said nutrient, should be modulated in an appetite-dependent manner.
An essential area for exploration is thus the degree to which homeostatic and reinforcement learning processes are coupled in the central nervous system. RL processes have been most closely associated with mesolimbic circuitry, namely the midbrain DA neurons and their major target, the striatum [
7,
8,
9]. While debate remains as to the role of DA in RL [
10], it is increasingly clear that midbrain DA neurons and their responses to essential nutrients are modulated by physiological state, through direct hormonal influence [
11,
12,
13,
14] or via interactions with homeostatic and/or related circuits [
15,
16,
17,
18,
19,
20]. A particularly powerful example of the impact of physiological need on motivated behavior and DA signaling is sodium appetite. Sodium appetite is a natural behavior [
21] whereby a sodium deficit generates sodium-seeking behaviors and selective consumption of sodium over other nutrients. Under homeostatic conditions, rodents avoid consumption of hypertonic sodium solutions. However, sodium depletion (via injection of a diuretic/natriuretic, e.g., furosemide) or removal of the adrenal glands [
22] induces avid consumption of hypertonic sodium solutions and appetitive taste reactivity [
23]. Importantly, phasic DA responses to the taste of a hypertonic sodium solution are dynamically sensitive to sodium balance [
16,
17]. As with behavior, the DA response in sodium-depleted rats is blocked by lingual application of the epithelial sodium channel blocker amiloride [
16] and is selective for sodium solutions [
17]. Lithium chloride, a notable exception, is equally preferred [
17,
24], likely due to sodium taste fibers responding to lithium as well (but not potassium) [
25]. These data argue strongly that information related to the current state of sodium balance is communicated to midbrain DA neurons to regulate brain signals thought to drive RL. Taken together, these data pose a major challenge to current state of the art RL theories, and novel RL models need to be developed that account for the impact of physiological need and the role of gustatory information on reward learning. Sodium appetite is an ideal paradigm to address this issue.
We recently put forth a homeostatic reinforcement learning (HRRL) framework that was developed to study how animals learn need-based adaptive behavioral strategies in their environment to obtain rewarding outcomes [
26,
27]. The HRRL agent learns to maximize the total cumulative reward by performing actions and predicting the impact of their outcome on its internal state. This framework relies on a new definition of rewards: the rewarding value of an action is a function of the predicted impact on the difference between the current internal state and the ideal one (i.e., “setpoint”). The function that links the internal states to rewards is called the drive function. In other words, the reinforcing value of a stimulus is modulated by the degree to which it alleviates or exacerbates a physiological need. In this way, HRRL joins the predictive homeostatic regulation and reinforcement learning theories by positing that minimizing deviations from a homeostatic setpoint and maximizing reward are equivalent. In other words HRRL synthesizes RL algorithms with the drive reduction theories of motivation [
28]. HRRL has been used to simulate the consumption of various resources and reproduce experimental data. It can also be used to represent complex behavior such as anticipatory responding, binge eating [
26] and cocaine addiction [
29]. Interestingly, it can be shown mathematically that HRRL agents show predictive allostatic behavior and HRRL accounts for the incentive salience proposals: the internal state of the HRRL agents is dynamically changed according to upcoming challenges and the action values (incentives) are modulated dynamically by the internal state of the animal.
Here, we show that the HRRL model can account for sodium-seeking behavior and DA signaling in rats. We first required the HRRL models to reproduce behavioral data showing that sodium-deprived rats preferred sodium and lithium over potassium solutions. We then showed that such HRRL agents also reproduce the dynamics of DA signals. We then used the models to make several predictions about satiety-dependent modulation of behavior and how exposure to lithium may only modulate the behavior and the reinforcing value sodium.
3. Results
We first optimized the free parameters of the model (see Methods) to generate a cohort of individual agents whose simulated behavior reproduces the results of the 10 min two-bottle intake test conducted by Fortin and Roitman [
17]. The parameters sampled and optimized were the setpoint, the learning rate, the exploration rate and the quantity of sodium lost between each trial. They were tuned for the potassium preference score of the simulated sodium-deprived agents to be as close as possible to the experimentally observed values. Our goal was to capture the preference scores for the different salt solutions as a function of the animal’s internal state and choices in the experiment. To illustrate the results, we picked a parameter set (see
Appendix A Table A1) with nearly optimal parameter values producing a simulated individual “rat” (N.B. for the rest of the manuscript we will denote such simulated animal by agent).
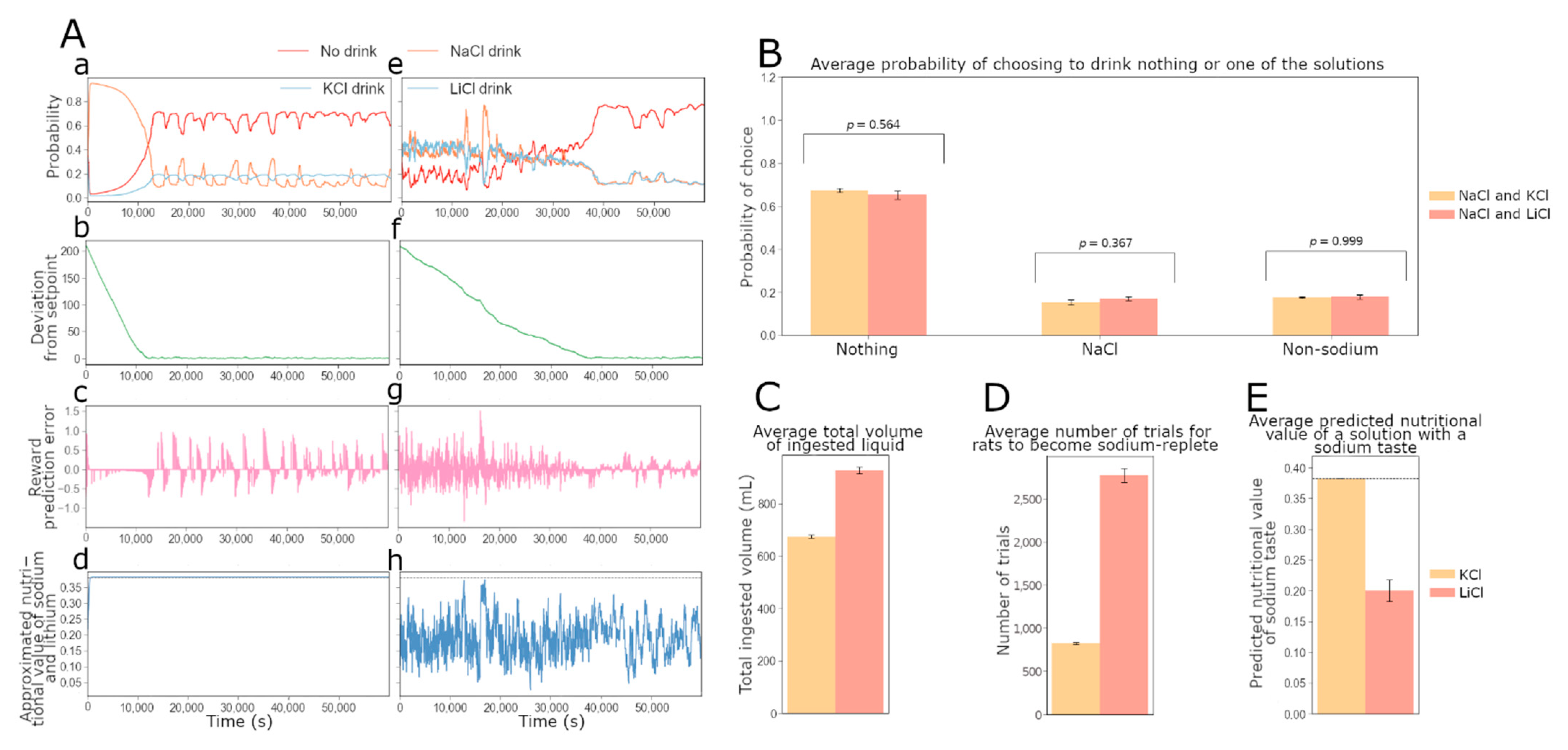
Figure 2 shows the behavior of such an individual agent throughout the experiments, and indicates that the model accounts for the qualitative observations made by Fortin and Roitman [
17] on the preference for sodium and lithium over potassium. In
Figure 2A, the evolution of the probability for an agent with optimized free parameters to consume either NaCl, KCl or nothing (left column), and the evolution of the probability for the same agent to consume either NaCl, LiCl or nothing (right column) are shown. In both simulations, the agent was initialized with a simulated depleted sodium internal state variable. As expected, when sodium and potassium are available, the probability of consuming NaCl increases greatly, while the probability of KCl consumption decreases and becomes lower than the chances of drinking nothing. This suggests that sodium-depleted agents selectively target the taste of sodium in their strategies to regulate their sodium level (as seen in the experiment). On the other hand, the probability of consuming NaCl or LiCl remains around 0.4, higher than the probability of drinking nothing. This indicates that the taste of sodium and lithium are both expected to restore sodium balance.
The individual choices made by the agent are also shown in
Figure 2A(a,e). This allows us to understand how the preference for sodium relative to a non-sodium salt evolves depending on the learned subjective value of each solution and the deviation from the setpoint (
Figure 2A(b,f)). We can make an inference about the dynamics of DA signaling in the NAc by studying the reward prediction errors (RPEs) of the agents during the simulated experiments (
Figure 2A(c,g)). Notice that NaCl and LiCl consumption gives rise to positive RPE signals, which correspond in our model to the experimentally observed positive DA responses in the NAc. Note that in the NaCl/LiCl task, the RPE signals are rapidly quenched, as the agent rapidly learns that both of these outcomes have an equal orosensory quality. We also tracked how the approximation of sodium nutritive value may evolve throughout the experiments (
Figure 2A(d,h)). We can see that when NaCl and KCl are present, the value of NaCl choice increases (the value of KCl decreases, result not shown), whereas in the NaCl/LiCl task, the value of NaCl stays relatively constant since their orosensory quality is equal. Indeed, our HRRL agent simulations show how DA dynamics are linked to internal state fluctuations, and also how the animals’ learned estimation of the nutritional value is based on gustatory information.
The model quantitatively reproduced the experimental results [
17] for the amount of ingested liquid and the individual preference for sodium, lithium or potassium.
Figure 2B(a,b) show that the average amount of liquid ingested during the experiment and the preference scores for the non-sodium solutions obtained with the simulations are consistent with the experimental values. We further confirmed qualitative observations for simulated individual agents (shown in
Figure 2A): at the end of the 10 min experiment, rats (as well as the simulated agents) with access to NaCl and LiCl (N = 15) are, approximately, equally likely to drink either of the two solutions. Rats with access to NaCl and KCl (N = 14), however, are unlikely to drink KCl, with a choice probability close to zero (see
Figure 2B(c)).
Based on the behaviorally validated model, we asked what would be predicted for the dopaminergic signal (in our model this corresponds to the PRE) and the predicted value associated with the sodium gustatory cue during the final part of the experiment.
Figure 2B(d) shows that the inter-individual-average phasic DA signal strength (as measured experimentally by the DA concentration) in the NAc during the 10 min experiment is higher when KCl is available than when LiCl is present as a choice, while in
Figure 2B(e) we show the average predicted value of a lick of sodium (or lithium) associated with the corresponding taste for the model agents at the end of the 10 min simulated experiment. The true nutritive value of one lick of sodium is indicated with a dotted line. Our simulations predict that rats learn the true value of sodium associated with its taste when NaCl and KCl are available. However, their estimate is equal to about half of the true value when NaCl and LiCl are available. This higher value of the rats’ estimated value of sodium and lithium when KCl is available may explain why the average RPE is also higher in this condition as compared to the LiCl-available condition (
Figure 2B(d)). On the other hand, when NaCl and LiCl are both available, the taste-dependent rewards are equally distributed between the two solutions, and hence the RPE for NaCl is reduced and a positive RPE is misattributed to the LiCl choice (in the sense that it is based purely on the taste information and not on the internal impact). Hence LiCl acquires a positive predicted value at the expense of the NaCl choice.
We then set out to see if the behavior-optimized model could also account for experimentally observed NAc DA responses to intraoral NaCl delivery in sodium-depleted rats and how this response develops as the animal continues to consume NaCl.
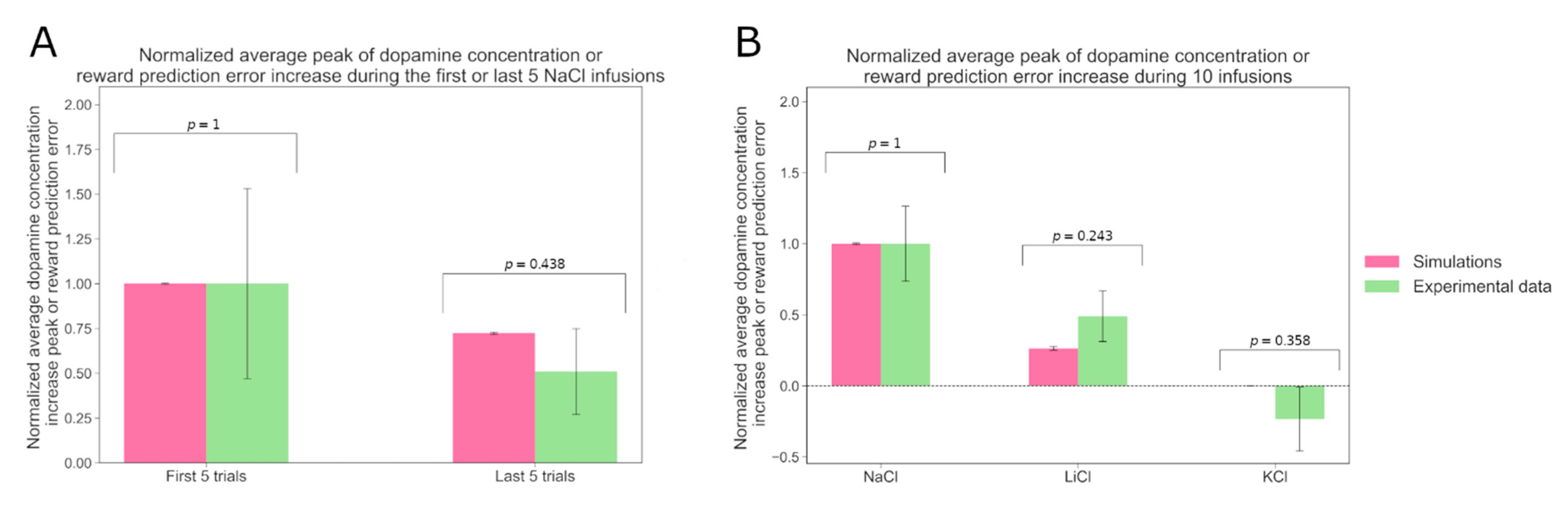
Figure 3 shows a simulated agent with parameters optimized to account for the experimental behavioral preference scores, as in the previous simulations. We can see that the simulated agents’ RPE signals are qualitatively consistent with the experimentally observed DA responses. Cone et al. [
16] measured the average DA response evoked by ten intraoral infusions of NaCl in sodium-depleted rats (N = 5). They observed that the first five infusions evoke larger DA responses than the last five.
Figure 3A shows the simulation results for the same experiment alongside the summary data from Cone et al. In order to simulate this experiment, we first measured the RPE for the naïve depleted model during the first five simulated trials of exposure to NaCl stimulus, then during the last five trials. The model was “depleted” by initializing the internal state significantly below the optimal value (variable
= 2). NaCl delivery was simulated as a series of 10 trials where the agent receives the palatable sodium reward. In the model, the impact of NaCl on the internal state was simulated by a dose-dependent shift in the internal state variable (here of
0.3819 per injection) and increase in the taste signal by
, with
=
(see methods). The results were averaged over five agents whose free parameter values were randomly sampled as previously presented. To compare the RPE with biological results, we referred to Cone et al.’s experiments [
16]. With their data, we calculated the baseline DA concentration for each trial and each rat as the average DA concentration during the 4 s preceding the NaCl infusion period. We subtracted this baseline from the DA concentration values during the 4 s infusion period. Then, for each rat, we computed the average peak of the DA concentration increase over the first and the last five trials. These two variables were finally averaged over the five rats. In order to compare the DA signal strength to the RPE, we normalized the DA signal from the first five trials and the RPE from the first five trials to unity. Consistent with the experimental results, we observed a decrease in the response between the first group of trials and the last. Indeed, Welch’s
t-test showed that the difference between the average responses to the first five trials and to the last ones was significant (
p = 6.93 × 10
−7). Moreover, the differences between the simulation and the experimental results were not statistically significant (Welch’s
t-test; see p-values on the figure). We then asked if the model can also account for the differential taste dependence of the phasic DA response. Fortin and Roitman (2018) tracked the average DA response of sodium-depleted rats during 10 intraoral infusions of NaCl, of KCl, of LiCl or of water and found that NaCl and LiCl evoke a strong DA response, while KCl does not. We simulated an analogue experiment.
Figure 3B compares the simulated and experimental results. Note that in our simulations we left out the response to water since that would, in the simulations, lead to a null result. With the experimental data from Fortin and Roitman [
17], we computed the peak of the DA concentration during the 4 s infusion period and subtracted the average DA concentration measured during the 4 s before the infusion onset as a baseline. This baseline was computed for each rat. We then averaged the DA increase over the rats. For the simulated data, we computed the average RPE signal evoked by 10 infusions of each solution. The results were averaged over six or five agents whose free parameter values were randomly sampled as previously. The baseline is null in our model. Then, in order to compare the DA data to the RPE, we normalized the response to NaCl to unity. We showed that in our simulations NaCl and LiCl are also the only solutions triggering a DA signal. Welch’s
t-test showed that the differences between the simulation and experimental results are not statistically significant.
We further reasoned that the original 10 min two-bottle intake test used by Fortin and Roitman [
17] may not give enough time for the acutely sodium-depleted rats to reach sodium satiety (or in terms of our model—to reach the optimal settling point of its internal state that corresponds to the minimum of the drive function). In order to study rat behavior when their sodium internal state approaches and reaches the optimal balance, we simulated the two-bottle intake test over a period that was sufficiently long for the agent to reach the satiation state.
Figure 4A shows simulations for the evolution of behavior and DA dynamics when the agents approach satiety and become replete in sodium.
Figure 4A(a,e) show the evolution of the probability for a simulated individual with optimized free parameters to drink either NaCl, KCl or nothing (a), and the evolution of the probability to drink either NaCl, LiCl or nothing (e). Interestingly, in both simulated conditions, the reduction in the consumption of NaCl or LiCl appears to anticipate satiety: the probability to drink starts to decrease before the amount of NaCl ingested (shown in
Figure 4A(b,f)) makes the individual reach satiety. We then tracked the RPE particularly when agents approach the replete state. In this case, consuming NaCl deviates the internal state away (beyond) from the setpoint. This deviation translates into a negative RPE. In our model, assuming that the baseline of DA outflow is sufficiently low, this corresponds to no DA being released in the NAc (should the baseline be high, the negative RPE would be interpreted as a phasic decrease in DA outflow). This is consistent with the fact that in sodium-repleted animals, intraoral infusions of hypertonic sodium chloride evoke no DA signal in the NAc: the DA concentration does not change from the baseline [
16,
17]. We also note the tell-tale oscillatory pattern in the RPE/DA over trials for the replete condition. This may be explained as follows: a small amount of sodium is lost between each trial; therefore, after having reached a replete state for the first time, as the agents have learned not to consume NaCl, the internal state can move below the setpoint again. When this happens, NaCl becomes rewarding again, which corresponds to the positive peaks of the RPE. The dynamics of RPE and the sodium-consumptive choice frequency are then determined by the physiological processes that regulate sodium loss.
When there is access to lithium chloride in the replete state, consuming this solution does not change the sodium internal state, but it can still be a punishment, similar to drinking sodium, since the two solutions acquire the same predictive value due to taste similarity. As in the 10 min experiment,
Figure 4A(d,h) indicates that the value of the predicted nutritional value of sodium associated to its taste,
, is learned when rats have access to NaCl and KCl. On the other hand, when rats consume both NaCl and LiCl, the long-term value of
oscillates around the value learned in the first 10 min of the experiment (equal to half the real nutritional value of one lick of NaCl).
In
Figure 4, the right panels show the average results for this simulated experiment, which could be tested with new experiments. First,
Figure 4B confirms the qualitative observation from
Figure 4A that in the replete state, the probability to drink nothing is much higher than the probability to drink one of the two solutions (NaCl or LiCl). Interestingly, agents with access to NaCl and LiCl (N = 15) appear to be slightly more likely to consume NaCl than agents in the other condition (N = 14). This is likely because the agent’s estimation of the nutritive value of sodium (under LiCl-NaCl access) is lower than under NaCl-KCl access (Panel 4e). Thus, consuming NaCl in a replete state under LiCl-NaCl access is a weaker punishment than for agents with access to NaCl and KCl. We are also interested in the amount of liquid agents consume during the experiment, in each condition (
Figure 4C). It appears that more liquid is consumed when NaCl and LiCl are the solutions available. This can be linked to the fact that more trials are necessary for the agent to reach satiety in this condition (
Figure 4D). Finally, in
Figure 4E, the agents appear to learn the true value of sodium associated to its taste when NaCl and KCl are available. However, their estimate is equal to approximately half of the true value (indicated by a dotted line) when NaCl and LiCl are available.
Evidence suggests that gastric distension is an early inhibitory signal of water ingestion in thirsty rats (Hoffmann et al., 2006). Hoffmann et al. show that dehydrated rats will almost continuously drink water or saline, yet stop drinking after 5 to 8 min before reaching satiety. The oropharynx is also likely to be involved in the anticipatory control of drinking behavior, by signaling the amount of water consumed (Zimmerman et al., 2017). Considering these results on thirst, we can hypothesize that animals would stop drinking before reaching sodium homeostasis because of early inhibitory signals. Arguably, an experiment where rats would consume sodium until fully replete would probably need to be conducted in several sessions to study the choices of the rats at different levels of internal sodium to avoid potential confounding due to gastric distension. This way, within a session, if rats stop drinking the solutions, we may assume it is because their internal need is satisfied and not because of sickness.
Therefore, we chose to simulate such experimental conditions by representing the extended two-bottle intake test as a series of short sessions. This different representation also allows us to zoom into the first and last minutes of the long experiments and compare depleted and repleted behaviors.
Figure 5 shows example data for the first and the last sessions of each version of the experiment (with NaCl and KCl or with NaCl and LiCl). In panels a, b and c, the data are collected from a sodium-depleted rat with access to NaCl and KCl, while in panels d, e and f, the data are collected from a sodium-depleted rat with access to NaCl and LiCl. As we can see in
Figure 5A, during the first session the probability of drinking NaCl increases significantly with sodium deprivation (left). During the last session, the rats are replete, so the choice not to drink anything is the most frequent one (right). In
Figure 5B, the choices of the rats are represented, and in
Figure 5C, we can see the reward prediction error signals evoked by the outcomes of these choices. We can observe that during the first session, KCl evokes a negative reward prediction error signal because it has an energy cost in our model. This means no DA is released in the NAc, which is consistent with Fortin and Roitman’s result [
17] that KCl does not evoke a DA response in the NAc. During the last session, sodium chloride triggers a weak negative reward prediction error as the rat is replete in sodium. This corresponds to the absence of DA release in the NAc observed by Fortin and Roitman in sodium-repleted rats receiving intraoral NaCl infusions [
17]. Interestingly, when we simulate an experiment where NaCl and LiCl are available, the probabilities of drinking NaCl and LiCl remain similar throughout the first and last sessions (
Figure 5D). We can see the actual simulated choices in
Figure 5E. We then can also track the reward prediction error signals evoked by the outcomes of these choices (see
Figure 5F). We note that during the first session, LiCl and NaCl both evoke positive reward prediction error signals, consistent with Fortin and Roitman’s results [
17]: intraoral infusions of NaCl and LiCl both trigger DA signals in the NAcs of sodium-depleted rats. Drinking LiCl makes the predicted nutritive value associated with the taste of sodium (and lithium) decrease, which is why after several successive licks of LiCl, the reward prediction error is negative in response to LiCl and NaCl. Drinking NaCl increases the predicted value of the sodium taste, making the taste of sodium more rewarding. Licks of NaCl thus increase the reward prediction error signal. During the last session, the rats reach the setpoint, so they drink sodium much less often. However, since rats lose some sodium after every trial, their internal sodium level can fall below the setpoint. In that case, NaCl and LiCl evoke a positive reward prediction error signal.
Finally, we wondered what our model would predict for the drinking behavior of rats in the presence of only KCl or LiCl. In particular, would sodium-depleted rats keep drinking LiCl, which appears to have the same taste as sodium, to try to satisfy their need? Conversely, would these rats eventually learn that LiCl has no impact on their sodium balance? We used the model to simulate the condition where only KCl or LiCl is available to sodium-depleted rats. Before this experiment, these two rats were trained while sodium-depleted as in the experiments described above: the rat with access to KCl could choose from NaCl and KCl and learned not to drink either as it became replete in sodium. The rat with access to LiCl could choose between NaCl and LiCl and also learned not to drink either once it became replete in sodium.
In order to see clearer what happens in the agent behavior and the corresponding agent internal variable (i.e., the RPE), we show examples of individual behavior and DA dynamics in
Figure 6F,G.
Figure 6F describes the experiment in which only KCl is available. The individual choices are shown in the middle panels. The reward prediction error dynamics are represented in
Figure 6, bottom panels. As we can see in the top panel, the individual agent’s probability to consume KCl smoothly decreases (null behavior probability decreases) because of the energy cost it imposes without any internal state benefit. Due to this cost, the KCl choice leads to negative RPE signals, which would correspond experimentally to an absence of DA release in the NAc. By the last session, the rat is much more likely to drink nothing (with a probability of about 0.8) than to drink KCl (with a probability of about 0.2). The probability of engaging with KCl is not null even after extended exposure because it represents the probability of making an exploratory decision. During the last session, sodium chloride triggers a weak negative reward prediction error in the model as the agent is replete in sodium. This may correspond to the absence of DA release in the NAc observed by Fortin and Roitman in sodium-repleted rats (2018). Panels
Figure 6D–F describe the experiment in which only LiCl is available. In
Figure 6G, on the left, we show the evolution of the probability to drink LiCl or nothing over time during the first session. On the right: the probability during the last session is shown. We can see the evolution of the relevant probabilities. We first notice that the probability of drinking LiCl is higher than that of drinking nothing only during the first session and a part of the second one. At the end of the last session, the difference in probability between drinking LiCl and nothing is similar to the one between drinking KCl and nothing, during the last session. The middle panels show the individual choices made. The bottom panels show the reward prediction error dynamics. It appears that, during the first session, the rat learns that LiCl does not increase its internal sodium level and imposes an energy cost. The reward prediction error signals in response to LiCl are first positive and become negative as the rat learns the value of lithium.
Figure 6 gives example data, represented over the entire duration of the experiments to show evolutions more clearly. It also gives average data that can be tested with future experiments.
Figure 6A shows the evolution of the probability for the rat to drink KCl or nothing over time (left), and the evolution of the probability for the rat to drink LiCl or nothing over time (right).
Figure 6B represents the reward prediction error signal of the same rats over time. This different representation gives us a global view of the evolution of the behavior of these individual rats throughout the whole experiment.
Figure 6C shows the average predicted value of a lick of sodium or lithium based on its taste for rats at the end of the 25 min experiment. The true nutritive value of one lick of sodium is indicated with a dotted line. This estimate is equal to half of the true value when KCl is available because it does not change in the absence of exposure to NaCl or LiCl. When LiCl is available, this value is close to zero (
p = 2.02 × 10
−30).
Figure 6E confirms that at the end of the experiment, rats are on average just as unlikely to drink LiCl (N = 15) as they are to drink KCl (N = 14), which does not taste like NaCl.
These average data allow us to propose an explanation for the individual behavior in
Figure 6A,B. The agent in panel a has already learned it is not worth it to drink KCl (the action value is initialized with the value the rat previously learned to satisfy its need in sodium). The probability of consuming potassium thus quickly drops to about 0.2. The agent in
Figure 6B has learned not to drink LiCl as it has kept its associated action value learned while sodium replete. This agent discovers through an exploratory decision that lithium is rewarding because of the previously learned
value, but lithium does not increase the internal state, so
decreases to 0. The reward prediction error signal therefore becomes negative in our model when the agent consumes LiCl, which has a cost but no homeostatic reward. Thus, the probability of consuming lithium quickly decreases to about 0.2. In
Figure 6D, we chose to represent the total liquid consumed during each version of the experiment. It appears that rats drink more liquid when they have access to LiCl than when KCl is the available solution (
p = 0.001).
4. Discussion
In this contribution, we show how sodium-directed behaviors and DA responses evoked by sodium and non-sodium stimuli following the induction of sodium appetite, can be accurately described by the homeostatic reinforcement (HRRL) theoretical framework. To do so, we optimized a simple HRRL agent to learn about the consequences of consuming different sodium (NaCl)- and non-sodium (KCl, LiCl)-containing solutions across various states of sodium balance. We show that the behavior of the HRRL model agents closely reproduced experimental data in which sodium-depleted rats were given access to NaCl, KCl or LiCl. Much like the rats, following the induction of sodium appetite, our HRRL agents strongly preferred solutions that contained sodium or lithium over potassium. We then examined the reward prediction error signals on single trials for the HRRL agents in response to consumption of salt-containing solutions. In our HRRL model, the RPE signal should correspond with phasic DA release in the NAc during sodium appetite. We show that the HRRL RPE is strongly modulated by internal state and the properties of the salt stimulus, which aligns well with experimentally observed DA signals in the NAc of sodium-depleted rats that are exposed to NaCl, LiCl and KCl. As in rats with sodium appetite, the HRRL RPE signals were positive for sodium tasting salts (NaCl and LiCl) under deplete conditions and attenuated as the agent approached a sodium-repleted state. Furthermore, the HRRL RPE for KCl was negligible, which also matched the experimentally observed phasic DA release.
We then used the HRRL framework to model sodium-seeking behavior in prolonged salt discrimination experiments, where sodium-depleted rats are allowed to consume sodium to satiety. Interestingly, our simulated agents began to reduce their consumption of NaCl before becoming sated. This suggested that the agent behavior reflects the anticipation of a future replete state and makes this as a prediction for the experiments. We further observed that after extensive experience with salt solutions while sodium depleted, the HRRL agent that had access to sodium and potassium chloride could predict the nutritive value of a lick of NaCl based on its taste. However, the estimated value of NaCl consumption was halved when the HRRL agents had access to both sodium and lithium chloride, which have been shown to taste similarly. We finally investigated the drinking behavior when only lithium chloride was available. Recall that lithium chloride tastes similar to sodium chloride but cannot restore the lost sodium. Our simulations predict that sodium-deprived rats learn that lithium chloride does not fulfill their sodium deficiency and thus should stop consuming it. Our simulation results can be tested with experiments that could give further insight into homeostatic state regulation, goal-directed behavior, reinforcement learning and how these phenomena depend on mesolimbic DA signaling.
In our HRRL framework, we modeled the state of sodium balance through a drive function that represents the deviation between the agents’ current state and an idealized homeostatic setpoint. In the model, the source of this sodium drive is ambiguous. However, in biological systems, sodium need is sensed via distributed neural systems. There are aldosterone-sensitive neurons in the nucleus of the solitary tract (NTS) that express 11β-hydroxysteroid dehydrogenase type 2 (HSD2+) that are activated by sodium depletion [
35]. Activation of NTS HSD2+ neurons can drive sodium consumption in sodium-repleted mice, whereas inhibition reduces sodium consumption in depleted animals [
36]. Importantly, NTS HSD2+ neurons project to other hindbrain areas such as the parabrachial complex (PB) and pre-locus coeruleus (pre-LC), which contribute to sodium appetite in distinct ways [
37,
38]. In addition to the NTS, sodium need is also sensed by neurons in the subfornical organ (SFO), which respond to changes in blood osmolality, among other things [
39], and has been shown to regulate sodium appetite [
40]. Notably, NTS HSD2+ neurons and SFO neurons that respond to osmolality challenges may influence sodium appetite through synergistic influences on neurons in the Bed Nucleus of the Stria Terminalis [
41]. Thus, in biological systems, state sensing, even for a single nutrient, is subject to complex multi-pathway regulation. This is to say nothing of how multiple competing needs interaction to influence behavior. In our HRRL models, the drive function was one-dimensional, as the current state of sodium balance was the only input under consideration.
In addition to sensing challenges to sodium balance to tune drive states, another key aspect of sodium appetite is the ability to detect sources of sodium in the environment. In the HRRL model, a “tastant” was evaluated by comparing its estimated reward value with the current state of sodium balance. If the agent was below an ideal setpoint, the tastant was evaluated as positively reinforcing. Otherwise the tastant was evaluated negatively as it further exacerbated deviations from homeostasis and cost energy to approach and consume. In vivo, sensing sodium primarily begins via Na+ selective epithelial sodium channels (eNACs), which are critical for sodium detection and discrimination [
42,
43,
44]. Sodium taste information is relayed to the brain via the chorda tympani (CT; [
45,
46]) and CT transection disrupts the expression of sodium appetite [
47,
48]. Interestingly, CT responses to sodium solutions are augmented by sodium appetite [
25], suggesting that changes in sodium balance can exert widespread effects on taste processing, even outside the CNS.
In the CNS, sodium appetite alters sodium taste responses in numerous brain areas, including hindbrain structures such as the NTS [
49,
50] and PB [
51] as well as circuits linked to reinforcement learning such as the striatum [
52] and the mesolimbic DA system [
16,
17]. Such widespread changes in sodium taste processing likely contribute to the robust changes in the consummatory responses and affective orosensory evaluation of sodium-containing solutions typically observed in sodium appetite [
23,
53].
Linking the gustatory properties of sodium-containing stimuli (taste, phasic) with sodium need (state, tonic) is essential for sodium appetite. Changes in the physiological state (tonic) serve to bias the organism’s behavioral repertoire towards sodium-seeking behaviors such that sodium intake is invigorated when tastants that contain sodium are identified. For example, consummatory responses such as bursts of licking, which are thought to reflect the palatability of a taste stimulus [
54], increase following sodium depletion [
53]. Prior work suggests that taste sensing and state interact in an additive fashion [
53], but if either is disrupted, the expression of sodium appetite is impaired [
36,
55].
Perhaps the key feature of the HRRL framework is that by incorporating a drive function that tracks deviations from homeostasis into a traditional RL-based agent, this enabled us to model the taste–state interactions that drive both current and future sodium-seeking behaviors associated with sodium appetite. At the moment of consumption (e.g., when an RPE is triggered), it is likely that state-dependent changes in taste information are relayed to DA neurons via the PB and pre-LC, both of which innervate the VTA [
38]. PB neurons express cFos following sodium consumption in sodium-depleted rats and this corresponds with reduced cFos staining in NTS HSD2+ neurons [
5]. Moreover, pre-LC FoxP2+ neurons that receive efferents from the NTS are strongly implicated in sodium appetite [
56] and project to the VTA [
17]. By tuning RPEs according to the current state of the animal, the HRRL model may mimic PB and pre-LC influences on VTA DA signaling that track physiological need.
Future work could explore whether the HRRL model also captures longer term plasticity in reinforcement circuits associated with sodium appetite. For example, sodium appetite is augmented by a single prior experience with sodium depletion [
57], while repeated depletions increase the need for free sodium intake long after sodium levels are replenished [
58,
59]. In terms of RPE signaling, mesolimbic DA neurons appear to encode sodium cues as reward predictive only after extensive experience with cue–sodium pairings while sodium depleted [
16]. However, after such associations are learned, phasic DA release to the sodium cue is only observed when the animals are in a state of need [
16]. It is likely the HRRL model would already account for this in its underlying math. Another challenging issue is how the proposed drive function is encoded in neural activity and how multiple drives may be prioritized with respect to each other (see also the discussion on multiple constraint satisfaction above).
An interesting point to consider in light of our results is whether the taste can be considered as another conditioned stimulus (CS) whose predicted impact of the consumed unconditioned stimulus (US) on the internal state is learned. A study on DA in mice consuming sucrose draws conclusions supporting this hypothesis [
32]. According to this study, a taste evokes a DA response only if the animal has associated through prior learning this taste with a nutritional value. In other words, the hedonic property of taste cannot alone be responsible for reinforcement. The study suggests that taste acts as a conditioned stimulus predictive of a food reward. This implies that the association between a taste and a nutritional value can be extinguished by giving the animal extensive experience with the taste in the absence of a value (an artificial sweetener instead of sucrose, for example). When it comes to sodium, however, taste does not seem to act simply as a conditioned stimulus and appetite appears to be regulated by a more complex interplay of both innate and learned mechanisms. This is reflected in our model by the non-linear drive function and the non-zero initial value of
. However, in our simulations, it is possible to extinguish seeking behavior towards the sodium taste after the exposure of sodium-depleted rats to LiCl. This suggests that the subjective value attached to sodium taste can be modified with learning, which should be investigated with new experiments.
Intriguingly, a recent proposal suggests that gustatory information could act as a hedonic predictor of the long-run worth of a good [
60]. This suggestion appears at first glance to be compatible with our work; for example, just as with the gustatory “hedonic” account in our simulation, the gustatory “reward/value” rapidly leads to the motivation of consumption behavior and is ultimately dominated by the nutritive lack of impact for LiCl with the end value converging to zero.
Our model, as all computational models, faces several limitations: the actions are necessarily chosen and performed by the agent at discrete and regular time steps. Moreover, the solutions are consumed at a fixed volume. A continuous time model, in which the internal state of the agent has to be constantly regulated with actions that maintain its homeostasis, would be closer to reality. Indeed, the temporality of physiological regulation is important as the deviation from the setpoint must be reduced as soon as possible. We have previously shown that taking the shortest path to reach the setpoint optimizes fitness and that HRRL agents learn to preemptively avoid life-threatening excursions far from the homeostatic optima [
61].
The proposed framework remains quite an abstract algorithmic model: how it relates to the neural circuitry mechanistically remains to be studied. For example, as discussed above, the circuits that mediate taste–state interactions in the brain are multi-faceted and could be communicated with the DA system through many convergent pathways. Another challenge that remains is how one might observe the drive function? A hint of predictive internal state encoding has been shown experimentally (see discussion above and [
4]); however, it is not clear if such neural traces represent the internal state itself or the drive function necessary for learning and generating the behaviors. In fact, perhaps the drive function properties could be a key to individual differences in homeostatically motivated learned behaviors. Thus, understanding how one may measure the properties of the drive function from behavioral observations remains a key challenge.
In conclusion, we showed that a homeostatic reinforcement learning theory can account for behaviors motivated by sodium appetite. A recent study also put forth a similar argument [
62]—focusing on a different dataset, they showed that HRRL agents can match two-bottle test behavior for sodium and water choices. Here, we critically extend these ideas to show that the HRRL framework can also quantitatively account for the taste- and state-dependent DA responses, arguing that such DA signaling may in fact be causal for the learning of such appetitive behaviors.