Analysis of Hepatic Lipid Metabolism Model: Simulation and Non-Stationary Global Sensitivity Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Recommendations for Menu Planning
2.1.2. Mathematical Model of Hepatic Lipid Metabolism
2.2. Methods
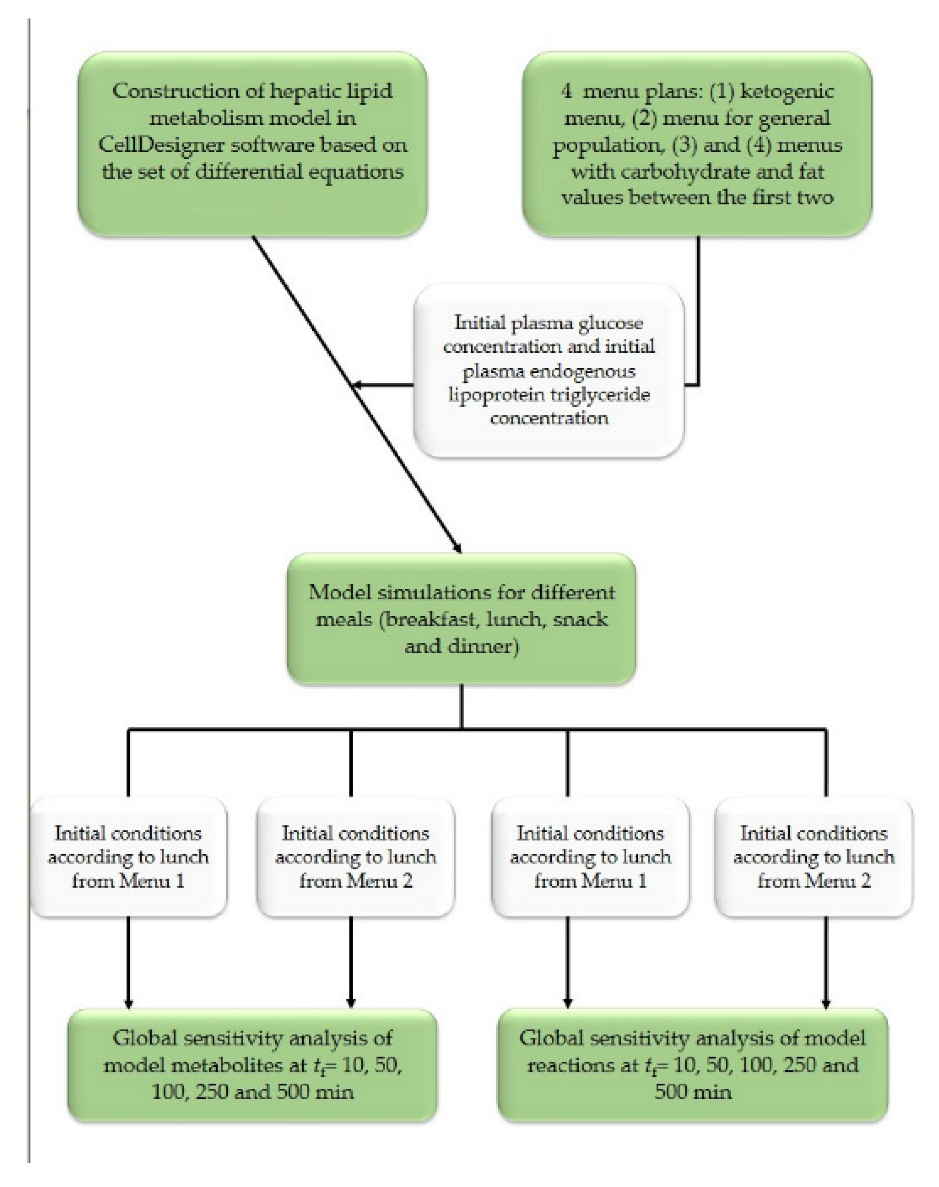
2.2.1. Hepatic Lipid Metabolism Model Simulation
2.2.2. Non-Stationary Global Sensitivity Analysis
3. Results and Discussion
3.1. Meal Plans
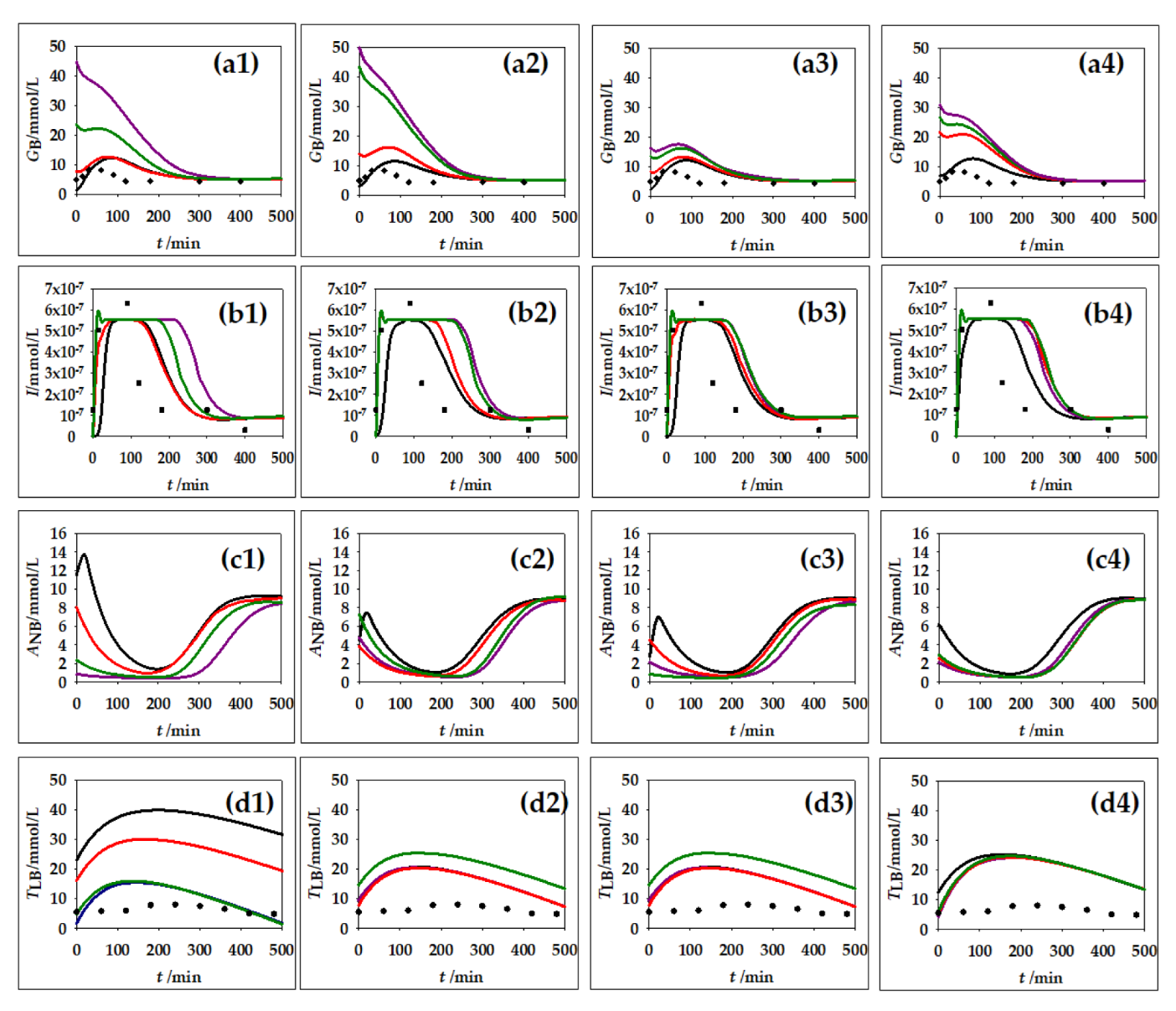
3.2. Hepatic Lipid Metabolism Construction and Simulation in CellDesigner
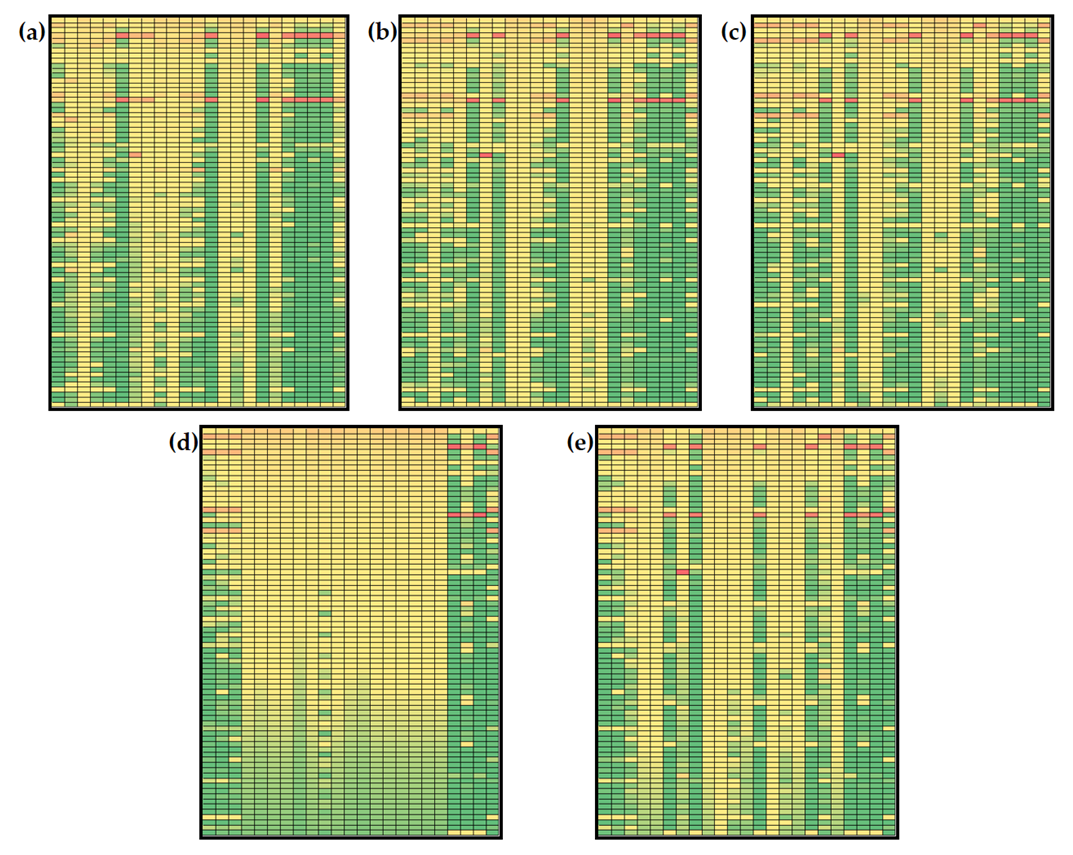
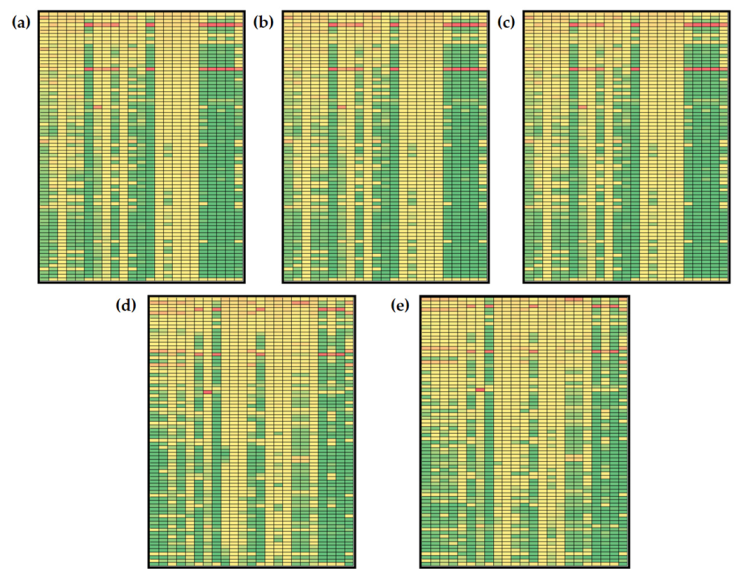
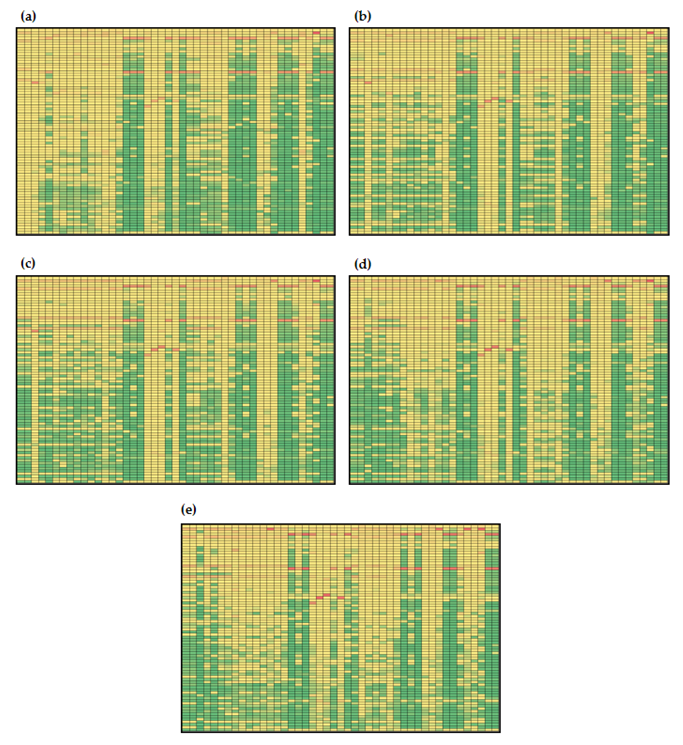
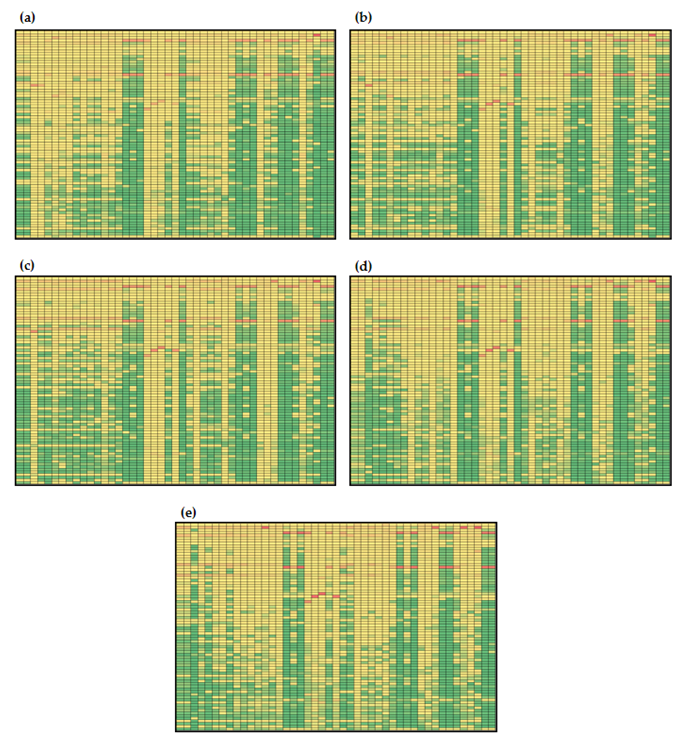
3.3. Non-Stationary Global Sensitivity Analysis
3.3.1. Global Sensitivities of the Model Metabolites
3.3.2. Global Sensitivities of the Model Reactions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Heer, M.; Egert, S. Nutrients other than carbohydrates: Their effects on glucose homeostasis in humans. Diabetes. Metab. Res. Rev. 2015, 31, 14–35. [Google Scholar] [CrossRef]
- van Ommen, B.; van den Broek, T.; de Hoogh, I.; van Erk, M.; van Someren, E.; Rouhani-Rankouhi, T.; Anthony, J.C.; Hogenelst, K.; Pasman, W.; Boorsma, A.; et al. Systems biology of personalized nutrition. Nutr. Rev. 2017, 75, 579–599. [Google Scholar] [CrossRef]
- Panagiotou, G.; Nielsen, J. Nutritional systems biology: Definitions and approaches. Annu. Rev. Nutr. 2009, 29, 329–339. [Google Scholar] [CrossRef]
- Badimon, L.; Vilahur, G.; Padro, T. Systems biology approaches to understand the effects of nutrition and promote health. Br. J. Clin. Pharmacol. 2017, 83, 38. [Google Scholar] [CrossRef]
- Hood, L.; Heath, J.R.; Phelps, M.E.; Lin, B. Systems biology and new technologies enable predictive and preventative medicine. Science 2004, 306, 640–643. [Google Scholar] [CrossRef] [PubMed]
- Mc Auley, M.T.; Proctor, C.J.; Corfe, B.M.; Cuskelly, G.C.; Mooney, K.M. Nutrition Research and the Impact of Computational Systems Biology. J. Comput. Sci. Syst. Biol. 2013, 6, 271–285. [Google Scholar] [CrossRef]
- De Graaf, A.A.; Freidig, A.P.; De Roos, B.; Jamshidi, N.; Heinemann, M.; Rullmann, J.A.C.; Hall, K.D.; Adiels, M.; Van Ommen, B. Nutritional systems biology modeling: From molecular mechanisms to physiology. PLoS Comput. Biol. 2009, 5, e1000554. [Google Scholar] [CrossRef]
- Jolicoeur, M.; Jolicoeur, M. Modeling cell behavior: Moving beyond intuition. AIMS Bioeng. 2014, 1, 1–12. [Google Scholar] [CrossRef]
- Yasemi, M.; Jolicoeur, M. Modelling Cell Metabolism: A Review on Constraint-Based Steady-State and Kinetic Approaches. Processes 2021, 9, 322. [Google Scholar] [CrossRef]
- Strutz, J.; Martin, J.; Greene, J.; Broadbelt, L.; Tyo, K. Metabolic kinetic modeling provides insight into complex biological questions, but hurdles remain. Curr. Opin. Biotechnol. 2019, 59, 24–30. [Google Scholar] [CrossRef] [PubMed]
- Nijhout, H.F.; Best, J.A.; Reed, M.C. Using mathematical models to understand metabolism, genes, and disease. BMC Biol. 2015, 13, 79. [Google Scholar] [CrossRef] [PubMed]
- Ederer, M.; Gilles, E.D. Thermodynamically Feasible Kinetic Models of Reaction Networks. Biophys. J. 2007, 92, 1846–1857. [Google Scholar] [CrossRef] [PubMed]
- Félix, G.; Ancheyta, J.; Trejo, F. Sensitivity analysis of kinetic parameters for heavy oil hydrocracking. Fuel 2019, 241, 836–844. [Google Scholar] [CrossRef]
- Wang, J.; Ye, J.; Yin, H.; Feng, E.; Wang, L. Sensitivity analysis and identification of kinetic parameters in batch fermentation of glycerol. J. Comput. Appl. Math. 2012, 236, 2268–2276. [Google Scholar] [CrossRef]
- Link, K.G.; Stobb, M.T.; Di Paola, J.; Neeves, K.B.; Fogelson, A.L.; Sindi, S.S.; Leiderman, K. A local and global sensitivity analysis of a mathematical model of coagulation and platelet deposition under flow. PLoS ONE 2018, 13, e0200917. [Google Scholar] [CrossRef]
- López-Cruz, I.L.; Rojano-Aguilar, A.; Salazar-Moreno, R.; Ruiz-García, A.; Goddard, J. A comparison of local and global sensitivity analyses for greenhouse crop models. Acta Hortic. 2012, 957, 267–273. [Google Scholar] [CrossRef]
- Lin, S.; Xie, M.; Wu, M.; Zhou, W. Global Sensitivity Analysis of Large Reaction Mechanisms Using Fourier Amplitude Sensitivity Test. J. Chem. 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Feng, K.; Lu, Z.; Yang, C. Enhanced Morris method for global sensitivity analysis: Good proxy of Sobol’ index. Struct. Multidiscip. Optim. 2019, 59, 373–387. [Google Scholar] [CrossRef]
- Ge, Q.; Menendez, M. Extending Morris method for qualitative global sensitivity analysis of models with dependent inputs. Reliab. Eng. Syst. Saf. 2017, 162, 28–39. [Google Scholar] [CrossRef]
- Silva, A.S.; Ghisi, E. Evaluation of capabilities of different global sensitivity analysis techniques for building energy simulation: Experiment on design variables. Ambient. Construído 2021, 21, 89–111. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Trame, M.N.; Lesko, L.J.; Schmidt, S. Sobol sensitivity analysis: A tool to guide the development and evaluation of systems pharmacology models. CPT Pharmacomet. Syst. Pharmacol. 2015, 4, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Carta, J.A.; Díaz, S.; Castañeda, A. A global sensitivity analysis method applied to wind farm power output estimation models. Appl. Energy 2020, 280, 115968. [Google Scholar] [CrossRef]
- Xu, C.; Gertner, G. Understanding and comparisons of different sampling approaches for the Fourier Amplitudes Sensitivity Test (FAST). Comput. Stat. Data Anal. 2011, 55, 184. [Google Scholar] [CrossRef] [PubMed]
- Ryan, E.; Wild, O.; Voulgarakis, A.; Lee, L. Fast sensitivity analysis methods for computationally expensive models with multi-dimensional output. Geosci. Model Dev. 2018, 11, 3131–3146. [Google Scholar] [CrossRef]
- Sobol’, I.M.; Kucherenko, S. Derivative based global sensitivity measures. Procedia Soc. Behav. Sci. 2010, 2, 7745–7746. [Google Scholar] [CrossRef]
- Nandi, S.; Singh, T.; Singla, P. Derivative based global sensitivity analysis using conjugate unscented transforms. Proc. Am. Control Conf. 2019, 2019, 2458–2463. [Google Scholar]
- Fang, S.; Gertner, G.Z.; Shinkareva, S.; Wang, G.; Anderson, A. Improved generalized Fourier amplitude sensitivity test (FAST) for model assessment. Stat. Comput. 2003, 13, 221–226. [Google Scholar] [CrossRef]
- Uys, L.; Hofmeyr, J.H.S.; Rohwer, J.M. Coupling kinetic models and advection–diffusion equations. 2. Sensitivity analysis of an advection–diffusion–reaction model. Silico Plants 2021, 3, 14. [Google Scholar] [CrossRef]
- Saltelli, A.; Bolado, R. An alternative way to compute Fourier amplitude sensitivity test (FAST). Comput. Stat. Data Anal. 1998, 26, 445–460. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.P.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Tušek, A.J.; Jurina, T.; Čurlin, M. Global Sensitivity Analysis of the Biological Part of the Integrated BTEX Bioremediation Model. Environ. Eng. Sci. 2016, 33, 404–422. Available online: https://home.liebertpub.com/ees (accessed on 20 June 2022). [CrossRef]
- Tušek, A.; Kurtanjek, Ž. MATHMOD Vienna 09 Proceedings; ARGESIM: Vienna, Austria, 2009. [Google Scholar]
- Jurinjak Tušek, A.; Čurlin, M.; Jurina, T.; Landeka Dragičević, T.; Kurtanjek, Ž. Parameter Sensitivity Analysis of Activated Sludge Models for Wastewater Treatment. Available online: https://www.researchgate.net/publication/268502503_Parameter_sensitivity_analysis_of_activated_sludge_models_for_wastewater_treatment (accessed on 13 October 2022).
- Phinney, S.D. Ketogenic diets and physical performance. Nutr. Metab. 2004, 1, 2. [Google Scholar] [CrossRef]
- Pratt, A.C.; Wattis, J.A.D.; Salter, A.M. Mathematical modelling of hepatic lipid metabolism. Math. Biosci. 2015, 262, 167–181. [Google Scholar] [CrossRef] [PubMed]
- Godinez, H.C.; Rougier, E.; Osthus, D.; Lei, Z.; Knight, E.; Srinivasan, G. Fourier amplitude sensitivity test applied to dynamic combined finite-discrete element methods–based simulations. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 30–44. [Google Scholar] [CrossRef]
- Bender, D.A. Introduction to Nutrition and Metabolism; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Scientific Opinion on Dietary Reference Values for carbohydrates and dietary fibre. EFSA J. 2016, 8, 1462.
- EFSA. Trusted Science for Safe Food. Available online: https://www.efsa.europa.eu/en (accessed on 12 October 2022).
- Funahashi, A.; Morohashi, M.; Kitano, H.; Tanimura, N. CellDesigner: A process diagram editor for gene-regulatory and biochemical networks. BIOSILICO 2003, 1, 159–162. [Google Scholar] [CrossRef]
- Funahashi, A.; Matsuoka, Y.; Jouraku, A.; Morohashi, M.; Kikuchi, N.; Kitano, H. CellDesigner 3.5: A versatile modeling tool for biochemical networks. Proc. IEEE 2008, 96, 1254–1265. [Google Scholar] [CrossRef]
- Berg, J.M.; Tymoczko, J.L.; Stryer, L. Good Hardcover 5th or Later Edition. In Biochemistry, 6th ed.; Palgrave MacMillan: London, UK, 2007; Available online: https://www.abebooks.com/Biochemistry-6th-ed-Berg-Jeremy-Tymoczko/14974066950/bd#&gid=1&pid=1 (accessed on 12 October 2022).
- Cruz, M.L.; Evans, K.; Frayn, K.N. Postprandial lipid metabolism and insulin sensitivity in young Northern Europeans, South Asians and Latin Americans in the UK. Atherosclerosis 2001, 159, 441–449. [Google Scholar] [CrossRef]
- Yoshizane, C.; Mizote, A.; Yamada, M.; Arai, N.; Arai, S.; Maruta, K.; Mitsuzumi, H.; Ariyasu, T.; Ushio, S.; Fukuda, S. Glycemic, insulinemic and incretin responses after oral trehalose ingestion in healthy subjects. Nutr. J. 2017, 16, 9. [Google Scholar] [CrossRef]
- Sarabhai, T.; Koliaki, C.; Mastrototaro, L.; Kahl, S.; Pesta, D.; Apostolopoulou, M.; Wolkersdorfer, M.; Bönner, A.C.; Bobrov, P.; Markgraf, D.F.; et al. Dietary palmitate and oleate differently modulate insulin sensitivity in human skeletal muscle. Diabetologia 2022, 65, 301–314. [Google Scholar] [CrossRef]
- Campbell, J.E.; Newgard, C.B. Mechanisms controlling pancreatic islet cell function in insulin secretion. Nat. Rev. Mol. Cell Biol. 2021, 22, 142–158. [Google Scholar] [CrossRef] [PubMed]
- Eliasson, L.; Abdulkader, F.; Braun, M.; Galvanovskis, J.; Hoppa, M.B.; Rorsman, P. Novel aspects of the molecular mechanisms controlling insulin secretion. J. Physiol. 2008, 586, 3313–3324. [Google Scholar] [CrossRef] [PubMed]
- Bermudez, B.; Ortega-Gomez, A.; Varela, L.M.; Villar, J.; Abia, R.; Muriana, F.J.G.; Lopez, S. Clustering effects on postprandial insulin secretion and sensitivity in response to meals with different fatty acid compositions. Food. Funct. 2014, 5, 1374–1380. [Google Scholar] [CrossRef] [PubMed]
- Iannello, S.; Milazzo, P.; Belfiore, F. Animal and human tissue Na,K-ATPase in normal and insulin-resistant states: Regulation, behaviour and interpretative hypothesis on NEFA effects. Obes. Rev. 2007, 8, 231–251. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Tan, K.W.J.; Lim, J.Z.; Magkos, F.; Henry, C.J. Dietary fat and carbohydrate quality have independent effects on postprandial glucose and lipid responses. Eur. J. Nutr. 2018, 57, 243–250. [Google Scholar] [CrossRef]
- Nguyen Quang, M.; Rogers, T.; Hofman, J.; Lanham, A.B. Global Sensitivity Analysis of Metabolic Models for Phosphorus Accumulating Organisms in Enhanced Biological Phosphorus Removal. Front. Bioeng. Biotechnol. 2019, 7, 234. [Google Scholar] [CrossRef]
- Kent, E.; Neumann, S.; Kummer, U.; Mendes, P. What Can We Learn from Global Sensitivity Analysis of Biochemical Systems? PLoS ONE 2013, 8, e79244. [Google Scholar] [CrossRef] [PubMed]
- Jurina, T.; Tušek, A.J.; Čurlin, M. Local sensitivity analysis and metabolic control analysis of the biological part of the BTEX bioremediation model. Biotechnol. Bioprocess Eng. 2015, 20, 1071–1087. [Google Scholar] [CrossRef]
- Zi, Z. Sensitivity analysis approaches applied to systems biology models. IET Syst. Biol. 2011, 5, 336–346. [Google Scholar] [CrossRef]


| Meal | Components with Corresponding Masses | |
|---|---|---|
| Menu 1 | Breakfast | 2 egg yolks (30 g), bacon (50 g) and gouda cheese (80 g) prepared in olive oil (5 g) |
| Lunch | Salmon (100 g) prepared in olive oil (10 g) and green salad (100 g) with flax seeds (10 g) and olive oil (5 g) | |
| Snack | Handful of walnuts (30 g) | |
| Dinner | Chicken (120 g) prepared with cooking cream (150 mL) and broccoli (100 g) with olive oil (5 g) | |
| Menu 2 | Breakfast | Cornflakes (80 g) with 2.8% m.f. yogurt (200 mL) and a cup of chamomile tea with sugar (5 g) |
| Lunch | Plate of vegetable soup (200 mL), chicken breast (200 g) prepared in olive oil (10 g) with couscous (50 g), tomato salad (100 g) with flax seeds (5 g), 2 slices of graham bread and a glass of orange juice (200 mL) | |
| Snack | Banana (100 g) and a handful of almonds (30 g) | |
| Dinner | Tuna steak (100 g) with potatoes (100 g) prepared with olive oil (10 g) and a cup of apple compote (200 mL) | |
| Menu 3 | Breakfast | 2 egg yolks (30 g) and bacon (50 g) prepared in olive oil (5 g) and a slice of bread (25 g) |
| Lunch | Plate of vegetable soup (200 mL), tuna steak (150 g) with potatoes (100 g) and Swiss chard prepared (100 g) in olive oil (10 g) | |
| Snack | 3.2% m.f. yogurt (150 mL) and mixed nuts (40 g) | |
| Dinner | Chicken (100 g), rice (60 g) with vegetable salad (150 g) and olive oil (15 g) | |
| Menu 4 | Breakfast | 2 slices of graham bread (50 g) with butter (15 g) and honey (20 g) and chamomile tea (200 mL) with sugar (5 g) |
| Lunch | Plate of vegetable soup (200 mL), beef stew (150 g) prepared with olive oil (10 g) with pasta (80 g) and vegetable salad (100 g) with olive oil (5 g) | |
| Snack | Sliced apple (100 g) with peanut butter (10 g) | |
| Dinner | Salmon (100 g) prepared in olive oil (5 g) with bulgur (50 g), vegetable salad (100 g) with olive oil (5 g) and a glass of orange juice (200 mL) |
| Variable | Balance | Initial Conditions |
|---|---|---|
| plasma insulin | 60 pmol/L | |
| liver glucose | 8 mmol/L | |
| liver glucose-6-phospahte | 2.06 mmol/L | |
| liver glycogen | 50 mmol/L | |
| liver pyruvate | 0.37 mmol/L | |
| free fatty acids in liver | 0.57 mmol/L | |
| triacylglycerides secretory pool in liver | 0.0149 mmol/L | |
| triacylglycerol storage pool in liver | 40 mmol/L | |
| glucose in muscles | 0.5 mmol/L | |
| glycogen in muscle | 20 mmol/L | |
| glucose-6-posphate in muscle | 0.133 mmol/L | |
| pyruvate in muscle | 0.009 mmol/L | |
| free fatty acids in muscle | 0.53 mmol/L | |
| triacylglycerides in muscle | 14.8 mmol/L | |
| AMP in muscles | 0 mmol/L | |
| adipose triacylglycerides | 500 mmol/L | |
| adipose free fatty acids | 0.57 mmol/L | |
| adipose glycerol | 0.17 mmol/L | |
| adipose glucose | 2.53 mmol/L | |
| exogenous plasma triacylglycerides | 0 mmol/L | |
| plasma free fatty acids | 0.5 mmol/L | |
| endogenous plasma triacylglycerides | Table 4 | |
| plasma glucose | Table 4 |
| Parameter | Value | |
|---|---|---|
| 1. | αA (adipose tissue volume) | 15.60 L |
| 2. | αL (liver tissue volume) | 1.60 L |
| 3. | αM (skeletal muscle volume) | 26.4 L |
| 4. | β6 (rate of liver de novo lipogenesis from pyruvate) | 31.6 L/min |
| 6. | βf (adipose release of triacylglycerides to non-esterified fatty acids) | 0.117 mmol/min |
| 7. | βL (liver glycogenolysis) | 12 L/min |
| 8. | βm (muscle glycogenolysis) | 82.5 L/min |
| 9. | µamp (national adenosine monophosphate/adenosine diphosphate creation rate) | 1.8 |
| 10. | µb (lactate production by red blood cells) | 0.133 mmol/min |
| 11. | µe (muscle triglyceride breakdown to free fatty acids) | 0.420 mmol/min |
| 12. | µs (muscle free fatty acid esterification to triglycerides) | 7.19 × 106 L mmol/min |
| 13. | µ1 (plasma glucose usage) | 0.588 mmol/min |
| 14. | µ3 (muscle glucose-6-phospahte usage) | 7.839 × 107 L mmol/min |
| 15. | µ4 (muscle free fatty acid usage) | 100 L/min |
| 16. | c0 (small parameters) | 0.1 mmol/L |
| 17. | cc (range of glucose concentrations over which excess insulin secretion occurs) | 2.5 mmol/L |
| 18. | dba (adipose uptake of glucose) | 0.3 mmol/min |
| 19. | k10 (affinity for hydrolysis of triglycerides to secretory pool) | 0.625 mmol/L |
| 20. | k11 (basal insulin secretion rate) | 48 mmol/min |
| 21. | k12 (increased fraction of very low-density lipoprotein 1 secretion by insulin) | 0.2 |
| 22. | k13 (rate at which insulin modifies the fraction of very low-density lipoprotein 1 to very low-density lipoprotein 2 secretion) | 15 mmol/L |
| 23. | k14 (basal very low-density lipoprotein 1 secretion fraction) | 0.6 |
| 24. | k22 (excess insulin secretion rate due to glucose stimulation) | 48 mmol/min |
| 25. | k5 (flux control coefficient for insulin inhibition of free fatty acid oxidation) | 8.23 × 107/mmol |
| 26. | k6 (affinity for very low-density lipoprotein 2 triglyceride secretion through secretory pathway) | 0.3 mmol/L |
| 27. | k61 (liver glucose dephosphorylation rate) | 4 L/min |
| 28. | k6p (muscle glucose-6-phospahte to pyruvate conversion rate) | 6.56 × 108 L2/mmol min |
| 29. | k7 (maximum rate of free fatty acid oxidation) | 0.759 L/min |
| 30. | k8 (affinity for esterification of free fatty acids to triglycerides) | 0.625 mmol/L |
| 31. | k9 (affinity of additional bulk lipidation) | 43.583 mmol/L |
| 32. | k9a (release of very low-density lipoproteins from secretory pathway) | 1 L/min |
| 33. | ka (adipose free fatty acid uptake of chylomicron triglycerides, insulin independent) | 0.1497 L/min |
| 34. | kaa (adipose free fatty acid esterification to triglycerides) | 3.11 × 105 L2/mmol min |
| 35. | kai (adipose free fatty acid uptake of chylomicron triglycerides, insulin dependent) | 2.08 × 106 1/mmol |
| 36. | kal (pyruvate to acetyl coenzyme A conversion rate) | 0.00002 L2/mmol min |
| 37. | kba (adipose uptake of endogenous lipoprotein triglycerides) | 0.0104 L/min |
| 38. | kbl (liver uptake of plasma non-esterified fatty acids) | 0.156 L/min |
| 39. | kbm (muscle uptake of plasma non-esterified fatty acids) | 0.226 L/min |
| 40. | kcl (liver free fatty acid uptake of chylomicron triglycerides) | 0.0075 L/min |
| 41. | kcm (muscle free fatty acid uptake of chylomicron triglycerides) | 0.0449 L/min |
| 42. | kd (insulin degradation rate) | 1.733 × 1014 L/mmol |
| 43. | kdl (liver glycogenolysis; insulin-inhibited rate) | 3.5 × 188 mmol/L |
| 44. | kdy (muscle glycogenolysis; insulin-inhibited rate) | 4 × 108 L/mmol |
| 45. | kft (adipose release of triglyceride to non-esterified fatty acids; insulin-inhibited rate) | 1.67 × 1014 L/mmol |
| 46. | kga (rate of glucose diffusion between plasma and adipose mediated by glucose 4 transporters) | 1.67 × 106 |
| 47. | kgi (glucose diffusion between plasma and muscles, insulin-mediated) | 2.632 × 108 mmol/L |
| 48. | kgl (plasma glucose diffusion rate to liver) | 0.9277 mmol/L |
| 49. | kgl2 (live glucose diffusion rate to blood) | 0.396 mmol/L |
| 50. | kgm (plasma glucose diffusion rate to muscle) | 0.0380 mmol/L |
| 51. | kgm2 (muscle glucose diffusion rate to plasma) | 0.0380 mmol/L |
| 52. | kgp (glucose-6-phospahte uptake from adipose glycerol) | 0.311 L/min |
| 53. | klp (rate of plasma triglyceride uptake by adipose tissue) | 0.25 |
| 54. | kLG (Michaelis–Menten constant of glucokinase in liver) | 8.95 mmol/L |
| 55. | kLH (Michaelis–Menten constant of hexokinase in liver) | 0.0115 mmol/L |
| 56. | kMH (Michaelis–Menten constant of hexokinase in muscle) | 8.98 mmol/L |
| 57. | kna (rate of plasma free fatty acid uptake into adipose free fatty acids) | 0.0697 L/min |
| 58. | kp (rate of insulin-mediated glucose-6-phoshate to pyruvate) | 1.41 × 107 mmol/L |
| 59. | kp6 (constant of pyruvate conversion to glucose-6-phospate) | 6.56 × 108 L2/mmol min |
| 60. | kpp (rate of muscle pyruvate transport to liver) | 0.5 |
| 61. | kr (rate of endogenously derived lipoprotein triglycerides by liver as free fatty acids) | 0.00058 mmol |
| 62. | krep (glucose-6-phospahte inhibition constant of hexokinase in muscle) | 2.98 mmol/L |
| 63. | kt (uptake rate of plasma endogenous triglycerides into muscle free fatty acids) | 0.00348 mmol/L |
| 64. | kyl (rate of the glycogen synthesis stimulated by insulin) | 1.28 × 106 |
| 65. | kym (glycogen synthesis rate) | 21.3641 mmol/L |
| 66. | lmax (maximum glycogen store of liver) | 400 mmol |
| 67. | mmax (maximum glycogen concentration) | 100 mmol |
| 68. | v (rate of glycogen transport) | 7 mmol |
| 69. | v10 (rate of triglyceride storage conversion to free fatty acids) | 0.1 mmol/min |
| 70. | v12 (constant in triglyceride release into plasma) | 40 mmol L−1 |
| 71. | v6 (rate of liver free fatty acid input to secretory pool) | 0.0158 mmol/L |
| 72. | v8 (rate of free fatty acid input to storage pool) | 0.333 mmol/min |
| 73. | v9 (rate of triglyceride release into plasma)) | 0.0159 mmol/L |
| 74. | vLG (maximum rate of glucokinase in liver) | 14.3 mmol/min |
| 76. | vLH (maximum rate of hexokinase in liver) | 5.57 mmol/min |
| 76. | vMH (muscle hexokinase maximum rate) | 54.288 mmol/min |
| 77. | y0 (range of liver glycogen concentration over which the release drops to zero) | 0.1 |
| 78. | αG (rate of glucose change in diet) | 2 mmol |
| 79. | αF (rate of fructose change in diet) | 2 mmol/L |
| 80. | ms (insulin-dependent rate of skeletal muscle storage of free fatty acids in the form of triglycerides) | 0.8 |
| 81. | me (rate of skeletal muscle triglyceride breakdown to free fatty acids) | 0.9 |
| Menu 1 | Menu 2 | Menu 3 | Menu 4 | |
|---|---|---|---|---|
| breakfast | GB0 = 1.5 mmol/L TLB0 = 23 mmol/L | GB0 = 44.7 mmol/L TLB0 = 1.6 mmol/L | GB0 = 7.7 mmol/L TLB0 = 16.1 mmol/L | GB0 = 23.6 mmol/L TLB0 = 4.7 mmol/L |
| lunch | GB0 = 3.2 mmol/L TLB0 = 9.1 mmol/L | GB0 = 49.8 mmol/L TLB0 = 9.5 mmol/L | GB0 = 14.0 mmol/L TLB0 = 7.7 mmol/L | GB0 = 43.2 mmol/L TLB0 = 14.5 mmol/L |
| snack | GB0 = 2.3 mmol/L TLB0 = 5.4 mmol/L | GB0 = 16.3 mmol/L TLB0 = 4.3 mmol/L | GB0 = 8.3 mmol/L TLB0 = 9.0 mmol/L | GB0 = 13.5 mmol/L TLB0 = 1.6 mmol/L |
| dinner | GB0 = 7.0 mmol/L TLB0 = 12.4 mmol/L | GB0 = 21.7 mmol/L TLB0 = 4.2 mmol/L | GB0 = 26.6 mmol/L TLB0 = 5.1 mmol/L | GB0 = 30.8 mmol/L TLB0 = 5.8 mmol/L |
| Meal | Carbohydrates/g | Fats/g | SFA/% | Energy/kcal | |
|---|---|---|---|---|---|
| Menu 1 | Breakfast | 2.7 | 82.4 | 859.2 | |
| Lunch | 5.7 | 32.6 | 408.6 | ||
| Snack | 4.1 | 19.5 | 209.9 | ||
| Dinner | 12.6 | 44.4 | 584.0 | ||
| Per day | 25.1 | 178.9 | 37.0 | 2061.7 | |
| Menu 2 | Breakfast | 80.4 | 5.9 | 421.9 | |
| Lunch | 89.7 | 33.9 | 904.7 | ||
| Snack | 29.3 | 15.3 | 284.1 | ||
| Dinner | 39.1 | 15.1 | 395.1 | ||
| Per day | 238.5 | 70.2 | 2.7 | 2005.8 | |
| Menu 3 | Breakfast | 13.9 | 57.7 | 612.9 | |
| Lunch | 25.2 | 27.7 | 517.3 | ||
| Snack | 14.9 | 32.4 | 403.6 | ||
| Dinner | 47.9 | 18.2 | 461.8 | ||
| Per day | 101.9 | 136.0 | 27.1 | 1995.6 | |
| Menu 4 | Breakfast | 42.5 | 16.7 | 343.9 | |
| Lunch | 77.8 | 52.0 | 971.2 | ||
| Snack | 24.3 | 5.6 | 164.4 | ||
| Dinner | 55.4 | 20.8 | 533.6 | ||
| Per day | 200 | 95.1 | 9.8 | 2013.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kosić, M.; Benković, M.; Jurina, T.; Valinger, D.; Gajdoš Kljusurić, J.; Tušek, A.J. Analysis of Hepatic Lipid Metabolism Model: Simulation and Non-Stationary Global Sensitivity Analysis. Nutrients 2022, 14, 4992. https://doi.org/10.3390/nu14234992
Kosić M, Benković M, Jurina T, Valinger D, Gajdoš Kljusurić J, Tušek AJ. Analysis of Hepatic Lipid Metabolism Model: Simulation and Non-Stationary Global Sensitivity Analysis. Nutrients. 2022; 14(23):4992. https://doi.org/10.3390/nu14234992
Chicago/Turabian StyleKosić, Martina, Maja Benković, Tamara Jurina, Davor Valinger, Jasenka Gajdoš Kljusurić, and Ana Jurinjak Tušek. 2022. "Analysis of Hepatic Lipid Metabolism Model: Simulation and Non-Stationary Global Sensitivity Analysis" Nutrients 14, no. 23: 4992. https://doi.org/10.3390/nu14234992
APA StyleKosić, M., Benković, M., Jurina, T., Valinger, D., Gajdoš Kljusurić, J., & Tušek, A. J. (2022). Analysis of Hepatic Lipid Metabolism Model: Simulation and Non-Stationary Global Sensitivity Analysis. Nutrients, 14(23), 4992. https://doi.org/10.3390/nu14234992










