Congruent Validity of Resting Energy Expenditure Predictive Equations in Young Adults
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Body Composition
2.3. Assessment of REE through Indirect Calorimetry
2.4. REE Predictive Equations
2.5. Statistical Analysis
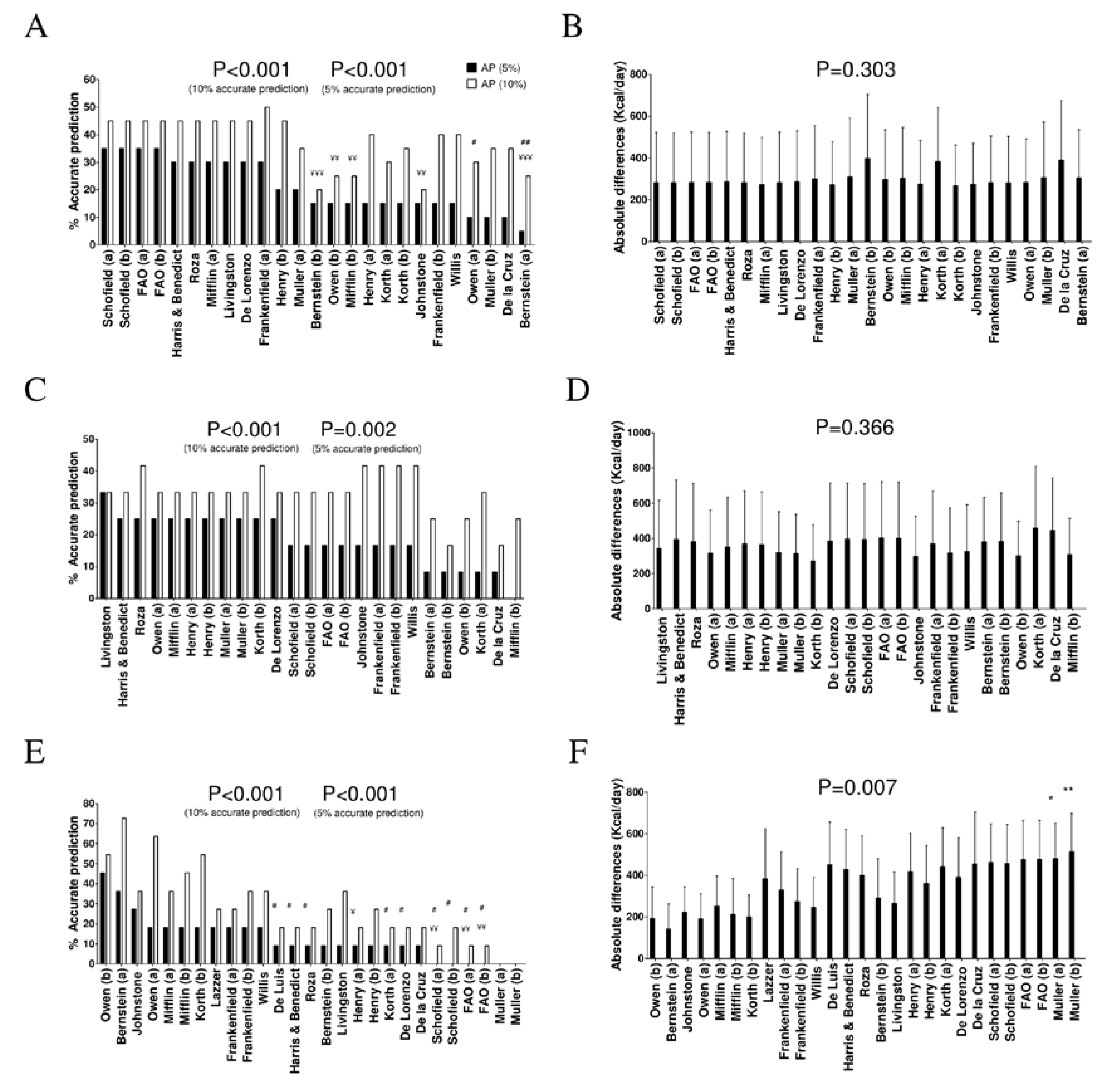
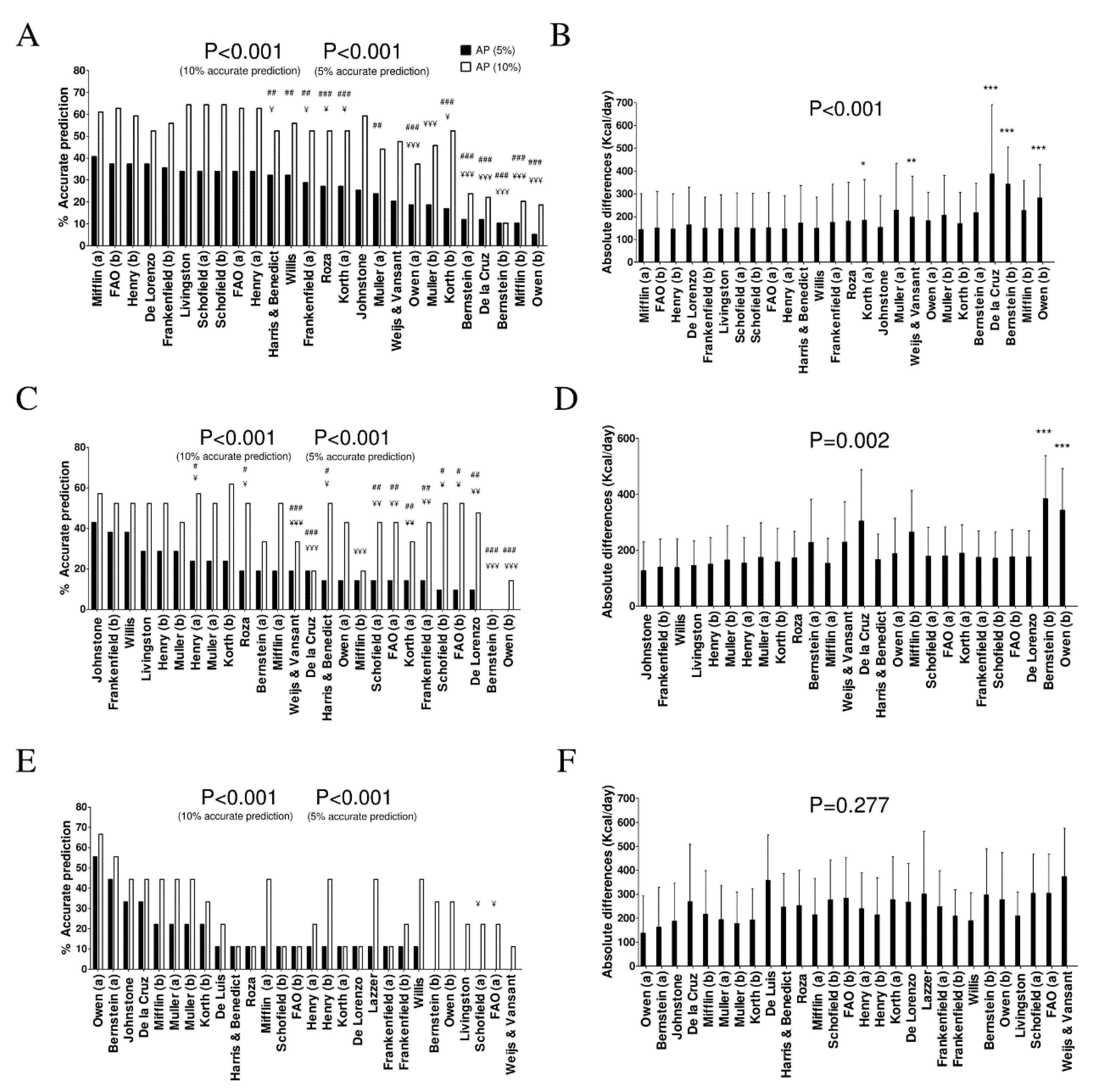
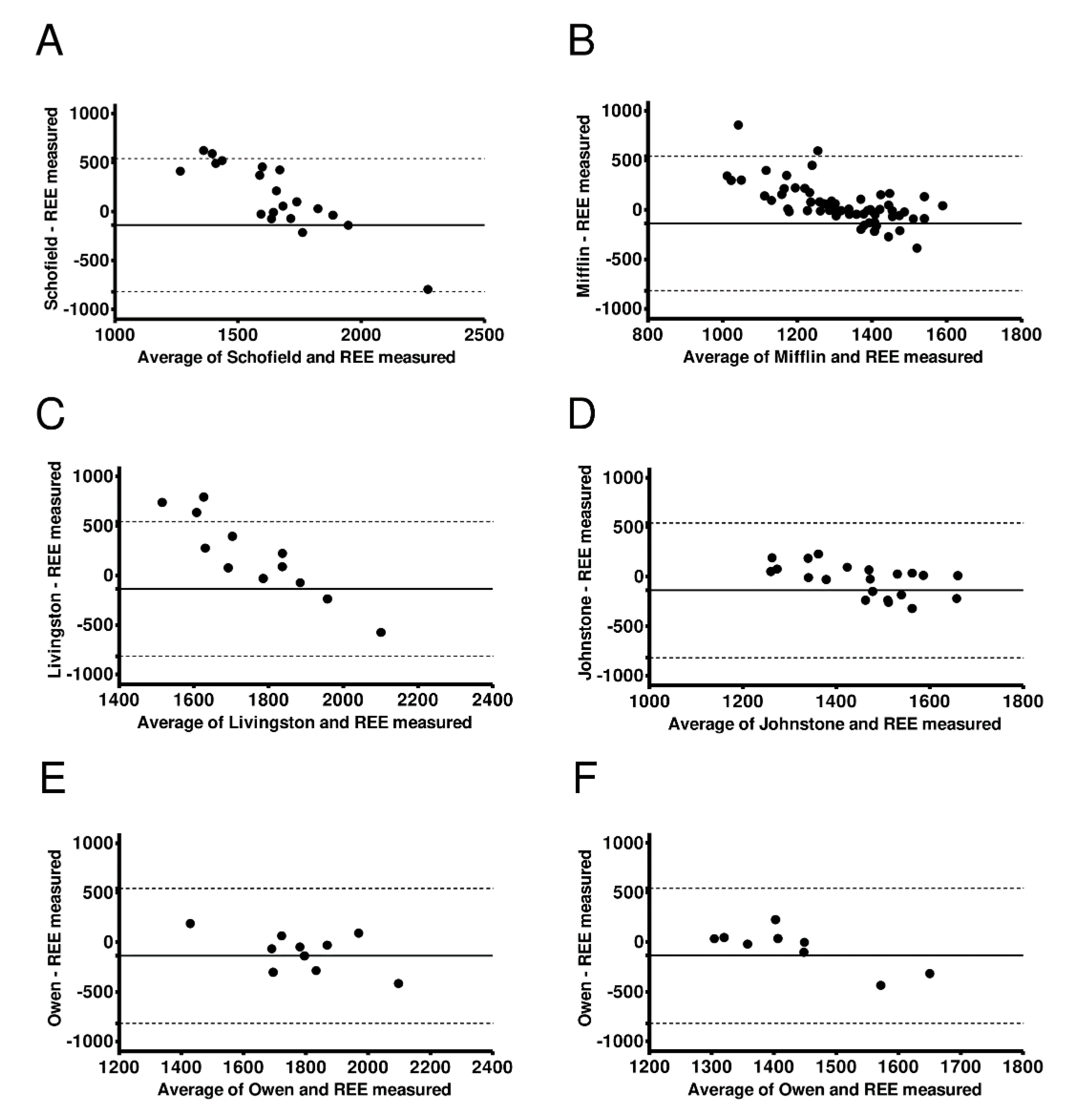
3. Results
4. Discussion
4.1. Normal Weight Men
4.2. Overweight Men
4.3. Obese Men
4.4. Normal Weight Women
4.5. Overweight Women
4.6. Obese Women
4.7. Limitations
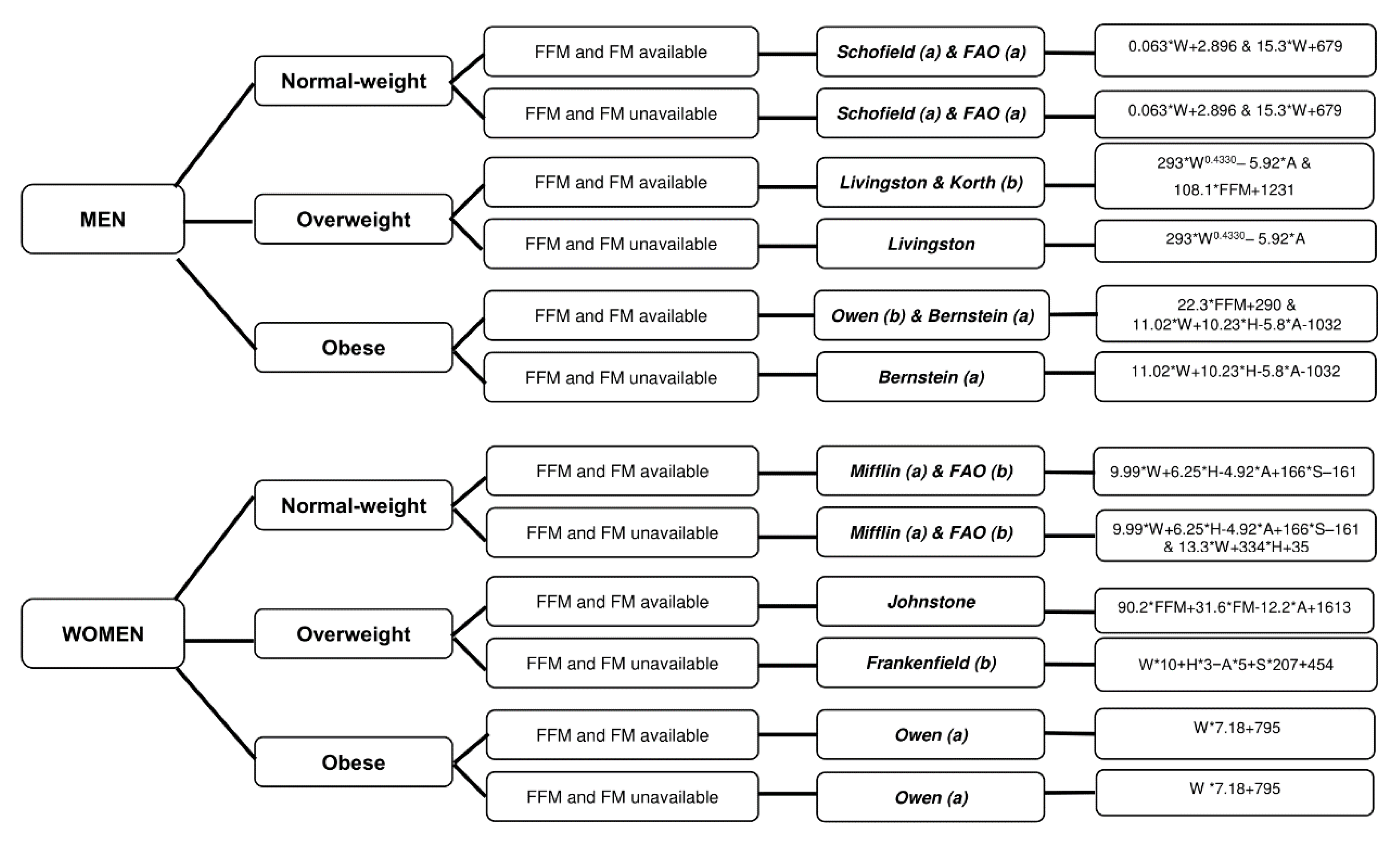
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pinheiro Volp, A.C.; Esteves de Oliveira, F.C.; Duarte Moreira Alves, R.; Esteves, E.A.; Bressan, J. Energy expenditure: Components and evaluation methods. Nutr. Hosp. 2011, 26, 430–440. [Google Scholar] [CrossRef] [PubMed]
- Weijs, P.J.M. Validity of predictive equations for resting energy expenditure in US and Dutch overweight and obese class I and II adults aged 18–65 y. Am. J. Clin. Nutr. 2008, 88, 959–970. [Google Scholar] [CrossRef] [PubMed]
- De Luis, D.A.; Aller, R.; Izaola, O.; Romero, E. Prediction equation of resting energy expenditure in an adult spanish population of obese adult population. Ann. Nutr. Metab. 2006, 50, 193–196. [Google Scholar] [CrossRef] [PubMed]
- Willis, E.A.; Herrmann, S.D.; Ptomey, L.T.; Honas, J.J.; Bessmer, C.T.; Donnelly, J.E.; Washburn, R.A. Predicting resting energy expenditure in young adults. Obes. Res. Clin. Pract. 2014, 8, 201–208. [Google Scholar] [CrossRef] [PubMed]
- FAO/WHO/UNU. Energy and Protein Requirements; FAO: Geneva, Switzerland, 1985. [Google Scholar]
- Lazzer, S.; Agosti, F.; Silvestri, P.; Derumeaux-Burel, H.; Sartorio, A. Prediction of resting energy expenditure in severely obese Italian women. J. Endocrinol. Investig. 2007, 30, 20–27. [Google Scholar] [CrossRef] [PubMed]
- Lazzer, S.; Agosti, F.; Resnik, M.; Marazzi, N.; Mornati, D.; Sartorio, A. Prediction of resting energy expenditure in severely obese Italian males. J. Endocrinol. Investig. 2007, 30, 754–761. [Google Scholar] [CrossRef] [PubMed]
- Müller, M.J.; Bosy-Westphal, A.; Klaus, S.; Kreymann, G.; Lührmann, P.M.; Neuhäuser-Berthold, M.; Noack, R.; Pirke, K.M.; Platte, P.; Selberg, O.; et al. World Health Organization equations have shortcomings for predicting resting energy expenditure in persons from a modern, affluent population: Generation of a new reference standard from a retrospective analysis of a German database of resting energy expe. Am. J. Clin. Nutr. 2004, 80, 1379–1390. [Google Scholar] [CrossRef] [PubMed]
- Schofield, W.N. Predicting basal metabolic rate, new standards and review of previous work. Hum. Nutr. Clin. Nutr. 1985, 39 (Suppl. 1), 5–41. [Google Scholar] [PubMed]
- Roza, A.M.; Shizgal, H.M. The Harris Benedict equation reevaluated: Resting energy requirements and the body cell mass. Am. J. Clin. Nutr. 1984, 40, 168–182. [Google Scholar] [CrossRef]
- de la Cruz Marcos, S.; de Mateo Silleras, B.; Camina Martín, M.A.; Carreño Enciso, L.; Miján de la Torre, A.; Galgani Fuentes, J.E.; Redondo del Río, M.P. Proposal for a new formula for estimating resting energy expenditure for healthy spanish population. Nutr. Hosp. 2015, 32, 2346–2352. [Google Scholar] [CrossRef] [PubMed]
- Harris, J.; Benedict, F. A biometric study of basal metabolism in man. Proc. Natl. Acad. Sci. USA 1918, 4, 370–373. [Google Scholar] [CrossRef] [PubMed]
- Livingston, E.H.; Kohlstadt, I. Simplified resting metabolic rate-predicting formulas for normal-sized and obese individuals. Obes. Res. 2005, 13, 1255–1262. [Google Scholar] [CrossRef] [PubMed]
- Owen, O.E.; Holup, J.L.; D’Alessio, D.A.; Craig, E.S.; Polansky, M.; Smalley, K.J.; Kavle, E.C.; Bushman, M.C.; Owen, L.R.; Mozzoli, M.A. A reappraisal of the caloric requirements of men. Am. J. Clin. Nutr. 1987, 46, 875–885. [Google Scholar] [CrossRef] [PubMed]
- Johnstone, A.M.; Rance, K.A.; Murison, S.D.; Duncan, J.S.; Speakman, J.R. Additional anthropometric measures may improve the predictability of basal metabolic rate in adult subjects. Eur. J. Clin. Nutr. 2006, 60, 1437–1444. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, R.S.; Thornton, J.C.; Yang, M.U.; Wang, J.; Redmond, A.M.; Pierson, R.N.; Pi-Sunyer, F.X.; Van Itallie, T.B. Prediction of the resting metabolic rate in obese patients. Am. J. Clin. Nutr. 1983, 37, 595–602. [Google Scholar] [CrossRef]
- De Lorenzo, A.; Tagliabue, A.; Andreoli, A.; Testolin, G.; Comelli, M.; Deurenberg, P. Measured and predicted resting metabolic rate in Italian males and females, aged 18–59 y. Eur. J. Clin. Nutr. 2001, 55, 208–214. [Google Scholar] [CrossRef]
- Henry, C.J.K. Basal metabolic rate studies in humans: Measurement and development of new equations. Public Health Nutr. 2005, 8, 1133–1152. [Google Scholar] [CrossRef]
- Mifflin, M.D.; St Jeor, S.T.; Hill, L.A.; Scott, B.J.; Daugherty, S.A.; Koh, Y.O. A new predictive equation for resting energy expenditure in healthy individuals. Am. J. Clin. Nutr. 1990, 51, 241–247. [Google Scholar] [CrossRef]
- Korth, O.; Bosy-Westphal, A.; Zschoche, P.; Glüer, C.C.; Heller, M.; Müller, M.J. Influence of methods used in body composition analysis on the prediction of resting energy expenditure. Eur. J. Clin. Nutr. 2007, 61, 582–589. [Google Scholar] [CrossRef]
- Owen, O.E.; Kavle, E.; Owen, R.S.; Polansky, M.; Caprio, S.; Mozzoli, M.A.; Kendrick, Z.V.; Bushman, M.C.; Boden, G. A reappraisal of caloric requirements in healthy women. Am. J. Clin. Nutr. 1986, 44, 1–19. [Google Scholar] [CrossRef]
- da Rocha, E.E.M.; Alves, V.G.F.; da Fonseca, R.B.V. Indirect calorimetry: Methodology, instruments and clinical application. Curr. Opin. Clin. Nutr. Metab. Care 2006, 9, 247–256. [Google Scholar] [CrossRef] [PubMed]
- Fullmer, S.; Benson-Davies, S.; Earthman, C.P.; Frankenfield, D.C.; Gradwell, E.; Lee, P.S.P.; Piemonte, T.; Trabulsi, J. Evidence analysis library review of best practices for performing indirect calorimetry in healthy and non-critically ill individuals. J. Acad. Nutr. Diet. 2015, 115, 1417–1446. [Google Scholar] [CrossRef] [PubMed]
- Compher, C.; Frankenfield, D.; Keim, N.; Roth-Yousey, L.; Evidence Analysis Working Group. Best practice methods to apply to measurement of resting metabolic rate in adults: A systematic review. J. Am. Diet. Assoc. 2006, 106, 881–903. [Google Scholar] [CrossRef] [PubMed]
- Weijs, P.J.M.; Vansant, G.A.A.M. Validity of predictive equations for resting energy expenditure in Belgian normal weight to morbid obese women. Clin. Nutr. 2010, 29, 347–351. [Google Scholar] [CrossRef] [PubMed]
- Lof, M.; Hannestad, U.; Forsum, E. Comparison of commonly used procedures, including the doubly-labelled water technique, in the estimation of total energy expenditure of women with special reference to the significance of body fatness. Br. J. Nutr. 2003, 90, 961. [Google Scholar] [CrossRef] [PubMed]
- Sanchez-Delgado, G.; Martinez-Tellez, B.; Olza, J.; Aguilera, C.M.; Labayen, I.; Ortega, F.B.; Chillon, P.; Fernandez-Reguera, C.; Alcantara, J.M.A.; Martinez-Avila, W.D.; et al. Activating brown adipose tissue through exercise (ACTIBATE) in young adults: Rationale, design and methodology. Contemp. Clin. Trials 2015, 45, 416–425. [Google Scholar] [CrossRef]
- World Health Organization. Obesity: Preventing and Managing the Global Epidemic; Executive Summary WHO Technical Report Series; WHO: Geneva, Switzerland, 2010; Volume 1997, pp. 5–8. [Google Scholar]
- Sanchez-Delgado, G.; Alcantara, J.M.A.; Ortiz-Alvarez, L.; Xu, H.; Martinez-Tellez, B.; Labayen, I.; Ruiz, J.R. Reliability of resting metabolic rate measurements in young adults: Impact of methods for data analysis. Clin. Nutr. 2018, 37, 1618–1624. [Google Scholar] [CrossRef]
- Alcantara, J.M.A.; Sanchez-Delgado, G.; Martinez-Tellez, B.; Merchan-Ramirez, E.; Labayen, I.; Ruiz, J.R. Congruent validity and inter-day reliability of two breath by breath metabolic carts to measure resting metabolic rate in young adults. Nutr. Metab. Cardiovasc Dis. 2018, 28, 929–936. [Google Scholar] [CrossRef] [PubMed]
- Weir, J. New methods for calculating metabolic rate with special reference to protein metabolism. J. Physiol. 1949, 109, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Frankenfield, D.; Roth-Yousey, L.; Compher, C. Comparison of predictive equations for resting metabolic rate in healthy nonobese and obese adults: A systematic review. J. Am. Diet. Assoc. 2005, 105, 775–789. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, J.R.; Ortega, F.B.; Rodríguez, G.; Alkorta, P.; Labayen, I. Validity of resting energy expenditure predictive equations before and after an energy-restricted diet intervention in obese women. PLoS ONE 2011, 6, e23759. [Google Scholar] [CrossRef] [PubMed]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar] [CrossRef]
- Frankenfield, D. Bias and accuracy of resting metabolic rate equations in non-obese and obese adults. Clin. Nutr. 2013, 32, 976–982. [Google Scholar] [CrossRef] [PubMed]
- Frankenfield, D.C.; Rowe, W.A.; Smith, J.S.; Cooney, R.N. Validation of several established equations for resting metabolic rate in obese and nonobese people. J. Am. Diet. Assoc. 2003, 103, 1152–1159. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, E.K. Accuracy of Predictive Equations for Resting Metabolic Rates and Daily Energy Expenditures of Police Officials Doing Shift Work by Type of Work. Clin. Nutr. Res. 2012, 1, 66. [Google Scholar] [CrossRef] [PubMed]
- Ramirez-Zea, M. Validation of three predictive equations for basal metabolic rate in adults. Public Health Nutr. 2005, 8, 1213–1228. [Google Scholar] [CrossRef] [PubMed]
- Wahrlicha, V.; Anjos, L. Validation of predictive equations of basal metabolic rate of women living in Southern Brazil. Rev. Saúde Pública 2001, 35, 39–45. [Google Scholar]
- Song, T.; Venkataraman, K.; Gluckman, P.; Seng, C.Y.; Meng, K.C.; Khoo, E.Y.H.; Leow, M.K.S.; Seng, L.Y.; Shyong, T.E. Validation of prediction equations for resting energy expenditure in Singaporean Chinese men. Obes. Res. Clin. Pract. 2014, 8, 201–208. [Google Scholar] [CrossRef]
- Cooper, J.A.; Watras, A.C.; O’Brien, M.J.; Luke, A.; Dobratz, J.R.; Earthman, C.P.; Schoeller, D.A. Assessing validity and reliability of resting metabolic rate in six gas analysis systems. J. Am. Diet. Assoc. 2009, 109, 128–132. [Google Scholar] [CrossRef]
- Vander Weg, M.W.; Watson, J.M.; Klesges, R.C.; Eck Clemens, L.H.; Slawson, D.L.; McClanahan, B.S. Development and cross-validation of a prediction equation for estimating resting energy expenditure in healthy African-American and European-American women. Eur. J. Clin. Nutr. 2004, 58, 474–480. [Google Scholar] [CrossRef]
- Dobratz, J.R.; Sibley, S.D.; Beckman, T.R.; Valentine, B.J.; Kellogg, T.A.; Ikramuddin, S.; Earthman, C.P. Predicting energy expenditure in extremely obese women. J. Parenter. Enter. Nutr. 2007, 31, 217–227. [Google Scholar] [CrossRef] [PubMed]
- Amaro-Gahete, F.J.; Jurado-Fasoli, L.; De-la-O, A.; Gutierrez, A.; Castillo, M.; Ruiz, J.R. Accuracy and Validity of Resting Energy Expenditure Predictive Equations in Middle-Aged Adults. Nutrients 2018, 10, 1635. [Google Scholar] [CrossRef] [PubMed]
| Men (n = 43) | Women (n = 79) | |||||
|---|---|---|---|---|---|---|
| Normal weight (n = 20) | Overweight (n = 12) | Obese (n = 11) | Normal weight (n = 59) | Overweight (n = 21) | Obese (n = 9) | |
| Age (years) | 21.5 (2.0) | 23.5 (2.1) | 23.0 (2.5) | 22.1 (2.1) | 22.6 (2.4) | 21.6 (2.0) |
| Weight (kg) | 69.0 (7.6) | 84.4 (7.6) | 109.0 (10.5) | 58.9 (7.1) | 74.6 (6.5) | 84.5 (9.7) |
| Height (m) | 1.75 (0.06) | 1.76 (0.06) | 1.78 (0.06) | 1.64 (0.07) | 1.64 (0.06) | 1.64 (0.09) |
| BMI (kg/m2) | 22.4 (1.8) | 27.1 (1.4) | 34.5 (2.2) | 21.8 (1.8) | 27.6 (1.2) | 31.3 (1.2) |
| Fat free mass (kg) | 50.9 (5.4) | 57.2 (4.1) | 66.3 (6.5) | 37.8 (4.1) | 41.7 (4.0) | 41.5 (6.0) |
| Fat mass (kg) | 18.1 (4.8) | 27.2 (6.8) | 42.7 (6.4) | 22.1 (4.5) | 32.9 (3.6) | 39.0 (5.0) |
| Fat mass (%) | 24.9 (5.3) | 30.6 (5.9) | 37.8 (3.4) | 35.2 (4.7) | 43.0 (3.0) | 45.1 (2.8) |
| REE (Kcal/day) | 1587 (390) | 1675 (363) | 1870 (251) | 1295 (222) | 1481 (179) | 1470 (203) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amaro-Gahete, F.J.; Sanchez-Delgado, G.; Alcantara, J.M.A.; Martinez-Tellez, B.; Muñoz-Hernandez, V.; Merchan-Ramirez, E.; Löf, M.; Labayen, I.; Ruiz, J.R. Congruent Validity of Resting Energy Expenditure Predictive Equations in Young Adults. Nutrients 2019, 11, 223. https://doi.org/10.3390/nu11020223
Amaro-Gahete FJ, Sanchez-Delgado G, Alcantara JMA, Martinez-Tellez B, Muñoz-Hernandez V, Merchan-Ramirez E, Löf M, Labayen I, Ruiz JR. Congruent Validity of Resting Energy Expenditure Predictive Equations in Young Adults. Nutrients. 2019; 11(2):223. https://doi.org/10.3390/nu11020223
Chicago/Turabian StyleAmaro-Gahete, Francisco J., Guillermo Sanchez-Delgado, Juan M.A. Alcantara, Borja Martinez-Tellez, Victoria Muñoz-Hernandez, Elisa Merchan-Ramirez, Marie Löf, Idoia Labayen, and Jonatan R. Ruiz. 2019. "Congruent Validity of Resting Energy Expenditure Predictive Equations in Young Adults" Nutrients 11, no. 2: 223. https://doi.org/10.3390/nu11020223
APA StyleAmaro-Gahete, F. J., Sanchez-Delgado, G., Alcantara, J. M. A., Martinez-Tellez, B., Muñoz-Hernandez, V., Merchan-Ramirez, E., Löf, M., Labayen, I., & Ruiz, J. R. (2019). Congruent Validity of Resting Energy Expenditure Predictive Equations in Young Adults. Nutrients, 11(2), 223. https://doi.org/10.3390/nu11020223







