A Stepwise Calibration of Global DMSP/OLS Stable Nighttime Light Data (1992–2013)
Abstract
:1. Introduction
2. DMSP/OLS NTL Time Series
3. Methodology
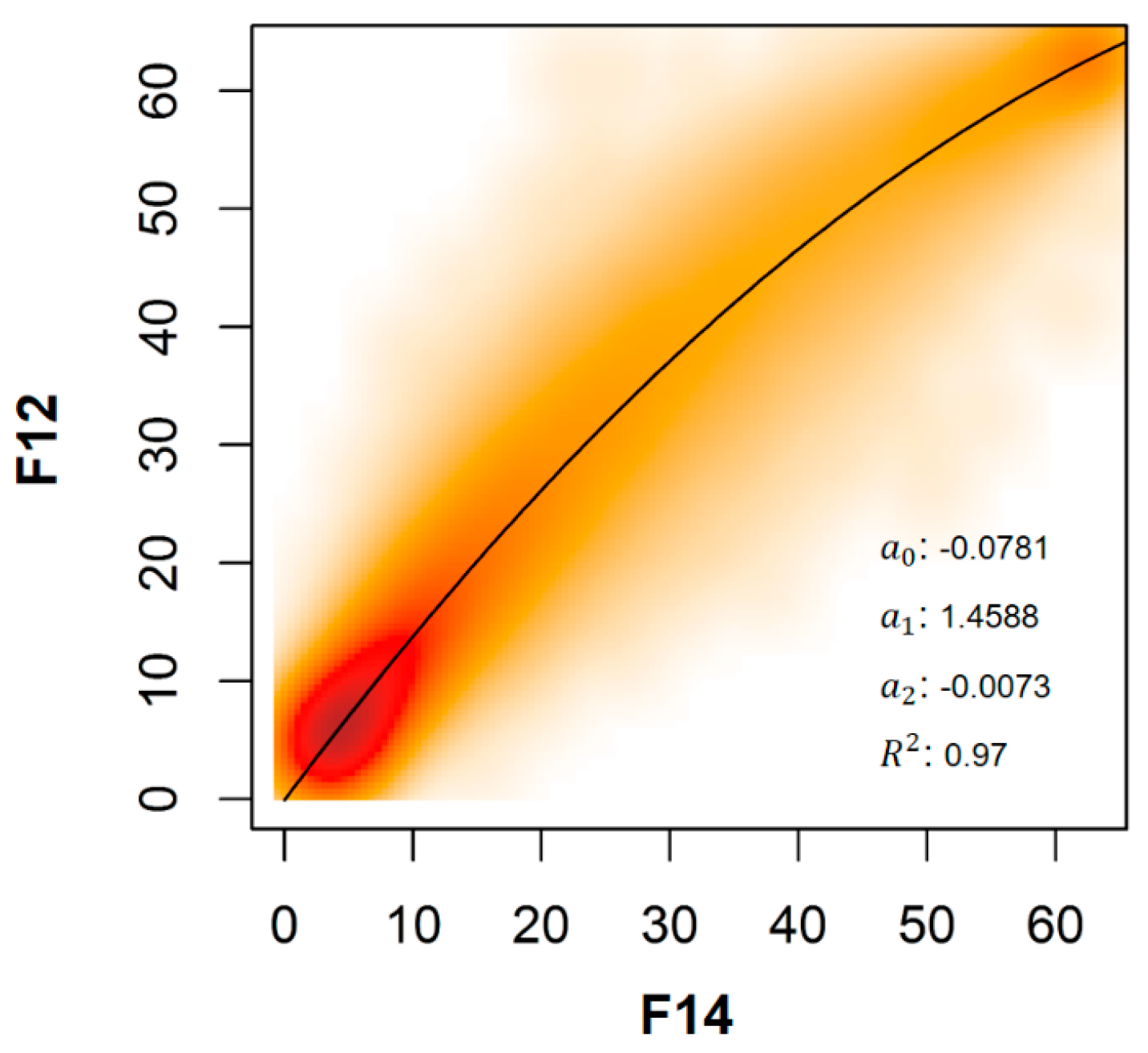
3.1. Step 1: Systematic Adjustment of F14
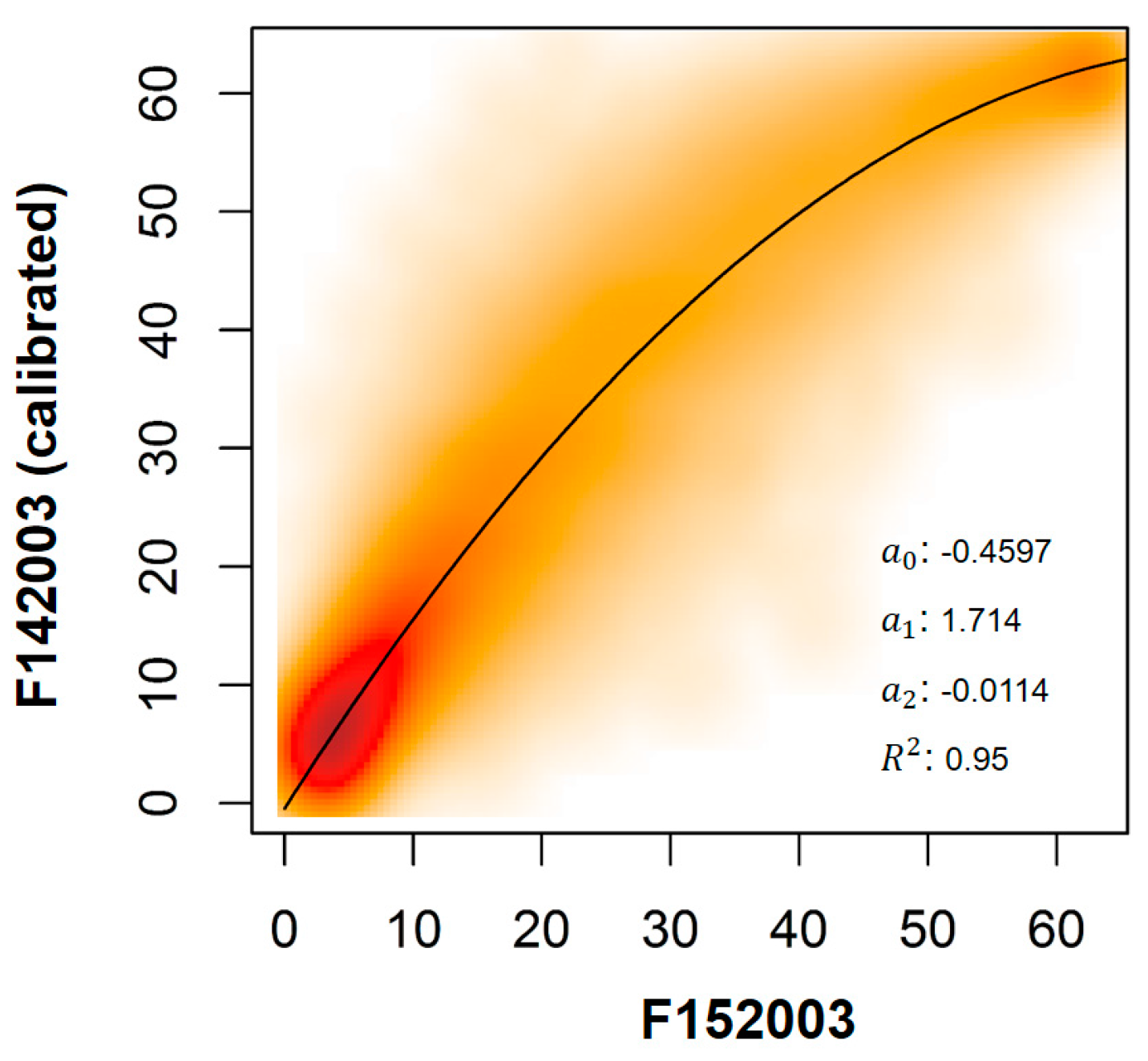
3.2. Step 2: Period-Based Adjustment of F15
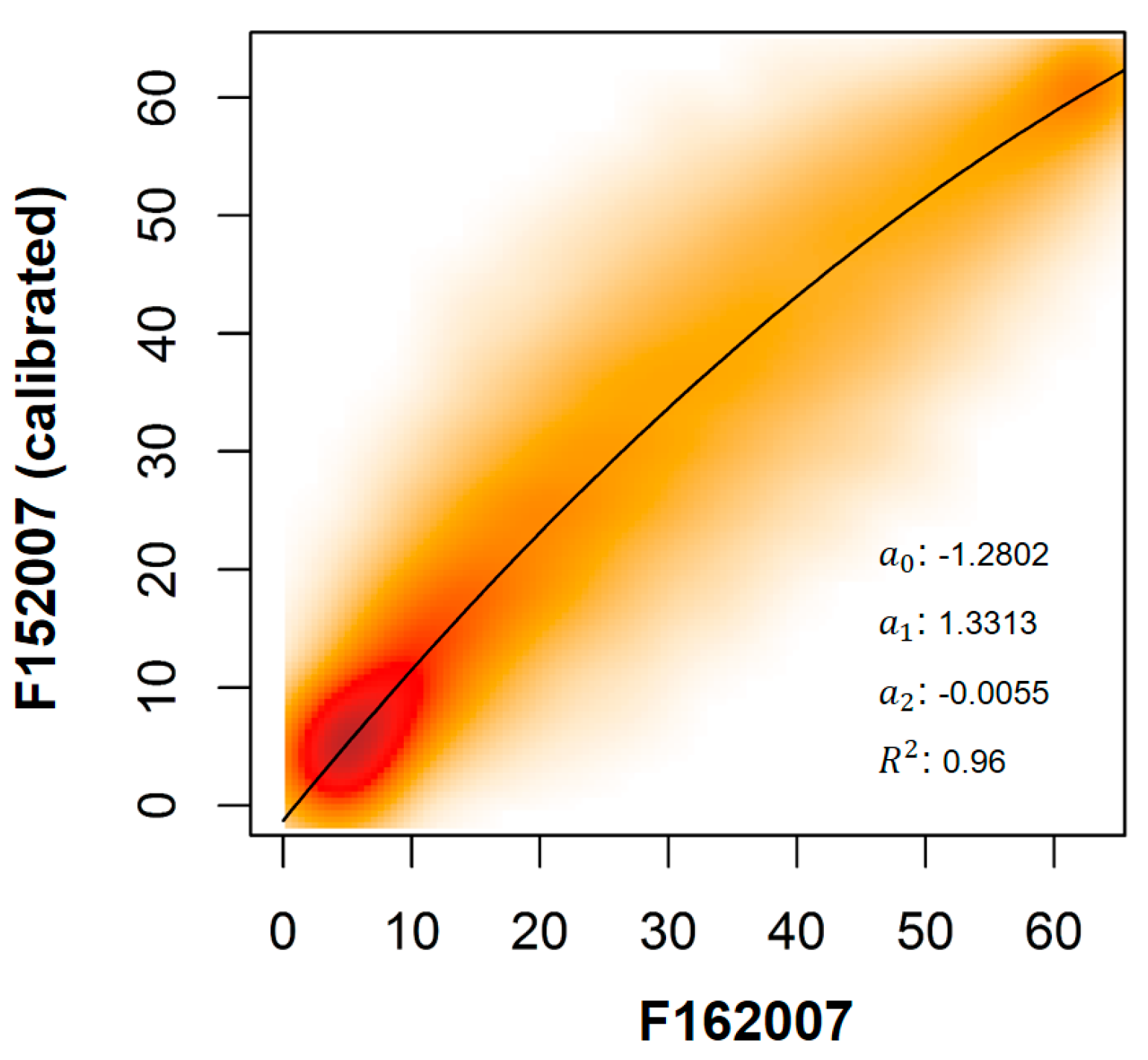
3.3. Step 3: A Hybrid Calibration of F16
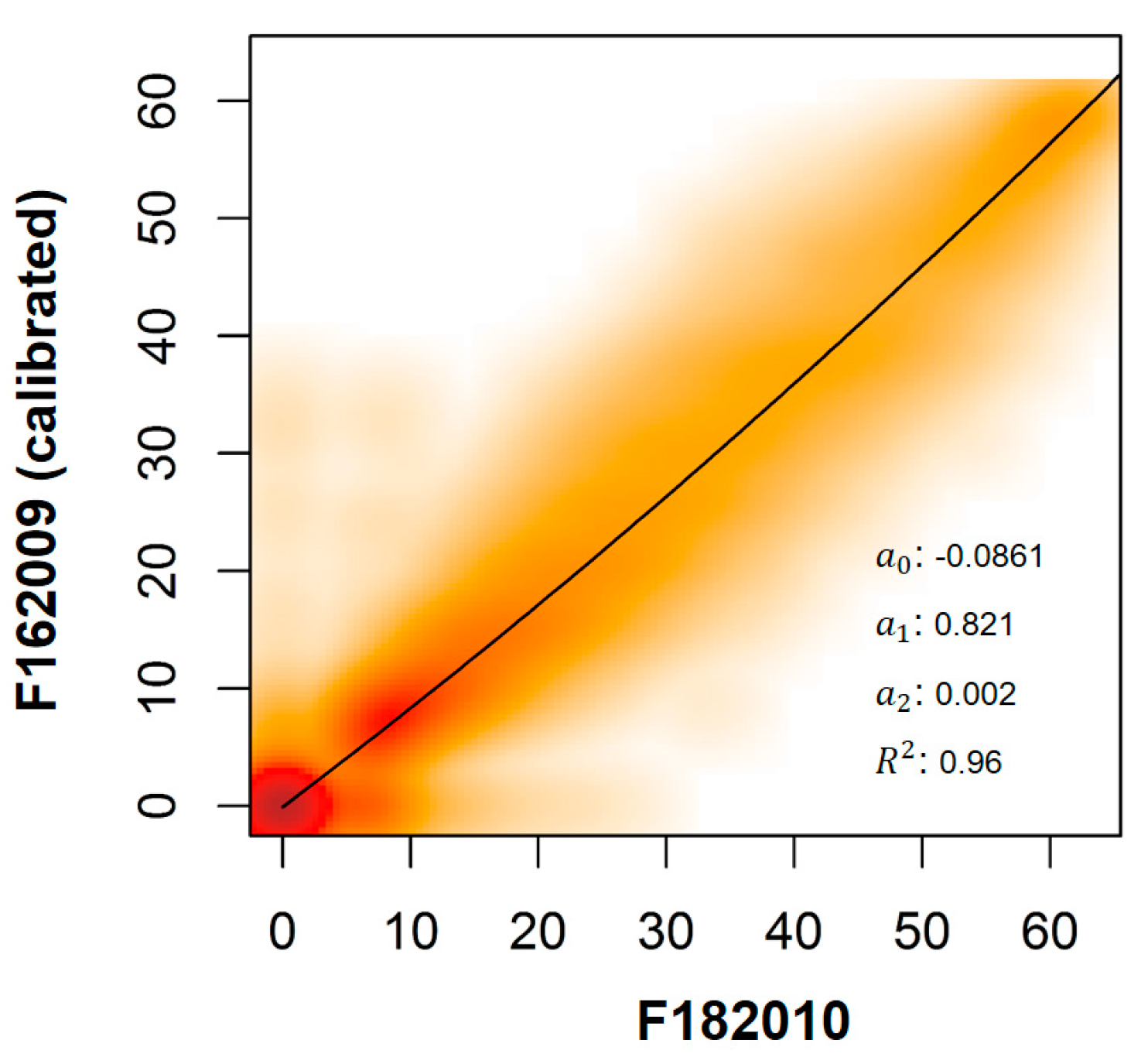
3.4. Step 4: Adjustment of F182010
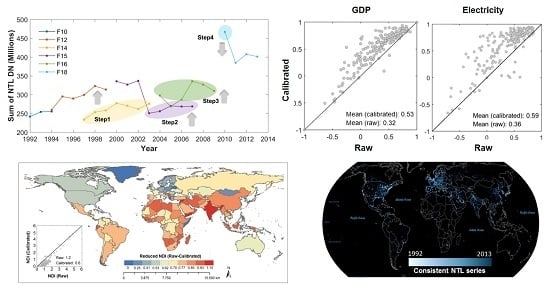
3.5. Evaluation of the Calibrated NTL Time Series
4. Results and Discussion
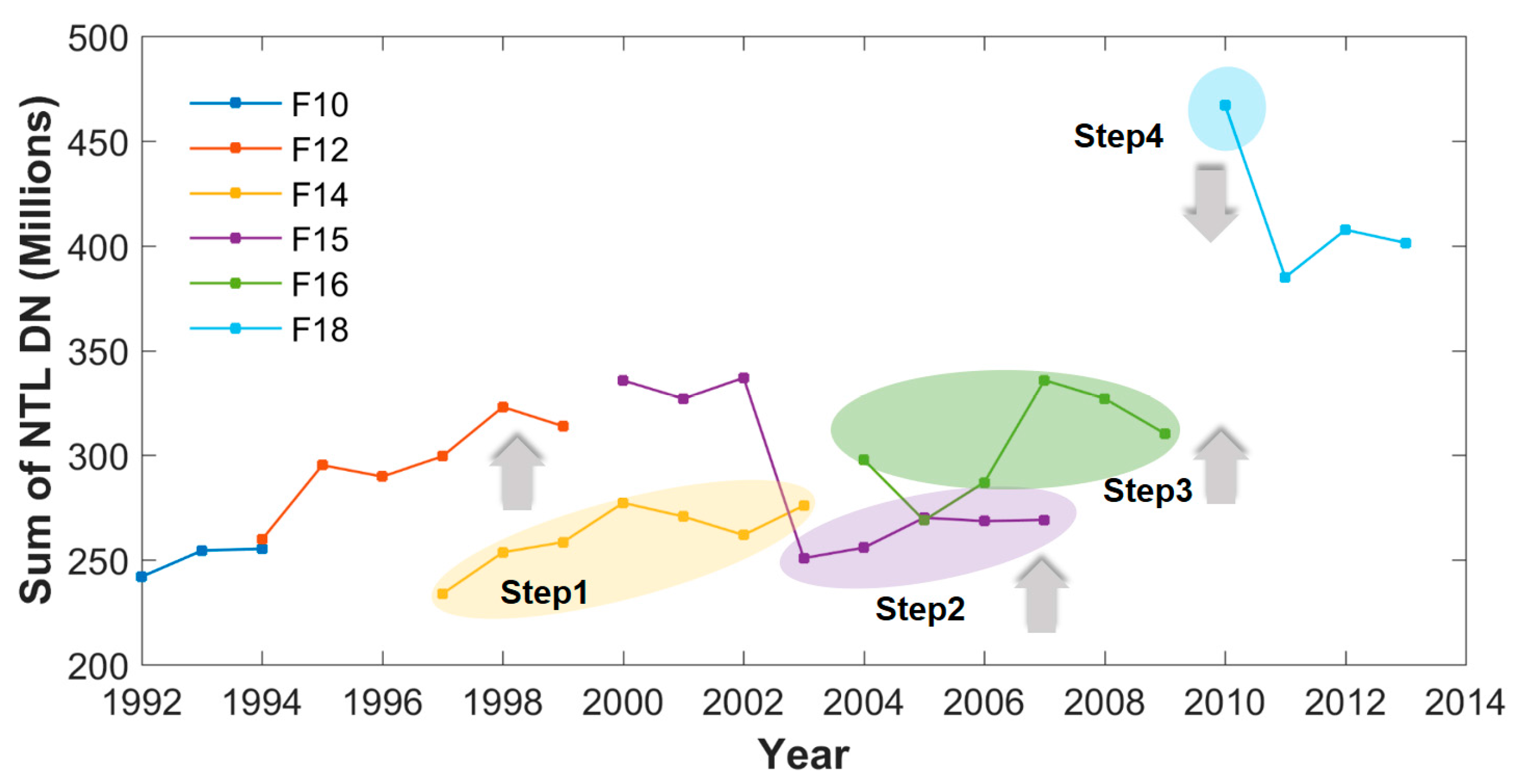
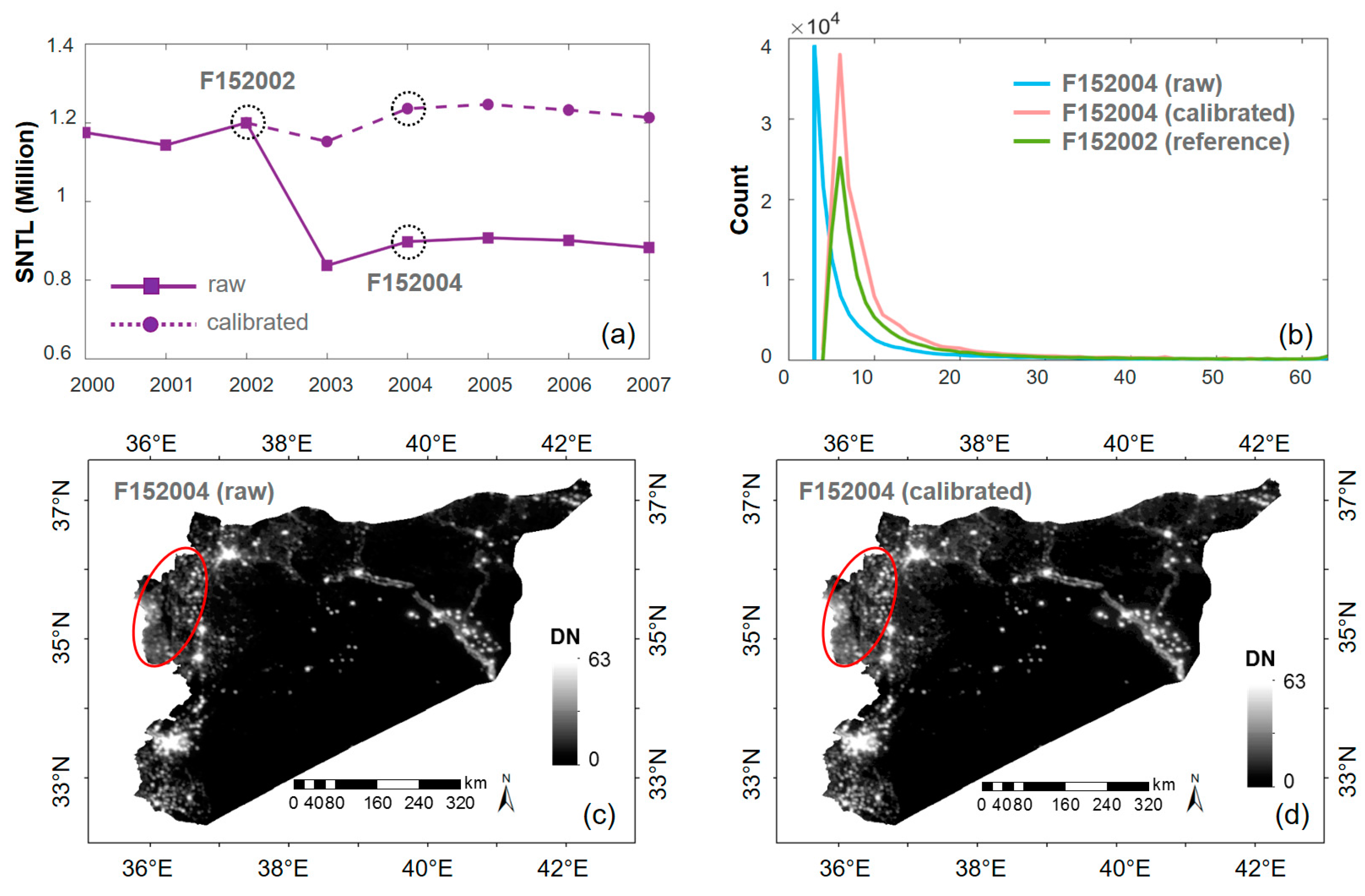
4.1. Improvement of NTL Data in Each Step
4.2. The Principle of Stepwise Calibration (Case of Satellite F15)
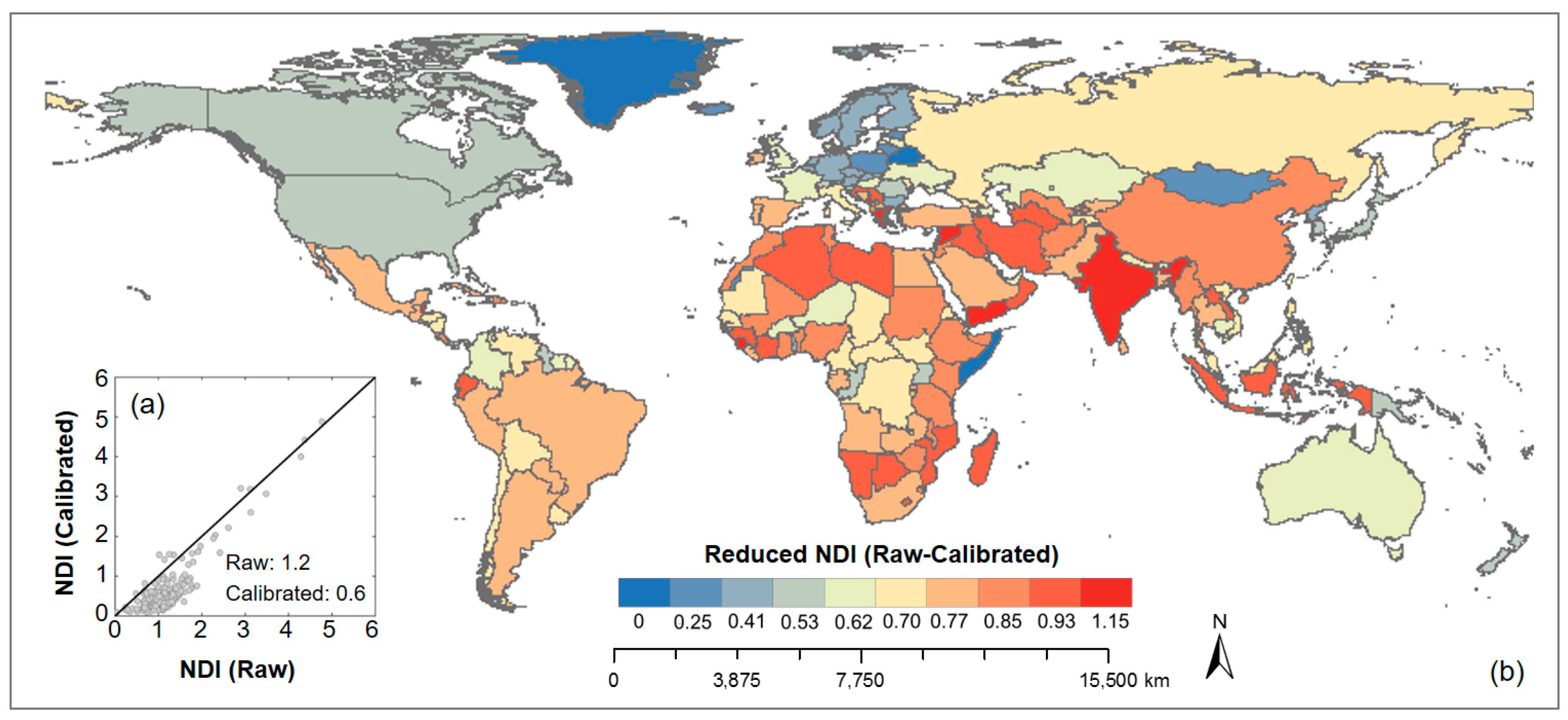
4.3. Evaluation of the Stepwise Calibration Based on SNTL
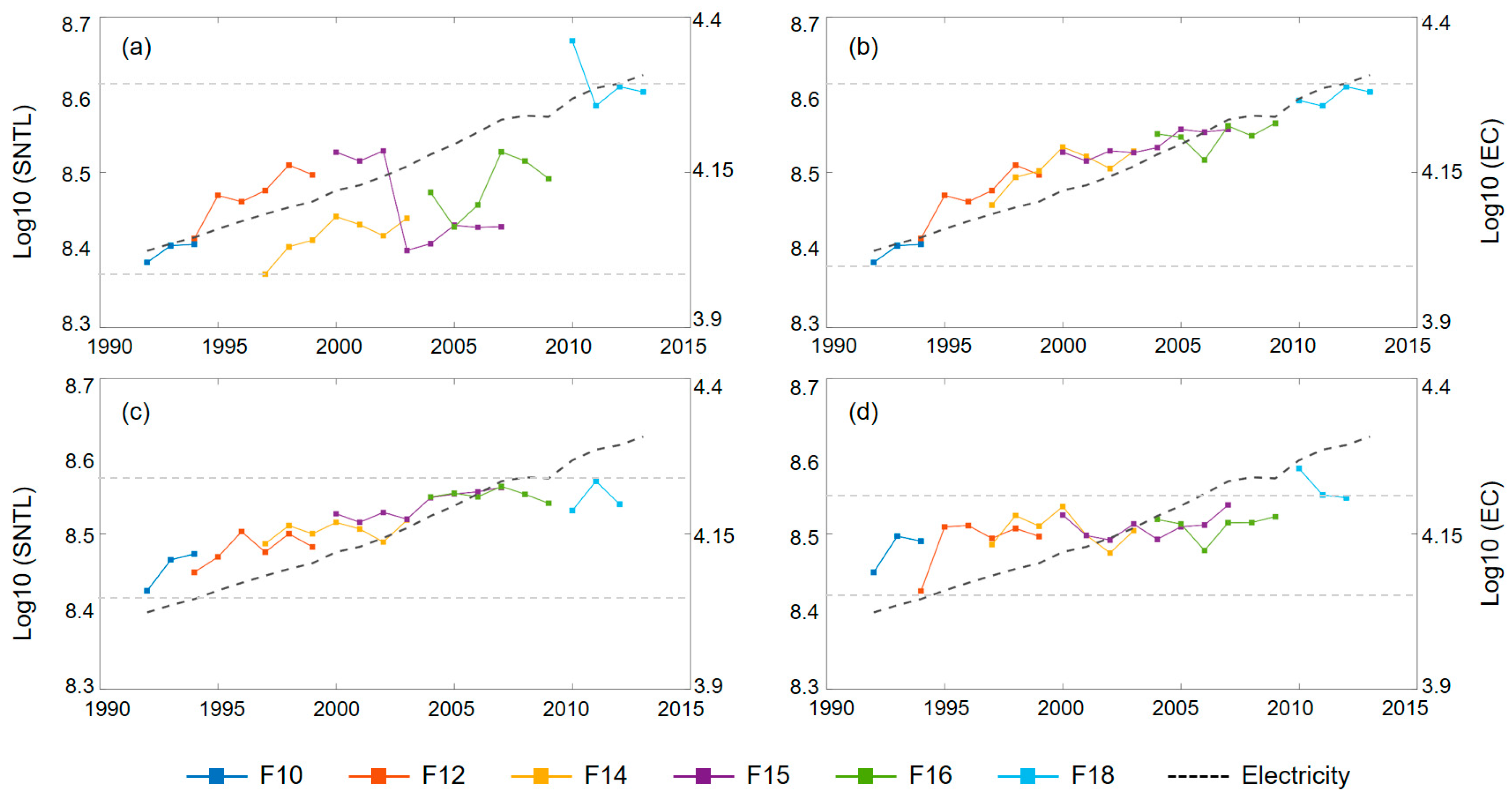
4.4. Comparison between Different Satellites in the Same Year
4.5. Comparison of NTL with Other Data
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, X.; Nordhaus, W.D. Using luminosity data as a proxy for economic statistics. Proc. Natl. Acad. Sci. USA 2011, 108, 8581–8594. [Google Scholar] [CrossRef] [PubMed]
- Amaral, S.; Monteiro, A.M.; Câmara, G.; Quintanilha, J. Dmsp/ols night-time light imagery for urban population estimates in the brazilian amazon. Int. J. Remote Sens. 2006, 27, 851–870. [Google Scholar] [CrossRef]
- Falchi, F.; Cinzano, P.; Duriscoe, D.; Kyba, C.C.M.; Elvidge, C.D.; Baugh, K.; Portnov, B.A.; Rybnikova, N.A.; Furgoni, R. The new world atlas of artificial night sky brightness. Sci. Adv. 2016, 2, e1600377. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Smith, S.J.; Zhao, K.; Imhoff, M.; Thomson, A.; Bond-Lamberty, B.; Asrar, G.R.; Zhang, X.; He, C.; Elvidge, C.D. A global map of urban extent from nightlights. Environ. Res. Lett. 2015, 10, 1–11. [Google Scholar] [CrossRef]
- Doll, C.H.; Muller, J.-P.; Elvidge, C.D. Night-time imagery as a tool for global mapping of socioeconomic parameters and greenhouse gas emissions. AMBIO 2000, 29, 151–162. [Google Scholar] [CrossRef]
- Zhuo, L.; Ichinose, T.; Zheng, J.; Chen, J.; Shi, P.J.; Li, X. Modelling the population density of china at the pixel level based on dmsp/ols non-radiance calibrated night time light images. Int. J. Remote Sens. 2009, 30, 1001–1018. [Google Scholar] [CrossRef]
- Doll, C.N.; Pachauri, S. Estimating rural populations without access to electricity in developing countries through night-time light satellite imagery. Energy Policy 2010, 38, 5661–5670. [Google Scholar] [CrossRef]
- Letu, H.; Hara, M.; Yagi, H.; Naoki, K.; Tana, G.; Nishio, F.; Shuhei, O. Estimating energy consumption from night-time dmps/ols imagery after correcting for saturation effects. Int. J. Remote Sens. 2010, 31, 4441–4458. [Google Scholar] [CrossRef]
- Croft, T.A. Nighttime images of the earth from space. Sci. Am. 1978, 239, 81–98. [Google Scholar] [CrossRef]
- Huang, Q.; Yang, X.; Gao, B.; Yang, Y.; Zhao, Y. Application of dmsp/ols nighttime light images: A meta-analysis and a systematic literature review. Remote Sens. 2014, 6, 6844. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y. Urban mapping using dmsp/ols stable night-time light: A review. Int. J. Remote Sens. 2017, 1–17. [Google Scholar] [CrossRef]
- Zhou, Y.; Smith, S.J.; Elvidge, C.D.; Zhao, K.; Thomson, A.; Imhoff, M. A cluster-based method to map urban area from dmsp/ols nightlights. Remote Sens. Environ. 2014, 147, 171–185. [Google Scholar] [CrossRef]
- Li, X.; Gong, P. Urban growth models: Progress and perspective. Sci. Bull. 2016, 61, 1631–1650. [Google Scholar] [CrossRef]
- Li, X.; Yu, L.; Sohl, T.; Clinton, N.; Li, W.; Zhu, Z.; Liu, X.; Gong, P. A cellular automata downscaling based 1 km global land use datasets (2010–2100). Sci. Bull. 2016, 61, 1651–1661. [Google Scholar] [CrossRef]
- Zhang, Q.; Pandey, B.; Seto, K.C. A robust method to generate a consistent time series from dmsp/ols nighttime light data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5821–5831. [Google Scholar] [CrossRef]
- Elvidge, C.; Ziskin, D.; Baugh, K.; Tuttle, B.; Ghosh, T.; Pack, D.; Erwin, E.; Zhizhin, M. A fifteen year record of global natural gas flaring derived from satellite data. Energies 2009, 2, 595–622. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Hsu, F.-C.; Baugh, K.E.; Ghosh, T. National trends in satellite-observed lighting. Global Urban Monit. Assess. Earth Obs. 2014, 91–118. [Google Scholar] [CrossRef]
- Li, X.; Chen, X.; Zhao, Y.; Xu, J.; Chen, F.; Li, H. Automatic intercalibration of night-time light imagery using robust regression. Remote Sens. Lett. 2013, 4, 41–54. [Google Scholar] [CrossRef]
- Stathakis, D. Intercalibration of dmsp/ols by parallel regressions. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1421–1424. [Google Scholar] [CrossRef]
- Zhao, N.; Zhou, Y.; Samson, E.L. Correcting incompatible dn values and geometric errors in nighttime lights time-series images. Geosci. Remote Sens. IEEE Trans. 2015, 53, 2031–2049. [Google Scholar] [CrossRef]
- Ma, T.; Zhou, C.; Pei, T.; Haynie, S.; Fan, J. Quantitative estimation of urbanization dynamics using time series of dmsp/ols nighttime light data: A comparative case study from china’s cities. Remote Sens. Environ. 2012, 124, 91–107. [Google Scholar] [CrossRef]
- Liu, Z.; He, C.; Zhang, Q.; Huang, Q.; Yang, Y. Extracting the dynamics of urban expansion in china using dmsp-ols nighttime light data from 1992 to 2008. Landsc. Urban Plan 2012, 106, 61–72. [Google Scholar] [CrossRef]
- Li, Q.; Lu, L.; Weng, Q.; Xie, Y.; Guo, H. Monitoring urban dynamics in the southeast U.S.A. Using time-series dmsp/ols nightlight imagery. Remote Sens. 2016, 8, 578. [Google Scholar] [CrossRef]
- Pandey, B.; Joshi, P.K.; Seto, K.C. Monitoring urbanization dynamics in india using dmsp/ols night time lights and spot-vgt data. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 41–61. [Google Scholar] [CrossRef]
- Wu, J.; He, S.; Peng, J.; Li, W.; Zhong, X. Intercalibration of dmsp-ols night-time light data by the invariant region method. Int. J. Remote Sens. 2013, 34, 7351–7368. [Google Scholar] [CrossRef]
- Li, C.; Ye, J.; Li, S.; Chen, G.; Xiong, H. Study on radiometric intercalibration methods for dmsp-ols night-time light imagery. Int. J. Remote Sens. 2016, 37, 3671–3695. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Erwin, E.H.; Baugh, K.E.; Ziskin, D.; Tuttle, B.T.; Ghosh, T.; Sutton, P.C. Overview of Dmsp Nightime Lights and Future Possibilities. In Proceedings of the 2009 Joint Urban Remote Sensing Event, Shanghai, China, 21–22 May 2009; pp. 1–5. [Google Scholar]
- Ju, Y.; Dronova, I.; Ma, Q.; Zhang, X. Analysis of urbanization dynamics in mainland china using pixel-based night-time light trajectories from 1992 to 2013. Int. J. Remote Sens. 2017, 1–26. [Google Scholar] [CrossRef]
- United Nations (UN). World Urbanization Prospects: The 2014 Revision; UN: New York, NY, USA, 2015. [Google Scholar]
- Shi, K.; Chen, Y.; Yu, B.; Xu, T.; Yang, C.; Li, L.; Huang, C.; Chen, Z.; Liu, R.; Wu, J. Detecting spatiotemporal dynamics of global electric power consumption using dmsp-ols nighttime stable light data. Appl. Energy 2016, 184, 451–463. [Google Scholar] [CrossRef]
- Yu, B.; Shu, S.; Liu, H.; Song, W.; Wu, J.; Wang, L.; Chen, Z. Object-based spatial cluster analysis of urban landscape pattern using nighttime light satellite images: A case study of china. Int. J. Geogr. Inf. Sci. 2014, 28, 2321–2355. [Google Scholar] [CrossRef]
- Pandey, B.; Zhang, Q.; Seto, K.C. Comparative evaluation of relative calibration methods for dmsp/ols nighttime lights. Remote Sens. Environ. 2017, 195, 61–78. [Google Scholar] [CrossRef]
- Miller, S.D.; Mills, S.P.; Elvidge, C.D.; Lindsey, D.T.; Lee, T.F.; Hawkins, J.D. Suomi satellite brings to light a unique frontier of nighttime environmental sensing capabilities. Proc. Natl. Acad. Sci. USA 2012, 109, 15701–15711. [Google Scholar] [CrossRef] [PubMed]



| Year | Satellite | |||||
|---|---|---|---|---|---|---|
| 1992 | F10 | |||||
| 1993 | F10 | |||||
| 1994 | F10 | F12 | ||||
| 1995 | F12 | |||||
| 1996 | F12 | |||||
| 1997 | F12 | F14 | ||||
| 1998 | F12 | F14 | ||||
| 1999 | F12 | F14 | ||||
| 2000 | F14 | F15 | ||||
| 2001 | F14 | F15 | ||||
| 2002 | F14 | F15 | ||||
| 2003 | F14 | F15 | ||||
| 2004 | F15 | F16 | ||||
| 2005 | F15 | F16 | ||||
| 2006 | F15 | F16 | ||||
| 2007 | F15 | F16 | ||||
| 2008 | F16 | |||||
| 2009 | F16 | |||||
| 2010 | F18 | |||||
| 2011 | F18 | |||||
| 2012 | F18 | |||||
| 2013 | F18 | |||||
| Year | ||||
|---|---|---|---|---|
| 2004 | 0.1194 | 1.2265 | −0.0041 | 0.9459 |
| 2005 | −0.3209 | 1.4619 | −0.0072 | 0.9765 |
| 2006 | 0.0877 | 1.1616 | −0.0021 | 0.9733 |
| 2007 | 0 | 1 | 0 | 1 |
| 2008 | 0.1100 | 1.0513 | −0.001 | 0.9820 |
| 2009 | 0.6294 | 1.1188 | −0.0024 | 0.9548 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhou, Y. A Stepwise Calibration of Global DMSP/OLS Stable Nighttime Light Data (1992–2013). Remote Sens. 2017, 9, 637. https://doi.org/10.3390/rs9060637
Li X, Zhou Y. A Stepwise Calibration of Global DMSP/OLS Stable Nighttime Light Data (1992–2013). Remote Sensing. 2017; 9(6):637. https://doi.org/10.3390/rs9060637
Chicago/Turabian StyleLi, Xuecao, and Yuyu Zhou. 2017. "A Stepwise Calibration of Global DMSP/OLS Stable Nighttime Light Data (1992–2013)" Remote Sensing 9, no. 6: 637. https://doi.org/10.3390/rs9060637
APA StyleLi, X., & Zhou, Y. (2017). A Stepwise Calibration of Global DMSP/OLS Stable Nighttime Light Data (1992–2013). Remote Sensing, 9(6), 637. https://doi.org/10.3390/rs9060637