2D Normalized Iterative Hard Thresholding Algorithm for Fast Compressive Radar Imaging

Abstract

Compressive radar imaging has attracted considerable attention because it substantially reduces imaging time through directly compressive sampling. However, a problem that must be addressed for compressive radar imaging systems is the high computational complexity of reconstruction of sparse signals. In this paper, a novel algorithm, called two-dimensional (2D) normalized iterative hard thresholding (NIHT) or 2D-NIHT algorithm, is proposed to directly reconstruct radar images in the matrix domain. The reconstruction performance of 2D-NIHT algorithm was validated by an experiment on recovering a synthetic 2D sparse signal, and the superiority of the 2D-NIHT algorithm to the NIHT algorithm was demonstrated by a comprehensive comparison of its reconstruction performance. Moreover, to be used in compressive radar imaging systems, a 2D sampling model was also proposed to compress the range and azimuth data simultaneously. The practical application of the 2D-NIHT algorithm in radar systems was validated by recovering two radar scenes with noise at different signal-to-noise ratios, and the results showed that the 2D-NIHT algorithm could reconstruct radar scenes with a high probability of exact recovery in the matrix domain. In addition, the reconstruction performance of the 2D-NIHT algorithm was compared with four existing efficient reconstruction algorithms using the two radar scenes, and the results illustrated that, compared to the other algorithms, the 2D-NIHT algorithm could dramatically reduce the computational complexity in signal reconstruction and successfully reconstruct 2D sparse images with a high probability of exact recovery.

1. Introduction

Radar, an object detection system using radio waves to detect objects and determine their spatial positions, has been applied in many fields, including radar astronomy, geographical environment surveillance system, and air defense systems. The demand of radar systems for high-resolution and high-speed imaging capabilities is increasing and results in a strong desire for higher bandwidths and more sampling time, which places significant pressure on radar hardware equipment and imaging costs. However, classical time–frequency uncertainty principles based on the Shannon sampling theorem have limited the development of high-resolution and high–speed radar imaging [1]. Compressive sensing, as an effective approach for direct compressive sampling, has great potential application for radar imaging and is able to solve the problems that radar systems currently face, that is, the mass time requirement of signal sampling and reconstruction for high–resolution imaging [2]. Meanwhile, a compressive imaging method can simplify the structure of a radar system, allowing elimination of the matched filter for pulse compression at the receiver and thereby reducing the need for analog-to-digital convertors [3,4,5,6].

Some achievements of radar imaging based on the compressive sensing principle have been reported [1,3,7,8]. Braniuk and co-workers first applied the compressive sensing theorem in radar imaging systems and confirmed the feasibility of compressive radar imaging by theoretical analysis and numerical experiments [3]. Zhang and co-workers proposed a framework to realize high–resolution inverse synthetic aperture radar (ISAR) imaging with limited measured data based on the theory of compressed sampling [4]. Ender presented generic system architectures and implementation considerations to address some further steps to compressive radar imaging and applied the compressive sensing in pulse compression, radar imaging and air space surveillance with array antennas [9]. An approach that employed pulse accumulation and weighted compressive sensing was also proposed by Zhang and co-workers under low signal-to-noise ratio (SNR) conditions, to realize high-resolution imaging and reduce sensitivity to noise [10]. Moreover, many reconstruction algorithms of compressive radar images have proposed. For example, Xie and co-workers proposed a smoothed L0 norm (SL0) algorithm to obtain fast radar imaging based on a compressive sensing [11]; Bhattacharya and co-workers used convex optimization through projection onto convex sets or greedy algorithms to decode compressive synthetic aperture radar (SAR) images [12,13]; and Yu and co-workers introduced a turbo-like iterative thresholding algorithm to recover SAR images [14]. The methods of compressive radar imaging based on these reconstruction algorithms can obtain high-resolution radar images with very small amounts of echo data, and improve the radar imaging speed remarkably, compared with conventional radar imaging methods. However, the radar imaging time is still very long, especially for high-resolution radar imaging, because the conventional strategies for 2D signal reconstruction usually involve stacking a matrix of 2D signals into a huge column vector based on the vector space model, and then recovering the huge vector signal with reconstruction algorithms in the 1D domain [15,16]. These approaches exponentially increase the computational complexity involved in recovering 2D sparse signals and the memory requirement for storing the large-bandwidth data of the radar images [17]. In addition, these approaches ignore the intrinsic spatial structure of 2D signals [16], especially the coupled range and azimuth information of radar imaging.

To address these drawbacks, some 2D reconstruction algorithms that directly leverage the matrix structure of 2D sparse signals have been proposed recently [16,17,18,19,20,21], and some have been used in radar imaging systems. For example, a fast reconstruction algorithm, called two-dimensional smoothed L0 norm (2D-SL0) algorithm, has been proposed to reduce computational complexity and economize on the memory required by directly utilizes the matrix structure to recover the 2D sparse signals and is designed [20], but the reconstruction quality of the natural image is poor. Another novel algorithm called the 2D orthogonal matching pursuit (2D-OMP) algorithm, which was extended from 1D-OMP, has been developed to reconstruct 2D sparse signals [17]. In this algorithm, each atom in the dictionary is a matrix. At each iteration, the best matched matrix atom is selected by projecting the sample matrix onto 2D atoms and the weights for the selected atoms are then updated via the least square. This algorithm significantly reduces the computational complexity with a matrix structure, but it still requires a great deal of memory usage and is suitable only for the square matrix of 2D sparse signals. In addition, an iterative gradient projection algorithm for 2D sparse image reconstruction has been proposed, in which the sparse solution is searched iteratively from the 2D solution space and then updated by gradient descent of the total variation. It recovers the natural image perfectly, being conducive to reduction in both computational complexity and memory requirements for the measurement matrix [18]; however, the algorithm suffers from the limitation that the sparse signals must be square.

In this paper, we propose a novel reconstruction algorithm of 2D sparse signals, called the 2D normalized iterative hard thresholding (2D-NIHT) algorithm, which is extended from the normalized iterative hard thresholding (NIHT) algorithm [22] to reduce the reconstruction time in radar imaging by recovering radar images in the matrix domain directly, and the effectiveness and superiority of the algorithm are theoretically proved and demonstrated by experiments. Moreover, we also present a 2D compressive sampling model of radar imaging systems, which compresses range and azimuth information simultaneously and also ensures that the 2D-NIHT algorithm can be implemented in a compressive radar imaging system.

This paper is organized as follows. In Section 2, we briefly present the compressive sensing theory and the NIHT algorithm. In Section 3, we introduce the radar imaging model based on compressive sensing. In Section 4, we describe the 2D-NIHT algorithm in detail and prove its convergence. In Section 5, some experiments using randomly synthetic 2D signals and actual radar images are presented. Finally, in Section 6, we draw conclusions.

2. Brief Introduction of Compressive Sensing and the NIHT Algorithm

2.1. Compressive Sensing

The basic theory of compressive sensing is formulated as follows. For a k-sparse signal $x\in R^N$, which contains no more than k nonzero elements, a measurement matrix $\Phi \in R^{M\times N}$, and an observation vector (or measurements) $y\in R^M$, where $M<N$, the core problem of compressive sensing is to reconstruct the sparse signal $x$ by solving the following linear equation:

$$y=\Phi x$$

(1)

which acquires no unique candidate signals $\overline{x}$ for $\Phi \overline{x}=y$ because it is under-determined. However, the signal $x$ can be recovered from $\Phi$ and $y$ through many available reconstruction algorithms, such as, compressive sampling matching pursuit (CoSaMP) [23], iterative hard thresholding (IHT) [24], and Smoothed L0 norm [25,26] algorithms, with high reliability if the measurement matrix $\Phi$ satisfies the restricted isometry property (RIP) condition [27] and the signal $x$ is sparse enough, that is, $k\ll N$ [2]. However, if the signals data are huge, these algorithms are inevitably costly in terms of the computational complexity for recovering sparse signals as well as the memory usage for storing the measurement matrices.

2.2. NIHT Algorithm

The NIHT algorithm, extended from the IHT algorithm, was first proposed by Blumensath [22] and has become an effective method to calculate near-optimal solutions. The algorithm solves the problem of Equation (1) using the following optimization problem:

$$x=arg\underset{x:{\Vert x\Vert }_0\le k}{\min }\Vert y-\Phi x\Vert +\lambda {\Vert x\Vert }_0$$

(2)

where $\Vert \Vert$ denotes the $l_2$-norm, ${\Vert \Vert }_0$ counts the nonzero elements, and $\lambda$ is the penalty factor. The algorithm is described as follows.

Let $x^1=0$; then,

$$x^{n+1}=H_k\left(x^n+{\mu }^n{\Phi }^T\left(y-\Phi x^n\right)\right)$$

(3)

where $H_k\left(x\right)$ is a nonlinear operator that sets all but the $k$ maximal elements in absolute terms of $x$ to be zero, and ${\mu }^n$ is the step size at the nth iteration. In the NIHT algorithm, ${\mu }^n$ is adaptively determined using the following procedures.

Let ${\Pi }^n=supp\left(x^n\right)$ denotes the support set of $x^n$, and $g^n={\Phi }^T\left(y-\Phi x^n\right)$ is the negative gradient of ${\Vert y-\Phi x\Vert }^2$ evaluated at $x^n$ at the $n\mathrm{th}$ iteration; then, $g_{{\Pi }^n}$ denotes the sub-vector of $g^n$ that contains only the elements in the set of ${\Pi }^n$, and ${\Phi }_{{\Pi }^n}$ is the sub-matrix of $\Phi$ that contains corresponding columns indexed by ${\Pi }^n$. The adaptive step size ${\mu }^n$ and new approximation of $x^{n+1}$ are updated as below.

Given the approximation of $x^n$ at the $n\mathrm{th}$ iteration and its support set ${\Pi }^n$, the adaptive step size ${\mu }^n$ is calculated by the following equation:

$${\mu }^n=g_{{\Pi }^n}^T{g}_{{\Pi }^n}/g_{{\Pi }^n}^T{\Phi }_{{\Pi }^n}^T{\Phi }_{{\Pi }^n}{g}_{{\Pi }^n}$$

(4)

and the new proposition ${\overline{x}}^{n+1}$ is obtained from $x^n$ by the following equation:

$${\overline{x}}^{n+1}=H_k\left(x^n+{\mu }^n{\Phi }^T\left(y-\Phi x^n\right)\right)$$

(5)

If the support set of ${\overline{x}}^{n+1}$ is equal to that of $x^n$, namely, ${\Pi }^{n+1}={\Pi }^n$, then $x^{n+1}={\overline{x}}^{n+1}$.

However, if ${\Pi }^{n+1}\ne {\Pi }^n$, the step size ${\mu }^n$ obtained in Equation (4) cannot guarantee that the Equation (2) has a maximal reduction, and the approximation of $x^n$ converges. In this case, the sufficient condition for the algorithm to guarantee convergent approximation of $x^n$ is that ${\mu }^n<{\omega }^n$, where

$${\omega }^n=\left(1-c\right){\Vert {\overline{x}}^{n+1}-x^n\Vert }_2^2/{\Vert \Phi \left({\overline{x}}^{n+1}-x^n\right)\Vert }_2^2$$

(6)

and $c$ is a small constant. Therefore, in the case that ${\Pi }^{n+1}\ne {\Pi }^n$, it is necessary to calculate ${\omega }^n$ and check whether ${\mu }^n<{\omega }^n$. If this holds, then $x^{n+1}={\overline{x}}^{n+1}$ and ${\Pi }^{n+1}=supp\left(x^{n+1}\right)$. Otherwise, the step size must be shrunk; in [22], it is proposed to shrink the step size ${\mu }^n$ by updating ${\mu }^n\leftarrow {\mu }^n/\left(\kappa \left(1-c\right)\right)$, where $\kappa >1/\left(1-c\right)$. A new proposition ${\overline{x}}^{n+1}$ is then calculated based on the shrunken step size ${\mu }^n$, and a new ${\omega }^n$ is obtained for rechecking whether ${\mu }^n<{\omega }^n$. These procedures are repeated until ${\mu }^n<{\omega }^n$, and then $x^{n+1}={\overline{x}}^{n+1}$ and ${\Pi }^{n+1}=supp\left(x^{n+1}\right)$.

The NIHT algorithm is a modification of the IHT algorithm by the introduction of a simple adaptive step size and line search, which not only makes the algorithm performance independent of arbitrary scaling of $\Phi$ but also guarantees its convergence regardless of whether the theoretical conditions for IHT are satisfied. Furthermore, the NIHT algorithm is faster than many other state-of-the-art approaches that show similar empirical performance, such as the $l_1$ norm algorithm and OMP algorithm [22].

3. Radar Imaging Model Based on Compressive Sensing

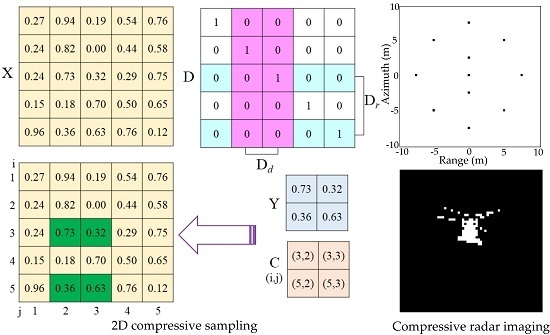
3.1. 2D Compressive Sensing

For a 2D K-sparse signal $X\in R^{N_1\times N_2}$, a measurement matrix pair $A\in R^{M_1\times N_1}$ and $B\in R^{M_2\times N_2}$, and an observation matrix $Y\in R^{M_1\times M_2}$, the 2D compressive sensing model is formulated as follows:

$$Y=AX{B}^T$$

(7)

where $B^T$ is the transpose of $B$, $M_1<N_1$, $M_2<N_2$ and $K<M_1{M}_2$. The sparsity $K$ of the 2D signal $X$ is defined as $Spa\left(X\right)={\displaystyle \sum _{i=1}^{N_2}}{\Vert x_i\Vert }_0\le K$, in which $x_i$ denotes the $i\mathrm{th}$ column vector of the matrix $X$, means that the 2D signal $X$ has no more than $K$ nonzero elements.

One-dimensional compressive sensing can be treated as a special form of 2D compressive sensing in the case that $M_2=N_2=1$. And the 2D compressive sensing model is also equivalent to the 1D compressive sensing model by the following operations:

$$\Phi =B\otimes A, y=vct\left(Y\right), x=vct\left(X\right)$$

(8)

where ‘$\otimes$’ denotes the operation of the Kronecker product and $vct( )$ denotes the vectorization of a matrix by stacking the columns of the matrix into a single column vector. Therefore, some properties of 1D compressive sensing are also suitable for 2D compressive sensing.

3.2. Compressive Radar Imaging Model

For a typical stepped frequency radar, the echo data of the $m\mathrm{th}$ ($m=0,1,\dots ,P-1$) aspect angle and $n\mathrm{th}$ ($n=0,1,\dots ,Q-1$) sampling frequency point can be described as:

$$u_{nm}={\displaystyle \sum _{p=0}^{P-1}{\displaystyle \sum _{q=0}^{Q-1}{\delta }_{pq}\exp \left(-j2\pi \frac{pn}{P}\right)\exp \left(-j2\pi \frac{qm}{Q}\right)}}$$

(9)

where ${\delta }_{pq}(p=0,1,\dots ,P-1,q=0,1,\dots ,Q-1)$ denotes the scattering intensity of the discrete position, $P$ is the number of aspect angles and $Q$ denotes the number of sub-pulse in a burst [21].

Suppose $N_1=P$ and $N_2=Q$, and let $U={\left[u_{nm}\right]}_{N_1\times N_2}$ and $\mathsf{\delta }={\left[{\delta }_{pq}\right]}_{N_1\times N_2}$ denote matrix of echo data and scattering intensity of the discrete position, respectively. ${\Psi }_d={\left[\exp \left(\frac{-j2\pi qm}{N_2}\right)\right]}_{N_2\times N_2}$ and ${\Psi }_r={\left[\exp \left(\frac{-j2\pi pn}{N_1}\right)\right]}_{N_1\times N_1}$ represent the discrete Fourier dictionary of azimuth and range, respectively. Then, a typical radar imaging model can be formulated as follows:

$$U={\Psi }_r\mathsf{\delta }{\Psi }_d$$

(10)

To apply the 2D compressive sensing in a radar imaging system, an effective compressive sampling method should be designed at first for reducing the length of observation signals. Compared with the 1D compressive sampling model by which a small number of either frequency points or aspect angles is randomly sampled [9,28], the 2D compressive sampling method compresses and randomly samples both of frequency points and aspect angles simultaneously. Moreover, in the process of compressive sampling of a radar system, any pixel ${\delta }_{pq}$ of a scene has just two states: sampled or un-sampled. So, the sampling matrix is designed specially and each entry of the matrix is either 1 or 0, indicating that the corresponding pixel of the radar imaging scene is sampled or un-sampled, respectively. The 2D compressive sampling method in radar imaging is designed by the following procedures: (i) set a matrix $D\in R^{N_2\times N_1}$, in which each entry $d_{ij}$ is either 0 ($i\ne j$) or 1 ($i=j$); (ii) randomly select $M_1$ rows of $D$ to produce a sampling matrix $D_r$, and $M_2$ columns of $D$ to produce a sampling matrix $D_d$, respectively. The sampling matrix pair $D_r$ and $D_d$ compress the range information from $N_1$ to $M_1$ and azimuth information from $N_2$ to $M_2$, respectively. In order to more clearly describe the 2D compressive sampling process, a simple example is given, as shown in Figure 1. It is obvious that the sampling process can compress a matrix $X$ to a matrix $Y$ of lower dimensions, and $Y$ can be also regarded as the set of $M_1{M}_2$ elements collected from the original scene $X$ at the rows and columns, which are determined by the column position of “1” of $D_r$ and $D_d^T$, respectively. Moreover, the compressive sampling method is actually feasible, which has been demonstrated by its application in compressive imaging with atomic force microscopy [29] and scanning ion conductance microscopy [30].

Then, the 2D compressive radar imaging model is formulated as follows:

$$Y=D_{r}U{D}_d=D_r{\Psi }_r\mathsf{\delta }{\Psi }_d{D}_d$$

(11)

The 2D compressive radar imaging model has the capability of dramatically reducing the sampled pixels of a radar scene from $N_1\times N_2$ dimensions to $M_1\times M_1$ dimensions and reconstructing the scene in matrix domain with much less reconstruction time using the 2D-NIHT algorithm presented as below.

4. 2D-NIHT Algorithm

4.1. Description of the 2D-NIHT Algorithm

In this study, inspired by the conventional NIHT algorithm, a 2D-NIHT algorithm is proposed to recover 2D sparse signals based on the 2D compressive sensing model, as described in the Equation (7), by solving the following optimization problem:

$$X^{*}=arg\underset{Spa\left(X\right)\le K}{\min }{\Vert Y-AX{B}^T\Vert }_F^2+\lambda *Spa\left(X\right)$$

(12)

where ${\Vert \Vert }_F$ denotes the Frobenius norm of a matrix, that is, ${\Vert X\Vert }_F=\sqrt{{\displaystyle \sum _{i=1}^{N_1}}{\displaystyle \sum _{j=1}^{N_2}}{x_{ij}}^2}$.

The above optimization problem can be solved by the following iterative procedures:

$$X^{n+1}={{\rm H}}_K\left[X^n+{\mu }^n{A}^T\left(Y-A{X}^n{B}^T\right)B\right]$$

(13)

where ${{\rm H}}_K\left[X\right]$ is the nonlinear operation that sets all elements of matrix $X$ as zero except for the maximum $K$ elements of $X$ in absolute terms.

At the $n\mathrm{th}$ iteration, ${\Gamma }^n=\mathrm{suppM}\left(X^n\right)=\left\{{\tau }_{ij}^n\right\}$ denotes the support matrix of $X^n$, in which ${\tau }_{ij}^n=\mathrm{sgn}(\mathrm{abs}(x_{ij}^n))$ and ${x_{ij}}^n$ are the entries of the matrices ${\Gamma }^n$ and $X^n$ at the $i\mathrm{th}$ row and the $j\mathrm{th}$ column, respectively, and $\mathrm{sgn}()$ is the signum function. $G^n=\left\{g_{ij}^n\right\}=A^T\left(Y-A{X}^n{B}^T\right)B$ is the negative gradient matrix of ${\Vert Y-AX{B}^T\Vert }_F^2$ evaluated at $X^n$. Then, $G_{{\Gamma }^n}=G^n.\times {\Gamma }^n$ denotes the matrix derived from $G^n$ by setting ${g_{ij}}^n=0$ if ${{\tau }_{ij}}^n=0$, in which the “$.\times$” is the element-wise multiplication, and ${\Phi }_{{\Gamma }^n}=A{G}_{{\Gamma }^n}{B}^T$. Similar to the arguments in [22], the step size ${\mu }^n$ is calculated by the following equation:

$${\mu }^n={\Vert G_{{\Gamma }^n}\Vert }_F^2/{\Vert {\Phi }_{{\Gamma }^n}{G}_{{\Gamma }^n}\Vert }_F^2$$

(14)

Hence, a new proposition ${\overline{X}}^{n+1}$ is calculated by the following equation:

$${\overline{X}}^{n+1}={{\rm H}}_K\left[X^n+{\mu }^n{A}^T\left(Y-A{X}^n{B}^T\right)B\right]$$

(15)

Next, it is necessary to determine whether the new proposition is an approximation solution $X^{n+1}$ to the problem in Equation (12) at the $(n+1)\mathrm{th}$ iteration by comparing the support matrices ${\Gamma }^n$ and ${\Gamma }^{n+1}=\mathrm{suppM}\left({\overline{X}}^{n+1}\right)$ described as follows.

If ${\Gamma }^n$ is equal to ${\Gamma }^{n+1}$, then $X^{n+1}={\overline{X}}^{n+1}$; otherwise, the sufficient condition must be satisfied to guarantee the convergence of the approximation solution of $X$, that is, ${\mu }^n<{\omega }^n$, where:

$${\omega }^n={\left(1-c\right){\Vert {\overline{X}}^{n+1}-X^n\Vert }_F^2/\Vert A\left({\overline{X}}^{n+1}-X^n\right)B^T\Vert }_F^2$$

(16)

and $c$ is a small constant. If ${\mu }^n\ge {\omega }^n$, then the step size ${\mu }^n$ must be shrunk by updating ${\mu }^n\leftarrow {\mu }^n/\left(\kappa \left(1-c\right)\right)$ with a constant $\kappa >1/\left(1-c\right)$, and a new proposition ${\overline{X}}^{n+1}$ is calculated based on the shrunk step size ${\mu }^n$ by Equation (15). The new ${\omega }^n$ is accordingly obtained for rechecking whether ${\mu }^n<{\omega }^n$. These procedures are repeated until ${\mu }^n<{\omega }^n$, and then $X^{n+1}={\overline{X}}^{n+1}$ and ${\Gamma }^{n+1}=\mathrm{suppM}\left(X^{n+1}\right)$.

The implementation of the 2D-NIHT algorithm is listed in Algorithm 1.

In general, compared with NIHT method, which places a great demand on memory space for measurement matrix storage, the 2D-NIHT algorithm realizes 2D sparse signal recovery in matrix domain with far less storage space requirement. The 2D-NIHT algorithm requires $M_1{N}_1+M_2{N}_2$ memory units to store the measurement matrices; in contrast, the measurement matrix of NIHT algorithm requires $M_1{N}_1\times M_2{N}_2$ memory units. The 2D-NIHT algorithm immensely reduces the storage space requirement for the measurement matrix, which is valuable in practice, especially for portable radar systems.

Algorithm 1. 2D normalized iterative hard thresholding algorithm.

Input: $A$, $B$, $Y$, $K$.

Initialize: $X^1=0$, ${\Gamma }^1=\mathrm{suppM}\left({\mathrm{H}}_K\left({\mathrm{A}}^{T}YB\right)\right)$.

Iterate for $n=1$, until the stopping criterion is met:

Step 1. $G^n=A^T\left(Y-A{X}^n{B}^T\right)B$;

Step 2. ${\mu }^n={\Vert G_{{\Gamma }^n}\Vert }_F^2/{\Vert {\Phi }_{{\Gamma }^n}{G}_{{\Gamma }^n}\Vert }_F^2$;

Step 3. ${\overline{X}}^{n+1}={{\rm H}}_K\left[X^n+{\mu }^n{G}^n\right]$;

Step 4. ${\Gamma }^{n+1}=\mathrm{suppM}\left({\overline{X}}^{n+1}\right)$;

Step 5. If ${\Gamma }^n$ is equal to ${\Gamma }^{n+1}$, then go to Step 6; otherwise

set ${\omega }^n={\left(1-c\right)\left({\Vert {\overline{X}}^{n+1}-X^n\Vert }_F^2\right)/\Vert A\left({\overline{X}}^{n+1}-X^n\right)B^T\Vert }_F^2$,

and repeat the following procedures until ${\mu }^n<{\omega }^n$:

${\mu }^n\leftarrow {\mu }^n/\left(\kappa \left(1-c\right)\right)$, ${\overline{X}}^{n+1}=H_K\left(X^n+{\mu }^n{G}^n\right)$,

${\omega }^n={\left(1-c\right)\left({\Vert {\overline{X}}^{n+1}-X^n\Vert }_F^2\right)/\Vert A\left({\overline{X}}^{n+1}-X^n\right)B^T\Vert }_F^2$;

Step 6. $X^{n+1}={\overline{X}}^{n+1}$;

Step 7. ${\Gamma }^{n+1}=\mathrm{suppM}\left(X^{n+1}\right)$;

Step 8. $n=n+1$.

Output: $X^{*}=X^{n+1}$.

4.2. Convergence of the 2D-NIHT Algorithm

The sufficient condition for the convergence the 2D-NIHT algorithm is given in the following convergence theorem.

Theorem 1.

Given a 2D compressive sensing model $Y=AX{B}^T$, where $X$ is a 2D K-sparse signal and $X^K$ is the best K-term approximation of the signal $X$, if the matrix $\Phi =B\otimes A$ satisfies the RIP condition for any 2K-sparse signal $x=vct(X)$:

$$0<{\alpha }_{2K}\le \frac{\Vert \Phi x\Vert }{\Vert x\Vert }\le {\beta }_{2K}$$

(17)

where ${\alpha }_{2K}$ and ${\beta }_{2K}$ are two constants, then the 2D-NIHT algorithm can recover $X$ by an approximation $X^n$ at the $n\mathrm{th}$ iteration, satisfying:

$${\Vert X-X^n\Vert }_F<2^{-3n/2}{\Vert X^K\Vert }_F+3.557/{\alpha }_{2K}^2{\Vert E\Vert }_F+{\Vert X-X^k\Vert }_F$$

(18)

where $E=Y-A{X}^K{B}^T$ is the observation error.

Furthermore, after no more than:

$$n*=\lceil \frac{2}{3}{\log }_2\left(\frac{{\Vert X^K\Vert }_F}{{\tilde{\epsilon }}_K}\right)\rceil$$

(19)

Iterations, the 2D-NIHT algorithm recovers $X$ with an accuracy of:

$${\Vert X-X^{n*}\Vert }_F\le 7.114/{\alpha }_{2K}^2{\Vert E\Vert }_F+2{\Vert X-X^k\Vert }_F$$

(20)

where:

$${\tilde{\epsilon }}_K=3.557/{\alpha }_{2K}^2{\Vert E\Vert }_F+{\Vert X-X^k\Vert }_F$$

(21)

Theorem 1 (proof shown in Appendix A) indicates that the 2D-NIHT algorithm can find an optimal solution that approximates the true signal with finite iterations, and the approximation is bounded by $2{\tilde{\epsilon }}_K$, which includes two parts: one is determined by the observation error $E$ and the other is determined by the deviation between the signal $X$ and the best $K$-term approximation. Assuming that the observation error is zero and $X$ is $K$-sparse, the algorithm can recover $X$ exactly. For practical radar imaging, the reconstruction error is naturally bounded by the observation error.

5. Results

In this section, on the one hand, an experiment with syncretic sparse images was conducted to demonstrate the feasibility of the 2D-NIHT algorithm and its superiority to the NIHT algorithm in reconstruction time. On the other hand, two SAR scenes were used to exam the reconstruction performance of the 2D-NIHT algorithm under different SNR levels and its superiority to other five efficient reconstruction algorithms of sparse signals in compressive radar imaging systems. All data were analyzed in the Matlab R2013a environment using an Intel Core 4, 3.20 GHz processor with 4.0 GB of memory under the Microsoft Windows 7 operating system. The reconstruction time, which is the CPU time, was utilized as an indicator of the computational complexity of signals reconstruction. The probability of exact recovery, which is a crucial criterion for evaluating the practicability of the algorithm, was calculated by the equation $P\left(X\right)=1-{\Vert X-X*\Vert }_0/\left(N_1\times N_2\right)$, where $X\in R^{N_1\times N_2}$, and $X*\in R^{N_1\times N_2}$ were original signals and the recovered signals, respectively.

5.1. Experiments on Synthetic Images

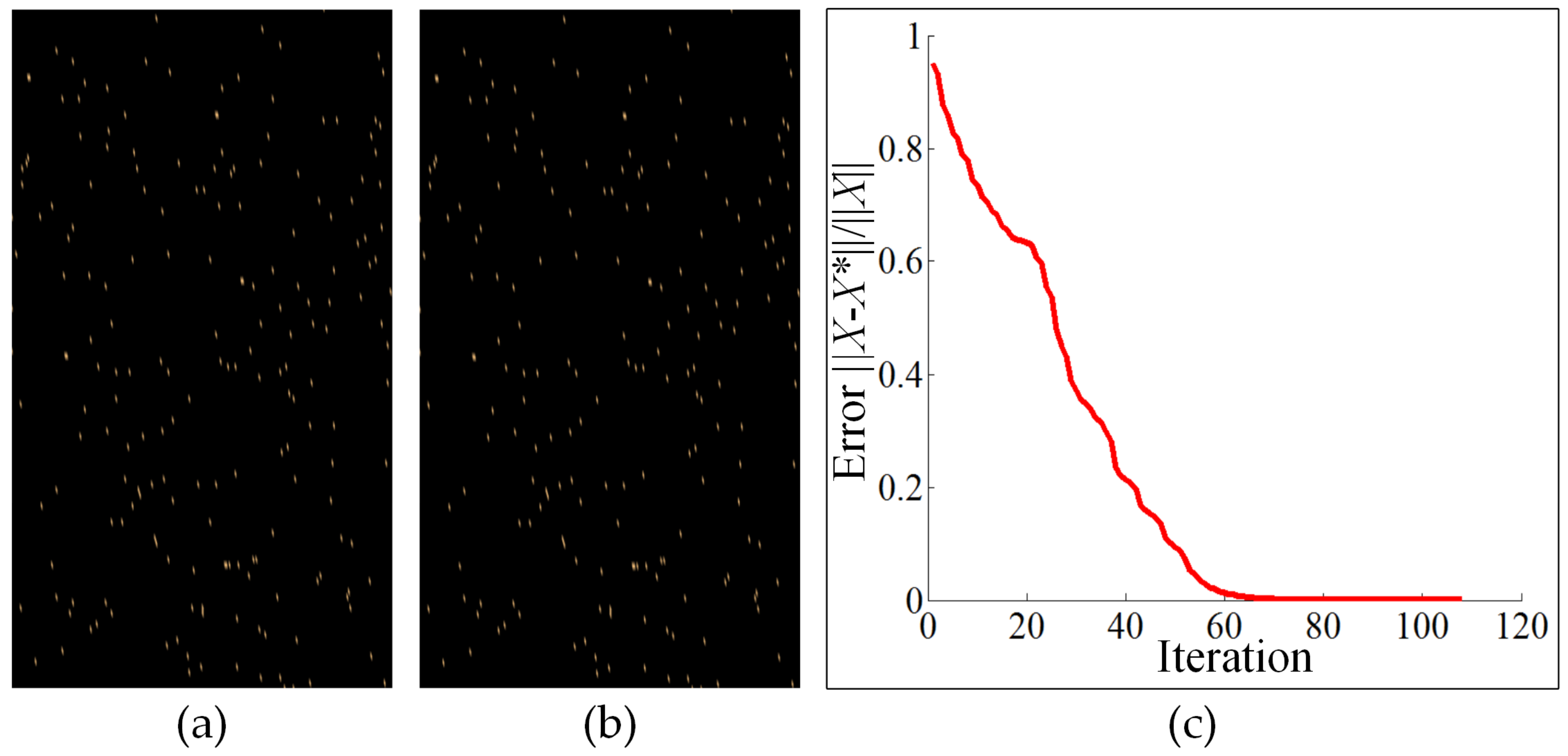
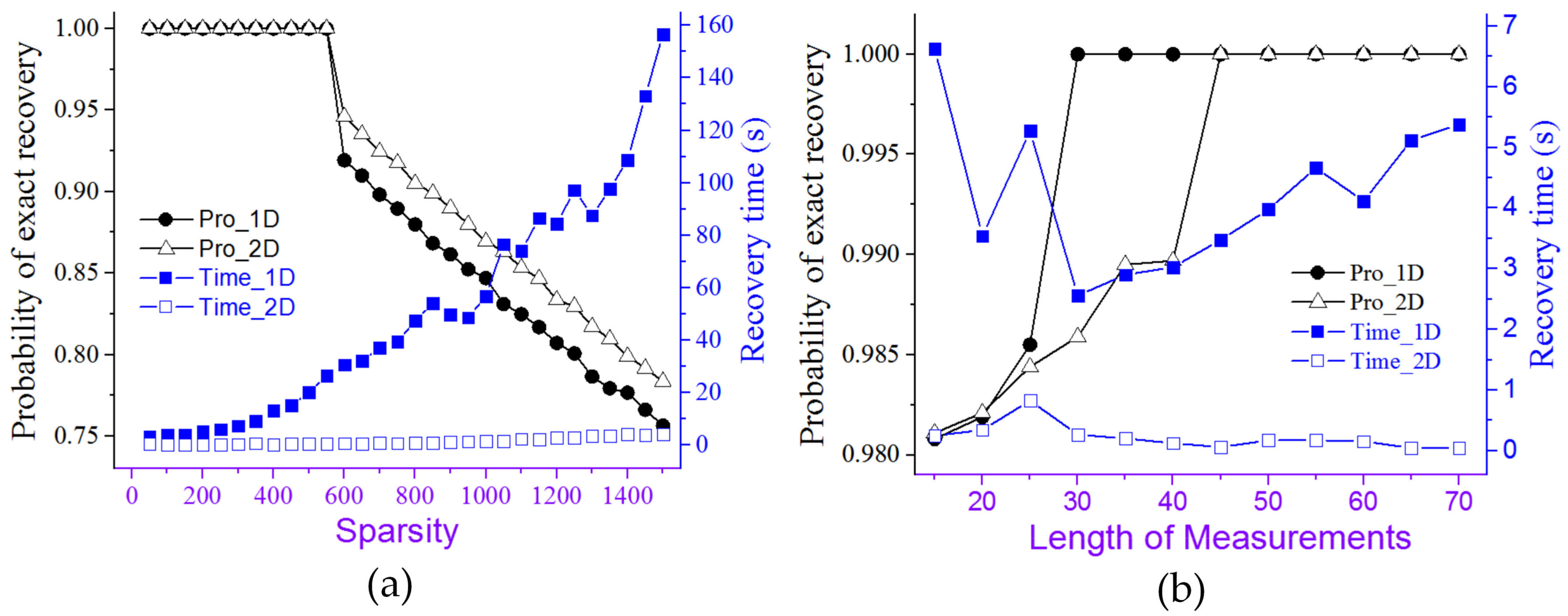
5.1.1. Efficiency of the 2D-NIHT Algorithm in 2D Signal Reconstruction

In this experiment, a randomly synthetic 2D sparse signal of $X$ with size of $256\times 128$ and a sparsity of 200, as shown in Figure 2a, was used to validate the efficiency of the 2D-NIHT algorithm. The observation matrix $Y$ was acquired by the model $Y=AX{B}^T$ with the compressive sampling rate of 0.5 in both row and column, and then the recovered signal $X*$ was reconstructed using the 2D-NIHT algorithm from $Y$. As shown in Figure 2b, it was obvious that the algorithm perfectly recovered the synthetic 2D sparse signal without any information loss. And, as shown in Figure 2c, it took a finite number of iterations, which was even far less than the sparsity $K$ of the signal. Moreover, only 0.25 s was spent on the whole process of the sparse signal recovery.

5.1.2. Comparison with the NIHT Algorithm

To demonstrate the superiority of the 2D-NIHT algorithm to the NIHT algorithm, a series of synthetic images were used to test their reconstruction performances. The reconstruction performances of the 2D-NIHT and the NIHT algorithms were comprehensively compared by varying the sparsities and lengths of measurements, respectively.

To test the reconstruction performance of the two algorithms under various sparsities, some randomly synthetic 2D sparse signals $X_i\left(i=1,2,\dots ,30\right)\in R^{100\times 100}$ with different sparsities were used as testing images, and the measurements of a fixed length were acquired with a constant compressive sampling rates of 0.5 for both rows and columns. To test the reconstruction performance of the NIHT algorithm, the 2D signals were also vectorized by $x_i=vct\left(X_i\right)\in R^{10000}$ firstly and the measurements were acquired based on Equation (1) with a constant compressive sampling rate of 0.25 for any signal $x_i$. The reconstruction performances of the two algorithms, as shown in Figure 3a, demonstrated that, on one hand, both algorithms could obtain the probability of exact recovery of 1 with a smaller sparsity (≤550), and then their probabilities of exact recovery of both algorithms decreased as the sparsity increased; on the other hand, the reconstruction time of the 2D-NIHT algorithm was far less than that of the NIHT algorithm, and the difference of recovery time between the two algorithms became larger with an increase in the signal sparsity.

To test the reconstruction performance of the two algorithms with measurements of various lengths, 2D sparse signals $X_i\left(i=1,2,\dots ,12\right)\in R^{100\times 100}$ with a fixed sparsity of $K=100$ were generated for testing and the measurements were obtained with different lengths. For the sparse signal $X_i$, the lengths of the measurement for the 2D-NIHT algorithm were set as $M_{1i}=M_{2i}=10+5i$ and the lengths of measurement for NIHT algorithm was set as $M_i=M_{1i}\times M_{2i}$ accordingly. The reconstruction performances of the two algorithms, as shown in Figure 3b, indicated that both algorithms could acquire a very high probability of exact recovery with measurements of large size (>40 × 40), while the reconstruction time of the NIHT algorithm was far greater than that of the 2D-NIHT algorithm.

Overall, the 2D-NIHT algorithm and the NIHT algorithm displayed a similar tendency in the probability of exact recovery with respect to the sparsity of signals and the size of measurements, indicating that they had consistent performances in the reconstruction convergence and accuracy, and the reconstruction time of the 2D-NIHT algorithm was much less than that of the NIHT algorithm, illustrating that the proposed 2D-NIHT algorithm dramatically reduced computational complexity in signal reconstruction.

5.2. Experiments on Actual Radar Images

In this section, two SAR scenes were used to verify the efficiency and superiority of the 2D-NIHT algorithm in compressive radar imaging systems, as shown in Figure 4. One was a simple scene that acquired 11 point targets (Figure 4a), and the other was a helicopter acquired by a SAR (Figure 4b). The SAR parameters were set such that the carrier frequency was 2 GHz, the working frequency was 9.5 GHz–10.5 GHz with a step size 20 MHz, the sampling number was $N_1=64$, the observation azimuth varied within −3.2°~3.0°, and corresponding sampling number was $N_2=64$. In addition, it was unavoidable that there were noises in the actual radar imaging system, so, the noises of different SNR levels were also added in the echo signals to explore the influence of the noise on the reconstruction performance of the 2D-NIHT algorithm.

To test radar imaging performance using the 2D-NIHT algorithm in the presence of noise, Gaussian white noises with different SNR levels (noise free, 30 dB and 20 dB) were added into the echo signals. Figure 5 shows the imaging results of the 11 point targets (Figure 5a) and the helicopter (Figure 5b) with different SNR levels of noises using the 2D-NIHT algorithm. The compressive sampling rates were 0.5 in the range and azimuth information for the two SAR scenes. The imaging results illustrated that the actual target positions and amplitudes of the both scenes were reconstructed without any information loss at the higher SNR level (noise free and 30 dB). At the low SNR level (20 dB), the imaging results contained some false values at the target positions for both scenes. Moreover, it was obvious that the reconstructed image using the 2D-NIHT algorithm was clean without any noise, because the nonlinear operation process of ${{\rm H}}_K\left[X\right]$ in the 2D-NIHT algorithm was capable of setting $N_1\times N_2-K$ elements of $X$ as 0 and these elements contained most of the noises. Therefore, the 2D-NIHT algorithm is an effective method to remove background noise used in compressive radar imaging systems.

In addition, four other algorithms, including CoSaMP, SL0, block-based compressive sensing (BCS) [31], and NIHT algorithms, were used to recover the two scenes without noises, and their reconstruction performances were compared with the 2D-NIHT algorithms in terms of reconstruction time and probability of exact recovery. The simulation for each SAR scene was repeated 20 times with every algorithm, and the statistical average values and standard deviations in reconstruction time and probability of exact recovery for the five algorithms were achieved, as shown in

Table 1. Comparison of the five algorithms, including CoSaMP, SL0, BCS, NIHT and 2D-NIHT algorithms, in terms of reconstruction time and probability of exact recovery.

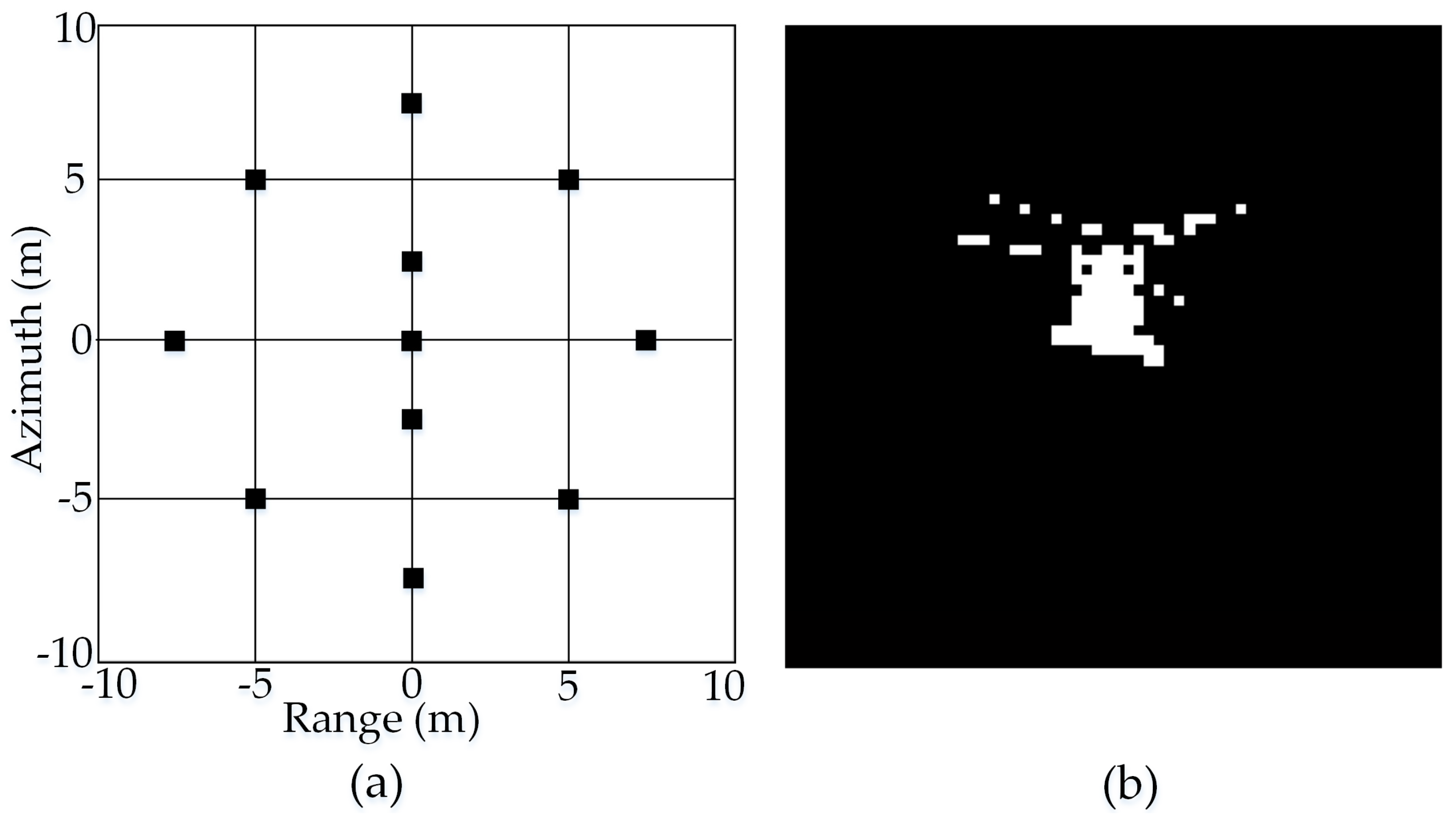
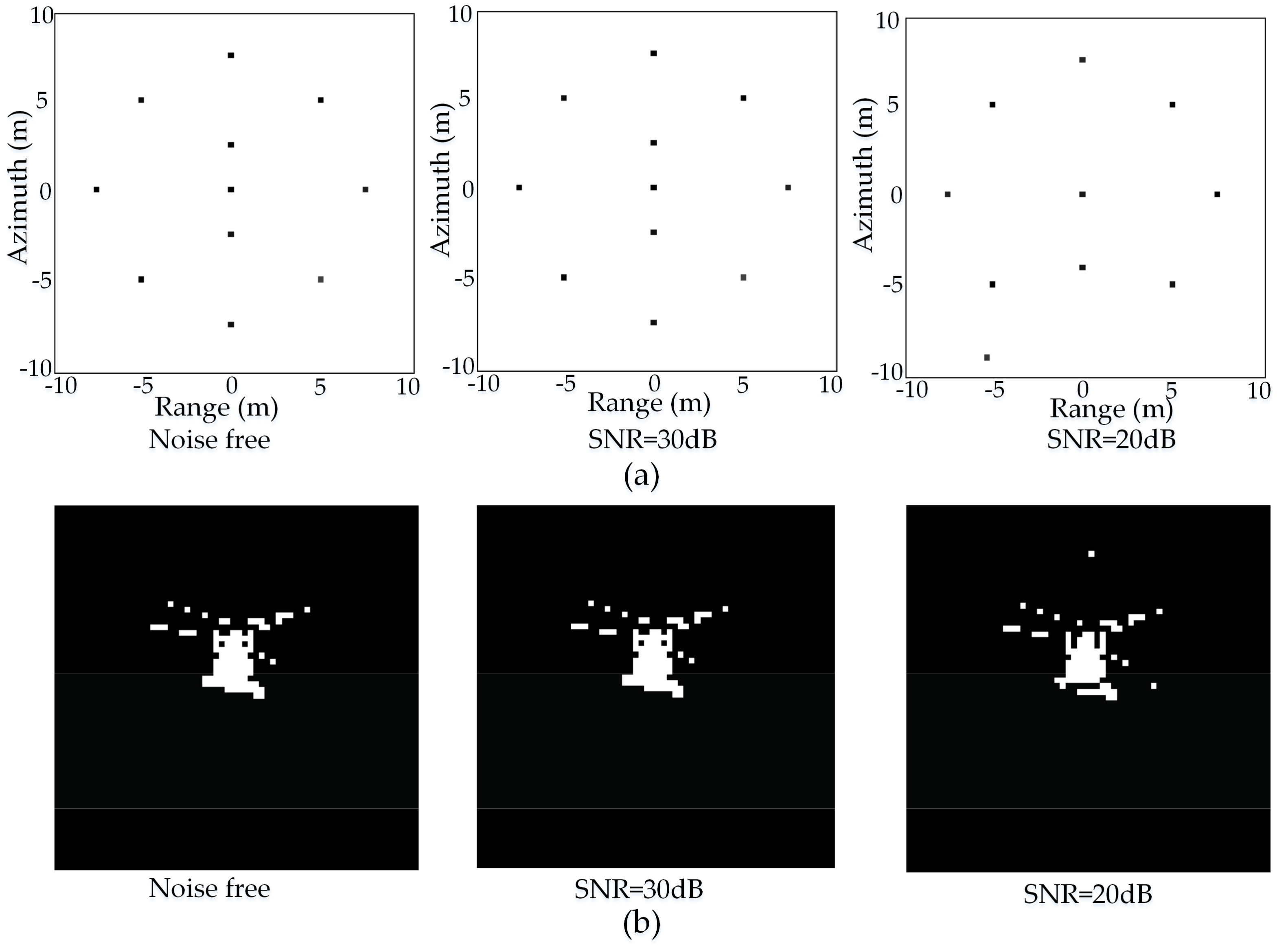
		CoSaMP	SL0	BCS	NIHT	2D-NIHT
11 point targets	Recovery time (s)	0.069 ± 0.134	30.80 ± 1.64	0.049 ± 0.024	0.629 ± 0.115	0.055 ± 0.037
	Probability of exact recovery	1	1	0.652 ± 0.038	1	1
helicopter	Recovery time (s)	128.79 ± 3.495	34.679 ± 0.902	0.172 ± 0.044	5.176 ± 0.13	0.237 ± 0.139
	Probability of exact recovery	0.976	1	0.476 ± 0.020	0.976	1

. The results demonstrate that, compared with the other four algorithms, the 2D-NIHT algorithm could acquire the reconstructed images with ultrahigh probability of exact recovery, and its performance in reconstruction time was only a little inferior to the BCS model, which, however, had the worst performance for the probability of exact recovery. Therefore, the 2D-NIHT is capable of significantly reducing the computational complexity and reconstruction time for recovering radar images and has an overall performance superior to the other four algorithms.

6. Conclusions

In this paper, a 2D-NIHT algorithm was proposed to solve the problem that compressive radar imaging systems confront, that is, the high computational complexity involved in recovering sparse signals. The algorithm recovered 2D sparse signals by directly leveraging the matrix structure of the signals with robust and ultra-high probability, as proved theoretically and demonstrated by experiments. The number of iterations of the 2D-NIHT algorithm in signal reconstruction is far fewer than the sparsity of the testing signals, and reconstruction time of the 2D-NIHT algorithm is far less than that of the NIHT algorithm, indicating that the 2D-NIHT algorithm dramatically reduces the computational complexity and reconstruction time compared with the NIHT algorithm. Particularly, the radar scenes can be also recovered successfully by the 2D-NIHT algorithm with high reconstruction performance, and the 2D-NIHT algorithm also displays significant superiority in overall reconstruction performance in radar imaging system to other four algorithms. Moreover, the 2D-NIHT algorithm offers great potential for general application of compressive sensing in electromagnetics and remote sensing to realize fast imaging.