Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation
Abstract
:1. Introduction
1.1. The Impact of UAVs on Photogrammetry and Remote Sensing
1.2. Trends in Block Georeferencing with UAV Photogrammetry
1.3. Requirements for DSO, ISO or GNSS-AT
1.3.1. Hardware and System Calibration
1.3.2. Camera Calibration
1.4. Previous Work on the Accuracy of Block Orientation with RTK-Enabled UAVs
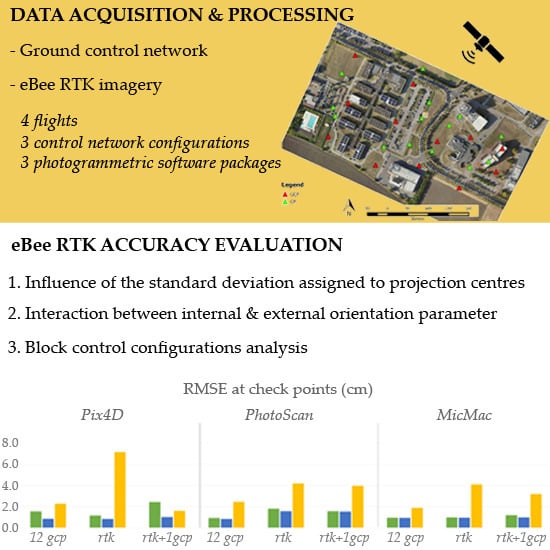
2. Materials and Methods
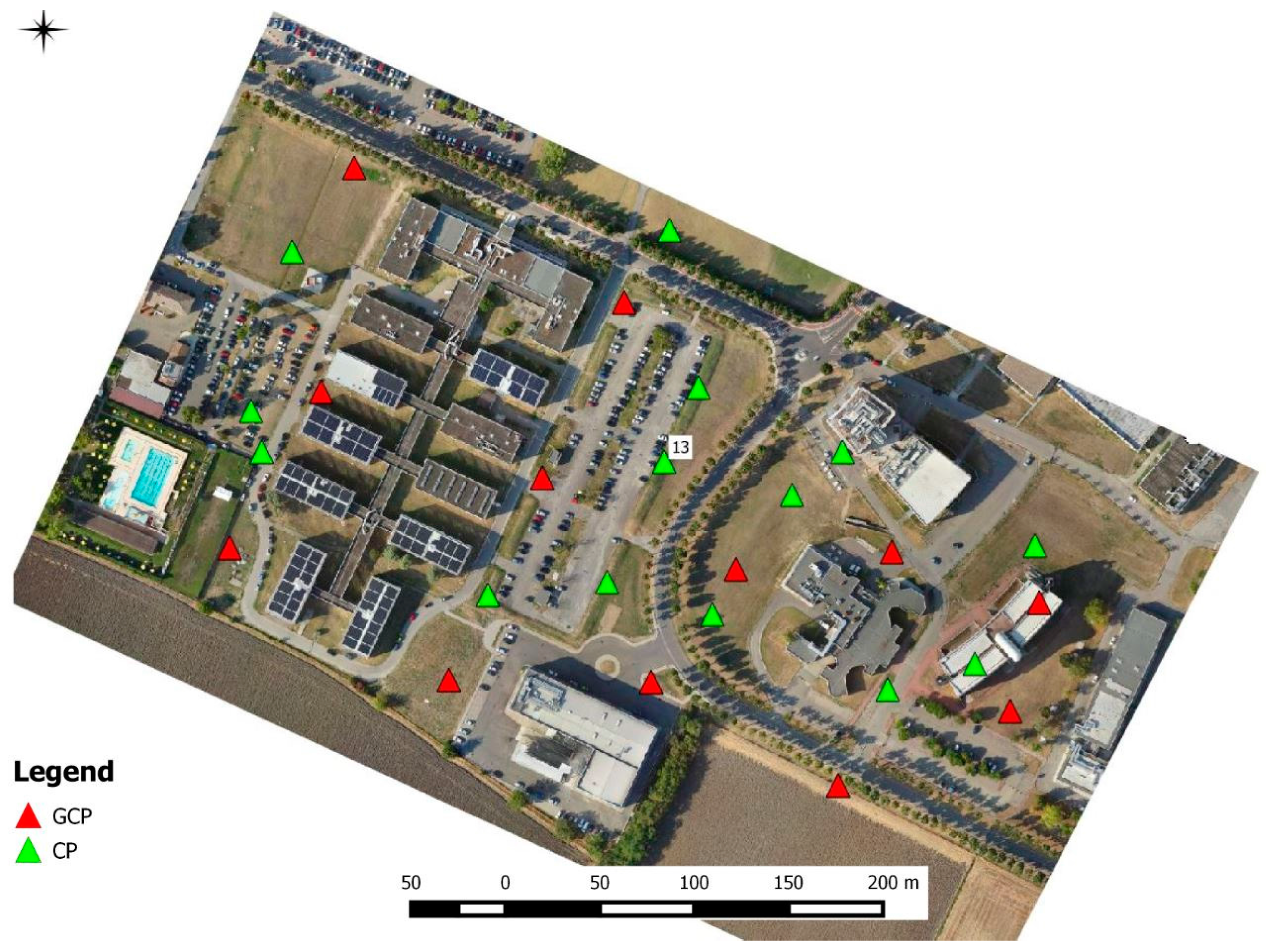
2.1. Test Site Description
Reference Network and GCP
2.2. Data Acquisition
2.3. Photogrammetric Data Processing
2.3.1. MicMac
2.3.2. Agisoft PhotoScan
2.3.3. Pix4Dmapper Pro
2.3.4. CALGE
2.4. Description of the Tests
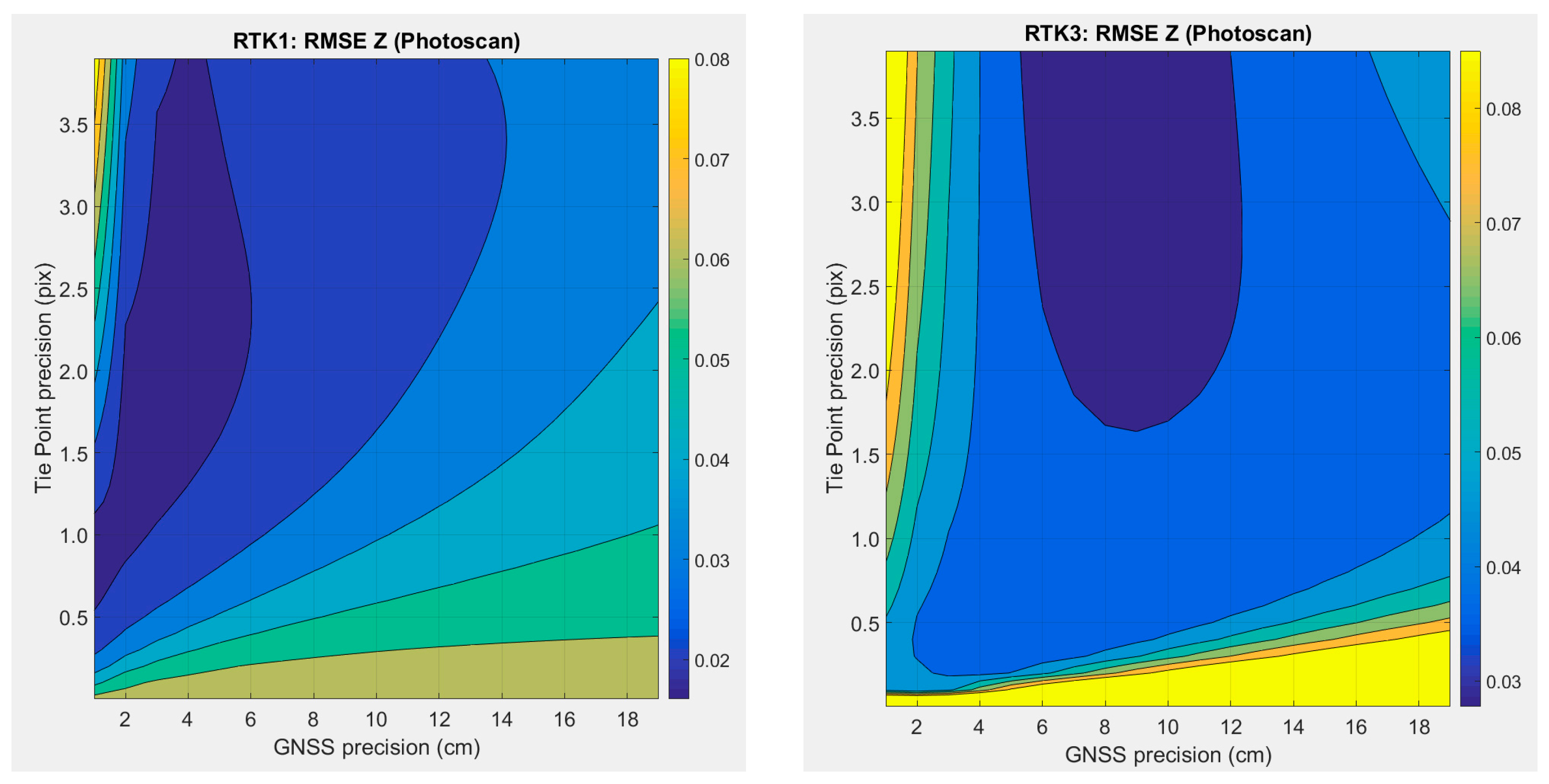
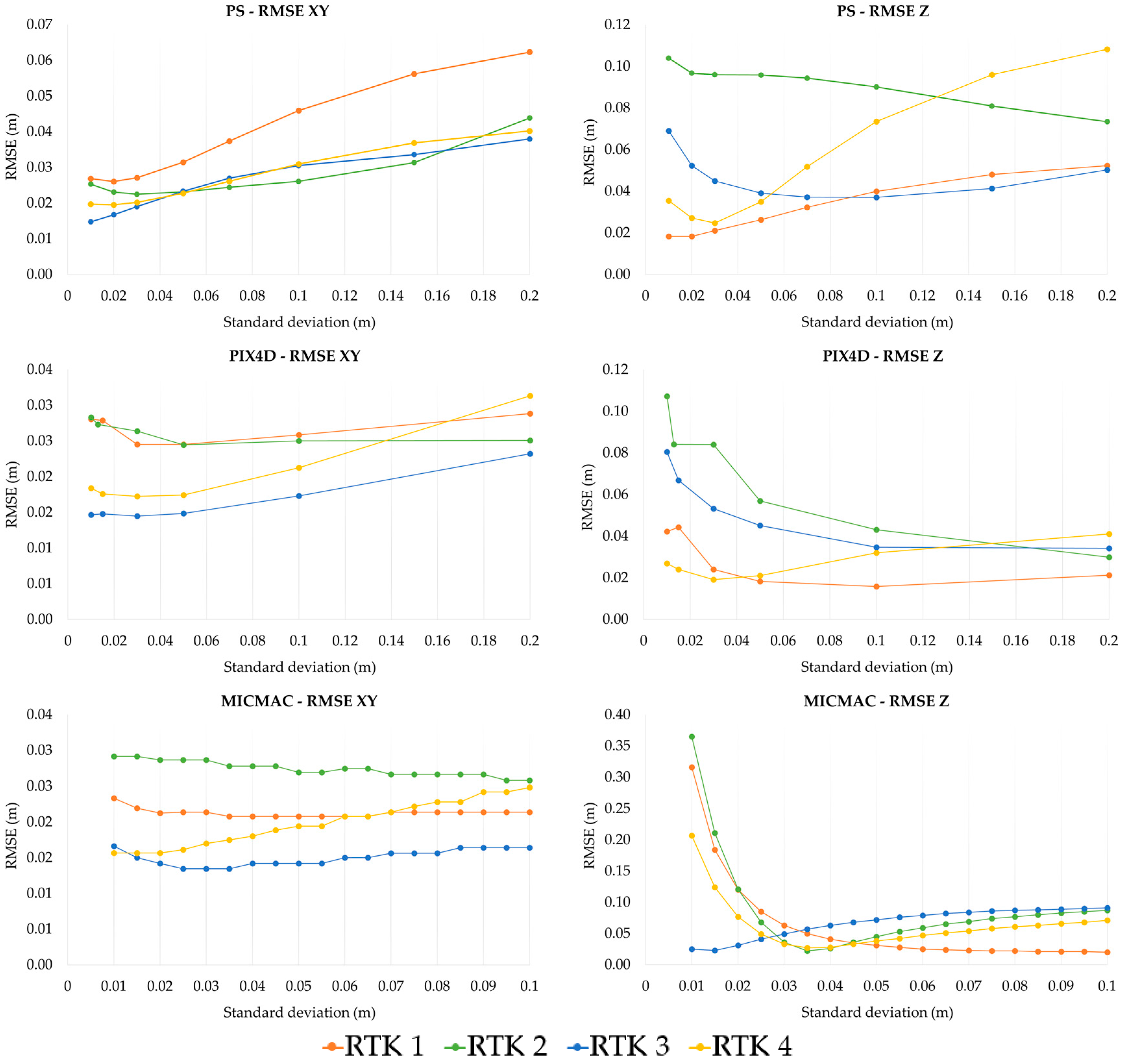
2.4.1. Influence of the Standard Deviation assigned to Projection Centers in the BBA
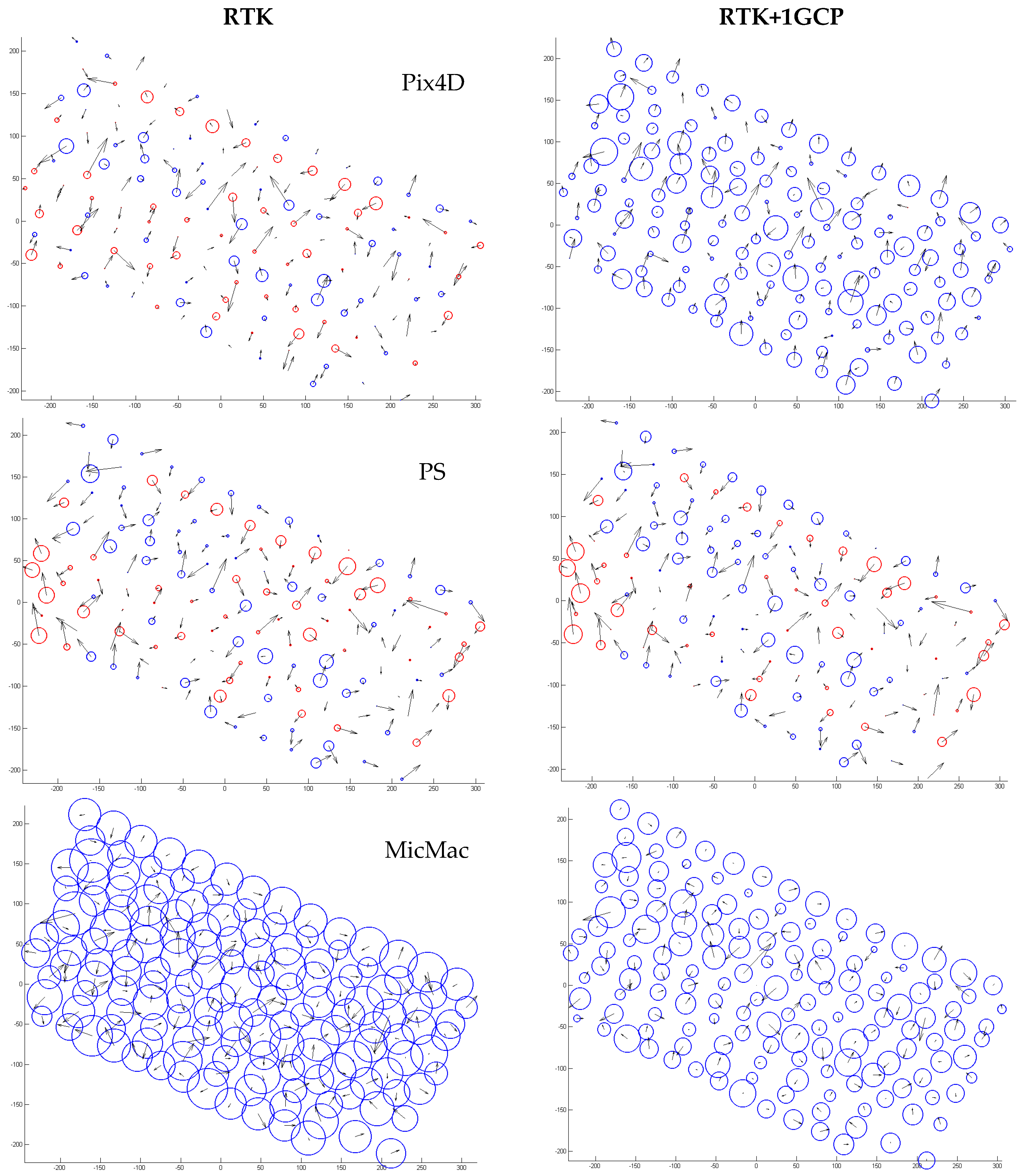
2.4.2. eBee RTK Survey Accuracy Assessment
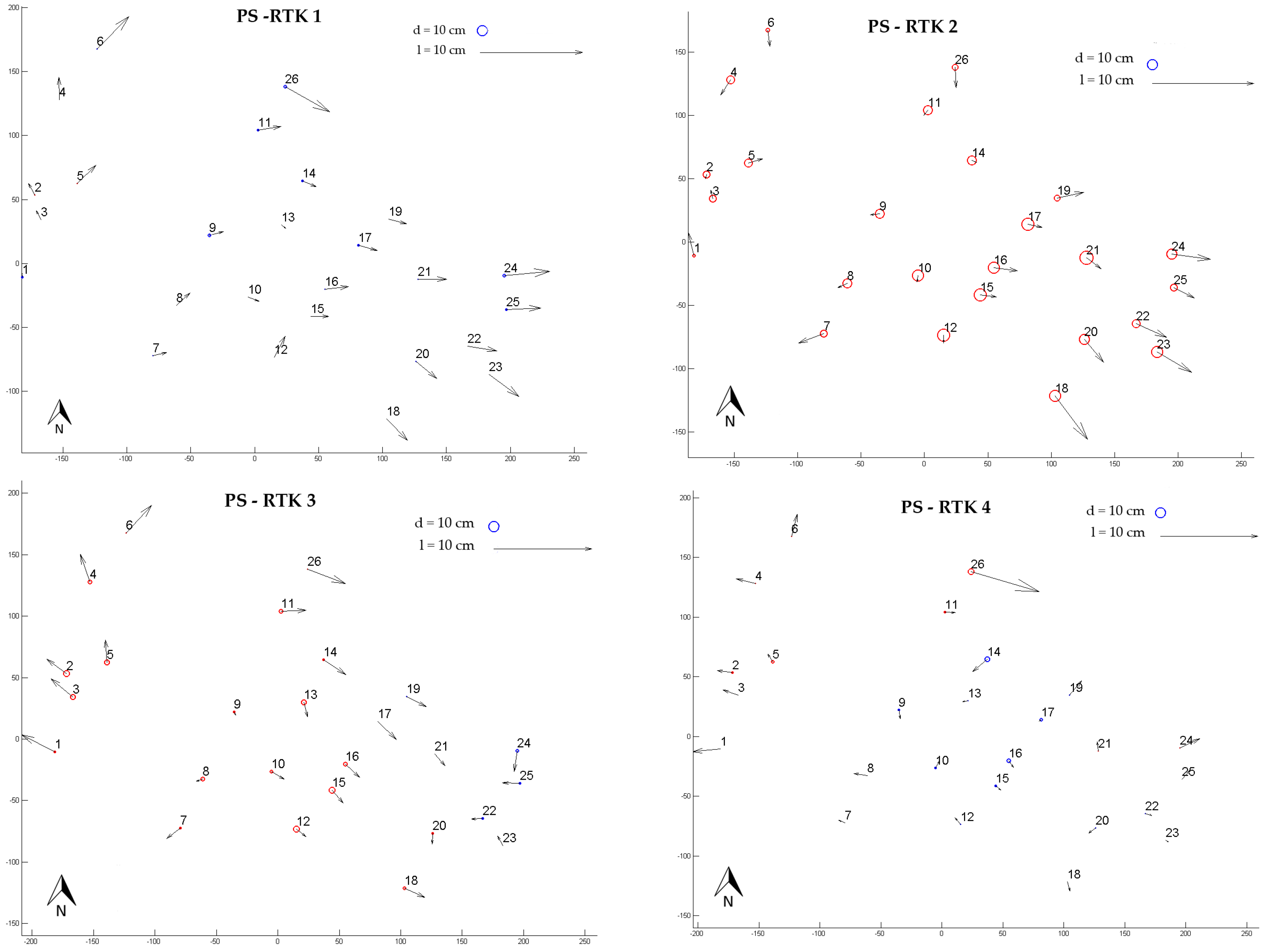
2.4.3. Interaction between Interior and Exterior Orientation Parameters
3. Results and Discussion
3.1. Influence of the Standard Deviation Assigned to the Observations
3.2. eBee RTK Survey Accuracy Assessment
3.3. Interaction between Interior and Exterior Orientation Parameters
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Interior Orientation and Self-Calibration Parameters | |
|---|---|
| PIX4D | Principal distance, Principal point coordinates, radial distortion parameters K1, K2, K3, tangential distortion parameters P1, P2 |
| PhotoScan | Principal distance, Principal point coordinates, radial distortion parameters K1, K2, K3, tangential distortion parameters P1, P2 |
| MicMac | Polynomial model (see MicMac manual [61]) |
| σ (cm) | 0.3 | 1 | 5 | 15 |
|---|---|---|---|---|
| RTK1 | 1.240 | 0.963 | 0.924 | 0.922 |
| RTK2 | 0.957 | 0.890 | 0.875 | 0.874 |
| RTK3 | 1.090 | 1.040 | 1.023 | 1.022 |
| RTK4 | 1.000 | 0.951 | 0.927 | 0.925 |
| MEAN X (m) | MEAN Y (m) | MEAN Z (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RTK 1 | |||||||||
| 12GCP | RTK | RTK+1GCP | 12GCP | RTK | RTK+1GCP | 12GCP | RTK | RTK+1GCP | |
| Pix4D | 0.001 | −0.014 | −0.011 | 0.007 | −0.003 | 0.002 | 0.005 | 0.012 | −0.002 |
| PS | −0.004 | 0.016 | 0.014 | −0.007 | −0.001 | 0.002 | −0.001 | 0.011 | 0.010 |
| MicMac | 0.003 | −0.011 | −0.010 | 0.004 | 0.002 | 0.001 | 0.003 | −0.085 | −0.004 |
| RTK 2 | |||||||||
| Pix4D | 0.002 | −0.005 | −0.006 | 0.003 | 0.008 | −0.004 | 0.006 | 0.083 | 0.001 |
| PS | −0.001 | 0.009 | 0.014 | −0.003 | −0.007 | 0.006 | −0.003 | −0.093 | −0.002 |
| MicMac | −0.003 | −0.008 | 0.014 | 0.002 | 0.003 | 0.006 | 0.000 | −0.063 | −0.002 |
| RTK 3 | |||||||||
| Pix4D | −0.002 | −0.004 | −0.006 | 0.004 | 0.004 | −0.004 | −0.011 | 0.069 | 0.001 |
| PS | −0.001 | 0.004 | 0.002 | −0.006 | −0.005 | 0.009 | −0.001 | −0.026 | 0.024 |
| MicMac | 0.000 | −0.002 | −0.001 | 0.006 | 0.007 | −0.001 | 0.004 | 0.035 | −0.019 |
| RTK 4 | |||||||||
| Pix4D | 0.000 | −0.008 | 0.008 | 0.005 | 0.004 | 0.004 | −0.008 | 0.013 | −0.026 |
| PS | 0.000 | 0.002 | 0.007 | −0.005 | 0.000 | 0.002 | 0.004 | 0.004 | −0.011 |
| MicMac | 0.004 | −0.003 | −0.002 | 0.003 | 0.000 | −0.006 | 0.010 | −0.039 | 0.000 |
| σ X (m) | σ Y (m) | σ Z (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RTK 1 | |||||||||
| 12GCP | RTK | RTK+1GCP | 12GCP | RTK | RTK+1GCP | 12GCP | RTK | RTK+1GCP | |
| Pix4D | 0.012 | 0.010 | 0.014 | 0.007 | 0.014 | 0.020 | 0.021 | 0.017 | 0.029 |
| PS | 0.011 | 0.016 | 0.016 | 0.010 | 0.012 | 0.012 | 0.018 | 0.015 | 0.015 |
| MicMac | 0.007 | 0.012 | 0.013 | 0.008 | 0.011 | 0.011 | 0.020 | 0.012 | 0.012 |
| RTK 2 | |||||||||
| Pix4D | 0.010 | 0.024 | 0.024 | 0.008 | 0.009 | 0.009 | 0.025 | 0.016 | 0.016 |
| PS | 0.010 | 0.015 | 0.009 | 0.008 | 0.009 | 0.011 | 0.018 | 0.020 | 0.021 |
| MicMac | 0.007 | 0.025 | 0.027 | 0.008 | 0.011 | 0.012 | 0.020 | 0.029 | 0.028 |
| RTK 3 | |||||||||
| Pix4D | 0.015 | 0.011 | 0.024 | 0.008 | 0.007 | 0.009 | 0.020 | 0.020 | 0.016 |
| PS | 0.009 | 0.018 | 0.015 | 0.005 | 0.015 | 0.012 | 0.024 | 0.033 | 0.032 |
| MicMac | 0.010 | 0.010 | 0.013 | 0.007 | 0.008 | 0.008 | 0.019 | 0.026 | 0.037 |
| RTK 4 | |||||||||
| Pix4D | 0.014 | 0.019 | 0.012 | 0.007 | 0.009 | 0.009 | 0.023 | 0.022 | 0.021 |
| PS | 0.018 | 0.023 | 0.025 | 0.008 | 0.009 | 0.012 | 0.017 | 0.028 | 0.027 |
| MicMac | 0.009 | 0.018 | 0.024 | 0.009 | 0.005 | 0.007 | 0.029 | 0.026 | 0.030 |
| RTK+1GCP | RTK+3 GCP | |||||
|---|---|---|---|---|---|---|
| RTK1 | ||||||
| X | Y | Z | X | Y | Z | |
| Mean (m) | 0.014 | 0.002 | 0.010 | −0.001 | −0.007 | −0.003 |
| σ (m) | 0.016 | 0.012 | 0.015 | 0.011 | 0.009 | 0.010 |
| RMSE (m) | 0.021 | 0.012 | 0.018 | 0.011 | 0.012 | 0.011 |
| RTK2 | ||||||
| Mean (m) | 0.014 | 0.006 | −0.002 | 0.009 | 0.001 | −0.002 |
| σ (m) | 0.009 | 0.011 | 0.021 | 0.008 | 0.009 | 0.019 |
| RMSE (m) | 0.017 | 0.013 | 0.021 | 0.012 | 0.009 | 0.019 |
| RTK 3 | ||||||
| Mean (m) | 0.002 | 0.009 | 0.024 | −0.002 | −0.002 | −0.011 |
| σ (m) | 0.015 | 0.012 | 0.032 | 0.014 | 0.006 | 0.027 |
| RMSE (m) | 0.015 | 0.015 | 0.039 | 0.014 | 0.006 | 0.029 |
| RTK4 | ||||||
| Mean (m) | 0.007 | 0.002 | −0.011 | 0.004 | −0.009 | 0.007 |
| σ (m) | 0.025 | 0.012 | 0.027 | 0.022 | 0.009 | 0.029 |
| RMSE (m) | 0.026 | 0.012 | 0.029 | 0.022 | 0.013 | 0.030 |
References
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sens. 2012, 4, 1671–1692. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Schellberg, J.; Hill, M.J.; Gerhards, R.; Rothmund, M.; Braun, M. Precision agriculture on grassland: Applications, perspectives and constraints. Eur. J. Agron. 2008, 29, 59–71. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Prec. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Villa, T.F.; Gonzalez, F.; Miljievic, B.; Ristovski, Z.D.; Morawska, L. An Overview of Small Unmanned Aerial Vehicles for Air Quality Measurements: Present Applications and Future Prospectives. Sensors 2016, 16, 1072. [Google Scholar] [CrossRef] [PubMed]
- Whitehead, K.; Hugenholtz, C.H. Remote sensing of the environment with small unmanned aircraft systems (UASs), part 1: A review of progress and challenges. J. Unmanned Veh. Syst. 2014, 2, 69–85. [Google Scholar] [CrossRef]
- Eisenbeiss, H. UAV Photogrammetry. Ph.D. Thesis, ETH Zuerich, Zuerich, Switzerland, 2009. [Google Scholar]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Hirschmüller, H. Accurate and efficient stereo processing by semi-global matching and mutual information. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; Volume 2, pp. 807–814.
- Haala, N.; Cramer, M.; Rothermel, M. Quality of 3D point clouds from highly overlapping UAV imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-1/W2, 183–188. [Google Scholar] [CrossRef]
- Santise, M. UAS Photogrammetric Blocks: Accuracy, Georeferencing and Control. Ph.D. Thesis, University of Parma, Parma, Italy, January 2016. [Google Scholar]
- Clapuyt, F.; Vanacker, V.; Van Oost, K. Reproducibility of UAV-based earth topography reconstructions based on Structure-from-Motion algorithms. Geomorphology 2016, 260, 4–15. [Google Scholar] [CrossRef]
- Jaud, M.; Passot, S.; Le Bivic, R.; Delacourt, C.; Grandjean, P.; Le Dantec, N. Assessing the accuracy of high resolution digital surface models computed by PhotoScan® and MicMac® in sub-optimal survey conditions. Remote Sens. 2016, 8, 465. [Google Scholar] [CrossRef]
- Naumann, M.; Geist, M.; Bill, R.; Niemeyer, F.; Grenzdörffer, G. Accuracy comparison of digital surface models created by unmanned aerial systems imagery and terrestrial laser scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-1/W2, 281–286. [Google Scholar] [CrossRef]
- Rock, G.; Ries, J.B.; Udelhoven, T. Sensitivity analysis of UAV-photogrammetry for creating digital elevation models (DEM). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, XXXVIII-1/C22, 69–73. [Google Scholar] [CrossRef]
- Shahbazi, M.; Sohn, G.; Théau, J.; Ménard, P. UAV-based point cloud generation for open-pit mine modelling. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40-1/W4, 313–320. [Google Scholar] [CrossRef]
- Siebert, S.; Teizer, J. Mobile 3D mapping for surveying earthwork projects using an Unmanned Aerial Vehicle (UAV) system. Autom. Constr. 2014, 41, 1–14. [Google Scholar] [CrossRef]
- Manyoky, M.; Theiler, P.; Steudler, D.; Eisenbeiss, H. Unmanned aerial vehicle in cadastral applications. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, XXXVIII -1/C22, 57–62. [Google Scholar] [CrossRef]
- Rau, J.Y.; Jhan, J.P.; Lo, C.F.; Lin, Y.S. Landslide mapping using imagery acquired by a fixed-wing UAV. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, XXXVIII -1/C22, 195–200. [Google Scholar] [CrossRef]
- Aicardi, I.; Nex, F.; Gerke, M.; Lingua, A.M. An Image-Based Approach for the Co-Registration of Multi-Temporal UAV Image Datasets. Remote Sens. 2016, 8, 779. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shea, J.M.; Shrestha, A.B.; Pellicciotti, F.; Bierkens, M.F.P.; de Jong, S.M. High-resolution monitoring of himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 2014, 150, 93–103. [Google Scholar] [CrossRef]
- Dall’Asta, E.; Forlani, G.; Roncella, R.; Santise, M.; Diotri, F.; di Cella, U.M. Unmanned Aerial Systems and DSM matching for rock glacier monitoring. ISPRS J. Photogramm. Remote Sens. 2016, in press. [Google Scholar] [CrossRef]
- Mancini, F.; Dubbini, M.; Gattelli, M.; Stecchi, F.; Fabbri, S.; Gabbianelli, G. Using unmanned aerial vehicles (UAV) for high-resolution reconstruction of topography: The structure from motion approach on coastal environments. Remote Sens. 2013, 5, 6880–6898. [Google Scholar] [CrossRef]
- Santise, M.; Fornari, M.; Forlani, G.; Roncella, R. Evaluation of DEM generation accuracy from UAS imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-5, 529–536. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; d’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV topographic surveys processed with structure-from-motion: Ground control quality, quantity and bundle adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef]
- Enac. Available online: https://www.enac.gov.it/repository/ContentManagement/information/N1220929004/Regulation_RPAS_Issue_2_Rev%202_eng.pdf (accessed on 22 January 2017).
- Federal Aviation Administration. Available online: https://www.faa.gov/uas/media/Part_107_Summary.pdf (accessed on 22 January 2107).
- Rango, A.; Laliberte, A.S.; Herrick, J.E.; Winters, C.; Havstad, K.; Steele, C.; Browning, D. Unmanned aerial vehicle-based remote sensing for rangeland assessment, monitoring, and management. J. Appl. Remote Sens. 2009, 3, 033542. [Google Scholar]
- Kraus, K. Photogrammetry, Volume 1: Fundamentals and Standard Processes; Fred. Dümmlers Verlag: Bonn, Germany, 1993. [Google Scholar]
- Schwarz, K.P.; Chapman, M.A.; Cannon, M.E.; Gong, P. An integrated INS/GPS approach to the georeferencing of remotely sensed data. Photogr. Eng. Remote Sens. 1993, 59, 1667–1674. [Google Scholar]
- Mostafa, M.M.; Hutton, J. Airborne kinematic positioning and attitude determination without base stations. In Proceedings of the International Symposium on Kinematic Systems in Geodesy, Geomatics, and Navigation (KIS 2001), Banff, AB, Canada, 5–8 June 2001.
- Heipke, C.; Jacobsen, K.; Wegmann, H.; Andersen, O.; Nilsen, B. Integrated sensor orientation-an OEEPE Test. Int. Arch. Photogramm. Remote Sens. 2000, XXXIII-B3/1, 373–380. [Google Scholar]
- Ackermann, F.; Schade, H. Application of GPS for aerial triangulation. Photogr. Eng. Remote Sens. 1993, 59, 1625–1632. [Google Scholar]
- Forlani, G.; Pinto, L. Experiences of combined block adjustment with GPS data. In Proceedings of the SPIE, ISPRS Commission III Symposium: Spatial Information from Digital Photogrammetry and Computer Vision, Munich, Germany, 5–9 September 1994; Heinrich, E., Christian, H., Konrad, E., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 1994; pp. 219–226. [Google Scholar]
- Bilker, M.; Honkavaara, E.; Jaakkola, J. GPS supported Aerial Triangulation using untargeted ground control. Int. Arch. Photogramm. Remote Sens. 1998, XXXII-3/W1, 2–9. [Google Scholar]
- Küng, O.; Strecha, C.; Beyeler, A.; Zufferey, J.-C.; Floreano, D.; Fua, P.; Gervaix, F. The accuracy of automatic photogrammetric techniques on ultra-light UAV imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, XXXVIII-1/C22, 125–130. [Google Scholar] [CrossRef]
- Pfeifer, N.; Glira, P.; Briese, C. Direct Georeferencing With on Board Navigation Components of Light Weight UAV Platforms. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2012, XXXIX-W7, 487–492. [Google Scholar] [CrossRef]
- Gerke, M.; Przybilla, H.J. Accuracy Analysis of Photogrammetric UAV Image Blocks: Influence of On board RTKGNSS and Cross Flight Patterns. Photogramm. Fernerkund. Geoinf. 2016, 1, 17–30. [Google Scholar] [CrossRef]
- Nocerino, E.; Menna, F.; Remondino, F.; Saleri, R. Accuracy and Block Deformation Analysis in Automatic UAV and Terrestrial Photogrammetry—Lessons learnt. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2013, II-5/W1, 203–208. [Google Scholar] [CrossRef]
- Cramer, M.; Stallmann, D.; Haala, N. Direct georeferencing using GPS/inertial exterior orientations for photogrammetric applications. Int. Arch. Photogramm. Remote Sens. 2000, XXXIII-B3/1, 198–205. [Google Scholar]
- Cina, A.; Piras, M. Performance of low-cost GNSS receiver for landslides monitoring: Test and results. Geomat. Nat. Hazards Risk 2015, 6, 497–514. [Google Scholar] [CrossRef]
- Daakir, M.; Pierrot-Deseilligny, M.; Bosser, P.; Pichard, F.; Thom, C. UAV onboard photogrammetry and GPS positionning for earthworks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-3/W3, 293–298. [Google Scholar] [CrossRef]
- Rehak, M.; Skaloud, J. Fixed-wing micro aerial vehicle for accurate corridor mapping. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2015, II-1/W1, 23–31. [Google Scholar]
- Pinto, L.; Forlani, G. A single step calibration procedure for IMU/GPS in aerial photogrammetry. Int. Arch. Photogramm. Remote Sens. 2002, XXXIV/B3, 210–213. [Google Scholar]
- Daakir, M.; Pierrot-Deseilligny, M.; Bosser, P.; Pichard, F.; Thom, C.; Rabot, Y. Study of lever-arm effect using embedded photogrammetry and on-board GPS receiver on UAV for metrological mapping purpose and proposal of a free ground measurements calibration procedure. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XL-3/W4, 65–70. [Google Scholar] [CrossRef]
- Harwin, S.; Lucieer, A. Assessing the accuracy of georeferenced point clouds produced via multi-view stereopsis from unmanned aerial vehicle (UAV) imagery. Remote Sens. 2012, 4, 1573–1599. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Proc. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Vallet, J.; Panissod, F.; Strecha, C.; Tracol, M. Photogrammetric performance of an ultra light weight swinglet “UAV”. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, XXXVIII-1/C22, 253–258. [Google Scholar] [CrossRef]
- Rosnell, T.; Honkavaara, E. Point cloud generation from aerial image data acquired by a quadrocopter type micro unmanned aerial vehicle and a digital still camera. Sensors 2012, 12, 453–480. [Google Scholar] [CrossRef] [PubMed]
- Turner, D.; Lucieer, A.; Wallace, L. Direct georeferencing of ultrahigh-resolution UAV imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2738–2745. [Google Scholar] [CrossRef]
- Hugenholtz, C.; Brown, O.; Walker, J.; Barchyn, T.; Nesbit, P.; Kucharczyk, M.; Myshak, S. Spatial Accuracy of UAV-Derived Orthoimagery and Topography: Comparing Photogrammetric Models Processed with Direct Geo-Referencing and Ground Control Points. Geomatica 2016, 70, 21–30. [Google Scholar] [CrossRef]
- MAVinci. Available online: www.mavinci.de/download/2016_04_SIRIUS_whitepaper.pdf (accessed on 24 November 2016).
- senseFly. Available online: https://www.sensefly.com/fileadmin/user_upload/sensefly/documents/eBee-RTK-Accuracy-Assessment.pdf (accessed on 28 November 2016).
- Pierrot Deseilligny, M.; Clery, I. Apero, An Open Source Bundle Adjusment Software For Automatic Calibration And Orientation Of Set Of Images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, XXXVIII-5/W16, 269–276. [Google Scholar] [CrossRef]
- Triggs, B.; McLauchlan, P.; Hartley, R.; Fitzgibbon, A. Bundle Adjustment—A Modern Synthesis. Lect. Notes Comput. Sci. 2000, 1883, 298–372. [Google Scholar]
- Agisoft PhotoScan. Available online: http://www.agisoft.com/forum/ (accessed on 15 December 2016).
- Pix4D, Pix4Dmapper Pro Version 3.0.17. Available online: https://pix4d.com/ (accessed on 24 November 2016).
- Lowe, D. Object recognition from local scale-invariant features. In Proceedings of the 7th International Conference on Computer Vision, Corfù, Greece, 20–27 September 1999; pp. 1150–1157.
- Fraser, C. Digital camera self-calibration. ISPRS J. Photogramm. Remote Sens. 1997, 52, 149–159. [Google Scholar] [CrossRef]
- IGN logiciels. Available online: http://logiciels.ign.fr/IMG/pdf/docmicmac-2.pdf (accessed on 22 January 2017).

| Method | Observations | BBA | Block Deform. Control | Reliable Self-Calibration |
|---|---|---|---|---|
| Indirect Sensor Orientation (InSO) | - Image coordinates of tie points and GCP - Object coordinates of GCP | Yes | Yes | Yes |
| Direct Sensor Orientation (DSO) | - Camera station position and attitude | No | No | No |
| Integrated Sensor Orientation (ISO) | - Image coordinates of tie points and GCP - Camera station position and attitude - Object coordinates of (a few) GCP (opt.) | Yes | Yes (with GCP) | Only with some GCPs |
| GNSS-supported Aerial Triangulation (GNSS-AT) | - Image coordinates of tie points and GCP - Camera station position - Object coordinates of (a few) GCP (opt.) | Yes | Yes (with GCP) | Only with some GCPs |
| Mean Wind Speed During Flight (m/s) | Wind Direction During Flight (° from North) | PDOP (Min–Max) | Images | |
|---|---|---|---|---|
| RTK1 | 2.2 | 320°–40 ° | 2.4–2.9 | 151 |
| RTK2 | 2.9 | 90° | 1.8–2.0 | 152 |
| RTK3 | 3.6–4.1 | 90° | 1.7–1.8 | 144 |
| RTK4 | 3.3–3.7 | 90° | 1.7–1.9 | 149 |
| MEAN Z (m) | |||||||
|---|---|---|---|---|---|---|---|
| RTK 1 | RTK 2 | ||||||
| 12GCP | RTK | RTK+1GCP | 12GCP | RTK | RTK+1GCP | ||
| Pix4D | 0.005 | 0.012 | −0.002 | Pix4D | 0.006 | 0.083 | 0.001 |
| PS | −0.001 | 0.011 | 0.010 | PS | −0.003 | −0.093 | −0.002 |
| MicMac | 0.003 | −0.085 | −0.004 | MicMac | 0.000 | −0.063 | −0.002 |
| RTK 3 | RTK 4 | ||||||
| 12GCP | RTK | RTK+1GCP | 12GCP | RTK | RTK+1GCP | ||
| Pix4D | −0.011 | 0.069 | 0.001 | Pix4D | −0.008 | 0.013 | −0.026 |
| PS | −0.001 | 0.006 | 0.024 | PS | 0.004 | 0.004 | −0.011 |
| MicMac | 0.004 | 0.035 | −0.019 | MicMac | 0.010 | −0.039 | 0.000 |
| RMSE XY (m) | RMSE XY (GSD) | |||||
| 12GCP | RTK | RTK+1GCP | 12GCP | RTK | RTK+1GCP | |
| Min | 0.012 | 0.014 | 0.016 | 0.48 | 0.57 | 0.67 |
| Max | 0.020 | 0.029 | 0.029 | 0.85 | 1.19 | 1.21 |
| RMSE Z (m) | RMSE Z (GSD) | |||||
| 12GCP | RTK | RTK+1GCP | 12GCP | RTK | RTK+1GCP | |
| Min | 0.016 | 0.019 | 0.014 | 0.67 | 0.79 | 0.58 |
| Max | 0.030 | 0.095 | 0.039 | 1.25 | 3.96 | 1.63 |
| RTK2—Estimated Principal Distance (mm) | |||
|---|---|---|---|
| 12 GCP | RTK | RTK+1GCP | |
| Pix4D | 4.5718 | 4.5771 | 4.5771 |
| PhotoScan | 4.5801 | 4.5853 | 4.5818 |
| MicMac | 4.6020 | 4.6134 | 4.6104 |
| MEAN DZ (m) | |||||||
|---|---|---|---|---|---|---|---|
| RTK1 | RTK2 | ||||||
| 12 GCP | RTK | RTK+1GCP | 12 GCP | RTK | RTK+1GCP | ||
| Pix4D | 0.024 | 0.000 | 0.046 | Pix4D | −0.041 | 0.000 | 0.083 |
| PhotoScan | 0.025 | 0.000 | 0.000 | PhotoScan | −0.017 | 0.000 | 0.007 |
| MicMac | −0.137 | 0.15 | −0.006 | MicMac | 0.010 | 0.256 | 0.154 |
| RTK3 | RTK4 | ||||||
| 12 GCP | RTK | RTK+1GCP | 12 GCP | RTK | RTK+1GCP | ||
| Pix4D | −0.025 | 0.000 | 0.079 | Pix4D | −0.043 | 0.000 | 0.025 |
| PhotoScan | −0.083 | 0.000 | 0.003 | PhotoScan | −0.033 | 0.000 | −0.001 |
| MicMac | −0.028 | 0.06 | 0.167 | MicMac | −0.146 | 0.122 | 0.034 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benassi, F.; Dall’Asta, E.; Diotri, F.; Forlani, G.; Morra di Cella, U.; Roncella, R.; Santise, M. Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation. Remote Sens. 2017, 9, 172. https://doi.org/10.3390/rs9020172
Benassi F, Dall’Asta E, Diotri F, Forlani G, Morra di Cella U, Roncella R, Santise M. Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation. Remote Sensing. 2017; 9(2):172. https://doi.org/10.3390/rs9020172
Chicago/Turabian StyleBenassi, Francesco, Elisa Dall’Asta, Fabrizio Diotri, Gianfranco Forlani, Umberto Morra di Cella, Riccardo Roncella, and Marina Santise. 2017. "Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation" Remote Sensing 9, no. 2: 172. https://doi.org/10.3390/rs9020172
APA StyleBenassi, F., Dall’Asta, E., Diotri, F., Forlani, G., Morra di Cella, U., Roncella, R., & Santise, M. (2017). Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation. Remote Sensing, 9(2), 172. https://doi.org/10.3390/rs9020172