Abstract
Unmanned aerial vehicles (UAVs) provide a flexible and low-cost solution for the acquisition of high-resolution data. The potential of high-resolution UAV imagery to create and update cadastral maps is being increasingly investigated. Existing procedures generally involve substantial fieldwork and many manual processes. Arguably, multiple parts of UAV-based cadastral mapping workflows could be automated. Specifically, as many cadastral boundaries coincide with visible boundaries, they could be extracted automatically using image analysis methods. This study investigates the transferability of gPb contour detection, a state-of-the-art computer vision method, to remotely sensed UAV images and UAV-based cadastral mapping. Results show that the approach is transferable to UAV data and automated cadastral mapping: object contours are comprehensively detected at completeness and correctness rates of up to 80%. The detection quality is optimal when the entire scene is covered with one orthoimage, due to the global optimization of gPb contour detection. However, a balance between high completeness and correctness is hard to achieve, so a combination with area-based segmentation and further object knowledge is proposed. The localization quality exhibits the usual dependency on ground resolution. The approach has the potential to accelerate the process of general boundary delineation during the creation and updating of cadastral maps.
1. Introduction
Unmanned aerial vehicles (UAVs) have gained increasing popularity in remote sensing as they provide a rapid, low-cost and flexible acquisition system for high-resolution data including digital surface models (DSMs), orthoimages and point clouds [1,2,3]. Recently, cadastral mapping has emerged as a field of application for UAVs [4,5,6,7,8]. Cadastral maps show the extent, value and ownership of land, are combinable with a corresponding register [9] and are considered crucial for a continuous and sustainable recording of land rights [10]. In contemporary settings, UAV data is employed both to create and to update cadastral maps, mostly through manual delineation of visible cadastral boundaries. An overview of case studies investigating the potential of UAVs for cadastral mapping and their approaches for boundary delineation is provided in [11]. However, none of the case studies described provide an automated approach for cadastral boundary delineation. In particular, visible boundaries, manifested through physical objects, could potentially be extracted automatically [12]. A large number of cadastral boundaries are assumed to be visible, as they coincide with natural or manmade object contours [13,14]. Contours refer to outlines of visible objects and will be used synonymously below. Such visible boundaries might be extractable with computer vision methods that detect object contours in images. Those contours could be used as basis for a delineation of cadastral boundaries that incorporate further knowledge and require further legal adjudication.
1.1. Contour Detection
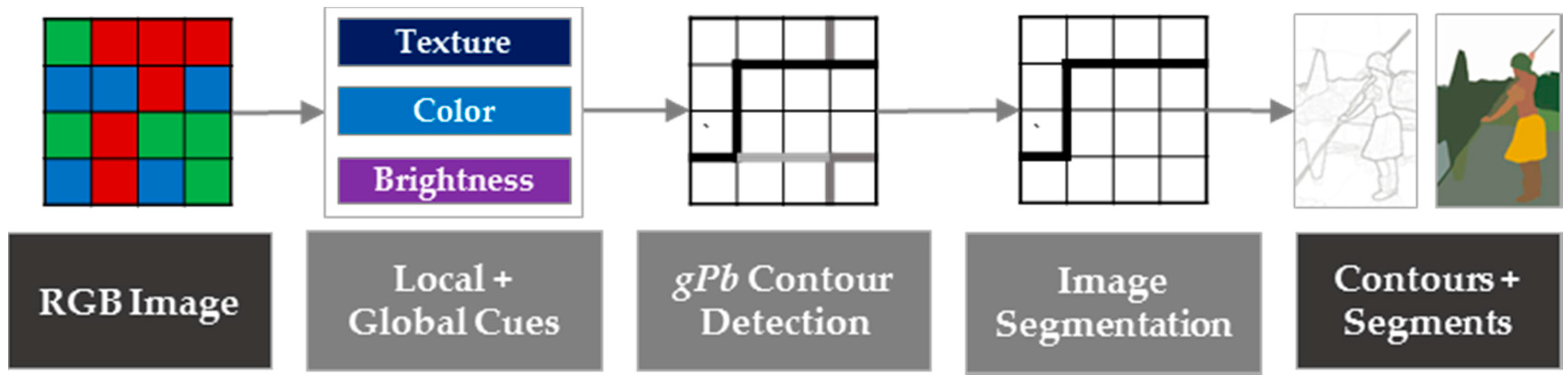
Contour detection, especially in computer vision, refers to finding boundaries between objects or segments. Early approaches, such as Canny edge detection [15], extract edges by calculating gradients of local brightness, which are thereafter combined to form contours. The approach typically detects irrelevant edges in textured regions. Later approaches include additional cues such as texture [16] and color [17] to identify contours. Maire et al. extended these approaches to consider multiple cues on both the local and global image scales through spectral partitioning [18]. Image information on a global scale allows for identification of contours not initially recognized by generating closed object outlines and eliminating irrelevant contours in textured regions. In [19,20], the closing of object outlines is provided by a hierarchical segmentation that partitions an image into meaningful objects. Detecting contours and assigning probabilities as presented in [18,19,20] is referred to as gPb (globalized probability of boundary). The concept is summarized in Figure 1. The justification for using the method is based on [11], in which a workflow and feature extraction methods suitable for cadastral mapping are provided. gPb contour detection combines the proposed workflow steps of image segmentation, line extraction and contour generation. A combination of other methods, as proposed in [11], might also be applicable. Due to the novelty of this research field, it cannot be definitively stated which approach has the most potential to bridge the described research gap. This study does not compare the usability of different approaches. Instead, it investigates the potential and limitations of gPb contour detection as an initial step in a workflow that needs to be extended for a final approximation of visible cadastral boundaries.
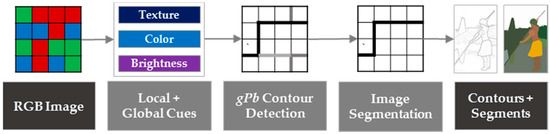
Figure 1.
Combined gPb contour detection and hierarchical image segmentation for the delineation of closed object contours from RGB images described in [19]. The example image is taken from the ‘Berkeley Segmentation Dataset and Benchmark’ [21] and is processed with the publicly available source code for gPb contour detection [22].
In a first step of gPb contour detection, oriented gradient operators for brightness, color and texture cues are calculated by measuring their differences on two halves of a differently scaled disc. Results are stored in an affinity matrix that represents similarities between pixels. Small similarities, i.e., a strongly oriented gradient, indicate a boundary between two distinct regions. Subsequently, all cues are merged based on a logistic regression classifier to predict the orientation and the posterior probability of a boundary, i.e., edge strength, at each image pixel. The image information on a global scale is obtained through spectral clustering. The local and global image scales convey different information: the former extracts all edges, while the latter extracts only the most salient edges. Both are combined through learning techniques as a weighted sum of local and spectral signals. This allows the assignment of a probability to each contour, resulting in the gPb contour detector. The following step, i.e., image segmentation, consists of (i) an Oriented Watershed Transform (OWT) that forms initial regions from contours; and (ii) the construction of an Ultrametric Contour Map (UCM) that defines a hierarchical segmentation [23]. The OWT is a variant of the watershed algorithm and constructs a set of initial regions from the oriented contour signal provided by a contour detector. UCM represents a hierarchy of these regions obtained by weighting each boundary and their agglomerative clustering. The image segmentation, consisting of the two steps of OWT and UCM, can be applied to the output of any contour detector. However, it has been proven to work optimally on the output of the gPb contour detector [20]. The overall results are (i) a contour map, in which each pixel is assigned a probability for being a boundary pixel; and (ii) a binary boundary map, in which each pixel is labeled as either ‘boundary’ or ‘no boundary’ and from which closed segments can be derived. The number of contours transferred from the contour map to closed segments in the boundary map is defined by a threshold, which is referred to as scale k in [19,20] and in the following. The processing pipeline of gPb-owt-ucm is referred to as gPb contour detection in this study.
gPb contour detection provides accurate results compared to other approaches on image segmentation (e.g., mean shift, multiscale normalized cuts and region merging) and edge detection (e.g., Prewitt, Sobel, Roberts operator and Canny detector) [19] and is often referred to as a state-of-the-art method for contour detection [24,25,26]. These comparisons are based on computer vision images, while its performance on remote sensing data has not been evaluated as extensively against comparable approaches. The main advantage of the method is its combination of edge detection and hierarchical image segmentation, while integrating image information on texture, color and brightness on a both a local and global scale. As the cue combination is learned, based on a large number of natural images from the ‘Berkeley Segmentation Dataset and Benchmark’ [21], the approach seeks to be transferable to images of different contexts. Nevertheless, gPb contour detection has hardly been applied to remotely sensed data [27,28] and, to the best of the authors’ knowledge, never to UAV data. The transferability of methods from computer vision to remote sensing is challenging, as both are often developed for image data with different characteristics: a benchmark dataset used in computer vision, such as the ‘Berkeley Segmentation Dataset and Benchmark’, contains natural images of maximal 1000 pixels in width and height, whereas a benchmark dataset used in remote sensing, such as the ‘ISPRS Benchmark’ [29], contains images from multiple sensors with higher numbers of pixels and larger ground sample distances (GSD).
1.2. Objective and Organization of the Study
This study investigates which processing is required for a state-of-the-art contour detection method from computer vision—namely gPb contour detection—to be applied to remotely sensed data with a high resolution—namely UAV data. Once the technical transferability is defined, the applicability of the method within the application field of cadastral mapping is investigated. This study aims to outline the potential of gPb contour detection for an automated delineation of visible objects that indicate cadastral boundaries.
Overall, the study addresses the research gaps of transferring a method developed within computer vision to an application in remote sensing, where images have different characteristics. Further, it encounters the lack of automation within cadastral boundary delineation by investigating the applicability of gPb contour detection.
The paper is structured as follows: after having described the context of this research (Section 1), the UAV datasets as well as the methodological approach are described (Section 2). Then, the results are described (Section 3) and discussed (Section 4). Concluding remarks include generic statements about the transferability and applicability of gPb contour detection for UAV-based delineation of visible cadastral boundaries (Section 5).
2. Materials and Methods
2.1. UAV Data
Three UAV orthoimages of different extents showing rural areas in Germany, France and Indonesia were selected for this study. Rural areas were chosen because the number of visible boundaries is usually higher in rural areas compared to high-density urban areas. For Amtsvenn and Lunyuk, data was captured with indirect georeferencing, i.e., Ground Control Points (GCPs) were distributed within the field and measured with a Global Navigation Satellite System (GNSS). For Toulouse, data was captured with direct georeferencing, i.e., through an on-board Post-Processing Kinematic (PPK) unit. All orthoimages were generated with Pix4DMapper. Table 1 shows specifications of the data capture, while Figure 2 shows orthoimages of the study areas.

Table 1.
Specifications of UAV datasets per study area.
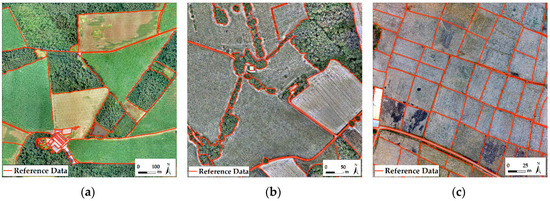
Figure 2.
Manually delineated object contours used as reference data to determine the detection quality overlaid on UAV orthoimages of (a) Amtsvenn, Germany; (b) Toulouse, France and (c) Lunyuk, Indonesia.
2.2. Reference Data
The study is based on the assumption that large portions of cadastral boundaries are visible [14]. Therefore, the method is intended to extract contours of physical objects that demarcate cadastral boundaries. A general list of such objects is rarely available in the literature and strongly depends on the area of investigation [11]. From a list of objects provided in [11], the following objects were assumed to indicate cadastral boundaries for the investigated study areas: roads, fences, hedges, stone walls, roof outlines, agricultural field outlines as well as outlines of tree groups. The contours of these objects were manually digitized for all three orthoimages (Figure 2). The reference data does not aim to delineate cadastral boundaries, since a subset of these, i.e., visible boundaries, are considered in this study. Cadastral boundaries are assumed to be more regular than the outlines of visible objects delineated as reference data. A workflow for cadastral boundary delineation would need to contain a step in which extracted contours are generalized to be more likely to be cadastral boundaries. This study is not designed to provide such a complete workflow; it seeks to delineate object contours as a first workflow step. Further workflow steps as proposed in [11] would need to be added, in order to derive data that is comparable with cadastral data.
2.3. Image Processing Workflow
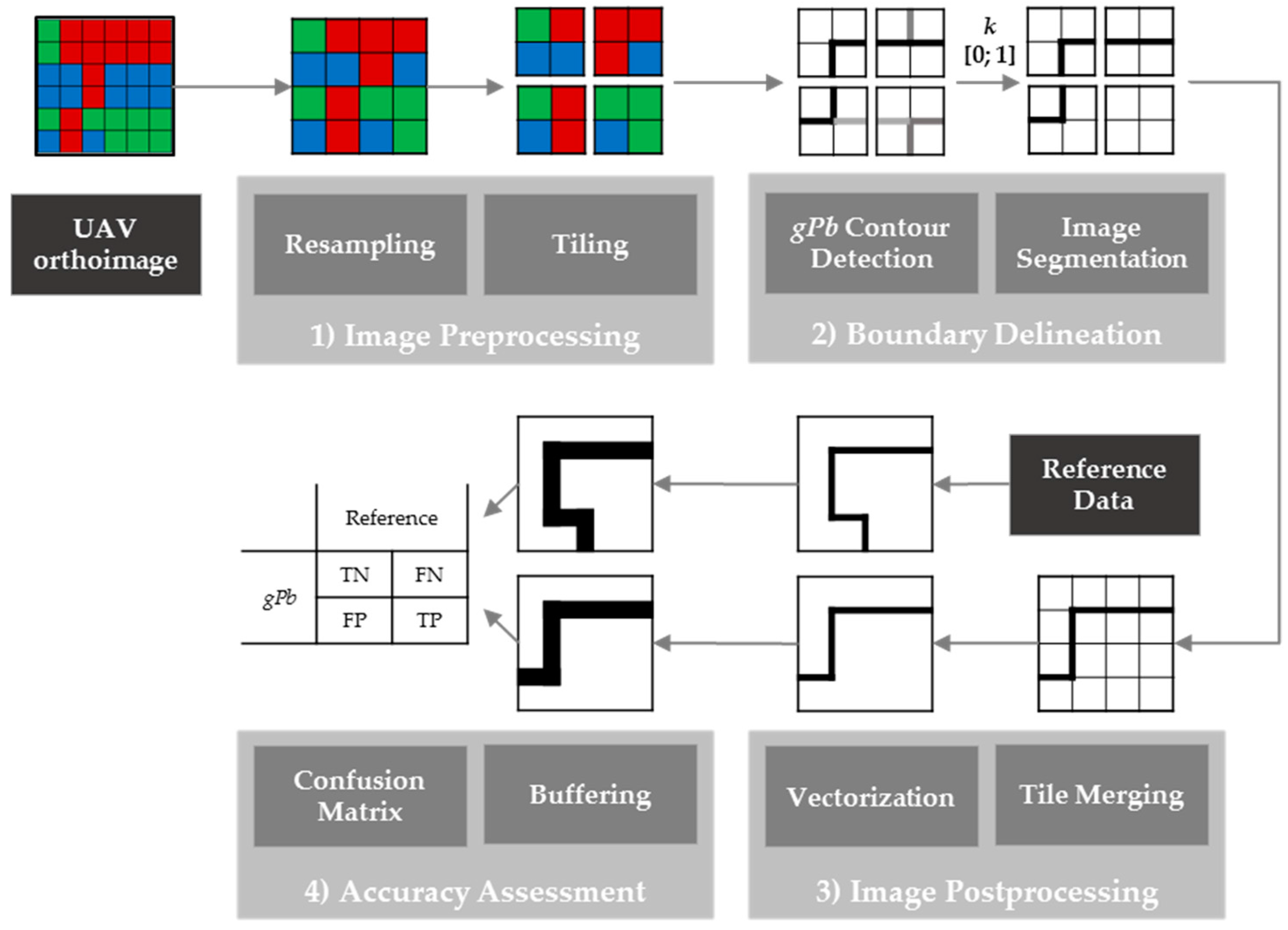
The method investigated, gPb contour detection, is open-source and available as a precompiled Matlab package [22]. This implementation was found to be inapplicable because of long computing time and insufficient memory when processing images of more than 1000 pixels in width and height. Therefore, an image processing workflow that reduces the original image size to 1000 × 1000 pixels was designed (Figure 3). The workflow consists of four steps, which are explained in the following. Apart from the Matlab implementation for gPb contour detection, all workflow steps were implemented in Python as QGIS processing scripts making use of QGIS [30], GRASS [31], SAGA [32] and GDAL [33] functionalities.
- (1)
- Image Preprocessing: The UAV orthoimage was first resampled to lower resolutions ranging from 5 to 100 cm GSD. All resampling was based on nearest neighbor resampling, as it is computationally least expensive. Initial tests with further resampling methods (bilinear, cubic, lanczos, average, mode) did not show significant differences in the gPb contour detection output. The resampling to different GSDs enabled investigation of the influence of GSD in detecting object contours. The resampled images of 1000 to 5000 pixels in width and height were then tiled to tiles of 1000 × 1000 pixels. The smaller the GSD, the more tiles were created (Table 2). The range of GSDs varied per study area, due to the varying extents per study area and the constant number of tiles amounting to 1, 9, 16 and 25 (Table 2): for Amtsvenn, the orthoimage covers an extent of 1000 × 1000 m, which results in a GSD of 50 cm, if the image is tiled to 4 tiles. The same number of tiles results in a GSD of 12.5 m for Lunyuk, since that orthoimage covers an extent of 250 × 250 m.
 Table 2. Number of pixels and ground sample distance (GSD) per tile after image preprocessing.
Table 2. Number of pixels and ground sample distance (GSD) per tile after image preprocessing. - (2)
- Boundary Delineation: Then, gPb contour detection was applied to each tile of different GSDs. This resulted in contour maps containing probabilities for contours per pixel. By applying hierarchical image segmentation at scale k within the range [0; 1], contours of a certain probability were closed and transferred to a binary raster map containing pixels for the classes ‘boundary’ and ‘no boundary’. The resulting boundary map was created for all levels of k. This processing pipeline refers to gPb-owt-ucm, which is described in Section 1.1.
- (3)
- Image Postprocessing: All tiles belonging to the same set were merged to one contour map and one binary boundary map, which was then vectorized. This creates polygons for all connected regions of pixels in a raster sharing a common pixel value, which produces dense polygon geometries, with edges following exactly pixel boundaries.
- (4)
- Accuracy Assessment: The assessment was pixel-based and investigated the confusion matrix in terms of pixels labeled as true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN) [34,35]. The accuracy assessment can equally be applied to a vector format by comparing the percentage of overlapping polygon areas per category. The accuracy assessment is designed to determine the accuracy in terms of (i) the detection quality, i.e., errors of commission and omission, and (ii) the localization quality, i.e., the accuracy of boundaries in a geometric sense:
- (i)
- For the detection quality, each line was buffered with a radius distance of 2 m and converted to a raster format. The same buffering and rasterization was applied to the reference data. From the confusion matrix, the following errors were calculated: the error of commission within the range of [0; 100], showing the percentage of pixels erroneously labeled as ‘boundary’ and the error of omission within the range of [0; 100], showing the percentage of pixels erroneously labeled as ‘no boundary’. A generous buffer of 2 m was chosen in order to account for uncertainties in conjunction with manual digitization and resampling effects.
- (ii)
- Since multiple objects, such as trees and bushes, do not provide exactly localizable contours, the localization accuracy requires a different set of reference data. Therefore, a subset of the reference data was evaluated containing exactly locatable object contours only, i.e., road and roof outlines. This subset was rasterized to a raster of 5 cm GSD and each boundary pixel was buffered with distances from 0 to 2 m at increments of 20 cm. The binary boundary map was resampled to a GSD of 5 cm to be comparable to the reference raster. During the resampling, only one center pixel of 5 × 5 cm was kept per pixel of a larger GSD to avoid having a higher number of pixels after resampling a boundary map of a larger GSD. The resampled binary boundary map was then compared to the reference raster. Based on the confusion matrix, the number of TPs per buffer zone was calculated to investigate the distance between TPs and the reference data and thus the influence of GSD on the localization quality.
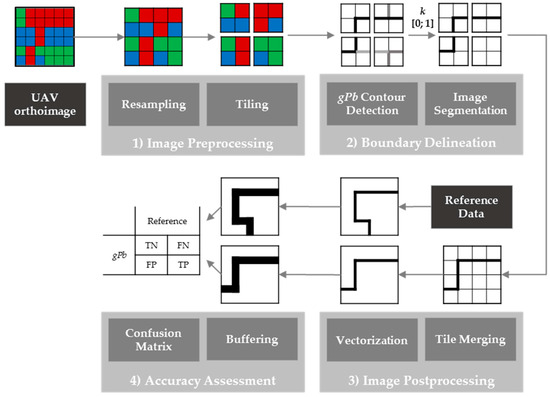
Figure 3.
Image processing workflow for delineation of visual object contours from UAV orthoimages and its assessment based on the comparison to reference data.
3. Results
Resampling and tiling the UAV orthoimages to tiles of 1000 × 1000 pixels results in a higher number of tiles for images of a smaller GSD (Table 2). Applying gPb contour detection on each tile of 1000 × 1000 pixels belonging to the same set of tiles with an identical GSD results in a contour map and a binary boundary map (Figure 4). The lower the level of k, the fewer contours are transferred from the contour map to the binary boundary map (Figure 5). The processing time for each tile ranged from 10 to 13 min and was 11 min on average, with gPb contour detection running single-threaded. The accuracy assessment is shown in terms of detection quality (Figure 6) and localization quality (Figure 7). To separate the influence of GSD and tiling on the detection quality, each untiled image of the largest GSD per study area was tiled to 25 tiles and assessed (Table 3).
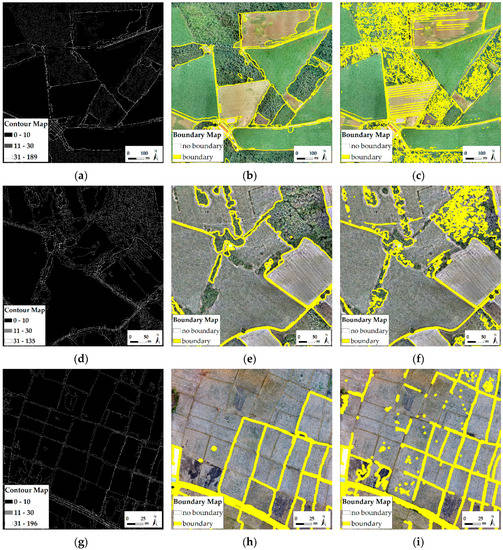
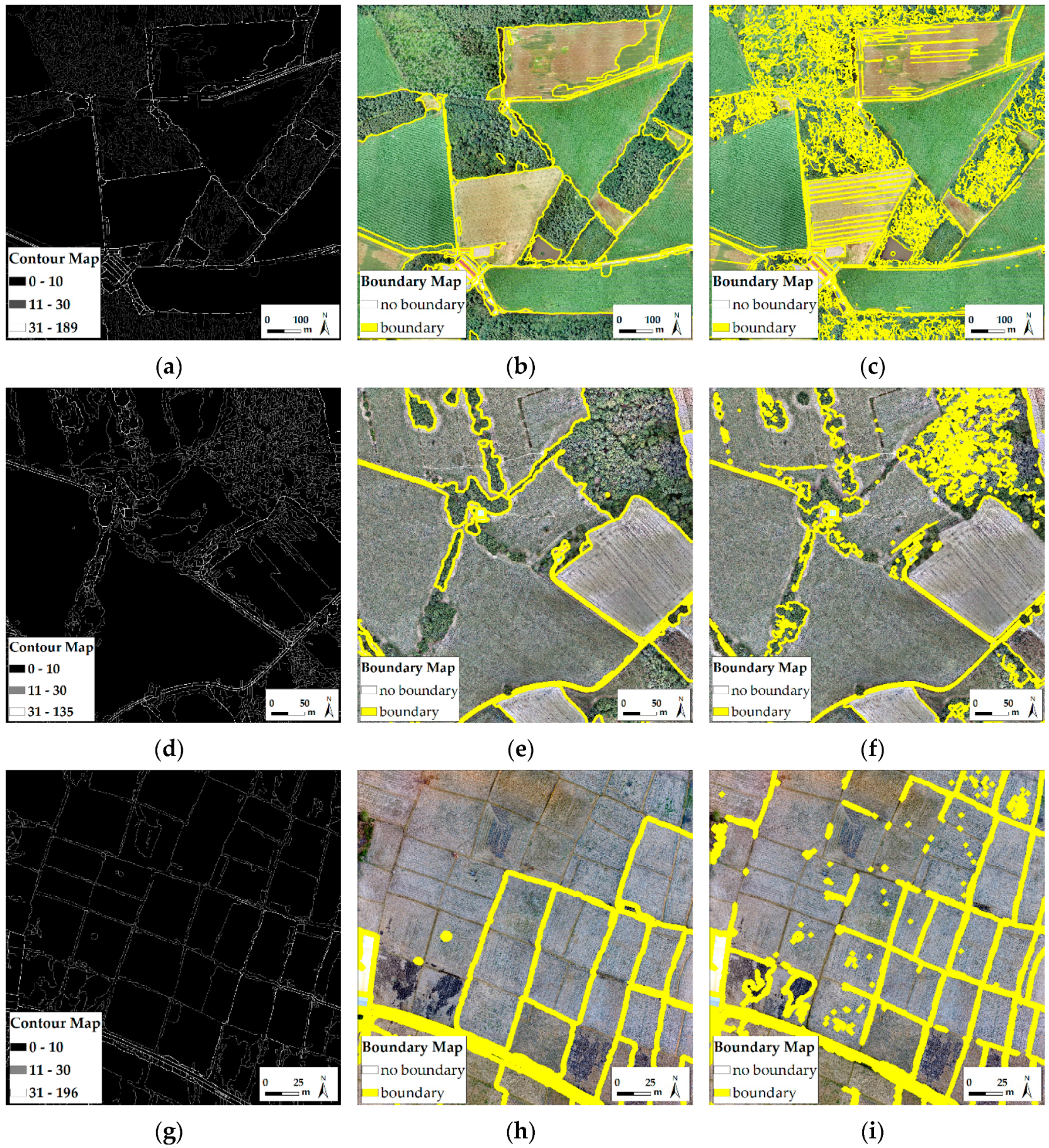
Figure 4.
(a–i) Examples of contour maps (a,d,g) and binary boundary maps (k = 0.1) of Amtsvenn (a–c), Toulouse (d–f) and Lunyuk (g–i). The boundary maps are buffered with 2 m to increase their visibility. (a,b,d,e,g,h) result from an untiled input image of 1000 × 1000 pixels, (c,f,i) from an input image of 5000 × 5000 pixels merged from 25 tiles.
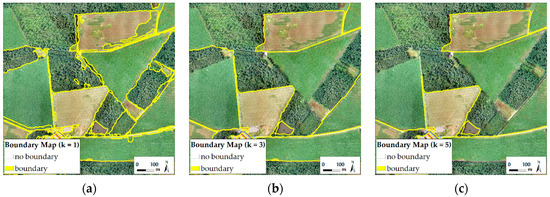
Figure 5.
Binary boundary maps derived from untiled UAV orthoimage of Amtsvenn with a size of 1000 × 1000 pixels and 100 cm GSD at level (a) k = 0.1; (b) k = 0.3; and (c) k = 0.5.
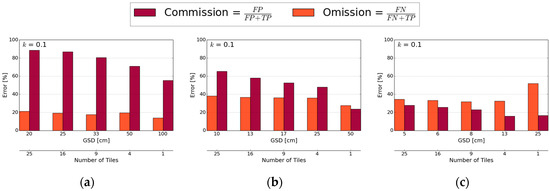
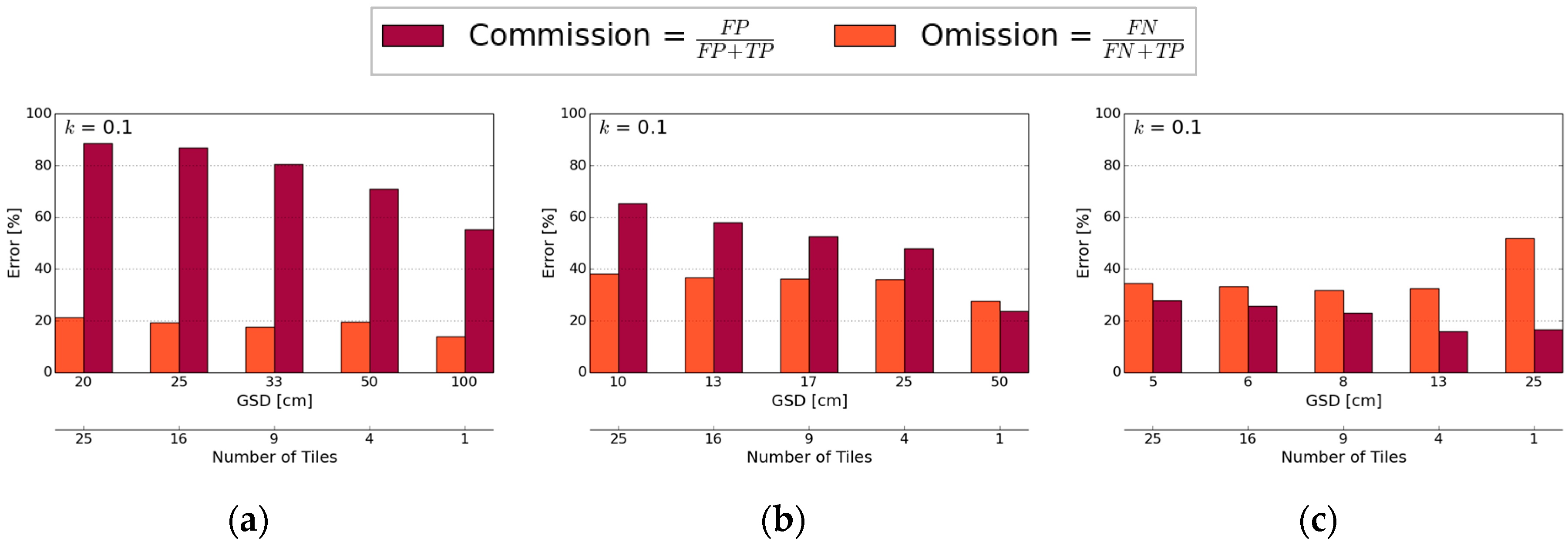
Figure 6.
Detection quality: the errors of commission and omission is shown for binary boundary maps of different Ground Sample Distances (GSD) derived for (a) Amtsvenn; (b) Toulouse; and (c) Lunyuk at level k = 0.1.
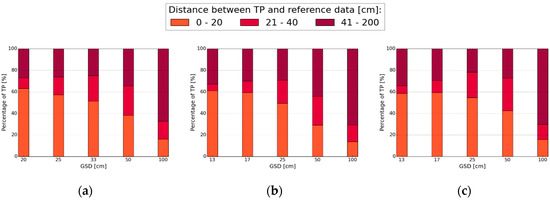
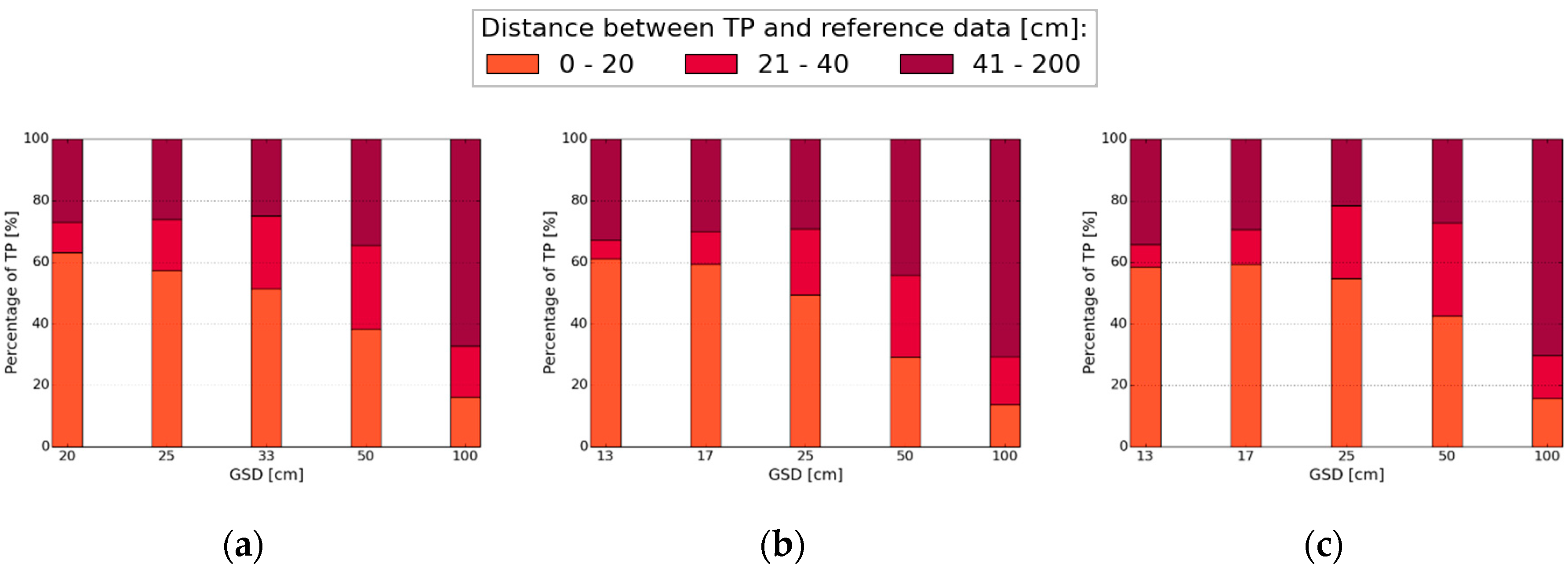
Figure 7.
Localization quality: the distance between pixels being True Positives (TP) and the reference data relative to the total number of TPs per Ground Sample Distance (GSD) is shown for (a) Amtsvenn; (b) Toulouse and (c) Lunyuk at level k = 0.1.

Table 3.
Comparison of detection quality for images of largest ground sample distance (GSD) per study area for the untiled image and the same image merged from 25 tiles. Lower errors are marked in bold.
4. Discussion
4.1. Detection Quality
The error of commission, i.e., excessive detection, increases with parallel decreasing of GSD and increasing of tiles and is mostly lowest for the untiled input image regardless of scale k (Figure 6). Both the errors of commission and omission are higher when applying gPb contour detection on the tiled image compared to the untiled image of the same GSD (Table 3). Therefore, the detection quality depends on the number of tiles, i.e., the area of the captured scene, rather than the GSD for the three study areas: gPb contour detection considers the global extent of one image or one single tile, respectively. When taking a small tile of the UAV orthoimage into account, the global optimization is not efficient. This results in a higher number of contours detected in textured regions (oversegmentation). Therefore, more boundaries are detected in Figure 4c,f,i, which consist of 25 tiles compared to Figure 4b,e,h, which consist of one single tile. Overall, the global optimization works optimally if the entire scene is covered in one orthoimage.
The error of omission, i.e., missed boundaries, varies less than the error of commission per binary boundary map. It can be concluded that a higher number of tiles that cover smaller parts of the entire scene, does not lead to an increase in the error of omission (Figure 6). The lowest number of errors of omission are obtained for k = 0.1, since fewer boundaries are missed in the over-segmented binary boundary map (Figure 5).
The overall detection accuracy is close to 100%, since many pixels are classified correctly as ‘no boundary’. It is therefore not visualized in Figure 6. A low level of k leads to an oversegmentation of the image, while a higher level of k leads to an undersegmentation or even no boundaries being contained in the binary boundary map (Figure 5), which influences the errors of commission and omission accordingly. However, even for the lowest level of k, contours indicated in the contour map (Figure 4g) might not be transferred to the binary boundary map (Figure 4h). This indicates that when aiming for a high completeness of detected contours, i.e., a low error of omission, which is considered optimal in [36] before integrating user interaction, the contour map should be considered for further processing.
The results for Amtsvenn show the highest number of errors of commission, due to many textured regions in which boundaries are erroneously detected. The error of commission is lowest for Lunyuk, since the image contains barely any textured regions or small objects. The high errors of omission for the Toulouse and Lunyuk data reveal that boundaries are less definite and visible in these images.
4.2. Localization Quality
The number of TPs within 20 cm distance of the reference data relative to the total number of TPs per GSD decreases for larger GSDs, for all study areas (Figure 7). The total number of TPs was comparable, as only one center pixel was kept in the gPb contour detection raster of 5 cm GSD that was compared to the reference data of the same GSD. For GSDs of 20–33 cm (Amtsvenn) and 10–25 cm (Toulouse and Lunyuk), the amount of TP localized within 20 cm distance from the reference data ranges between 50% and 60%. This percentage decreases for all study areas when the GSD is increased to 100 cm. The results indicate that contours are more accurately localized for UAV images of a higher resolution.
4.3. Discussion of the Evaluation Approach
The study results (Section 4.1, Section 4.2) strongly depend on the applied buffer distance. For detection quality, a buffer distance of 2 m was chosen. This does not represent the following two visually observed cases: (i) some boundaries run along the shadow of an object and are therefore shifted compared to the reference data that runs along the actual object contour; (ii) some boundaries are covered by other objects, e.g., trees covering streets. Merging contours of smaller objects with the applied buffer distance does not represent such cases. Such issues could be resolved with an object detection that includes semantics, i.e., knowledge about the objects to be extracted. UAV-based approaches have the potential to extract such object knowledge through incorporation of high-resolution imagery, pointclouds and DSMs. According to Mayer, the use of such additional information makes object extraction more robust and reliable [36]. The approach to detection quality is employed similarly in other studies [34,35,37,38]. The authors argue that despite its strong dependency on the buffer size and its focus on positional accuracy while neglecting factors such as topological accuracy, the buffer approach provides a simple and comprehensive accuracy measure. Further, it can be used on both a vector and a raster representation and is easy to implement [38]. For a comparison to cadastral data, a smaller buffer size, according to local accuracy requirements, should be considered.
Apart from the accuracy assessment method, the manually drawn reference data strongly influences the results. Manually drawn reference data is argued to be valid for measuring the degree to which an automated system, as proposed in this study, outperforms a human operator [36]. However, each human might draw different reference data. Averaging a large amount of manually drawn reference data, as proposed in [17], might reduce errors produced by an individual. Manually drawn reference data was chosen instead of real cadastral data, as the approach does not aim to delineate final cadastral boundaries, but the outlines of physical objects demarcating visible cadastral boundaries. To which extent these visible boundaries coincide with cadastral data, appears to be highly case-depended and needs to be investigated in future work. Our approach is designed for cases in which cadastral data is largely visible.
4.4. Transferability and Applicability of gPb for Boundary Delineation
gPb contour detection appears to be transferable to UAV orthoimages, when reducing the images’ resolution. The approach shows potential for the automation of cadastral boundary delineation in cases where cadastral maps are scarcely available and concepts such as fit-for-purpose and responsible land administration are in place [39,40]. Such concepts accept general boundaries, for which the positional correctness is of lower importance [14]. In cases where a map needs to be created or updated, and general boundaries are accepted, editing automatically generated visible boundaries of high completeness, correctness and topological accuracy on a UAV orthoimage might be less cost- and time-intensive than manually digitizing all boundaries. This would need to be verified by comparing both cadastral mapping workflows as a whole. Hence, future work is required to determine to which degree the object contours coincide with cadastral boundaries and which level of accuracy is required to outperform a manual cadastral mapping workflow. For road extraction, which is closely related to the object detection of this study, Mayer et al. propose a correctness of around 85% and a completeness of around 70% for an approach to be of real practical importance, which relates to an error of commission of 15% and an error of omission of 30% [41]. Such values can hardly be achieved when applying solely gPb contour detection for cadastral boundary delineation. The contours of gPb contour detection should be considered as an initial workflow step in a complete processing chain, as proposed in [11]. One idea would be to use the gPb contour detection for a general localization of potential visible boundaries and to integrate further approaches taking into account the full resolution provided by UAVs to decide on the final probability and localization for a visible boundary. Those boundaries would then need to be connected and regularized to form a closed network of potential cadastral boundaries, before integrating human interaction. Once such a complete workflow is developed, a comparison to direct techniques and indirect techniques using aerial or satellite images of lower resolutions is feasible. However, even if UAV-based cadastral mapping fulfills the expected criteria, the approach is unlikely to substitute convention approaches, as UAVs are currently not suitable to map large areas and are limited in use due to regulations [5].
Furthermore, there might be cases in which only a small portion of cadastral boundaries is visible or object contours do not coincide with cadastral boundaries. Then, the proposed data-driven approach will need to be combined with a knowledge-driven approach. To reliably delineate a closed and geometrically and topologically correct network of boundaries, further object knowledge should be incorporated, e.g., through semi-supervised machine learning approaches and thus derived complementary data. The contour map containing the probability for each contour detected and for which the level of k does not need to be defined, could be employed as a first workflow step. The salient contours detected in this step could be balanced by incorporating an area-based segmentation, resulting in more homogeneous areas. Adding further steps to the workflow could generate an output directly comparable to cadastral boundaries. In future, the authors aim to develop a workflow that remains as automatic, generic and adaptive to different scenarios as possible, similarly formulated in [42] as a need for contemporary boundary detection schemes.
5. Conclusions
This study examines the recent endeavor of making the process of cadastral mapping more reproducible, transparent, automated, scalable and cost-effective. This is investigated by proposing the application of UAV orthoimages combined with automated image analysis, i.e., a state-of-the-art computer vision method that has never been applied to UAV data. The approach does not require prior knowledge (learning) and automatically detects object contours from UAV orthoimages that indicate visible cadastral boundaries. More specifically, this study investigates the transferability of gPb contour detection to UAV images and its applicability for automated delineation of objects demarcating visible cadastral boundaries. This is investigated in terms of detection and localization quality for three different study areas.
The results show the potential and limitations of gPb contour detection within the described application field. The approach is most suitable for areas in which object contours are clearly visible and coincide with cadastral boundaries. However, the approach is of limited usability as a standalone approach for cadastral mapping: it can be employed for an initial localization of candidate object boundaries, which need to be verified and located exactly by integrating further workflow steps. The design and implementation of such a complete workflow that incorporates the high resolution that UAV data provides is the focus of our future work. To establish the comparability of the detected object contours with cadastral boundaries, future work will focus on incorporating the approach proposed here with machine learning methods to integrate further object knowledge. The goal is to generate a tool for cadastral boundary delineation that is highly automatic, generic and adaptive to different scenarios.
Acknowledgments
This work was supported by its4land, which is part of the Horizon 2020 program of the European Union (project number 687828). We are grateful to Claudia Stöcker, Sheilla Ayu Ramadhani and DelAirTech for capturing, processing and providing the UAV data. We acknowledge the financial support of the Open Science Fund of the University of Twente, which supports open access publishing.
Author Contributions
Sophie Crommelinck processed all the data for this paper. Markus Gerke, Rohan Bennett, Michael Ying Yang and George Vosselman contributed to the analysis and interpretation of the data. The manuscript was written by Sophie Crommelinck with contributions from Markus Gerke, Rohan Bennett, Michael Ying Yang and George Vosselman.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DSM | Digital Surface Model |
| FN | False Negative |
| FP | False Positive |
| GCP | Ground Control Points |
| GNSS | Global Navigation Satellite System |
| gPb | Globalized Probability of Boundary |
| GSD | Ground Sample Distance |
| OWT | Oriented Watershed Transform |
| PPK | Post Processing Kinematic |
| TN | True Negative |
| TP | True Positive |
| UAV | Unmanned Aerial Vehicle |
| UCM | Ultrametric Contour Map |
References
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Pajares, G. Overview and current status of remote sensing applications based on unmanned aerial vehicles (UAVs). Photogramm. Eng. Remote Sens. 2015, 81, 281–329. [Google Scholar] [CrossRef]
- Manyoky, M.; Theiler, P.; Steudler, D.; Eisenbeiss, H. Unmanned aerial vehicle in cadastral applications. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 63, 1–6. [Google Scholar] [CrossRef]
- Barnes, G.; Volkmann, W. High-resolution mapping with unmanned aerial systems. Surv. Land Inf. Sci. 2015, 74, 5–13. [Google Scholar]
- Mumbone, M.; Bennett, R.; Gerke, M.; Volkmann, W. Innovations in boundary mapping: Namibia, customary lands and UAVs. In Proceedings of the World Bank Conference on Land and Poverty, Washington, DC, USA, 23–27 March 2015; pp. 1–22.
- Volkmann, W.; Barnes, G. Virtual surveying: Mapping and modeling cadastral boundaries using Unmanned Aerial Systems (UAS). In Proceedings of the FIG Congress: Engaging the Challenges—Enhancing the Relevance, Kuala Lumpur, Malaysia, 16–21 June 2014; pp. 1–13.
- Maurice, M.J.; Koeva, M.N.; Gerke, M.; Nex, F.; Gevaert, C. A photogrammetric approach for map updating using UAV in Rwanda. In Proceedings of the GeoTech Rwanda—International Conference on Geospatial Technologies for Sustainable Urban and Rural Development, Kigali, Rwanda, 18–20 November 2015; pp. 1–8.
- Binns, B.O.; Dale, P.F. Cadastral Surveys and Records of Rights in Land Administration. Available online: http://www.fao.org/docrep/006/v4860e/v4860e03.htm (accessed on 10 November 2016).
- Williamson, I.; Enemark, S.; Wallace, J.; Rajabifard, A. Land Administration for Sustainable Development; ESRI Press Academic: Redlands, CA, USA, 2010; p. 472. [Google Scholar]
- Crommelinck, S.; Bennett, R.; Gerke, M.; Nex, F.; Yang, M.; Vosselman, G. Review of automatic feature extraction from high-resolution optical sensor data for UAV-based cadastral mapping. Remote Sens. 2016, 8, 1–28. [Google Scholar] [CrossRef]
- Jazayeri, I.; Rajabifard, A.; Kalantari, M. A geometric and semantic evaluation of 3D data sourcing methods for land and property information. Land Use Policy 2014, 36, 219–230. [Google Scholar] [CrossRef]
- Bennett, R.; Kitchingman, A.; Leach, J. On the nature and utility of natural boundaries for land and marine administration. Land Use policy 2010, 27, 772–779. [Google Scholar] [CrossRef]
- Zevenbergen, J.; Bennett, R. The visible boundary: More than just a line between coordinates. In Proceedings of the GeoTech Rwanda—International Conference on Geospatial Technologies for Sustainable Urban and Rural Development, Kigali, Rwanda, 18–20 November 2015; pp. 1–4.
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 6, 679–698. [Google Scholar] [CrossRef]
- Malik, J.; Belongie, S.; Leung, T.; Shi, J. Contour and texture analysis for image segmentation. Int. J. Comput. Vis. 2001, 43, 7–27. [Google Scholar] [CrossRef]
- Martin, D.R.; Fowlkes, C.C.; Malik, J. Learning to detect natural image boundaries using local brightness, color, and texture cues. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 530–549. [Google Scholar] [CrossRef] [PubMed]
- Maire, M.; Arbeláez, P.; Fowlkes, C.; Malik, J. Using contours to detect and localize junctions in natural images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8.
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour detection and hierarchical image segmentation. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. From contours to regions: An empirical evaluation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami Beach, FL, USA, 20–25 June 2009; pp. 2294–2301.
- Arbeláez, P.; Fowlkes, C.; Martin, D. Berkeley Segmentation Dataset and Benchmark. Available online: https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/bsds/ (accessed on 10 November 2016).
- Arbeláez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour Detection and Image Segmentation Resources. Available online: https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/grouping/resources.html (accessed on 10 November 2016).
- Arbelaez, P. Boundary extraction in natural images using ultrametric contour maps. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshop (CVPRW), New York, NY, USA, 17–22 June 2006. [CrossRef]
- Jevnisek, R.J.; Avidan, S. Semi global boundary detection. Comput. Vis. Image Understand. 2016, 152, 21–28. [Google Scholar] [CrossRef]
- Zhang, X.; Xiao, P.; Song, X.; She, J. Boundary-constrained multi-scale segmentation method for remote sensing images. ISPRS J. Photogramm. Remote Sens. 2013, 78, 15–25. [Google Scholar] [CrossRef]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer: London, UK, 2010; p. 812. [Google Scholar]
- Dornaika, F.; Moujahid, A.; El Merabet, Y.; Ruichek, Y. Building detection from orthophotos using a machine learning approach: An empirical study on image segmentation and descriptors. Expert Syst. Appl. 2016, 58, 130–142. [Google Scholar] [CrossRef]
- Hou, B.; Kou, H.; Jiao, L. Classification of polarimetric SAR images using multilayer autoencoders and superpixels. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2016, 9, 3072–3081. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Gerke, M.; Wegner, J.D.; Breitkopf, U.; Jung, J. Results of the ISPRS benchmark on urban object detection and 3D building reconstruction. ISPRS J. Photogramm. Remote Sens. 2014, 93, 256–271. [Google Scholar] [CrossRef]
- QGIS Development Team. QGIS Geographic Information System; Open Source Geospatial Foundation: Chicago, CA, USA, 2009. Available online: www.qgis.osgeo.org (accessed on 21 June 2016).
- GRASS Developmnet Team. Geographic Resources Analysis Support System (GRASS) Software, Version 7.0. Available online: www.grass.osgeo.org (accessed on 21 June 2016).
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for automated geoscientific analyses (SAGA) Version 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- GDAL Development Team. GDAL—Geospatial Data Abstraction Library, version 2.1.2; Open Source Geospatial Foundation: Chicago, CA, USA, 2016. Available online: www.gdal.org (accessed on 5 January 2017).
- Wiedemann, C.; Heipke, C.; Mayer, H.; Jamet, O. Empirical evaluation of automatically extracted road axes. In Empirical Evaluation Techniques in Computer Vision; IEEE Computer Society Press: Los Alamitos, CA, USA, 1998; pp. 172–187. [Google Scholar]
- Shi, W.; Cheung, C.K.; Zhu, C. Modelling error propagation in vector-based buffer analysis. Int. J. Geogr. Inf. Sci. 2003, 17, 251–271. [Google Scholar] [CrossRef]
- Mayer, H. Object extraction in photogrammetric computer vision. ISPRS J. Photogramm. Remote Sens. 2008, 63, 213–222. [Google Scholar]
- Kumar, M.; Singh, R.; Raju, P.; Krishnamurthy, Y. Road network extraction from high resolution multispectral satellite imagery based on object oriented techniques. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 107–110. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Hunter, G.J. A simple positional accuracy measure for linear features. Int. J. Geogr. Inf. Sci. 1997, 11, 299–306. [Google Scholar] [CrossRef]
- Enemark, S.; Bell, K.C.; Lemmen, C.; McLaren, R. Fit-For-Purpose Land Administration; International Federation of Surveyors: Frederiksberg, Denmark, 2014; p. 42. [Google Scholar]
- Zevenbergen, J.; de Vries, W.; Bennett, R.M. Advances in Responsible Land Administration; CRC Press: Padstow, UK, 2015; p. 279. [Google Scholar]
- Mayer, H.; Hinz, S.; Bacher, U.; Baltsavias, E. A test of automatic road extraction approaches. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2006, 36, 209–214. [Google Scholar]
- Basaeed, E.; Bhaskar, H.; Al-Mualla, M. CNN-based multi-band fused boundary detection for remotely sensed images. In Proceedings of the International Conference on Imaging for Crime Prevention and Detection, London, UK, 15–17 July 2015; pp. 1–6.
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).