Fusion of Ultrasonic and Spectral Sensor Data for Improving the Estimation of Biomass in Grasslands with Heterogeneous Sward Structure
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Site Characteristics
2.2. Field Measurements
2.2.1. Ground-Based Remote Sensing Measurements
2.2.2. Sampling of Reference Data
2.3. Data Analysis
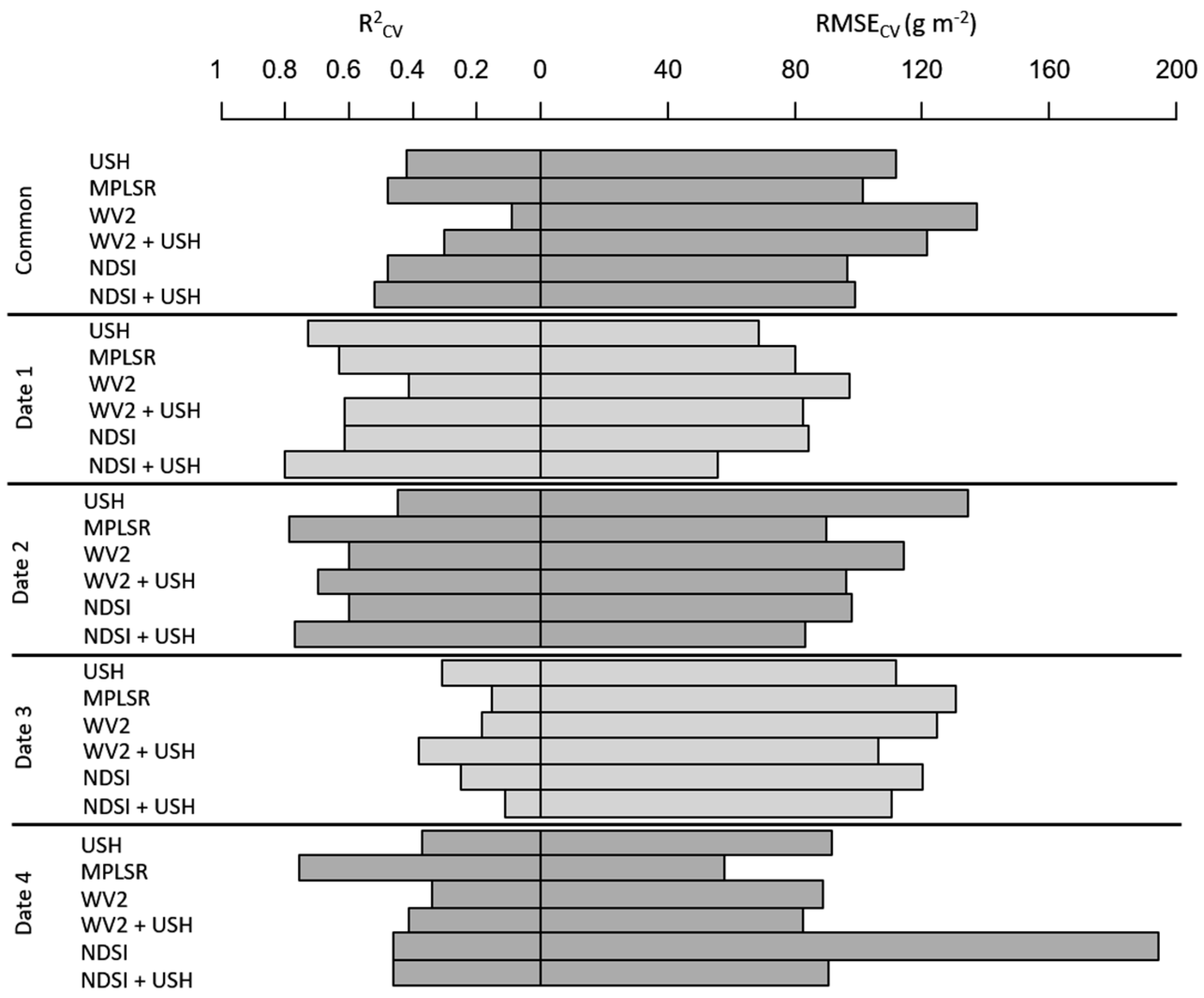
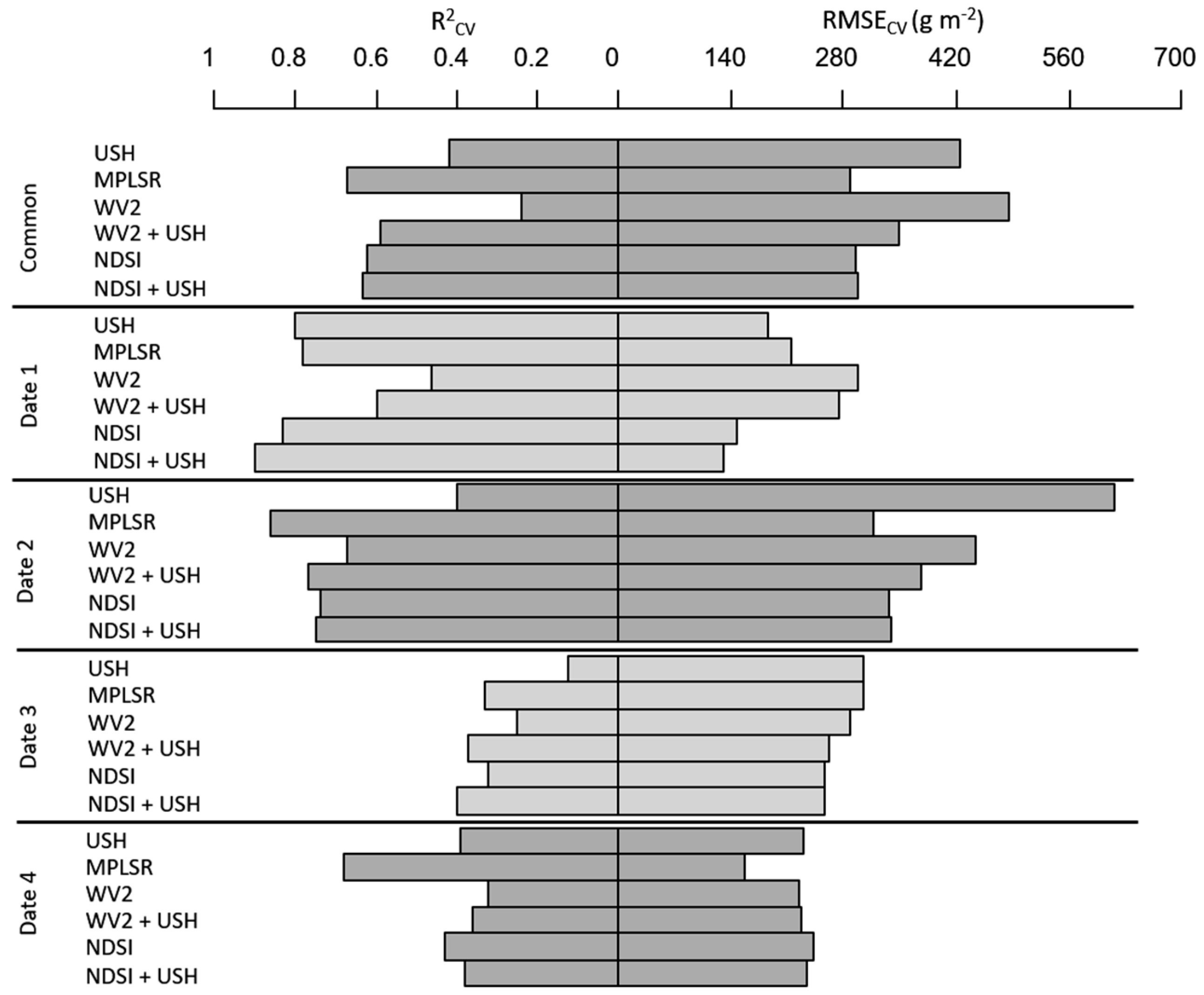
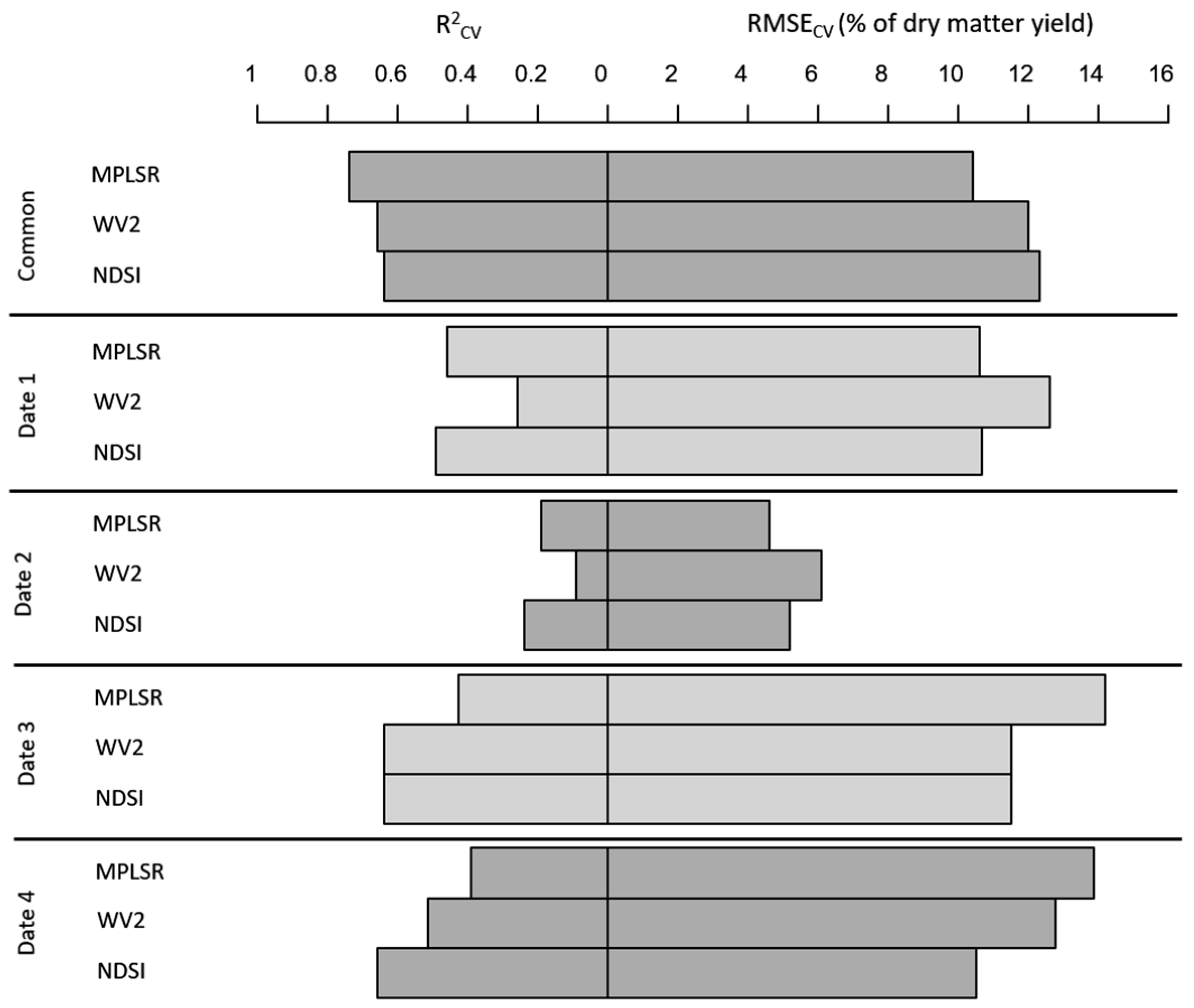
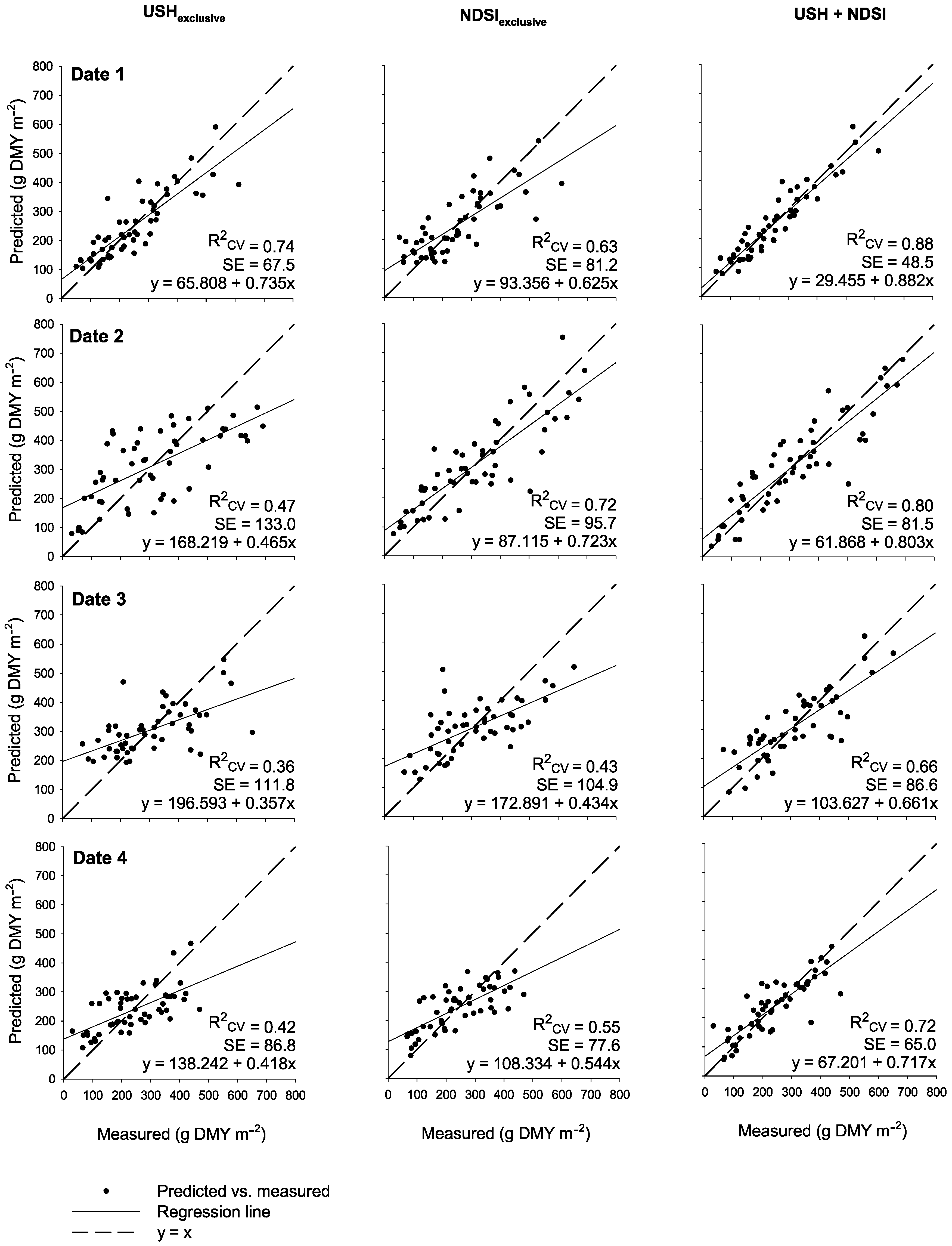
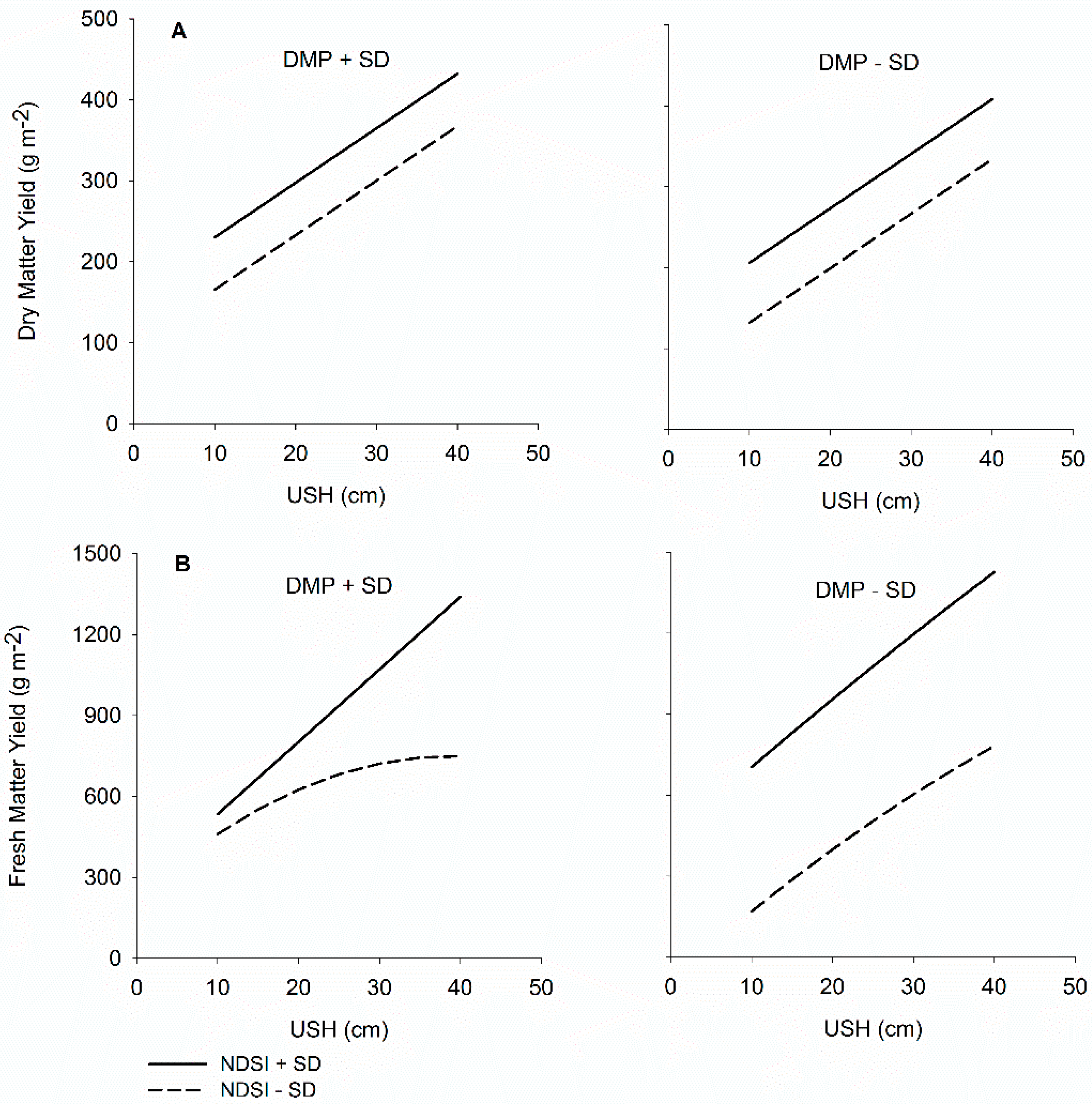
3. Results
3.1. Sward Characteristics
3.2. Exclusive use of Ultrasonic Sward Height
3.3. Exclusive Use of Spectral Data
3.4. Sensor Data Fusion Using Combinations of USH and Spectral Variables
4. Discussion
4.1. Exclusive Use of USH
4.2. Exclusive Use of Spectral Data
4.3. Sensor Fusion
5. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
Appendix A
| Species | Min | Max | Mean | Const. (%) | Species | Min | Max | Mean | Const. (%) |
|---|---|---|---|---|---|---|---|---|---|
| Grasses | Herbs | ||||||||
| Agrostis stolonifera | 0.0 | 79.4 | 9.22 | 54.2 | Achillea millefolium | 0.0 | 85.0 | 0.92 | 5.1 |
| Alopecurus pratensis | 0.0 | 95.0 | 3.83 | 13.6 | Anthriscus sylvestris | 0.0 | 28.0 | 0.13 | 0.5 |
| Arrhenatherum elatius | 0.0 | 1.0 | 0.00 | 0.5 | Bellis perennis | 0.0 | 59.0 | 0.31 | 2.3 |
| Bromus mollis | 0.0 | 7.0 | 0.10 | 3.7 | Centaurea jacea | 0.0 | 1.0 | 0.00 | 0.5 |
| Cynosurus cristatus | 0.0 | 59.6 | 1.77 | 10.3 | Cerastium holosteoides | 0.0 | 4.0 | 0.23 | 19.6 |
| Dactylis glomerata | 0.0 | 94.0 | 25.68 | 89.7 | Cirsium arvense | 0.0 | 40.0 | 1.14 | 9.3 |
| Deschampsia caespitosa | 0.0 | 90.0 | 0.59 | 0.9 | Cirsium vulgare | 0.0 | 15.0 | 0.30 | 7.0 |
| Elymus repens | 0.0 | 80.0 | 5.82 | 36.9 | Convolvulus arvensis | 0.0 | 28.6 | 0.39 | 6.1 |
| Festuca pratensis | 0.0 | 85.0 | 0.71 | 5.6 | Crepis capillaris | 0.0 | 20.0 | 0.38 | 6.1 |
| Festuca rubra | 0.0 | 95.4 | 4.85 | 21.0 | Erophila verna | 0.0 | 4.0 | 0.04 | 4.7 |
| Lolium perenne | 0.0 | 88.6 | 15.64 | 70.1 | Epilobium spec. | 0.0 | 16.0 | 0.20 | 4.7 |
| Phleum pratense | 0.0 | 4.0 | 0.06 | 2.3 | Galium mollugo | 0.0 | 88.0 | 9.67 | 40.7 |
| Poa annua | 0.0 | 1.0 | 0.01 | 0.9 | Geranium dissectum | 0.0 | 13.0 | 0.20 | 13.6 |
| Poa pratensis | 0.0 | 45.0 | 2.32 | 27.6 | Geum urbanum | 0.0 | 30.0 | 0.19 | 3.3 |
| Poa trivialis | 0.0 | 16.0 | 1.28 | 25.2 | Hieracium pilosella | 0.0 | 0.2 | 0.00 | 0.5 |
| Lamium purpureum | 0.0 | 38.0 | 0.21 | 2.3 | |||||
| Legumes | Leontodon hispidus | 0.0 | 2.0 | 0.02 | 1.9 | ||||
| Medicago lupulina | 0.0 | 5.0 | 0.03 | 0.9 | Plantago lanceolata | 0.0 | 35.0 | 0.56 | 10.7 |
| Trifolium campestre | 0.0 | 20.0 | 0.17 | 1.9 | Plantago major | 0.0 | 3.0 | 0.01 | 0.5 |
| Trifolium dubium | 0.0 | 25.0 | 0.18 | 3.7 | Taraxacum officinale | 0.0 | 83.0 | 5.89 | 57.5 |
| Trifolium pratense | 0.0 | 61.0 | 1.50 | 17.8 | Ranunculus acris | 0.0 | 10.0 | 0.20 | 6.5 |
| Trifolium repens | 0.0 | 49.6 | 2.49 | 39.7 | Ranunculus repens | 0.0 | 71.8 | 1.35 | 23.8 |
| Vicia cracca | 0.0 | 1.0 | 0.00 | 0.5 | Rosa spec. | 0.0 | 5.0 | 0.04 | 0.9 |
| Rumex acetosa | 0.0 | 4.0 | 0.03 | 1.4 | |||||
| Urtica dioica | 0.0 | 84.0 | 1.09 | 2.8 | |||||
| Veronica chamaedrys | 0.0 | 4.0 | 0.03 | 1.9 | |||||
| Veronica serpyllifolia | 0.0 | 35.0 | 0.19 | 1.9 |
References
- Cho, M.A.; Skidmore, A.; Corsi, F.; van Wieren, S.E.; Sobhan, I. Estimation of green grass/herb biomass from airborne hyperspectral imagery using spectral indices and partial least squares regression. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 414–424. [Google Scholar] [CrossRef]
- Fava, F.; Colombo, R.; Bocchi, S.; Meroni, M.; Sitzia, M.; Fois, N.; Zucca, C. Identification of hyperspectral vegetation indices for Mediterranean pasture characterization. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 233–243. [Google Scholar] [CrossRef]
- Xiaoping, W.; Ni, G.; Kai, Z.; Jing, W. Hyperspectral remote sensing estimation models of aboveground biomass in Gannan rangelands. Proc. Environ. Sci. 2011, 10, 697–702. [Google Scholar] [CrossRef]
- Fricke, T.; Wachendorf, M. Combining ultrasonic sward height and spectral signatures to assess the biomass of legume-grass swards. Comput. Electron. Agric. 2013, 99, 236–247. [Google Scholar] [CrossRef]
- Fricke, T.; Richter, F.; Wachendorf, M. Assessment of forage mass from grassland swards by height measurement using an ultrasonic sensor. Comput. Electron. Agric. 2011, 79, 142–152. [Google Scholar] [CrossRef]
- Lee, H.-J.; Kawamura, K.; Watanabe, N.; Sakanoue, S.; Sakuno, Y.; Itano, S.; Nakagoshi, N. Estimating the spatial distribution of green herbage biomass and quality by geostatistical analysis with field hyperspectral measurements. Grassl. Sci. 2011, 57, 142–149. [Google Scholar] [CrossRef]
- Schellberg, J.; Hill, M.J.; Gerhards, R.; Rothmund, M.; Braun, M. Precision agriculture on grassland: Applications, perspectives and constraints. Eur. J. Agron. 2008, 29, 59–71. [Google Scholar] [CrossRef]
- Pullanagari, R.R.; Yule, I.J.; Hedley, M.J.; Tuohy, M.P.; Dynes, R.A.; King, W.M. Multi-spectral radiometry to estimate pasture quality components. Precis. Agric. 2012, 13, 442–456. [Google Scholar] [CrossRef]
- Adamchuk, V.I.; Sudduth, K.A.; Lammers, P.S.; Rossel, R.A.V. Sensor Fusion for Precision Agriculture; In-Tech: Rijeka, Croatia, 2011. [Google Scholar]
- Jones, C.L.; Maness, N.O.; Stone, M.L.; Jayasekara, R. Chlorophyll estimation using multispectral reflectance and height sensing. Trans. ASABE 2007, 50, 1867–1872. [Google Scholar] [CrossRef]
- Mazzetto, F.; Calcante, A.; Mena, A.; Vercesi, A. Integration of optical and analogue sensors for monitoring canopy health and vigour in precision viticulture. Precis. Agric. 2010, 11, 636–649. [Google Scholar] [CrossRef]
- Scotford, I.M.; Miller, P. Combination of spectral reflectance and ultrasonic sensing to monitor the growth of winter wheat. Biosyst. Eng. 2004, 87, 27–38. [Google Scholar] [CrossRef]
- Scotford, I.; Miller, P. Estimating tiller density and leaf area index of winter wheat using spectral reflectance and ultrasonic sensing techniques. Biosyst. Eng. 2004, 89, 395–408. [Google Scholar] [CrossRef]
- Farooque, A.A.; Chang, Y.K.; Zaman, Q.U.; Groulx, D.; Schumann, A.W.; Esau, T.J. Performance evaluation of multiple ground based sensors mounted on a commercial wild blueberry harvester to sense plant height, fruit yield and topographic features in real-time. Comput. Electron. Agric. 2013, 91, 135–144. [Google Scholar] [CrossRef]
- Sui, R.; Thomasson, J.A. Ground-Based Sensing System for Cotton Nitrogen Status Determination. Trans. ASABE 2006, 49, 1983–1991. [Google Scholar] [CrossRef]
- Hutchings, N.J.; Phillips, A.H.; Dobson, R.C. An ultrasonic rangefinder for measuring the undisturbed surface height of continuously grazed grass swards. Grass Forage Sci. 1990, 45, 119–127. [Google Scholar] [CrossRef]
- Hutchings, N.J. Factors affecting sonic sward stick measurements: the effect of different leaf characteristics and the area of sward sampled. Grass Forage Sci. 1992, 47, 153–160. [Google Scholar] [CrossRef]
- Boschetti, M.; Bocchi, S.; Brivio, P.A. Assessment of pasture production in the Italian Alps using spectrometric and remote sensing information. Agric. Ecosyst. Environ. 2007, 118, 267–272. [Google Scholar] [CrossRef]
- Yang, X.; Guo, X. Quantifying Responses of spectral vegetation indices to dead materials in mixed grasslands. Remote Sens. 2014, 6, 4289–4304. [Google Scholar] [CrossRef]
- Jackson, R.D.; Huete, A.R. Interpreting vegetation indices. Interpreting vegetation indices. Prev. Vet. Med. 1991, 11, 185–200. [Google Scholar] [CrossRef]
- Duan, M.; Gao, Q.; Wan, Y.; Li, Y.; Guo, Y.; Ganzhu, Z.; Liu, Y.; Qin, X. Biomass estimation of alpine grasslands under different grazing intensities using spectral vegetation indices. Can. J. Remote Sens. 2014, 37, 413–421. [Google Scholar] [CrossRef]
- Numata, I.; Roberts, D.; Chadwick, O.; Schimel, J.; Galvao, L.; Soares, J. Evaluation of hyperspectral data for pasture estimate in the Brazilian Amazon using field and imaging spectrometers. Remote Sens. Environ. 2008, 112, 1569–1583. [Google Scholar] [CrossRef]
- Biewer, S.; Fricke, T.; Wachendorf, M. Determination of dry matter yield from legume–grass swards by field spectroscopy. Crop Sci. 2009, 49, 1927–1936. [Google Scholar] [CrossRef]
- Kumar, L.; Sinha, P.; Taylor, S.; Alqurashi, A.F. Review of the use of remote sensing for biomass estimation to support renewable energy generation. J. Appl. Remote Sens 2015, 9, 097696. [Google Scholar] [CrossRef]
- Wrage, N.; Şahin Demirbağ, N.; Hofmann, M.; Isselstein, J. Vegetation height of patch more important for phytodiversity than that of paddock. Agric. Ecosyst. Environ. 2012, 155, 111–116. [Google Scholar] [CrossRef]
- Scimone, M.; Rook, A.J.; Garel, J.P.; Sahin, N. Effects of livestock breed and grazing intensity on grazing systems: 3. Effects on diversity of vegetation. Grass Forage Sci. 2007, 62, 172–184. [Google Scholar] [CrossRef]
- Jerrentrup, J.S.; Wrage-Mönnig, N.; Röver, K.-U.; Isselstein, J.; McKenzie, A. Grazing intensity affects insect diversity via sward structure and heterogeneity in a long-term experiment. J. Appl. Ecol. 2014, 51, 968–977. [Google Scholar] [CrossRef]
- Pepperl; Fuchs. Sensing your needs: ENU Part No. 200237. 2010. Available online: http://www.pepperl-fuchs.us/usa/downloads_USA/Sensing-your-needs-2010-01-EN.pdf (accessed on 19 January 2017).
- Klapp, E.; Stählin, A. Standorte, Pflanzengesellschaften und Leistung des Grünlandes. 122 Seiten mit 3 Karten und 20 Abbildungen. Verlag Eugen Ulmer, Stuttgart-S. 1936. Z. Pflanzenernaehr. Dueng. Bodenk. 1936, 43, 221–222. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Inoue, Y.; Penuelas, J.; Miyata, A.; Mano, M. Normalized difference spectral indices for estimating photosynthetic efficiency and capacity at a canopy scale derived from hyperspectral and CO2 flux measurements in rice. Remote Sens. Environ. 2008, 112, 156–172. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In Third ERTS-1 Symposium; Fraden, S.C., Marcanti, E.P., Becker, M.A., Eds.; Scientific and Technical Information Office, National Aeronautics and Space Administration: Washington, DC, USA, 1974; pp. 309–317. [Google Scholar]
- Nelder, J.A. The statistics of linear models: back to basics. Stat. Comput. 1994, 4, 221–234. [Google Scholar] [CrossRef]
- Nelder, J.A.; Lane, P.W. The computer analysis of factorial experiments: In memoriam—Frank Yates. Am. Stat. 1995, 49, 382–385. [Google Scholar] [CrossRef]
- Diaconis, P.; Efron, B. Computer-intensive methods in statistics. Sci. Am. 1983, 248, 116–130. [Google Scholar] [CrossRef]
- Biewer, S.; Fricke, T.; Wachendorf, M. Development of canopy reflectance models to predict forage quality of legume–grass mixtures. Crop Sci. 2009, 49, 1917. [Google Scholar] [CrossRef]
- Marabel, M.; Alvarez-Taboada, F. Spectroscopic determination of aboveground biomass in grasslands using spectral transformations, support vector machine and partial least squares regression. Sensors 2013, 13, 10027–10051. [Google Scholar] [CrossRef] [PubMed]
- Möckel, T.; Dalmayne, J.; Prentice, H.C.; Eklundh, L.; Purschke, O.; Schmidtlein, S.; Hall, K. Classification of grassland successional stages using airborne hyperspectral imagery. Remote Sens. 2014, 6, 7732–7761. [Google Scholar] [CrossRef]
- Möckel, T.; Dalmayne, J.; Schmid, B.C.; Prentice, H.C.; Hall, K. Airborne hyperspectral data predict fine-scale plant species diversity in grazed dry grasslands. Remote Sens. 2016, 8, 133. [Google Scholar] [CrossRef]
- Möckel, T.; Löfgren, O.; Prentice, H.C.; Eklundh, L.; Hall, K. Airborne hyperspectral data predict Ellenberg indicator values for nutrient and moisture availability in dry grazed grasslands within a local agricultural landscape. Ecol. Indic. 2016, 66, 503–516. [Google Scholar] [CrossRef]
- Reddersen, B.; Fricke, T.; Wachendorf, M. A multi-sensor approach for predicting biomass of extensively managed grassland. Comput. Electron. Agric. 2014, 109, 247–260. [Google Scholar] [CrossRef]
- Chen, P.; Haboudane, D.; Tremblay, N.; Wang, J.; Vigneault, P.; Li, B. New spectral indicator assessing the efficiency of crop nitrogen treatment in corn and wheat. Remote Sens. Environ. 2010, 114, 1987–1997. [Google Scholar] [CrossRef]
- Anderson, M.; Neale, C.; LI, F.; Normann, J.; Kustas, W.; Jayanthi, H.; Chavez, J. Upscaling ground observations of vegetation water content, canopy height, and leaf area index during SMEX02 using aircraft and Landsat imagery. Remote Sens. Environ. 2004, 92, 447–464. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K. Narrow band vegetation indices overcome the saturation problem in biomass estimation. Int. J. Remote Sens. 2004, 25, 3999–4014. [Google Scholar] [CrossRef]
- Psomas, A.; Kneubühler, M.; Huber, S.; Itten, K.; Zimmermann, N.E. Hyperspectral remote sensing for estimating aboveground biomass and for exploring species richness patterns of grassland habitats. Int. J. Remote Sens. 2011, 32, 9007–9031. [Google Scholar] [CrossRef]
- Gherbin, P.; de Franchi, A.S.; Monteleone, M.; Rivelli, A.R. Adaptability and productivity of some warm-season pasture species in a Mediterranean environment. Grass Forage Sci. 2007, 62, 78–86. [Google Scholar] [CrossRef]
| N | Min | Max | Mean | Sd | Min | Max | Mean | Sd | |
|---|---|---|---|---|---|---|---|---|---|
| Dry matter yield (g·m−2) | Fresh matter yield (g·m−2) | ||||||||
| Common | 214 | 29.2 | 691.9 | 276.4 | 145.5 | 68.8 | 3207.0 | 823.9 | 554.6 |
| Date 1 | 54 | 51.9 | 612.1 | 248.8 | 130.0 | 140.0 | 1883.0 | 739.6 | 416.9 |
| Date 2 | 54 | 31.9 | 691.9 | 314.5 | 180.2 | 107.2 | 3207.0 | 1240.0 | 785.6 |
| Date 3 | 52 | 68.2 | 654.8 | 305.7 | 138.1 | 148.0 | 1822.0 | 745.4 | 337.0 |
| Date 4 | 54 | 29.2 | 468.8 | 237.6 | 112.7 | 68.8 | 1325.0 | 567.5 | 281.7 |
| Ultrasonic sward height (mm) | Grass proportion (% of DM) | ||||||||
| Common | 214 | 7 | 646 | 252 | 151 | 8.0 | 93.7 | 50.6 | 23.9 |
| Date 1 | 54 | 7 | 438 | 136 | 99 | 12.9 | 81.1 | 44.9 | 16.8 |
| Date 2 | 54 | 31 | 646 | 364 | 174 | 8.2 | 93.7 | 72.2 | 19.0 |
| Date 3 | 52 | 105 | 615 | 268 | 119 | 8.8 | 92.9 | 41.9 | 24.8 |
| Date 4 | 54 | 48 | 576 | 240 | 107 | 8.0 | 85.3 | 43.1 | 20.6 |
| Legume proportion (% of DM) | Moss proportion (% of DM) | ||||||||
| Common | 214 | 0.0 | 39.6 | 2.9 | 6.8 | 0.0 | 27.5 | 1.9 | 4.4 |
| Date 1 | 54 | 0.0 | 36.4 | 4.7 | 8.2 | 0.0 | 21.3 | 4.9 | 6.1 |
| Date 2 | 54 | 0.0 | 39.6 | 4.1 | 9.0 | 0.0 | 14.7 | 0.7 | 2.4 |
| Date 3 | 52 | 0.0 | 31.2 | 1.9 | 5.0 | 0.0 | 27.5 | 1.6 | 4.4 |
| Date 4 | 54 | 0.0 | 7.1 | 0.6 | 1.6 | 0.0 | 5.8 | 0.3 | 0.9 |
| Herb proportion (% of DM) | Dead material proportion (% of DM) | ||||||||
| Common | 214 | 0.0 | 63.7 | 13.1 | 12.9 | 1.4 | 83.6 | 31.6 | 20.5 |
| Date 1 | 54 | 0.0 | 44.6 | 13.6 | 12.7 | 2.5 | 70.3 | 31.9 | 14.9 |
| Date 2 | 54 | 0.0 | 63.7 | 13.9 | 15.0 | 1.4 | 37.6 | 9.2 | 6.4 |
| Date 3 | 52 | 0.0 | 47.5 | 14.6 | 12.8 | 3.9 | 76.3 | 40.0 | 18.8 |
| Date 4 | 54 | 0.0 | 42.1 | 10.3 | 10.8 | 10.5 | 83.6 | 45.7 | 17.7 |
| Common (n = 214) | Date 1 (n = 54) | Date 2 (n = 54) | Date 3 (n = 52) | Date 4 (n = 54) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| b1 | b2 | b1 | b2 | b1 | b2 | b1 | b2 | b1 | b2 | |
| Dry matter yield (g·m−2) | ||||||||||
| NDSI | 1035 | 1051 | 389 | 609 | 1097 | 1139 | 1122 | 1128 | 769 | 778 |
| USH + NDSI | 521 | 578 | 1215 | 1225 | 1024 | 1031 | 1116 | 1118 | 1622 | 1633 |
| Fresh matter yield (g·m−2) | ||||||||||
| NDSI | 1117 | 1134 | 1040 | 1073 | 1080 | 1104 | 1122 | 1128 | 751 | 782 |
| USH + NDSI | 1077 | 1086 | 996 | 1005 | 536 | 564 | 1122 | 1135 | 1621 | 1633 |
| Dead material proportion (% of dry matter yield) | ||||||||||
| NDSI | 1242 | 1305 | 1231 | 1285 | 1188 | 1202 | 1236 | 1281 | 1187 | 1206 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moeckel, T.; Safari, H.; Reddersen, B.; Fricke, T.; Wachendorf, M. Fusion of Ultrasonic and Spectral Sensor Data for Improving the Estimation of Biomass in Grasslands with Heterogeneous Sward Structure. Remote Sens. 2017, 9, 98. https://doi.org/10.3390/rs9010098
Moeckel T, Safari H, Reddersen B, Fricke T, Wachendorf M. Fusion of Ultrasonic and Spectral Sensor Data for Improving the Estimation of Biomass in Grasslands with Heterogeneous Sward Structure. Remote Sensing. 2017; 9(1):98. https://doi.org/10.3390/rs9010098
Chicago/Turabian StyleMoeckel, Thomas, Hanieh Safari, Björn Reddersen, Thomas Fricke, and Michael Wachendorf. 2017. "Fusion of Ultrasonic and Spectral Sensor Data for Improving the Estimation of Biomass in Grasslands with Heterogeneous Sward Structure" Remote Sensing 9, no. 1: 98. https://doi.org/10.3390/rs9010098
APA StyleMoeckel, T., Safari, H., Reddersen, B., Fricke, T., & Wachendorf, M. (2017). Fusion of Ultrasonic and Spectral Sensor Data for Improving the Estimation of Biomass in Grasslands with Heterogeneous Sward Structure. Remote Sensing, 9(1), 98. https://doi.org/10.3390/rs9010098






