Measuring Leaf Water Content with Dual-Wavelength Intensity Data from Terrestrial Laser Scanners
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment Design
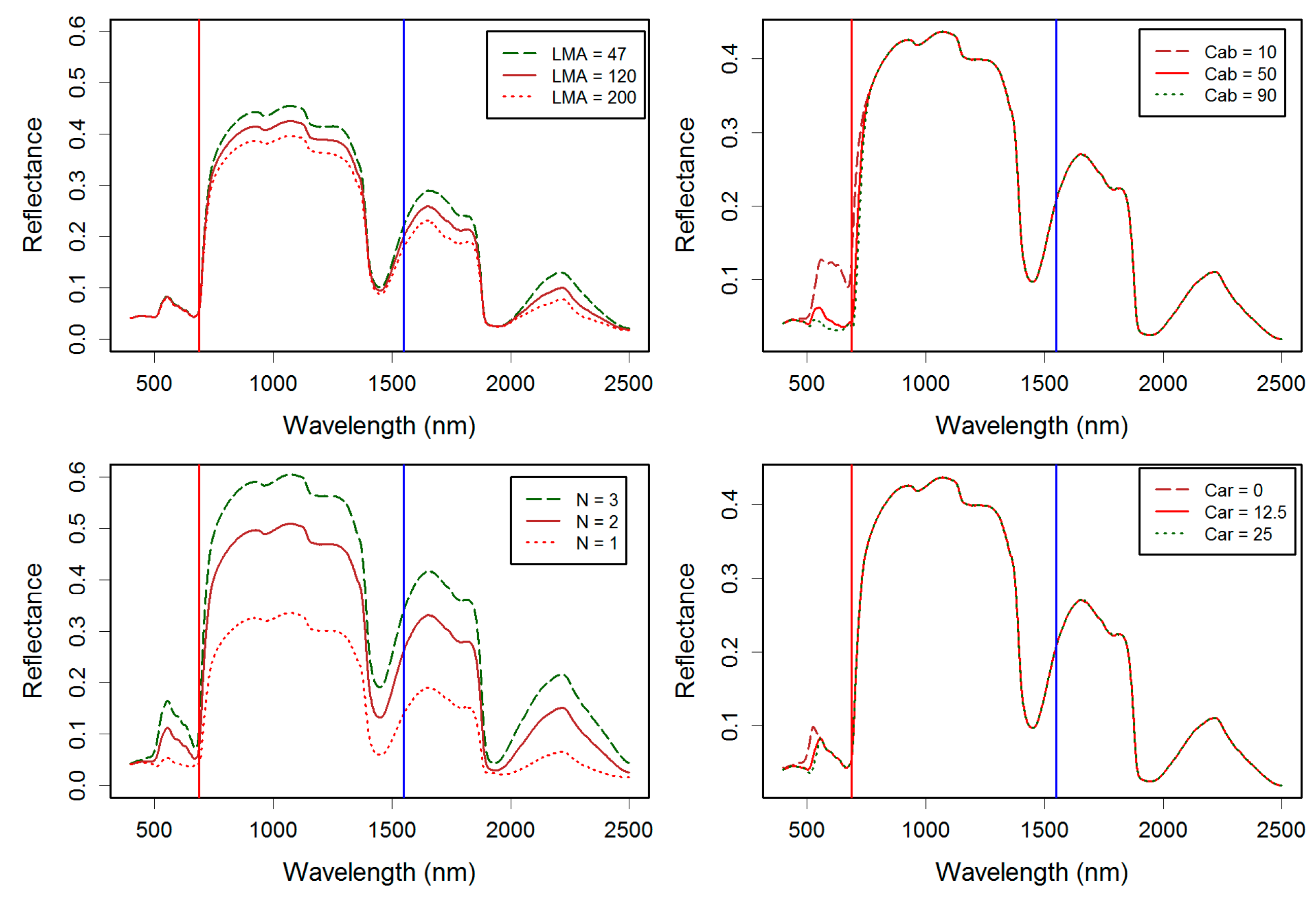
2.2. The Calculation of Eco-Physiological Parameters
2.3. Terrestrial Laser Scanners
2.4. Pre-Processing of TLS Data
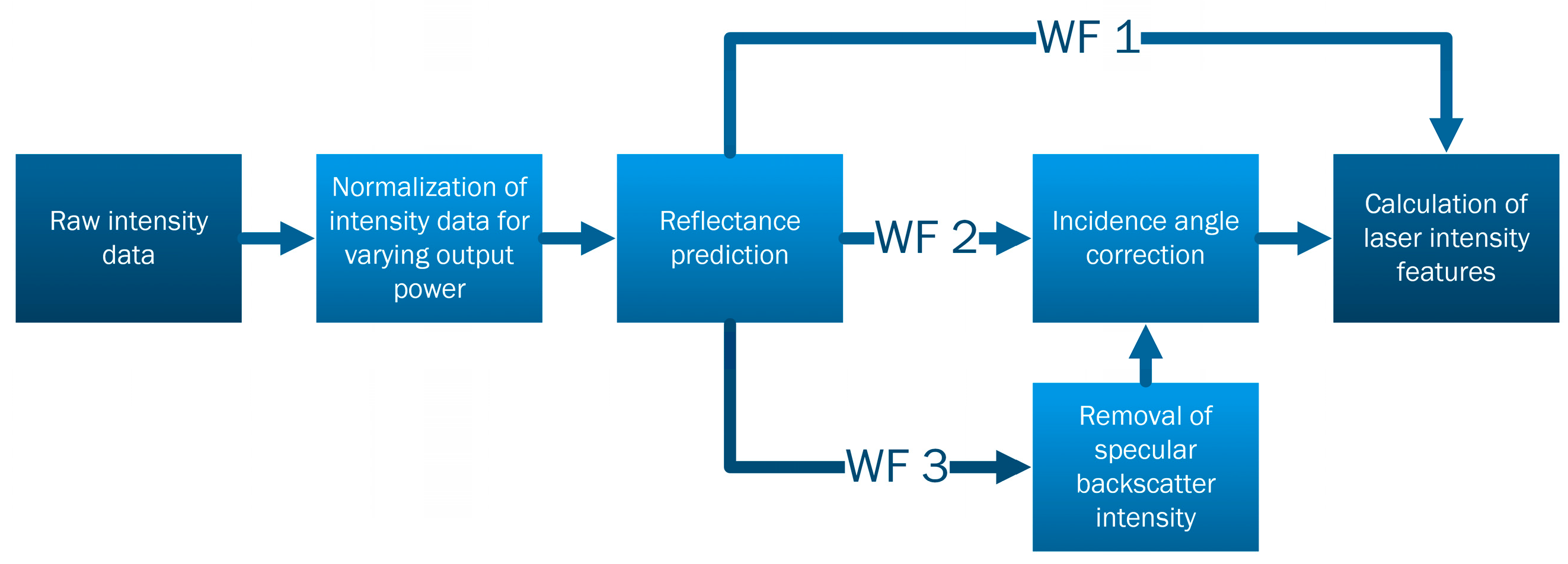
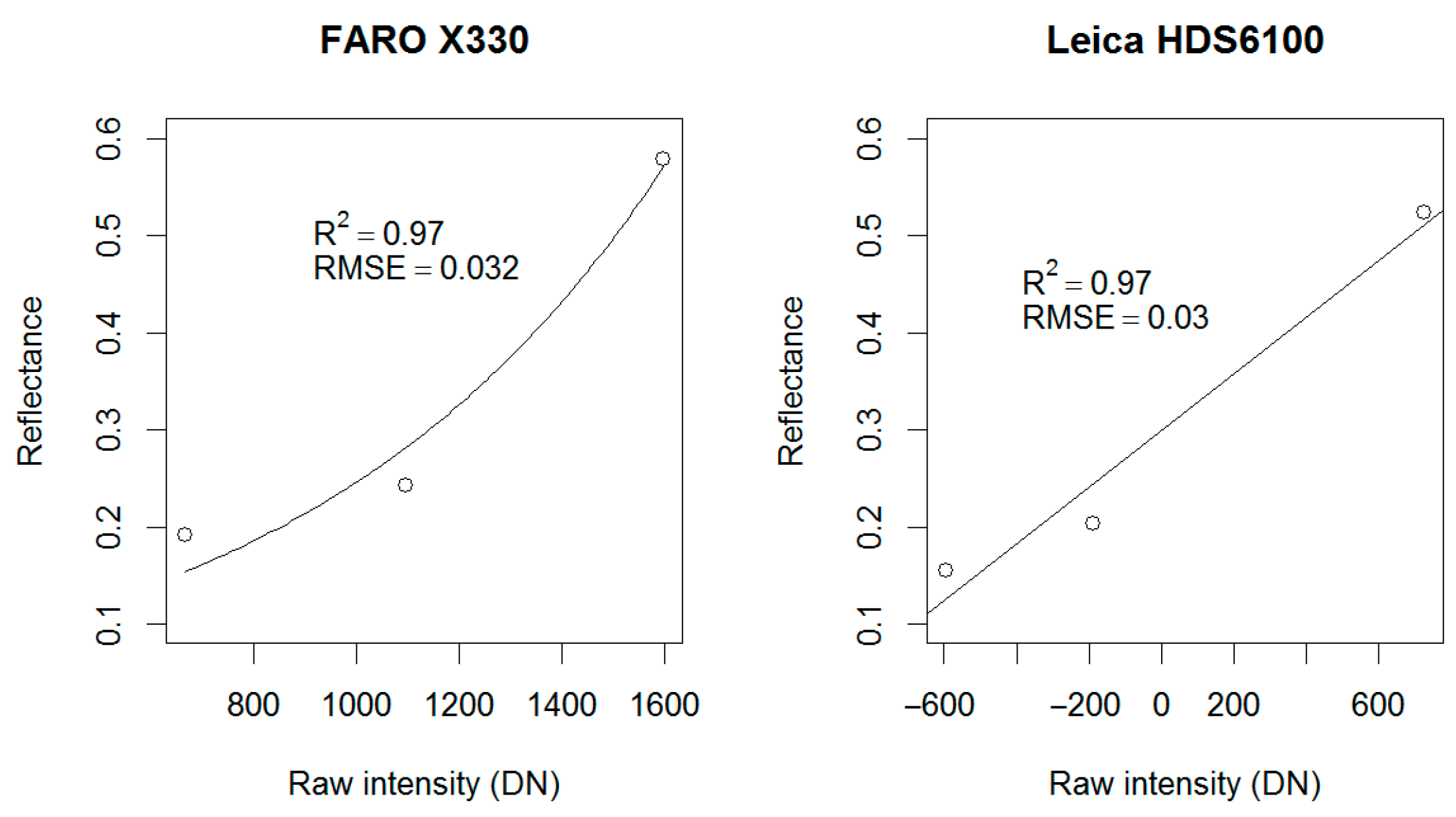
2.5. Intensity Calibration
2.6. Incidence Angle Correction
2.6.1. Incidence Angle
2.6.2. Model for Correcting the Incidence Angle Effect on Backscatter Intensity
2.7. Removal of Specular Backscatter Intensity
2.8. Laser Intensity Features
2.9. Statistical Analysis
3. Results
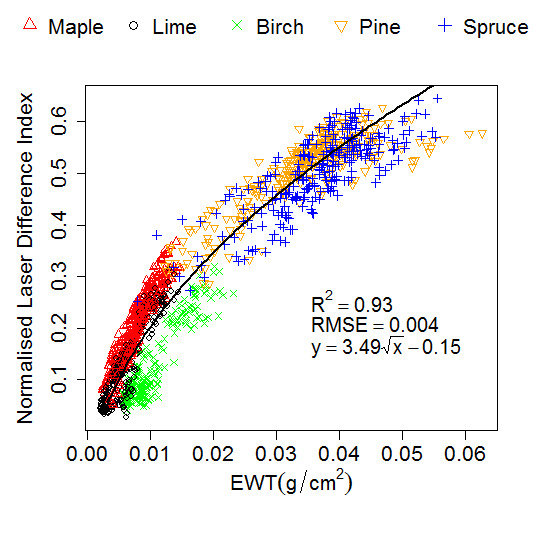
3.1. Correlation between Calibrated Intensity and EWT
3.2. Correlation between Calibrated Intensity and EWT after Incidence Angle Correction
3.3. Correlation between Calibrated Intensity and EWT after Incidence Angle Correction and the Removal of Specular Backscatter Intensity
3.4. The Effect of Leaf Dry Mass on Calibrated Intensity
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.; Tignor, M.; Miller, H. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Dale, V.H.; Joyce, L.A.; McNulty, S.; Neilson, R.P.; Ayres, M.P.; Flannigan, M.D.; Hanson, P.J.; Irland, L.C.; Lugo, A.E.; Peterson, C.J. Climate change and forest disturbances: Climate change can affect forests by altering the frequency, intensity, duration, and timing of fire, drought, introduced species, insect and pathogen outbreaks, hurricanes, windstorms, ice storms, or landslides. Bioscience 2001, 51, 723–734. [Google Scholar] [CrossRef]
- Eitel, J.U.; Höfle, B.; Vierling, L.A.; Abellán, A.; Asner, G.P.; Deems, J.S.; Glennie, C.L.; Joerg, P.C.; LeWinter, A.L.; Magney, T.S. Beyond 3-d: The new spectrum of lidar applications for earth and ecological sciences. Remote Sens. Environ. 2016, 186, 372–392. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Kantola, T.; Lyytikäinen-Saarenmaa, P.; Vastaranta, M.; Kankare, V.; Yu, X.; Holopainen, M.; Talvitie, M.; Solberg, S.; Puolakka, P.; Hyyppä, J. Using high density als data in plot level estimation of the defoliation by the common pine sawfly. In Procedings of the 2011 SilviLaser, Hobart, Australia, 16–20 October 2011.
- Douglas, E.S.; Strahler, A.; Martel, J.; Cook, T.; Mendillo, C.; Marshall, R.; Chakrabarti, S.; Schaaf, C.; Woodcock, C.; Li, Z.; et al. Dwel: A dual-wavelength echidna lidar for ground-based forest scanning. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 4998–5001.
- Li, W.; Niu, Z.; Sun, G.; Gao, S.; Wu, M. Deriving backscatter reflective factors from 32-channel full-waveform lidar data for the estimation of leaf biochemical contents. Opt. Express 2016, 24, 4771–4785. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Korpela, I.; Maltamo, M.; Tokola, T. Imputation of single-tree attributes using airborne laser scanning-based height, intensity, and alpha shape metrics. Remote Sens. Environ. 2010, 114, 1263–1276. [Google Scholar] [CrossRef]
- Korpela, I.; Ørka, H.O.; Maltamo, M.; Tokola, T.; Hyyppä, J. Tree species classification using airborne lidar—Effects of stand and tree parameters, downsizing of training set, intensity normalization, and sensor type. Silva Fenn. 2010, 44, 319–339. [Google Scholar] [CrossRef]
- Korpela, I.; Hovi, A.; Morsdorf, F. Understory trees in airborne lidar data—Selective mapping due to transmission losses and echo-triggering mechanisms. Remote Sens. Environ. 2012, 119, 92–104. [Google Scholar] [CrossRef]
- Béland, M.; Widlowski, J.-L.; Fournier, R.A.; Côté, J.-F.; Verstraete, M.M. Estimating leaf area distribution in savanna trees from terrestrial lidar measurements. Agric. For. Meteorol. 2011, 151, 1252–1266. [Google Scholar] [CrossRef]
- Lovell, J.; Jupp, D.; Newnham, G.; Culvenor, D. Measuring tree stem diameters using intensity profiles from ground-based scanning lidar from a fixed viewpoint. ISPRS J. Photogramm. Remote Sens. 2011, 66, 46–55. [Google Scholar] [CrossRef]
- Franceschi, M.; Teza, G.; Preto, N.; Pesci, A.; Galgaro, A.; Girardi, S. Discrimination between marls and limestones using intensity data from terrestrial laser scanner. ISPRS J. Photogramm. Remote Sens. 2009, 64, 522–528. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Ahokas, E.; Hyyppä, J.; Suomalainen, J. Study of surface brightness from backscattered laser intensity: Calibration of laser data. Geosci. Remote Sens. Lett. 2005, 2, 255–259. [Google Scholar] [CrossRef]
- Eitel, J.U.; Vierling, L.A.; Long, D.S. Simultaneous measurements of plant structure and chlorophyll content in broadleaf saplings with a terrestrial laser scanner. Remote Sens. Environ. 2010, 114, 2229–2237. [Google Scholar] [CrossRef]
- Balduzzi, M.A.; Van der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Coppin, P. The properties of terrestrial laser system intensity for measuring leaf geometries: A case study with conference pear trees (pyrus communis). Sensors 2011, 11, 1657–1681. [Google Scholar] [CrossRef] [PubMed]
- Kaasalainen, S.; Krooks, A.; Kukko, A.; Kaartinen, H. Radiometric calibration of terrestrial laser scanners with external reference targets. Remote Sens. 2009, 1, 144–158. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Jaakkola, A.; Kaasalainen, M.; Krooks, A.; Kukko, A. Analysis of incidence angle and distance effects on terrestrial laser scanner intensity: Search for correction methods. Remote Sens. 2011, 3, 2207–2221. [Google Scholar] [CrossRef]
- Lichti, D.D. Spectral filtering and classification of terrestrial laser scanner point clouds. Photogramm. Rec. 2005, 20, 218–240. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Nevalainen, O.; Hakala, T.; Anttila, K. Incidence angle dependency of leaf vegetation indices from hyperspectral lidar measurements. Photogramm. Fernerkund. Geoinform. 2016, 2016, 75–84. [Google Scholar] [CrossRef]
- Höfle, B. Radiometric correction of terrestrial lidar point cloud data for individual maize plant detection. IEEE Geosci. Remote Sens. Lett. 2014, 11, 94–98. [Google Scholar] [CrossRef]
- Sanchez, R.; Hall, A.; Trapani, N.; De Hunau, R.C. Effects of water stress on the chlorophyll content, nitrogen level and photosynthesis of leaves of two maize genotypes. Photosynth. Res. 1983, 4, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Wulder, M.A.; Dymond, C.C.; White, J.C.; Leckie, D.G.; Carroll, A.L. Surveying mountain pine beetle damage of forests: A review of remote sensing opportunities. For. Ecol. Manag. 2006, 221, 27–41. [Google Scholar] [CrossRef]
- Skakun, R.S.; Wulder, M.A.; Franklin, S.E. Sensitivity of the thematic mapper enhanced wetness difference index to detect mountain pine beetle red-attack damage. Remote Sens. Environ. 2003, 86, 433–443. [Google Scholar] [CrossRef]
- Wermelinger, B. Ecology and management of the spruce bark beetle ips typographus—A review of recent research. For. Ecol. Manag. 2004, 202, 67–82. [Google Scholar] [CrossRef]
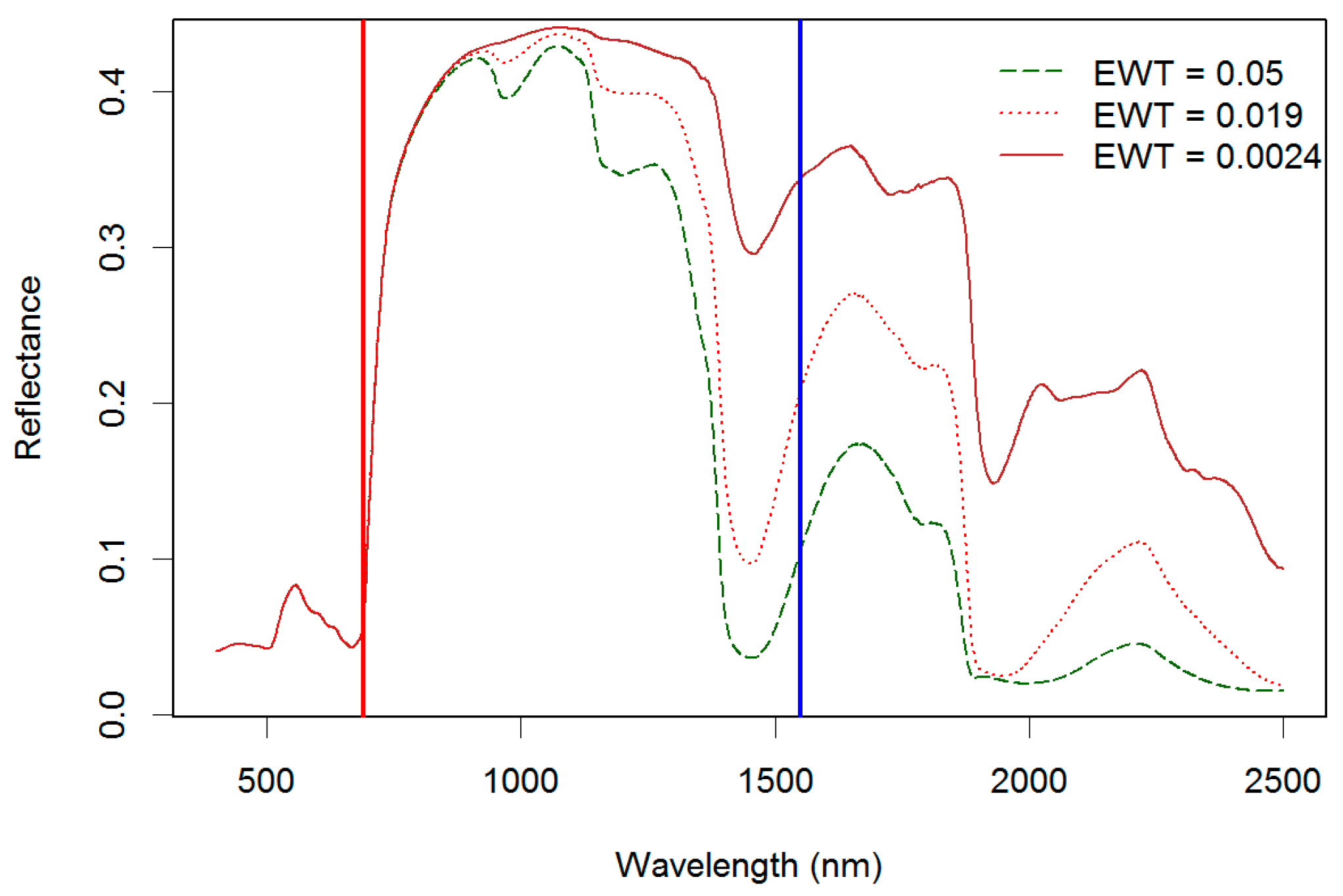
- Ceccato, P.; Flasse, S.; Tarantola, S.; Jacquemoud, S.; Grégoire, J.-M. Detecting vegetation leaf water content using reflectance in the optical domain. Remote Sens. Environ. 2001, 77, 22–33. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, T.; Darvishzadeh, R.; Skidmore, A.K.; Niemann, K.O. 3d leaf water content mapping using terrestrial laser scanner backscatter intensity with radiometric correction. ISPRS J. Photogramm. Remote Sens. 2015, 110, 14–23. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, T.; Skidmore, A.K.; Darvishzadeh, R.; Niemann, K.O.; Liu, J. Canopy leaf water content estimated using terrestrial lidar. Agric. For. Meteorol. 2017, 232, 152–162. [Google Scholar] [CrossRef]
- Gaulton, R.; Danson, F.; Ramirez, F.; Gunawan, O. The potential of dual-wavelength laser scanning for estimating vegetation moisture content. Remote Sens. Environ. 2013, 132, 32–39. [Google Scholar] [CrossRef]
- Junttila, S.; Kaasalainen, S.; Vastaranta, M.; Hakala, T.; Nevalainen, O.; Holopainen, M. Investigating bi-temporal hyperspectral lidar measurements from declined trees—Experiences from laboratory test. Remote Sens. 2015, 7, 13863–13877. [Google Scholar] [CrossRef]
- Eitel, J.U.; Magney, T.S.; Vierling, L.A.; Dittmar, G. Assessment of crop foliar nitrogen using a novel dual-wavelength laser system and implications for conducting laser-based plant physiology. ISPRS J. Photogramm. Remote Sens. 2014, 97, 229–240. [Google Scholar] [CrossRef]
- Danson, F.M.; Gaulton, R.; Armitage, R.P.; Disney, M.; Gunawan, O.; Lewis, P.; Pearson, G.; Ramirez, A.F. Developing a dual-wavelength full-waveform terrestrial laser scanner to characterize forest canopy structure. Agric. For. Meteorol. 2014, 198, 7–14. [Google Scholar] [CrossRef]
- Nevalainen, O.; Hakala, T.; Suomalainen, J.; Mäkipää, R.; Peltoniemi, M.; Krooks, A.; Kaasalainen, S. Fast and nondestructive method for leaf level chlorophyll estimation using hyperspectral lidar. Agric. For. Meteorol. 2014, 198, 250–258. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. Prospect-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Cajander, A.K. Theory of forest types. Acta For. Fenn. 1926, 29, 1–108. [Google Scholar]
- Warren, C.; Ethier, G.; Livingston, N.; Grant, N.; Turpin, D.; Harrison, D.; Black, T. Transfer conductance in second growth Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco) canopies. Plant Cell Environ. 2003, 26, 1215–1227. [Google Scholar] [CrossRef]
- Easlon, H.M.; Bloom, A.J. Easy leaf area: Automated digital image analysis for rapid and accurate measurement of leaf area. Appl. Plant Sci. 2014, 2. [Google Scholar] [CrossRef] [PubMed]
- Danson, F.; Steven, M.; Malthus, T.; Clark, J. High-spectral resolution data for determining leaf water content. Int. J. Remote Sens. 1992, 13, 461–470. [Google Scholar] [CrossRef]
- Kaasalainen, S.; Kukko, A.; Lindroos, T.; Litkey, P.; Kaartinen, H.; Hyyppa, J.; Ahokas, E. Brightness measurements and calibration with airborne and terrestrial laser scanners. IEEE Trans. Geosci. Remote Sens. 2008, 46, 528–534. [Google Scholar] [CrossRef]
- Hoffman, R.; Jain, A.K. Segmentation and classification of range images. IEEE Trans. Pattern Anal. Mach. Intell. 1987, PAMI-9, 608–620. [Google Scholar] [CrossRef]
- Fairbairn, M.B. Planetary photometry: The lommel-seeliger law. J. R. Astron. Soc. Can. 2005, 99, 92–93. [Google Scholar]
- Poullain, E.; Garestier, F.; Bretel, P.; Levoy, F. Modeling of ALS intensity behavior as a function of incidence angle for coastal zone surface study. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 2849–2852.
- Beckmann, P.; Spizzichino, A. The Scattering of Electromagnetic Waves from Rough Surfaces; Artech Print on Demand: Norwood, MA, USA, 1987. [Google Scholar]
- Smith, R.J. Use and misuse of the reduced major axis for line-fitting. Am. J. Phys. Anthropol. 2009, 140, 476–486. [Google Scholar] [CrossRef] [PubMed]
- Team, R.C. R: A Language and Environment for Statistical Computing; Foundation for Statistical Computing; Erste Bank AG: Vienna, Austria, 2013. [Google Scholar]
- Cui, Z.-W.; Xu, S.-Y.; Sun, D.-W. Effect of microwave-vacuum drying on the carotenoids retention of carrot slices and chlorophyll retention of chinese chive leaves. Dry. Technol. 2004, 22, 563–575. [Google Scholar] [CrossRef]
- Vicré, M.; Sherwin, H.; Driouich, A.; Jaffer, M.; Farrant, J. Cell wall characteristics and structure of hydrated and dry leaves of the resurrection plant craterostigma wilmsii, a microscopical study. J. Plant Physiol. 1999, 155, 719–726. [Google Scholar] [CrossRef]
- Alberte, R.S.; Thornber, J.P.; Fiscus, E.L. Water stress effects on the content and organization of chlorophyll in mesophyll and bundle sheath chloroplasts of maize. Plant Physiol. 1977, 59, 351–353. [Google Scholar] [CrossRef] [PubMed]
- Zahedi, H.; Alahrnadi, S.J. Effects of drought stress on chlorophyll fluorescence parameters, chlorophyll content and grain yield of wheat cultivars. J. Biol. Sci. 2007, 7, 841–847. [Google Scholar]
- Chasmer, L.; Hopkinson, C.; Smith, B.; Treitz, P. Examining the influence of changing laser pulse repetition frequencies on conifer forest canopy returns. Photogramm. Eng. Remote Sens. 2006, 72, 1359–1367. [Google Scholar] [CrossRef]
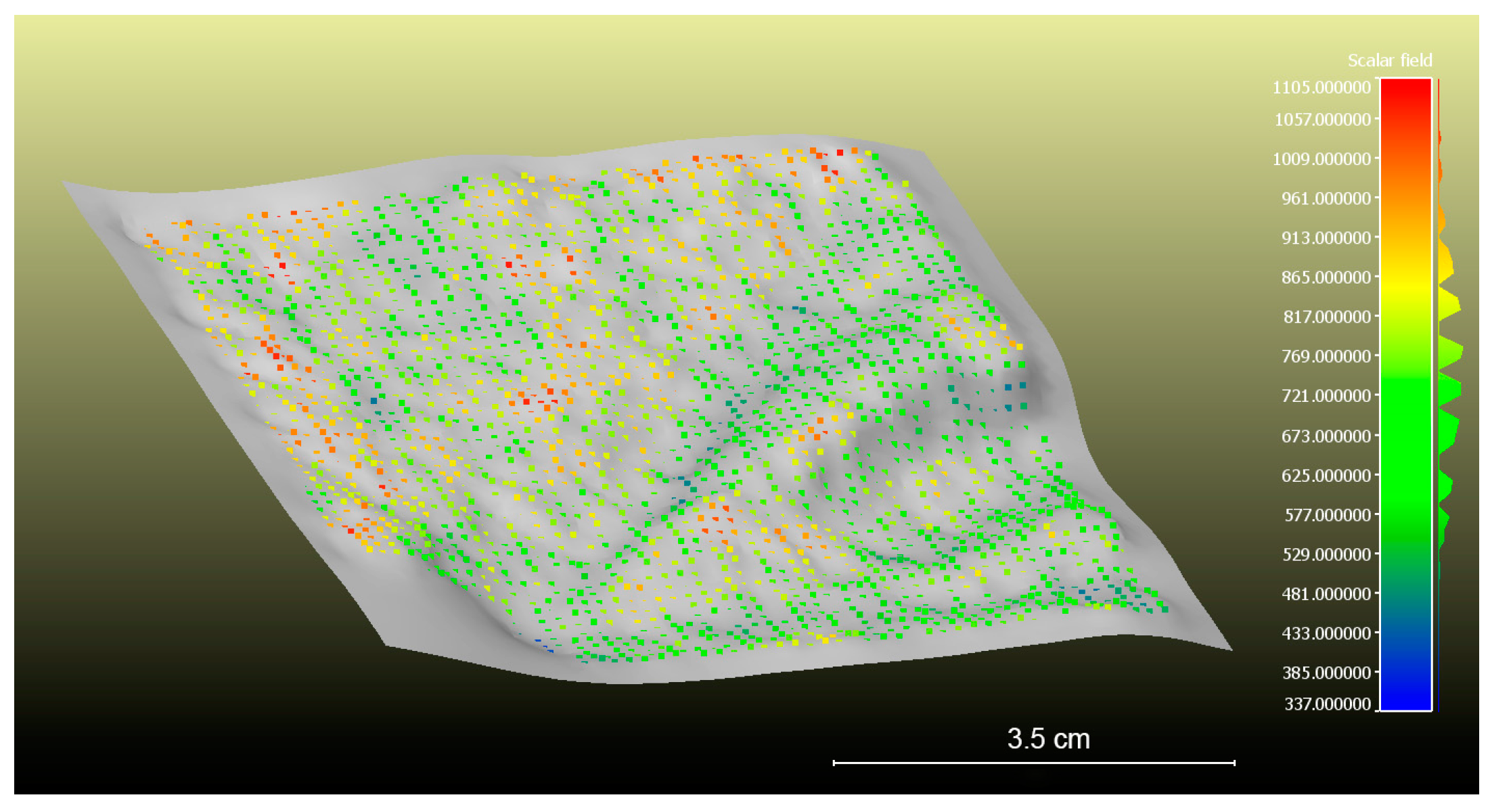
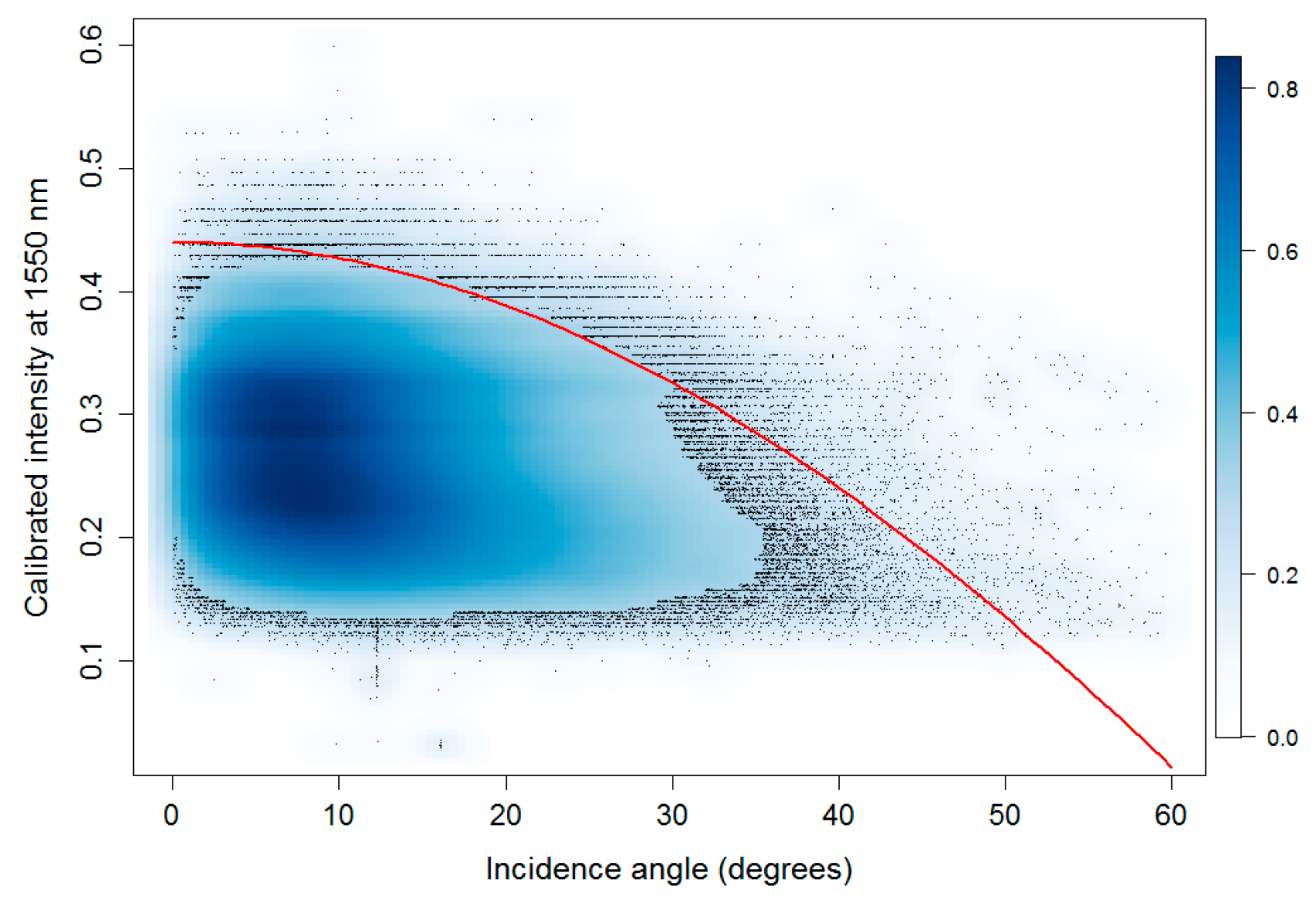
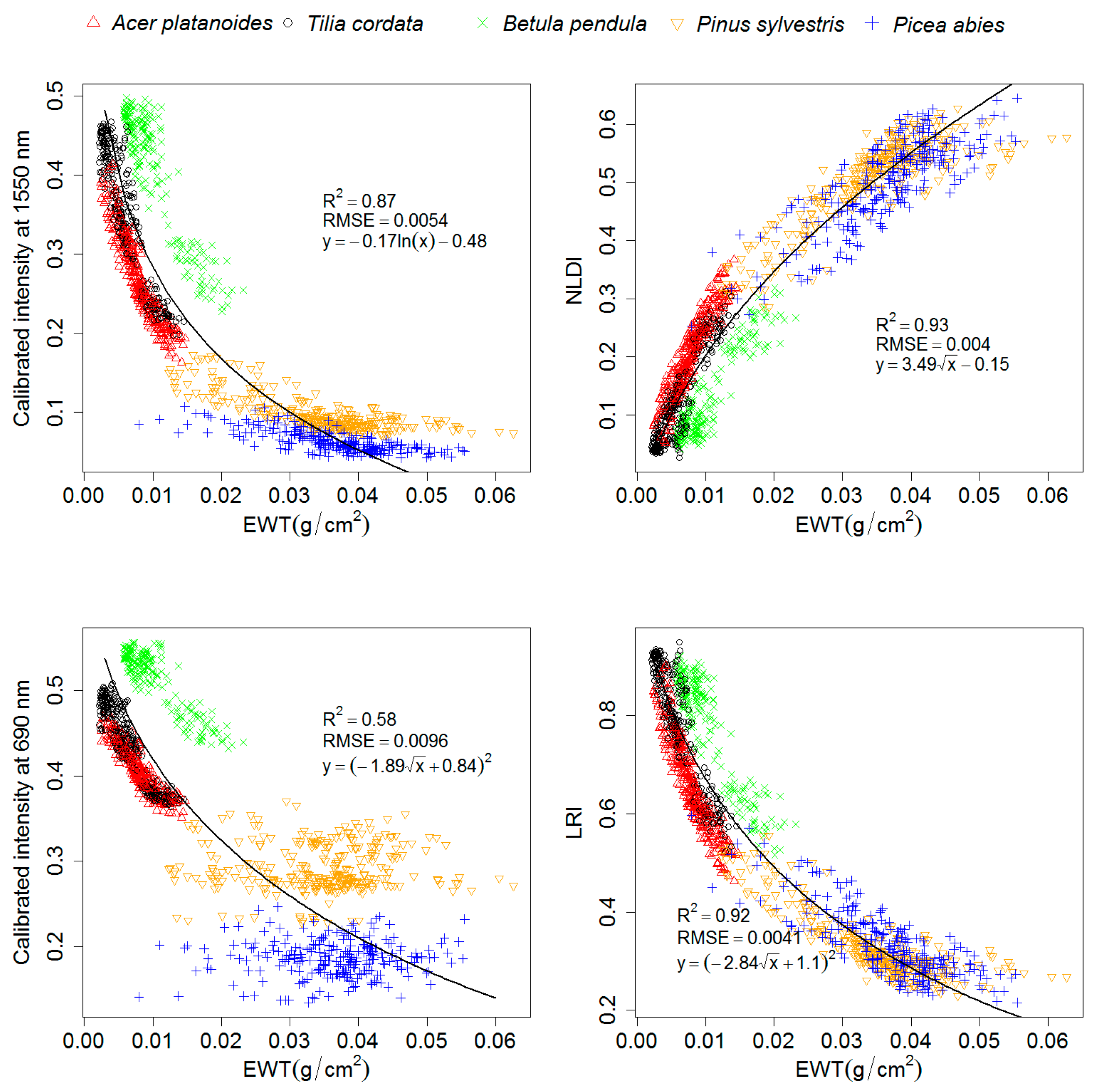
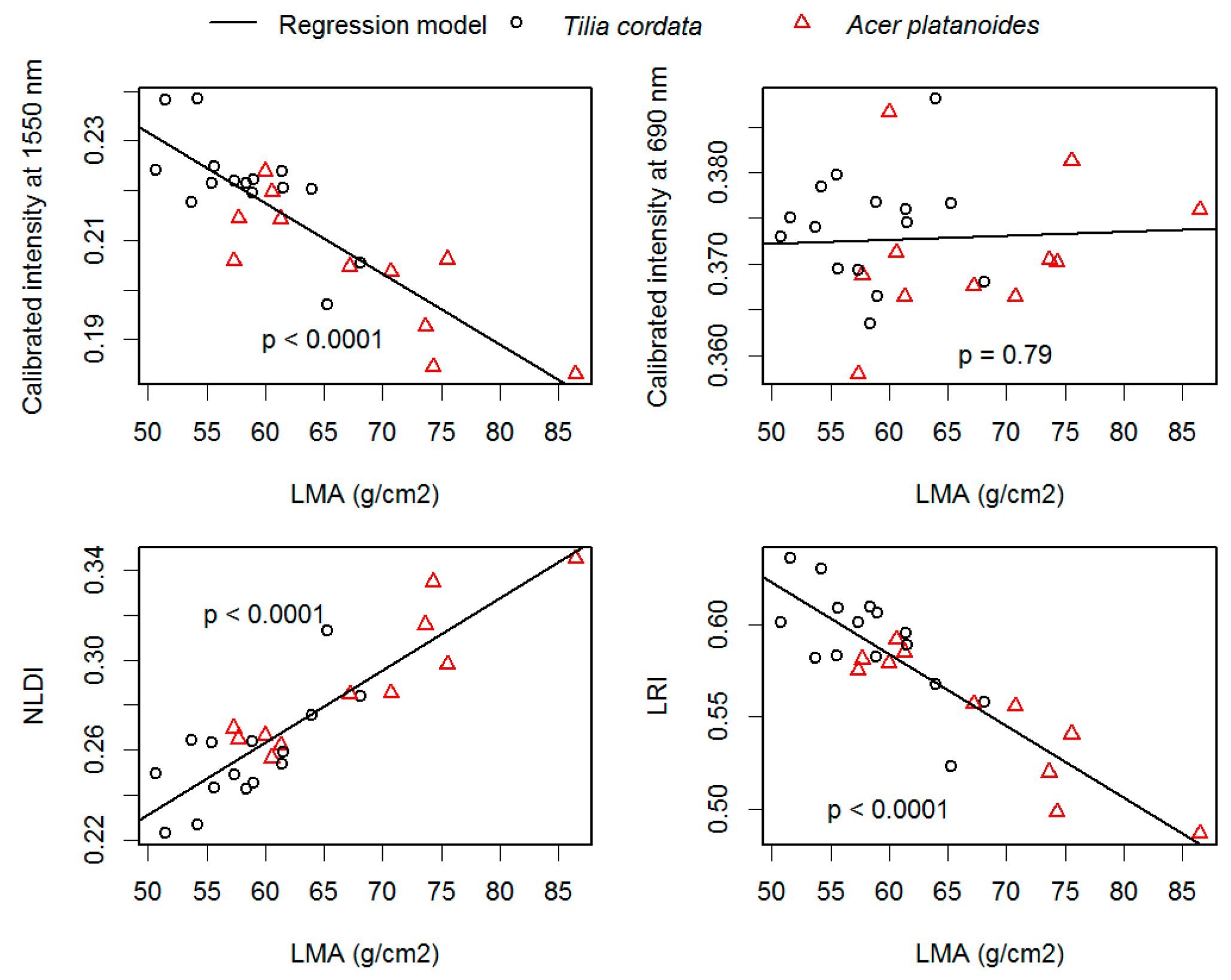
| Species Name | Measurements | EWT | Standard Deviation of EWT (g/cm2) | ||
| Mean EWT (g/cm2) | Min EWT (g/cm2) | Max EWT (g/cm2) | |||
| Tilia cordata L. | 248 | 0.0062 | 0.0021 | 0.0145 | 0.0084 |
| Betula pendula L. | 140 | 0.0117 | 0.0058 | 0.0232 | 0.0045 |
| Acer platanoides L. | 298 | 0.0082 | 0.0024 | 0.0147 | 0.0028 |
| Picea abies L. | 242 | 0.0364 | 0.0079 | 0.0552 | 0.0083 |
| Pinus sylvestris L. | 252 | 0.0329 | 0.0123 | 0.0527 | 0.0084 |
| Species Name | Measurements | LMA | Standard Deviation of LMA (g/m2) | ||
| Mean LMA (g/m2) | Min LMA (g/m2) | Max LMA (g/m2) | |||
| Tilia cordata L. | 248 | 58.9 | 50.7 | 70.8 | 5.1 |
| Betula pendula L. | 140 | 94.1 | 87.9 | 101.8 | 4.4 |
| Acer platanoides L. | 298 | 72.7 | 57.7 | 88.3 | 9.1 |
| Picea abies L. | 242 | 502.7 | 434.8 | 589.2 | 49.7 |
| Pinus sylvestris L. | 252 | 248.2 | 212.1 | 325.6 | 31.8 |
| Scanner Type | Beam Divergence (mrad) | Beam Diameter at Exit (mm) | Wavelength (nm) | Output Power (mW) | Scan Rate (kHz) | Intensity Recording (DN) | Ranging Error (mm) |
|---|---|---|---|---|---|---|---|
| FARO X330 | 0.19 | 2.25 | 1550 | 500 | 488 | −2048 to 2033 | ±2 |
| Leica HDS6100 | 0.22 | 3 | 690 | 30 | 508 | −1228 to 2048 | ±2 |
| Model for Correcting the Incidence Angle | ||||
| Species | FARO X330 | Leica HDS6100 | ||
| b | b | |||
| Tilia cordata L. | 1.78 | 0.82 | ||
| Betula pendula L. | 2.3 | 0.71 | ||
| Acer platanoides L. | 1.74 | 0.75 | ||
| Picea abies L. | 0.58 | 0.25 | ||
| Pinus sylvestris L. | 0.82 | 0.82 | ||
| Model for Simulating Backscatter Intensity | ||||
| Species | FARO X330 | Leica HDS6100 | ||
| kd | m | kd | m | |
| Tilia cordata L. | 0.60 | 0.49 | 0.7 | 0.59 |
| Betula pendula L. | 0.45 | 0.45 | 0.78 | 0.58 |
| Acer platanoides L. | 0.49 | 0.55 | 0.91 | 0.55 |
| Picea abies L. | 0.95 | 0.58 | 0.99 | 0.6 |
| Pinus sylvestris L. | 0.99 | 0.58 | 0.99 | 0.6 |
| Calibrated Intensity | |||||
| Species/Wavelength or Spectral Index | 1550 nm | 690 nm | NLDI | LRI | |
| Tilia cordata | R2 | 0.84 | 0.83 | 0.85 | 0.86 |
| RMSE | 0.0012 | 0.0013 | 0.0012 | 0.0011 | |
| Betula pendula | R2 | 0.86 | 0.82 | 0.86 | 0.86 |
| RMSE | 0.0017 | 0.0019 | 0.0017 | 0.0017 | |
| Acer platanoides | R2 | 0.87 | 0.83 | 0.86 | 0.86 |
| RMSE | 0.0010 | 0.0011 | 0.0010 | 0.0010 | |
| Picea abies | R2 | 0.48 | 0.01 | 0.61 | 0.56 |
| RMSE | 0.0059 | 0.011 | 0.0051 | 0.0054 | |
| Pinus sylvestris | R2 | 0.53 | 0.01 | 0.69 | 0.67 |
| RMSE | 0.0051 | 0.012 | 0.0051 | 0.0052 | |
| All species | R2 | 0.87 a | 0.58 b | 0.93 c | 0.92 b |
| RMSE | 0.0054 | 0.0096 | 0.004 | 0.0042 | |
| Incidence Angle Corrected Calibrated Intensity | |||||
| Tilia cordata | R2 | 0.80 | 0.82 | 0.82 | 0.84 |
| RMSE | 0.0014 | 0.0013 | 0.0013 | 0.0012 | |
| Betula pendula | R2 | 0.82 | 0.79 | 0.83 | 0.84 |
| RMSE | 0.0018 | 0.0019 | 0.0018 | 0.0017 | |
| Acer platanoides | R2 | 0.84 | 0.77 | 0.85 | 0.85 |
| RMSE | 0.0011 | 0.0013 | 0.0011 | 0.0011 | |
| Picea abies | R2 | 0.51 | 0.01 | 0.64 | 0.59 |
| RMSE | 0.0058 | 0.011 | 0.0050 | 0.0053 | |
| Pinus sylvestris | R2 | 0.54 | 0.01 | 0.69 | 0.68 |
| RMSE | 0.0062 | 0.012 | 0.0050 | 0.0052 | |
| All species | R2 | 0.86 a | 0.53 b | 0.92 c | 0.91 b |
| RMSE | 0.0055 | 0.01 | 0.0043 | 0.0046 | |
| Calibrated Intensity after Incidence Angle Correction and Removal of Specular Fraction of Backscatter Intensity | |||||
| All species | R2 | 0.69 | 0.12 b | 0.45 c | 0.36 b |
| RMSE | 0.0083 | 0.016 | 0.012 | 0.011 | |
| EWT (g/cm2) | 1550 nm | 690 nm | NLDI | LRI | Number of Samples |
|---|---|---|---|---|---|
| 0.011–0.013 | −0.85 | 0.05 | 0.89 | −0.88 | 26 |
| 0.013–0.015 | −0.87 | −0.50 | 0.88 | −0.89 | 12 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Junttila, S.; Vastaranta, M.; Liang, X.; Kaartinen, H.; Kukko, A.; Kaasalainen, S.; Holopainen, M.; Hyyppä, H.; Hyyppä, J. Measuring Leaf Water Content with Dual-Wavelength Intensity Data from Terrestrial Laser Scanners. Remote Sens. 2017, 9, 8. https://doi.org/10.3390/rs9010008
Junttila S, Vastaranta M, Liang X, Kaartinen H, Kukko A, Kaasalainen S, Holopainen M, Hyyppä H, Hyyppä J. Measuring Leaf Water Content with Dual-Wavelength Intensity Data from Terrestrial Laser Scanners. Remote Sensing. 2017; 9(1):8. https://doi.org/10.3390/rs9010008
Chicago/Turabian StyleJunttila, Samuli, Mikko Vastaranta, Xinlian Liang, Harri Kaartinen, Antero Kukko, Sanna Kaasalainen, Markus Holopainen, Hannu Hyyppä, and Juha Hyyppä. 2017. "Measuring Leaf Water Content with Dual-Wavelength Intensity Data from Terrestrial Laser Scanners" Remote Sensing 9, no. 1: 8. https://doi.org/10.3390/rs9010008
APA StyleJunttila, S., Vastaranta, M., Liang, X., Kaartinen, H., Kukko, A., Kaasalainen, S., Holopainen, M., Hyyppä, H., & Hyyppä, J. (2017). Measuring Leaf Water Content with Dual-Wavelength Intensity Data from Terrestrial Laser Scanners. Remote Sensing, 9(1), 8. https://doi.org/10.3390/rs9010008