Characteristics of Decomposition Powers of L-Band Multi-Polarimetric SAR in Assessing Tree Growth of Industrial Plantation Forests in the Tropics
Abstract
:1. Introduction
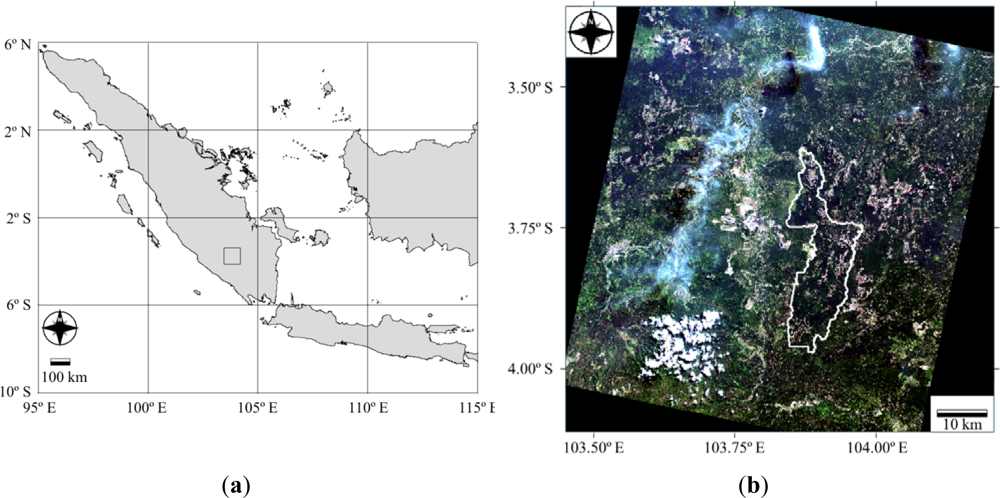
2. Study Area
3. Data Sets
3.1. Field Measured Forest Biometric Data
3.2. Satellite Data Sets
4. Analysis Methodology
4.1. Forest Biometric Parameters
4.2. Satellite Remote Sensing Data
4.2.1. Covariance and Coherency Matrix
4.2.2 Pre-Processing of the PALSAR Data
4.2.3. Rotation of Coherency Matrix
4.2.4. Decomposition of Covariance and Rotated Covariance Matrices
4.3. Correlation Analysis between Forest Biometric Parameters and Decomposition Powers
5. Data Analysis Results
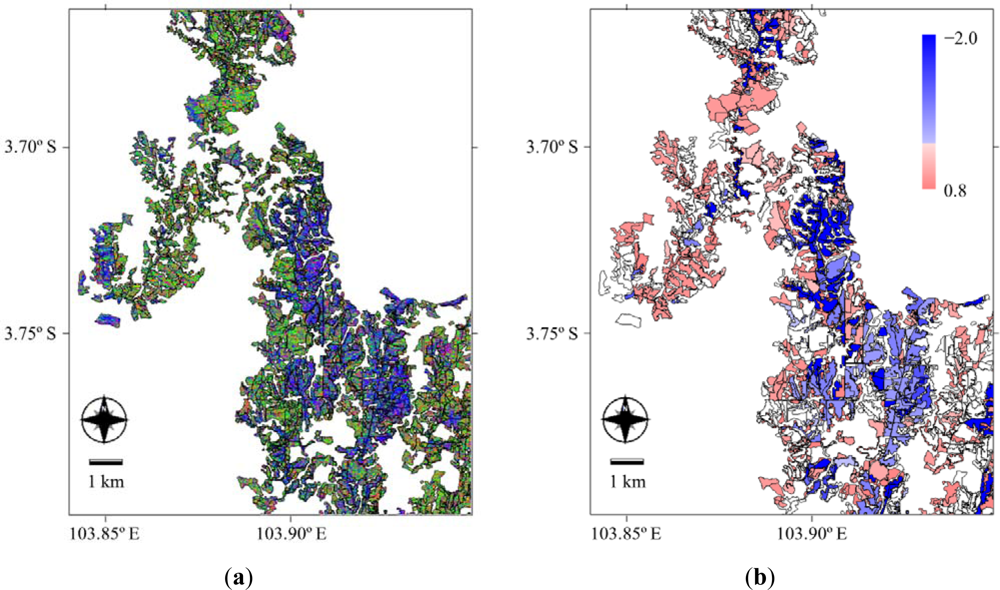
5.1. Visual Interpretation of Decomposition SAR Image
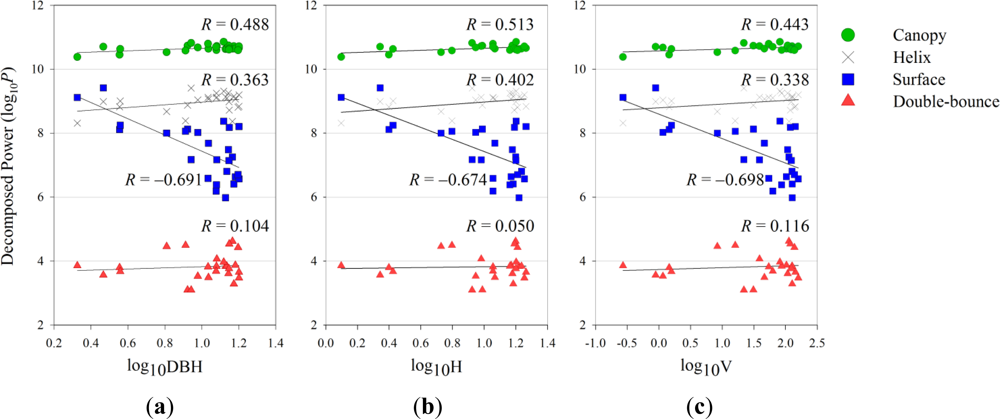
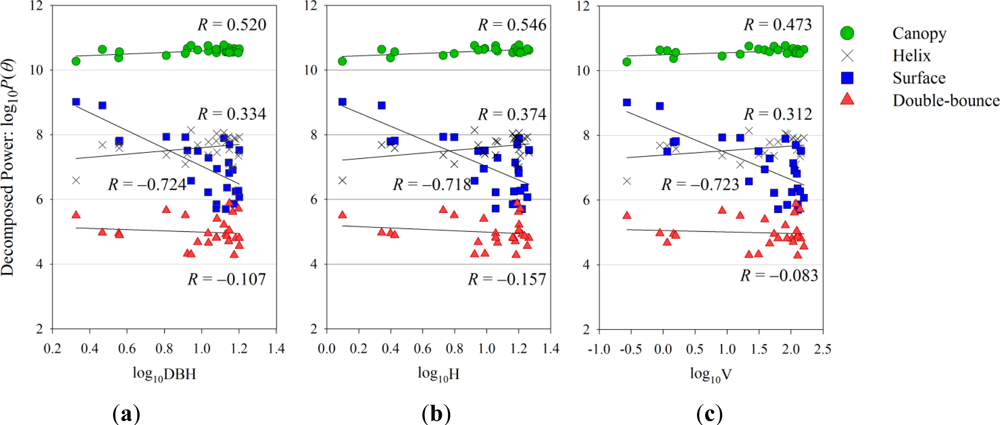
5.2. Forest Biometric Parameters and Decomposition Powers
5.3. Forest Stand Volume Estimation using Decomposition Powers
6. Discussion
6.1. Differences among Decomposition Powers
6.2. Physical Understanding of Scattering Characteristics
6.3. Possibility of Estimating the Forest Stand Volume
6.4. Uncertainties in the Relationship between the Decomposition Powers and Forest Structural Parameters
7. Concluding Remarks
Acknowledgments
References and Notes
- Garestier, F.; Dubois-Fernandez, P.C.; Guyon, D.; Le Toan, T. Forest biophysical parameter estimation using L-and P-band polarimetric SAR data. IEEE Trans. Geosci. Remote Sens 2009, 47, 3379–3388. [Google Scholar]
- Gama, F.F.; Dos Santos, J.R.; Mura, J.C. Eucalyptus biomass and volume estimation using interferometric and polarimetric SAR data. Remote Sens 2010, 2, 939–956. [Google Scholar]
- Lonnqvist, A.; Rauste, Y.; Molinier, M.; Hame, T. Polarimetric SAR data in land cover mapping in boreal zone. IEEE Trans. Geosci. Remote Sens 2010, 48, 3652–3662. [Google Scholar]
- Goncalves, F.; Santos, J.; Treuhaft, R. Stem volume of tropical forests from polarimetric radar. Int. J. Remote Sens 2011, 32, 503–522. [Google Scholar]
- He, Q.S.; Cao, C.X.; Chen, E.X.; Sun, G.Q.; Ling, F.L.; Pang, Y.; Zhang, H.; Ni, W.J.; Xu, M.; Li, Z.Y. Forest stand biomass estimation using ALOS PALSAR data based on LiDAR-derived prior knowledge in the Qilian Mountain, Western China. Int. J. Remote Sens 2012, 33, 710–729. [Google Scholar]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, J.E.S. Assessing performance of L- and P-band polarimetric interferometric SAR data in estimating boreal forest above-ground biomass. IEEE Trans. Geosci. Remote Sens 2012, 50, 714–726. [Google Scholar]
- Paradzayi, C.; Annegarn, H.J. Estimating potential woody biomass in communal savanna woodlands from synthetic aperture radar (SAR). Int. J. Appl. Geospat. Res 2012, 3, 53–62. [Google Scholar]
- Santoro, M.; Fransson, J.E.S.; Eriksson, L.E.B.; Magnusson, M.; Ulander, L.M.H.; Olsson, H. Signatures of ALOS PALSAR L-band backscatter in Swedish forest. IEEE Trans. Geosci. Remote Sens 2009, 47, 4001–4019. [Google Scholar]
- Clewley, D.; Lucas, R.; Accad, A.; Armston, J.; Bowen, M.; Dwyer, J.; Pollock, S.; Bunting, P.; McAlpine, C.; Eyre, T.; et al. An approach to mapping forest growth stages in Queensland, Australia through integration of ALOS PALSAR and Landsat sensor data. Remote Sens 2012, 4, 2236–2255. [Google Scholar]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens 1998, 36, 963–973. [Google Scholar]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens 1997, 35, 68–78. [Google Scholar]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens 2005, 43, 1699–1706. [Google Scholar]
- Yamaguchi, Y.; Sato, A.; Boerner, W.M.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens 2011, 49, 2251–2258. [Google Scholar]
- Cui, Y.; Yamaguchi, Y.; Yang, J.; Park, S.-E.; Kobayashi, H.; Singh, G. Three-component power decomposition for polarimetric SAR data based on adaptive volume scatter modeling. Remote Sens 2012, 4, 1559–1572. [Google Scholar]
- Sugimoto, M.; Ouchi, K.; Nakamura, Y. Four-component scattering power decomposition algorithm with rotation of covariance matrix using ALOS-PALSAR polarimetric data. Remote Sens 2012, 4, 2199–2209. [Google Scholar]
- Richards, J.A. Remote Sensing with Imaging Radar. Signals and Communication Technology Series; Springer-Verlag; Berlin/Heidelberg, Germany, 2009. Available online: http://www.springer.com/engineering/electronics/book/978-3-642-02019-3 (accessed on 3 September 2012).
- Austin, J.M.; Mackey, B.G.; Van Niel, K.P. Estimating forest biomass using satellite radar: An exploratory study in a temperate Australian Eucalyptus forest. For. Ecol. Manag 2003, 176, 575–583. [Google Scholar]
- Hoekman, D.H.; Quiriones, M. Land cover type and biomass classification using AirSAR data for evaluation of monitoring scenarios in the Colombian Amazon. IEEE Trans. Geosci. Remote Sens 2000, 38, 685–696. [Google Scholar]
- Balzter, H.; Baker, J.R.; Hallikainen, M.; Tomppo, E. Retrieval of timber volume and snow water equivalent over a Finnish boreal forest from airborne polarimetric synthetic aperture radar. Int. J. Remote Sens 2002, 23, 3185–3208. [Google Scholar]
- Rowland, C.S.; Balzter, H.; Dawson, T.P.; Luckman, A.; Patenaude, G.; Skinner, L. Airborne SAR monitoring of tree growth in a coniferous plantation. Int. J. Remote Sens 2008, 29, 3873–3889. [Google Scholar] [Green Version]
- Macelloni, G.; Paloscia, S.; Pampaloni, P.; Marliani, F.; Gai, M. The relationship between the backscattering coefficient and the biomass of narrow and broad leaf crops. IEEE Trans. Geosci. Remote Sens 2001, 39, 873–884. [Google Scholar]
- Kobayashi, S.; Widyorini, R.; Kawai, S.; Omura, Y.; Sanga-Ngoie, K.; Supriadi, B. Backscattering characteristics of L-band polarimetric and optical satellite imagery over planted acacia forests in Sumatra, Indonesia. J. Appl. Remote Sens 2012, 6, 063525. [Google Scholar]
- Kawai, S.; Widyorini, R. Sustainable Forest Management and Regional Environment in South-East Asia. Proceedings of the Second International Conference of Kyoto University Global COE Program in Search of Sustainable Humanosphere in Asia and Africa, Kyoto, Japan, 12–14 March 2008.
- Gunawan, R.; Wahyono, R. Faktor Bentuk (Form Factor) Acacia Mangium (in Indonesian); Technical Note of Research and Development Division; PT Musi Hutan Persada: South Sumatera, Indonesia, 2004; pp. 1–3. [Google Scholar]
- Yamaguchi, Y. Radar Polarimetry from Basic to Applications: Radar Remote Sensing Using Polarimetric Information (in Japanese); The Institute of Electrtonics, information and Communication Engineers Press: Tokyo, Japan, 2007; pp. 80–100. [Google Scholar]
- Lee, J.S.; Pottier, E. Polarimetric SAR Speckle Filtering. In Polarimetric Radar Imaging: from Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009; pp. 143–178. [Google Scholar]
- McNeill, S.; Pairman, D. Stand age retrieval in production forest stands in New Zealand using C-and L-band polarimetric radar. IEEE Trans. Geosci. Remote Sens 2005, 43, 2503–2515. [Google Scholar]



| (a) | (b) | |||||
|---|---|---|---|---|---|---|
| Decomposition Power | log10DBH | log10H | log10V | log10DBH | log10H | log10V |
| Surface | −0.691 | −0.674 | −0.698 | −0.724 | −0.718 | −0.723 |
| Double-bounce | 0.104 | 0.050 | 0.116 | −0.107 | −0.157 | −0.083 |
| Canopy | 0.488 | 0.513 | 0.443 | 0.520 | 0.546 | 0.473 |
| Helix | 0.363 | 0.402 | 0.338 | 0.334 | 0.374 | 0.312 |
| log10DBH | log10H | log10V | ||||
|---|---|---|---|---|---|---|
| Decomposition power | R | P-value | R | P-value | R | P-value |
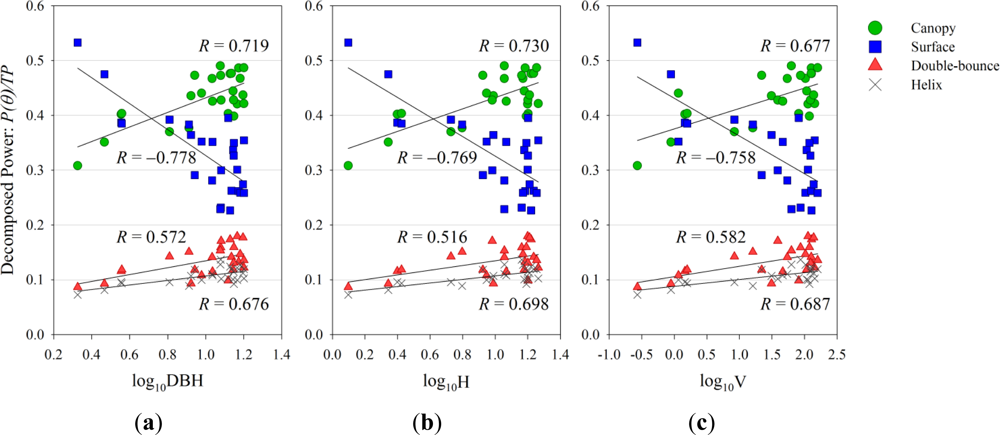
| Surface | −0.778 | <0.001 | −0.769 | <0.001 | −0.758 | <0.001 |
| Double-bounce | 0.572 | 0.002 | 0.516 | 0.007 | 0.582 | 0.002 |
| Canopy | 0.719 | <0.001 | 0.730 | <0.001 | 0.677 | <0.001 |
| Helix | 0.676 | <0.001 | 0.698 | <0.001 | 0.687 | <0.001 |
| R2 = 0.557, Standard Error of Estimate = 0.563 | |||||
|---|---|---|---|---|---|
| DF | SS | MS | F | P-value | |
| Regression | 1 | 9.552 | 9.552 | 30.164 | <0.001 |
| Residual | 24 | 7.600 | 0.317 | ||
| Total | 25 | 17.152 | 0.686 | ||
Share and Cite
Kobayashi, S.; Omura, Y.; Sanga-Ngoie, K.; Widyorini, R.; Kawai, S.; Supriadi, B.; Yamaguchi, Y. Characteristics of Decomposition Powers of L-Band Multi-Polarimetric SAR in Assessing Tree Growth of Industrial Plantation Forests in the Tropics. Remote Sens. 2012, 4, 3058-3077. https://doi.org/10.3390/rs4103058
Kobayashi S, Omura Y, Sanga-Ngoie K, Widyorini R, Kawai S, Supriadi B, Yamaguchi Y. Characteristics of Decomposition Powers of L-Band Multi-Polarimetric SAR in Assessing Tree Growth of Industrial Plantation Forests in the Tropics. Remote Sensing. 2012; 4(10):3058-3077. https://doi.org/10.3390/rs4103058
Chicago/Turabian StyleKobayashi, Shoko, Yoshiharu Omura, Kazadi Sanga-Ngoie, Ragil Widyorini, Shuichi Kawai, Bambang Supriadi, and Yoshio Yamaguchi. 2012. "Characteristics of Decomposition Powers of L-Band Multi-Polarimetric SAR in Assessing Tree Growth of Industrial Plantation Forests in the Tropics" Remote Sensing 4, no. 10: 3058-3077. https://doi.org/10.3390/rs4103058
APA StyleKobayashi, S., Omura, Y., Sanga-Ngoie, K., Widyorini, R., Kawai, S., Supriadi, B., & Yamaguchi, Y. (2012). Characteristics of Decomposition Powers of L-Band Multi-Polarimetric SAR in Assessing Tree Growth of Industrial Plantation Forests in the Tropics. Remote Sensing, 4(10), 3058-3077. https://doi.org/10.3390/rs4103058




