Mapping of Ice Motion in Antarctica Using Synthetic-Aperture Radar Data
Abstract
:1. Introduction
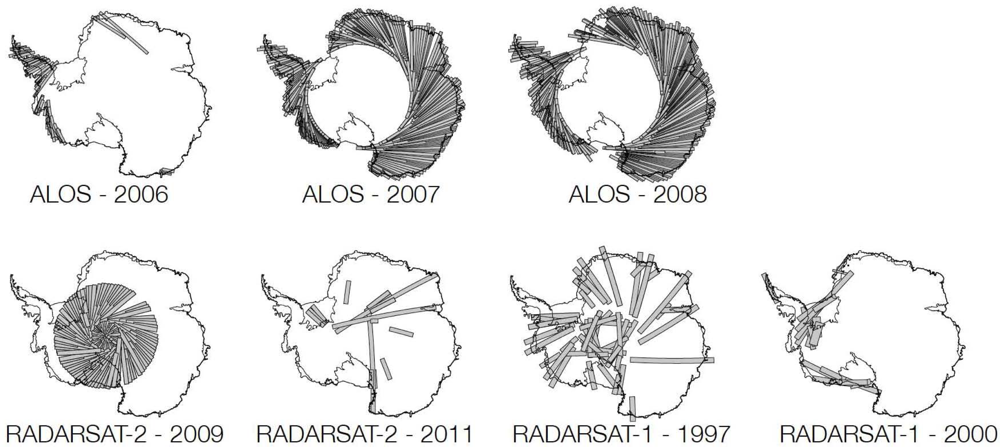
2. Data
3. Methods
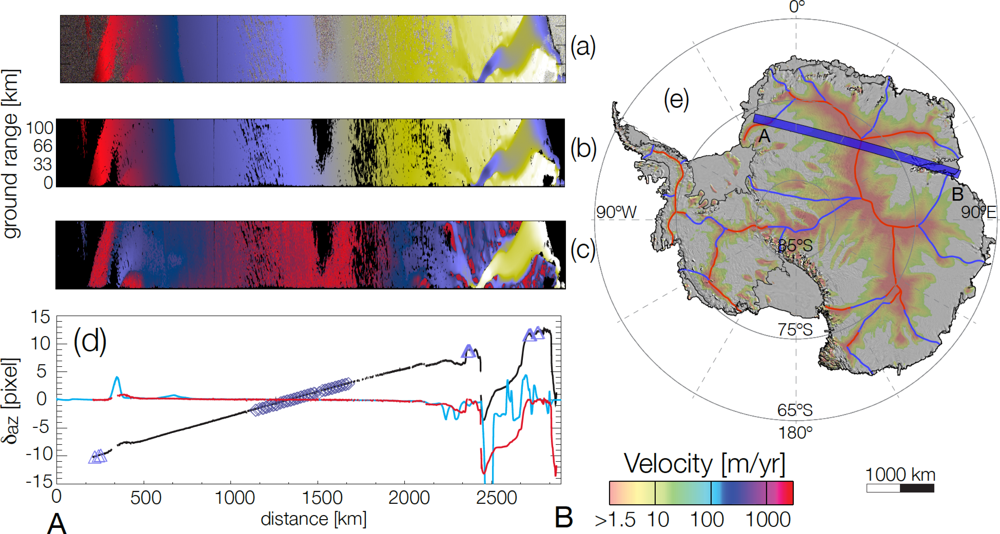
3.1. Speckle Tracking
3.2. Calibration
3.3. Combining Speckle Tracking and Interferometric Phase
3.4. Gap Filling with Historic Data
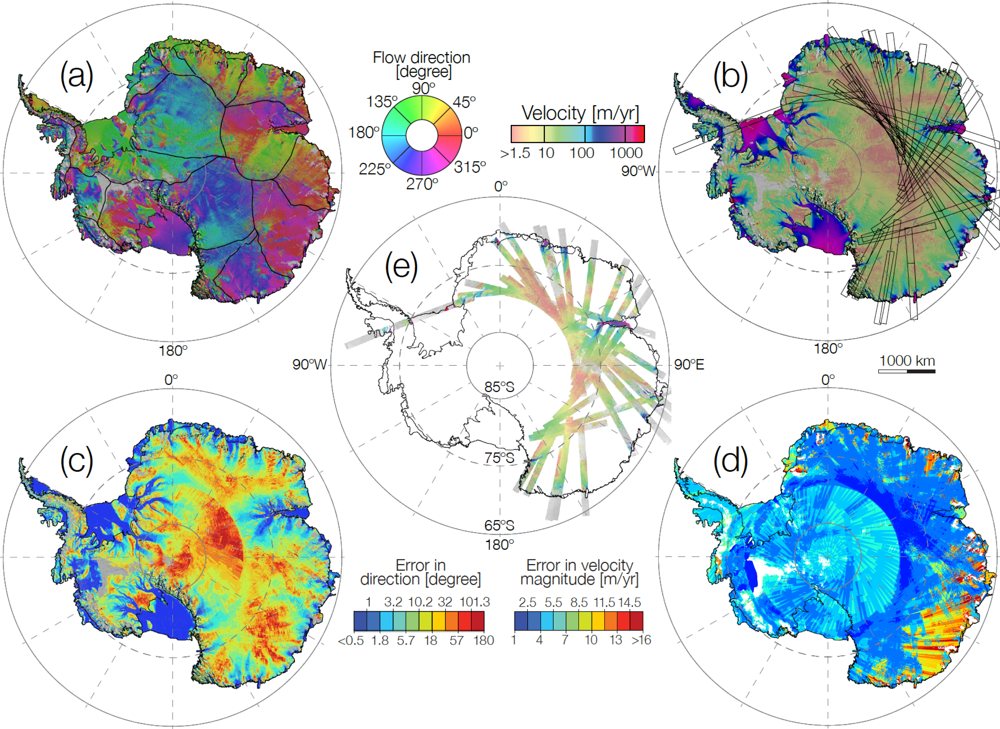
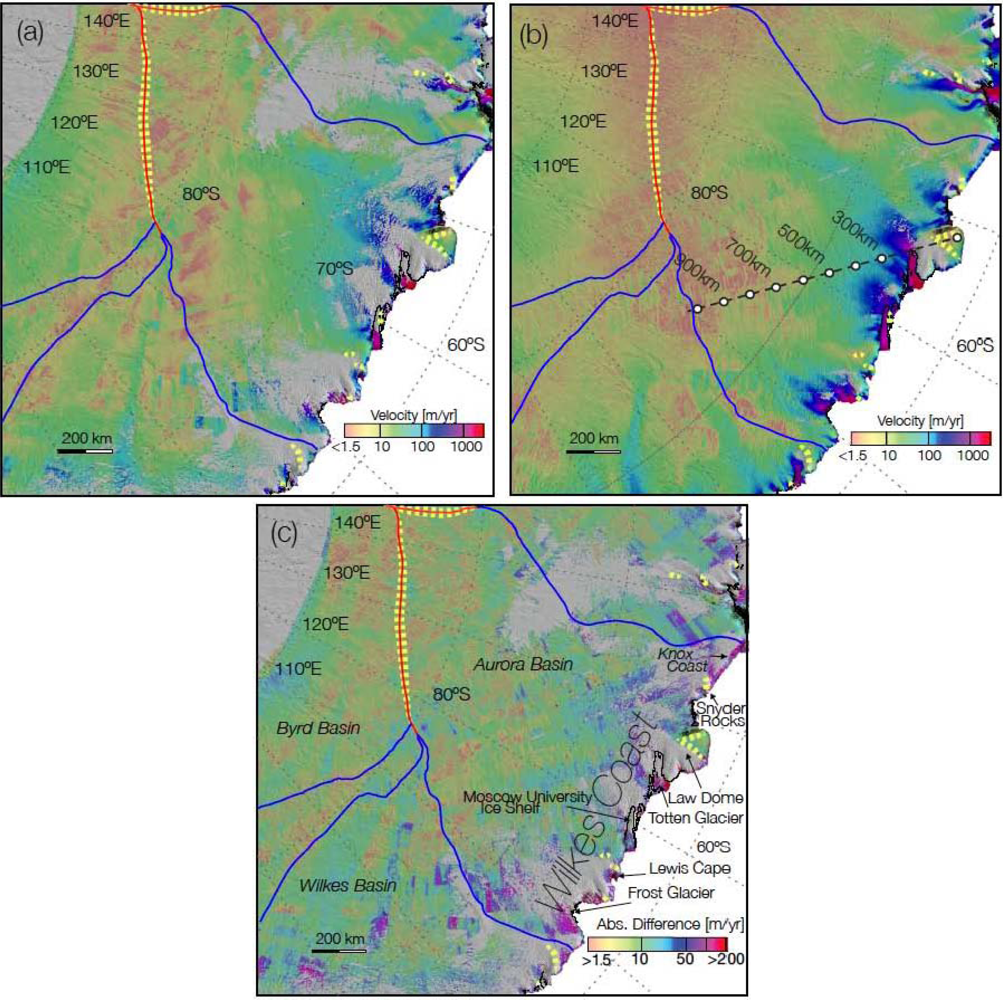
4. Results
4.1. Error Analysis
4.2. Validation
5. Discussion
6. Conclusions
Acknowledgments
References
- Rignot, E.; Bamber, J.L.; van den Broeke, M.R.; Davis, C.; Li, Y.; van de Berg, W.J.; van Meijgaard, E. Recent Antarctic ice mass loss from radar interferometry and regional climate modelling. Nat. Geosci 2008, 1, 106–110. [Google Scholar]
- Rignot, E.; Velicogna, I.; van den Broeke, M.R.; Monaghan, A.; Lenaerts, J. Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett, 2011. [Google Scholar] [CrossRef]
- Joughin, I.; Smith, B.E.; Abdalati, W. Glaciological advances made with interferometric synthetic aperture radar. J. Glaciol 2011, 56, 1026–1042. [Google Scholar]
- Rignot, E. Radar interferometry detection of hinge-line migration on Rutford Ice Stream and Carlson Inlet, Antarctica. Ann. Glaciol 1998, 27, 25–32. [Google Scholar]
- Jezek, K.C. Glaciological properties of the Antarctic ice sheet from RADARSAT-1 synthetic aperture radar imagery. Ann. Glaciol 1999, 29, 286–290. [Google Scholar]
- Jezek, K.C.; Farness, K.; Carande, R.; Wu, X.; Labelle-Hamer, N. RADARSAT 1 synthetic aperture radar observations of Antarctica: Modified Antarctic mapping mission, 2000. Radio Sci, 2003. [Google Scholar] [CrossRef]
- Michel, R.; Rignot, E. Flow of Glaciar Moreno, Argentina, from repeat-pass Shuttle Imaging Radar images: Comparison of the phase correlation method with radar interferometry. J. Glaciol 1999, 45, 93–100. [Google Scholar]
- Rosen, P.A.; Henley, S.; Peltzer, G.; Simons, M. Update repeat orbit interferometry package released. EOS Trans. AGU 2004, 85, 47. [Google Scholar]
- Bamber, J.L.; Gomez-Dans, J.L.; Griggs, J.A. A new 1 km digital elevation model of the Antarctic derived from combined satellite radar and laser data—Part 1: Data and methods. Cryosphere 2009, 3, 101–111. [Google Scholar]
- Gray, A.L.; Mattar, K.E.; Sofko, G. Influence of ionospheric electron density fluctuations on satellite radar interferometry. Geophys. Res. Lett, 2000. [Google Scholar] [CrossRef]
- Meyer, F.; Bamler, R.; Jakowski, N.; Fritz, T. The potential of low-frequency SAR systems for mapping ionospheric TEC distributions. IEEE Geosci. Remote Sens. Lett 2006, 3, 560–564. [Google Scholar]
- Bamber, J.L.; Vaughan, D.G.; Joughin, I. Widespread complex flow in the interior of the antarctic ice sheet. Science 2000, 287, 1248–1250. [Google Scholar]
- Rignot, E.; Mouginot, J.; Scheuchl, B. Ice flow of the Antarctic ice sheet. Science 2011, 333, 1427–1430. [Google Scholar]
- Haran, T.; Bohlander, J.; Scambos, T.; Painter, T.; Fahnestock, M. MODIS Mosaic of Antarctica (MOA) Image Map; National Snow and Ice Data Center Digital Media: Boulder, CO, USA, 2006. [Google Scholar]
- Joughin, I.R.; Kwok, R.; Fahnestock, M.A. Interferometric estimation of three-dimensional ice-flow using ascending and descending passes. IEEE Trans. Geosci. Remote Sens 1998, 36, 25–37. [Google Scholar]
- Hoen, W.E.; Zebker, H. Penetration depths inferred from interferometric volume decorrelation observed over the Greenland Ice Sheet. IEEE Trans. Geosci. Remote Sens 2000, 38, 2571–2583. [Google Scholar]
- Rignot, E.; Echelmeyer, K.; Krabill, W. Penetration depth of interferometric synthetic-aperture radar signals in snow and ice. Geophys. Res. Lett 2001, 28, 3501–3504. [Google Scholar]
- Joughin, I. Ice-sheet velocity mapping: A combined interferometric and speckle-tracking approach. Ann. Glaciol 2002, 34, 195–201. [Google Scholar]
- Griggs, J.A.; Bamber, J.L. A new 1 km digital elevation model of Antarctica derived from combined radar and laser data—Part 2: Validation and error estimates. Cryosphere 2009, 3, 113–123. [Google Scholar]
- Rignot, E.; Mouginot, J.; Scheuchl, B. Antarctic grounding line mapping from differential satellite radar interferometry. Geophys. Res. Lett, 2011. [Google Scholar] [CrossRef]
- Rignot, E.; Mouginot, J.; Scheuchl, B. MEaSUREs InSAR-Based Antarctica Velocity Map; NASA EOSDIS DAAC at NSIDC: Boulder, CO, USA, 2011. [Google Scholar]

| Platform | Look Dir. | Mode | Repeat Cycle [day] | Incidence Angle [degree] | Spacing Rg×Az [m] | Swath [km] | Frequency [GHz] | # of tracks | Raw data volume [Tbyte] | Season Year |
|---|---|---|---|---|---|---|---|---|---|---|
| ERS-1 & -2 | Right | IS2 | 1 | 23 | 13×4 | 100 | 5.3 | 60 | 0.5 | Spring 1996 |
| RADARSAT-1 | Left | S2–S7 | 24 | 28–47 1 | 12×5–17×6 1 | 100 | 5.3 | 72 | 0.5 | Fall 1997 |
| Right | various | 24 | 18–38 1 | 7×5–12×5 1 | 50–100 1 | 5.3 | 84 | 0.5 | Fall 2000 | |
| ENVISAT | Right | IS2 | 35 | 23 | 13×5 | 100 | 5.331 | 115/130/210 2 | 1/1/2 2 | Summer 2007/2008/2009 |
| RADARSAT-2 | Left | S5-EH4 | 24 | 41–57 1 | 12×5–12×5 1 | 100 | 5.405 | 135/14 2 | 4/1 2 | Spring 2009/2011 |
| ALOS/PALSAR | Right | FBS | 46 | 39 | 7×4 | 70 | 1.27 | 64/204/296 2 | 2/6/9 2 | Fall 2006/2007/2008 |
| Track Length [km] | Velocity [m/yr] | Speed Error Flux at the GL [%] | Error [Gt/yr] |
|---|---|---|---|
| 1,000 | 1.8 | >0.1 | >0.1 |
| 900 | 6.4 | 0.3 | 0.2 |
| 800 | 4.3 | 0.2 | 0.2 |
| 700 | 4.3 | 0.3 | 0.2 |
| 600 | 7.1 | 0.5 | 0.4 |
| 500 | 22.4 | 1.8 | 1.4 |
| 400 | 43.9 | 4.5 | 3.3 |
| 300 | 65.8 | 9.0 | 6.7 |
Share and Cite
Mouginot, J.; Scheuchl, B.; Rignot, E. Mapping of Ice Motion in Antarctica Using Synthetic-Aperture Radar Data. Remote Sens. 2012, 4, 2753-2767. https://doi.org/10.3390/rs4092753
Mouginot J, Scheuchl B, Rignot E. Mapping of Ice Motion in Antarctica Using Synthetic-Aperture Radar Data. Remote Sensing. 2012; 4(9):2753-2767. https://doi.org/10.3390/rs4092753
Chicago/Turabian StyleMouginot, Jeremie, Bernd Scheuchl, and Eric Rignot. 2012. "Mapping of Ice Motion in Antarctica Using Synthetic-Aperture Radar Data" Remote Sensing 4, no. 9: 2753-2767. https://doi.org/10.3390/rs4092753
APA StyleMouginot, J., Scheuchl, B., & Rignot, E. (2012). Mapping of Ice Motion in Antarctica Using Synthetic-Aperture Radar Data. Remote Sensing, 4(9), 2753-2767. https://doi.org/10.3390/rs4092753





