Long-Term (2015–2024) Daily PM2.5 Estimation in China by Using XGBoost Combining Empirical Orthogonal Function Decomposition
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Datasets
2.2.1. PM2.5 Station Data
2.2.2. AOD Data
2.2.3. Meteorological Fields
2.2.4. Additional Data
2.2.5. Data Reprocessing
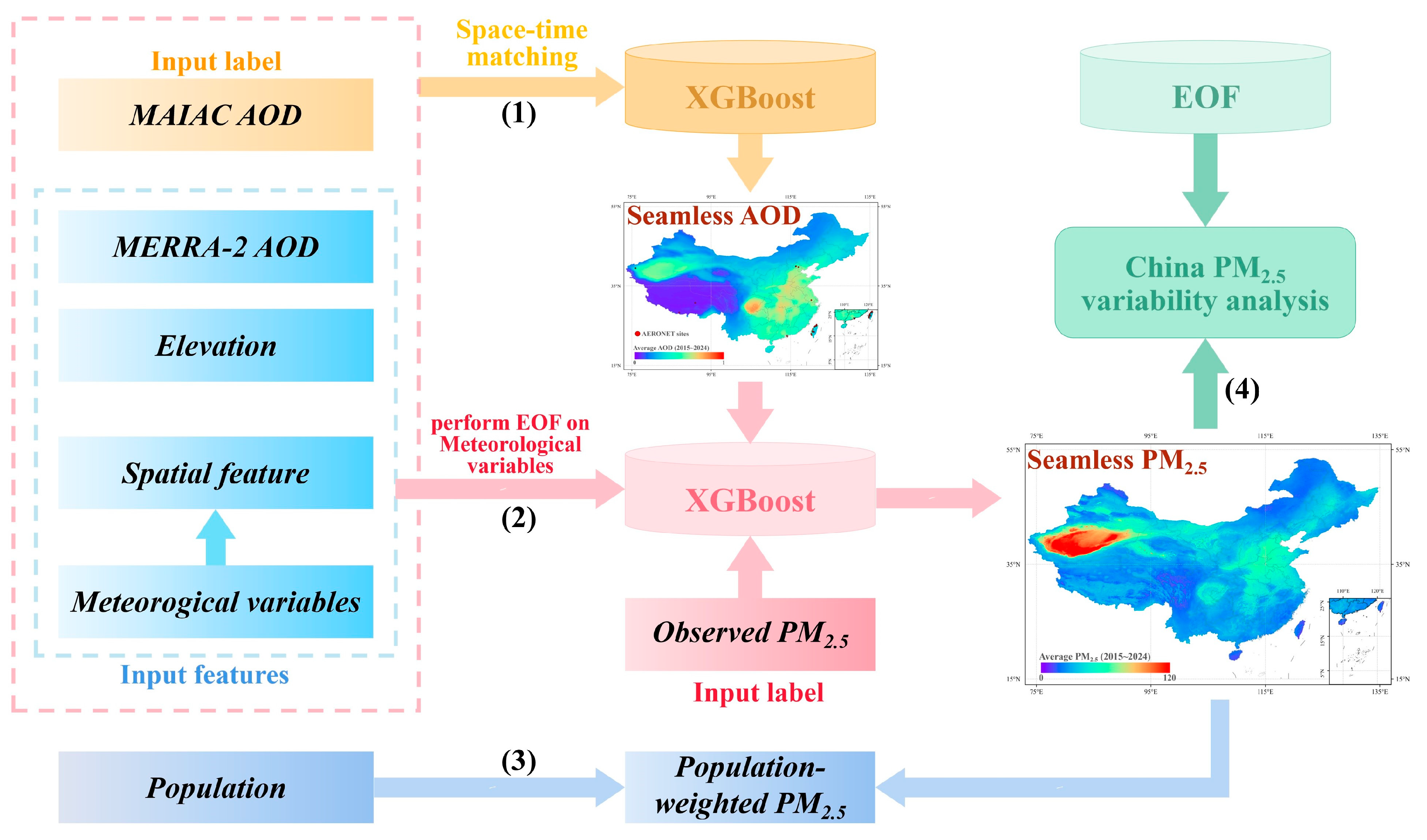
2.3. Methodology
2.3.1. AOD Reconstruction Model
2.3.2. PM2.5 Estimation Model
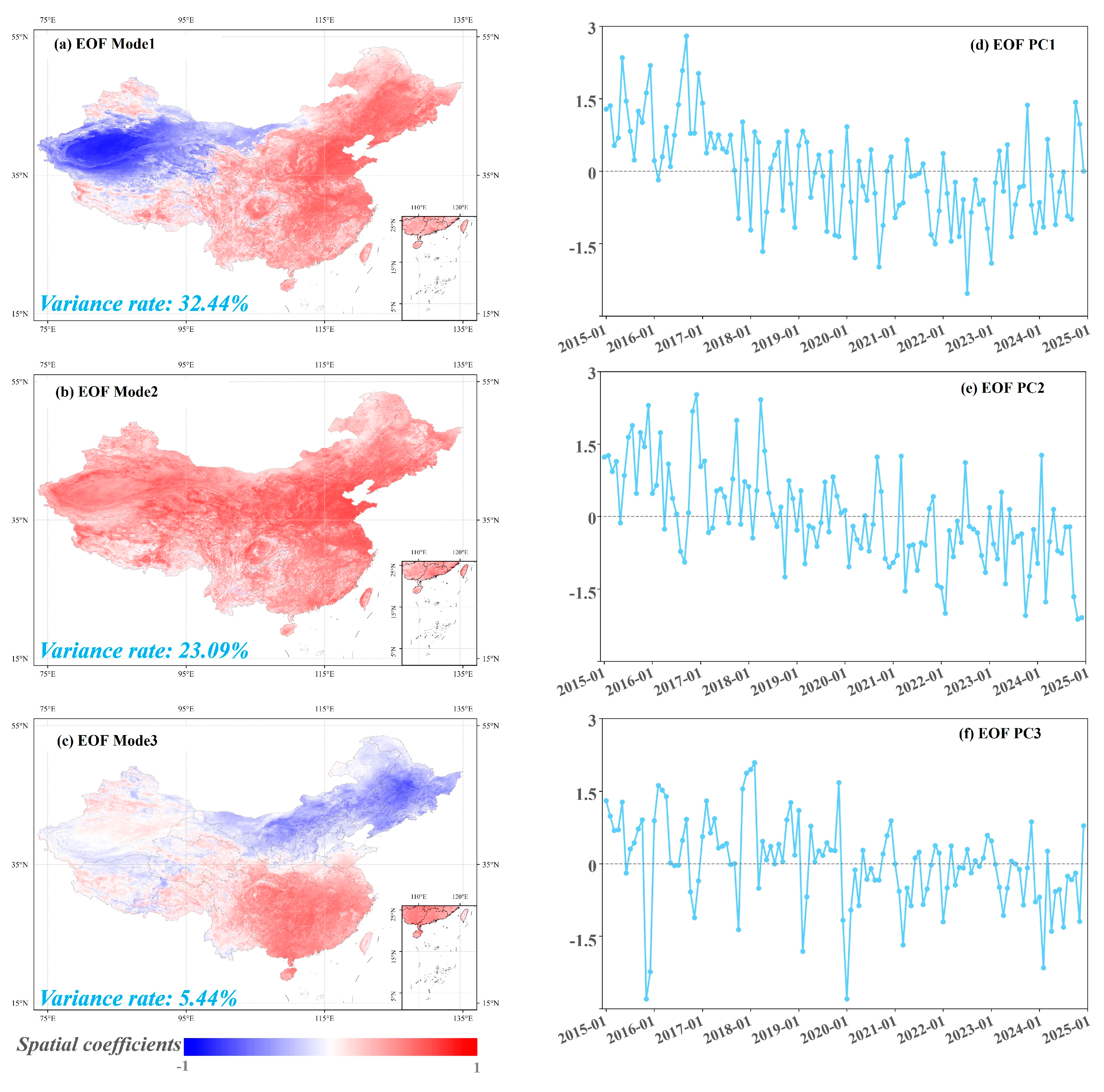
2.3.3. Empirical Orthogonal Function Analysis
2.3.4. Population-Weighted PM2.5 Calculation
2.3.5. Model Performance Evaluation
3. Results
3.1. AOD Reconstruction
3.2. PM2.5 Estimation
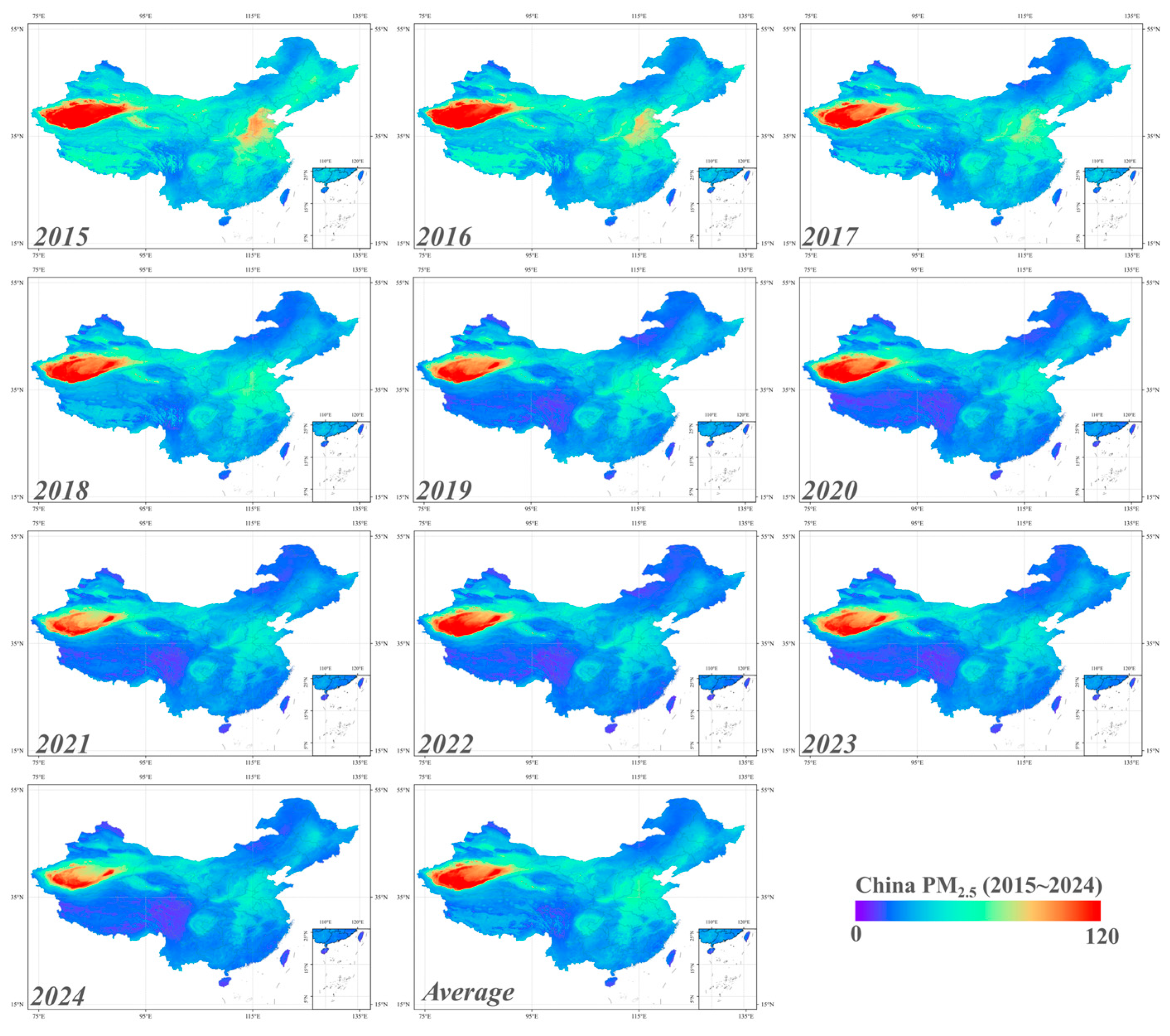
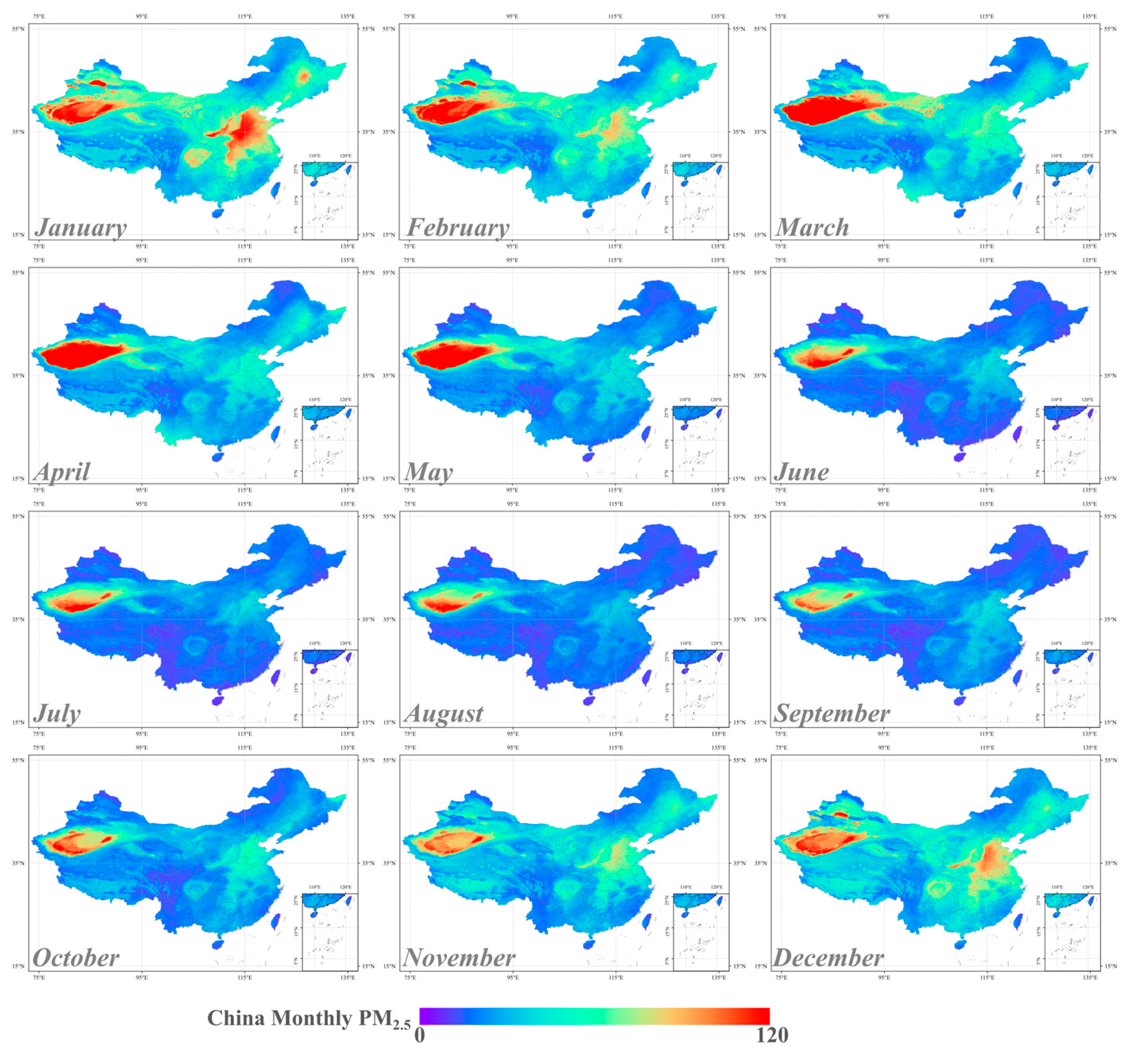
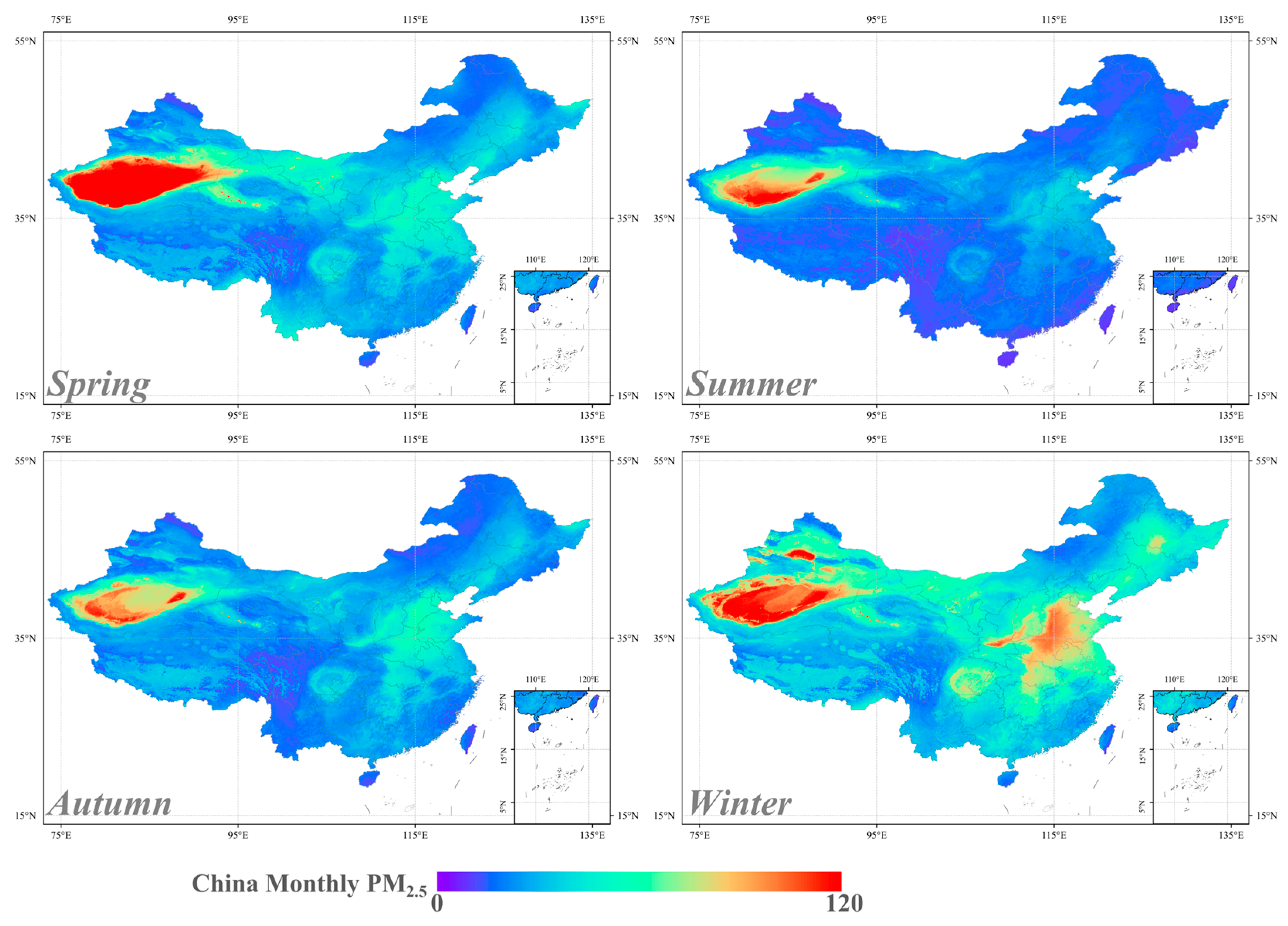
3.3. Spatio-Temporal Distribution of China PM2.5
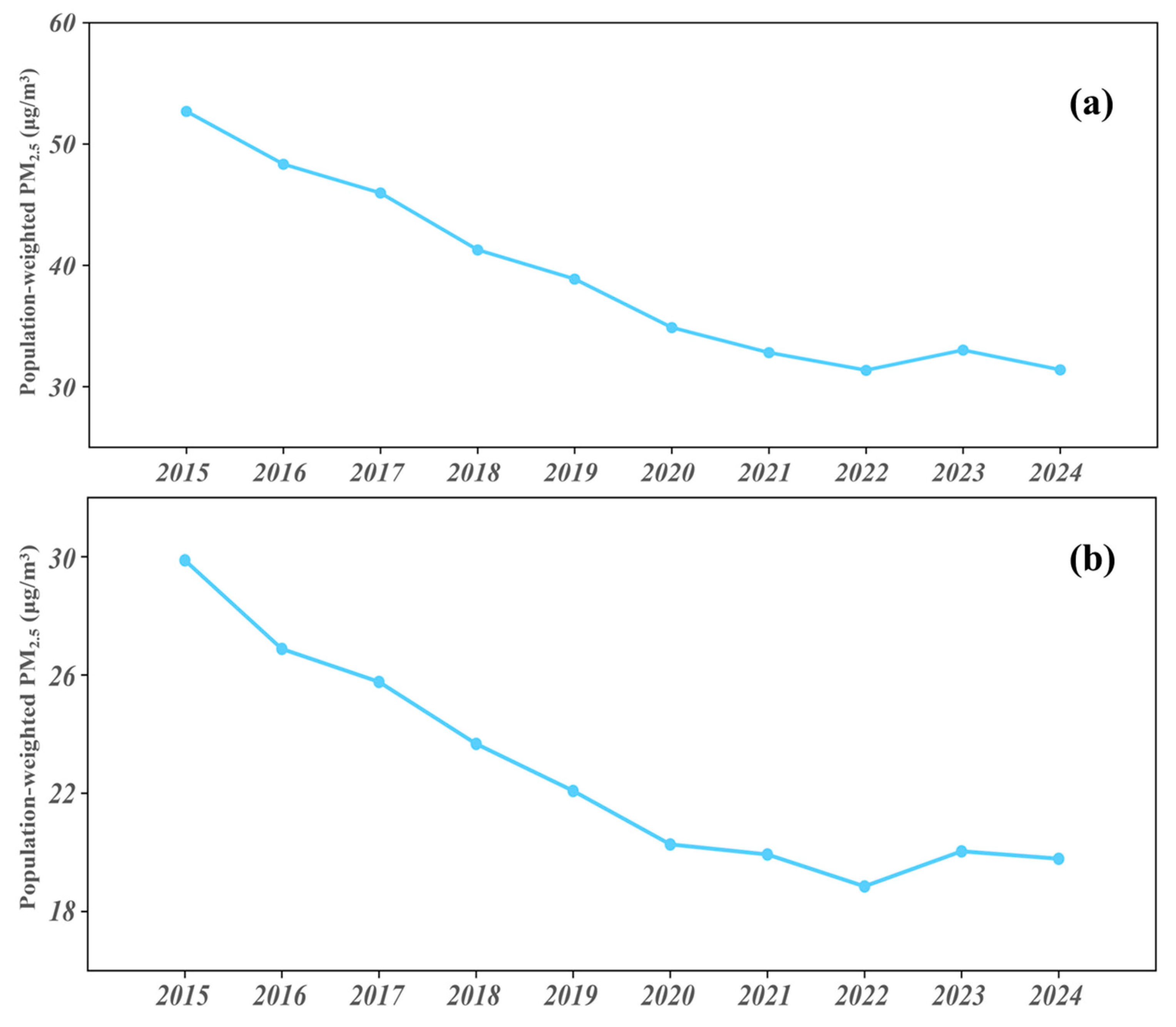
3.4. Population-Weighted PM2.5 Concentration Trends
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AERONET | Aerosol Robotic Network |
| AOD | Aerosol Optical Depth |
| CI | Confidence Interval |
| CNEMC | China National Environmental Monitoring Centre |
| COVID-19 | Coronavirus disease, the disease caused by the SARS-CoV-2 coronavirus |
| CV | Cross validation |
| DEM | Digital Elevation Model |
| EOF | Empirical Orthogonal Function |
| ERA5 | European Centre for Medium-Range Weather Forecasts (ECWMF) Reanalysis v5 |
| GIS | Geographic Information Systems |
| MAIAC | Multi-Angle Implementation of Atmospheric Correction |
| MERRA-2 | Modern-Era Retrospective Analysis for Research and Applications Version 2 |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| NASA | National Aeronautics and Space Administration |
| ORNL | Oak Ridge National Laboratory |
| PC | Principle Component |
| PCA | Principal Component Analysis |
| PM2.5 | Fine particulate matter with aerodynamic diameter less than 2.5 μm |
| R2 | The coefficient of determination |
| RMSE | Root Mean Square Error |
| SRTM | Shuttle Radar Topography Mission |
| SVD | Singular Value Decomposition |
| WHO | World Health Organization |
| WRF-CMAQ | Weather Research and Forecasting-Community Multiscale Air Quality |
| XGBoost | EXtreme Gradient Boosting |
References
- Pui, D.Y.; Chen, S.C.; Zuo, Z. Pm2.5 in China: Measurements, Sources, Visibility and Health Effects, and Mitigation. Particuology 2014, 13, 1–26. [Google Scholar] [CrossRef]
- Geng, G.; Zheng, Y.; Zhang, Q.; Xue, T.; Zhao, H.; Tong, D.; Zheng, B.; Li, M.; Liu, F.; Hong, C.; et al. Drivers of Pm2.5 Air Pollution Deaths in China 2002–2017. Nat. Geosci. 2021, 14, 645–650. [Google Scholar] [CrossRef]
- Song, C.; He, J.; Wu, L.; Jin, T.; Chen, X.; Li, R.; Ren, P.; Zhang, L.; Mao, H. Health Burden Attributable to Ambient Pm2.5 in China. Environ. Pollut. 2017, 223, 575–586. [Google Scholar] [CrossRef]
- Wang, F.; Chen, T.; Chang, Q.; Kao, Y.-W.; Li, J.; Chen, M.; Li, Y.; Shia, B.-C. Respiratory Diseases Are Positively Associated with Pm2.5 Concentrations in Different Areas of Taiwan. PLoS ONE 2021, 16, e0249694. [Google Scholar] [CrossRef] [PubMed]
- Hayes, R.B.; Lim, C.; Zhang, Y.; Cromar, K.; Shao, Y.; Reynolds, H.R.; Silverman, D.T.; Jones, R.R.; Park, Y.; Jerrett, M.; et al. Pm2.5 Air Pollution and Cause-Specific Cardiovascular Disease Mortality. Int. J. Epidemiol. 2020, 49, 25–35. [Google Scholar] [CrossRef]
- State Council of the People’s Republic of China; Central People’s Government of the State Republic of China. Air Pollution Prevention and Control Action Plan; State Council of the People’s Republic of China, Central People’s Government of the State Republic of China: Beijing, China, 2013. [Google Scholar]
- Guo, B.; Wu, H.; Pei, L.; Zhu, X.; Zhang, D.; Wang, Y.; Luo, P. Study on the Spatiotemporal Dynamic of Ground-Level Ozone Concentrations on Multiple Scales across China during the Blue Sky Protection Campaign. Environ. Int. 2022, 170, 107606. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Ahlers, A.L. Blue Sky Fabrication in China: Science-Policy Integration in Air Pollution Regulation Campaigns for Mega-Events. Environ. Sci. Policy 2019, 94, 135–142. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, X. Blue Sky Protection Campaign: Assessing the Role of Digital Technology in Reducing Air Pollution. Systems 2024, 12, 55. [Google Scholar] [CrossRef]
- Yu, Y.; Dai, C.; Wei, Y.; Ren, H.; Zhou, J. Air Pollution Prevention and Control Action Plan Substantially Reduced Pm2.5 Concentration in China. Energy Econ. 2022, 113, 106206. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Zeng, C.; Yuan, Q.; Zhang, L. Point-Surface Fusion of Station Measurements and Satellite Observations for Mapping Pm2.5 Distribution in China: Methods and Assessment. Atmos. Environ. 2017, 152, 477–489. [Google Scholar] [CrossRef]
- Kim, K.Y.; Kim, Y.S.; Roh, Y.M.; Lee, C.M.; Kim, C.N. Spatial Distribution of Particulate Matter (Pm10 and Pm2.5) in Seoul Metropolitan Subway Stations. J. Hazard. Mater. 2008, 154, 440–443. [Google Scholar] [CrossRef] [PubMed]
- Cavaliere, A.; Carotenuto, F.; Di Gennaro, F.; Gioli, B.; Gualtieri, G.; Martelli, F.; Matese, A.; Toscano, P.; Vagnoli, C.; Zaldei, A. Development of Low-Cost Air Quality Stations for Next Generation Monitoring Networks: Calibration and Validation of Pm2.5 and Pm10 Sensors. Sensors 2018, 18, 2843. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Belle, J.H.; Meng, X.; Wildani, A.; Waller, L.A.; Strickland, M.J.; Liu, Y. Estimating Pm2.5 Concentrations in the Conterminous United States Using the Random Forest Approach. Environ. Sci. Technol. 2017, 51, 6936–6944. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Jia, H.; Huang, J.; Zhang, Y. A Satellite-Based Geographically Weighted Regression Model for Regional Pm2.5 Estimation over the Pearl River Delta Region in China. Remote Sens. Environ. 2014, 154, 1–7. [Google Scholar] [CrossRef]
- Zhang, G.; Rui, X.; Fan, Y. Critical Review of Methods to Estimate Pm2.5 Concentrations within Specified Research Region. ISPRS Int. J. Geo-Inf. 2018, 7, 368. [Google Scholar] [CrossRef]
- Fang, X.; Zou, B.; Liu, X.; Sternberg, T.; Zhai, L. Satellite-Based Ground Pm2.5 Estimation Using Timely Structure Adaptive Modeling. Remote Sens. Environ. 2016, 186, 152–163. [Google Scholar] [CrossRef]
- Diao, M.; Holloway, T.; Choi, S.; O’Neill, S.M.; Al-Hamdan, M.Z.; Van Donkelaar, A.; Martin, R.V.; Jin, X.; Fiore, A.M.; Henze, D.K.; et al. Methods, Availability, and Applications of Pm2.5 Exposure Estimates Derived from Ground Measurements, Satellite, and Atmospheric Models. J. Air Waste Manag. Assoc. 2019, 69, 1391–1414. [Google Scholar] [CrossRef]
- Baker, K.R.; Foley, K.M. A Nonlinear Regression Model Estimating Single Source Concentrations of Primary and Secondarily Formed Pm2.5. Atmos. Environ. 2011, 45, 3758–3767. [Google Scholar] [CrossRef]
- Liu, Y.; Sarnat, J.A.; Kilaru, V.; Jacob, D.J.; Koutrakis, P. Estimating Ground-Level Pm2.5 in the Eastern United States Using Satellite Remote Sensing. Environ. Sci. Technol. 2005, 39, 3269–3278. [Google Scholar] [CrossRef]
- Hien, P.D.; Bac, V.T.; Tham, H.C.; Nhan, D.D.; Vinh, L.D. Influence of Meteorological Conditions on Pm2.5 and Pm2.5−10 Concentrations during the Monsoon Season in Hanoi, Vietnam. Atmos. Environ. 2002, 36, 3473–3484. [Google Scholar] [CrossRef]
- Chen, L.W.A.; Watson, J.G.; Chow, J.C.; Magliano, K.L. Quantifying Pm2.5 Source Contributions for the San Joaquin Valley with Multivariate Receptor Models. Environ. Sci. Technol. 2007, 41, 2818–2826. [Google Scholar] [CrossRef] [PubMed]
- Vallius, M.; Janssen, N.A.H.; Heinrich, J.; Hoek, G.; Ruuskanen, J.; Cyrys, J.; Van Grieken, R.; de Hartog, J.J.; Kreyling, W.G.; Pekkanen, J. Sources and Elemental Composition of Ambient Pm2.5 in Three European Cities. Sci. Total Environ. 2005, 337, 147–162. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, F.-J.; Chang, L.-C.; Kao, I.-F.; Wang, Y.-S.; Kang, C.-C. Multi-Output Support Vector Machine for Regional Multi-Step-Ahead Pm2.5 Forecasting. Sci. Total Environ. 2019, 651, 230–240. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, G.; Zhao, N.; Mulligan, K.; Ye, X. Improve Ground-Level Pm2.5 Concentration Mapping Using a Random Forests-Based Geostatistical Approach. Environ. Pollut. 2018, 235, 272–282. [Google Scholar] [CrossRef]
- Kow, P.-Y.; Chang, L.-C.; Lin, C.-Y.; Chou, C.C.-K.; Chang, F.-J. Deep Neural Networks for Spatiotemporal Pm2.5 Forecasts Based on Atmospheric Chemical Transport Model Output and Monitoring Data. Environ. Pollut. 2022, 306, 119348. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ogawa, S. Effects of Meteorological Conditions on Pm2.5 Concentrations in Nagasaki, Japan. Int. J. Environ. Res. Public Health 2015, 12, 9089–9101. [Google Scholar] [CrossRef]
- Xu, Y.; Xue, W.; Lei, Y.; Zhao, Y.; Cheng, S.; Ren, Z.; Huang, Q. Impact of Meteorological Conditions on Pm2.5 Pollution in China during Winter. Atmosphere 2018, 9, 429. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, D.; Zhao, C.; Kwan, M.P.; Cai, J.; Zhuang, Y.; Zhao, B.; Wang, X.; Chen, B.; Yang, J.; et al. Influence of Meteorological Conditions on Pm2.5 Concentrations across China: A Review of Methodology and Mechanism. Environ. Int. 2020, 139, 105558. [Google Scholar] [CrossRef]
- Xu, Y.; Xue, W.; Lei, Y.; Huang, Q.; Zhao, Y.; Cheng, S.; Ren, Z.; Wang, J. Spatiotemporal Variation in the Impact of Meteorological Conditions on Pm2.5 Pollution in China from 2000 to 2017. Atmos. Environ. 2020, 223, 117215. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, Z.; Lu, W.; Wang, X. A Catboost Approach with Wavelet Decomposition to Improve Satellite-Derived High-Resolution Pm2.5 Estimates in Beijing-Tianjin-Hebei. Atmos. Environ. 2021, 249, 118212. [Google Scholar] [CrossRef]
- Ding, Y.; Li, S.; Xing, J.; Li, X.; Ma, X.; Song, G.; Teng, M.; Yang, J.; Dong, J.; Meng, S. Retrieving Hourly Seamless Pm2.5 Concentration across China with Physically Informed Spatiotemporal Connection. Remote Sens. Environ. 2024, 301, 113901. [Google Scholar] [CrossRef]
- Pruthi, D.; Zhu, Q.; Wang, W.; Liu, Y. Multiresolution Analysis of Hrrr Meteorological Parameters and Goes-R Aod for Hourly Pm2.5 Prediction. Environ. Sci. Technol. 2024, 58, 20040–20048. [Google Scholar] [CrossRef] [PubMed]
- Yoo, C.; Kim, S. Eof Analysis of Surface Soil Moisture Field Variability. Adv. Water Resour. 2004, 27, 831–842. [Google Scholar] [CrossRef]
- Ludwig, F.L.; Horel, J.; Whiteman, C.D. Using Eof Analysis to Identify Important Surface Wind Patterns in Mountain Valleys. J. Appl. Meteorol. 2004, 43, 969–983. [Google Scholar] [CrossRef]
- Xiao-Feng, L.; Pietrafesa, L.; Shu-Fang, L.; Li-An, X. Significance Test for Empirical Orthogonal Function (Eof) Analysis of Meteorological and Oceanic Data. Chin. J. Oceanol. Limnol. 2000, 18, 10–17. [Google Scholar] [CrossRef]
- Zhou, K.; Yang, S. Emission Reduction of China’s Steel Industry: Progress and Challenges. Renew. Sustain. Energy Rev. 2016, 61, 319–327. [Google Scholar] [CrossRef]
- Xu, C.; Huo, X.; Hong, Y.; Yu, C.; de Jong, M.; Cheng, B. How Urban Greening Policy Affects Urban Ecological Resilience: Quasi-Natural Experimental Evidence from Three Megacity Clusters in China. J. Clean. Prod. 2024, 452, 142233. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Korkin, S.; Huang, D. Modis Collection 6 Maiac Algorithm. Atmos. Meas. Tech. 2018, 11, 5741–5765. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Laszlo, I.; Kahn, R.; Korkin, S.; Remer, L.; Levy, R.; Reid, J.S. Multiangle Implementation of Atmospheric Correction (Maiac): 2. Aerosol Algorithm. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Lyapustin, A.I.; Wang, Y.; Laszlo, I.; Hilker, T.; Hall, F.G.; Sellers, P.J.; Tucker, C.J.; Korkin, S.V. Multi-Angle Implementation of Atmospheric Correction for Modis (Maiac): 3. Atmospheric Correction. Remote Sens. Environ. 2012, 127, 385–393. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (Merra-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Buchard, V.; Randles, C.A.; Da Silva, A.M.; Darmenov, A.; Colarco, P.R.; Govindaraju, R.; Ferrare, R.; Hair, J.; Beyersdorf, A.J.; Ziemba, L.D.; et al. The Merra-2 Aerosol Reanalysis, 1980 Onward. Part Ii: Evaluation and Case Studies. J. Clim. 2017, 30, 6851–6872. [Google Scholar] [CrossRef] [PubMed]
- Sun, E.; Xu, X.; Che, H.; Tang, Z.; Gui, K.; An, L.; Lu, C.; Shi, G. Variation in Merra-2 Aerosol Optical Depth and Absorption Aerosol Optical Depth over China from 1980 to 2017. J. Atmos. Sol.-Terr. Phys. 2019, 186, 8–19. [Google Scholar] [CrossRef]
- Andrews, E.; Ogren, J.A.; Kinne, S.; Samset, B. Comparison of Aod, Aaod and Column Single Scattering Albedo from Aeronet Retrievals and in Situ Profiling Measurements. Atmos. Chem. Phys. 2017, 17, 6041–6072. [Google Scholar] [CrossRef]
- Sorek-Hamer, M.; Franklin, M.; Chau, K.; Garay, M.; Kalashnikova, O. Spatiotemporal Characteristics of the Association between Aod and Pm over the California Central Valley. Remote Sens. 2020, 12, 685. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The Era5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hallgren, C.; Aird, J.A.; Ivanell, S.; Körnich, H.; Vakkari, V.; Barthelmie, R.J.; Pryor, S.C.; Sahlée, E. Machine Learning Methods to Improve Spatial Predictions of Coastal Wind Speed Profiles and Low-Level Jets Using Single-Level Era5 Data. Wind Energ. Sci. 2024, 9, 821–840. [Google Scholar] [CrossRef]
- Han, H.; Zeng, Q.; Jiao, J. Quality Assessment of Tandem-X Dems, Srtm and Aster Gdem on Selected Chinese Sites. Remote Sens. 2021, 13, 1304. [Google Scholar] [CrossRef]
- Hanberry, B.B. Imposing Consistent Global Definitions of Urban Populations with Gridded Population Density Models: Irreconcilable Differences at the National Scale. Landsc. Urban Plan. 2022, 226, 104493. [Google Scholar] [CrossRef]
- Ni, W.; Ding, Y.; Li, S.; Teng, M.; Yang, J. Estimation of Daily Seamless Pm2.5 Concentrations with Climate Feature in Hubei Province, China. Remote Sens. 2023, 15, 3822. [Google Scholar] [CrossRef]
- Kim, K.Y.; Wu, Q. A Comparison Study of Eof Techniques: Analysis of Nonstationary Data with Periodic Statistics. J. Clim. 1999, 12, 185–199. [Google Scholar] [CrossRef]
- Sauquet, E.; Krasovskaia, I.; Leblois, E. Mapping Mean Monthly Runoff Pattern Using Eof Analysis. Hydrol. Earth Syst. Sci. 2000, 4, 79–93. [Google Scholar] [CrossRef]
- Aunan, K.; Ma, Q.; Lund, M.T.; Wang, S. Population-Weighted Exposure to Pm2.5 Pollution in China: An Integrated Approach. Environ. Int. 2018, 120, 111–120. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.J.; Brauer, M.; Burnett, R.; Anderson, H.R.; Frostad, J.; Estep, K.; Balakrishnan, K.; Brunekreef, B.; Dandona, L.; Dandona, R.; et al. Forouzanfar. Estimates and 25-Year Trends of the Global Burden of Disease Attributable to Ambient Air Pollution: An Analysis of Data from the Global Burden of Diseases Study 2015. Lancet 2017, 389, 1907–1918. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Zheng, Y.; Tong, D.; Shao, M.; Wang, S.; Zhang, Y.; Xu, X.; Wang, J.; He, H.; Liu, W.; et al. Drivers of Improved Pm2.5 Air Quality in China from 2013 to 2017. Proc. Natl. Acad. Sci. USA 2019, 116, 24463–24469. [Google Scholar] [CrossRef]
- Xiao, Q.; Geng, G.; Xue, T.; Liu, S.; Cai, C.; He, K.; Zhang, Q. Tracking Pm and O3 Pollution and the Related Health Burden in China 2013–2020. Environ. Sci. Technol. 2022, 56, 6922–6932. [Google Scholar] [CrossRef]
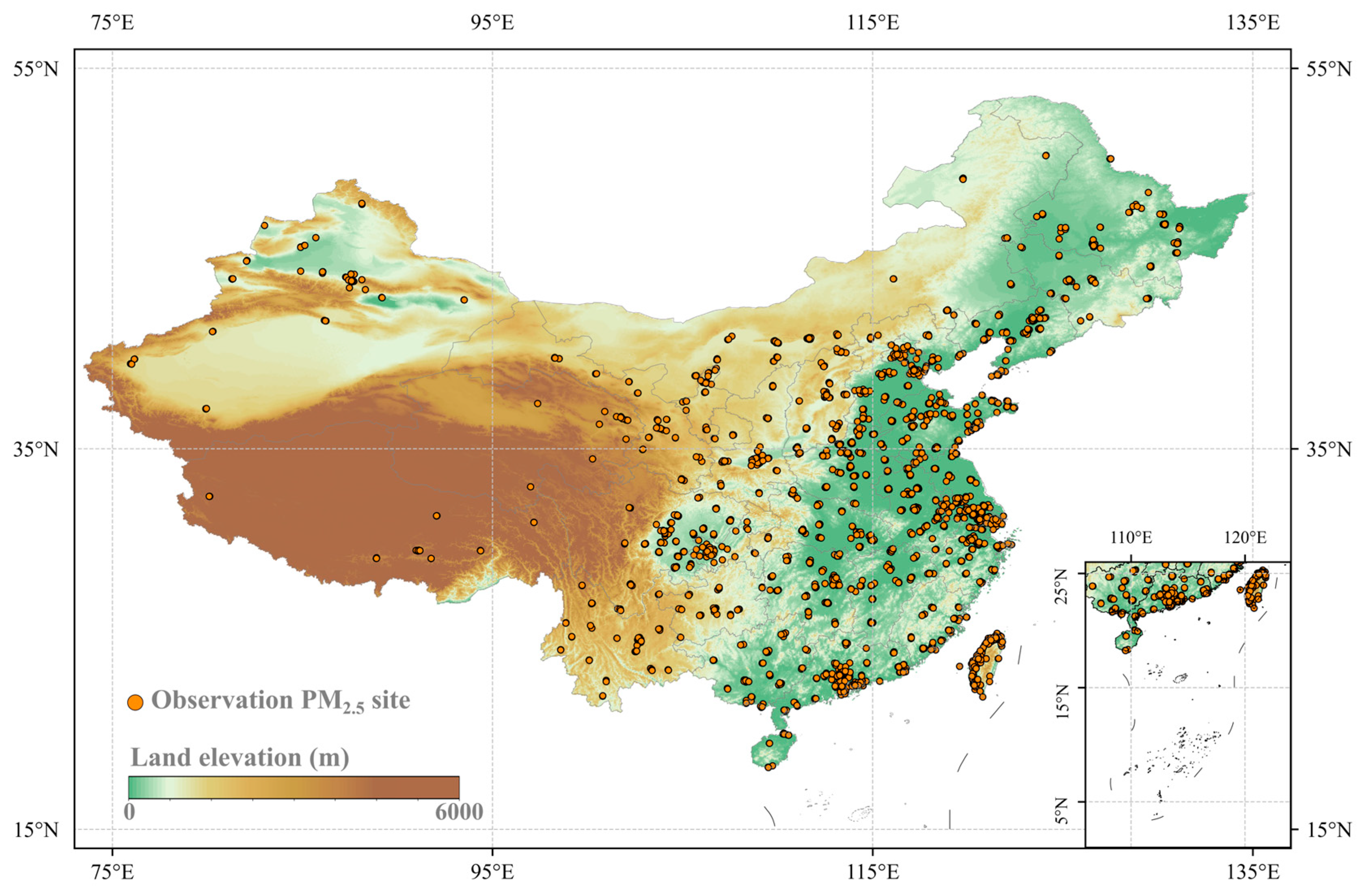
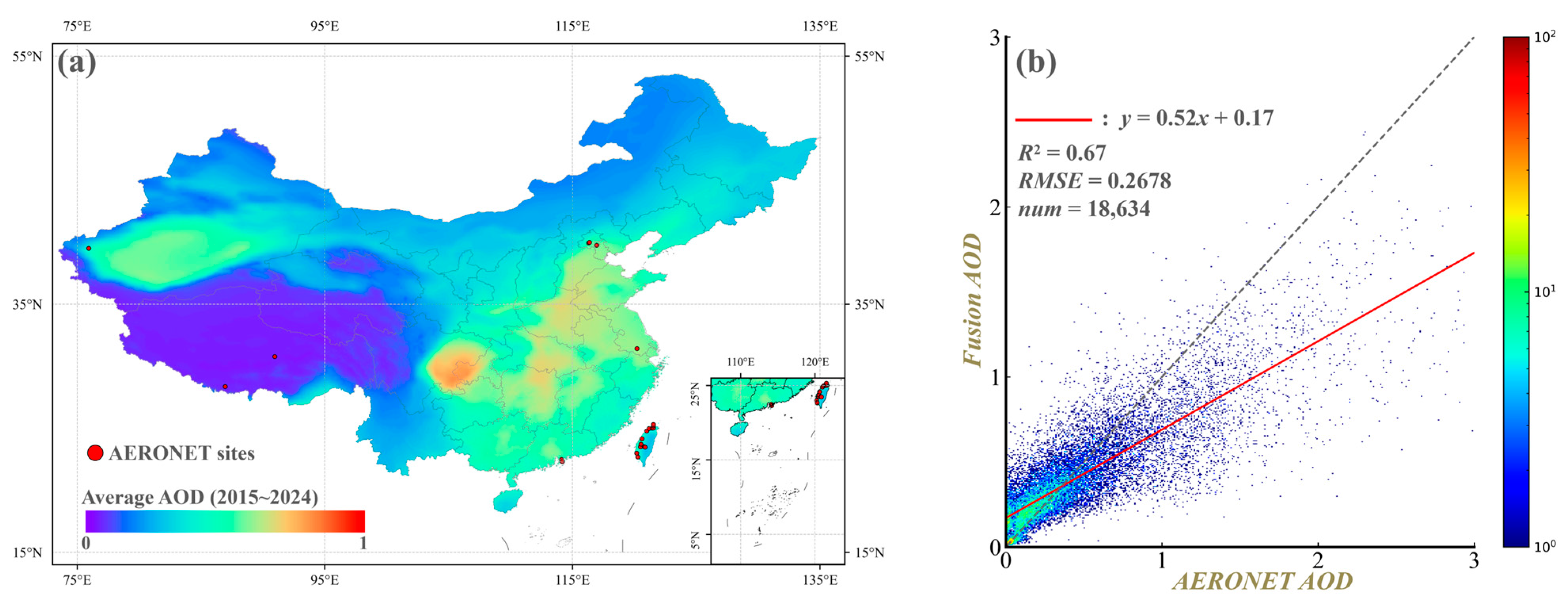
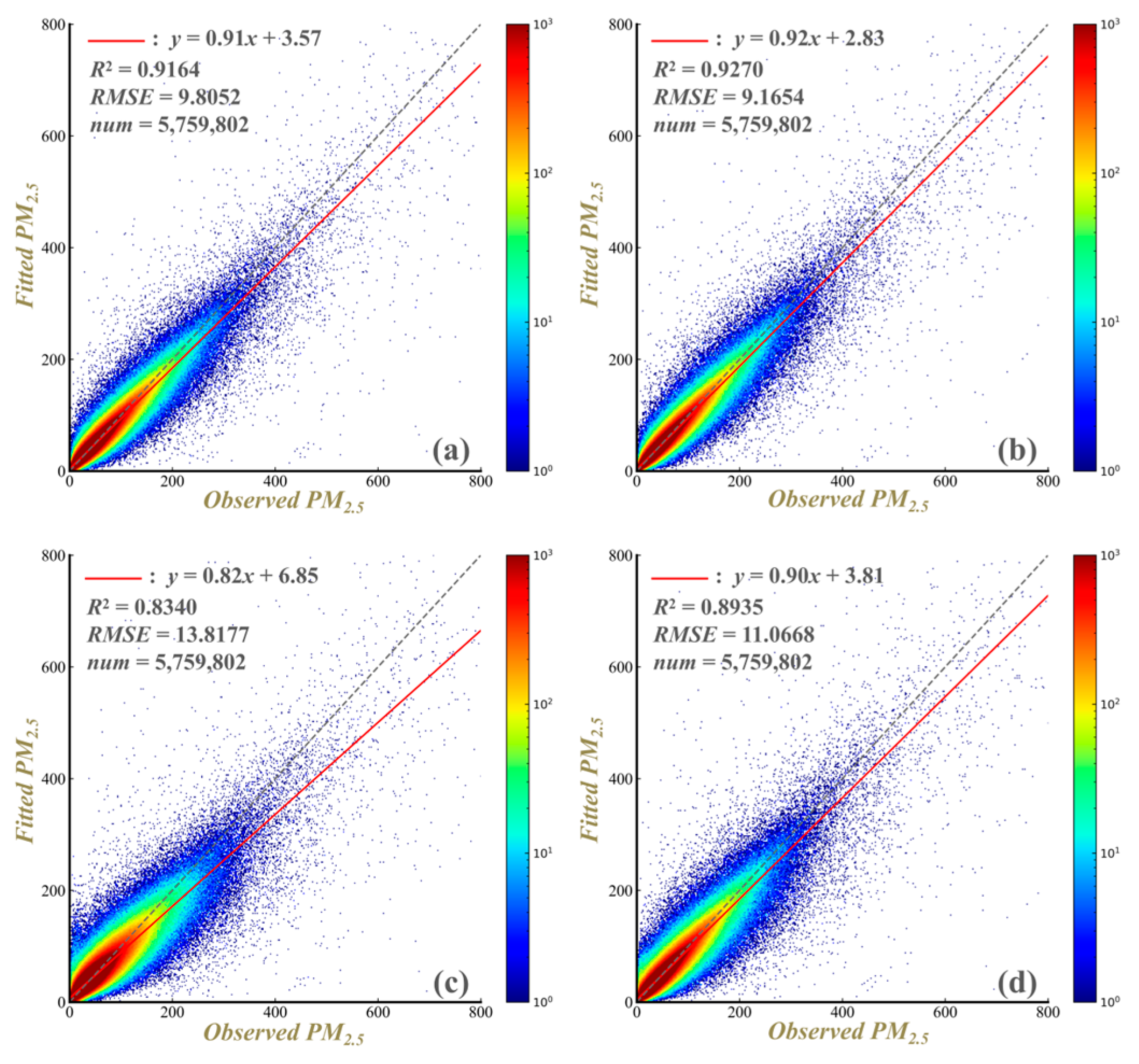
| Hyperparameters | Value | Explanation |
|---|---|---|
| num_boost_round | 500 | Number of boosting iterations, equal to trees to build, as each iteration will build a new tree. |
| objective | reg:squarederror | Loss function, squarederror means squared error is a loss function and needs to be minimized. |
| tree_method | hist | Tree construction method, here we choose histogram-based splitting for its high speed. |
| device | cuda | Uses NVIDIA GPU acceleration via CUDA |
| eval_metric | rmse | Evaluation metric, Root Mean Squared Error, is chosen here (for validation). |
| learning_rate | 0.23 | Shrinkage factor, controls step size in updates (higher = faster convergence). |
| max_depth | 15 | Maximum tree depth, controls complexity of model (higher = deeper interactions). |
| booster | gbtree | The type of base learner, we choose gradient-boosted decision trees. |
| Site | Altitude(m) | Latitude (°) | Longitude (°) | Level 2.0 Period |
|---|---|---|---|---|
| Kashi | 1298 | 39.504 | 75.930 | 2019.03–2019.04 |
| NAM_CO | 4737 | 30.773 | 90.962 | 2015.01–2017.11 2020.07–2024.06 |
| QOMS_CAS | 4288 | 28.365 | 86.948 | 2015.01–2019.08 2021.08–2022.06 |
| Hong_Kong_Sheung | 37 | 22.483 | 114.117 | 2015.04–2022.07 |
| Hong_Kong_PolyU | 12 | 22.303 | 114.180 | 2015.01–2019.01 2020.05–2023.06 |
| Chen-Kung_Univ | 18 | 22.993 | 120.205 | 2015.01–2023.08 |
| Xitun | 91 | 24.162 | 120.617 | 2018.01–2024.04 |
| Douliu | 60 | 23.712 | 120.545 | 2015.01–2018.01 2022.01–2024.02 |
| Kaohsiung | 15 | 22.676 | 120.292 | 2018.01–2024.11 |
| Alishan | 2416 | 23.508 | 120.813 | 2016.04–2016.04 |
| Lulin | 2868 | 23.469 | 120.874 | 2015.01–2024.12 |
| Chiayi | 62 | 23.496 | 120.496 | 2015.01–2018.04 |
| TASA_Taiwan | 99 | 24.784 | 121.001 | 2018.01–2024.06 |
| Banqiao | 16 | 24.998 | 121.4425 | 2017.06–2017.09 |
| Taipei_CWB | 26 | 25.015 | 121.539 | 2015.01–2023.01 |
| Bamboo | 1050 | 25.187 | 121.535 | 2016.11–2017.03 |
| Fuguei_Cape | 50 | 25.298 | 121.538 | 2015.10–2015.11 |
| Taihu | 16 | 31.421 | 120.215 | 2015.10–2016.08 |
| XiangHe | 15 | 39.754 | 116.962 | 2015.01–2017.05 2019.05–2022.02 |
| Beijing | 58 | 39.977 | 116.381 | 2015.01–2019.03 |
| Beijing-CAMS | 59 | 39.933 | 116.317 | 2015.01–2024.01 2024.09–2024.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Dong, J.; Ding, Y.; Ni, W.; Yang, J.; Li, S. Long-Term (2015–2024) Daily PM2.5 Estimation in China by Using XGBoost Combining Empirical Orthogonal Function Decomposition. Remote Sens. 2025, 17, 1632. https://doi.org/10.3390/rs17091632
Jiang J, Dong J, Ding Y, Ni W, Yang J, Li S. Long-Term (2015–2024) Daily PM2.5 Estimation in China by Using XGBoost Combining Empirical Orthogonal Function Decomposition. Remote Sensing. 2025; 17(9):1632. https://doi.org/10.3390/rs17091632
Chicago/Turabian StyleJiang, Jiacheng, Jiaxin Dong, Yu Ding, Wenjia Ni, Jie Yang, and Siwei Li. 2025. "Long-Term (2015–2024) Daily PM2.5 Estimation in China by Using XGBoost Combining Empirical Orthogonal Function Decomposition" Remote Sensing 17, no. 9: 1632. https://doi.org/10.3390/rs17091632
APA StyleJiang, J., Dong, J., Ding, Y., Ni, W., Yang, J., & Li, S. (2025). Long-Term (2015–2024) Daily PM2.5 Estimation in China by Using XGBoost Combining Empirical Orthogonal Function Decomposition. Remote Sensing, 17(9), 1632. https://doi.org/10.3390/rs17091632








