Structural Similarity-Guided Siamese U-Net Model for Detecting Changes in Snow Water Equivalent
Abstract
1. Introduction
2. Related Work and Recent Progress
2.1. Progress in Snow Parameter Analysis
2.2. Siamese Models for Pattern Comparison
3. Materials and Methods
3.1. SWE Data and Study Location
3.2. SWE Data Processing
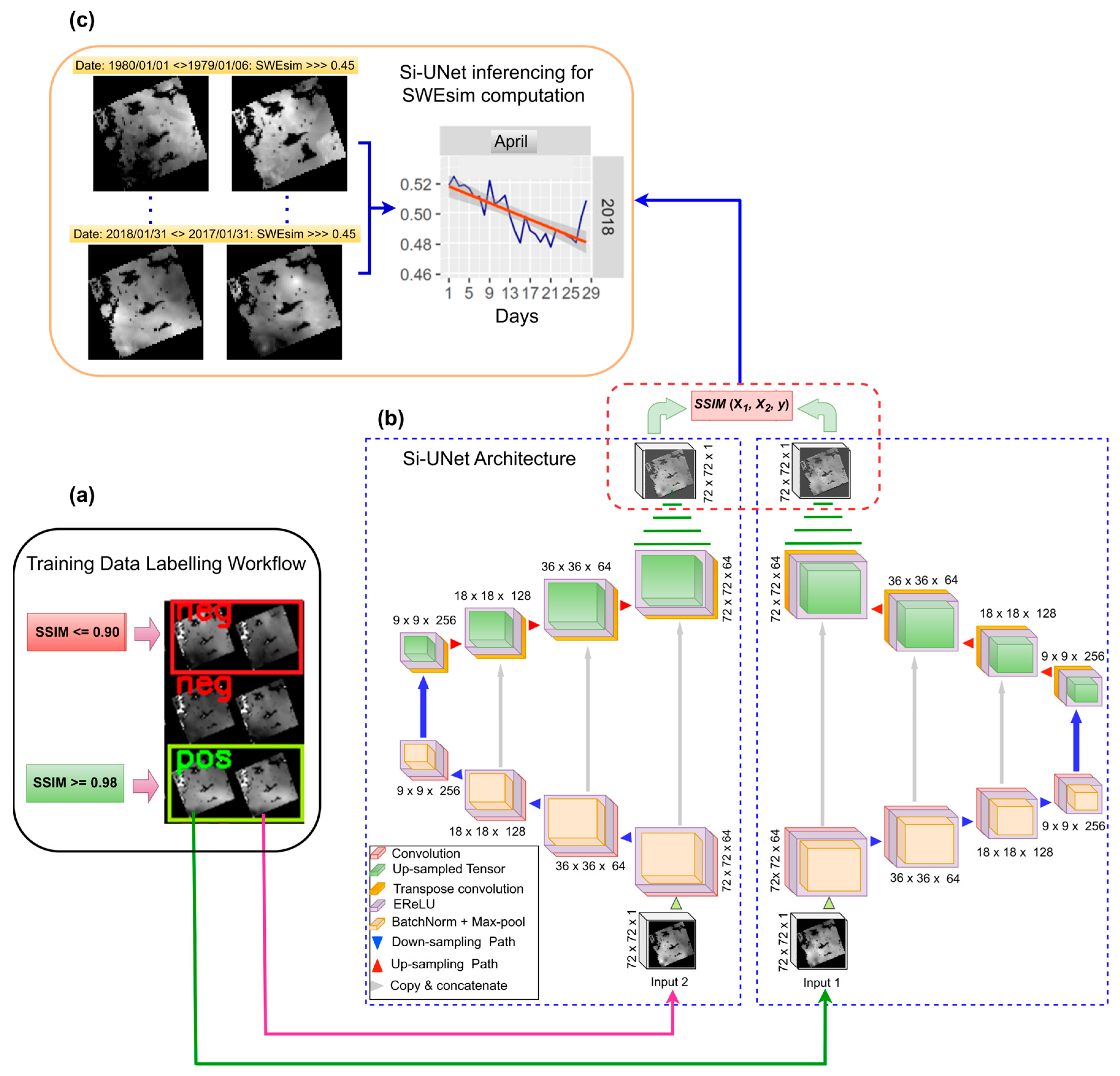
3.3. Siamese U-Net Model Architecture
3.4. Training Data and SWE Labelling
3.5. SSIM Index Properties
3.6. Combining the SSIM Index and the Contrastive Loss Function
3.7. Model Architecture, Loss Function, and Similarity Metrics
3.8. Deriving Time Series SWE Similarity Vectors
4. Results
4.1. Ablation Studies
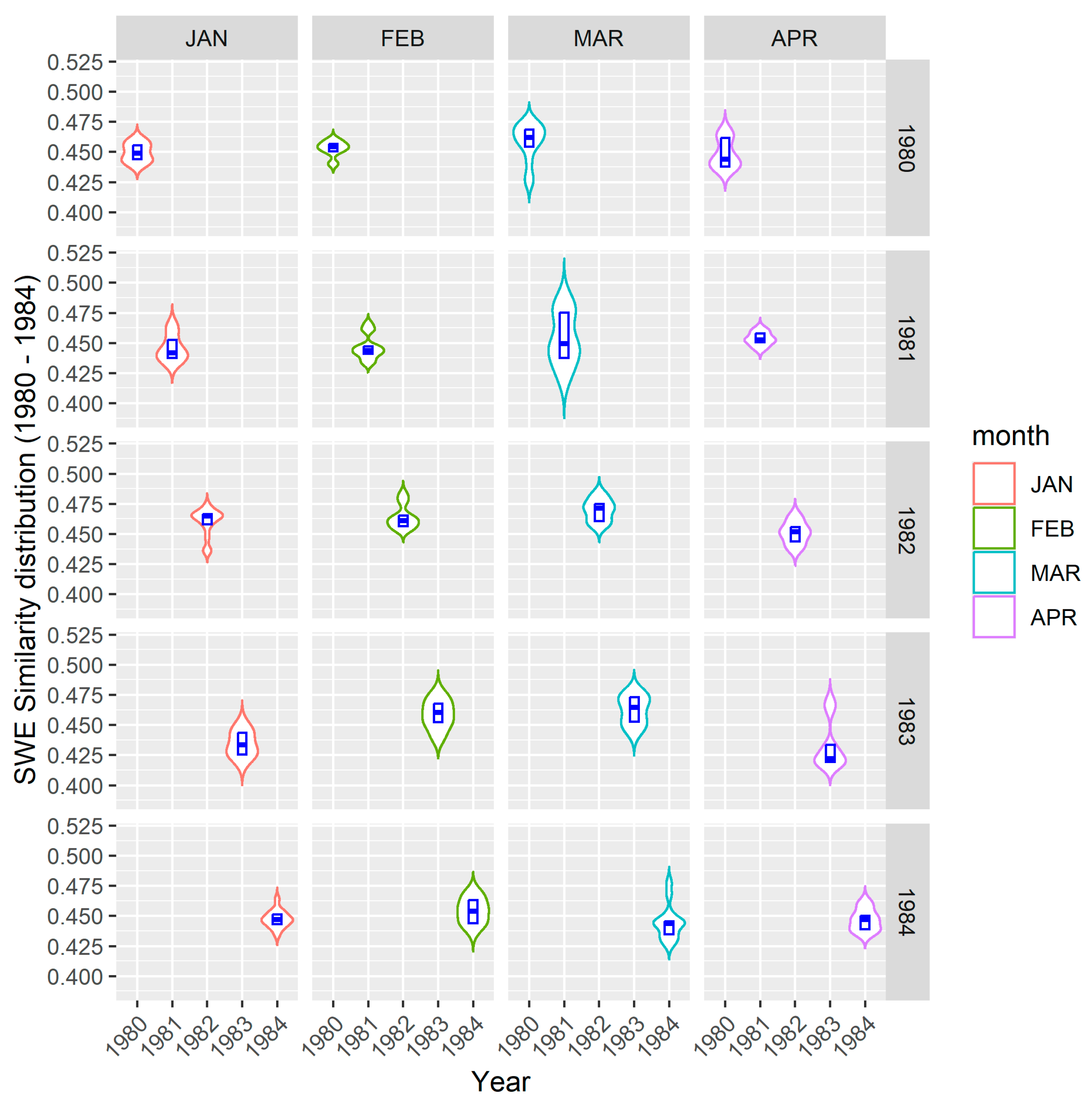
4.2. A Comparison of Monthly Changes in SWE Distribution over 5 Years
4.2.1. SWE Distribution—1980 to 1984
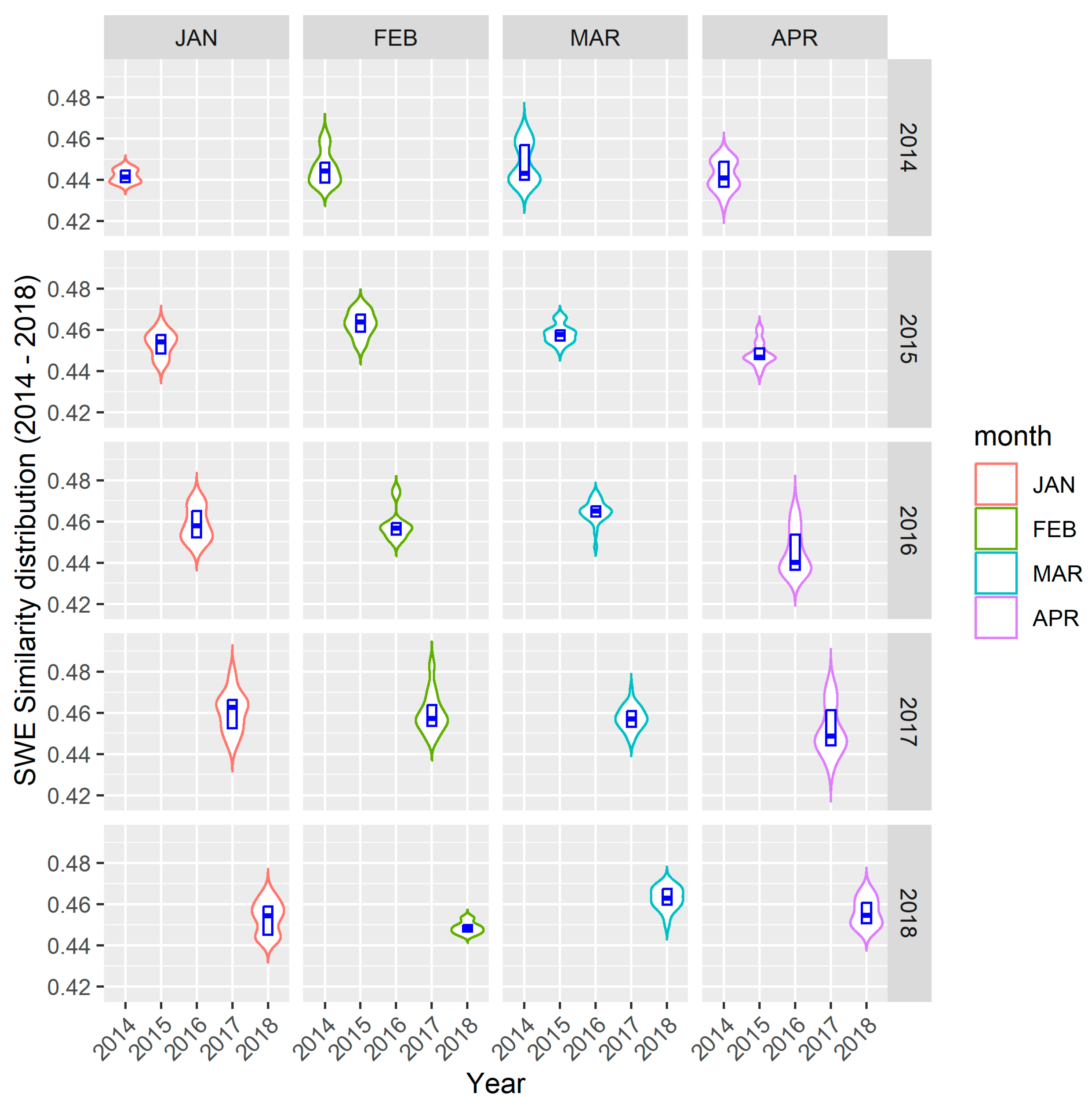
4.2.2. SWE Distribution—2014 to 2018
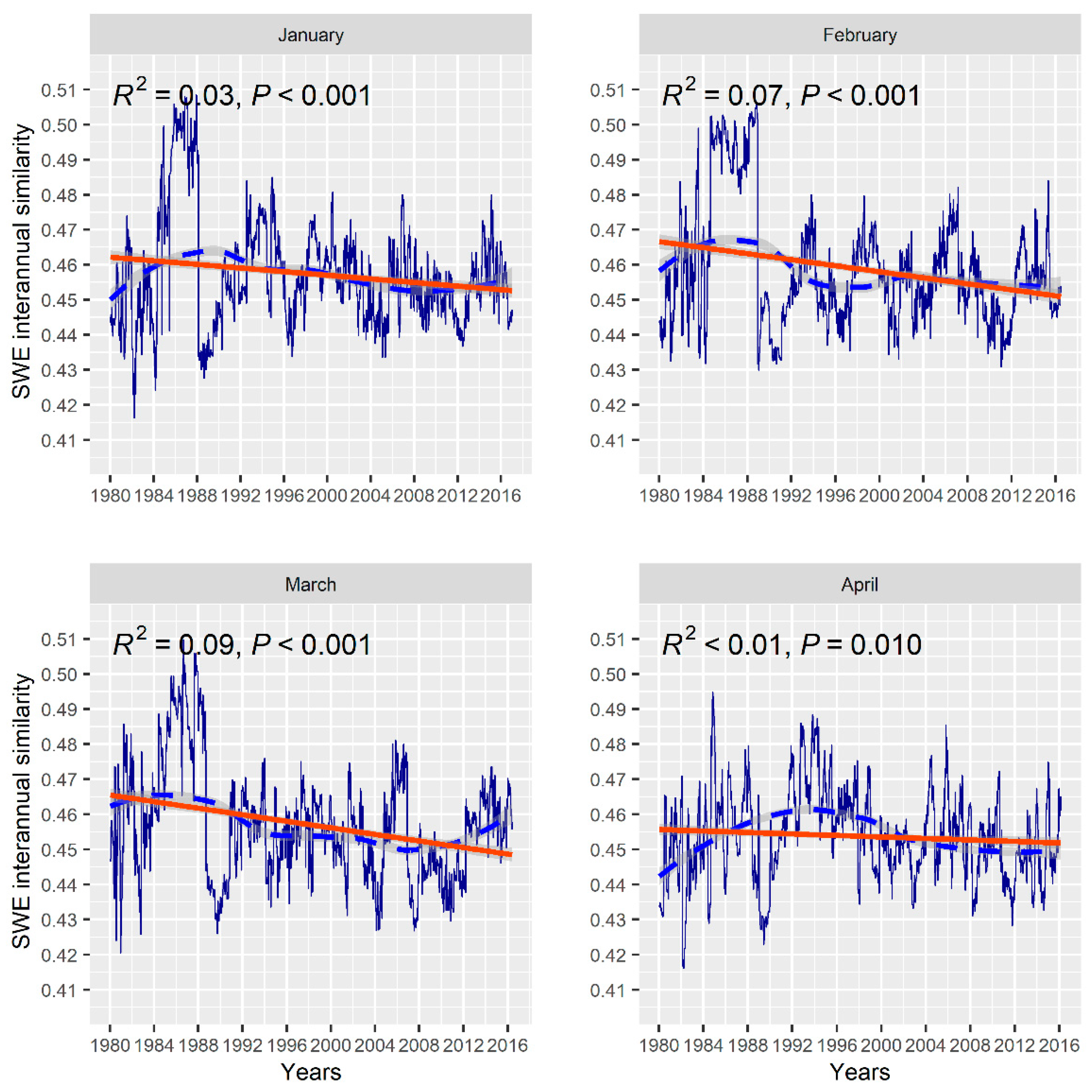
4.3. Interannual SWE Trends—1979 to 2018
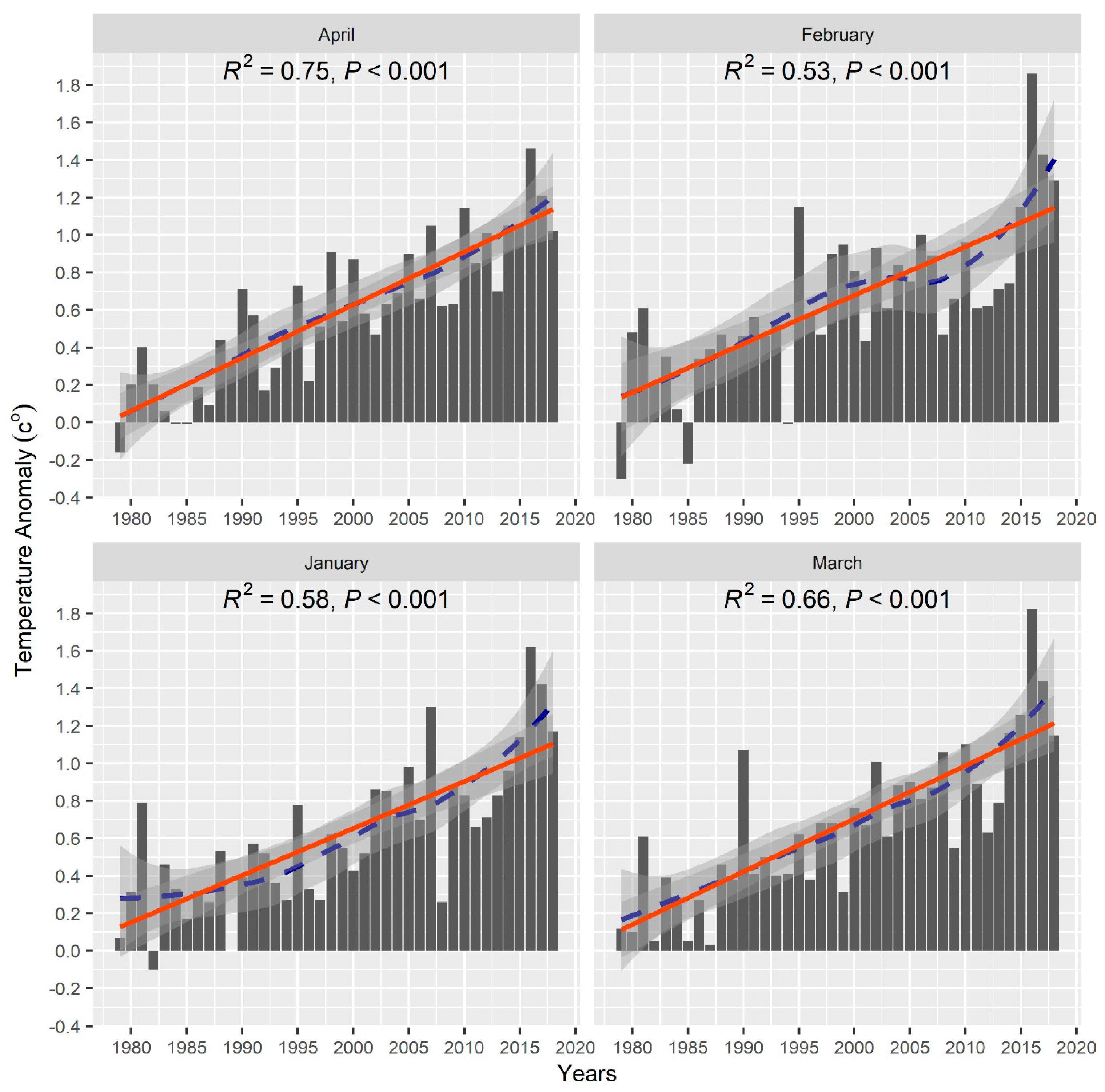
4.4. Northern Hemisphere Temperature Anomalies
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Month | N | S | tau | p-Value | R2 |
|---|---|---|---|---|---|
| January | 1019 | –3.31 × 104 | –6.37 × 10−2 | 2.31 × 10−3 | 3.0 × 10−2 |
| February | 950 | –4.38 × 104 | –9.72 × 10−2 | 7.34 × 10−6 | 7.0 × 10−2 |
| March | 1019 | –8.16 × 104 | –1.57 × 10−2 | 5.62 × 10−14 | 9.0 × 10−2 |
| April | 940 | –3.47 × 104 | –7.85 × 10−2 | 3.13 × 10−4 | 1.0 × 10−2 |
Appendix B
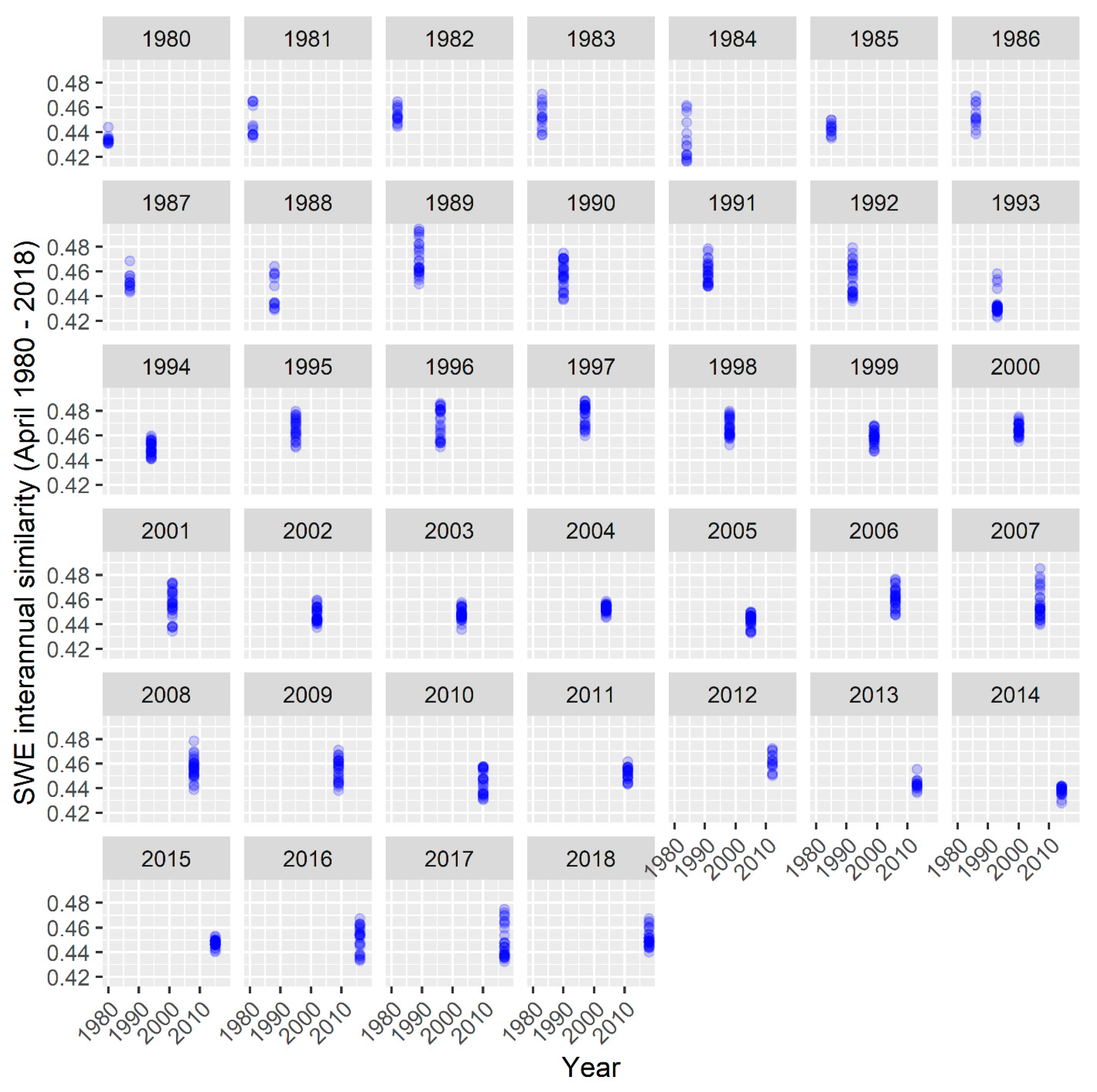
Appendix C
References
- Thackeray, C.W.; Derksen, C.; Fletcher, C.G.; Hall, A. Snow and Climate: Feedbacks, Drivers, and Indices of Change; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Schilling, S.; Dietz, A.; Kuenzer, C. Snow Water Equivalent Monitoring—A Review of Large-Scale Remote Sensing Applications. Remote Sens. 2024, 16, 1085. [Google Scholar] [CrossRef]
- Callaghan, T.V.; Johansson, M.; Brown, R.D.; Groisman, P.Y.; Labba, N.; Radionov, V.; Bradley, R.S.; Blangy, S.; Bulygina, O.N.; Christensen, T.R.; et al. Multiple effects of changes in arctic snow cover. Ambio 2011, 40 (Suppl. S1), 32–45. [Google Scholar] [CrossRef]
- Rupp, D.E.; Mote, P.W.; Bindoff, N.L.; Stott, P.A.; Robinson, D.A. Detection and attribution of observed changes in northern hemisphere spring snow cover. J. Clim. 2013, 26, 6904–6914. [Google Scholar] [CrossRef]
- Pulliainen, J.; Luojus, K.; Derksen, C.; Mudryk, L.; Lemmetyinen, J.; Salminen, M.; Ikonen, J.; Takala, M.; Cohen, J.; Smolander, T.; et al. Patterns and trends of Northern Hemisphere snow mass from 1980 to 2018. Nature 2020, 581, 294–298. [Google Scholar] [CrossRef]
- Mudryk, L.R.; Kushner, P.J.; Derksen, C.; Thackeray, C. Snow cover response to temperature in observational and climate model ensembles. Geophys. Res. Lett. 2017, 44, 919–926. [Google Scholar] [CrossRef]
- Brown, R.D.; Fang, B.; Mudryk, L. Update of Canadian Historical Snow Survey Data and Analysis of Snow Water Equivalent Trends, 1967–2016. Atmos. Ocean 2019, 57, 149–156. [Google Scholar] [CrossRef]
- Räisänen, J. Changes in March mean snow water equivalent since the mid-20th century and the contributing factors in reanalyses and CMIP6 climate models. Cryosphere 2023, 17, 1913–1934. [Google Scholar] [CrossRef]
- Cordero, R.R.; Asencio, V.; Feron, S.; Damiani, A.; Llanillo, P.J.; Sepulveda, E.; Jorquera, J.; Carrasco, J.; Casassa, G. Dry-Season Snow Cover Losses in the Andes (18°–40°S) driven by Changes in Large-Scale Climate Modes. Sci. Rep. 2019, 9, 16945. [Google Scholar] [CrossRef]
- Brown, R.D.; Robinson, D.A. Northern Hemisphere spring snow cover variability and change over 1922–2010 including an assessment of uncertainty. Cryosphere 2011, 5, 219–229. [Google Scholar] [CrossRef]
- Luojus, K.; Pulliainen, J.; Takala, M.; Derksen, C.; Rott, H.; Nagler, T.; Solberg, R.; Wiesmann, A.; Metsamaki, S.; Malnes, E.; et al. Investigating the feasibility of the globsnow snow water equivalent data for climate research purposes. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; Volume 19, pp. 4851–4853. [Google Scholar] [CrossRef]
- Fontrodona-Bach, A.; Schaefli, B.; Woods, R.; Teuling, A.J.; Larsen, J.R. NH-SWE: Northern Hemisphere Snow Water Equivalent dataset based on in situ snow depth time series. Earth Syst. Sci. Data 2023, 15, 2577–2599. [Google Scholar] [CrossRef]
- Luomaranta, A.; Aalto, J.; Jylhä, K. Snow cover trends in Finland over 1961–2014 based on gridded snow depth observations. Int. J. Climatol. 2019, 39, 3147–3159. [Google Scholar] [CrossRef]
- Brown, R.D.; Brasnett, B.; Robinson, D. Gridded North American monthly snow depth and snow water equivalent for GCM evaluation. Atmos. Ocean 2003, 41, 1–14. [Google Scholar] [CrossRef]
- Gan, T.Y.; Barry, R.G.; Gizaw, M.; Gobena, A.; Balaji, R. Changes in North American snowpacks for 1979–2007 detected from the snow water equivalent data of SMMR and SSM/I passive microwave and related climatic factors. J. Geophys. Res. Atmos. 2013, 118, 7682–7697. [Google Scholar] [CrossRef]
- Räisänen, J. Snow conditions in northern Europe: The dynamics of interannual variability versus projected long-term change. Cryosphere 2021, 15, 1677–1696. [Google Scholar] [CrossRef]
- Kim, R.S.; Kumar, S.; Vuyovich, C.; Houser, P.; Lundquist, J.; Mudryk, L.; Durand, M.; Barros, A.; Kim, E.J.; Forman, B.A.; et al. Snow Ensemble Uncertainty Project (SEUP): Quantification of snow water equivalent uncertainty across North America via ensemble land surface modeling. Cryosphere 2021, 15, 771–791. [Google Scholar] [CrossRef]
- Urraca, R.; Gobron, N. Temporal stability of long-term satellite and reanalysis products to monitor snow cover trends. Cryosphere 2023, 17, 1023–1052. [Google Scholar] [CrossRef]
- Cheng, K.; Wei, Z.; Li, X.; Ma, L. Multi-Source Dataset Assessment and Variation Characteristics of Snow Depth in Eurasia from 1980 to 2018. Atmosphere 2024, 15, 530. [Google Scholar] [CrossRef]
- Hale, K.E.; Jennings, K.S.; Musselman, K.N.; Livneh, B.; Molotch, N.P. Recent decreases in snow water storage in western North America. Commun. Earth Environ. 2023, 4, 170. [Google Scholar] [CrossRef]
- Mote, P.W.; Li, S.; Lettenmaier, D.P.; Xiao, M.; Engel, R. Dramatic declines in snowpack in the western US. NPJ Clim. Atmos. Sci. 2018, 1, 2. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, N. Spatiotemporal variability of snow cover and snow water equivalent in the last three decades over Eurasia. J. Hydrol. 2018, 559, 238–251. [Google Scholar] [CrossRef]
- Dierauer, J.R.; Allen, D.M.; Whitfield, P.H. Climate change impacts on snow and streamflow drought regimes in four ecoregions of British Columbia. Can. Water Resour. J. 2021, 46, 168–193. [Google Scholar] [CrossRef]
- Santi, E.; Pettinato, S.; Paloscia, S.; Pampaloni, P.; Fontanelli, G.; Crepaz, A.; Valt, M. Monitoring of Alpine snow using satellite radiometers and artificial neural networks. Remote Sens. Environ. 2014, 144, 179–186. [Google Scholar] [CrossRef]
- Malik, K.; Robertson, C. Exploring the Use of Computer Vision Metrics for Spatial Pattern Comparison. Geogr. Anal. 2019, 52, 617–641. [Google Scholar] [CrossRef]
- Bromley, R.S.J.; Guyon, I.; LeCun, Y.; Sickinger, E. Signature Verification using a ‘Siamese’ Time Delay Neural Network. Adv. Neural Inf. Process. Syst. 1993, 6, 737–744. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, C.; Li, X.; Kim, H.J.; Wang, J. A full convolutional network based on DenseNet for remote sensing scene classification. Math. Biosci. Eng. 2019, 16, 3345–3367. [Google Scholar] [CrossRef]
- Cao, K.; Zhang, X. An improved Res-UNet model for tree species classification using airborne high-resolution images. Remote Sens. 2020, 12, 1128. [Google Scholar] [CrossRef]
- Thomas, E.; Pawan, S.J.; Kumar, S.; Horo, A.; Niyas, S.; Vinayagamani, S.; Kesavadas, C.; Rajan, J. Multi-Res-Attention UNet: A CNN Model for the Segmentation of Focal Cortical Dysplasia Lesions from Magnetic Resonance Images. IEEE J. Biomed. Health Inform. 2020, 25, 1724–1734. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Z.; Feng, J.; Liu, L.; Jiao, L. Remote Sensing Image Change Detection Based on Deep Multi-Scale Multi-Attention Siamese Transformer Network. Remote Sens. 2023, 15, 842. [Google Scholar] [CrossRef]
- Wu, L.; Wang, Y.; Gao, J.; Li, X. Where-and-When to Look: Deep Siamese Attention Networks for Video-Based Person Re-Identification. IEEE Trans. Multimed. 2019, 21, 1412–1424. [Google Scholar] [CrossRef]
- Yuan, P.; Zhao, Q.; Zhao, X.; Wang, X.; Long, X.; Zheng, Y. A transformer-based Siamese network and an open optical dataset for semantic change detection of remote sensing images. Int. J. Digit. Earth 2022, 15, 1506–1525. [Google Scholar] [CrossRef]
- Michal, D.; Eugene, V.; Gabriel, C.; Samuel, K.; Chris, P. The Importance of Skip Connections in Biomedical Image Segmentation. In Deep Learning and Data Labeling for Medical Applications; Springer International Publishing: Cham, Switzerland, 2016; pp. 179–187. [Google Scholar] [CrossRef]
- Tang, Y.; Cao, Z.; Guo, N.; Jiang, M. A Siamese Swin-Unet for image change detection. Sci. Rep. 2024, 14, 4577. [Google Scholar] [CrossRef] [PubMed]
- Canadian Environmental Sustainability Indicators. Environment and Climate Change Canada (2024). Canadian Environmental Sustainability Indicators: Snow Cover. Consulted on Month Day, Year. July 2024. Available online: www.canada.ca/en/environment-climate-change/services/environmental-indicators/snow-cover.html (accessed on 2 February 2025).
- Luojus, K.; Pulliainen, J.; Takala, M.; Lemmetyinen, J.; Mortimer, C.; Derksen, C.; Mudryk, L.; Moisander, M.; Hiltunen, M.; Smolander, T.; et al. GlobSnow v3.0 Northern Hemisphere snow water equivalent dataset. Sci. Data 2021, 8, 163. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Member, S.; Simoncelli, E.P.; Member, S. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Chopra, S.; Hadsell, R.; Lecun, Y. Learning a Similarity Metric Discriminatively, with Application to Face Verification. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 539–546. [Google Scholar]
- Malik, K.; McLeman, R.; Robertson, C.; Lawrence, H. Reconstruction of past backyard skating seasons in the Original Six NHL cities from citizen science data. Can. Geogr. 2020, 64, 564–575. [Google Scholar] [CrossRef]
- Dey, S.; Dutta, A.; Toledo, J.I.; Ghosh, S.K.; Llados, J.; Pal, U. SigNet: Convolutional Siamese Network for Writer Independent Offline Signature Verification. July 2017. Available online: http://arxiv.org/abs/1707.02131 (accessed on 1 February 2025).
- NOAA National Centers for Environmental Information, Climate at a Glance: Global Time Series. Available online: https://www.ncei.noaa.gov/access/monitoring/climate-at-a-glance/global/time-series (accessed on 8 March 2025).
- Räisänen, J. Warmer climate: Less or more snow? Clim. Dyn. 2008, 30, 307–319. [Google Scholar] [CrossRef]
- Mudryk, L.; Santolaria-Otín, M.; Krinner, G.; Ménégoz, M.; Derksen, C.; Brutel-Vuilmet, C.; Brady, M.; Essery, R. Historical Northern Hemisphere snow cover trends and projected changes in the CMIP6 multi-model ensemble. Cryosphere 2020, 14, 2495–2514. [Google Scholar] [CrossRef]
- Erlat, E.; Aydin-Kandemir, F. Changes in snow cover extent in the Central Taurus Mountains from 1981 to 2021 in relation to temperature, precipitation, and atmospheric teleconnections. J. Mt. Sci. 2024, 21, 49–67. [Google Scholar] [CrossRef]
- Ishida, K.; Ohara, N.; Ercan, A.; Jang, S.; Trinh, T.; Kavvas, M.L.; Carr, K.; Anderson, M.L. Impacts of climate change on snow accumulation and melting processes over mountainous regions in Northern California during the 21st century. Sci. Total Environ. 2019, 685, 104–115. [Google Scholar] [CrossRef] [PubMed]
- Mankin, J.S.; Diffenbaugh, N.S. Influence of temperature and precipitation variability on near-term snow trends. Clim. Dyn. 2015, 45, 1099–1116. [Google Scholar] [CrossRef]
- Malik, K.; Robertson, C.; Roberts, S.A.; Remmel, T.K.; Jed, A. Computer vision models for comparing spatial patterns: Understanding spatial scale. Int. J. Geogr. Inf. Sci. 2022, 37, 1–35. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Palecki, M.A.; Hubbard, K.G.; Robinson, D.A.; Redmond, K.T.; Easterling, D.R. Trend identification in twentieth-century U.S. snowfall: The challenges. J. Atmos. Ocean Technol. 2007, 24, 64–73. [Google Scholar] [CrossRef]
- Derksen, C.; Mudryk, L. Assessment of Arctic seasonal snow cover rates of change. Cryosphere 2023, 17, 1431–1443. [Google Scholar] [CrossRef]
- Mudryk, L.R.; Derksen, C.; Howell, S.; Laliberté, F.; Thackeray, C.; Sospedra-Alfonso, R.; Vionnet, V.; Kushner, P.J.; Brown, R. Canadian snow and sea ice: Historical trends and projections. Cryosphere 2018, 12, 1157–1176. [Google Scholar] [CrossRef]
- Klein, G.; Vitasse, Y.; Rixen, C.; Marty, C.; Rebetez, M. Shorter snow cover duration since 1970 in the swiss alps due to earlier snowmelt more than to later snow onset. Clim Chang. 2016, 139, 637–649. [Google Scholar] [CrossRef]
- Essery, R.; Kim, H.; Wang, L.; Bartlett, P.; Boone, A.; Brutel-Vuilmet, C.; Burke, E.; Cuntz, M.; Decharme, B.; Dutra, E.; et al. Snow cover duration trends observed at sites and predicted by multiple models. Cryosphere 2020, 14, 4687–4698. [Google Scholar] [CrossRef]
- Musselman, K.N.; Addor, N.; Vano, J.A.; Molotch, N.P. Winter melt trends portend widespread declines in snow water resources. Nat. Clim. Chang. 2021, 11, 418–421. [Google Scholar] [CrossRef]
- Kouki, K.; Luojus, K.; Riihelä, A. Evaluation of snow cover properties in ERA5 and ERA5-Land with several satellite-based datasets in the Northern Hemisphere in spring 1982–2018. Cryosphere 2023, 17, 5007–5026. [Google Scholar] [CrossRef]
- Mortimer, C.; Mudryk, L.; Derksen, C.; Luojus, K.; Brown, R.; Kelly, R.; Tedesco, M. Evaluation of long-term Northern Hemisphere snow water equivalent products. Cryosphere 2020, 14, 1579–1594. [Google Scholar] [CrossRef]

| Model Architecture | Model Parameters | Confidence Threshold | Loss Functions | Similarity Metrics | Accuracy Metrics | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BCE | Cont. Loss | ECD | SSIM | TPR | TNR | PR | F1-Score | OA | |||
| CNN base | 1,773,190 | 50% | Yes | No | Yes | No | 78.65 | 95.56 | 88.65 | 83 | 90.38 |
| Si-UNet | 2,560,646 | 50% | Yes | No | Yes | No | 87.5 | 89.74 | 79.5 | 83 | 89.05 |
| Si-UNet | 2,560,646 | 70% | Yes | No | No | Yes | 100 | 99.23 | 98.29 | 99 | 99.56 |
| Si-Att-UNet | 8,134,593 | 70% | Yes | No | No | Yes | 95.49 | 99.85 | 99.64 | 98 | 98.51 |
| Si-UNet | 2,560,646 | 50% | No | Yes | No | Yes | 100 | 98.93 | 97.63 | 99 | 99.25 |
| Si-Att-UNet | 8,134,593 | 50% | No | Yes | No | Yes | 98.61 | 100 | 100 | 99 | 99.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, K.; Robertson, C. Structural Similarity-Guided Siamese U-Net Model for Detecting Changes in Snow Water Equivalent. Remote Sens. 2025, 17, 1631. https://doi.org/10.3390/rs17091631
Malik K, Robertson C. Structural Similarity-Guided Siamese U-Net Model for Detecting Changes in Snow Water Equivalent. Remote Sensing. 2025; 17(9):1631. https://doi.org/10.3390/rs17091631
Chicago/Turabian StyleMalik, Karim, and Colin Robertson. 2025. "Structural Similarity-Guided Siamese U-Net Model for Detecting Changes in Snow Water Equivalent" Remote Sensing 17, no. 9: 1631. https://doi.org/10.3390/rs17091631
APA StyleMalik, K., & Robertson, C. (2025). Structural Similarity-Guided Siamese U-Net Model for Detecting Changes in Snow Water Equivalent. Remote Sensing, 17(9), 1631. https://doi.org/10.3390/rs17091631








