Research on Effective Radius Retrievals of Aerosol Particles Based on Dual-Wavelength Lidar
Abstract
1. Introduction
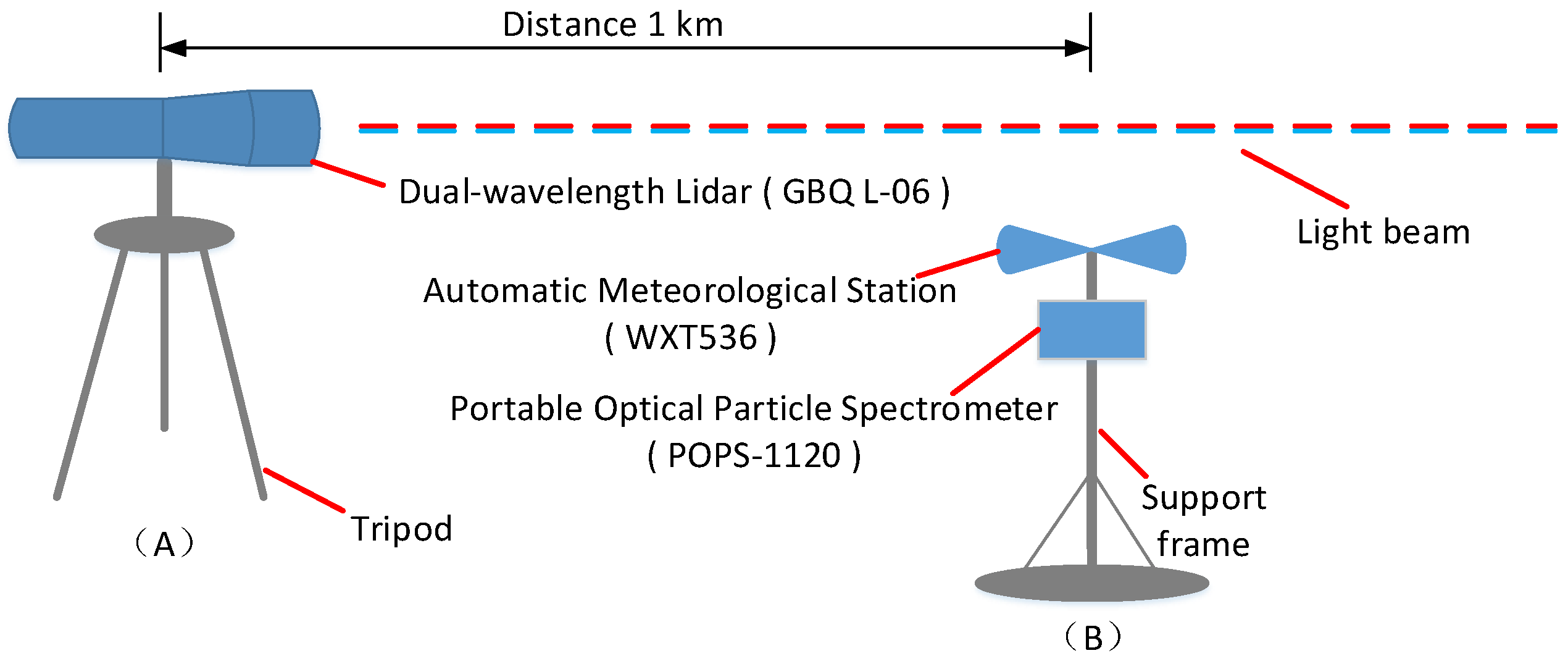
2. Instrument
2.1. Dual-Wavelength Lidar System
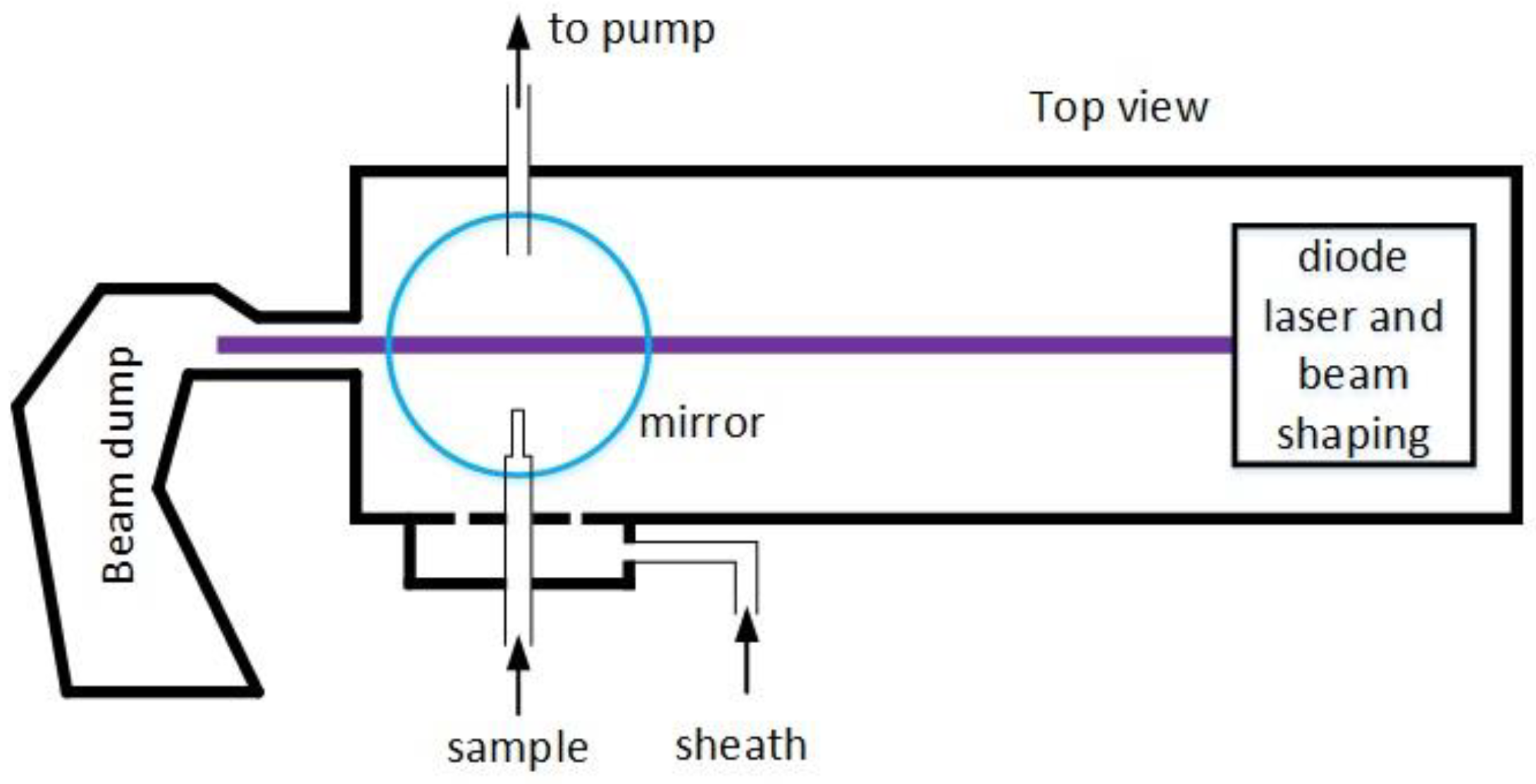
2.2. Portable Optical Particle Spectrometer
- Both the particle spectrometer and the lidar operate based on optical scattering and are influenced by the same complex refractive index, particularly its real part [8]. When the refractive index variation is minimal, these instruments can effectively reflect the consistency of aerosol optical responses.
- Although they measure different physical quantities [9], in atmospheric aerosols, where absorption effects are weak, extinction is primarily governed by scattering. Therefore, the target parameters measured by both instruments are consistent.
- Both instruments are capable of continuous 24 h field observations, enabling real-time detection of atmospheric aerosol samples within the same region. This ensures that the data originate from the same location and time, eliminating the impact of sample differences that could undermine the validity of the experiment.
- The particle spectrometer is cost-effective, requires low maintenance, and exhibits strong environmental adaptability, making it suitable for field deployments. This provides the most cost-effective solution for the present study.
3. Aerosol Particle Effective Radius Retrieval Method
3.1. Overview of the Retrieval Process
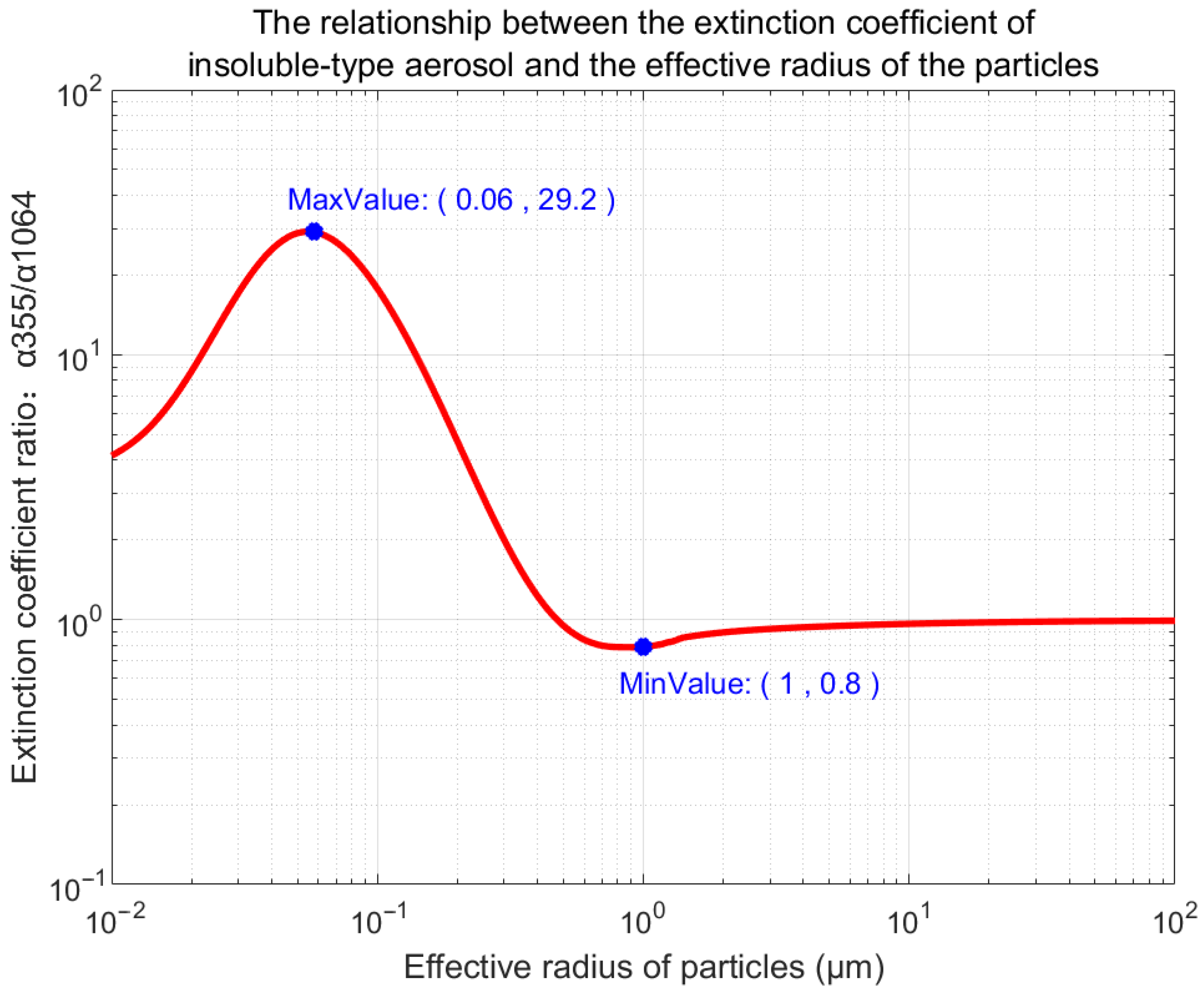
- Establishment of the extinction coefficient ratio to particle effective radius lookup table: Using the complex refractive index provided by the OPAC (Optical Properties of Aerosols and Clouds) database [15], the extinction efficiency factor of aerosol particles in the range of [0.01, 100] μm is calculated. By combining the Gamma distribution, the extinction coefficient ratio at wavelengths of 355 nm and 1064 nm can be derived. From the relationship between the extinction coefficient ratio and the particle effective radius, it is found that the extinction coefficient ratio is monotonic and unique in the range of [0.06, 1] μm, allowing for the construction of a lookup table that relates the extinction coefficient ratio to the particle effective radius within this range.
- Inversion of the measured extinction coefficient ratios for aerosol particles at two wavelengths: The real-time backscattered signals of atmospheric aerosol retrieved by the dual-wavelength lidar are used to determine the effective retrievals range of the lidar. By applying the Mie scattering lidar equation and using the slope method, the aerosol extinction coefficients at both wavelengths are calculated, leading to the calculation of the extinction coefficient ratio.
- Lookup of the real-time aerosol particle effective radius: The measured extinction coefficient ratio is combined with the extinction coefficient ratio to particle effective radius lookup table, allowing the aerosol effective radius of atmospheric aerosol particles to be determined.
3.2. Establishment of the Lookup Table for the Relationship Between Extinction Coefficient Ratio and Particle Effective Radius
3.2.1. Theoretical Basis for Establishing the Lookup Table
3.2.2. Implementation Process for Establishing the Lookup Table
3.3. Retrieval of the Measured Extinction Coefficient Ratios at Two Wavelengths
3.3.1. Theoretical Basis for Extinction Coefficient Retrieval
3.3.2. Implementation Process for Extinction Coefficient Retrieval
4. Results
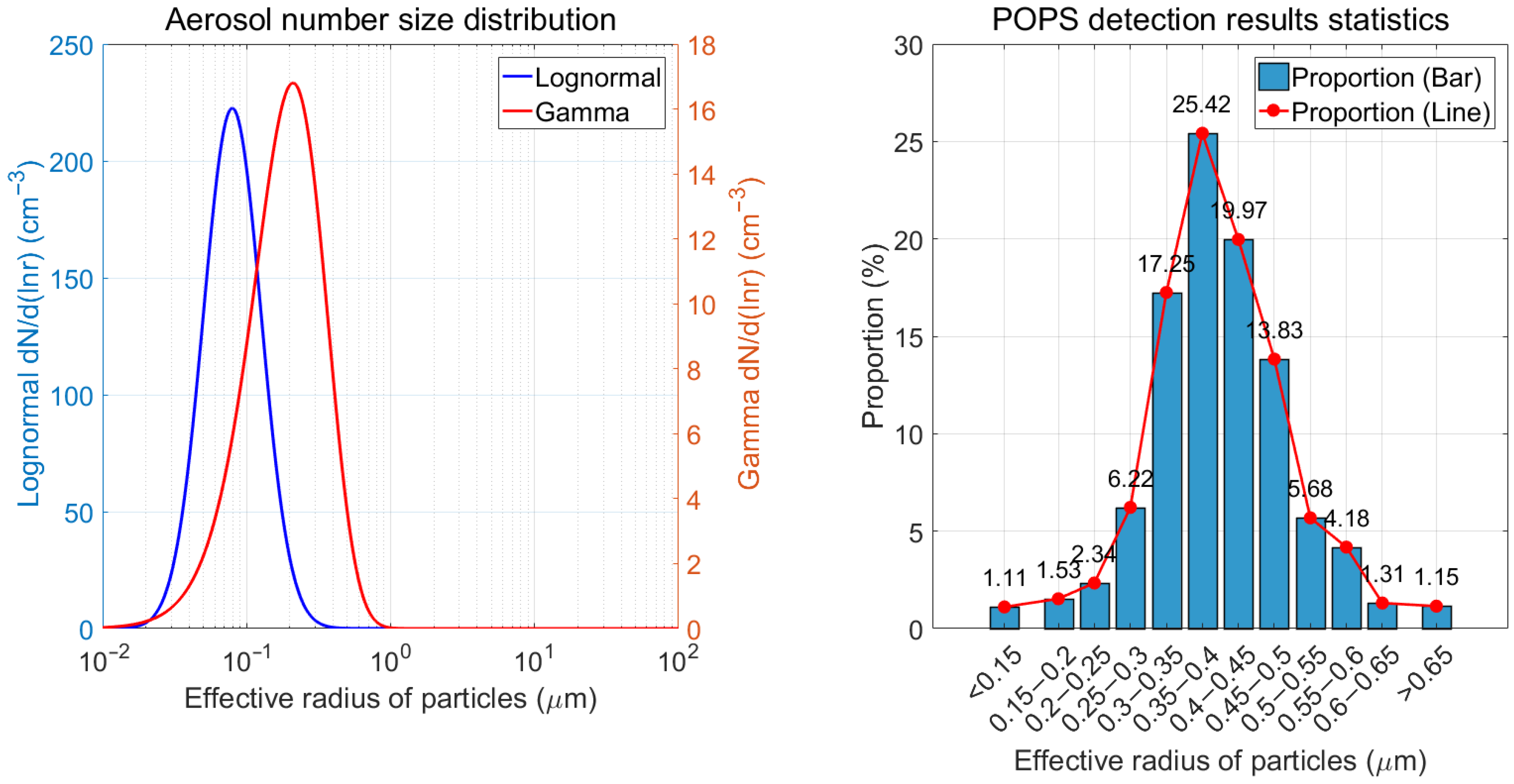
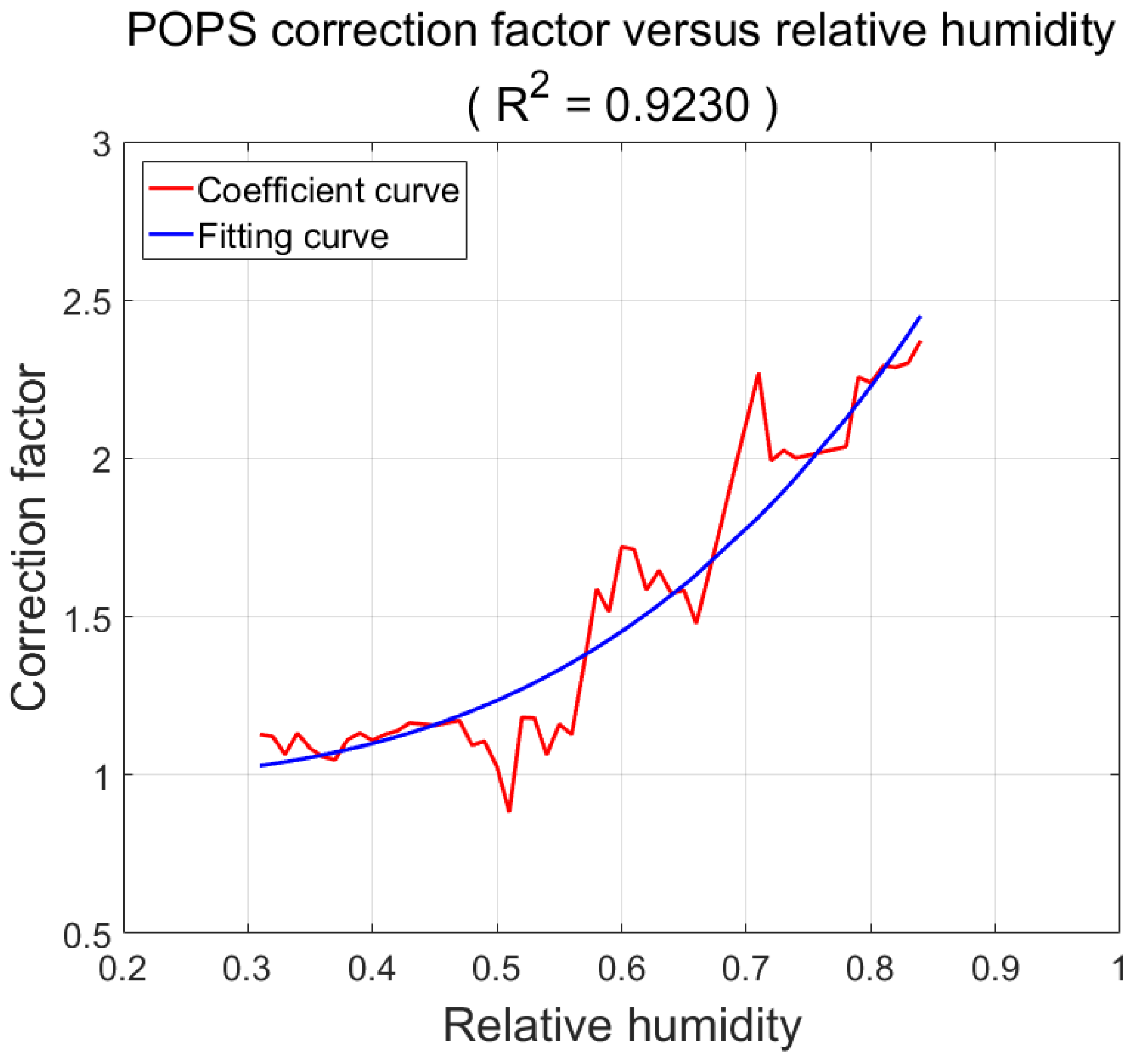
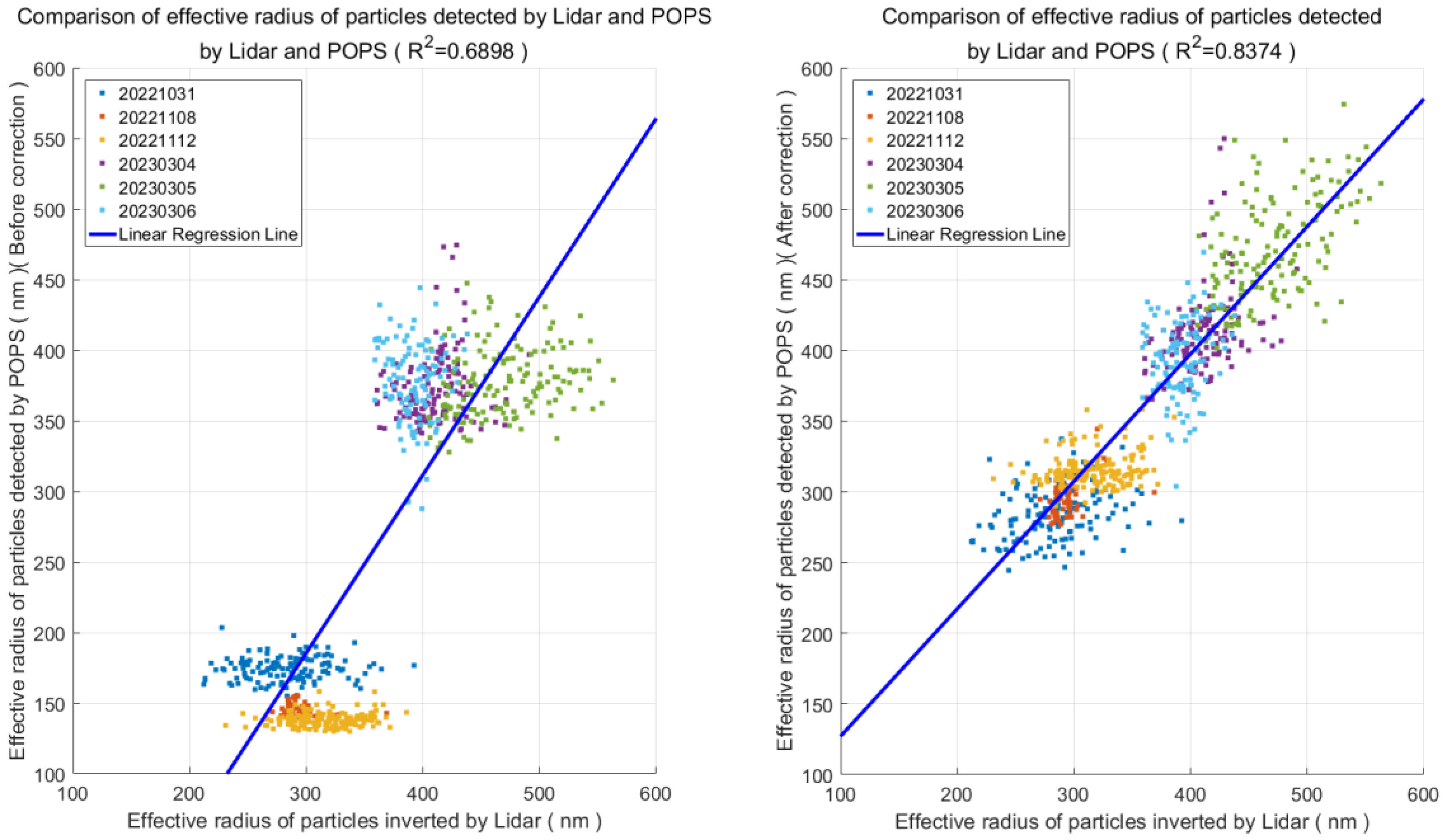
4.1. Correction of the Particle Spectrometer Detection Results
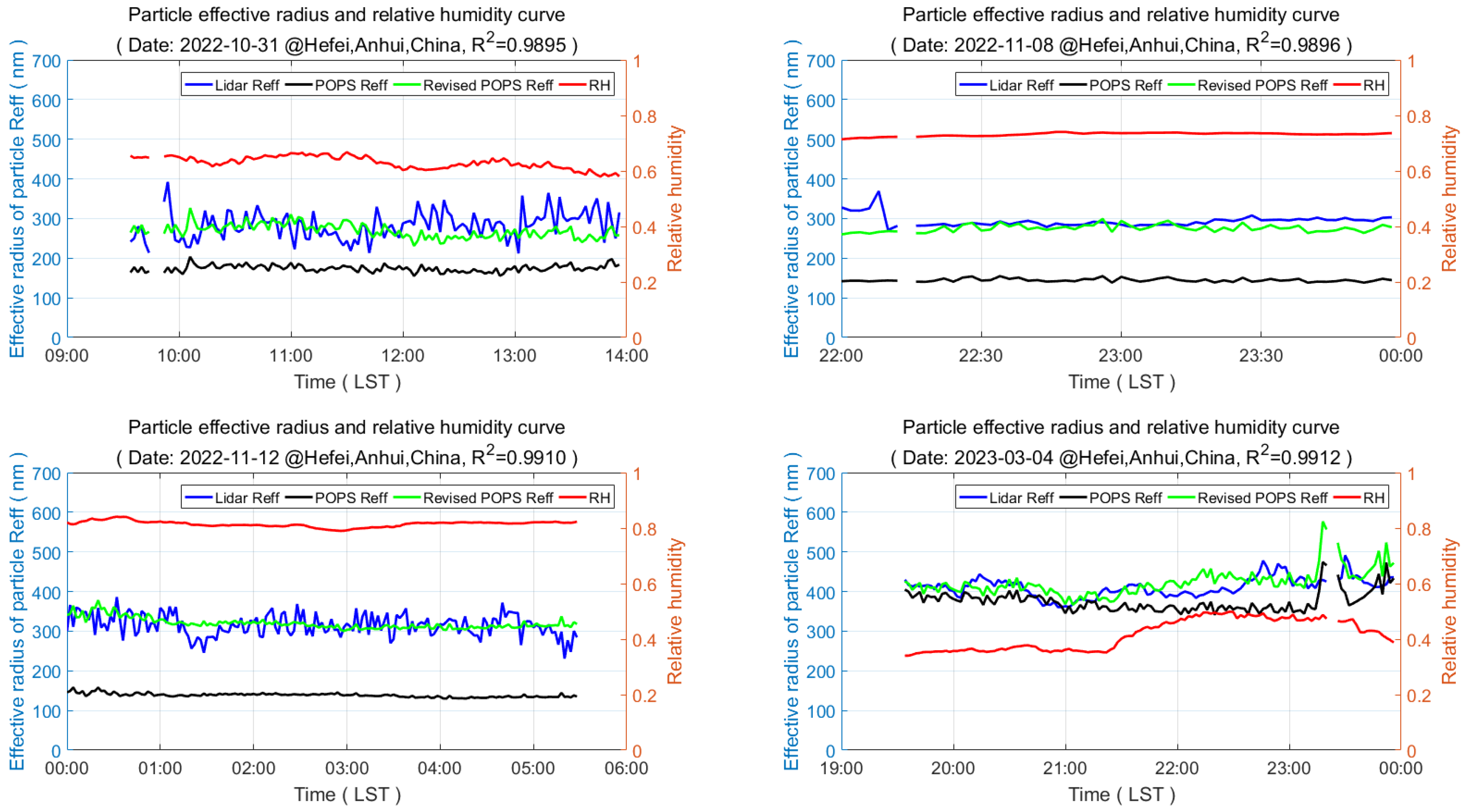
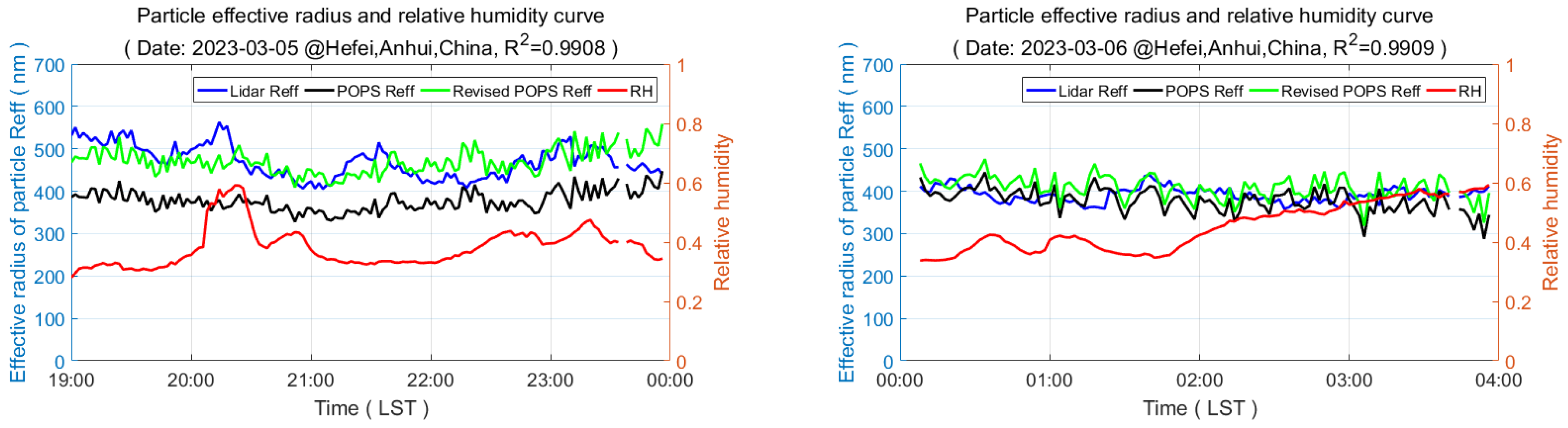
4.2. Comparison of the Dual-Wavelength Lidar and Particle Spectrometer Detection Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.J.; Hu, S.X.; Zhou, J.; Hu, H.L.; Xie, C.B.; Dong, J.H.; Yuan, K.E.; Zhang, C.Y.; Wu, X.Q.; Huang, Y.B.; et al. Lidar Atmospheric Parameter Measurement; Science Press: Beijing, China, 2014. [Google Scholar]
- Hou, H.Y.; Liu, J.; Zhong, W.T.; Yan, K.J.; Di, H.G. Aerosol particle size distribution retrieval algorithm and error analysis based on multi-wavelength radar. In Proceedings of the Tenth International Symposium on Precision Engineering Measurements and Instrumentation, Kunming, China, 8–10 August 2018; pp. 476–481. [Google Scholar]
- Bott, A. A numerical model of the cloud-topped planetary boundary-layer: Influence of the physico-chemical properties of aerosol particles on the effective radius of stratiform clouds. Atmos. Res. 2000, 53, 15–27. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, D.R.; Huo, J. Retrieval of cloud optical thickness and effective particle radius using transmitting solar radiation: Method study. Prog. Nat. Sci. 2006, 16, 850–858. [Google Scholar]
- Jiang, J.H.; Su, H.; Zhai, C.; Massie, S.T.; Schoeberl, M.R.; Colarco, P.R.; Platnick, S.; Gu, Y.; Liou, K.-N. Influence of convection and aerosol pollution on ice cloud particle effective radius. Atmos. Chem. Phys. 2011, 11, 457–463. [Google Scholar] [CrossRef]
- Chen, Q.Y.; Mao, S.; Yin, Z.P.; Yi, Y.; Li, X.; Wang, A.Z.; Wang, X. Compact and efficient 1064 nm up-conversion atmospheric lidar. Opt. Express 2023, 31, 23931–23943. [Google Scholar] [CrossRef] [PubMed]
- Donovan, D.P.; Carswell, A.I. Principal component analysis applied to multiwavelength lidar aerosol backscatter and extinction measurements. Appl. Opt. 1997, 36, 9406–9424. [Google Scholar] [CrossRef] [PubMed]
- Mei, F.; McMeeking, G.; Pekour, M.; Gao, R.-S.; Kulkarni, G.; China, S.; Telg, H.; Dexheimer, D.; Tomlinson, J.; Schmid, B. Performance Assessment of Portable Optical Particle Spectrometer (POPS). Sensors 2020, 20, 6294. [Google Scholar] [CrossRef] [PubMed]
- Mei, F.; Pekour, M. Portable Optical Particle Spectrometer (POPS) Instrument Handbook; Oak Ridge National Laboratory (ORNL): Oak Ridge, TN, USA; Atmospheric Radiation Measurement (ARM) Data Center, Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2020. [Google Scholar]
- Gao, R.S.; Telg, H.; McLaughlin, R.J.; Ciciora, S.J.; Watts, L.A.; Richardson, M.S.; Schwarz, J.P.; Perring, A.E.; Thornberry, T.D.; Rollins, A.W. A light-weight, high-sensitivity particle spectrometer for PM2.5 aerosol measurements. Aerosol Sci. Technol. 2016, 50, 88–99. [Google Scholar] [CrossRef]
- Yu, P.F.; Rosenlof, K.H.; Liu, S.; Telg, H.; Thornberry, T.D.; Rollins, A.W.; Portmann, R.W.; Bai, Z.X.; Ray, E.A.; Duan, Y.J. Efficient transport of tropospheric aerosol into the stratosphere via the Asian summer monsoon anticyclone. Proc. Natl. Acad. Sci. USA 2017, 114, 6972–6977. [Google Scholar] [CrossRef] [PubMed]
- Wang, L. Radiation Characteristics of Aerosol Particles/Particle System Under Different Relative Humidity. Master’s Thesis, Wuhan University of Science and Technology, Wuhan, China, 2022. [Google Scholar]
- Xia, C. Effects of Hygroscopicity on Aerosol Optical Properties and Direct Radiative Forcing in Beijing. Ph.D. Thesis, Nanjing University of Information Science & Technology, Nanjing, China, 2023. [Google Scholar]
- Zhang, L. Observation Study of Relative Humidity Effects on Aerosol Light Scattering at a Regional Backgound Site in the Yangtze Delta Region. Master’s Thesis, Chinese Academy of Meteorological Sciences, Beijing, China, 2014. [Google Scholar]
- Hess, M.; Koepke, P.; Schult, I. Optical Properties of Aerosols and Clouds: The Software Package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Wang, Z.X. The Precise Detection of Aerosol Particle Size Distributions of Fog/Haze the Open Atmosphere. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2019. [Google Scholar]
- Liu, B.L. Aerosol Effective Radius Retrieval Based on Dual-Wavelength Lidar Measurement. Master’s Thesis, University of Science and Technology of China, Hefei, China, 2023. [Google Scholar]
- Müller, D.; Wagner, F.; Wandinger, U.; Ansmann, A.; Wendisch, M.; Althausen, D.; von Hoyningen-Huene, W. Microphysical particle parameters from extinction and backscatter lidar data by inversion with regularization: Experiment. Appl. Opt. 2000, 39, 1879–1892. [Google Scholar] [CrossRef] [PubMed]
- AboEl-Fetouh, Y.; O’Neill, N.; Ranjbar, K.; Hesaraki, S.; Abboud, I.; Sobolewski, P. Climatological-scale analysis of intensive and semi-intensive aerosol parameters derived from AERONET retrievals over the Arctic. J. Geophys. Res. Atmos. 2020, 125, e2019JD031569. [Google Scholar] [CrossRef]
- Xiong, F.L. Study of Fitting Gamma Raindrop Size Distribution. Master’s Thesis, Nanjing University of Information Science and Technology, Nanjing, China, 2016. [Google Scholar]
- Liu, D. Development of Polarization-Meter Lidar and Lidar Detection in the Atmospheric Boundary Layer. Ph.D. Thesis, Graduate School of the Chinese Academy of Sciences, Beijing, China, 2005. [Google Scholar]
- Tao, Z.M.; Zhang, Y.C.; Zhang, G.X.; Lv, Y.H.; Liu, X.Q.; Tan, K.; Shao, S.S.; Hu, H.L. Properties of extinction efficiency factor of aerosol particles and fitting of scale spectrum. Chin. J. Quantum Electron. 2004, 21, 103–109. [Google Scholar]
- Zhao, H. Atmospheric Aerosol Detection and Experimental Research Based on Multiwavelength Lidar and In-Situ Instruments. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2017. [Google Scholar]
- Hansen, J.E.; Travis, L.D. Light scattering in planetary atmospheres. Space Sci. Rev. 1974, 16, 527–610. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Zhang, Z.Y.; Su, L.; Chen, L.F. Retrieval and analysis of aerosol lidar ratio at several typical regions in China. Chin. J. Lasers 2013, 40, 1–6. [Google Scholar]
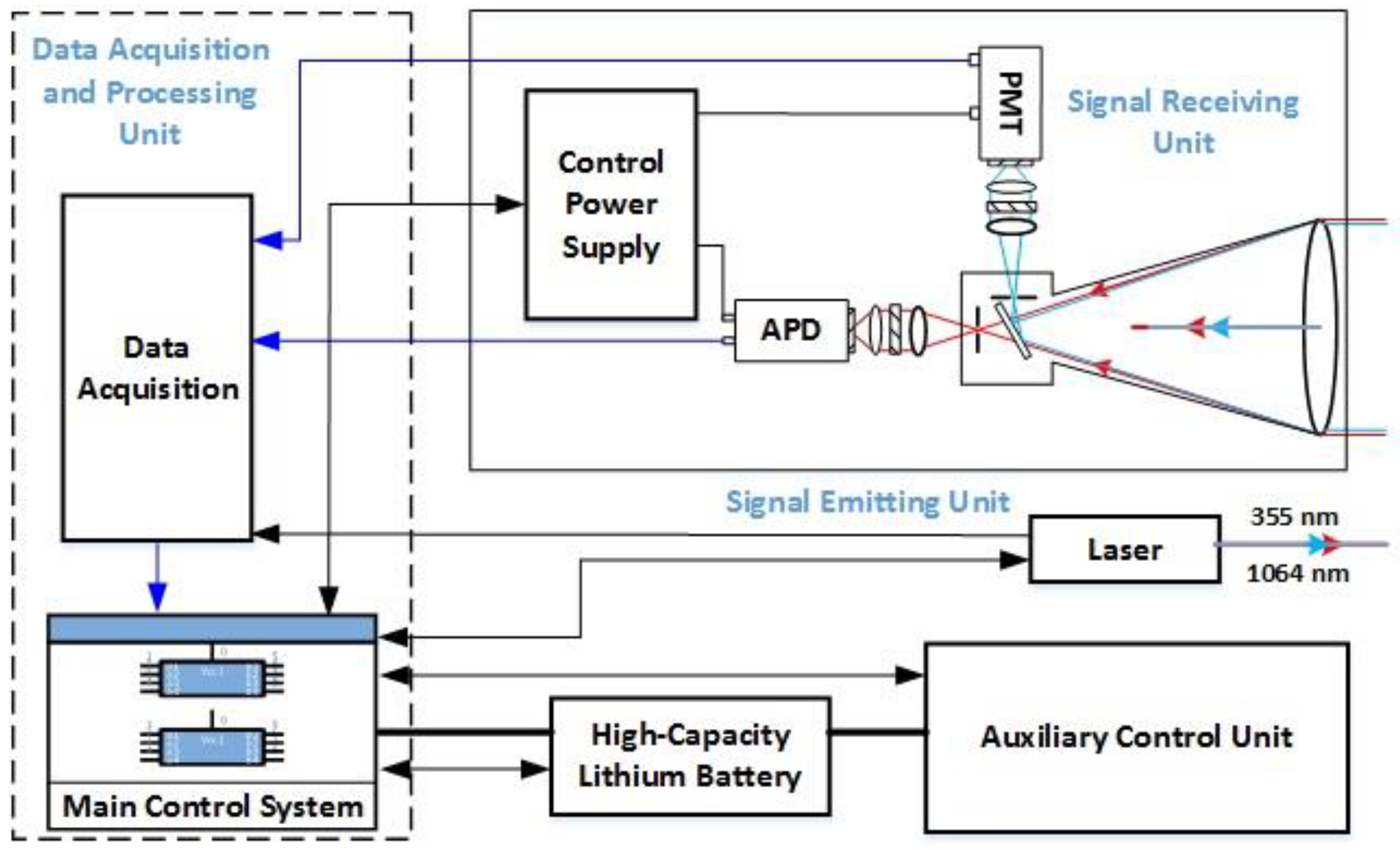


| Parameter Name | Channel 1 | Channel 2 | |
|---|---|---|---|
| Overall Performance | Wavelength | 355 nm | 1064 nm |
| Temporal Resolution | 5 s~300 s | 5 s~300 s | |
| Spatial Resolution | 7.5 m | 7.5 m | |
| Detection Range | 3 km (Under the condition of horizontal visibility 10 km) | ||
| Weight | 11.7 kg | ||
| Power Consumption | 150 W | ||
| Battery Life | 4.8 h | ||
| Laser Transmitter Unit | Single Pulse Energy | 40 μJ | 40 μJ |
| Laser Repetition Frequency | 1 kHz | 1 kHz | |
| Pulse Width | 0.6 ns | 0.6 ns | |
| Beam Expansion Gain | 22 times | ||
| Signal Receiving Unit | Detector Type | PMT | APD |
| Telescope Type | Transmissive | ||
| Telescope Diameter | 150 mm | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Z.; Liu, D.; Mao, J.; Wang, Z.; Wu, D.; Zhang, S.; Kuang, Z.; Shi, Q.; Wang, Y. Research on Effective Radius Retrievals of Aerosol Particles Based on Dual-Wavelength Lidar. Remote Sens. 2025, 17, 1383. https://doi.org/10.3390/rs17081383
Lv Z, Liu D, Mao J, Wang Z, Wu D, Zhang S, Kuang Z, Shi Q, Wang Y. Research on Effective Radius Retrievals of Aerosol Particles Based on Dual-Wavelength Lidar. Remote Sensing. 2025; 17(8):1383. https://doi.org/10.3390/rs17081383
Chicago/Turabian StyleLv, Zuokun, Dong Liu, Jietai Mao, Zhenzhu Wang, Decheng Wu, Shuai Zhang, Zhiqiang Kuang, Qibing Shi, and Yingjian Wang. 2025. "Research on Effective Radius Retrievals of Aerosol Particles Based on Dual-Wavelength Lidar" Remote Sensing 17, no. 8: 1383. https://doi.org/10.3390/rs17081383
APA StyleLv, Z., Liu, D., Mao, J., Wang, Z., Wu, D., Zhang, S., Kuang, Z., Shi, Q., & Wang, Y. (2025). Research on Effective Radius Retrievals of Aerosol Particles Based on Dual-Wavelength Lidar. Remote Sensing, 17(8), 1383. https://doi.org/10.3390/rs17081383








