Abstract
Multi-temporal synthetic aperture radar interferometry (MT-InSAR) has evolved from a niche research technique into a powerful global monitoring tool. With the launch of nationwide and continent-wide ground motion services (GMSs), freely available deformation data can now be analyzed on a large scale. However, their applicability for monitoring critical infrastructure, such as dams, has not yet been thoroughly assessed, and several challenges have hindered the integration of MT-InSAR into existing monitoring frameworks. These challenges include technical limitations, difficulties in interpreting deformation results, and the rigidity of existing safety protocols, which often restrict the adoption of remote sensing techniques for operational dam monitoring. This study evaluates the effectiveness of persistent scatterer (PS) data from the German ground motion service (Bodenbewegungsdienst Deutschland, BBD) in complementing time-consuming in situ techniques. By analyzing a gravity dam in Germany, BBD time series were compared with in situ pendulum data. We propose a two-stage assessment procedure: First, we evaluate the dam’s suitability for PS analysis using the CR-Index to identify areas with good radar visibility. Second, we assess the interpretability of BBD data for radial deformations by introducing a novel index that quantifies the radial sensitivity of individual PS points on the dam. This index is universally applicable and can be transferred to other types of infrastructure. The results revealed a fair correlation between PS deformations and pendulum data for many PS points (up to = 0.7). A priori feasibility assessments are essential, as factors such as topography, land cover, and dam type influence the applicability of the PS technique. The dam’s orientation relative to the look direction of the sensor emerged as a key criterion for interpreting radial deformations. For angle differences () of up to 20° between the true north radial angle of a PS point and the satellite’s look direction, the line-of-sight (LOS) sensitivity accounts for approximately 50 to 70% of the true radial deformation, depending on the satellite’s incidence angle. This criterion is best fulfilled by dams aligned in a north–south direction. For the dam investigated in this study, the LOS sensitivity to radial deformations was low due to its east–west orientation, resulting in significantly higher errors (6 mm mm) compared to in situ pendulum data. Eliminating PS points with an unfavorable alignment with the sensor should be considered before interpreting radial deformations. For implementation into operational monitoring programs, greater effort must be spent on near-real-time updates of BBD datasets.
1. Introduction
As critical infrastructure, dams require regular monitoring to ensure their safe operation. Depending on their size, a comprehensive measurement setup is installed to monitor deformations over short- and long-term periods. These measurements are typically conducted using in situ geodetic methods such as pendulum systems and trigonometry [1]. Although trigonometric measurements cover the entire dam, field campaigns are time-consuming and are often conducted only twice a year. Pendulum systems enable continuous monitoring, usually with one or more measurements per day [2]. However, they are not installed on every dam and only capture deformations at specific locations (e.g., in the middle of the crest), which may not be representative of deformation patterns across other dam sections.
Advancements in multi-temporal synthetic aperture radar interferometry (MT-InSAR) have addressed these challenges by combining temporally dense time series with a high number of observation points. Interferometric techniques, such as the persistent scatterer interferometry (PSI), enable the monitoring of deformations with millimeter-level precision. With the implementation of ESA’s Sentinel-1 (S-1) data into nationwide ground motion services (GMSs), persistent scatterer (PS) time series are now freely available as analysis-ready datasets. In Germany, the German ground motion service (Bodenbewegungsdienst Deutschland, BBD) provides data spanning from 2015 to 2021 [3]. With revisit intervals ranging from 6 to 12 days, the BBD offers valuable insights into the structural behavior of dams and their long-term deformation characteristics.
1.1. MT-InSAR Employed for Dam Monitoring in Scientific Studies
MT-InSAR has evolved from a niche technique to a valuable monitoring tool, with its effectiveness in deformation analysis demonstrated on embankment dams [4,5,6,7,8,9,10,11], gravity dams [2,12,13,14,15,16], arch-gravity dams [17], and tailings dams [18,19]. Most of these studies are based on data that have been individually processed for each analysis. However, due to time constraints and limited technical expertise, dam operators may prefer analysis-ready datasets over independently processing PS data. This underscores the necessity of evaluating the potential of PS time series provided through GMS. Few studies have focused on the use of analysis-ready PS data for incorporation into operational monitoring programs. Table 1 shows a selection of recent studies. Even et al. [20] compared the accuracy of BBD time series with those provided by the European ground motion service (EGMS) against external leveling and GNSS data, reporting slightly higher biases in the EGMS data.

Table 1.
Selection of studies relevant to this work in the context of MT-InSAR. Some of them utilize analysis-ready time series as the data source.
Marchamalo-Sacristán et al. [11] examined the integration of MT-InSAR with other monitoring techniques in a pilot monitoring system for embankment dams in Spain. While this study focused primarily on developing an application programming interface (API) for operational monitoring, it did not consider analysis-ready PS data. Dubois et al. [15] investigated the deformation of a gravity dam in Germany using S-1 data from the BBD. The recent nature of these studies highlights the increasing efforts in this field; however, PS data have not yet been integrated into operational monitoring procedures.
1.2. Challenges for Incorporation into Operational Monitoring Programs
Although the potential of PSI for dam monitoring has been well researched, several challenges have so far hindered the integration of this technique into existing monitoring methods [11]. These challenges include administrative and technical barriers related to data processing, interpretation, and integration:
- Lack of interoperability: The rigidity of existing monitoring procedures presents a considerable challenge, as they may not be easily adaptable to new technologies. This includes discrepancies in data formats and incompatibility with different monitoring software. Standardization of data formats is crucial to fully leverage advanced technologies such as PSI [11].
- Lack of interpretability: One of the primary challenges for dam operators is the interpretation of PS-derived deformations, which are measured in the sensor’s line of sight (LOS) [21,22]. Since LOS deformations include both vertical and horizontal displacement components, direct comparison with pendulum data, acquired radially to the dam, is challenging. Given that the highest deformation on a gravity dam typically occurs perpendicular to the dam crest, PS data must be converted to ensure comparability with in situ measurements, improving interpretability for dam operators.
- Lack of standardized workflows: For effective implementation, the benefits and limitations of PSI for dam monitoring must be more clearly defined. Since PSI applications are highly case-specific, greater effort is required to assess their feasibility for individual dams. The development of standardized guidelines could facilitate this assessment, addressing aspects such as
- A: Assessment of topography: Steep slopes and other topographic features can influence the applicability of PSI due to the sensor geometry (e.g., layover, foreshortening, shadow). Therefore, it is crucial to evaluate the impact of topography prior to analysis.
- B: Assessment of land cover: Different land cover types affect the number of detected PS points. Temporal coherence is usually low in vegetated areas, making PSI applications more challenging.
- C: Assessment of dam type: Since the number of PS points is essentially dependent on the material properties of the building, the dam type is one of the key factors for successful PS analysis. In contrast to gravity or arch dams, typically made of masonry or concrete, embankment dams are built on various compositions of rock or soil, often covered by vegetation. This can limit the detection of PS points.
- D: Assessment of dam orientation: The dam’s orientation relative to the sensor’s look direction is one of the most important criteria for interpreting PSI-derived deformations. Most satellites used for infrastructure monitoring, such as Cosmo-SkyMed, TerraSAR-X, and Sentinel-1 operate with an east–west-looking direction. Consequently, dams oriented north–south provide the highest sensitivity for detecting deformations perpendicular to their crest.
1.3. Research Approach
This study evaluates the potential of BBD-provided PS time series for interpreting radial deformations on a gravity dam and comparing them to traditional in situ pendulum data. We propose a two-stage assessment procedure: First, we analyze the selected dam concerning key factors such as topography and land cover to determine its suitability for PS analysis. Second, we assess the interpretability of radial PS time series for comparability with pendulum data, highlighting the impact of dam orientation on PS time series accuracy. By introducing a novel index applicable to various types of infrastructure, the sensitivity of LOS measurements to radial deformations can be effectively assessed. To the best of our knowledge, this study is the first to assess the feasibility of incorporating freely available, analysis-ready PS data from the BBD into the monitoring program of gravity dams.
2. Study Site and Data
2.1. Study Site
This study was conducted on the Ennepe Dam, a 50 m high arched gravity dam with a crest length of 320 m. It is located in the Sauerland region, North Rhine-Westphalia, Germany. The middle of its downstream side is oriented towards the north (radial orientation: 10°). The Ennepe Dam serves the water supply of the Ruhr area and plays a vital role in flood protection and low water elevation [23]. The dam is operated and monitored by the Ruhrverband, a non-profit-oriented water management company. Its monitoring setup consists of 40 trigonometric measurement points and two pendulum systems (PL1 and PL2), located on the two towers in the middle of the dam crest (Figure 1).
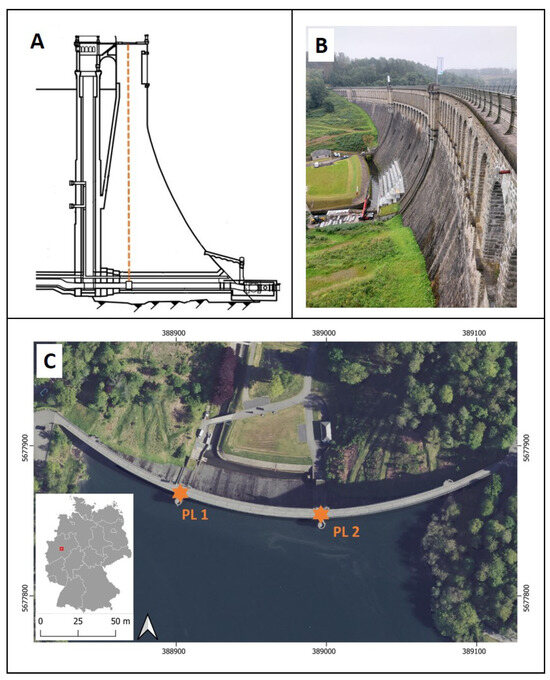
Figure 1.
Characteristics of the Ennepe Dam: (A) Cross section (adapted by [23]). (B) Downstream side of the dam as viewed from the west section and (C) on a digital orthophoto. The location of the pendulum systems is marked in orange. Orthophoto: GDI-NRW [24], EPSG: 25832.
2.2. Data
This study covered more than six years, spanning from April 2015 to December 2021.
2.2.1. Topography and Land Cover Information
To assess the topographic conditions and land cover of the dam, we utilized a high-resolution digital elevation model (DEM) with a 1-m spatial resolution, provided by the Geodata Infrastructure North Rhine-Westphalia (GDI-NRW) [24]. Additionally, freely available land cover data from GDI-NRW were incorporated into the analysis [24].
2.2.2. German Ground Motion Service (BBD)
The BBD provides high-resolution, nationwide monitoring of ground movements across Germany. Operated by the Federal Institute for Geosciences and Natural Resources (BGR), it delivers PS-based deformation data derived from ESA’s Copernicus S-1 satellites. The raw data are processed using a PSI processor specifically optimized for large-area analysis by the German Aerospace Center (DLR), and made available as wide-area products (WAPs) [25,26,27] on a WebGIS. Each dataset is filtered applying a temporal coherence threshold for quality assurance. For calibration and validation, external GNSS data are utilized [28]. The time series data are freely accessible from both ascending and descending orbits in the sensor’s line of sight. In addition, the BBD provides products related to vertical and east–west displacements, available on a 50 m2; grid [3]. All datasets can be downloaded in standard formats (.csv/.gdb) at no cost. The S-1 satellites offer a high temporal resolution, with revisit times ranging between six and 12 days [28]. The deformation data are updated annually by BGR, with each update extending the dataset by one year. Further details on BBD’s WebGIS platform can be found in Kalia et al. [28].
In this study, all available PS LOS data from April 2015 to December 2021, acquired in both ascending and descending orbits, were utilized. Table 2 summarizes the characteristics of the datasets, which were provided with a temporal coherence threshold of >0.75.

Table 2.
Characteristics of the S-1 data stacks utilized in the analysis [3].
2.2.3. In Situ Data
In situ data recorded by two pendulum systems at the center of the dam were utilized. These systems measure radial deformation data perpendicular to the dam crest, providing a detailed representation of movement in these dam sections. The pendulum data were provided by the Ruhrverband in a daily resolution. Additionally, trigonometric data spanning several decades were available. However, due to time-consuming field campaigns, these data are acquired only biannually, limiting their temporal resolution to only 14 recordings within the study period. Therefore, they were not used for comparison with PS data. To determine the radial angle of each PS point on the dam, the coordinates of the circle center defining the dam’s alignment were obtained from the Ruhrverband using TIM-online, a publicly accessible web application provided by the state of North Rhine-Westphalia for geospatial data visualization [29].
3. Methods
The methodology is divided into two sections: First, we introduce an index for assessing the general feasibility of a dam for PS-based monitoring with regard to topography and land cover. Second, we describe the methodological procedure for converting LOS data into radial deformation time series. In addition, we develop a metric for evaluating the sensitivity of LOS measurements to radial deformations depending on dam orientation.
3.1. Evaluation of Topography and Land Cover: The CR-Index
To assess the feasibility of a PS-based monitoring strategy for individual dams, the CR-Index was used, incorporating information on topography and land cover. The CR-Index enables the pixel-wise identification of areas with good radar visibility by assigning probabilistic values for detecting PS points [30,31]. It consists of two components, land cover information and the R-Index. The R-Index is calculated as follows:
where S represents the slope (i.e., the steepness of the land surface), denotes the S-1 incidence angle [32], and is the local aspect angle of the S-1 flight path in the ascending () or descending direction (), respectively. The complete derivation for both trajectories is provided in Appendix A Equations (A1) and (A2). Table 3 presents the range of index values along with the corresponding class descriptions [30].

Table 3.
Range of R-Index values along with the corresponding class descriptions (adapted from [30]).
By combining the R-Index visibility map with additional land cover information, the CR-Index is derived. In this study, we used the CR-Index to assess the likelihood of detecting PS points on the Ennepe Dam using BBD S-1 data. Values greater than 75 indicate excellent preconditions for PS analysis. We followed the same approach proposed by Notti et al. [30], adapted from Jänichen et al. [32]: a land use index (LUI) specifically tailored to Germany was developed, addressing the limitations of existing LUI values for Great Britain, which cannot be directly applied due to differing land cover classifications. Detailed information about this adaption can be found in Jänichen et al. [32]. The waterbody of the reservoir was masked prior to analysis.
3.2. Converting PS LOS Data to Radial Deformation Time Series
MT-InSAR measures deformations in the LOS geometry of the satellite. This geometry is defined as the projection of a 3D displacement vector d, with deformation components , , and in the north, east, and up directions, respectively, into the LOS direction [33]. The complete relationship between these components is provided in Appendix A Equation (A3). A conversion from a single LOS direction (dLOS) to a displacement d, corresponding to the expected direction of the detected movement, is performed as follows [34,35]:
where represents the angle between the vertical direction and the true deformation direction. The angular difference between the true north radial angle of a detected scatterer (), and the S-1 look direction () is referred to as . Its values range between 0° and 90° and are determined as follows:
On gravity dams, the highest proportion of movement is generally expected in the horizontal plane compared to the vertical component [2,36]. For the Ennepe Dam, this assumption was confirmed by trigonometric measurements, which indicated no significant vertical deformation within the study period [37]. Consequently, the S-1 LOS data could be converted to purely horizontal deformations (dHOR) by neglecting the vertical component (i.e., = 90°). As a result, Equation (2) simplifies to Equations (4) and (5):
We followed a similar approach proposed in Jänichen et al. [2]. However, we defined the LOS displacement as a projection of the true radial deformation, rather than vice versa. Importantly, this conversion is only valid if the displacements in one of the two dimensions are sufficiently small to be neglected [38,39].
Since the Ennepe Dam was built as a gravity dam with an arched crest, the orientation of the axes varies for each PS point, leading to variations in the angle between the true north and the radial axis [2]. To derive the true radial deformation (dRAD) from the horizontal deformation component, we applied the following conversion:
Figure 2 illustrates all relevant conversions between LOS geometry and the true radial deformation of a dam.
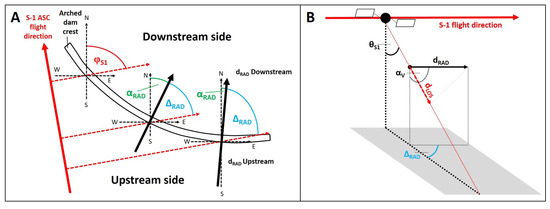
Figure 2.
Relationship between true radial dam deformations and their projection onto the LOS geometry of the sensor: (A) Variations in (blue) as a function of the true north radial angle of the corresponding PS point (, green), and the S-1 look direction ( = 84°, red dashed arrow). The effect is illustrated for the ascending flight direction. (B) A 3D representation of the projection of true radial deformations onto the sensor’s LOS geometry [35].
Descriptive statistics, including root mean square error (RMSE) and mean absolute error (MAE), were used to compare radial PS data with pendulum measurements. All PS points located near the two pendulum systems (i.e., <50 m) were analyzed. Outliers in the time series of each PS point were filtered using the 1.5 interquartile range of the dataset’s distribution. Since BBD data and pendulum measurements were not acquired on the same dates and had different temporal resolutions, only pendulum data corresponding to the acquisition dates of the PS time series were used. Finally, linear regression analysis was performed.
3.3. Evaluating the Sensitivity of PS Data to Radial Dam Deformations
We developed an index to assess the sensitivity of each PS point to radial deformations, based on its location on the dam. This metric expresses the LOS deformation of a PS point as a proportion of the true radial deformation (Figure 3). Importantly, LOS measurements depend primarily on the sensor’s incidence angle and its azimuthal alignment with the true deformation direction. Since MT-InSAR measures a combination of vertical and horizontal components, the true deformation amplitude decreases when projected onto the sensor’s LOS. The sensitivity to radial deformations, referred to as “LOS Sensitivity” in the following, was derived from the measured LOS deformation.
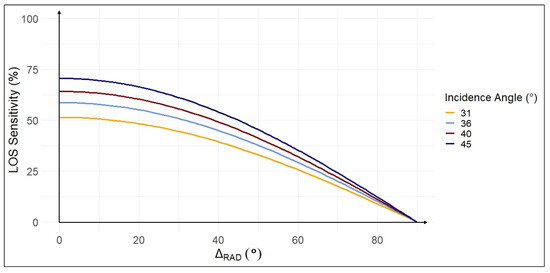
Figure 3.
LOS sensitivity (%) to radial deformations, expressed as a proportion of the true radial deformation (mm). The sensitivity of deformations projected onto the LOS of the sensor is described as a function of and . LOS sensitivity is presented for all datasets used in this study, along with their corresponding values.
As shown in Figure 3, the graphs follow a nonlinear cosine curve, revealing maximum LOS sensitivity for purely horizontal deformations at shallow incidence angles (i.e., = 45°) and = 0°. Dams oriented perpendicular to the sensor’s look direction provide the most favorable conditions, resulting in the highest possible sensitivity to radial deformations. In practical terms, a PS point perfectly aligned with the azimuth look direction of the sensor at = 45° exhibits an LOS sensitivity of 71% of the true radial deformation amplitude. Figure 3 summarizes the LOS sensitivity for all datasets used in this study, along with their corresponding incidence angles. As decreases (i.e., steeper incidence angles), the LOS sensitivity to radial deformations declines to 64% for = 40°, 59% for = 36°, and 52% for = 31°. Notably, LOS sensitivity remains approximately constant as long as 20°. The minimum sensitivity occurs at = 90° (i.e., is perpendicular to ), where LOS sensitivity is 0%, regardless of the incidence angle.
Importantly, the index is not limited to dams but can be applied to other types of infrastructure, such as bridges, making it universally applicable for infrastructure monitoring. Moreover, the index remains consistent for both ascending and descending flight directions and is independent of the SAR wavelength, as it relies solely on the geometric relationship between the satellite’s look direction and the orientation of the building.
4. Results
First, the results of the CR-Index are presented and compared to the distribution of PS points on the dam. Second, the PS time series is analyzed and compared with pendulum data.
4.1. Feasibility Assessment
A total of 30 PS points were detected on the Ennepe Dam, with 13 in the ascending direction and 17 in the descending data stacks. Figure 4 shows their distribution on the Ennepe Dam. With the exception of two PS points in the ascending direction (i.e., ASC #088-02 & ASC #015-06), all points were located on the crest of the wall.
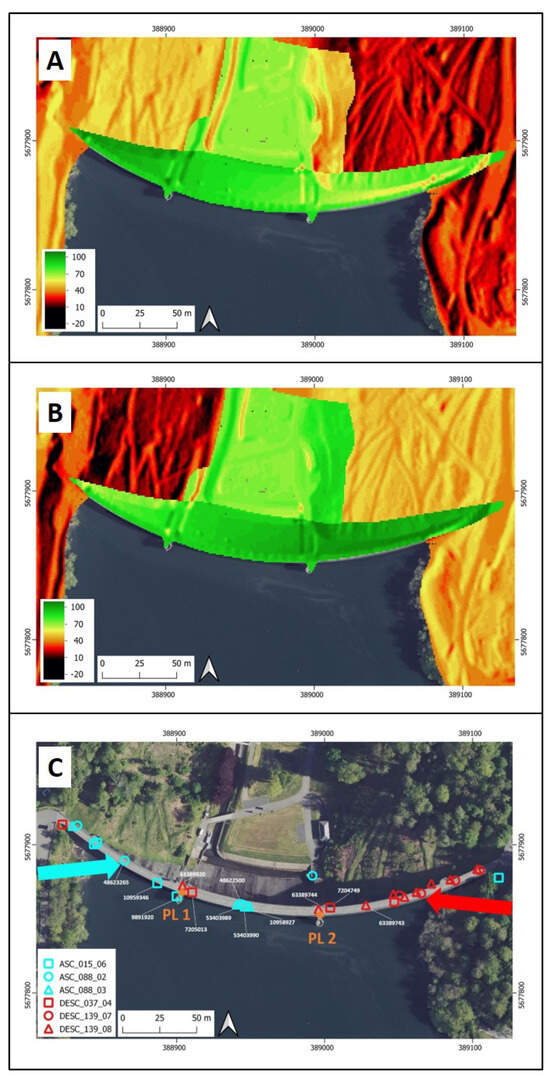
Figure 4.
Feasibility analysis on the Ennepe Dam using the CR-Index: (A) Ascending direction. (B) Descending direction. Values greater than 75 can be considered ideal for observation. (C) Distribution of PS points on the dam. Ascending points are shown in cyan, and descending points are shown in red. The arrows indicate the look direction of the S-1 satellites. The shape of the points corresponds to their affiliation with the respective data stack. The closest points to PL1 and PL2 are illustrated with their corresponding ID. Orthophoto: GDI-NRW [24], EPSG: 25832.
According to the CR-Index, 9 out of the 13 points in the ascending direction showed values of 75 or higher. In the descending orbits, this accounted for 95% of all points (16/17). As evident in Figure 4, notable differences in visibility occurred between the two side segments of the dam. While the ascending direction performed better in the western section, descending visibility increased towards the east. These variations can be attributed to the differing azimuth look angles of the ascending and descending trajectories, which result in layover or shadowing effects on the dam’s side sections. The western section of the Ennepe Dam is better aligned with the ascending orbits, whereas the eastern part exhibits higher visibility with the descending datasets. This pattern aligns with the distribution of PS points along the crest, where 11 out of the 13 points in the ascending data stacks were concentrated in the western section. In contrast, 14 out of 17 PS points in the descending direction were located on the eastern side of the dam. The temporal coherence of the points ranged from 0.76 to 0.92 in the ascending stacks and from 0.77 to 0.96 in the descending direction, indicating generally high data quality. Based on these aspects, the dam was considered suitable for further analysis.
4.2. Sensitivity to Radial Deformations and Time Series Analysis
Figure 5 illustrates the LOS sensitivity to radial deformations for all PS points on the Ennepe Dam, based on their location along the crest. The maximum LOS sensitivity could theoretically be achieved in the ascending data stacks at = 84° and = 264°. In the descending direction, the theoretical maxima occured at = 96° and = 276°. The difference between the maxima in the ascending and descending datasets was only 12°.
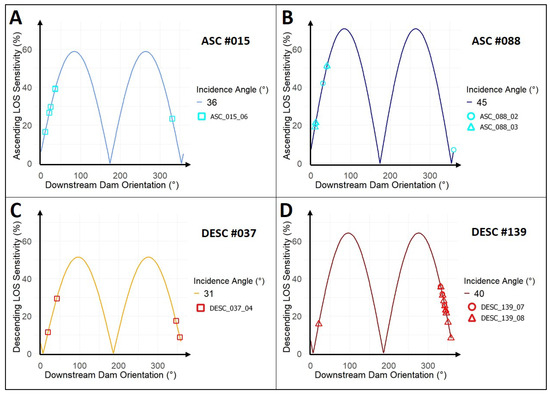
Figure 5.
LOS sensitivities (%), expressed as the proportion of the true radial deformation (mm), analyzed for all datasets and their corresponding PS points on the dam: (A) ASC #015. (B) ASC #088. (C) DESC #037. (D) DESC #139. The theoretical maxima between ascending and descending datasets differ by 12° in for congruence. Ascending points are shown in cyan, descending points in red. The shape of each point indicates its affiliation with the respective data stack.
Notably, due to the steeper incidence angles, the theoretical maxima for LOS sensitivity were generally lower in the descending direction compared to the ascending direction. As shown in Figure 5, none of the PS points on the Ennepe Dam were located near these maxima, either in the ascending or descending direction. The maximum LOS sensitivity in the ascending direction reached 51% of dRAD for two PS points in data stack #088, whereas the descending values were considerably lower, peaking at 36% of dRAD for two PS points in dataset #139. Overall, three out of 30 PS points exhibited LOS sensitivities of 40% or higher. In the descending direction, none of the PS points exceeded 40% sensitivity, making their interpretation and comparison with the pendulum data challenging. The limited number of PS points suitable for comparison with radial pendulum data is primarily due to the dam’s alignment with the satellite sensor, as its crest is oriented from west to east.
Table 4 summarizes the statistics of the PS points analyzed near the two pendulum systems. Most points exhibited a moderate correlation between the radial PS time series and the pendulum data. Errors ranged from 6.2 to 43 mm in RMSE and from 5.1 to 34.8 mm in MAE. Notably, the differences between ascending and descending orbits were remarkable. On PL1, the ascending direction achieved a high correlation of up to 0.7 in and mean absolute errors as low as 5 mm for PS point #48623265. The other PS points in the ascending direction showed moderate correlations () but considerably higher errors, ranging from 11.6 to 19.4 mm in RMSE and from 9.2 to 15.7 mm in MAE. This is due to the higher (see Table 4), as errors increase with increasing . Other contributing factors may include a lower signal-to-noise ratio (SNR) for these points compared to #48623265. The SNR values for all PS points are summarized in Appendix C Table A1 and Table A2.

Table 4.
Descriptive statistics of all PS points close to PL1 (left) and PL2 (right), along with their corresponding ID (#). The metrics refer to the radial PS time series, using the pendulum data as a reference. is given in degrees. RMSE and MAE are given in mm. All points indicate a significant correlation between PS data and pendulum measurements (p < 0.001).
The descending data stacks demonstrated lower correlations on PL1 but also lower errors compared to the ascending points (except #48623265). This is a result of the extremely small LOS amplitude for these two descending PS points. Since the look direction of the sensor is almost parallel to the dam crest, the SAR sensor is sensitive to measuring tangential deformations, which make up only a fraction of the radial deformation. In contrast, the descending orbits showed fair agreement with the pendulum data on PL2, reaching an of up to 0.7. However, RMSE and MAE were considerably higher compared to PL1. Since no ascending points were available on PL2, no comparison could be made with the descending datasets.
Figure 6 compares the deformation amplitudes of two PS points on PL1 and PL2 with respect to their radial position on the dam. As evident, both points exhibited the same seasonal deformation pattern as the in situ pendulum measurements, which led to correlations of up to 0.7 in . The deformation is primarily driven by seasonal fluctuations in water level and temperature, with an upstream radial movement during the summer, and a downstream movement in the winter [36]. However, considerable differences in deformation amplitudes were observed, not only between the two points on PL1 and PL2 but also across the different projections dLOS, dHOR, and dRAD. While the amplitudes for dLOS and dHOR nearly matched the amplitude of the pendulum data, the dRAD amplitudes were considerably higher.
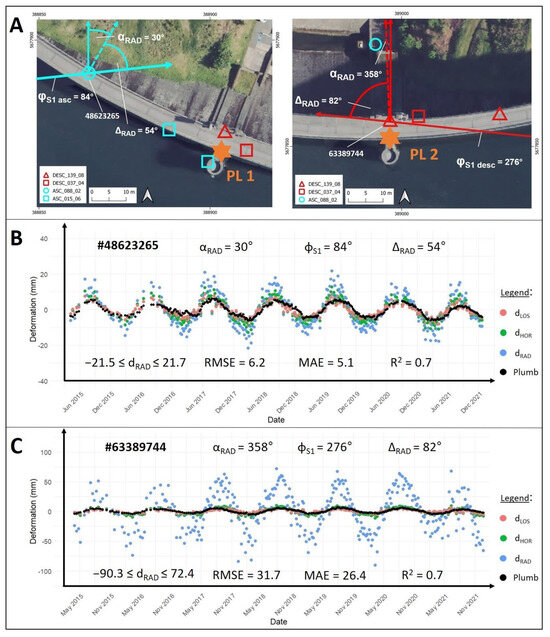
Figure 6.
Interpreting radial deformation time series: (A) Location of two PS points near to PL1 (left) and PL2 (right), along with the look direction () of the S-1 satellites (solid line) and the radial position () of the PS points (dashed line) in cyan (ascending), and red (descending). (B) Deformation time series of PS point #48623265 in the ascending direction, near PL1. (C) Deformation time series of PS point #63389744 in the descending direction, near PL2. The values for dLOS are illustrated in red, dHOR in green, and dRAD in blue. Black dots represent the pendulum time series. Notably, for visualization, the scaling of the y-axis differs between (B,C). of the PS points and their corresponding are provided in degrees. The amplitude of the radial time series is presented as an interval in mm. RMSE and MAE values are also provided in mm. Orthophoto: GDI-NRW [24], EPSG: 25832.
For the ascending PS point #48623265, the radial amplitude ranged between ±21 mm. In contrast, the time series of the descending PS point #63389744 on PL2 showed significantly higher amplitude differences compared to dLOS, dHOR, and pendulum data (Figure 6C). Although this point exhibited the same , the radial time series showed a considerable increase in deformation amplitude (−90 mm 70 mm), which led to higher RMSE and MAE values. This could be attributed to the largest for all PS points analyzed (82.5°). Since the descending look direction of the satellite is nearly parallel to the dam crest (Figure 6A), the LOS sensitivity for this PS point was minimal (8.5%). As a result, the derived radial deformation amplitude was an order of magnitude higher than the in situ pendulum measurements (±7 mm). It can be concluded that deriving radial deformations for this PS point is not plausible.
5. Discussion
This study examined the applicability of PS datasets for operational dam monitoring, presenting a selection of key considerations for assessing the suitability of individual dams for PS-based monitoring approaches. Importantly, these considerations represented only a subset of relevant factors and can be supplemented by additional variables based on the type of dam investigated or the specific requirements of dam operators.
As demonstrated, a priori analyses are beneficial in evaluating the general suitability of individual dams for PS-based monitoring. Geometric distortions (i.e., layover, foreshortening, and shadow) could influence their monitoring capability due to challenging topographic conditions. Therefore, a priori analyses are crucial in highlighting the limitations of the PS technique, as not all dams are equally well-suited.
The dam type and its relative orientation to the sensor’s look direction were among the most important criteria for interpreting PS data and ensuring comparability to in situ geodetic methods. Variations in also contributed to minor variations in the deformation amplitude of the time series. However, as can be seen in Figure 6, these variations accounted for only a fraction of the total deviation between and (see graph). Atmospheric effects can also impact radar signal quality, primarily due to variations in atmospheric pressure, temperature, and water vapor. Fluctuations in water vapor—especially in the lower troposphere (i.e., up to 2 km above ground)—can introduce significant, localized phase artifacts due to turbulent mixing [40]. These variations in water vapor content differ between morning and evening, potentially affecting the quality of MT-InSAR measurements and contributing to differences between ascending and descending acquisitions. Integrating information on the signal-to-noise ratio of PS points can be useful for filtering those with high noise. The BBD datasets used in this study provide the SNR of each PS point (see Appendix C Table A1 and Table A2), thereby facilitating decision-making.
As shown in Figure 5, the sensitivity to radial deformations between ascending and descending S-1 tracks differed by only 12°. However, due to the arched shape of the Ennepe Dam, the sensitivity to radial deformations varied considerably across different PS points (see Figure 6). Notable differences in deformation amplitude can arise between PS points, depending on the data stack and the projection used for analysis. The fact that the radial time series exceeded the deformation amplitude of the pendulum data by a significant margin limits their applicability for operational dam monitoring. Notably, the required monitoring accuracy for each dam varies depending on factors such as its dimensions, material composition, and interaction with the foundation bedrock [1,5,41]. According to Corsetti et al., concrete dams, such as the Ennepe Dam, require measurement precision approximately five times higher than that needed for embankment dams [5]. This may necessitate filtering adequate points or deriving segments with high radial deformation sensitivity to meet operational standards. Such a procedure could also be integrated into a priori assessments to support decision-making. On the Ennepe Dam, the specified accuracy for concrete dams (i.e., 5 mm) [5] was only achieved by one PS point (#48623265: MAE = 5.1 mm, RMSE = 6.2 mm), based on its radial time series. Importantly, this does not necessarily imply that a PS point significantly overestimating the radial deformation provides no valuable information regarding the LOS geometry. For dams without a vertical monitoring system, the LOS time series—which combines vertical and horizontal deformations—may serve as a crucial supplementary data source for dam operators assessing structural stability. At this stage, we refrain from making recommendations regarding which acquisition geometry to use for deformation assessment, noting that the decision remains at the discretion of the dam operators, based on their individual needs.
For a comprehensive monitoring strategy, it is beneficial to incorporate both ascending and descending orbits where available. Using data from both directions increases the PS density and allows for a more comprehensive monitoring of a dam. As demonstrated for the Ennepe Dam, BBD data provided sufficient PS points to monitor all dam sections. However, this does not apply to all cases, as the number of detected PS points varies from dam to dam. Appendix D Table A3 and Table A4 give an overview of the dams operated by the Ruhrverband, illustrating the approximate number of detected PS points based on dam type and crest length. Importantly, the number of detected PS points depends not only on the radar signal’s wavelength, but also on the dam’s material properties, size, alignment with the satellite, and the sensor’s spatial resolution. Certain dam sections may not be adequately monitored due to insufficient PS points, limiting the applicability of BBD datasets on these dams. As for the Ruhrverband, this applies to four of the seven dams illustrated in Appendix D Table A3 and Table A4, detecting less than 10 PS points. This highlights the importance of a priori assessments to support decision-making. Notably, we used BBD data, providing filtered PS point datasets based on their temporal coherence to meet the required quality standards. The dataset analyzed in this study (i.e., spanning from 2015 to 2021) was provided with a temporal coherence threshold of >0.75. As an alternative, data from the European ground motion service (EGMS), which now includes LOS measurements in its latest update, can be considered. Unlike BBD data, EGMS employs multi-temporal interferometric processing that integrates both persistent scatterers and distributed scatterers (DSs) [20,42]. While the PS technique relies on single dominant scatterers with a high-quality interferometric phase [43], the DS approach focuses on areas of moderate coherence, where multiple neighboring pixels share similar reflectivity values as they belong to the same object [44]. Unlike PS, DS lack a single dominant reflector, making them particularly advantageous in rural areas with lower coherence. The combination of both, as implemented in EGMS, increases the number of measurement points available for deformation monitoring. However, filtering out points with low temporal coherence, poor signal-to-noise ratio, or unfavorable sensor orientation remains essential for reliable analysis. Otherwise, several dozen PS points on a dam may be far less effective for decision-making than a smaller number of high-quality points. Finally, considering that many dams have only a single pendulum system installed—if any—limiting deformation assessments to one specific point on the dam, the PS technique remains valuable even when only a small number of PS points are detected on the dam.
Further considerations imply that radial deformation analysis is only possible on dams with no discernible vertical deformation [2]. Due to their foundation on solid rock formations [45], gravity dams and arch dams are well-suited for this approach, as vertical deformations are typically much smaller than horizontal deformations. Trigonometric measurements on the Ennepe Dam confirmed that vertical deformation accounts for only a fraction of the total movement [37]. This assumption does not hold for embankment dams affected by the consolidation of fill material. In such cases, PS data in the sensor’s line of sight may not be directly comparable to in situ radial measurements but can be used as a supplementary data source for deformation interpretation. Ultimately, the decision regarding which geometry to use rests with the dam operators. Both LOS and radial deformations can be implemented for operational use, regardless of dam type.
The ability to provide analysis-ready data in different geometries positions nationwide ground motion services as reliable data providers for dam operators. With annual updates, long-term deformations can yet be effectively monitored [15]. With freely available PS data provided in common formats (.csv/.gdb), technical integration into existing monitoring programs could be possible at minimal cost. However, a key challenge lies in the implementation of near-real-time data, as current BBD datasets only cover time series from 2015 to 2021 [3]. Dam operators often require near-real-time assessments to detect potentially critical deformations on their infrastructure—particularly during extreme weather events—which is not yet integrated. Implementing this functionality requires greater effort for quicker decision-making and operational applicability of BBD datasets.
A dedicated API could facilitate the assessment of PSI applications for individual dams by standardizing workflows and streamlining the data [11]. Integrating near-real-time processing, optionally enhanced with complementary X-band data, could provide deeper insights into deformation characteristics on a local scale. Additionally, the functionality of this service could be tailored to meet the specific requirements of dam operators.
6. Conclusions
In this study, we assessed the feasibility of analysis-ready PS data provided by the German ground motion service for operational dam monitoring. Two key aspects proved crucial in evaluating the applicability of the PS technique on gravity dams: first, determining the dam’s general suitability for PS analysis using the CR-Index, which incorporates topography and land cover information to identify areas with good radar visibility; and second, assessing the interpretability of BBD data for radial deformations. For this purpose, we introduced a novel index that quantifies the radial sensitivity of PS points on the dam.
Freely available BBD time series demonstrated fair agreement with in situ pendulum data (up to = 0.7) for many PS points, highlighting their potential for integration into operational monitoring procedures. The capability to provide consistent deformation data with frequent updates positions PSI as a valuable complement to time-consuming in situ campaigns. Importantly, not all dams are equally suited for a PS-based monitoring strategy. A priori analysis of the dam’s characteristics (i.e., topography, land cover, dam type, dam orientation) is crucial to assess its general feasibility for PSI applications.
The sensitivity of PS data to deformations perpendicular to the dam wall emerged as an essential criterion for interpretability. For up to 20°, the LOS sensitivity captures approximately 50 to 70% of the true radial deformation, depending on the satellite’s incidence angle. This condition is best fulfilled by dam crests aligned in a north–south direction. However, when exceeds 20°, the sensitivity to LOS deformations decreases considerably. The Ennepe Dam investigated in this study exhibited generally low LOS sensitivity to radial deformations due to its east–west orientation, with exceeding 20° for all PS points. As a result, the estimated radial deformation amplitudes were up to an order of magnitude greater (−90 mm 70 mm) than those measured by pendulum systems. For these points, errors ranged from 6 to 43 mm in RMSE and from 5 to 35 mm in MAE. Eliminating points with low temporal coherence or an unfavorable alignment with the sensor should be considered before interpreting their radial deformations. For dams that are not optimally aligned with the sensor, LOS data can serve as a valuable supplementary data source—combining both horizontal and vertical deformation components. The final decision on which acquisition geometry to use remains at the discretion of the dam operators. For integration into operational monitoring programs, greater effort must be spent on near-real-time updates of BBD datasets.
Future research could focus on developing a freely available API specifically designed for dams, enabling the transfer of the proposed methodology to a nationwide dam monitoring service with standardized data products.
Author Contributions
Conceptualization, J.Z. and C.D.; methodology, J.Z., J.J., K.L. and C.D.; validation, J.Z.; formal analysis, J.Z.; investigation, J.Z.; resources, A.K., T.L., C.W., D.K. and K.L.; data curation, J.Z.; writing—original draft preparation, J.Z.; writing—review and editing, C.D., J.J., C.W. and D.K.; visualization, J.Z.; supervision, C.D., K.L. and C.S.; project administration, C.D., J.Z. and C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received external funding provided by the Federal Ministry for Economic Affairs and Climate Action (BMWK) due to an enactment of the German Bundestag under Grant No. 50EE2202A. We also acknowledge support by the German Research Foundation Projekt-Nr. 512648189 and the Open Access Publication Fund of the Thüringer Universitäts- und Landesbibliothek Jena.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
We acknowledge financial support through DLR with funds provided by the Federal Ministry for Economic Affairs and Climate Action (BMWK) due to an enactment of the German Bundestag under Grant No. 50EE2202A.
Conflicts of Interest
The Author Carolin Wicker, Daniel Klöpper, Katja Last are employed by Department for Water Economy, Ruhrverband. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
The CR-Index is derived from three key variables: the slope S, the S-1 incidence angle , and the aspect angle between the target object and the S-1 flight path A. Depending on the flight direction, AS1 from Equation (1) is replaced by for the ascending orbit (Equation (A1)) and for the descending trajectory (Equation (A2)) [30]:
where A represents the aspect angle of the target object on the ground, and and denote the angular difference between the true north and the S-1 flight direction in the ascending and descending orbits, respectively.
Appendix B
The LOS deformation () represents the projection of a 3D displacement vector d with its components , , and , in North, East, and Up direction, into the line-of-sight direction of the satellite sensor, as described by Equation (A3):
where represents the S-1 incidence angle, and denotes the angle difference between the true north radial angle and the S-1 look direction.
Appendix C

Table A1.
Signal-to-noise ratio (SNR) for the PS points located near PL1 [3].
Table A1.
Signal-to-noise ratio (SNR) for the PS points located near PL1 [3].
| Stack-ID | Point-ID | SNR |
|---|---|---|
| ASC 015-06 | #10959346 | 3.7 |
| ASC 015-06 | #9891920 | 4.7 |
| ASC 015-06 | #10958927 | 3.6 |
| ASC 088-02 | #48623265 | 10.1 |
| ASC 088-02 | #48622500 | 4.6 |
| ASC 088-03 | #53403989 | 4.5 |
| ASC 088-03 | #53403990 | 6.5 |
| DESC 037-04 | #7205013 | 14.3 |
| DESC 139-08 | #63389920 | 7.3 |

Table A2.
Signal-to-noise ratio (SNR) for the PS points located near PL2 [3].
Table A2.
Signal-to-noise ratio (SNR) for the PS points located near PL2 [3].
| Stack-ID | Point-ID | SNR |
|---|---|---|
| DESC 037-04 | #7204749 | 5.2 |
| DESC 139-08 | #63389743 | 2.0 |
| DESC 139-08 | #63389744 | 8.0 |
Appendix D

Table A3.
Approximate number of detected PS points (i.e., ascending and descending data stacks) compared to the crest length (in m) of selected gravity dams operated by the Ruhrverband, based on the BBD S-1 dataset used in this study (spanning from 2015 to 2021) [3,46].
Table A3.
Approximate number of detected PS points (i.e., ascending and descending data stacks) compared to the crest length (in m) of selected gravity dams operated by the Ruhrverband, based on the BBD S-1 dataset used in this study (spanning from 2015 to 2021) [3,46].
| Gravity Dam | Crest Length (m) | Approximate No. of PS Points Associated with the Dam |
|---|---|---|
| Fürwigge Dam | 166 | <10 |
| Lister Dam | 264 | <10 |
| Ennepe Dam | 320 | >25 |
| Möhne Dam | 650 | >50 |

Table A4.
Approximate number of detected PS points (i.e., ascending and descending data stacks) compared to the crest length (in m) of selected embankment dams operated by the Ruhrverband, based on the BBD S-1 dataset used in this study (spanning from 2015 to 2021) [3,46].
Table A4.
Approximate number of detected PS points (i.e., ascending and descending data stacks) compared to the crest length (in m) of selected embankment dams operated by the Ruhrverband, based on the BBD S-1 dataset used in this study (spanning from 2015 to 2021) [3,46].
| Embankment Dam | Crest Length (m) | Approximate No. of PS Points Associated with the Dam |
|---|---|---|
| Verse Dam | 320 | <10 |
| Bigge Dam | 640 | <10 |
| Sorpe Dam | 700 | >25 |
References
- Bettzieche, V. Satellite monitoring of the deformations of dams. Wasserwirtschaft 2020, 110, 48–51. [Google Scholar] [CrossRef]
- Jänichen, J.; Schmullius, C.; Baade, J.; Last, K.; Bettzieche, V.; Dubois, C. Monitoring of Radial Deformations of a Gravity Dam Using Sentinel-1 Persistent Scatterer Interferometry. Remote Sens. 2022, 14, 1112. [Google Scholar] [CrossRef]
- BGR. Federal Institute for Geosciences and Natural Resources. BodenBewegungsdienst Deutschland (BBD). 2021. Available online: https://bodenbewegungsdienst.bgr.de/mapapps/resources/apps/bbd/index.html?lang=de (accessed on 11 October 2024).
- Milillo, P.; Porcu, M.C.; Lundgren, P.; Soccodato, F.; Salzer, J.; Fielding, E.; Bürgmann, R.; Milillo, G.; Perissin, D.; Biondi, F. The ongoing destabilization of the Mosul dam as observed by synthetic aperture radar interferometry. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 6279–6282. [Google Scholar] [CrossRef]
- Corsetti, M.; Fossati, F.; Manunta, M.; Marsella, M. Advanced SBAS-DInSAR technique for controlling large civil infrastructures: An application to the Genzano di Lucania dam. Sensors 2018, 18, 2371. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Armenteros, A.M.; Lazecky, M.; Hlaváčová, I.; Bakoň, M.; Delgado, J.M.; Sousa, J.J.; Lamas-Fernández, F.; Marchamalo, M.; Caro-Cuenca, M.; Papco, J.; et al. Deformation monitoring of dam infrastructures via spaceborne MT-InSAR. The case of La Viñuela (Málaga, southern Spain). Procedia Comput. Sci. 2018, 138, 346–353. [Google Scholar] [CrossRef]
- Othman, A.A.; Al-Maamar, A.F.; Al-Manmi, D.A.M.; Liesenberg, V.; Hasan, S.E.; Al-Saady, Y.I.; Shihab, A.T.; Khwedim, K. Application of DInSAR-PSI technology for deformation monitoring of the Mosul Dam, Iraq. Remote Sens. 2019, 11, 2632. [Google Scholar] [CrossRef]
- Bayik, C.; Abdikan, S.; Arıkan, M. Long term displacement observation of the Atatürk Dam, Turkey by multi-temporal InSAR analysis. Acta Astronaut. 2021, 189, 483–491. [Google Scholar] [CrossRef]
- Abo, H.; Osawa, T.; Ge, P.; Takahashi, A.; Yamagishi, K. Deformation Monitoring of Large-Scale Rockfill Dam Applying Persistent Scatterer Interferometry (PSI) Using Sentinel-1 SAR Data. In Proceedings of the 2021 7th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Bali, Indonesia, 1–3 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Marchamalo-Sacristán, M.; Ruiz-Armenteros, A.M.; Lamas-Fernández, F.; González-Rodrigo, B.; Martínez-Marín, R.; Delgado-Blasco, J.M.; Bakon, M.; Lazecky, M.; Perissin, D.; Papco, J.; et al. MT-InSAR and dam modeling for the comprehensive monitoring of an Earth-fill dam: The case of the Benínar dam (Almería, Spain). Remote Sens. 2023, 15, 2802. [Google Scholar] [CrossRef]
- Marchamalo-Sacristán, M.; Fernández-Landa, A.; Sancho, C.; Hernández-Cabezudo, A.; Krishnakumar, V.; García-Lanchares, C.; Sánchez, J.; Rubén, M.M.; Rejas-Ayuga, J.; González-Tejada, I.; et al. EyeRADAR-Dam: Integration of MT-InSAR with monitoring technologies in a pilot monitoring system for embankment dams. Procedia Comput. Sci. 2024, 239, 2286–2292. [Google Scholar] [CrossRef]
- Wang, Z.; Perissin, D. Cosmo SkyMed AO projects-3D reconstruction and stability monitoring of the Three Gorges Dam. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 3831–3834. [Google Scholar] [CrossRef]
- Lazecky, M.; Perissin, D.; Lei, L.; Qin, Y.; Scaioni, M. Plover Cove Dam Monitoring with Spaceborne InSAR Technique in Hong Kong. In Proceedings of the 2nd Joint International Symposium on Deformation Monitoring, Nottingham, UK, 9–10 September 2013; pp. 9–11. Available online: http://www.sarproz.com/wp-content/papercite-data/pdf/lazecky-pcdmwsitihk2013.pdf (accessed on 11 October 2024).
- Tomás, R.; Cano, M.; Garcia-Barba, J.; Vicente, F.; Herrera, G.; Lopez-Sanchez, J.M.; Mallorquí, J. Monitoring an earthfill dam using differential SAR interferometry: La Pedrera dam, Alicante, Spain. Eng. Geol. 2013, 157, 21–32. [Google Scholar] [CrossRef]
- Dubois, C.; Ziemer, J.; Jänichen, J.; Stumpf, N.; Liedel, C.; Sabrowski, M.; Schmullius, C. Dam Monitoring With Ground Motion Services–A Case Study of a Gravity Dam with the German Ground Motion Service. In Proceedings of the IGARSS 2024–2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 4670–4673. [Google Scholar] [CrossRef]
- Stein, G.; Ziemer, J.; Wicker, C.; Jänichen, J.; Demisch, G.; Klöpper, D.; Last, K.; Denzler, J.; Schmullius, C.; Shadaydeh, M.; et al. Data-Driven Prediction of Large Infrastructure Movements Through Persistent Scatterer Time Series Modeling. In Proceedings of the IGARSS 2024–2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 8669–8673. [Google Scholar] [CrossRef]
- Milillo, P.; Perissin, D.; Salzer, J.T.; Lundgren, P.; Lacava, G.; Milillo, G.; Serio, C. Monitoring dam structural health from space: Insights from novel InSAR techniques and multi-parametric modeling applied to the Pertusillo dam Basilicata, Italy. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 221–229. [Google Scholar] [CrossRef]
- Grebby, S.; Sowter, A.; Gluyas, J.; Toll, D.; Gee, D.; Athab, A.; Girindran, R. Advanced analysis of satellite data reveals ground deformation precursors to the Brumadinho Tailings Dam collapse. Commun. Earth Environ. 2021, 2, 2. [Google Scholar] [CrossRef]
- Rana, N.M.; Delaney, K.B.; Evans, S.G.; Deane, E.; Small, A.; Adria, D.A.; McDougall, S.; Ghahramani, N.; Take, W.A. Application of Sentinel-1 InSAR to monitor tailings dams and predict geotechnical instability: Practical considerations based on case study insights. Bull. Eng. Geol. Environ. 2024, 83, 204. [Google Scholar] [CrossRef]
- Even, M.; Westerhaus, M.; Kutterer, H. German and European Ground Motion Service: A Comparison. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2024, 92, 253–270. [Google Scholar] [CrossRef]
- Hanssen, R.; Van Leijen, F.; Van Zwieten, G.; Dortland, S.; Bremmer, C.; Kleuskens, M. Validation of PSI Results of Alkmaar and Amsterdam Within the Terrafirma Validation Project. In Proceedings of the Fringe Workshop “Adv. SAR Interferometry Envisat ERS Missions, Frascati, Italy, 26–30 November 2007. [Google Scholar]
- Pratesi, F.; Tapete, D.; Terenzi, G.; Del Ventisette, C.; Moretti, S. Rating health and stability of engineering structures via classification indexes of InSAR Persistent Scatterers. Int. J. Appl. Earth Obs. Geoinf. 2015, 40, 81–90. [Google Scholar] [CrossRef]
- Ruhrverband. Ennepetalsperre. Sicherheitsbericht. Teil A. Unpublished Security Report. 2016; unpublished. [Google Scholar]
- GDI-NRW. Geodateninfrastruktur Nordrhein-Westfalen. Geoportal NRW. 2021. Available online: https://www.gdi.nrw (accessed on 11 October 2024).
- Adam, N.; Gonzalez, F.R.; Parizzi, A.; Brcic, R. Wide area Persistent Scatterer Interferometry: Current developments, algorithms and examples. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1857–1860. [Google Scholar] [CrossRef]
- Goel, K.; Adam, N.; Shau, R.; Rodriguez-Gonzalez, F. Improving the reference network in wide-area Persistent Scatterer Interferometry for non-urban areas. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1448–1451. [Google Scholar] [CrossRef]
- Adam, N. Methodology of a troposphere effect mitigation processor for SAR interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 5334–5344. [Google Scholar] [CrossRef]
- Kalia, A.C.; Frei, M.; Lege, T. BodenBewegungsdienst Deutschland (BBD): Konzept, Umsetzung und Service-Plattform. ZfV-Z. Geodäsie Geoinf. Landmanagement 2021, 4. [Google Scholar] [CrossRef]
- GDI-NRW. Topographisches Informationsmanagement (TIM-Online). 2025. Available online: https://www.tim-online.nrw.de/tim-online2/ (accessed on 10 March 2025).
- Notti, D.; Meisina, C.; Zucca, F.; Colombo, A. Models to predict Persistent Scatterers Data Distribution and Their Capacity to Register Movement Along the Slope. In Proceedings of the Fringe 2011 Workshop, Frascati, Italy, 9–23 September 2011; pp. 19–23. Available online: https://earth.esa.int/eogateway/documents/20142/37627/Models_predict_persistent_scatterers_data_distribution.pdf (accessed on 10 October 2024).
- Francesca, C.; Luke, B.; Colm, J.; Claire, D. Nationwide monitoring of geohazards in Great Britain with InSAR: Feasibility mapping based on ERS-1/2 and ENVISAT imagery. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 672–675. [Google Scholar] [CrossRef]
- Jänichen, J.; Ziemer, J.; Fischer, N.; Wolsza, M.; Klöpper, D.; Weltmann, S.; Wicker, C.; Last, K.; Schmullius, C.; Dubois, C. Towards Operational Dam Monitoring with DInSAR-PSI and Electronic Corner Reflectors (submitted). Remote Sens. 2025, in progress. [Google Scholar]
- Samieie-Esfahany, S.; Hanssen, R.F.; van Thienen-Visser, K.; Muntendam-Bos, A. On the effect of horizontal deformation on InSAR subsidence estimates. In Proceedings of the Fringe 2009, Proceedings of the Workshop, Frascati, Italy, 30 November–4 December 2009; ESA-SP Volume 677, ISBN 978-92-9221-241-4. [Google Scholar]
- Cumming, I.; Zhang, J. Measuring the 3-D flow of the Lowell Glacier with InSAR. In Proceedings of the FRINGE’99 SAR Workshop, Liege, Belgium, 10–12 November 1999; Volume 99. [Google Scholar]
- Lazecky, M.; Hlavacova, I.; Bakon, M.; Sousa, J.J.; Perissin, D.; Patricio, G. Bridge displacements monitoring using space-borne X-band SAR interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 205–210. [Google Scholar] [CrossRef]
- Fleischer, H. Load-bearing behaviour of old dams and conclusions for structural monitoring. Wasserwirtschaft 2022, 112, 12–18. [Google Scholar] [CrossRef]
- Ruhrverband. Ennepetalsperre. Sicherheitsbericht. Teil B. Unpublished Security Report. 2021; unpublished. [Google Scholar]
- Haghighi, M.H.; Motagh, M. Sentinel-1 InSAR over Germany: Large-scale interferometry, atmospheric effects, and ground deformation mapping. ZfV-Z. Geodäsie Geoinf. Landmanagement 2017. [Google Scholar] [CrossRef]
- Duan, L.; Gong, H.; Chen, B.; Zhou, C.; Lei, K.; Gao, M.; Yu, H.; Cao, Q.; Cao, J. An improved multi-sensor MTI time-series fusion method to monitor the subsidence of Beijing subway network during the Past 15 Years. Remote Sens. 2020, 12, 2125. [Google Scholar] [CrossRef]
- Ding, X.l.; Li, Z.w.; Zhu, J.j.; Feng, G.c.; Long, J.p. Atmospheric effects on InSAR measurements and their mitigation. Sensors 2008, 8, 5426–5448. [Google Scholar] [CrossRef]
- DIN. German Institute for Standardization. DIN 19700-10: 2004-07, Stauanlagen-Teil 11: Talsperren; Beuth Verlag GmbH: Berlin, Germany, 2004. [Google Scholar] [CrossRef]
- Mele, A.; Crosetto, M.; Miano, A.; Prota, A. Adafinder tool applied to EGMS data for the structural health monitoring of urban settlements. Remote Sens. 2023, 15, 324. [Google Scholar] [CrossRef]
- Shen, P.; Wang, C.; An, B. AdpPL: An adaptive phase linking-based distributed scatterer interferometry with emphasis on interferometric pair selection optimization and adaptive regularization. Remote Sens. Environ. 2023, 295, 113687. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Wittke, W.; Wittke, M.; Kiehl, J.R. Interaction of a masonry dam and the rock foundation. Geotech. Geol. Eng. 2012, 30, 581–601. [Google Scholar] [CrossRef]
- Ruhrverband. Das Talsperrensystem des Ruhrverbands. 2024. Available online: https://ruhrverband.de/flussgebiet/talsperren (accessed on 7 February 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).