Enhancing the Prediction of Dam Deformations: A Novel Data-Driven Approach
Abstract
1. Introduction
1.1. MT-InSAR Employed for Dam Monitoring in Scientific Studies
1.2. Research Approach
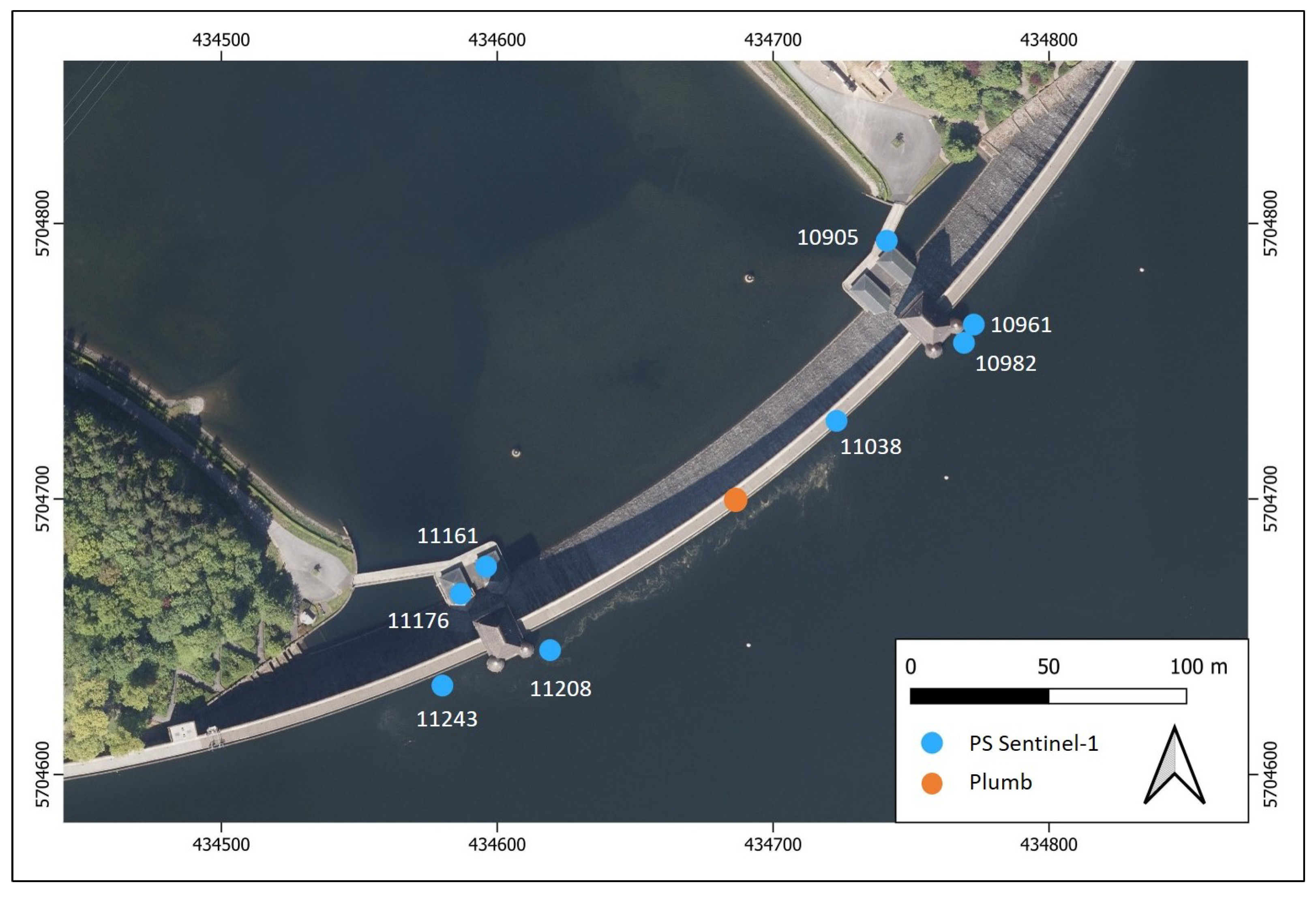
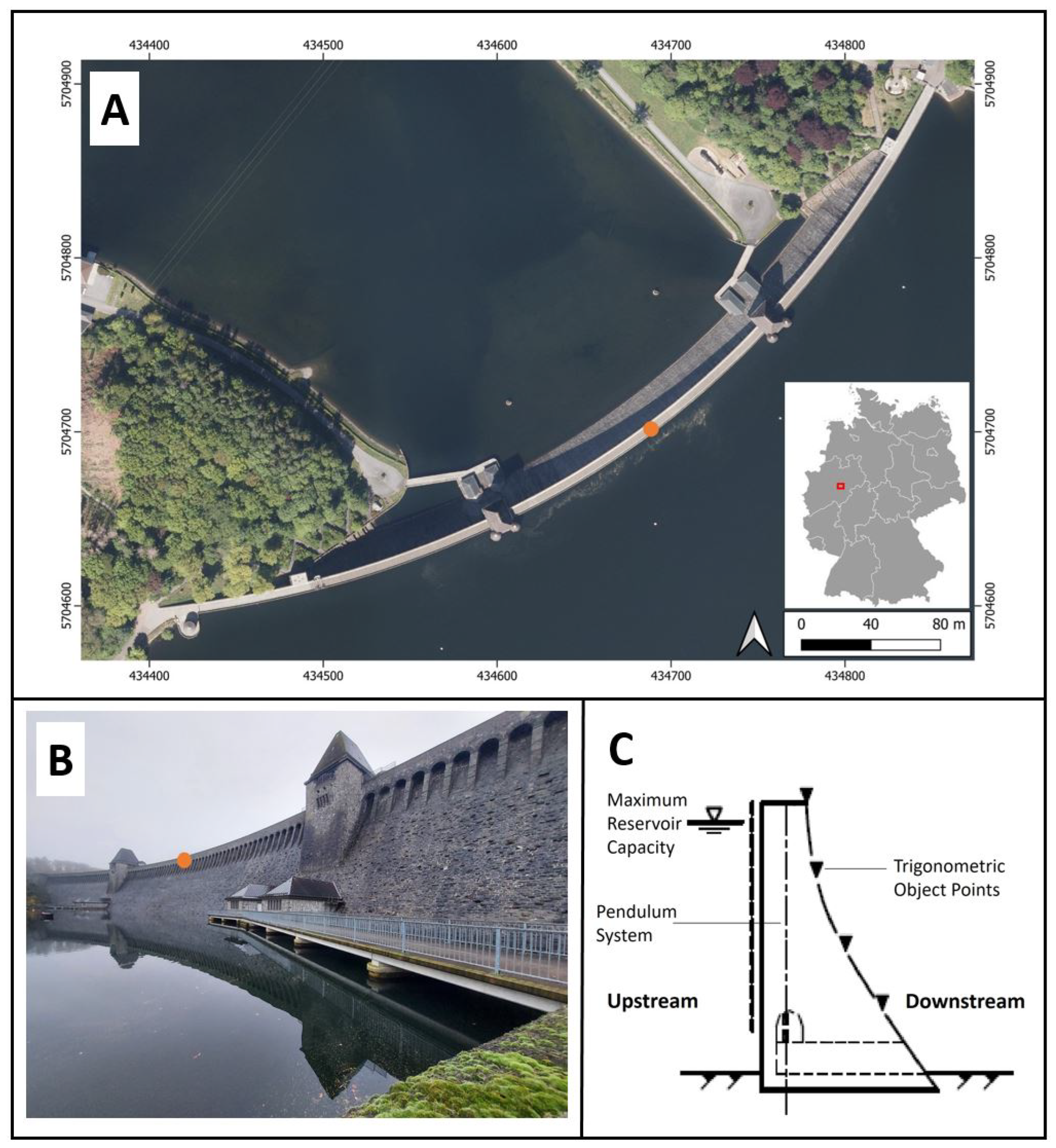
2. Study Site and Data
2.1. Study Site
2.2. Data
2.2.1. In Situ Data
2.2.2. BBD Data
| DESC #066 | |
|---|---|
| Start Date | 8 April 2015 |
| End Date | 31 December 2020 |
| Reference Scene | 19 September 2018 |
| No. of Scenes | 287 |
| Temporal Resolution | 12 days |
| Incidence Angle | 46° |
| Look Angle | 276° |
| Max. Perpendicular Baseline | +167 m |
| Min. Perpendicular Baseline | −139 m |

3. Methods
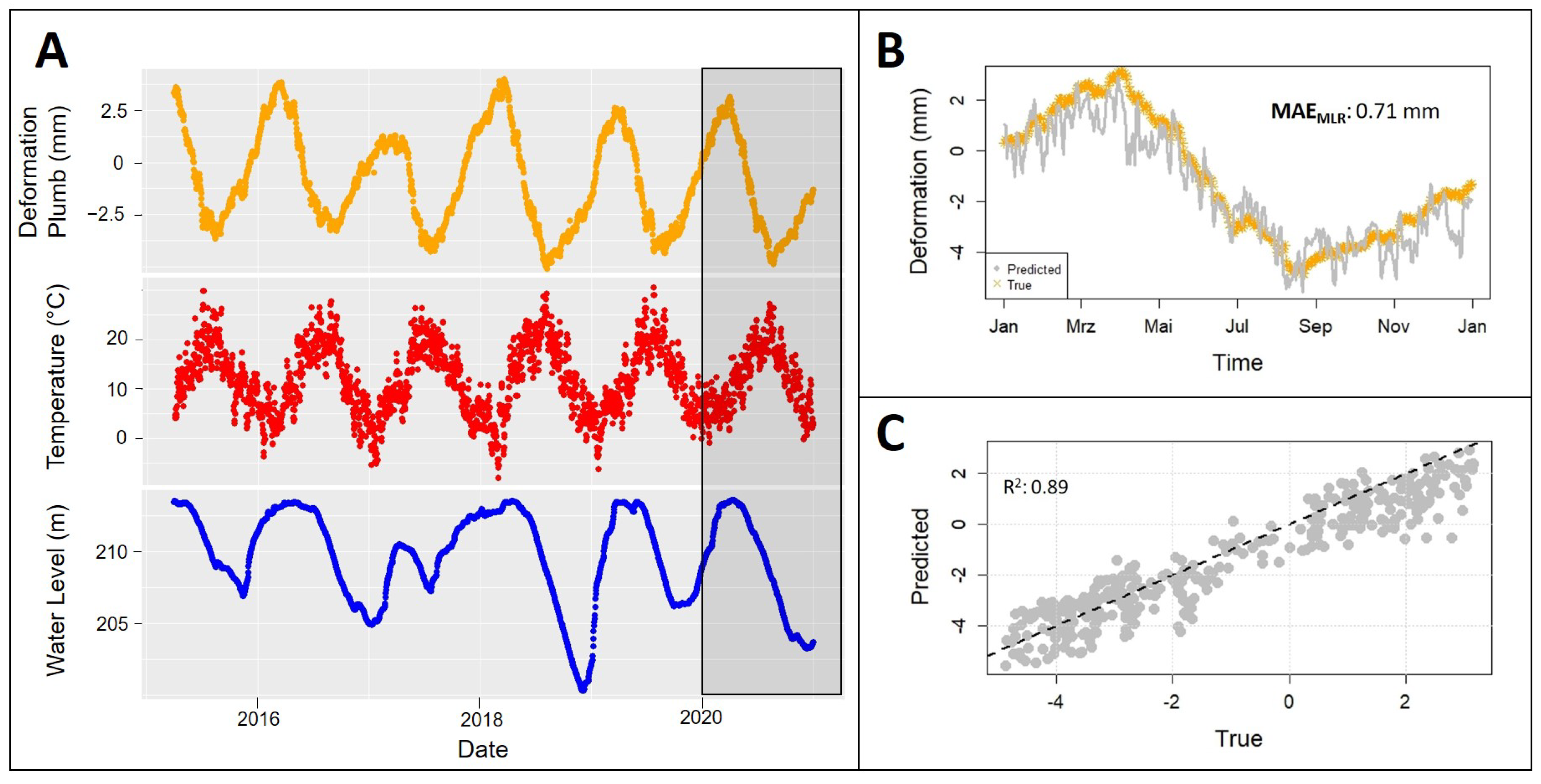
3.1. Baseline Model: Multiple Linear Regression Using Pendulum Data
3.2. Data-Driven Approach
3.2.1. Model Classes
3.2.2. Exogenous Variables
3.2.3. Model Search
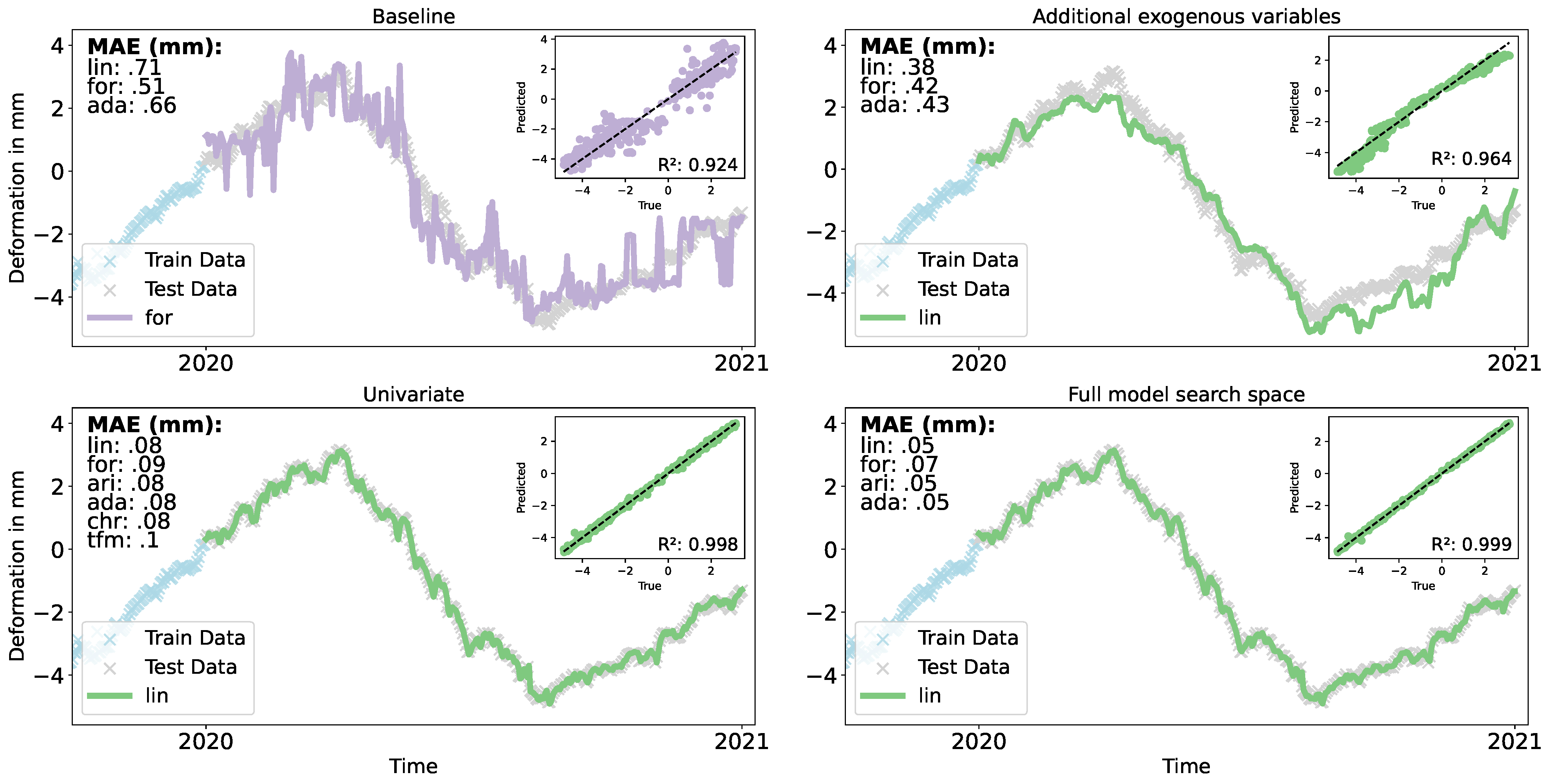
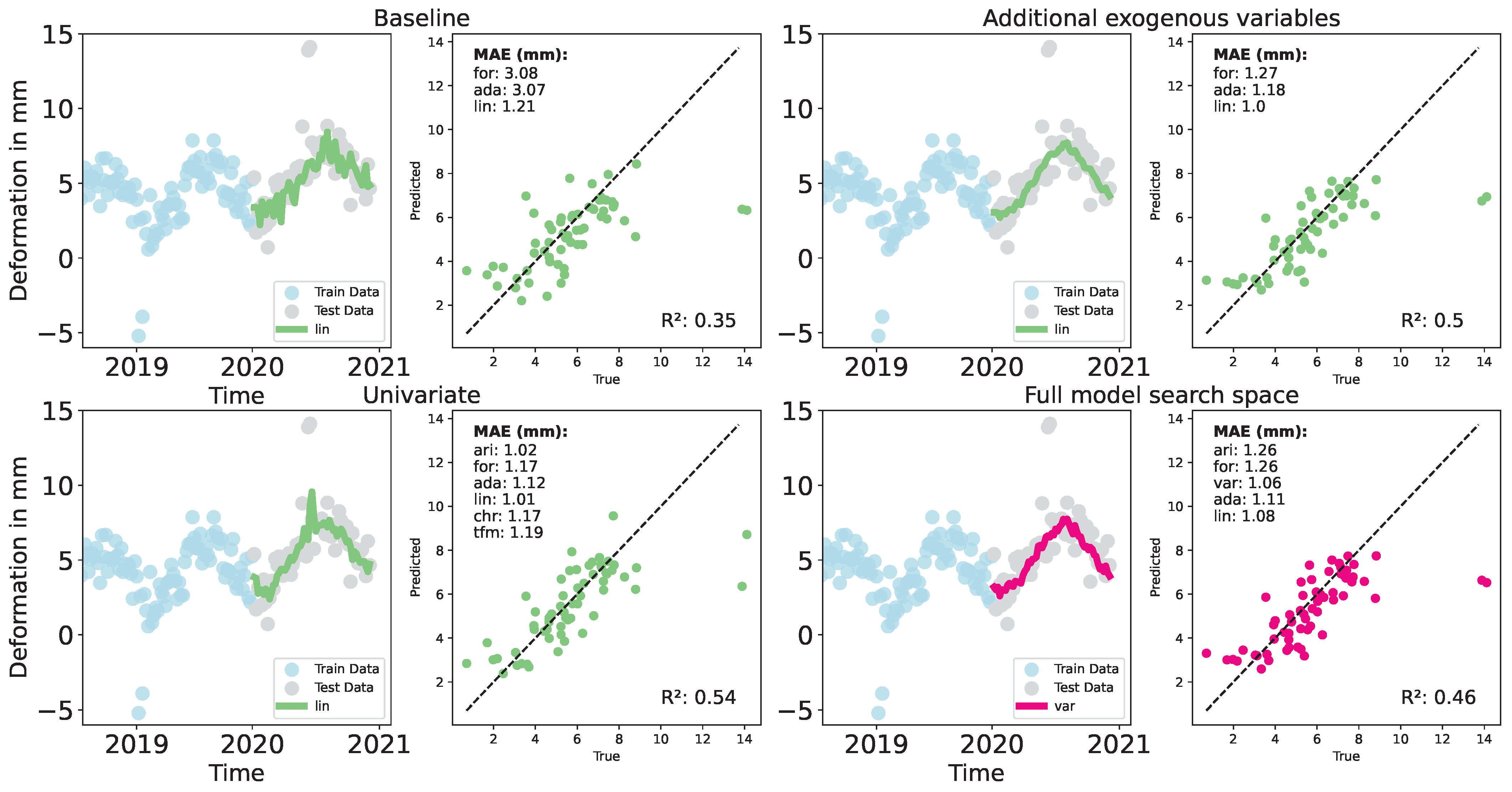
4. Results
4.1. Deformation Prediction Obtained Through In Situ Data and Pendulum Measurements
4.2. Deformation Prediction Obtained Through In Situ Data and Sentinel-1 PS Time Series
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Point-ID | SNR |
|---|---|
| 10905 | 5.8 |
| 10961 | 10.6 |
| 10982 | 5.2 |
| 11038 | N/A |
| 11161 | N/A |
| 11176 | 16.2 |
| 11208 | 5.9 |
| 11243 | N/A |
References
- Böcker, D.; Schumann, A.; Bettzieche, V. Analysis of Shifts and Trends of Monitoring Data at Dams with Consideration of the Influence of Variables Measured Externally. JOT-Int. Surf. Technol. 2010, 3, 8–11. [Google Scholar] [CrossRef]
- German Association for Water and Waste (DWA). Mess- und Kontrolleinrichtungen zur Überprüfung der Standsicherheit von Staumauern und Staudämmen. In DVWK-Merkblätter zur Wasserwirtschaft; Parey-Verlag Hamburg: Hamburg, Germany, 1991; Volume Heft 222. [Google Scholar]
- Bettzieche, V. Mathematical-Statistical Analysis of Measurements from Dam Monitoring. Wasserwirtschaft 2004, 94, 30–34. [Google Scholar] [CrossRef]
- Bettzieche, V. Satellite monitoring of the deformations of dams. Wasserwirtschaft 2020, 110, 48–51. [Google Scholar] [CrossRef]
- Fleischer, H. Load-bearing behaviour of old dams and conclusions for structural monitoring. Wasserwirtschaft 2022, 112, 12–18. [Google Scholar] [CrossRef]
- Milillo, P.; Perissin, D.; Salzer, J.T.; Lundgren, P.; Lacava, G.; Milillo, G.; Serio, C. Monitoring dam structural health from space: Insights from novel InSAR techniques and multi-parametric modeling applied to the Pertusillo dam Basilicata, Italy. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 221–229. [Google Scholar] [CrossRef]
- Corsetti, M.; Fossati, F.; Manunta, M.; Marsella, M. Advanced SBAS-DInSAR technique for controlling large civil infrastructures: An application to the Genzano di Lucania dam. Sensors 2018, 18, 2371. [Google Scholar] [CrossRef]
- Bayik, C.; Abdikan, S.; Arıkan, M. Long term displacement observation of the Atatürk Dam, Turkey by multi-temporal InSAR analysis. Acta Astronaut. 2021, 189, 483–491. [Google Scholar] [CrossRef]
- Grebby, S.; Sowter, A.; Gluyas, J.; Toll, D.; Gee, D.; Athab, A.; Girindran, R. Advanced analysis of satellite data reveals ground deformation precursors to the Brumadinho Tailings Dam collapse. Commun. Earth Environ. 2021, 2, 2. [Google Scholar] [CrossRef]
- Milillo, P.; Porcu, M.C.; Lundgren, P.; Soccodato, F.; Salzer, J.; Fielding, E.; Bürgmann, R.; Milillo, G.; Perissin, D.; Biondi, F. The ongoing destabilization of the Mosul dam as observed by synthetic aperture radar interferometry. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 6279–6282. [Google Scholar] [CrossRef]
- Ruiz-Armenteros, A.M.; Lazecky, M.; Hlaváčová, I.; Bakoň, M.; Delgado, J.M.; Sousa, J.J.; Lamas-Fernández, F.; Marchamalo, M.; Caro-Cuenca, M.; Papco, J.; et al. Deformation monitoring of dam infrastructures via spaceborne MT-InSAR. The case of La Viñuela (Málaga, southern Spain). Procedia Comput. Sci. 2018, 138, 346–353. [Google Scholar] [CrossRef]
- Othman, A.A.; Al-Maamar, A.F.; Al-Manmi, D.A.M.; Liesenberg, V.; Hasan, S.E.; Al-Saady, Y.I.; Shihab, A.T.; Khwedim, K. Application of DInSAR-PSI technology for deformation monitoring of the Mosul Dam, Iraq. Remote Sens. 2019, 11, 2632. [Google Scholar] [CrossRef]
- Abo, H.; Osawa, T.; Ge, P.; Takahashi, A.; Yamagishi, K. Deformation Monitoring of Large-Scale Rockfill Dam Applying Persistent Scatterer Interferometry (PSI) Using Sentinel-1 SAR Data. In Proceedings of the IEEE 2021 7th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Virtual, 1–3 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Marchamalo-Sacristán, M.; Ruiz-Armenteros, A.M.; Lamas-Fernández, F.; González-Rodrigo, B.; Martínez-Marín, R.; Delgado-Blasco, J.M.; Bakon, M.; Lazecky, M.; Perissin, D.; Papco, J.; et al. MT-InSAR and dam modeling for the comprehensive monitoring of an Earth-fill dam: The case of the Benínar dam (Almería, Spain). Remote Sens. 2023, 15, 2802. [Google Scholar] [CrossRef]
- Marchamalo-Sacristán, M.; Fernández-Landa, A.; Sancho, C.; Hernández-Cabezudo, A.; Krishnakumar, V.; García-Lanchares, C.; Sánchez, J.; Rubén, M.M.; Rejas-Ayuga, J.; González-Tejada, I.; et al. EyeRADAR-Dam: Integration of MT-InSAR with monitoring technologies in a pilot monitoring system for embankment dams. Procedia Comput. Sci. 2024, 239, 2286–2292. [Google Scholar] [CrossRef]
- Wang, Z.; Perissin, D. Cosmo SkyMed AO projects-3D reconstruction and stability monitoring of the Three Gorges Dam. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3831–3834. [Google Scholar] [CrossRef]
- Lazecky, M.; Perissin, D.; Lei, L.; Qin, Y.; Scaioni, M. Plover Cove dam monitoring with spaceborne InSAR technique in Hong Kong. In Proceedings of the 2nd Joint International Symposium on Deformation Monitoring, Nottingham, UK, 9–11 September 2013; pp. 9–11. Available online: http://www.sarproz.com/wp-content/papercite-data/pdf/lazecky-pcdmwsitihk2013.pdf (accessed on 11 October 2024).
- Tomás, R.; Cano, M.; Garcia-Barba, J.; Vicente, F.; Herrera, G.; Lopez-Sanchez, J.M.; Mallorquí, J. Monitoring an earthfill dam using differential SAR interferometry: La Pedrera dam, Alicante, Spain. Eng. Geol. 2013, 157, 21–32. [Google Scholar] [CrossRef]
- Jänichen, J.; Schmullius, C.; Baade, J.; Last, K.; Bettzieche, V.; Dubois, C. Monitoring of Radial Deformations of a Gravity Dam Using Sentinel-1 Persistent Scatterer Interferometry. Remote Sens. 2022, 14, 1112. [Google Scholar] [CrossRef]
- Dubois, C.; Ziemer, J.; Jänichen, J.; Stumpf, N.; Liedel, C.; Sabrowski, M.; Schmullius, C. Dam Monitoring with Ground Motion Services—A Case Study of a Gravity Dam with the German Ground Motion Service. In Proceedings of the IGARSS 2024-2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 4670–4673. [Google Scholar] [CrossRef]
- Stein, G.; Ziemer, J.; Wicker, C.; Jänichen, J.; Demisch, G.; Klöpper, D.; Last, K.; Denzler, J.; Schmullius, C.; Shadaydeh, M.; et al. Data-Driven Prediction of Large Infrastructure Movements Through Persistent Scatterer Time Series Modeling. In Proceedings of the IGARSS 2024-2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 8669–8673. [Google Scholar] [CrossRef]
- Rana, N.M.; Delaney, K.B.; Evans, S.G.; Deane, E.; Small, A.; Adria, D.A.; McDougall, S.; Ghahramani, N.; Take, W.A. Application of Sentinel-1 InSAR to monitor tailings dams and predict geotechnical instability: Practical considerations based on case study insights. Bull. Eng. Geol. Environ. 2024, 83, 204. [Google Scholar] [CrossRef]
- Ruhrverband. Möhnetalsperre. Sicherheitsbericht. Teil A. Unpublished Security Report. 2013. [Google Scholar]
- GDI-NRW. Geodateninfrastruktur Nordrhein-Westfalen. Geoportal NRW. 2021. Available online: https://www.gdi.nrw (accessed on 11 October 2024).
- Ruhrverband. Möhnetalsperre. Vertiefte Überprüfung. Analyse der Messdaten. Unpublished Security Report. 2018. [Google Scholar]
- Kalia, A.; Frei, M.; Lege, T. A Copernicus downstream-service for the nationwide monitoring of surface displacements in Germany. Remote Sens. Environ. 2017, 202, 234–249. [Google Scholar] [CrossRef]
- Kalia, A.C.; Frei, M.; Lege, T. BodenBewegungsdienst Deutschland (BBD): Konzept, Umsetzung und Service-Plattform. ZfV-Z. Geod. Geoinf. Landmanag. 2021, 4. [Google Scholar] [CrossRef]
- Ziemer, J.; Jänichen, J.; Wicker, C.; Klöpper, D.; Last, K.; Kalia, A.; Lege, T.; Schmullius, C.; Dubois, C. Assessing the Feasibility of Persistent Scatterer Data for Operational Dam Monitoring in Germany: A Case Study (submitted). Remote Sens. 2025. [Google Scholar]
- Kumar, H.; Syed, T.H.; Amelung, F.; Agrawal, R.; Venkatesh, A. Space-time evolution of land subsidence in the National Capital Region of India using ALOS-1 and Sentinel-1 SAR data: Evidence for groundwater overexploitation. J. Hydrol. 2022, 605, 127329. [Google Scholar] [CrossRef]
- BGR. Federal Institute for Geosciences and Natural Resources. BodenBewegungsdienst Deutschland (BBD). 2020. Available online: https://bodenbewegungsdienst.bgr.de/mapapps/resources/apps/bbd/index.html?lang=de (accessed on 11 October 2024).
- Alaska Satellite Facility. ASF DAAC Vertex Data Search. 2025. Available online: https://search.asf.alaska.edu/#/ (accessed on 17 February 2025).
- Glötzl. Vektorlotsystem, Zweiachsig. Product Sheet. 2005. Available online: http://www.gloetzl.de/fileadmin/produkte/1%20Messwertaufnehmer/4%20Neigung%20und%20Deformation/P%20082.50%20Vektorlot%20de.pdf (accessed on 11 October 2024).
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with python. SciPy 2010, 7, 92–96. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the IEEE 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–15 August 1995; Volume 1, pp. 278–282. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Ansari, A.F.; Stella, L.; Turkmen, C.; Zhang, X.; Mercado, P.; Shen, H.; Shchur, O.; Rangapuram, S.S.; Arango, S.P.; Kapoor, S.; et al. Chronos: Learning the language of time series. arXiv 2024, arXiv:2403.07815. [Google Scholar] [CrossRef]
- Liang, Y.; Wen, H.; Nie, Y.; Jiang, Y.; Jin, M.; Song, D.; Pan, S.; Wen, Q. Foundation models for time series analysis: A tutorial and survey. In Proceedings of the 30th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Barcelona, Spain, 25–29 August 2024; pp. 6555–6565. [Google Scholar] [CrossRef]
- Mele, A.; Crosetto, M.; Miano, A.; Prota, A. Adafinder tool applied to EGMS data for the structural health monitoring of urban settlements. Remote Sens. 2023, 15, 324. [Google Scholar] [CrossRef]
- Even, M.; Westerhaus, M.; Kutterer, H. German and European Ground Motion Service: A Comparison. PFG—J. Photogramm. Remote Sens. Geoinf. Sci. 2024, 92, 253–270. [Google Scholar] [CrossRef]
- Shen, P.; Wang, C.; An, B. AdpPL: An adaptive phase linking-based distributed scatterer interferometry with emphasis on interferometric pair selection optimization and adaptive regularization. Remote Sens. Environ. 2023, 295, 113687. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Xu, G.; Gao, Y.; Li, J.; Xing, M. InSAR phase denoising: A review of current technologies and future directions. IEEE Geosci. Remote Sens. Mag. 2020, 8, 64–82. [Google Scholar] [CrossRef]

| Dam Type | Study | Research Focus |
|---|---|---|
| Embankment Dam | Milillo et al., 2017 [10] | Deformation Monitoring, Dam Modeling |
| Embankment Dam | Corsetti et al., 2018 [7] | Deformation Monitoring, Dam Modeling |
| Embankment Dam | Abo et al., 2021 [13] | Deformation Monitoring |
| Embankment Dam | Bayik et al., 2021 [8] | Deformation Monitoring |
| Embankment Dam | Marchamalo-Sacristán et al., 2023 [14] | Deformation Monitoring, Dam Modeling |
| Embankment Dam | Marchamalo-Sacristán et al., 2024 [15] | Deformation Monitoring, API |
| Arch-Gravity Dam | Milillo et al., 2016 [6] | Deformation Monitoring, Dam Modeling |
| Gravity Dam | Jänichen et al., 2022 [19] | Deformation Monitoring |
| Gravity Dam | Dubois et al., 2024 [20] | Deformation Monitoring |
| Gravity Dam | Stein et al., 2024 [21] | Deformation Prediction |
| Tailings Dam | Grebby et al., 2021 [9] | Deformation Monitoring, Failure Prediction |
| Tailings Dam | Rana et al., 2024 [22] | Deformation Monitoring, Failure Prediction |
| Data | Temporal Resolution |
|---|---|
| Pendulum Data (mm) | daily |
| Water Level (m) | daily |
| Temperature (°C) | daily |
| Linear | Arimax | VARMAX | Random Forest | AdaBoost | |
|---|---|---|---|---|---|
| (P, Equation (2)) | -, 1, 2 | -, 1, 2 | -, 1, 2 | -, 1, 2 | -, 1, 2 |
| -, 0, 1, 2 | -, 0, 1, 2 | -, 0, 1, 2 | -, 0, 1, 2 | -, 0, 1, 2 | |
| -, 0, 1, 2 | -, 0, 1, 2 | -, 0, 1, 2 | -, 0, 1, 2 | -, 0, 1, 2 | |
| -, 7 | -, 7 | -, 7 | -, 7 | -, 7 | |
| -, 7 | -, 7 | -, 7 | -, 7 | -, 7 | |
| Decomposition | Y, N | Y, N | Y, N | Y, N | Y, N |
| Interaction Effect | -, (3), (4) | -, (3), (4) | -, (3), (4) | -, (3), (4) | -, (3), (4) |
| Estimator | - | - | - | - | DT, Lin |
| N Estimators | - | - | - | 50, 250 | 50, 250 |
| Learning Rate | - | - | - | - | 1, 0.1 |
| Max Depth | - | - | - | -, 3, 7 | - |
| D (Equation (2)) | - | 0, 1 | - | - | - |
| Q (Equation (2)) | - | 0, 1, 2 | 0, 1, 2 | - | - |
| Search Space | Model Class | 10905 | 10961 | 10982 | 11038 | 11161 | 11176 | 11208 | 11243 |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | lin | 1.52 | 1.02 | 1.18 | 3.85 | 2.05 | 1.21 | 1.56 | 3.16 |
| for | 3.41 | 3.03 | 3.71 | 5.01 | 3.03 | 3.08 | 2.76 | 4.18 | |
| ada | 3.48 | 3.06 | 3.62 | 4.84 | 2.83 | 3.07 | 2.53 | 3.93 | |
| Baseline + Exogenous | lin | 1.56 | 0.98 | 1.12 | 3.64 | 2.09 | 1.00 | 1.42 | 3.26 |
| for | 1.72 | 1.39 | 1.24 | 4.18 | 2.23 | 1.27 | 1.49 | 3.27 | |
| ada | 1.57 | 1.81 | 1.34 | 4.66 | 2.19 | 1.18 | 1.57 | 3.51 | |
| Univariate | lin | 1.50 | 0.81 | 1.06 | 3.72 | 2.06 | 1.01 | 1.40 | 3.25 |
| ari | 1.34 | 0.94 | 1.06 | 3.73 | 2.05 | 1.02 | 1.39 | 3.26 | |
| for | 1.64 | 1.02 | 1.50 | 4.09 | 2.22 | 1.17 | 1.76 | 3.27 | |
| ada | 1.40 | 0.84 | 0.97 | 3.68 | 2.10 | 1.12 | 1.65 | 3.11 | |
| tfm | 1.50 | 0.88 | 1.16 | 4.18 | 2.16 | 1.19 | 1.54 | 3.34 | |
| chr | 1.55 | 0.87 | 1.17 | 4.22 | 2.28 | 1.17 | 1.69 | 3.40 | |
| Full | lin | 1.51 | 0.98 | 1.08 | 3.59 | 2.04 | 1.08 | 1.42 | 3.26 |
| ari | 1.86 | 1.05 | 1.44 | 3.71 | 2.74 | 1.26 | 1.61 | 4.26 | |
| var | 1.56 | 1.09 | 1.13 | 3.64 | 2.11 | 1.06 | 1.42 | 3.37 | |
| for | 1.72 | 0.95 | 1.24 | 4.21 | 2.04 | 1.26 | 1.49 | 3.27 | |
| ada | 1.57 | 0.93 | 1.34 | 4.55 | 2.19 | 1.11 | 1.57 | 3.21 | |
| tfm | 1.50 | 0.88 | 1.16 | 4.18 | 2.16 | 1.19 | 1.54 | 3.34 | |
| chr | 1.55 | 0.87 | 1.17 | 4.22 | 2.28 | 1.17 | 1.69 | 3.40 |
| 10905 | 10961 | 10982 | 11038 | 11161 | 11176 | 11208 | 11243 | |
|---|---|---|---|---|---|---|---|---|
| ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✓ | ✓ | |
| ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | |
| ✗ | ✗ | ✗ | ✓ | ✓ | ✗ | ✓ | ✓ | |
| ✗ | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✗ | |
| ✗ | ✗ | ✓ | ✓ | ✗ | ✓ | ✗ | ✓ | |
| Interaction | ✗ | ✗ | ✓ | ✓ | ✓ | ✗ | ✓ | ✗ |
| Decompose | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziemer, J.; Stein, G.; Wicker, C.; Jänichen, J.; Klöpper, D.; Last, K.; Denzler, J.; Schmullius, C.; Shadaydeh, M.; Dubois, C. Enhancing the Prediction of Dam Deformations: A Novel Data-Driven Approach. Remote Sens. 2025, 17, 1026. https://doi.org/10.3390/rs17061026
Ziemer J, Stein G, Wicker C, Jänichen J, Klöpper D, Last K, Denzler J, Schmullius C, Shadaydeh M, Dubois C. Enhancing the Prediction of Dam Deformations: A Novel Data-Driven Approach. Remote Sensing. 2025; 17(6):1026. https://doi.org/10.3390/rs17061026
Chicago/Turabian StyleZiemer, Jonas, Gideon Stein, Carolin Wicker, Jannik Jänichen, Daniel Klöpper, Katja Last, Joachim Denzler, Christiane Schmullius, Maha Shadaydeh, and Clémence Dubois. 2025. "Enhancing the Prediction of Dam Deformations: A Novel Data-Driven Approach" Remote Sensing 17, no. 6: 1026. https://doi.org/10.3390/rs17061026
APA StyleZiemer, J., Stein, G., Wicker, C., Jänichen, J., Klöpper, D., Last, K., Denzler, J., Schmullius, C., Shadaydeh, M., & Dubois, C. (2025). Enhancing the Prediction of Dam Deformations: A Novel Data-Driven Approach. Remote Sensing, 17(6), 1026. https://doi.org/10.3390/rs17061026








