Prediction of Vanadium Contamination Distribution Pattern Through Remote Sensing Image Fusion and Machine Learning
Abstract
1. Introduction
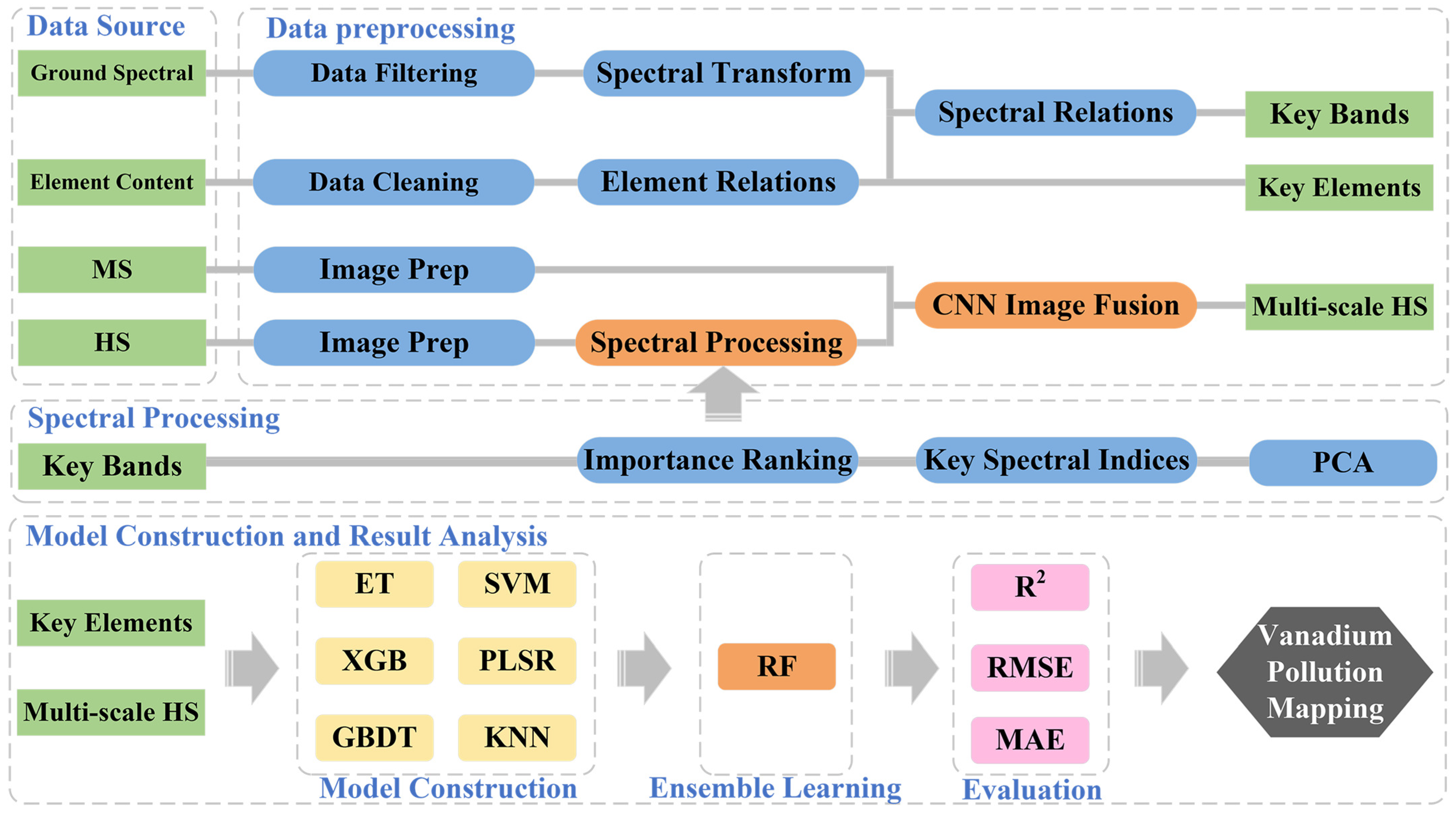
2. Materials and Methods
2.1. Overview of the Study Area
2.2. Data Acquisition
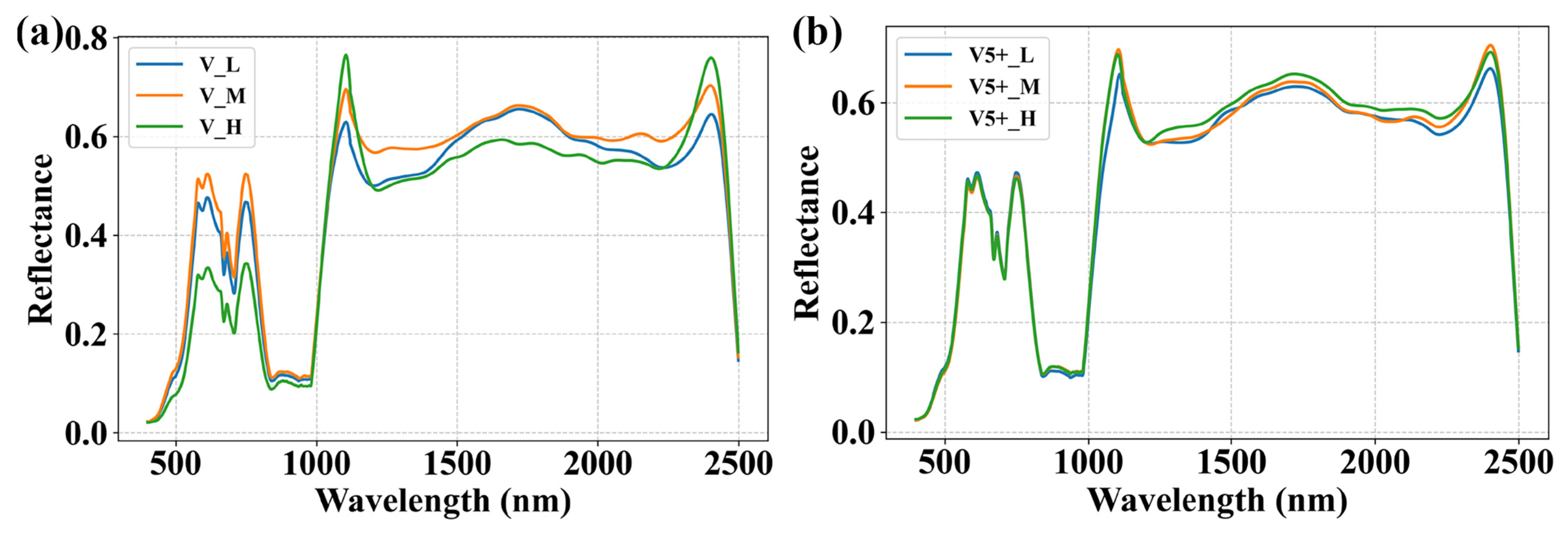
2.2.1. Soil Investigation Data
2.2.2. Remote Sensing Data
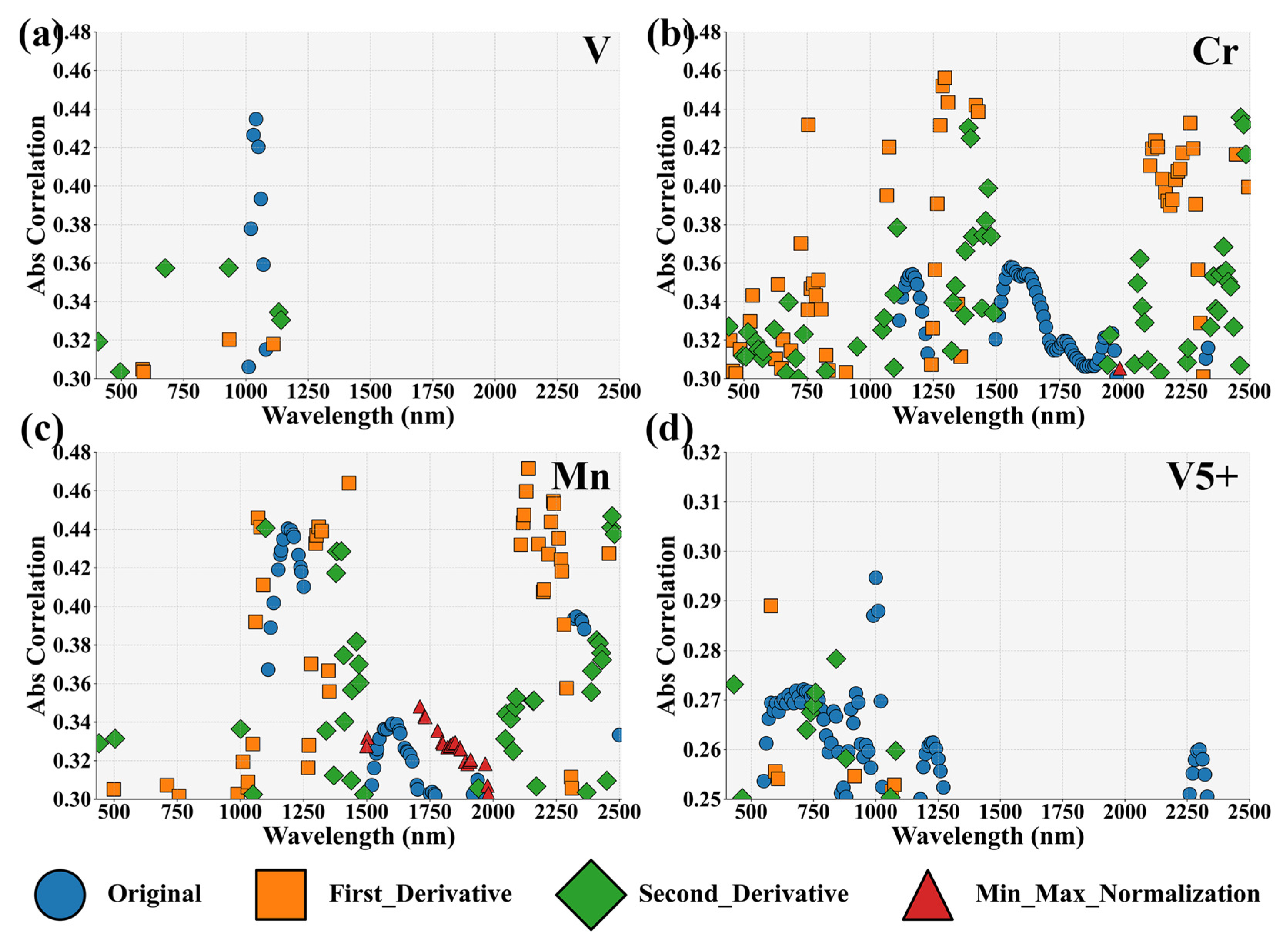
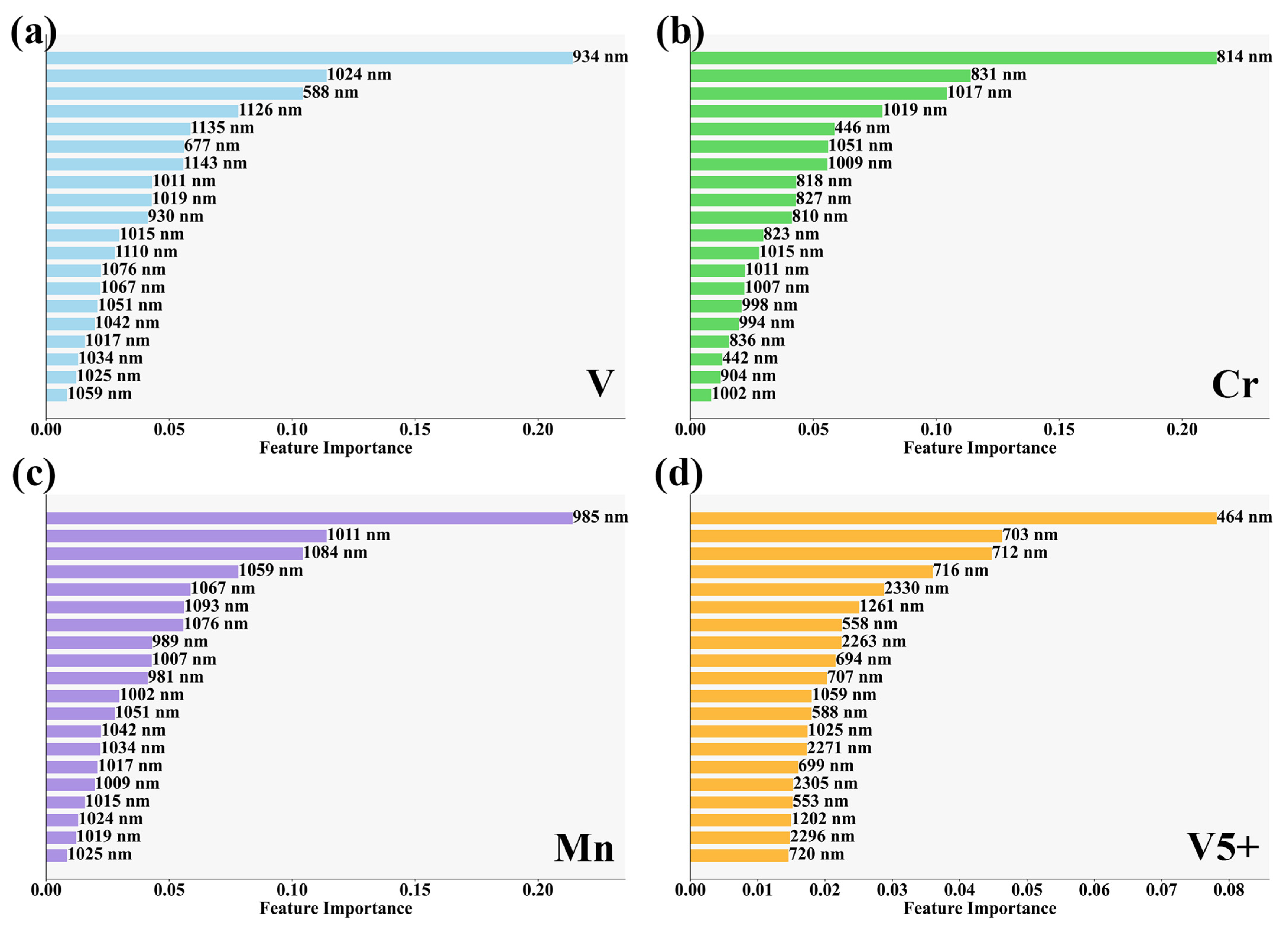
2.3. Characteristic Band Extraction
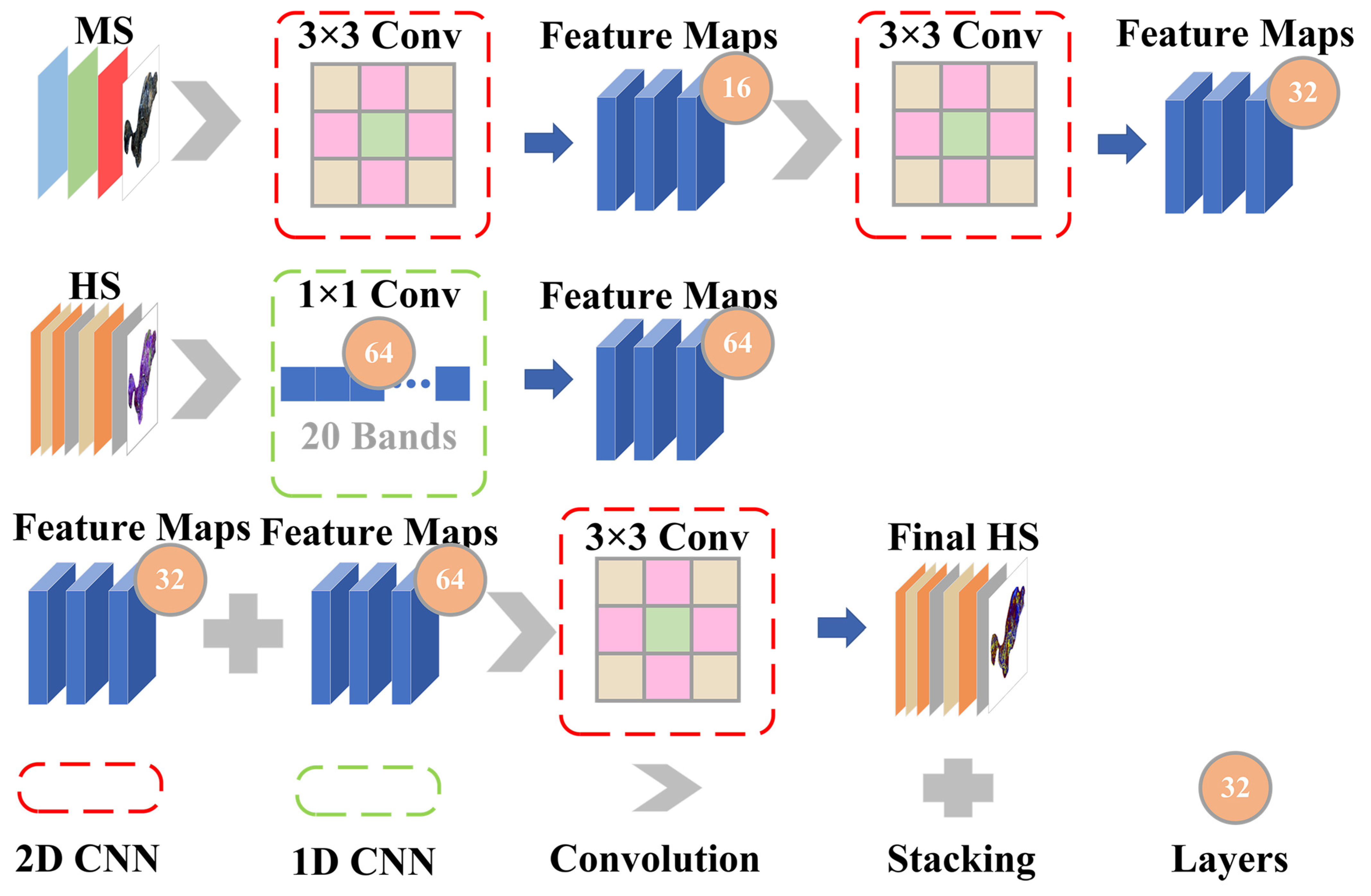
2.4. Image Fusion
2.5. Construction of Spectral Indices
2.6. Model Building Methods
2.6.1. Ensemble Learning
| Model | Parameter | Search Range |
|---|---|---|
| ET | n_estimators | [100, 300] |
| max_depth | [5, 15] | |
| min_samples_split | [2, 10] | |
| min_samples_leaf | [1, 4] | |
| XGB | learning_rate | [0.01, 0.3] |
| n_estimators | [100, 300] | |
| max_depth | [3, 9] | |
| reg_alpha | [0, 10] | |
| reg_lambda | [1, 20] | |
| min_child_weight | [1, 5] | |
| GBDT | n_estimators | [100, 300] |
| max_depth | [3, 7] | |
| learning_rate | [0.01, 0.3] | |
| SVR | C | [1, 100] |
| gamma | [0.001, 1] | |
| epsilon | [0.05, 0.5] | |
| PLSR | n_components | [2, 8] |
| RF | n_estimators | [100, 300] |
| max_depth | [5, 15] | |
| min_samples_split | [2, 10] | |
| min_samples_leaf | [1, 4] | |
| alpha | [0.1, 1.0] |
2.6.2. Model Evaluation
2.7. Spatial Mapping
3. Results
3.1. Feature Extraction
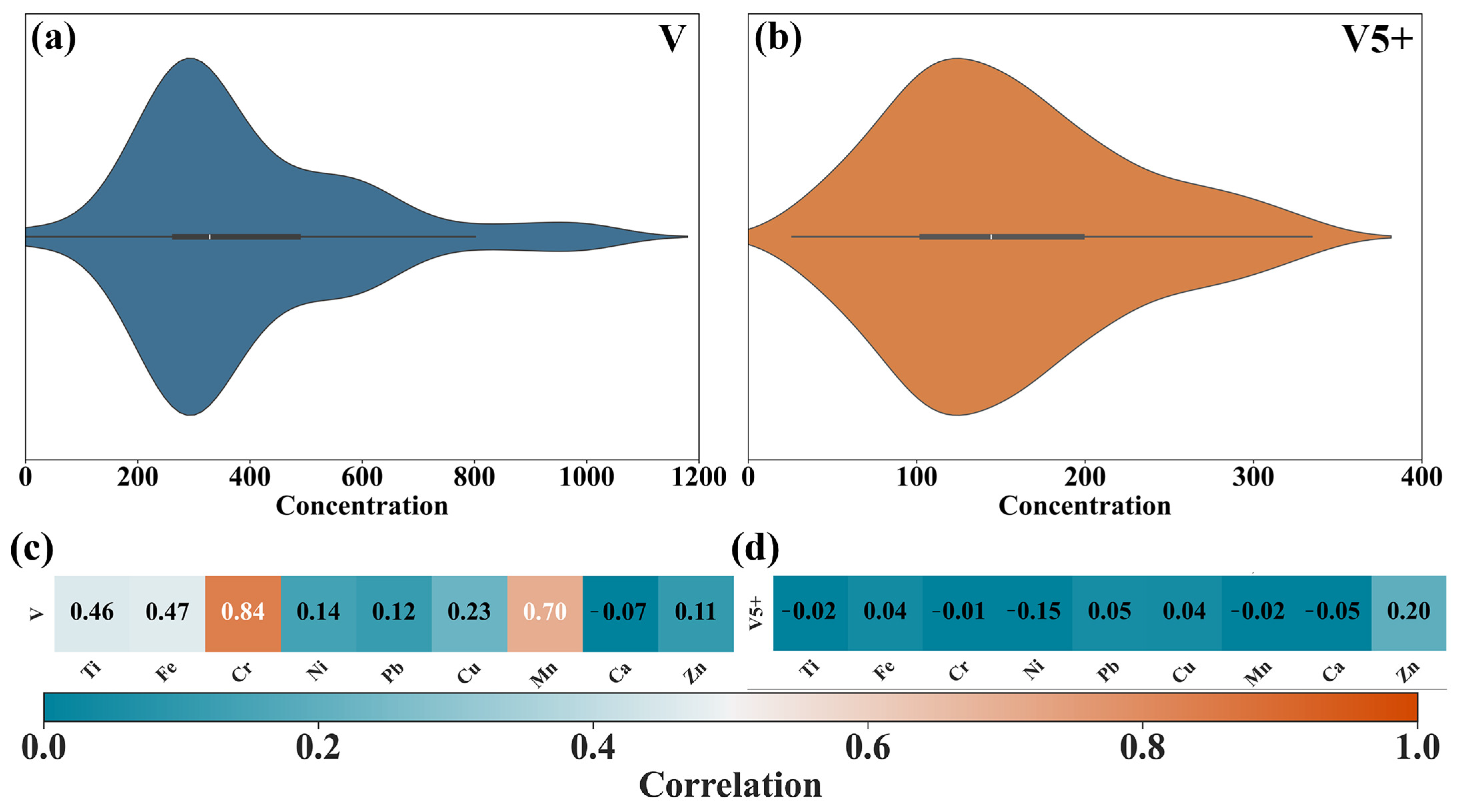
3.1.1. Soil Element Content Analysis
3.1.2. Spectral Feature Extraction
3.1.3. Performance of Characteristic Band Importance
3.2. Performance of Image Fusion
3.3. Model Construction
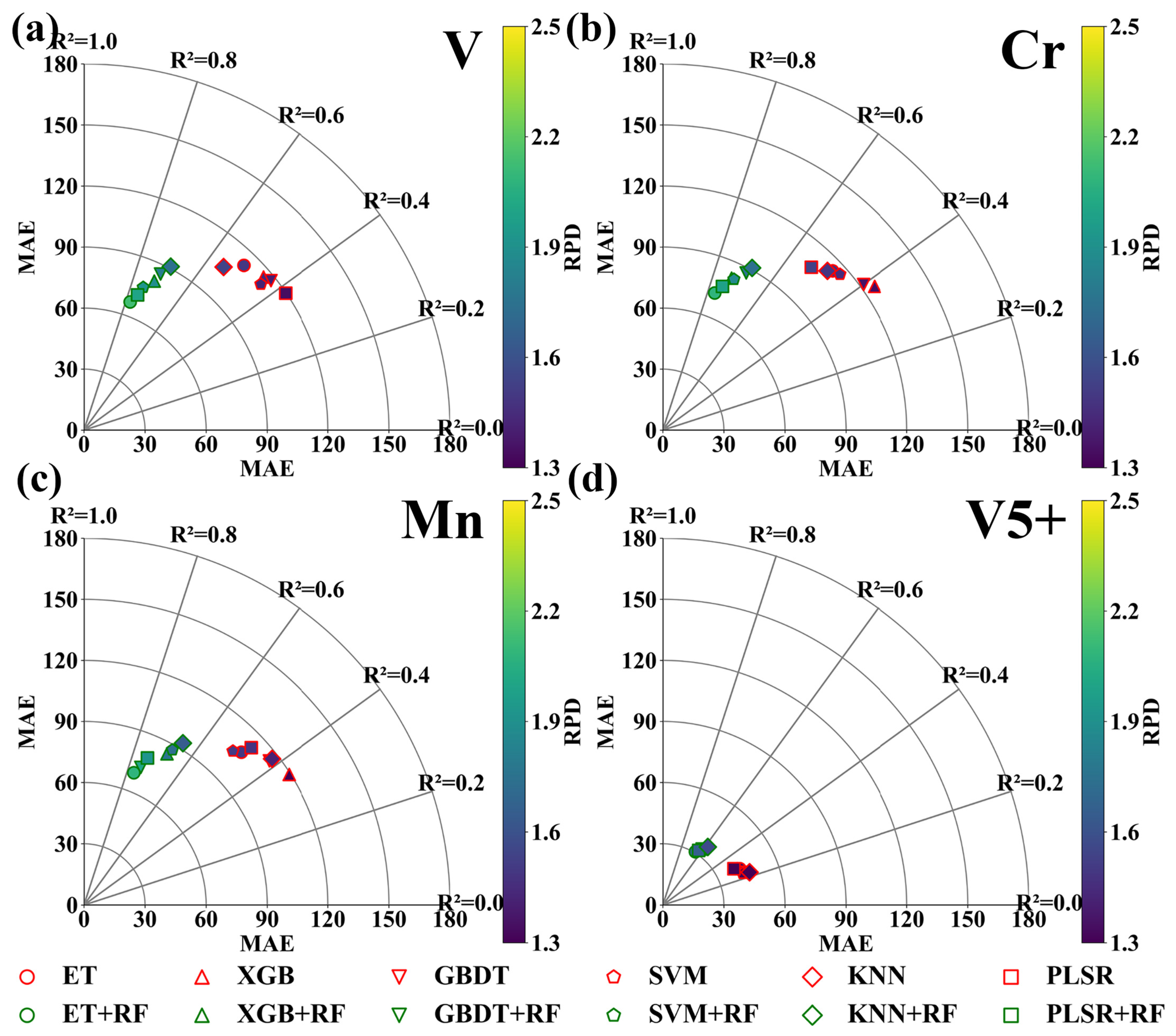
3.3.1. Traditional Machine Learning Models
3.3.2. Optimized Random Forest Model
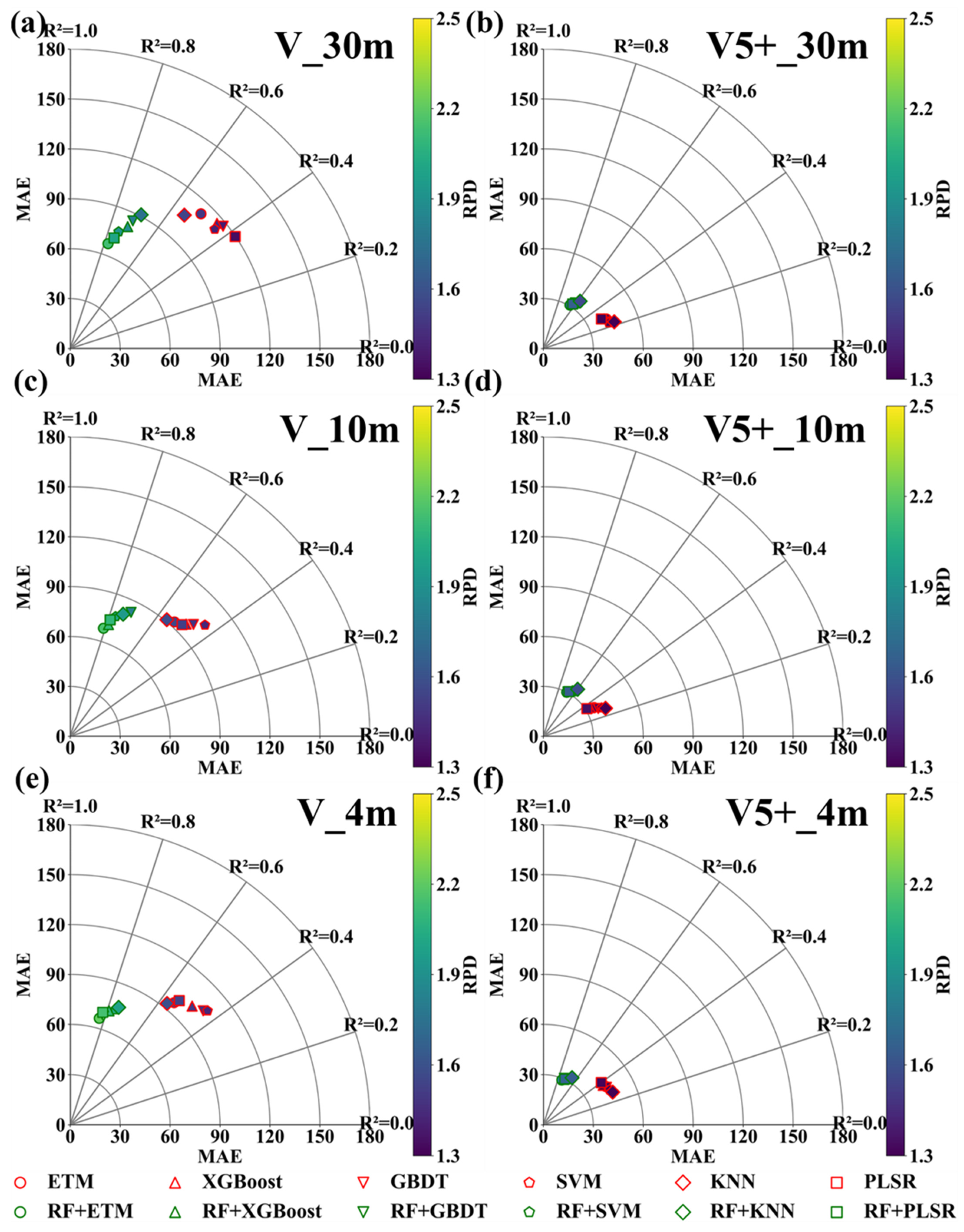
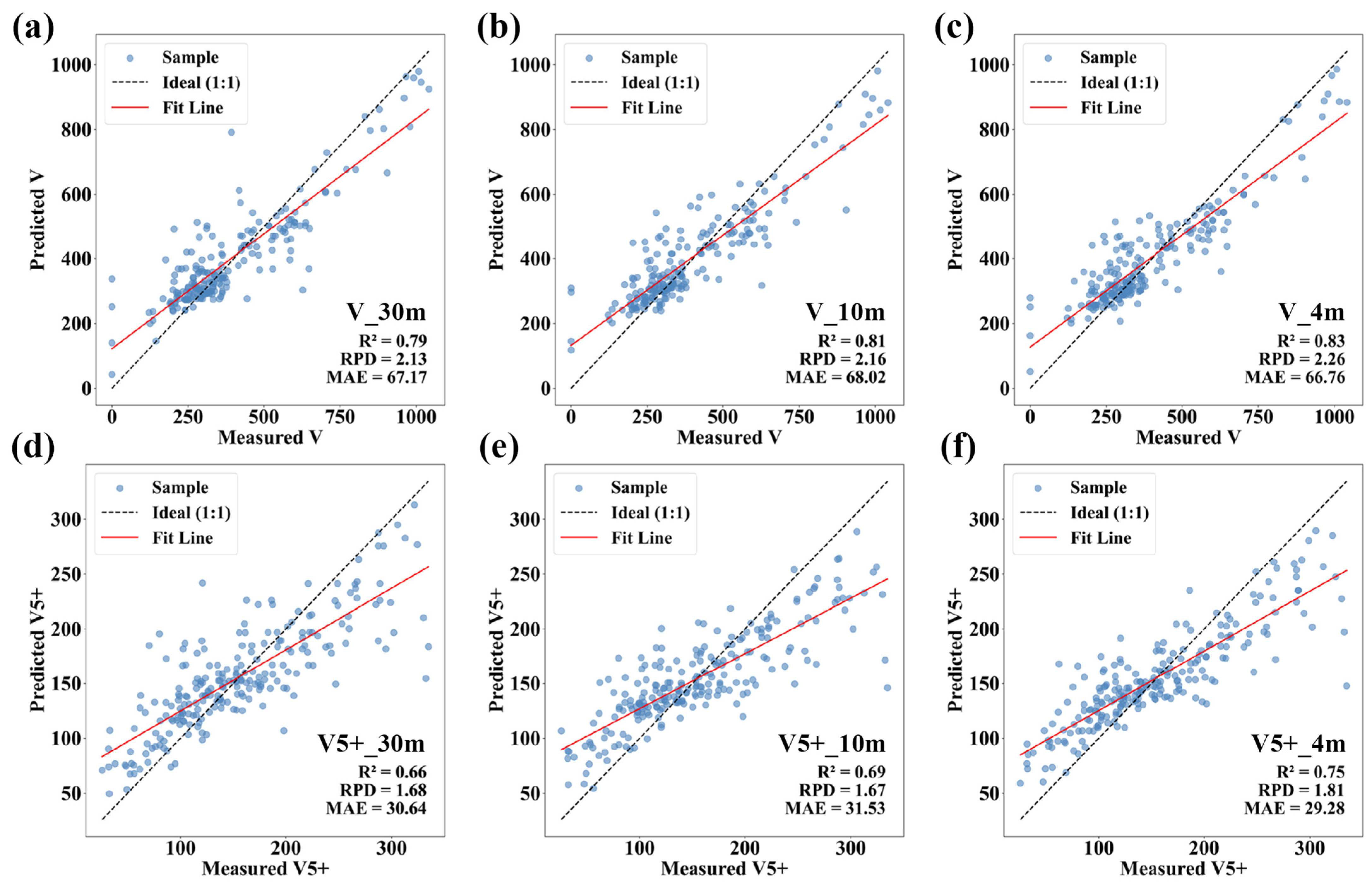
3.3.3. Random Forest Optimization Model Based on Image Fusion
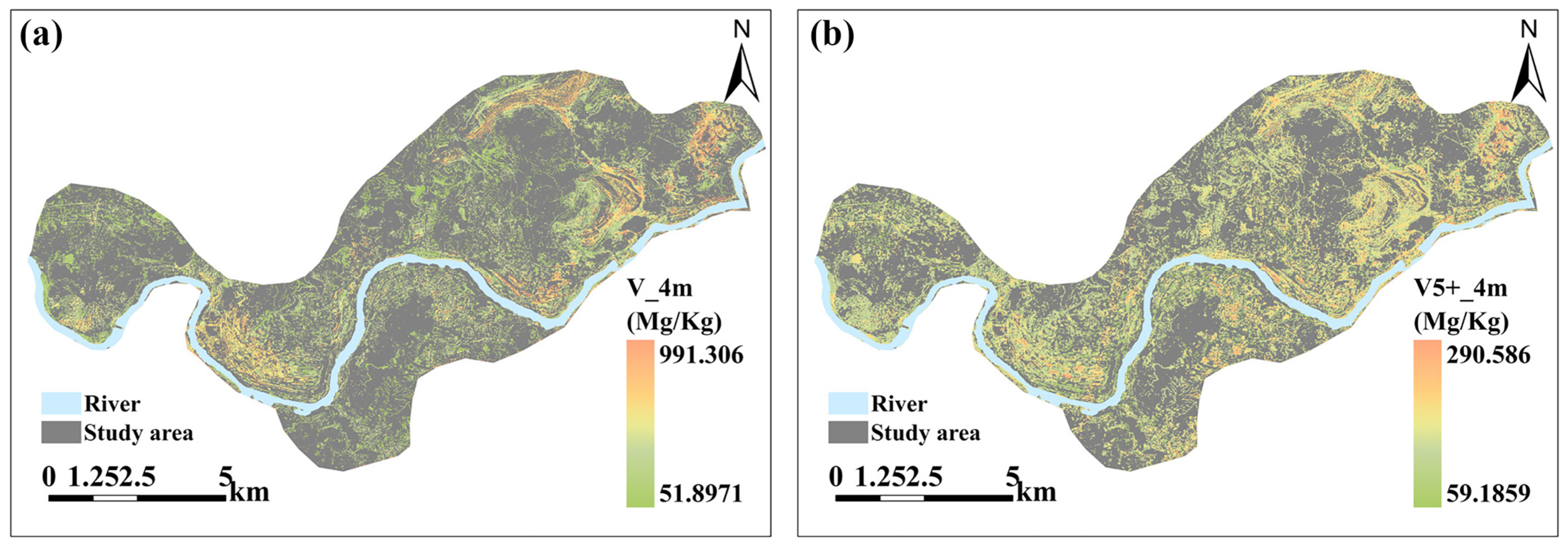
3.4. Soil Vanadium Concentration Map
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Islam, S.; Ahmed, K.; Habibullah-Al-Mamun; Masunaga, S. Potential Ecological Risk of Hazardous Elements in Different Land-Use Urban Soils of Bangladesh. Sci. Total Environ. 2015, 512–513, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Adnan, M.; Xiao, B.; Ali, M.U.; Xiao, P.; Zhao, P.; Wang, H.; Bibi, S. Heavy Metals Pollution from Smelting Activities: A Threat to Soil and Groundwater. Ecotoxicol. Environ. Saf. 2024, 274, 116189. [Google Scholar] [CrossRef] [PubMed]
- Schlesinger, W.H.; Klein, E.M.; Vengosh, A. Global Biogeochemical Cycle of Vanadium. Proc. Natl. Acad. Sci. USA 2017, 114, E11092–E11100. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Huang, Y.; Li, Y.; Yang, Y.; Cheng, X.; Jiao, G.; Dai, H. The Response of Bacterial Communities to V and Cr and Novel Reducing Bacteria near a Vanadium-titanium Magnetite Refinery. Sci. Total Environ. 2022, 806, 151214. [Google Scholar] [CrossRef]
- Gan, C.; Yang, J.; Li, J.; Yang, M.; Du, X.; Nikitin, A. Transcriptome Analysis Reveals Vanadium Reduction Mechanisms in a Bacterium of Pseudomonas Balearica. J. Clean. Prod. 2024, 454, 142258. [Google Scholar] [CrossRef]
- Cheng, M.; Yin, X.; Zhang, H. Insights into the Hydrogen-Fueled Bioreduction of Vanadium(V) by Marine Shewanella Sp. FDA-1: Process and Mechanism. J. Hazard. Mater. 2025, 483, 136585. [Google Scholar] [CrossRef]
- Cao, X.; Diao, M.; Zhang, B.; Liu, H.; Wang, S.; Yang, M. Spatial Distribution of Vanadium and Microbial Community Responses in Surface Soil of Panzhihua Mining and Smelting Area, China. Chemosphere 2017, 183, 9–17. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, B.; Liu, Z.; Wang, S.; Yao, J.; Borthwick, A.G.L. Vanadium Contamination and Associated Health Risk of Farmland Soil near Smelters throughout China. Environ. Pollut. 2020, 263, 114540. [Google Scholar] [CrossRef]
- Ścibior, A.; Wnuk, E.; Gołębiowska, D. Wild Animals in Studies on Vanadium Bioaccumulation—Potential Animal Models of Environmental Vanadium Contamination: A Comprehensive Overview with a Polish Accent. Sci. Total Environ. 2021, 785, 147205. [Google Scholar] [CrossRef]
- Yang, N.; Han, L.; Liu, M. Inversion of Soil Heavy Metals in Metal Tailings Area Based on Different Spectral Transformation and Modeling Methods. Heliyon 2023, 9, e19782. [Google Scholar] [CrossRef]
- Gholizadeh, A.; Saberioon, M.; Ben-Dor, E.; Borůvka, L. Monitoring of Selected Soil Contaminants Using Proximal and Remote Sensing Techniques: Background, State-of-the-Art and Future Perspectives. Crit. Rev. Environ. Sci. Technol. 2018, 48, 243–278. [Google Scholar] [CrossRef]
- Shi, T.; Liu, H.; Chen, Y.; Wang, J.; Wu, G. Estimation of Arsenic in Agricultural Soils Using Hyperspectral Vegetation Indices of Rice. J. Hazard. Mater. 2016, 308, 243–252. [Google Scholar] [CrossRef] [PubMed]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Tajik, S.; Finke, P. Digital Mapping of Soil Properties Using Multiple Machine Learning in a Semi-Arid Region, Central Iran. Geoderma 2019, 338, 445–452. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, T.; Lei, M.; Yang, J.; Guo, Q.; Song, B.; Zhou, X. Spatial Distribution of Soil Heavy Metal Pollution Estimated by Different Interpolation Methods: Accuracy and Uncertainty Analysis. Chemosphere 2011, 82, 468–476. [Google Scholar] [CrossRef] [PubMed]
- Shi, T.; Guo, L.; Chen, Y.; Wang, W.; Shi, Z.; Li, Q.; Wu, G. Proximal and Remote Sensing Techniques for Mapping of Soil Contamination with Heavy Metals. Appl. Spectrosc. Rev. 2018, 53, 783–805. [Google Scholar] [CrossRef]
- Zahra, A.; Qureshi, R.; Sajjad, M.; Sadak, F.; Nawaz, M.; Khan, H.A.; Uzair, M. Current Advances in Imaging Spectroscopy and Its State-of-the-Art Applications. Expert Syst. Appl. 2024, 238, 122172. [Google Scholar] [CrossRef]
- Song, Y.; Sun, N.; Zhang, L.; Wang, L.; Su, H.; Chen, Z.; Yu, H.; Li, B. Using Multispectral Variables to Estimate Heavy Metals Content in Agricultural Soils: A Case of Suburban Area in Tianjin, China. Geoderma Reg. 2022, 29, e00540. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, S.; Dai, X.; Li, D.; Jiang, H.; Jia, K. Coupled Retrieval of Heavy Metal Nickel Concentration in Agricultural Soil from Spaceborne Hyperspectral Imagery. J. Hazard. Mater. 2023, 446, 130722. [Google Scholar] [CrossRef]
- Tan, K.; Wang, H.; Chen, L.; Du, Q.; Du, P.; Pan, C. Estimation of the Spatial Distribution of Heavy Metal in Agricultural Soils Using Airborne Hyperspectral Imaging and Random Forest. J. Hazard. Mater. 2020, 382, 120987. [Google Scholar] [CrossRef]
- Wang, J.; Hu, X.; Shi, T.; He, L.; Hu, W.; Wu, G. Assessing Toxic Metal Chromium in the Soil in Coal Mining Areas via Proximal Sensing: Prerequisites for Land Rehabilitation and Sustainable Development. Geoderma 2022, 405, 115399. [Google Scholar] [CrossRef]
- Wang, F.; Gao, J.; Zha, Y. Hyperspectral Sensing of Heavy Metals in Soil and Vegetation: Feasibility and Challenges. ISPRS J. Photogramm. Remote Sens. 2018, 136, 73–84. [Google Scholar] [CrossRef]
- Shi, T.; Chen, Y.; Liu, Y.; Wu, G. Visible and Near-Infrared Reflectance Spectroscopy—An Alternative for Monitoring Soil Contamination by Heavy Metals. J. Hazard. Mater. 2014, 265, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Laparrcr, V.; Santos-Rodriguez, R. Spatial/Spectral Information Trade-off in Hyperspectral Images. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1124–1127. [Google Scholar]
- Bhargava, A.; Sachdeva, A.; Sharma, K.; Alsharif, M.H.; Uthansakul, P.; Uthansakul, M. Hyperspectral Imaging and Its Applications: A Review. Heliyon 2024, 10, e33208. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Sun, W.; Wang, J.; Ding, S.; Liu, S. Effects of Hyperspectral Data with Different Spectral Resolutions on the Estimation of Soil Heavy Metal Content: From Ground-Based and Airborne Data to Satellite-Simulated Data. Sci. Total Environ. 2022, 838, 156129. [Google Scholar] [CrossRef] [PubMed]
- Yao, L.; Xu, M.; Liu, Y.; Niu, R.; Wu, X.; Song, Y. Estimating of Heavy Metal Concentration in Agricultural Soils from Hyperspectral Satellite Sensor Imagery: Considering the Sources and Migration Pathways of Pollutants. Ecol. Indic. 2024, 158, 111416. [Google Scholar] [CrossRef]
- Melser, R.; Coops, N.C.; Wulder, M.A.; Derksen, C. Multi-Source Remote Sensing Based Modeling of Vegetation Productivity in the Boreal: Issues & Opportunities. Can. J. Remote Sens. 2023, 49, 2256895. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, C.; Wang, J.; Zhang, M.-W.; Wang, X.; Zeng, L.-T.; Cui, Y.-P.; Wang, H.; Sun, X.-L. Monitoring Soil Arsenic Content in Densely Vegetated Agricultural Areas Using UAV Hyperspectral, Satellite Multispectral and SAR Data. J. Hazard. Mater. 2025, 484, 136689. [Google Scholar] [CrossRef]
- Sara, D.; Mandava, A.K.; Kumar, A.; Duela, S.; Jude, A. Hyperspectral and Multispectral Image Fusion Techniques for High Resolution Applications: A Review. Earth Sci. Inform. 2021, 14, 1685–1705. [Google Scholar] [CrossRef]
- Allu, A.R.; Mesapam, S. Impact of Remote Sensing Data Fusion on Agriculture Applications: A Review. Eur. J. Agron. 2025, 164, 127478. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral Image Classification With Deep Feature Fusion Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Vivone, G. Multispectral and Hyperspectral Image Fusion in Remote Sensing: A Survey. Inf. Fusion 2023, 89, 405–417. [Google Scholar] [CrossRef]
- Dian, R.; Li, S.; Sun, B.; Guo, A. Recent Advances and New Guidelines on Hyperspectral and Multispectral Image Fusion. Inf. Fusion 2021, 69, 40–51. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.-Q.; Chan, J.C.-W. Hyperspectral and Multispectral Image Fusion via Deep Two-Branches Convolutional Neural Network. Remote Sens. 2018, 10, 800. [Google Scholar] [CrossRef]
- Laszlo, E.; Szolgay, P.; Nagy, Z. Analysis of a GPU Based CNN Implementation. In Proceedings of the 2012 13th International Workshop on Cellular Nanoscale Networks and their Applications, Turin, Italy, 29–31 August 2012; pp. 1–5. [Google Scholar]
- Nkinahamira, F.; Feng, A.; Zhang, L.; Rong, H.; Ndagijimana, P.; Guo, D.; Cui, B.; Zhang, H. Machine Learning Approaches for Monitoring Environmental Metal Pollutants: Recent Advances in Source Apportionment, Detection, Quantification, and Risk Assessment. TrAC Trends Anal. Chem. 2024, 180, 117980. [Google Scholar] [CrossRef]
- Lovynska, V.; Bayat, B.; Bol, R.; Moradi, S.; Rahmati, M.; Raj, R.; Sytnyk, S.; Wiche, O.; Wu, B.; Montzka, C. Monitoring Heavy Metals and Metalloids in Soils and Vegetation by Remote Sensing: A Review. Remote Sens. 2024, 16, 3221. [Google Scholar] [CrossRef]
- Koldasbayeva, D.; Tregubova, P.; Gasanov, M.; Zaytsev, A.; Petrovskaia, A.; Burnaev, E. Challenges in Data-Driven Geospatial Modeling for Environmental Research and Practice. Nat. Commun. 2024, 15, 10700. [Google Scholar] [CrossRef]
- Al-Shboul, K.F. Unraveling the Complex Interplay between Soil Characteristics and Radon Surface Exhalation Rates through Machine Learning Models and Multivariate Analysis. Environ. Pollut. 2023, 336, 122440. [Google Scholar] [CrossRef]
- Zou, Z.; Wang, Q.; Wu, Q.; Li, M.; Zhen, J.; Yuan, D.; Zhou, M.; Xu, C.; Wang, Y.; Zhao, Y.; et al. Inversion of Heavy Metal Content in Soil Using Hyperspectral Characteristic Bands-Based Machine Learning Method. J. Environ. Manag. 2024, 355, 120503. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Shen, W. A Review of Ensemble Learning Algorithms Used in Remote Sensing Applications. Appl. Sci. 2022, 12, 8654. [Google Scholar] [CrossRef]
- Khan, Z.; Gul, A.; Perperoglou, A.; Miftahuddin, M.; Mahmoud, O.; Adler, W.; Lausen, B. Ensemble of Optimal Trees, Random Forest and Random Projection Ensemble Classification. Adv. Data Anal. Classif. 2020, 14, 97–116. [Google Scholar] [CrossRef]
- Luo, Y.; Su, S. SpatioTemporal Random Forest and SpatioTemporal Stacking Tree: A Novel Spatially Explicit Ensemble Learning Approach to Modeling Non-Linearity in Spatiotemporal Non-Stationarity. Int. J. Appl. Earth Obs. Geoinf. 2025, 136, 104315. [Google Scholar] [CrossRef]
- Gan, C.; Yang, J.; Liu, R.; Li, X.; Tang, Q. Contrasted Speciation Distribution of Toxic Metal(Loid)s and Microbial Community Structure in Vanadium-Titanium Magnetite Tailings under Dry and Wet Disposal Methods. J. Hazard. Mater. 2022, 439, 129624. [Google Scholar] [CrossRef] [PubMed]
- HJ/T 166-2004; State Environmental Protection Administration of the People’s Republic of China Technical Specification for Soil Environmental Monitoring. State Environmental Protection Administration of the People’s Republic of China: Shenzhen, China, 2004.
- Ma, X.; Wang, J.; Zhou, K.; Zhang, W.; Zhang, Z.; Zhou, S.; Bai, Y.; De Maeyer, P.; Van De Voorde, T. Quantitative Evaluation of the Impact of Band Optimization Methods on the Accuracy of the Hyperspectral Metal Element Inversion Models. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104011. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation Forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Zhang, B.; Guo, B.; Zou, B.; Wei, W.; Lei, Y.; Li, T. Retrieving Soil Heavy Metals Concentrations Based on GaoFen-5 Hyperspectral Satellite Image at an Opencast Coal Mine, Inner Mongolia, China. Environ. Pollut. 2022, 300, 118981. [Google Scholar] [CrossRef]
- Ding, S.; Zhang, X.; Sun, W.; Shang, K.; Wang, Y. Estimation of Soil Lead Content Based on GF-5 Hyperspectral Images, Considering the Influence of Soil Environmental Factors. J. Soils Sediments 2022, 22, 1431–1445. [Google Scholar] [CrossRef]
- Yin, F.; Wu, M.; Liu, L.; Zhu, Y.; Feng, J.; Yin, D.; Yin, C.; Yin, C. Predicting the Abundance of Copper in Soil Using Reflectance Spectroscopy and GF5 Hyperspectral Imagery. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102420. [Google Scholar] [CrossRef]
- He, Z.; Gao, L.; Liang, M.; Zeng, Z.-C. A Survey of Methane Point Source Emissions from Coal Mines in Shanxi Province of China Using AHSI on Board Gaofen-5B. Atmos. Meas. Tech. 2024, 17, 2937–2956. [Google Scholar] [CrossRef]
- Ren, K.; Sun, W.; Meng, X.; Yang, G.; Du, Q. Fusing China GF-5 Hyperspectral Data with GF-1, GF-2 and Sentinel-2A Multispectral Data: Which Methods Should Be Used? Remote Sens. 2020, 12, 882. [Google Scholar] [CrossRef]
- Shen, Q.; Xia, K.; Zhang, S.; Kong, C.; Hu, Q.; Yang, S. Hyperspectral Indirect Inversion of Heavy-Metal Copper in Reclaimed Soil of Iron Ore Area. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 222, 117191. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2014; Volume 8689, pp. 818–833. ISBN 978-3-319-10589-5. [Google Scholar]
- Vasanthakumari, R.K.; Nair, R.V.; Krishnappa, V.G. Improved Learning by Using a Modified Activation Function of a Convolutional Neural Network in Multi-Spectral Image Classification. Mach. Learn. Appl. 2023, 14, 100502. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Zhao, K.; Zhao, X.; Song, C. FSL-Unet: Full-Scale Linked Unet With Spatial–Spectral Joint Perceptual Attention for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Wu, H.; Gui, J.; Xu, Y.; Wu, Z.; Tang, Y.Y.; Wei, Z. An Efficient Cross-Modality Self-Calibrated Network for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Kalamkar, S.; Geetha, M.A. Multimodal Image Fusion: A Systematic Review. Decis. Anal. J. 2023, 9, 100327. [Google Scholar] [CrossRef]
- Gelvez-Barrera, T.; Arguello, H.; Foi, A. Joint Nonlocal, Spectral, and Similarity Low-Rank Priors for Hyperspectral–Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Xie, Q.; Zhou, M.; Zhao, Q.; Xu, Z.; Meng, D. MHF-Net: An Interpretable Deep Network for Multispectral and Hyperspectral Image Fusion. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 1457–1473. [Google Scholar] [CrossRef]
- Huang, S.; Tang, L.; Hupy, J.P.; Wang, Y.; Shao, G. A Commentary Review on the Use of Normalized Difference Vegetation Index (NDVI) in the Era of Popular Remote Sensing. J. For. Res. 2021, 32, 1–6. [Google Scholar] [CrossRef]
- Jia, X.; Hou, D. Mapping Soil Arsenic Pollution at a Brownfield Site Using Satellite Hyperspectral Imagery and Machine Learning. Sci. Total Environ. 2023, 857, 159387. [Google Scholar] [CrossRef]
- Tan, K.; Chen, L.; Wang, H.; Liu, Z.; Ding, J.; Wang, X. Estimation of the Distribution Patterns of Heavy Metal in Soil from Airborne Hyperspectral Imagery Based on Spectral Absorption Characteristics. J. Environ. Manag. 2023, 347, 119196. [Google Scholar] [CrossRef]
- Wang, Q.; Zou, X.; Chen, Y.; Zhu, Z.; Yan, C.; Shan, P.; Wang, S.; Fu, Y. XGBoost Algorithm Assisted Multi-Component Quantitative Analysis with Raman Spectroscopy. Spectrochim. Acta Part A 2024, 323, 124917. [Google Scholar] [CrossRef]
- Li, S.; Sun, L.; Tian, Y.; Lu, X.; Fu, Z.; Lv, G.; Zhang, L.; Xu, Y.; Che, W. Research on Non-Destructive Identification Technology of Rice Varieties Based on HSI and GBDT. Infrared Phys. Technol. 2024, 142, 105511. [Google Scholar] [CrossRef]
- Salazar-Rojas, T.; Cejudo-Ruiz, F.R.; Calvo-Brenes, G. Comparison between Machine Linear Regression (MLR) and Support Vector Machine (SVM) as Model Generators for Heavy Metal Assessment Captured in Biomonitors and Road Dust. Environ. Pollut. 2022, 314, 120227. [Google Scholar] [CrossRef] [PubMed]
- Xie, R.; Darvishzadeh, R.; Skidmore, A.; Van Der Meer, F. Characterizing Foliar Phenolic Compounds and Their Absorption Features in Temperate Forests Using Leaf Spectroscopy. ISPRS J. Photogramm. Remote Sens. 2024, 212, 338–356. [Google Scholar] [CrossRef]
- Cimusa Kulimushi, L.; Bigabwa Bashagaluke, J.; Prasad, P.; Heri-Kazi, A.B.; Lal Kushwaha, N.; Masroor, M.; Choudhari, P.; Elbeltagi, A.; Sajjad, H.; Mohammed, S. Soil Erosion Susceptibility Mapping Using Ensemble Machine Learning Models: A Case Study of Upper Congo River Sub-Basin. Catena 2023, 222, 106858. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random Forest in Remote Sensing: A Review of Applications and Future Directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Huang, C.; Yang, Q.; Zhang, H. Temporal and Spatial Variation of NDVI and Its Driving Factors in Qinling Mountain. Water 2021, 13, 3154. [Google Scholar] [CrossRef]
- Zheng, Y.; Tang, L.; Wang, H. An Improved Approach for Monitoring Urban Built-up Areas by Combining NPP-VIIRS Nighttime Light, NDVI, NDWI, and NDBI. J. Clean. Prod. 2021, 328, 129488. [Google Scholar] [CrossRef]
- Guha, S.; Govil, H.; Dey, A.; Gill, N. Analytical Study of Land Surface Temperature with NDVI and NDBI Using Landsat 8 OLI and TIRS Data in Florence and Naples City, Italy. Eur. J. Remote Sens. 2018, 51, 667–678. [Google Scholar] [CrossRef]
- Laukamp, C.; Rodger, A.; LeGras, M.; Lampinen, H.; Lau, I.C.; Pejcic, B.; Stromberg, J.; Francis, N.; Ramanaidou, E. Mineral Physicochemistry Underlying Feature-Based Extraction of Mineral Abundance and Composition from Shortwave, Mid and Thermal Infrared Reflectance Spectra. Minerals 2021, 11, 347. [Google Scholar] [CrossRef]
- Hao, H.; Li, P.; Jiao, W.; Ge, D.; Hu, C.; Li, J.; Lv, Y.; Chen, W. Ensemble Learning-Based Applied Research on Heavy Metals Prediction in a Soil-Rice System. Sci. Total Environ. 2023, 898, 165456. [Google Scholar] [CrossRef]
- Baltrėnaitė, E.; Baltrėnas, P.; Lietuvninkas, A.; Šerevičienė, V.; Zuokaitė, E. Integrated Evaluation of Aerogenic Pollution by Air-Transported Heavy Metals (Pb, Cd, Ni, Zn, Mn and Cu) in the Analysis of the Main Deposit Media. Environ. Sci. Pollut. Res. 2014, 21, 299–313. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, J.; Wu, X.; Tian, Q.; Ji, J.; Qin, Z. Possibilities of Reflectance Spectroscopy for the Assessment of Contaminant Elements in Suburban Soils. Appl. Geochem. 2005, 20, 1051–1059. [Google Scholar] [CrossRef]
- Pandit, C.M.; Filippelli, G.M.; Li, L. Estimation of Heavy-Metal Contamination in Soil Using Reflectance Spectroscopy and Partial Least-Squares Regression. Int. J. Remote Sens. 2010, 31, 4111–4123. [Google Scholar] [CrossRef]
- Murphy, R.J.; Schneider, S.; Monteiro, S.T. Consistency of Measurements of Wavelength Position From Hyperspectral Imagery: Use of the Ferric Iron Crystal Field Absorption at $\sim$900 Nm as an Indicator of Mineralogy. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2843–2857. [Google Scholar] [CrossRef]
- Li, W.; Liu, X.; Liu, D.; Han, Y. Mineralogical Reconstruction of Titanium-Vanadium Hematite and Magnetic Separation Mechanism of Titanium and Iron Minerals. Adv. Powder Technol. 2022, 33, 103408. [Google Scholar] [CrossRef]
- Nohair, M.; Aymes, D.; Perriat, P.; Gillot, B. Infrared Spectra-Structure Correlation Study of Vanadium-Iron Spinels and of Their Oxidation Products. Vib. Spectrosc. 1995, 9, 181–190. [Google Scholar] [CrossRef]
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A.; et al. Recent Advances in Techniques for Hyperspectral Image Processing. Remote Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, Z.; Ghamisi, P.; Rasti, B.; Liu, X.; Cai, Z. Transformer-Based Contrastive Prototypical Clustering for Multimodal Remote Sensing Data. Inf. Sci. 2023, 649, 119655. [Google Scholar] [CrossRef]
- Stevens, A.; Udelhoven, T.; Denis, A.; Tychon, B.; Lioy, R.; Hoffmann, L.; Van Wesemael, B. Measuring Soil Organic Carbon in Croplands at Regional Scale Using Airborne Imaging Spectroscopy. Geoderma 2010, 158, 32–45. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, R.; Lin, G.; Xiao, Y.; Ma, H.; Zhao, L. Estimate of Soil Heavy Metal in a Mining Region Using PCC-SVM-RFECV-AdaBoost Combined with Reflectance Spectroscopy. Environ. Geochem. Health 2023, 45, 9103–9121. [Google Scholar] [CrossRef]
- Ye, M.; Zhu, L.; Li, X.; Ke, Y.; Huang, Y.; Chen, B.; Yu, H.; Li, H.; Feng, H. Estimation of the Soil Arsenic Concentration Using a Geographically Weighted XGBoost Model Based on Hyperspectral Data. Sci. Total Environ. 2023, 858, 159798. [Google Scholar] [CrossRef]
- Lv, L.; Chen, T.; Dou, J.; Plaza, A. A Hybrid Ensemble-Based Deep-Learning Framework for Landslide Susceptibility Mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102713. [Google Scholar] [CrossRef]
- Somarathna, P.D.S.N.; Minasny, B.; Malone, B.P. More Data or a Better Model? Figuring Out What Matters Most for the Spatial Prediction of Soil Carbon. Soil Sci. Soc. Am. J. 2017, 81, 1413–1426. [Google Scholar] [CrossRef]
- Licciardi, G.A.; Villa, A.; Khan, M.M.; Chanussot, J. Image Fusion and Spectral Unmixing of Hyperspectral Images for Spatial Improvement of Classification Maps. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 7290–7293. [Google Scholar]
- Trentin, C.; Ampatzidis, Y.; Lacerda, C.; Shiratsuchi, L. Tree Crop Yield Estimation and Prediction Using Remote Sensing and Machine Learning: A Systematic Review. Smart Agric. Technol. 2024, 9, 100556. [Google Scholar] [CrossRef]

| Type | Data | Data ID | Date |
|---|---|---|---|
| HS | GF-5B | GF5B_AHSI_E101.8_N26.4_20230413_008494_L10000316410 | 13 April 2023 |
| MS | Sentinel-2A | 20230409T034541_20230409T040008_T47RQK | 9 April 2023 |
| GF-2 | GF2_PMS1_E101.5_N26.5_20230410_L1A0007216553 | 10 April 2023 | |
| GF2_PMS2_E101.7_N26.5_20230410_L1A0007216706 | |||
| GF2_PMS2_E101.8_N26.7_20230410_L1A0007216704 |
| Order | Method | Combination |
|---|---|---|
| 1 | ND | |
| 2 | MP | |
| 3 | RT | |
| 4 | SP | |
| 5 | ALN | |
| 6 | SB |
| Statistic | Unit | V | V5+ |
|---|---|---|---|
| Max | mg/kg | 1041.37 | 324.15 |
| Min | mg/kg | 0.00 | 26.10 |
| Mean | mg/kg | 396.72 | 154.41 |
| Std | mg/kg | 204.67 | 69.34 |
| CV | % | 51.59 | 44.91 |
| Model (S-2A) | PSNR (db) | SSIM | FSIM | Model (GF-2) | PSNR (db) | SSIM | FSIM |
|---|---|---|---|---|---|---|---|
| 31.253 | 0.946 | 0.964 | 31.066 | 0.937 | 0.952 | ||
| 30.377 | 0.937 | 0.955 | 29.517 | 0.924 | 0.947 | ||
| 30.534 | 0.949 | 0.957 | 29.870 | 0.938 | 0.953 | ||
| 32.307 | 0.957 | 0.969 | 31.363 | 0.953 | 0.949 |
| Element | Metric | ET | XGB | GBDT | SVM | KNN | PLSR |
|---|---|---|---|---|---|---|---|
| R2 | 0.51 | 0.45 | 0.43 | 0.44 | 0.38 | 0.54 | |
| V | RPD | 1.49 | 1.43 | 1.39 | 1.41 | 1.34 | 1.54 |
| MAE | 112.83 | 115.91 | 117.6 | 112.63 | 119.82 | 105.51 | |
| R2 | 0.48 | 0.38 | 0.4 | 0.46 | 0.53 | 0.49 | |
| Cr | RPD | 1.46 | 1.34 | 1.36 | 1.45 | 1.53 | 1.48 |
| MAE | 114.37 | 125.76 | 121.84 | 115.94 | 108.28 | 112.53 | |
| R2 | 0.49 | 0.36 | 0.42 | 0.51 | 0.48 | 0.42 | |
| Mn | RPD | 1.49 | 1.3 | 1.37 | 1.5 | 1.48 | 1.41 |
| MAE | 107.59 | 119.36 | 115.25 | 105.09 | 112.62 | 116.84 | |
| R2 | 0.28 | 0.29 | 0.25 | 0.24 | 0.3 | 0.23 | |
| V5+ | RPD | 1.27 | 1.28 | 1.24 | 1.23 | 1.29 | 1.21 |
| MAE | 41.82 | 40.69 | 41.95 | 42.24 | 39.16 | 45.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Sun, Y.; Jia, W.; Yang, J.; Wang, F. Prediction of Vanadium Contamination Distribution Pattern Through Remote Sensing Image Fusion and Machine Learning. Remote Sens. 2025, 17, 1164. https://doi.org/10.3390/rs17071164
Zhao Z, Sun Y, Jia W, Yang J, Wang F. Prediction of Vanadium Contamination Distribution Pattern Through Remote Sensing Image Fusion and Machine Learning. Remote Sensing. 2025; 17(7):1164. https://doi.org/10.3390/rs17071164
Chicago/Turabian StyleZhao, Zipeng, Yuman Sun, Weiwei Jia, Jinyan Yang, and Fan Wang. 2025. "Prediction of Vanadium Contamination Distribution Pattern Through Remote Sensing Image Fusion and Machine Learning" Remote Sensing 17, no. 7: 1164. https://doi.org/10.3390/rs17071164
APA StyleZhao, Z., Sun, Y., Jia, W., Yang, J., & Wang, F. (2025). Prediction of Vanadium Contamination Distribution Pattern Through Remote Sensing Image Fusion and Machine Learning. Remote Sensing, 17(7), 1164. https://doi.org/10.3390/rs17071164










