Exploiting Weighted Multidirectional Sparsity for Prior Enhanced Anomaly Detection in Hyperspectral Images
Abstract
1. Introduction
- We propose a novel AD method named WMS-LRTR that incorporates both the low-rank property of the background and the structured sparsity of the anomaly and enhances the robustness of AD.
- We extend the anomaly tensor to multimodal and design an adaptive dictionary construction method to generate a clean background dictionary. WTNN is employed to effectively allocate singular value contributions, while WMS leverages the correlations between abnormal pixels across different dimensions, thereby enhancing the ability to explore structured features in abnormal regions.
- We construct an efficient algorithm based on ADMM, where all subproblems are relatively easy to solve. Besides, numerical experiments on eight datasets demonstrate that the detection ability of WMS-LRTR surpasses nine benchmark AD methods.
2. Preliminaries
2.1. Notations
2.2. Related Work
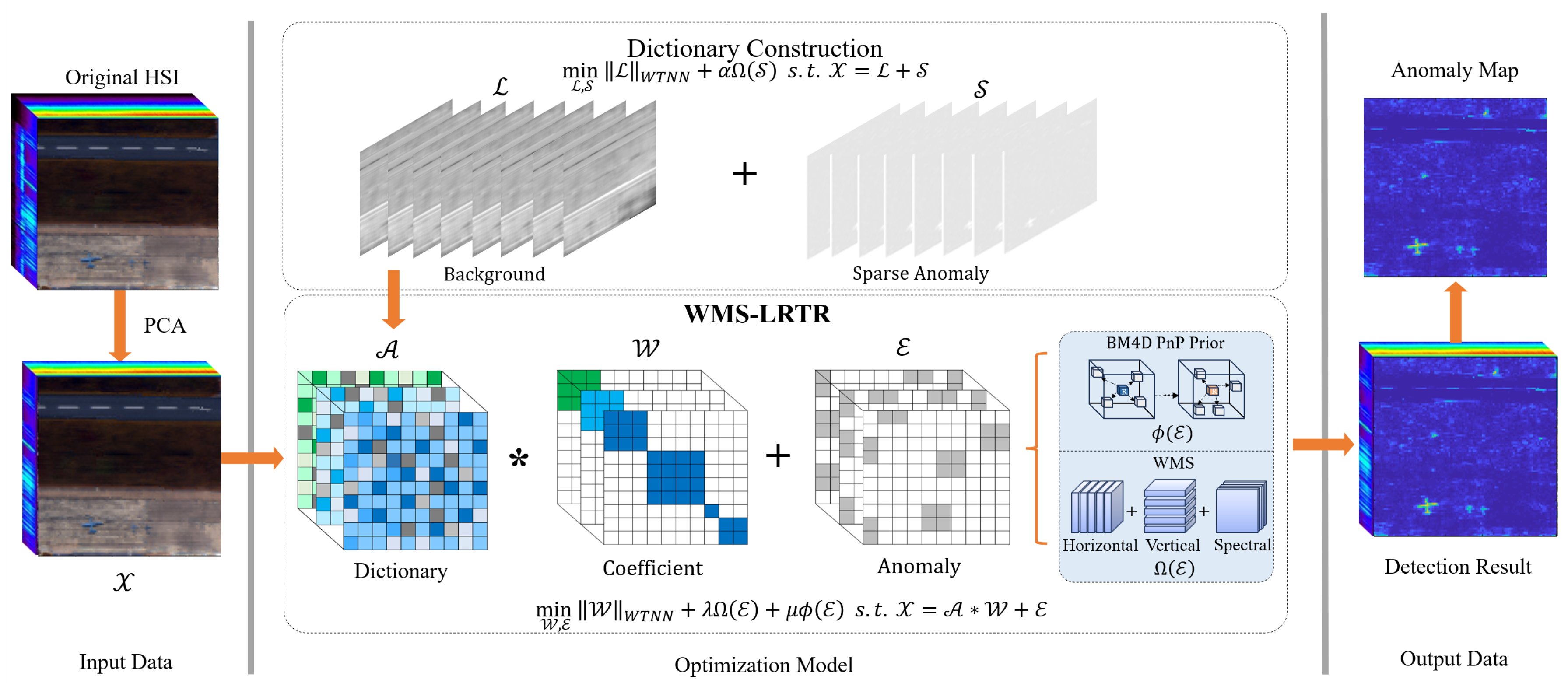
3. The Proposed Method
3.1. New Formulation
- considers the correlation between abnormal pixels across different dimensions and captures multidirectional structured features than , thereby preserving more spatially local anomaly characteristics.
- complements by filtering out noise to preserve the background low-rank structure and facilitate the separation of sparse anomalous regions, thus improving the robustness of AD.
3.2. Optimization Algorithm
- The -subproblem can be solved by:which is equivalent to:where . Then, Equation (21) can be written as:where According to [59], Equation (22) can be solved through the proximal operator. It then follows from the quadratic min-cost flow technique that:then the solution can be obtained by folding and assigning weights to the above tensors, respectively, that is:
- The -subproblem can be rewritten as:where is the PnP information, serving as a method for prior denoising supported by BM4D. For convenience, the solution of (25) is given by:where is the noise level.
- The -subproblem can be transformed to:which can be solved by:where is the transpose of .
- The Lagrange multipliers are updated by:
| Algorithm 1 Optimization framework |
| Input: Given data , dictionary , parameters Initialize: initialized to 0, set iteration number While not converged do
Output: |
3.3. Dictionary Construction
- The -subproblem can be simplified to:which has a closed-form solution similar to (22).
- The Lagrange multipliers is updated by:
4. Experiments and Discussions
4.1. Dataset Description
4.2. Implementation Details
4.2.1. Performance Indicators
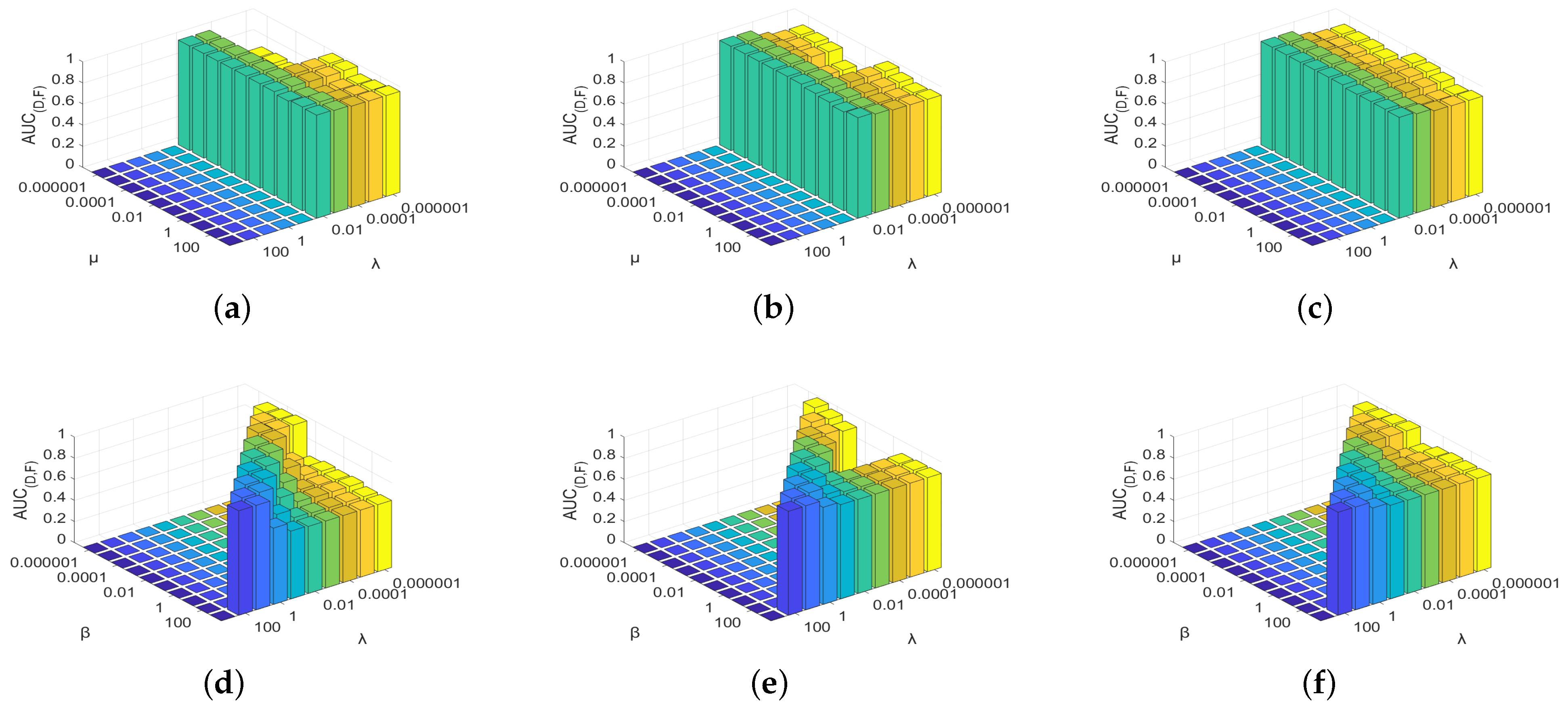
4.2.2. Parameter Selection
4.3. Numerical Results
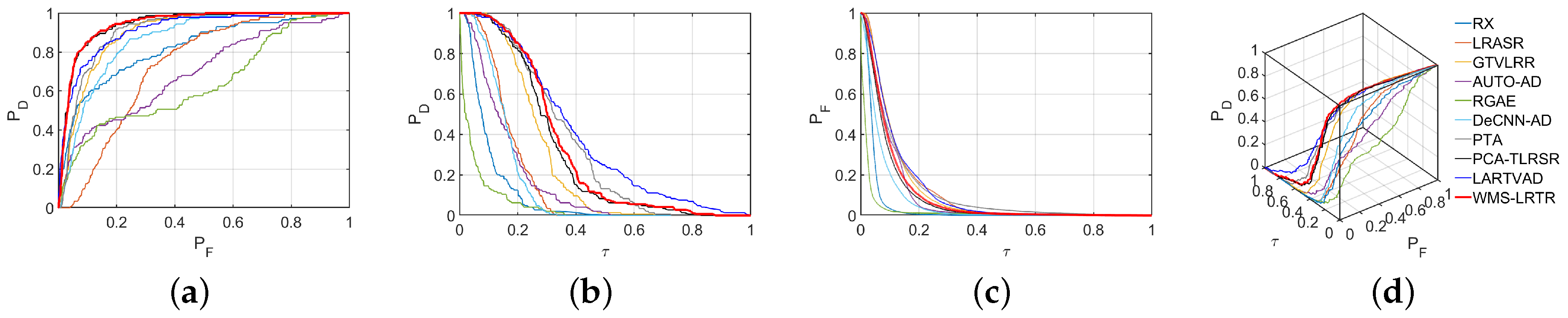
4.3.1. Experiments on the Airport Scenes
4.3.2. Experiments on the Beach Scenes
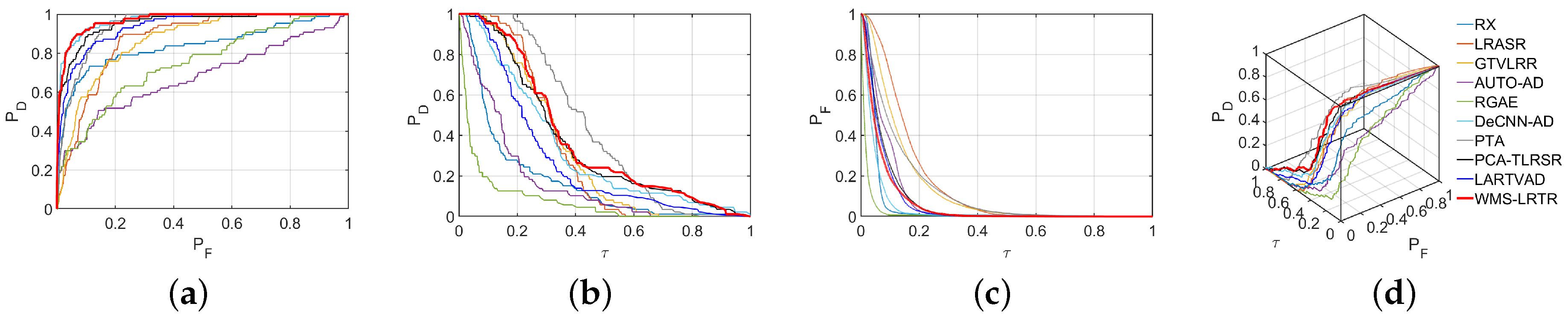
4.3.3. Experiments on the Urban Scenes
4.4. Discussion
4.4.1. Statistical Separability Analysis
4.4.2. Noise Resistance Analysis
4.4.3. Ablation Analysis
4.4.4. Block Size Analysis
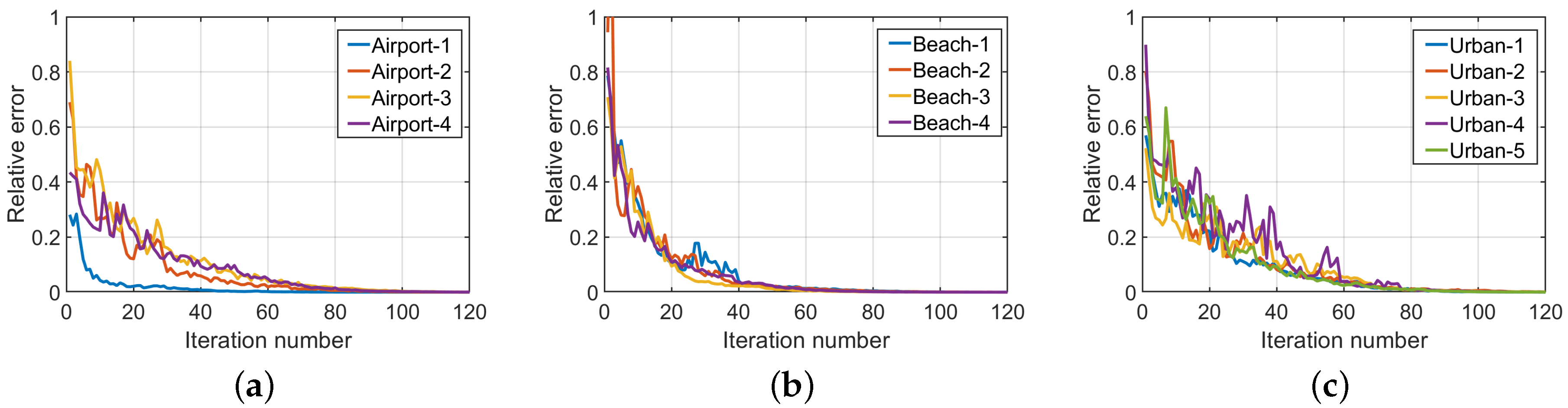
4.4.5. Convergence Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Chen, H.; Yang, G.; Zhang, L. LR-Net: Low-Rank Spatial-Spectral Network for Hyperspectral Image Denoising. IEEE Trans. Image Process. 2021, 30, 8743–8758. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, L.; Ng, M.K.; Gao, L.; Wang, Z. Eigen-CNN: Eigenimages Plus Eigennoise Level Maps Guided Network for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5512018. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, Y.; Yuan, Q.; Song, M.; Yu, H.; Xiao, Y. Hyperspectral Image Denoising: From Model-Driven, Data-Driven, to Model-Data-Driven. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 13143–13163. [Google Scholar] [CrossRef]
- Dong, Y.; Shi, W.; Du, B.; Hu, X.; Zhang, L. Asymmetric Weighted Logistic Metric Learning for Hyperspectral Target Detection. IEEE Trans. Cybern. 2022, 52, 11093–11106. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Zhang, B.; Hong, D.; Yao, J.; Chanussot, J. LRR-Net: An Interpretable Deep Unfolding Network for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5513412. [Google Scholar] [CrossRef]
- Chang, C.I.; Chen, S.; Zhong, S.; Shi, Y. Exploration of Data Scene Characterization and 3D ROC Evaluation for Hyperspectral Anomaly Detection. Remote Sens. 2024, 16, 135. [Google Scholar] [CrossRef]
- Han, Y.; Zhu, H.; Jiao, L.; Yi, X.; Li, X.; Hou, B.; Ma, W.; Wang, S. SSMU-Net: A Style Separation and Mode Unification Network for Multimodal Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5407115. [Google Scholar] [CrossRef]
- Chen, H.; Ru, J.; Long, H.; He, J.; Chen, T.; Deng, W. Semi-Supervised Adaptive Pseudo-Label Feature Learning for Hyperspectral Image Classification in Internet of Things. IEEE Internet Things J. 2024, 11, 30754–30768. [Google Scholar] [CrossRef]
- Huang, S.; Liu, Z.; Jin, W.; Mu, Y. Superpixel-based multi-scale multi-instance learning for hyperspectral image classification. Pattern Recognit. 2024, 149, 110257. [Google Scholar]
- Gao, H.; Li, S.; Dian, R. Hyperspectral and Multispectral Image Fusion Via Self-Supervised Loss and Separable Loss. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5537712. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Zhao, K.; Zhao, X.; Song, C. FSL-Unet: Full-Scale Linked Unet With Spatial–Spectral Joint Perceptual Attention for Hyperspectral and Multispectral Image Fusion. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5539114. [Google Scholar] [CrossRef]
- Li, H.C.; Feng, X.R.; Wang, R.; Gao, L.; Du, Q. Superpixel-Based Low-Rank Tensor Factorization for Blind Nonlinear Hyperspectral Unmixing. IEEE Sens. J. 2024, 24, 13055–13072. [Google Scholar] [CrossRef]
- Li, M.; Yang, B.; Wang, B. EMLM-Net: An Extended Multilinear Mixing Model-Inspired Dual-Stream Network for Unsupervised Nonlinear Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5509116. [Google Scholar] [CrossRef]
- Reed, I.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Chang, C.I.; Chiang, S.S. Anomaly detection and classification for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1314–1325. [Google Scholar] [CrossRef]
- Kwon, H.; Nasrabadi, N. Kernel RX-algorithm: A nonlinear anomaly detector for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 388–397. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, B.; Ran, Q.; Gao, L.; Li, J.; Plaza, A. Weighted-RXD and Linear Filter-Based RXD: Improving Background Statistics Estimation for Anomaly Detection in Hyperspectral Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2351–2366. [Google Scholar] [CrossRef]
- Zhou, J.; Kwan, C.; Ayhan, B.; Eismann, M.T. A Novel Cluster Kernel RX Algorithm for Anomaly and Change Detection Using Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6497–6504. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, L.; Wang, Y. A Superpixel-Based Dual Window RX for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1233–1237. [Google Scholar] [CrossRef]
- Donoho, D. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust Recovery of Subspace Structures by Low-Rank Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse Representation for Target Detection in Hyperspectral Imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L.; Ma, L. Hyperspectral Anomaly Detection by the Use of Background Joint Sparse Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2523–2533. [Google Scholar] [CrossRef]
- Ling, Q.; Guo, Y.; Lin, Z.; An, W. A Constrained Sparse Representation Model for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2358–2371. [Google Scholar] [CrossRef]
- Qin, H.; Shen, Q.; Zeng, H.; Chen, Y.; Lu, G. Generalized Nonconvex Low-Rank Tensor Representation for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5526612. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly Detection in Hyperspectral Images Based on Low-Rank and Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1990–2000. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L.; Wang, S. A Low-Rank and Sparse Matrix Decomposition-Based Mahalanobis Distance Method for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1376–1389. [Google Scholar] [CrossRef]
- Cheng, T.; Wang, B. Graph and Total Variation Regularized Low-Rank Representation for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 391–406. [Google Scholar] [CrossRef]
- Shen, X.; Liu, H.; Nie, J.; Zhou, X. Matrix Factorization With Framelet and Saliency Priors for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5504413. [Google Scholar] [CrossRef]
- Lin, J.T.; Lin, C.H. SuperRPCA: A Collaborative Superpixel Representation Prior-Aided RPCA for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5532516. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, G.; Dai, W. A Tensor Decomposition-Based Anomaly Detection Algorithm for Hyperspectral Image. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5801–5820. [Google Scholar] [CrossRef]
- Zhou, P.; Lu, C.; Feng, J.; Lin, Z.; Yan, S. Tensor Low-Rank Representation for Data Recovery and Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 1718–1732. [Google Scholar] [CrossRef]
- A, R.; Mu, X.; He, J. Enhance Tensor RPCA-Based Mahalanobis Distance Method for Hyperspectral Anomaly Detection. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6008305. [Google Scholar] [CrossRef]
- Shang, W.; Jouni, M.; Wu, Z.; Xu, Y.; Dalla Mura, M.; Wei, Z. Hyperspectral Anomaly Detection Based on Regularized Background Abundance Tensor Decomposition. Remote Sens. 2023, 15, 1679. [Google Scholar] [CrossRef]
- Sun, S.; Liu, J.; Zhang, Z.; Li, W. Hyperspectral Anomaly Detection Based on Adaptive Low-Rank Transformed Tensor. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 9787–9799. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Qu, Y.; Zhao, C.; Tao, R.; Du, Q. Prior-Based Tensor Approximation for Anomaly Detection in Hyperspectral Imagery. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1037–1050. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Wang, Q.; Hong, D.; Roy, S.K.; Chanussot, J. Learning Tensor Low-Rank Representation for Hyperspectral Anomaly Detection. IEEE Trans. Cybern. 2023, 53, 679–691. [Google Scholar] [CrossRef]
- Sun, S.; Liu, J.; Chen, X.; Li, W.; Li, H. Hyperspectral Anomaly Detection With Tensor Average Rank and Piecewise Smoothness Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 8679–8692. [Google Scholar] [CrossRef] [PubMed]
- Feng, M.; Chen, W.; Yang, Y.; Shu, Q.; Li, H.; Huang, Y. Hyperspectral Anomaly Detection Based on Tensor Ring Decomposition With Factors TV Regularization. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5514114. [Google Scholar] [CrossRef]
- Ren, L.; Gao, L.; Wang, M.; Sun, X.; Chanussot, J. HADGSM: A Unified Nonconvex Framework for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5503415. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhao, L.; Chen, S.; Li, X. Robust Tensor Low-Rank Sparse Representation With Saliency Prior for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5529920. [Google Scholar] [CrossRef]
- Cheng, X.; Mu, R.; Lin, S.; Zhang, M.; Wang, H. Hyperspectral Anomaly Detection via Low-Rank Representation with Dual Graph Regularizations and Adaptive Dictionary. Remote Sens. 2024, 16, 1837. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Zhang, L.; Zhong, Y. Auto-AD: Autonomous Hyperspectral Anomaly Detection Network Based on Fully Convolutional Autoencoder. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5503314. [Google Scholar] [CrossRef]
- Fan, G.; Ma, Y.; Mei, X.; Fan, F.; Huang, J.; Ma, J. Hyperspectral Anomaly Detection With Robust Graph Autoencoders. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5511314. [Google Scholar] [CrossRef]
- Xiang, P.; Ali, S.; Jung, S.K.; Zhou, H. Hyperspectral Anomaly Detection With Guided Autoencoder. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5538818. [Google Scholar] [CrossRef]
- Mu, Z.; Wang, Y.; Zhang, Y.; Song, C.; Wang, X. MPDA: Multivariate Probability Distribution Autoencoder for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5538513. [Google Scholar] [CrossRef]
- Liu, H.; Su, X.; Shen, X.; Zhou, X. MSNet: Self-Supervised Multiscale Network With Enhanced Separation Training for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5520313. [Google Scholar] [CrossRef]
- Wang, X.; Chen, J.; Richard, C. Tuning-Free Plug-and-Play Hyperspectral Image Deconvolution With Deep Priors. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5506413. [Google Scholar] [CrossRef]
- He, Y.; Zhang, C.; Zhang, B.; Chen, Z. FSPnP: Plug-and-Play Frequency–Spatial-Domain Hybrid Denoiser for Thermal Infrared Image. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5000416. [Google Scholar] [CrossRef]
- Zhuang, L.; Bioucas-Dias, J.M. Fast Hyperspectral Image Denoising and Inpainting Based on Low-Rank and Sparse Representations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 730–742. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Maggioni, M.; Katkovnik, V.; Egiazarian, K.; Foi, A. Nonlocal Transform-Domain Filter for Volumetric Data Denoising and Reconstruction. IEEE Trans. Image Process. 2013, 22, 119–133. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Jia, S.; Zhuang, L.; Xu, M.; Zhou, J.; Li, Q. Hyperspectral Anomaly Detection via Deep Plug-and-Play Denoising CNN Regularization. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9553–9568. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Zhao, X.L.; Zheng, Y.B.; Ma, T.H.; Zhang, H. Hyperspectral Image Restoration by Tensor Fibered Rank Constrained Optimization and Plug-and-Play Regularization. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5500717. [Google Scholar] [CrossRef]
- Zhuang, L.; Ng, M.K. FastHyMix: Fast and Parameter-Free Hyperspectral Image Mixed Noise Removal. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 4702–4716. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a Fast and Flexible Solution for CNN-Based Image Denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor Robust Principal Component Analysis with a New Tensor Nuclear Norm. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 925–938. [Google Scholar] [CrossRef] [PubMed]
- Mu, Y.; Wang, P.; Lu, L.; Zhang, X.; Qi, L. Weighted tensor nuclear norm minimization for tensor completion using tensor-SVD. Pattern Recognit. Lett. 2020, 130, 4–11. [Google Scholar] [CrossRef]
- Mairal, J.; Jenatton, R.; Bach, F.; Obozinski, G.R. Network Flow Algorithms for Structured Sparsity. Adv. Neural Inf. Process. Syst. 2010, 23, 1–9. [Google Scholar]
- Liu, X.; Zhao, G.; Yao, J.; Qi, C. Background Subtraction Based on Low-Rank and Structured Sparse Decomposition. IEEE Trans. Image Process. 2015, 24, 2502–2514. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- He, X.; Wu, J.; Ling, Q.; Li, Z.; Lin, Z.; Zhou, S. Anomaly Detection for Hyperspectral Imagery via Tensor Low-Rank Approximation With Multiple Subspace Learning. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5509917. [Google Scholar] [CrossRef]
- Sun, S.; Liu, J.; Li, W. Spatial Invariant Tensor Self-Representation Model for Hyperspectral Anomaly Detection. IEEE Trans. Cybern. 2024, 54, 3120–3131. [Google Scholar] [CrossRef]
- Chang, C.I. An Effective Evaluation Tool for Hyperspectral Target Detection: 3D Receiver Operating Characteristic Curve Analysis. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5131–5153. [Google Scholar] [CrossRef]







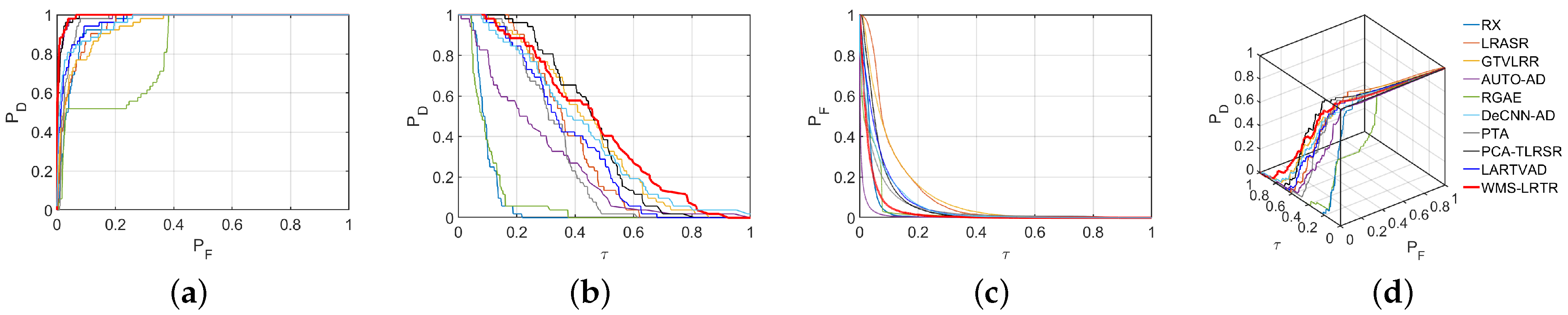



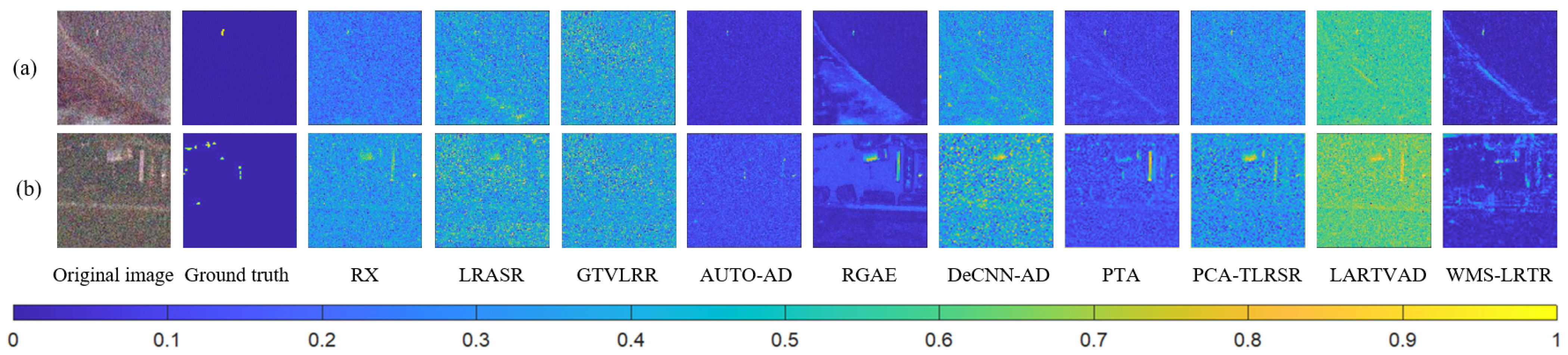
| Dataset | Sensor | Location | Size | Bands | Spatial Resolution (m) | Spectral Resolution (nm) |
|---|---|---|---|---|---|---|
| Airport-1 | AVIRIS | Los Angeles | 100 × 100 | 205 | 7.1 | 10.0 |
| Airport-2 | AVIRIS | Los Angeles | 100 × 100 | 205 | 7.1 | 10.0 |
| Airport-3 | AVIRIS | Los Angeles | 100 × 100 | 205 | 7.1 | 10.0 |
| Airport-4 | AVIRIS | Gulfport | 100 × 100 | 191 | 3.4 | 10.0 |
| Beach-1 | AVIRIS | Cat Island | 150 × 150 | 188 | 17.2 | 10.0 |
| Beach-2 | AVIRIS | San Diego | 100 × 100 | 193 | 7.5 | 10.0 |
| Beach-3 | AVIRIS | Bay Champagne | 100 × 100 | 188 | 4.4 | 10.0 |
| Beach-4 | ROSIS | Pavia | 150 × 150 | 102 | 1.3 | 10.0 |
| Urabn-1 | AVIRIS | Texas Coast | 100 × 100 | 204 | 17.2 | 10.0 |
| Urabn-2 | AVIRIS | Texas Coast | 100 × 100 | 207 | 17.2 | 10.0 |
| Urabn-3 | AVIRIS | Gainesville | 100 × 100 | 191 | 3.5 | 10.0 |
| Urabn-4 | AVIRIS | Los Angeles | 100 × 100 | 205 | 7.1 | 10.0 |
| Urabn-5 | AVIRIS | Los Angeles | 100 × 100 | 205 | 7.1 | 10.0 |
| Dataset | AUC | RX [14] | LRASR [26] | GTVLRR [28] | AUTO-AD [43] | RGAE [44] | DeCNN-AD [53] | PTA [36] | PCA-TLRSR [37] | LARTVAD [38] | WMS-LRTR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Airport-1 | 0.8221 | 0.7284 | 0.8997 | 0.6941 | 0.6387 | 0.8662 | 0.9109 | 0.9420 | 0.9202 | 0.9435 | |
| 0.0987 | 0.1711 | 0.2665 | 0.1595 | 0.0506 | 0.1562 | 0.3471 | 0.3088 | 0.2540 | 0.3284 | ||
| 0.0424 | 0.1209 | 0.1153 | 0.0991 | 0.0255 | 0.0689 | 0.1191 | 0.0918 | 0.0816 | 0.1001 | ||
| 0.9208 | 0.8996 | 1.1647 | 0.8536 | 0.6889 | 1.0224 | 1.2580 | 1.2508 | 1.1742 | 1.2718 | ||
| 0.7797 | 0.6075 | 0.7844 | 0.5950 | 0.6128 | 0.7974 | 0.7918 | 0.8502 | 0.8386 | 0.8433 | ||
| 0.0563 | 0.0502 | 0.1496 | 0.0603 | 0.0252 | 0.0873 | 0.2279 | 0.2170 | 0.1724 | 0.2282 | ||
| 0.8784 | 0.7786 | 1.0493 | 0.7544 | 0.6635 | 0.9536 | 1.1388 | 1.1590 | 1.0927 | 1.1717 | ||
| Airport-2 | 0.8403 | 0.8707 | 0.8670 | 0.6764 | 0.7470 | 0.9656 | 0.9411 | 0.9543 | 0.9387 | 0.9704 | |
| 0.1841 | 0.3156 | 0.3175 | 0.1976 | 0.0770 | 0.3257 | 0.4334 | 0.3705 | 0.2845 | 0.3807 | ||
| 0.0516 | 0.1613 | 0.1379 | 0.0862 | 0.0196 | 0.0476 | 0.1292 | 0.0753 | 0.0692 | 0.0652 | ||
| 1.0245 | 1.1863 | 1.1845 | 0.8439 | 0.8239 | 1.2913 | 1.3745 | 1.3248 | 1.2233 | 1.3511 | ||
| 0.7888 | 0.7094 | 0.7291 | 0.5902 | 0.7274 | 0.9180 | 0.8119 | 0.8790 | 0.8696 | 0.9052 | ||
| 0.1325 | 0.1542 | 0.1797 | 0.0814 | 0.0574 | 0.2781 | 0.3042 | 0.2952 | 0.2154 | 0.3155 | ||
| 0.9709 | 1.0249 | 1.0467 | 0.7578 | 0.8044 | 1.2437 | 1.2453 | 1.2495 | 1.1541 | 1.2859 | ||
| Airport-3 | 0.9288 | 0.9234 | 0.9231 | 0.9210 | 0.8873 | 0.9235 | 0.9247 | 0.9540 | 0.8877 | 0.9579 | |
| 0.0660 | 0.0562 | 0.0695 | 0.1278 | 0.0511 | 0.0676 | 0.1665 | 0.1398 | 0.1203 | 0.1333 | ||
| 0.0145 | 0.0126 | 0.0155 | 0.0395 | 0.0057 | 0.0123 | 0.0416 | 0.0279 | 0.0326 | 0.0194 | ||
| 0.9948 | 0.9796 | 0.9927 | 1.0488 | 0.9384 | 0.9916 | 1.0911 | 1.0945 | 1.0080 | 1.0912 | ||
| 0.9144 | 0.9108 | 0.9077 | 0.8815 | 0.8816 | 0.9117 | 0.8831 | 0.9268 | 0.8551 | 0.9385 | ||
| 0.0516 | 0.0436 | 0.0540 | 0.0883 | 0.0454 | 0.0553 | 0.1249 | 0.1119 | 0.0877 | 0.1139 | ||
| 0.9804 | 0.9670 | 0.9772 | 1.0094 | 0.9327 | 0.9793 | 1.0496 | 1.0666 | 0.9754 | 1.0718 | ||
| Airport-4 | 0.9526 | 0.9566 | 0.9836 | 0.9840 | 0.7508 | 0.9239 | 0.9841 | 0.9933 | 0.9173 | 0.9961 | |
| 0.0736 | 0.3747 | 0.4437 | 0.4071 | 0.1172 | 0.4229 | 0.6476 | 0.4350 | 0.0931 | 0.5110 | ||
| 0.0248 | 0.1053 | 0.0942 | 0.0267 | 0.0749 | 0.1646 | 0.1044 | 0.0924 | 0.0311 | 0.0427 | ||
| 1.0262 | 1.3313 | 1.4273 | 1.3911 | 0.8679 | 1.3467 | 1.6317 | 1.4283 | 1.0104 | 1.5071 | ||
| 0.9278 | 0.8513 | 0.8894 | 0.9573 | 0.6759 | 0.7593 | 0.8798 | 0.9008 | 0.8862 | 0.9534 | ||
| 0.0489 | 0.2693 | 0.3496 | 0.3804 | 0.0423 | 0.2583 | 0.5432 | 0.3426 | 0.0620 | 0.4684 | ||
| 1.0015 | 1.2260 | 1.3332 | 1.3644 | 0.7930 | 1.1822 | 1.5273 | 1.3358 | 0.9793 | 1.4645 |
| Dataset | AUC | RX [14] | LRASR [26] | GTVLRR [28] | AUTO-AD [43] | RGAE [44] | DeCNN-AD [53] | PTA [36] | PCA-TLRSR [37] | LARTVAD [38] | WMS-LRTR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Beach-1 | 0.9804 | 0.9155 | 0.9720 | 0.9510 | 0.9395 | 0.9635 | 0.9742 | 0.9673 | 0.9606 | 0.9883 | |
| 0.2496 | 0.2161 | 0.3081 | 0.1288 | 0.1055 | 0.2778 | 0.2711 | 0.3298 | 0.2265 | 0.3715 | ||
| 0.0065 | 0.0460 | 0.0237 | 0.0183 | 0.0142 | 0.0181 | 0.0177 | 0.0235 | 0.0145 | 0.0111 | ||
| 1.2304 | 1.1316 | 1.2801 | 1.0798 | 1.0450 | 1.1913 | 1.2452 | 1.2971 | 1.1871 | 1.3598 | ||
| 0.9742 | 0.8694 | 0.9483 | 0.9327 | 0.9253 | 0.9454 | 0.9565 | 0.9437 | 0.9460 | 0.9772 | ||
| 0.2431 | 0.1701 | 0.2845 | 0.1105 | 0.0913 | 0.2096 | 0.2534 | 0.3063 | 0.2119 | 0.3604 | ||
| 1.2238 | 1.0856 | 1.2565 | 1.0615 | 1.0308 | 1.1732 | 1.2275 | 1.2735 | 1.1725 | 1.3487 | ||
| Beach-2 | 0.9106 | 0.6357 | 0.9274 | 0.8803 | 0.9020 | 0.9067 | 0.9167 | 0.9273 | 0.9230 | 0.9604 | |
| 0.1530 | 0.1335 | 0.2236 | 0.0472 | 0.0200 | 0.1774 | 0.1701 | 0.2454 | 0.1154 | 0.2820 | ||
| 0.0488 | 0.0907 | 0.0469 | 0.0173 | 0.0180 | 0.0320 | 0.0536 | 0.0477 | 0.0253 | 0.0398 | ||
| 1.0636 | 0.7692 | 1.1510 | 0.9275 | 0.9220 | 1.0841 | 1.0868 | 1.1727 | 1.0384 | 1.2424 | ||
| 0.8618 | 0.5450 | 0.8805 | 0.8630 | 0.8840 | 0.8747 | 0.8631 | 0.8796 | 0.8977 | 0.9206 | ||
| 0.1042 | 0.0428 | 0.1767 | 0.0299 | 0.0020 | 0.1454 | 0.1165 | 0.1977 | 0.0901 | 0.2422 | ||
| 1.0148 | 0.6786 | 1.1041 | 0.9101 | 0.9040 | 1.0522 | 1.0333 | 1.1250 | 1.0130 | 1.2026 | ||
| Beach-3 | 0.9998 | 0.9953 | 0.9923 | 0.9991 | 0.8668 | 0.9985 | 0.9989 | 0.9985 | 0.9939 | 0.9993 | |
| 0.5314 | 0.5578 | 0.6527 | 0.3724 | 0.3569 | 0.5439 | 0.5679 | 0.6387 | 0.5640 | 0.6765 | ||
| 0.0259 | 0.0796 | 0.1430 | 0.0029 | 0.0397 | 0.0428 | 0.0459 | 0.0629 | 0.0490 | 0.0639 | ||
| 1.5312 | 1.5531 | 1.6450 | 1.3715 | 1.2237 | 1.5424 | 1.5668 | 1.6372 | 1.5579 | 1.6758 | ||
| 0.9739 | 0.9157 | 0.8493 | 0.9962 | 0.8271 | 0.9557 | 0.9530 | 0.9356 | 0.9449 | 0.9354 | ||
| 0.5055 | 0.4782 | 0.5097 | 0.3695 | 0.3172 | 0.5011 | 0.5220 | 0.5758 | 0.5150 | 0.6126 | ||
| 1.5053 | 1.4736 | 1.5020 | 1.3685 | 1.1840 | 1.4996 | 1.5209 | 1.5743 | 1.5089 | 1.6118 | ||
| Beach-4 | 0.9538 | 0.9216 | 0.9796 | 0.9838 | 0.9041 | 0.9680 | 0.9701 | 0.9463 | 0.9578 | 0.9724 | |
| 0.1343 | 0.1949 | 0.2420 | 0.1047 | 0.2210 | 0.1882 | 0.3579 | 0.2991 | 0.3090 | 0.3287 | ||
| 0.0233 | 0.0510 | 0.0236 | 0.0012 | 0.0377 | 0.0081 | 0.0353 | 0.0807 | 0.0717 | 0.0694 | ||
| 1.0881 | 1.1167 | 1.2217 | 1.0885 | 1.1252 | 1.1562 | 1.3280 | 1.2454 | 1.2668 | 1.3010 | ||
| 0.9305 | 0.8708 | 0.9560 | 0.9826 | 0.8664 | 0.9599 | 0.9349 | 0.8656 | 0.8861 | 0.9030 | ||
| 0.1110 | 0.1440 | 0.2185 | 0.1036 | 0.1834 | 0.1801 | 0.3226 | 0.2184 | 0.2373 | 0.2593 | ||
| 1.0648 | 1.0657 | 1.1981 | 1.0873 | 1.0875 | 1.1481 | 1.2927 | 1.1647 | 1.1951 | 1.2317 |
| Dataset | AUC | RX [14] | LRASR [26] | GTVLRR [28] | AUTO-AD [43] | RGAE [44] | DeCNN-AD [53] | PTA [36] | PCA-TLRSR [37] | LARTVAD [38] | WMS-LRTR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Urban-1 | 0.9907 | 0.9452 | 0.8278 | 0.9886 | 0.9821 | 0.9238 | 0.9808 | 0.9810 | 0.9773 | 0.9942 | |
| 0.3143 | 0.4198 | 0.3212 | 0.2245 | 0.3749 | 0.4661 | 0.5001 | 0.4977 | 0.5206 | 0.5271 | ||
| 0.0556 | 0.1707 | 0.1681 | 0.0050 | 0.0168 | 0.1499 | 0.0882 | 0.0621 | 0.0657 | 0.0682 | ||
| 1.3050 | 1.3650 | 1.1490 | 1.2131 | 1.3570 | 1.3899 | 1.4809 | 1.4787 | 1.4979 | 1.5213 | ||
| 0.9351 | 0.7745 | 0.6597 | 0.9836 | 0.9653 | 0.7739 | 0.8926 | 0.9189 | 0.9116 | 0.9260 | ||
| 0.2587 | 0.2491 | 0.1531 | 0.2195 | 0.3581 | 0.3162 | 0.4119 | 0.4356 | 0.4549 | 0.4589 | ||
| 1.2494 | 1.1942 | 0.9810 | 1.2081 | 1.3402 | 1.2400 | 1.3927 | 1.4166 | 1.4322 | 1.4531 | ||
| Urban-2 | 0.9946 | 0.8640 | 0.8499 | 0.9893 | 0.9871 | 0.9340 | 0.9592 | 0.9854 | 0.9597 | 0.9959 | |
| 0.1178 | 0.0636 | 0.1324 | 0.0812 | 0.1101 | 0.2047 | 0.2001 | 0.1870 | 0.1320 | 0.2144 | ||
| 0.0135 | 0.0186 | 0.0424 | 0.0014 | 0.0053 | 0.0392 | 0.0130 | 0.0228 | 0.0142 | 0.0243 | ||
| 1.1124 | 0.9276 | 0.9823 | 1.0705 | 1.0973 | 1.1387 | 1.1593 | 1.1724 | 1.0917 | 1.2103 | ||
| 0.9811 | 0.8454 | 0.8075 | 0.9879 | 0.9819 | 0.8948 | 0.9462 | 0.9626 | 0.9455 | 0.9716 | ||
| 0.1043 | 0.0450 | 0.0900 | 0.0798 | 0.1049 | 0.1655 | 0.1871 | 0.1642 | 0.1178 | 0.1901 | ||
| 1.0989 | 0.9090 | 0.9399 | 1.0690 | 1.0920 | 1.0995 | 1.1464 | 1.1496 | 1.0776 | 1.1861 | ||
| Urban-3 | 0.9513 | 0.9521 | 0.9430 | 0.9891 | 0.8223 | 0.9635 | 0.9684 | 0.9906 | 0.9679 | 0.9936 | |
| 0.0963 | 0.3686 | 0.4351 | 0.2654 | 0.1018 | 0.4163 | 0.3170 | 0.4459 | 0.3643 | 0.4608 | ||
| 0.0351 | 0.1135 | 0.1106 | 0.0089 | 0.0376 | 0.0601 | 0.0562 | 0.0693 | 0.0672 | 0.0346 | ||
| 1.0476 | 1.3207 | 1.3781 | 1.2545 | 0.9241 | 1.3779 | 1.2854 | 1.4365 | 1.3322 | 1.4544 | ||
| 0.9162 | 0.8386 | 0.8324 | 0.9802 | 0.7847 | 0.9035 | 0.9122 | 0.9213 | 0.9007 | 0.9590 | ||
| 0.0612 | 0.2551 | 0.3245 | 0.2565 | 0.0642 | 0.3563 | 0.2608 | 0.3766 | 0.2971 | 0.4262 | ||
| 1.0125 | 1.2072 | 1.2676 | 1.2457 | 0.8865 | 1.3198 | 1.2292 | 1.3672 | 1.2651 | 1.4198 | ||
| Urban-4 | 0.9887 | 0.5991 | 0.9326 | 0.9867 | 0.9862 | 0.9744 | 0.9632 | 0.9313 | 0.9796 | 0.9887 | |
| 0.0891 | 0.0562 | 0.0682 | 0.0379 | 0.0372 | 0.0993 | 0.1034 | 0.1113 | 0.0593 | 0.1130 | ||
| 0.0114 | 0.0191 | 0.0089 | 0.0008 | 0.0014 | 0.0183 | 0.0054 | 0.0162 | 0.0074 | 0.0146 | ||
| 1.0778 | 0.8188 | 1.0085 | 1.0246 | 1.0234 | 1.0737 | 1.0666 | 1.0426 | 1.0389 | 1.1017 | ||
| 0.9773 | 0.7767 | 0.9283 | 0.9859 | 0.9848 | 0.9561 | 0.9578 | 0.9151 | 0.9722 | 0.9741 | ||
| 0.0777 | 0.0291 | 0.0622 | 0.0371 | 0.0358 | 0.0810 | 0.0980 | 0.0951 | 0.0519 | 0.0984 | ||
| 1.0664 | 0.6362 | 0.9919 | 1.0238 | 1.0220 | 1.0554 | 1.0612 | 1.0263 | 1.0316 | 1.0871 | ||
| Urban-5 | 0.9692 | 0.9076 | 0.9304 | 0.8728 | 0.9569 | 0.8339 | 0.9136 | 0.9691 | 0.9043 | 0.9804 | |
| 0.1461 | 0.2138 | 0.2611 | 0.0707 | 0.2533 | 0.3065 | 0.2852 | 0.2853 | 0.1721 | 0.3158 | ||
| 0.0437 | 0.0899 | 0.0844 | 0.0062 | 0.0179 | 0.1742 | 0.0417 | 0.0688 | 0.0660 | 0.0627 | ||
| 1.1153 | 1.1214 | 1.1915 | 0.9435 | 1.2102 | 1.1404 | 1.1988 | 1.2544 | 1.0764 | 1.2962 | ||
| 0.9255 | 0.8177 | 0.8460 | 0.8666 | 0.9390 | 0.6597 | 0.8719 | 0.9003 | 0.8383 | 0.9177 | ||
| 0.1024 | 0.1239 | 0.1767 | 0.0645 | 0.2354 | 0.1323 | 0.2435 | 0.2165 | 0.1061 | 0.2531 | ||
| 1.0716 | 1.0314 | 1.1072 | 0.9372 | 1.1922 | 0.9662 | 1.1570 | 1.1856 | 1.0104 | 1.2335 |
| Dataset | AUC | RX [14] | LRASR [26] | GTVLRR [28] | AUTO-AD [43] | RGAE [44] | DeCNN-AD [53] | PTA [36] | PCA-TLRSR [37] | LARTVAD [38] | WMS-LRTR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Average | 0.9448 | 0.8627 | 0.9253 | 0.9166 | 0.8747 | 0.9343 | 0.9543 | 0.9646 | 0.9452 | 0.9801 | |
| 0.1734 | 0.2417 | 0.2878 | 0.1711 | 0.1444 | 0.2810 | 0.3360 | 0.3303 | 0.2473 | 0.3572 | ||
| 0.0305 | 0.0830 | 0.0780 | 0.0241 | 0.0242 | 0.0643 | 0.0578 | 0.0570 | 0.0458 | 0.0474 | ||
| 1.1183 | 1.1170 | 1.2136 | 1.0855 | 1.0190 | 1.2113 | 1.2902 | 1.2950 | 1.1926 | 1.3372 | ||
| 0.9143 | 0.7948 | 0.8476 | 0.8925 | 0.8505 | 0.8700 | 0.8965 | 0.9077 | 0.8994 | 0.9327 | ||
| 0.1429 | 0.1580 | 0.2099 | 0.1447 | 0.1202 | 0.2128 | 0.2782 | 0.2733 | 0.2015 | 0.3098 | ||
| 1.0876 | 1.0214 | 1.1350 | 1.0613 | 0.9948 | 1.1471 | 1.2325 | 1.2380 | 1.1468 | 1.2899 |
| Dataset | AUC | RX [14] | LRASR [26] | GTVLRR [28] | AUTO-AD [43] | RGAE [44] | DeCNN-AD [53] | PTA [36] | PCA-TLRSR [37] | LARTVAD [38] | WMS-LRTR |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Noisy Beach-3 | 0.9267 | 0.7543 | 0.6208 | 0.7905 | 0.8067 | 0.7806 | 0.9740 | 0.8109 | 0.8602 | 0.9755 | |
| 0.5386 | 0.5523 | 0.5122 | 0.2924 | 0.3427 | 0.5665 | 0.5110 | 0.5785 | 0.7330 | 0.4833 | ||
| 0.2453 | 0.3667 | 0.4267 | 0.0607 | 0.0630 | 0.3506 | 0.1056 | 0.3105 | 0.5712 | 0.0491 | ||
| 1.4652 | 1.3066 | 1.1330 | 1.0829 | 1.1494 | 1.3470 | 1.4850 | 1.3894 | 1.5932 | 1.4589 | ||
| 0.6814 | 0.3876 | 0.1941 | 0.7297 | 0.7437 | 0.4300 | 0.8684 | 0.5004 | 0.2889 | 0.9264 | ||
| 0.2933 | 0.1856 | 0.0854 | 0.2316 | 0.2797 | 0.2158 | 0.4054 | 0.2680 | 0.1618 | 0.4342 | ||
| 1.2200 | 0.9400 | 0.7063 | 1.0221 | 1.0864 | 0.9964 | 1.3794 | 1.0790 | 1.0220 | 1.4097 | ||
| Noisy Urban-3 | 0.6873 | 0.5919 | 0.5124 | 0.6794 | 0.4518 | 0.5492 | 0.9085 | 0.6180 | 0.6893 | 0.9281 | |
| 0.4440 | 0.4611 | 0.4061 | 0.2357 | 0.0781 | 0.4445 | 0.3519 | 0.4470 | 0.6803 | 0.2803 | ||
| 0.3539 | 0.4127 | 0.3971 | 0.1358 | 0.0955 | 0.4177 | 0.1543 | 0.3956 | 0.6219 | 0.0714 | ||
| 1.1312 | 1.0530 | 0.9185 | 0.9151 | 0.5299 | 0.9937 | 1.2604 | 1.0650 | 1.3696 | 1.2084 | ||
| 0.3334 | 0.1791 | 0.1153 | 0.5436 | 0.3563 | 0.1315 | 0.7541 | 0.2225 | 0.0674 | 0.8567 | ||
| 0.0901 | 0.0484 | 0.0090 | 0.0998 | 0.0175 | 0.0268 | 0.1976 | 0.0514 | 0.0583 | 0.2089 | ||
| 0.7774 | 0.6403 | 0.5214 | 0.7792 | 0.4344 | 0.5760 | 1.1061 | 0.6695 | 0.7477 | 1.1370 |
| Dataset | Without PCA | Without WTNN | Without WMS | Without PnP Prior | WMS-LRTR | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Time (s) | Time (s) | Time (s) | Time (s) | Time (s) | ||||||
| Airport-1 | 0.9076 | 14,801.741 | 0.8294 | 226.314 | 0.9350 | 46.210 | 0.9240 | 195.416 | 0.9435 | 222.551 |
| Airport-2 | 0.9322 | 12,431.595 | 0.9585 | 96.175 | 0.9627 | 26.713 | 0.9441 | 62.733 | 0.9704 | 92.963 |
| Airport-3 | 0.9274 | 15,124.256 | 0.9529 | 271.938 | 0.9546 | 132.316 | 0.9533 | 179.844 | 0.9579 | 297.676 |
| Airport-4 | 0.9779 | 13,547.221 | 0.9914 | 138.498 | 0.9952 | 41.520 | 0.9906 | 96.701 | 0.9961 | 130.514 |
| Average | 0.9363 | 13,976.203 | 0.9331 | 183.231 | 0.9619 | 61.690 | 0.9530 | 133.674 | 0.9670 | 185.926 |
| Dataset | Index | Horizontal | Vertical | Spectral | Multidirectional |
|---|---|---|---|---|---|
| Airport-1 | 0.9428 | 0.9415 | 0.9412 | 0.9435 | |
| Airport-2 | 0.9679 | 0.9686 | 0.9629 | 0.9704 | |
| Airport-3 | 0.9547 | 0.9526 | 0.9577 | 0.9579 | |
| Airport-4 | 0.9958 | 0.9956 | 0.9950 | 0.9961 |
| Dataset | RX [14] | LRASR [26] | GTVLRR [28] | AUTO-AD [43] | RGAE [44] | DeCNN-AD [53] | PTA [36] | PCA-TLRSR [37] | LARTVAD [38] | WMS-LRTR |
|---|---|---|---|---|---|---|---|---|---|---|
| Airport-1 | 0.102 | 36.594 | 214.276 | 53.080 | 151.695 | 56.391 | 41.515 | 5.185 | 46.579 | 222.551 |
| Airport-2 | 0.387 | 52.394 | 223.684 | 24.520 | 144.780 | 61.706 | 30.623 | 5.322 | 51.808 | 92.963 |
| Airport-3 | 0.089 | 47.754 | 171.489 | 20.675 | 152.961 | 73.266 | 36.622 | 21.625 | 40.472 | 297.676 |
| Airport-4 | 0.092 | 40.181 | 180.609 | 26.694 | 156.080 | 77.445 | 33.261 | 22.451 | 55.220 | 130.514 |
| Average | 0.168 | 44.231 | 197.515 | 31.242 | 151.379 | 67.202 | 35.505 | 13.646 | 48.520 | 185.926 |
| Dataset | Index | 2 × 2 | 3 × 3 | 4 × 4 | 5 × 5 |
|---|---|---|---|---|---|
| Airport-1 | 0.9435 | 0.9424 | 0.9379 | 0.9335 | |
| Time (s) | 222.551 | 240.222 | 313.199 | 506.953 | |
| Airport-2 | 0.9704 | 0.9663 | 0.9659 | 0.9612 | |
| Time (s) | 92.963 | 111.301 | 132.522 | 204.909 | |
| Airport-3 | 0.9579 | 0.9597 | 0.9587 | 0.9595 | |
| Time (s) | 297.676 | 358.482 | 419.583 | 494.698 | |
| Airport-4 | 0.9961 | 0.9960 | 0.9953 | 0.9955 | |
| Time (s) | 130.514 | 150.457 | 179.795 | 278.522 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Jin, J.; Xiu, X.; Liu, W.; Zhang, J. Exploiting Weighted Multidirectional Sparsity for Prior Enhanced Anomaly Detection in Hyperspectral Images. Remote Sens. 2025, 17, 602. https://doi.org/10.3390/rs17040602
Liu J, Jin J, Xiu X, Liu W, Zhang J. Exploiting Weighted Multidirectional Sparsity for Prior Enhanced Anomaly Detection in Hyperspectral Images. Remote Sensing. 2025; 17(4):602. https://doi.org/10.3390/rs17040602
Chicago/Turabian StyleLiu, Jingjing, Jiashun Jin, Xianchao Xiu, Wanquan Liu, and Jianhua Zhang. 2025. "Exploiting Weighted Multidirectional Sparsity for Prior Enhanced Anomaly Detection in Hyperspectral Images" Remote Sensing 17, no. 4: 602. https://doi.org/10.3390/rs17040602
APA StyleLiu, J., Jin, J., Xiu, X., Liu, W., & Zhang, J. (2025). Exploiting Weighted Multidirectional Sparsity for Prior Enhanced Anomaly Detection in Hyperspectral Images. Remote Sensing, 17(4), 602. https://doi.org/10.3390/rs17040602








