Automatic Registration of Remote Sensing High-Resolution Hyperspectral Images Based on Global and Local Features

Abstract

Automatic registration of remote sensing images is an important task, which requires the establishment of appropriate correspondence between the sensed image and the reference image. Nowadays, the trend of satellite remote sensing technology is shifting towards high-resolution hyperspectral imaging technology. Ever higher revisit cycles and image resolutions require higher accuracy and real-time performance for automatic registration. The push-broom payload is affected by the push-broom stability of the satellite platform and the elevation change of ground objects, and the obtained hyperspectral image may have distortions such as stretching or shrinking at different parts of the image. In order to solve this problem, a new automatic registration strategy for remote sensing hyperspectral images based on the combination of whole and local features of the image was established, and two granularity registrations were carried out, namely coarse-grained matching and fine-grained matching. The high-resolution spatial features are first employed for detecting scale-invariant features, while the spectral information is used for matching, and then the idea of image stitching is employed to fuse the image after fine registration to obtain high-precision registration results. In order to verify the proposed algorithm, a simulated on-orbit push-broom imaging experiment was carried out to obtain hyperspectral images with local complex distortions under different lighting conditions. The simulation results show that the proposed remote sensing hyperspectral image registration algorithm is superior to the existing automatic registration algorithms. The advantages of the proposed algorithm in terms of registration accuracy and real-time performance make it have a broad prospect for application in satellite ground application systems.

1. Introduction

Earth satellite remote sensing technology is developing towards high resolution, pursuing the “three highs”, that is, high spatial resolution, high spectral resolution, and high temporal resolution. Among them, high-resolution hyperspectral imaging technology has developed rapidly, and a number of high-resolution hyperspectral imagers have been launched at home and abroad, such as the EnMAP launched by Germany in 2022 with a spectral resolution of 6.5 nm and a spatial resolution of 30 m, and the PRISMA launched by Italy in 2019 with a spatial resolution of 30 m and a spectral resolution of 12 nm. China launched the ZY-1 02D satellite in 2019 with a hyperspectral camera with a spatial resolution of 30 m and a spectral resolution of 10 nm. The Jitianxing A-01 satellite launched in 2024 has meter-level resolution hyperspectral imaging capabilities through computational reconstruction. The high-resolution images obtained by the new technology have new characteristics and attributes. High-resolution hyperspectral images provide richer details and stronger quantitative resolution of objects. This information needs to be extracted and utilized by more advanced algorithms. However, the existing models do not match the characteristics and attributes of the new images, and new algorithms need to be developed urgently. Another aspect of the “three highs” technology in satellite remote sensing is high temporal resolution, which refers to a high revisit period. Existing satellites acquire data with a higher frequency or combine multiple satellites to increase the revisit period. Image registration is required for aligning high-resolution hyperspectral images acquired at different times to the same spatial reference coordinate system.

Remote sensing images are different from images in other fields and have some unique characteristics [1]. First, the image comes from different viewing angles, e.g., from a single pushing sensor or multiple sensors. It is difficult to ensure strict stability during the pushing process, especially on high-resolution images. Secondly, the images are captured at different times, the lighting conditions are different, and sometimes the gray value varies greatly. Due to the mismatch in the sweeping speed of the satellite platform and the change of the elevation of the scene, it is difficult for the existing image registration methods to register each part of a scene with high precision. Remote sensing images usually have a low signal-to-noise ratio, which aggravates the difficulty of feature matching.

The field of image registration includes classical methods and deep learning methods [2,3]. Some scholars have modified classical methods to improve the registration accuracy. For example, improvements were made to the Random Sample Consensus Algorithm (RANSAC) to improve the accuracy of matched sample pairs [4,5]. Ma et al. [6] improved the Scale Invariant Feature Transformation (SIFT) algorithm by introducing a new gradient definition to overcome image intensity differences between remote image pairs. Then, an enhanced feature matching method is introduced by combining the position, scale, and orientation of each key to increase the number of correct correspondences. Chang et al. [7] investigated a novel remote sensing image registration algorithm based on an improved SIFT scheme. In that paper, an outlier removal mechanism based on trilateral computation (TC) recipe and a homogeneity enforcement (HE) layout based on divide-and-conquer inclusion strategy are proposed. Finally, a game-based stochastic competition process is introduced to ensure that an appropriate number of matches are correctly matched in the proposed Tc and He (TcHe)-SIFT frameworks. In [8], a new method of mean adaptive RANSAC (MAR) based on graph transformation matching (GTM) is proposed, which combines MAR and GTM algorithms to effectively eliminate false matching. Zhao et al. [9] proposed a new spatial feature descriptor. In this method, the spatial information is encoded by using the distances and angles between the main scatterers to construct translational and rotational invariant feature descriptors. Ghannadi et al. [10] proposed the use of an optimal gradient filter (OGF) to extract details from the image and used the filtered image for image reconstruction. This method can enhance the texture of certain areas of the image. Gradient filter coefficients are optimized using particle swarm optimization. For the image matching process, the SIFT algorithm is utilized. Zhu et al. [11] proposed a curvature-scale space algorithm for feature detection and random sample consistency for robust matching. Li et al. [12] increased the number of duplicate feature points in a heterogeneous image by using a phase agreement transformation instead of a gradient edge map for chunked Harris feature point detection, resulting in a maximum moment map. In order to obtain the rotation invariance of the subsequent descriptors, a method for determining the principal phase angle is proposed. The phase angle of the area near the feature point is calculated, and the parabolic interpolation method is used to estimate the more accurate principal phase angle in the determined interval. Zhang et al. [13] proposed an improved algorithm based on SIFT to solve the problem that it is difficult to obtain a sufficiently correct correspondence in SIFT classical algorithms for multi-model data. In this method, the modified ratio of exponentially weighted averages (MROEWA) operator is introduced, and the Harris scale space is constructed to replace the traditional differences in the Gaussian (DoG) scale space, and the repeatable key points are identified by searching for local maxima, and the identified key points are located and refined to improve their accuracy.

When the image noise is strong, the number of image features obtained by the single feature extraction method is insufficient. Researchers utilize combinatorial registration techniques to increase the number of features, ultimately improving registration accuracy [14,15,16]. Kumawat et al. [17] proposed a hybrid feature detection method based on detectors such as BRISK, FAST, ORB, Harris, MinEigen, and MSER. Tang et al. [18] proposed an image registration method that combines nonlinear diffusion filtering, Hessian features, and edge points to reduce noise and obtain more image features. The proposed method uses an infinite symmetric exponential filter (ISEF) for image preprocessing and a nonlinear diffusion filter for scale space construction. These measures remove noise from the image while preserving the edges of the image. Hessian features and edge points are also used as image features to optimize the utilization of feature information. Zhang et al. [19] introduced a robust heterologous image registration technique based on region adaptive key point selection, which integrates image texture features and focuses on two key aspects: feature point extraction and matching point screening. Initially, the double-threshold criterion based on the information entropy and variance product of the block region effectively identified the weakly characteristic regions. Subsequently, it constructs feature descriptors to generate similarity maps, combining histogram parameter skewness with non-maximum suppression (NMS) to improve the accuracy of matching points. Chen et al. [20] proposed a feature descriptor based on directional gradient histogram (HOG) optimization, and added a new threshold strategy, in which the matching feature point set was determined by the multi-feature selection strategy. Finally, the hybrid Gaussian model is used to calculate the correspondence between multi-temporal and multi-modal images and complete the registration.

After the feature points are extracted, the matching pairs are identified by calculating the feature point similarity metric factor. The application of particle swarm optimization algorithm in registration is systematically described in [21]. Ji et al. [22] utilized the distributed alternating direction method of multipliers for optimization (DADMMreg). The optimization algorithm used in DADMMreg achieves better convergence by changing the optimization order of the similarity and regularization terms in the energy function compared to the optimization algorithm that uses the alternating direction multiplier method (ADMM). To overcome the limitations of intensity-based or structure-based similarity metrics, an improved structural similarity measure (SSIM) is proposed, which takes into account both strength and structure information. Considering that the uniform smoothing prior of the sliding surface will lead to inaccurate registration, a new regularization metric based on vector modulus is proposed to avoid the physically untrustworthy displacement fields. Sengupta et al. [23] proposed an effective similarity measure based on mutual information. The efficiency of this indicator lies in the computation of mutual information, which uses a modified algorithm to calculate entropy and joint entropy. Lv et al. [24] introduced the concept of the geometric similarity to the registration of multispectral images.

Deep learning methods require a training process, which usually includes two types, one is to use the network as a feature extractor, and the other is end-to-end registration. Some scholars use deep networks as feature extractors to replace traditional features. Zhou et al. [25] proposed a joint network for remote sensing image registration and change detection, which uses a single network to achieve multiple tasks. Quan et al. [26] introduced the attention learning mechanism into the feature learning network. In [27], a deep learning network based on wavelet transform was established to effectively extract the low-frequency part and the high-frequency part. Yang et al. [28] used deep convolutional neural networks as feature extractors. Ye et al. [29] fused traditional SIFT and convolutional neural network features to improve the feature level. Li et al. [30] proposed a remote sensing image registration method based on deep learning regression network, which pairs the image blocks of the perception image with the reference image, and then directly learns the displacement parameters of the four corners of the perception image block relative to the reference image.

Other scholars have proposed end-to-end networks, where the output of the network is the registered image. Jia et al. [31] proposed an end-to-end registration network based on Fourier transform and established a transformation layer for moving image transformation. Liu et al. [32] utilized Fourier transform and spatial reorganization (SR) and channel optimization (CR) networks for registration. Qiu et al. [33] proposed a unified learning network that would be used for transformation registration and segmentation. Chang [34] developed an efficient remote sensing image registration framework based on a convolutional neural network (CNN) architecture, called Geometric Correlation Regression for Dense Feature Networks (GcrDfNet). In order to obtain the depth features of remote sensing images, a dense convolutional network (DenseNet) related to partial transfer learning and partial parameter fine-tuning is utilized. The feature maps derived from the sensed and reference images were further analyzed using a geometrically matched model, and then a linear regression was performed to calculate their correlation and estimate the transformation coefficients.

Although deep learning has developed rapidly in the field of image registration, it has certain drawbacks. Deep learning models need to be trained with a large amount of annotated data to ensure the accuracy and generalization ability of the model. However, high-quality annotation of remote sensing images is a costly task. Secondly, deep learning models require a lot of computing resources and time to train and optimize, which is difficult to meet the real-time registration requirements in the field of remote sensing. In addition, the performance of deep learning models is largely dependent on initialization and parameter settings, and improper initialization or parameter settings may lead to slow convergence of the model or fall into local optimum, affecting the registration effect.

Although the aforementioned methods achieve better registration accuracy, they do not consider the processing strategies when complex deformations such as stretching and shrinking coexist locally in remote sensing images, and the aforementioned methods are not suitable for deployment in ground application systems for automated processing. In this paper, unsupervised hyperspectral image registration is researched in order to achieve automatic registration. Remote sensing high-resolution hyperspectral images possess rich spectral information. To utilize this information, the high-resolution spatial features are first employed for detecting scale-invariant features, while the spectral information is used for point matching.

In addition to the different starting positions, the images obtained by the multi-moment push-broom instrument are stretched and compressed at the local scale due to the influence of platform jitter, terrain undulation, and other factors. Existing methods cannot achieve high registration accuracy and good results. In this paper, an automatic registration algorithm for spaceborne high-resolution hyperspectral images based on the combination of local image registration and image stitching based on image fragmentation is proposed, and accurate registration is carried out in the whole image and the local image. Although the individual technologies are conventional, the combination of technologies and the registration framework presented in this paper demonstrates excellent application results in addressing local deformations in high-resolution images.

The main contributions of this paper are summarized as follows:

(1)

A new automatic registration strategy for remote sensing hyperspectral images based on the combination of whole and local features of the image was established, and two granularity registrations were carried out, namely coarse-grained matching and fine-grained matching. The high-resolution spatial features are first employed for detecting scale-invariant features, while the spectral information is used for point matching. This paper designs a joint matching using spectra to improve the matching accuracy.

(2)

The idea of image stitching is introduced into image registration, and the registration accuracy is improved. Due to the influence of distortion such as stretching or shrinking of the image scale, and the principle of partial overlap when the image is divided, at the same position of the reference image, there must be a situation where the block connection is greater than one image block, so the coincident part must be fused to obtain the stitched image.

(3)

A push-broom test scheme was established, and a hyperspectral image acquisition test was carried out to simulate the on-orbit push-broom process. A large number of pushing broom experiments were conducted. The paper adds images obtained at different times during the experimental phase to verify the universality of the algorithm. These images effectively present the various deformations of the local scanning process.

(4)

Compared with multiple remote sensing image registration methods, the effectiveness and superiority of the method are proven. Spectrally, this paper designs evaluation metrics for hyperspectral image registration to verify the spectral correlation before and after the registration.

The rest of this article is organized as follows. In Section 2, the proposed remote sensing hyperspectral image registration framework is described, which includes details such as coarse matching, fine matching, image blocking, principal component transformation, and image transformation. Section 3 presents the results of the push-broom test and image registration, comparison algorithms, and performance analysis. Finally, Section 4 draws the conclusion.

2. Algorithm

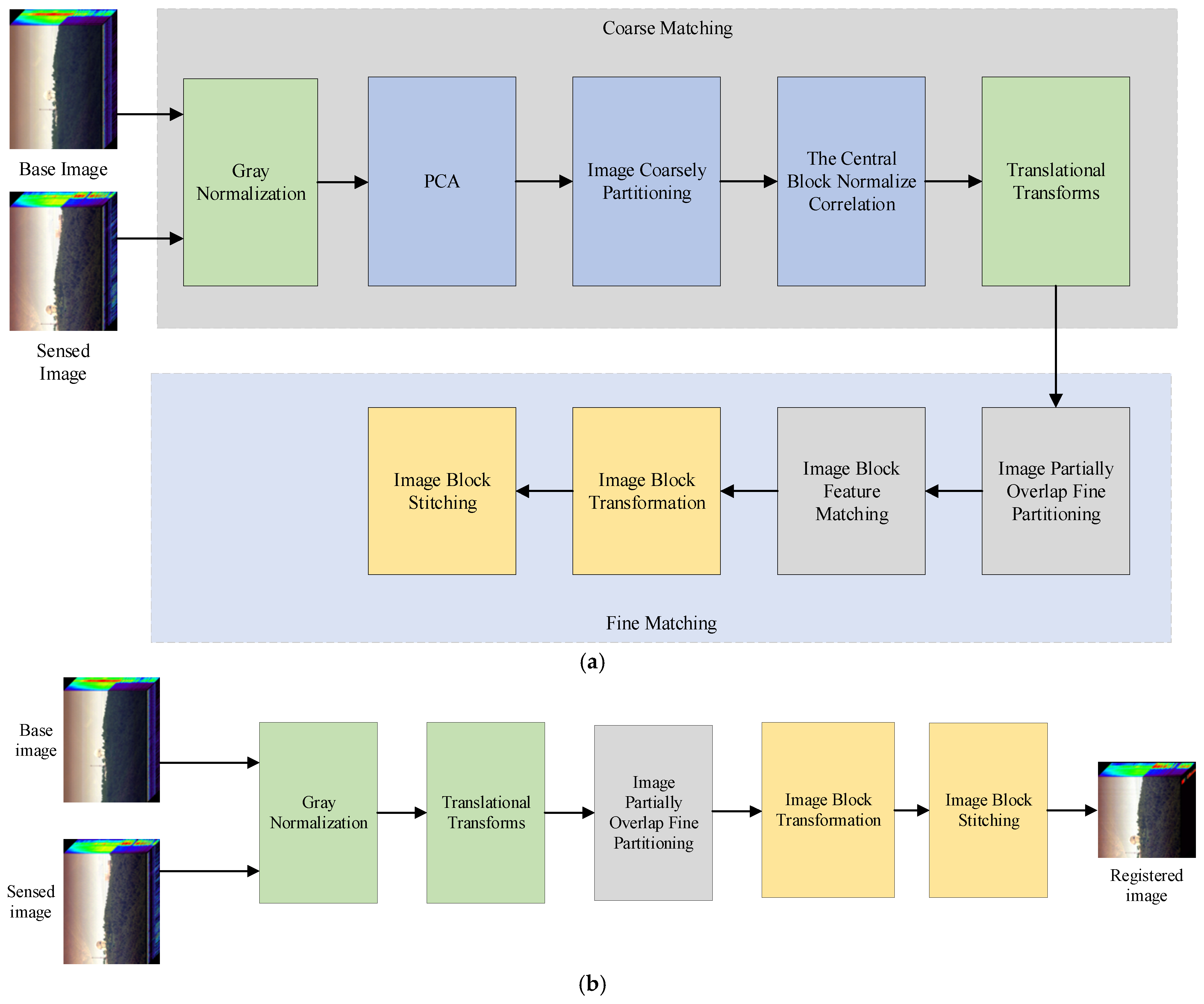
The algorithm mainly consists of two parts: one is the feature extraction stage and the other is the transformation application stage, as shown in Figure 1. The feature extraction stage is used to extract the transformation matrices of coarse-grained registration and fine-grained registration, while the algorithm application stage is used to apply the resulting transformation matrices to each band of the hyperspectral image.

The reference image, which we call the base image $f_{base}(x,y)$. The sensed image $f_{sensed}(x,y)$ is obtained at another moment and does not overlap with the field of view of the reference image. Their field of view may have significant deviations; therefore, our objective is to first perform a coarse alignment to overlap their fields of view as much as possible, and then to match them more precisely in specific areas. Both the base image and the sensed image are cut from strip pushing image of the satellite and they are assumed to be the same size. Due to the sun-synchronous orbit’s revisit pattern over a certain region, the position deviation of the two is mainly in the direction of pushing, and the deviation of the dimension of swath is small.

The core of the algorithm is described below.

(1)

Principal Component Transformation

Different types of imaging spectrometers obtain different band signal-to-noise ratios. Some instruments have poor signal-to-noise ratios in shorter wavelength regions, while others have poor signal-to-noise ratios in the infrared bands. Therefore, during image registration, the accuracy of selecting a single band for feature extraction will be greatly affected. Principal component analysis (PCA), on the other hand, transforms the hyperspectral image to concentrate energy in the first few bands, thereby suppressing noise while preserving texture details and other information. Figure 2 shows the 10 principal components of the base image. The first two principal components concentrate 90% of the energy. Using the first principal component for registration results in the loss of some texture information, and when taking the second principal component, it will lose more low-frequency energy. Therefore, this paper fuses the first two bands for feature extraction. The two principal component images are fused using alpha blending rules, as shown in Equation (1). Here, we take α as 0.5. This means that the average can take into account the information from both principal component channels.

$$I=\alpha I_{PC1}+(1-\alpha )I_{PC2}$$

(1)

where $I_{PC1}$ and $I_{PC2}$ are the first two principal components, respectively, $I$ is the fused principal component image. This paper adopts the average as a conventional practice.

(2)

Image coarse registration

The coarse registration performed in this paper is different from the previous methods, and the similarity of the two images with a large field of view is not directly calculated, or the region of interest (ROI) is manually selected for calculation. The adopted strategy is to automatically extract local image blocks for similarity matching. Principal component analysis is performed on the reference image and the sensed image, respectively, and the fused principal component image $I_{base}$ and $I_{sensed}$ are obtained. The main component of the base image is divided into blocks according to the block size $N_b$, and the center block $B_C$ is extracted. The blocks partitioning referred to here is in the direction of the pushing. The width of the block is the same as the width of the push image. By traversing the sensed image, block image B of the same size as the center block $B_C$ is extracted, and then it is matched with the center block $B_C$. In order to accurately obtain the offset position of the image block to be matched, when the image block to be matched is moved in the direction of pushing, it moves line by line, and the number of image blocks to be matched is the same as that of the sensed image pushing line. The process is shown in Figure 3.

The coordinate offset of the most relevant point in the image is calculated by normalized cross correlation (NCC) [3] between the center block and the image block to be matched.

$$NCC(u,v)={\displaystyle \frac{{\displaystyle {\sum }_{x,y}\left[f_B(x,y)-{\overline{f}}_{Bu,v}\right]}\left[f_{BC}(x-u,y-v)-{\overline{f}}_{BC}\right]}{\left\{{\left.{{\displaystyle {\sum }_{x,y}\left[f_B(x,y)-{\overline{f}}_{Bu,v}\right]}}^2{\displaystyle {\sum }_{x,y}{\left[f_{BC}(x-u,y-v)-{\overline{f}}_{BC}\right]}^2}\right\}}^{1/2}\right.}},$$

(2)

where ${\overline{f}}_{BC}$ is the mean of the central block, ${\overline{f}}_{Bu,v}$ is the mean of B in the area within the range of the central block.

From Equation (2), it can be concluded that there is a displacement in both the scanning dimension and the swath dimension for the coarse matching points (the point corresponding to the maximum value in the NCC), but the primary displacement occurs in the scanning dimension, where the obtained offset refers to the scanning dimension. Each matching finds the maximum value of NCC, and the sliding window moves pixel by pixel along the pushing dimension, resulting in a column vector of NCC maximum values that corresponds to the number of pushing lines. The maximum value of this column vector is identified, which corresponds to the image block that best matches the central block, thus determining the offset between the two images.

This offset and the coordinates of the first point in the upper-left corner of the center block in the base image are combined to form the offset between the base image and the sensed image. A translation transform is applied to align the base image with the sensed image.

(3)

Image fine division block

The aligned base image principal component ${\widehat{I}}_{base}$ and the sensed image principal component ${\widehat{I}}_{sensed}$ are then further registered at a finer scale. Due to the different position offsets and scale distortions of different parts of the sensed image, if the image is directly divided into blocks when coarse matching is used, there will be a gap in the connection of the transformed image blocks, so there is a certain overlap between adjacent image blocks when the image is blocked, and the overlapping ratio should be greater than the maximum offset of the block image. The parts ${\widehat{I}}_{base\_warped}$ and ${\widehat{I}}_{sensed\_warped}$ where the fields of view of ${\widehat{I}}_{base}$ and ${\widehat{I}}_{sensed}$ overlap are carried out according to the new division principle.

First of all, compared with the coarse registration stage, the block scale $N_b$ is smaller. Secondly, the adjacent blocks are partially overlapped, and the overlapping ratio is b. The same as before, the block is divided in the direction of pushing, and the width of the block is the same as the width of the push image. The obtained blocks are $B_{base}^i$ and $B_{Sensed}^i$, $i\in [0,N]$, where N is the number of blocks. The ith image block and the i + 1th image block partially overlapped, and the overlapping ratio is b.

(4)

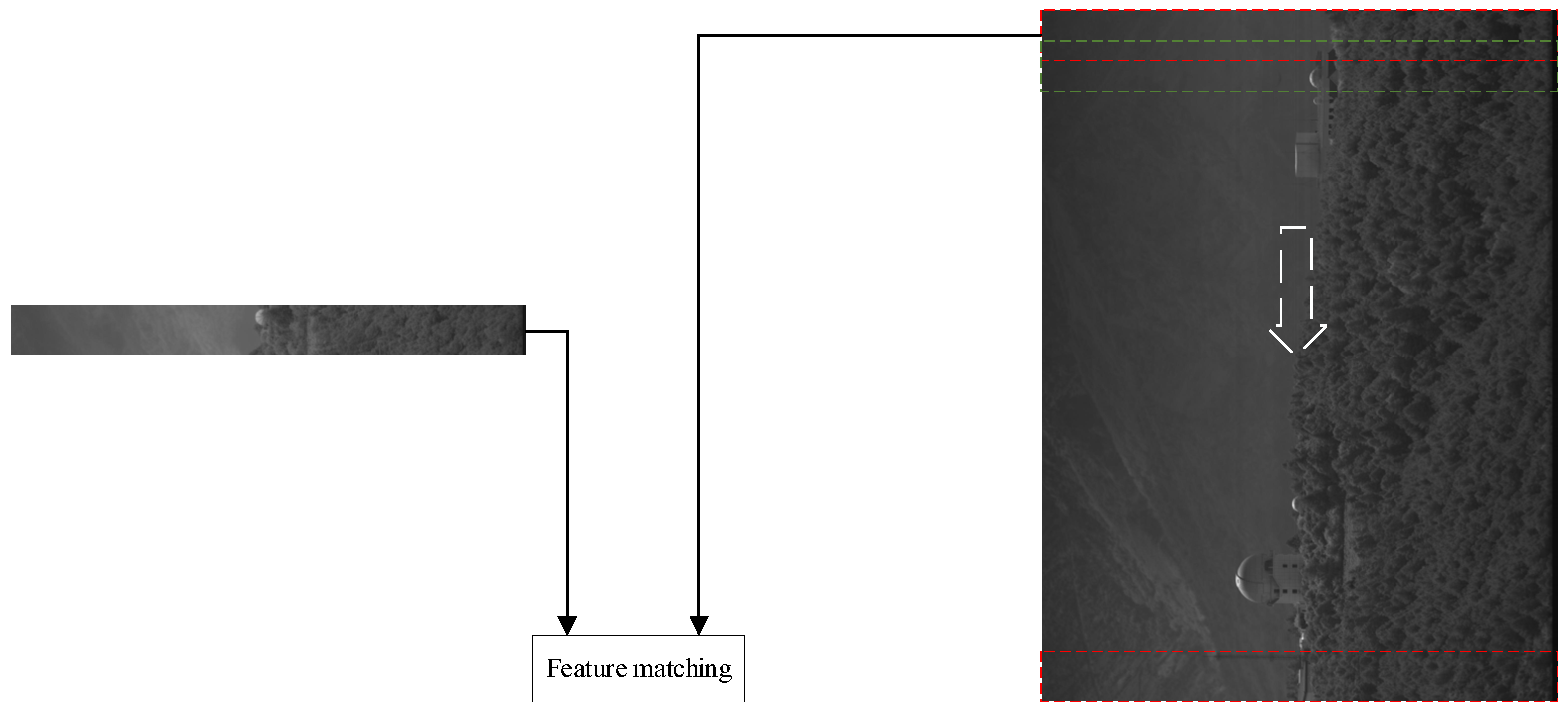
Image block feature matching

The features of image blocks $B_{base}^i$ and $B_{Sensed}^i$ are extracted one by one and matched. Gaussian filtering or mean filtering in the algorithm SIFT and SURF will destroy the image texture boundary information. KAZE uses nonlinear diffusion to establish a nonlinear scale space, filter noise interference, and maintain the overall clarity of the image, so as to obtain higher image feature point accuracy. Therefore, KAZE feature points are selected in this paper [35]. Additionally, to fully utilize the spectral information, the detected KAZE feature points will be matched using their spectral characteristics in conjunction with the KAZE feature vectors, thereby obtaining the correct matching point pairs between the two images. The exhaustion method was used to match the nearest neighbor of the joint feature vector points of the two images, and the matching points were obtained as shown in Figure 4. Despite the coarse registration performed, the two images still have distortions in position and scale locally. This distortion is not only reflected in the dimension of swath, but also in the pushing dimension.

After obtaining the matching point pairs, the block image transformation matrix $T^i$ is estimated to prepare for the subsequent sensed image block $B_{Sensed}^i$ to perform image block transformation.

(5)

Image block stitching

Image mosaic is a technique that stitches two or more overlapping images from the same scene into a larger image. This section utilizes image mosaic technology to stitch and merge local blocks of the high-resolution image.

The block image transformation matrix estimated by feature point matching is applied to the sensed image block $B_{Sensed}^i$, and the translation transformation is applied at the starting position of the base image according to the block image. Due to the influence of distortion such as stretching or shrinking of the image scale, as well as the principle of partial overlap when the image is divided, at the same position of the reference image, there must be a situation where the block connection is greater than one image block, so the coincident part must be fused to obtain the stitched image $I_{sensed}^{re\mathrm{cov}er}$. If the pixel value of $I_{sensed}^{re\mathrm{cov}er}$ at the position of the base image is 0 when the image block $B_{sensed\_r \mathrm{e} c}^i$ is fused and transformed, the pixel of the image block is directly filled. If the pixel value of the position is no longer 0, the pixel of the current $B_{sensed\_r \mathrm{e} c}^i$ is filled with the position. Here, a value of zero indicates the area where the image blocks do not overlap. At this time, it can be filled directly. A value of non-zero indicates an overlapping area of the image block, which is directly filled with a new image block.

(6)

Algorithm application stage

The feature extraction stage is for the single principal component after PCA transformation, and the actual algorithm application stage is for each band R in the cube image. The offset obtained by coarse matching in the feature extraction stage, subdivision block step, and block transformation matrix can be directly applied to each band R. The principle of band image block fusion also adopts the method of fine registration stage. In this way, each band of the sensed image is obtained, and the entire sensed image is recovered.

3. Experiment

3.1. Push-Broom Test and Data Acquisition

The ground prototype corresponding to the spaceborne interferometric Fourier transform imaging spectrometer was used to obtain the interference image by pushing and sweeping experiments, and then the spectrum was restored to obtain a standard hyperspectral data cube. The image width is 2048 pixels, 70 bands, and the band range is 450~900 nm. When it is imaged at a distance of 7 km, the corresponding resolution is 0.1 m.

Figure 5 shows the push-broom scene at the Lijiang Observatory in Yunnan, China, and the vegetation spectrum curve corresponding to the red dots in the figure is shown in Figure 6.

Vegetation areas were selected to calculate the signal-to-noise ratio of the base image and the sensed image, as shown in Figure 7. The signal-to-noise ratio of different bands varies greatly.

The four images were acquired at different times, and the lighting conditions were quite different, which was reflected in the obvious differences in the characteristics of vegetation areas in the images. In addition, the image is partially stretched or shrank. In addition to the distortion in the pushing direction, there is also distortion in the swath direction of the two images.

3.2. Parameter Settings

In this paper, the method based on feature point matching (Feat) [35], the registration method based on normalized cross-correlation (NCC) [7], the registration method based on control points (Control) [2], and the registration method based on a variety of combination features (multiscale histogram of local main orientation, HLMO) [36] are compared. The registration method based on normalized cross-correlation needs to select the ROI to reduce the computing resources, and the white dome is used as the matching target region. In the method of feature point matching, SIFT features and affine transformations were selected. The maximum threshold for feature matching is set to 10 and the maximum ratio is 0.7. The SIFT feature detects the correct match pair 234. This enhances its registration accuracy at various locations in the image.

The control points selected for the control point-based registration method are shown in Figure 8, the correction method is polynomial, and the resampling method is bilinear.

3.3. Evaluation Criteria

(1)

Target Registration Error (TRE) [7] is an important criterion to measure the accuracy of image registration, which is defined as:

$$TRE(I_{base},I_{sensed})={\displaystyle \frac{{\displaystyle \sum _{i=1}^{N_{key}}{\left[{(x_{base}^i-x_{sensed}^i)}^2+{(y_{base}^i-y_{sensed}^i)}^2\right]}^{1/2}}}{N_{key}}},$$

(3)

where $N_{key}$ is number of key points marked. $(x_{base}^i,y_{base}^i)$ and $(x_{sensed}^i,y_{sensed}^i)$ represent the coordinates of the ith key point marked in the image $I_{base}$ and $I_{sensed}$, respectively.

Registration accuracy is measured by calculating the Euclidean distance between the keys of a fixed and distorted image. The closer the TRE is to zero, the better the registration effect. The key points marked in this paper are shown in Figure 5.

The marked points are mainly the corners with obvious characteristics, which are distributed at the beginning and end positions of the push-broom scene to adapt to the distortion such as local stretching or shrinking caused by the instability of the push-broom platform or terrain factors.

(2)

Coherence coefficient method [7], which is defined as:

The coherence coefficient (CC) is used to measure the similarity of two images, and its values range from −1 to 1, with values closer to 1 indicating that the two images are more similar.

$$CC(I_{base},I_{sensed})={\displaystyle \frac{{\displaystyle \sum (I_{base}-{\overline{I}}_{base})(I_{sensed}-{\overline{I}}_{sensed})}}{\sqrt{{\displaystyle \sum {(I_{base}-{\overline{I}}_{base})}^2}\sqrt{{\displaystyle \sum {(I_{sensed}-{\overline{I}}_{sensed})}^2}}}}},$$

(4)

where ${\overline{I}}_{base}$ and ${\overline{I}}_{sensed}$ are the gray mean of $I_{base}$ and $I_{sensed}$, respectively.

(3)

Spectral Angle Mapper (SAM) measures spectral similarity, which is defined as:

$$\alpha ={\cos }^{-1}\left({\displaystyle \frac{{\displaystyle \sum _{i=1}^C{t}_i{r}_i}}{\sqrt{{\displaystyle \sum _{i=1}^C{t}_i^2}{\displaystyle \sum _{i=1}^C{r}_i^2}}}}\right),$$

(5)

where t is the test spectral vector and r is a reference spectral vector. C is the band number.

3.4. Experimental Results

As can be seen from Figure 7, the signal-to-noise ratio is poor in the shorter wavelength bands, which makes registration difficult. In this paper, band 50 is selected as the calculation target for different algorithm registration. The sensed image after registration is shown in Figure 9.

4. Discussion

We compare the registration results of typical targets, focusing on the trees in the red box and the towers in the yellow box in Figure 9. The two targets are located at opposite ends of the push-broom image. In this way, the scale distortion of stretching and shrinking of local images at different locations is compared. The red box target displays the base image and the registered image in a checkerboard, as shown in Figure 10. The tree stem is circled in red in Figure 10a. The NCC method has more offsets in the trunk part. The registration effect of our algorithm, the SIFT-based Feat algorithm, and HLMO are better, while the control point-based control’s registration effect is poor.

The red box target displays the base image and the registered image in a checkerboard, as shown in Figure 11. The NCC method and our algorithm have high registration accuracy, while Feat and HLMO still have shear translation in the push-broom dimension. The algorithm of Control prioritizes the registration accuracy at each control point, however, the registration accuracy in other parts is poor.

In addition to the visual representation of the registration effect, the registration accuracy was also evaluated by quantitative indicators. Here, the target registration error (TRE) of different methods for the marker points is compared, as shown in the first row of

Table 1. The evaluation results of the registered image of the sensed image 1 and the reference image. The bold text indicates the best performance.

Methods	Corr.	Feat	Control	HLMO	Ours
TRE	4.1583	2.9532	21.4252	2.6132	1.6105
CC	0.9491	0.9512	0.9392	0.9511	0.9623
SAM (radians)	0.1623	0.1606	0.1711	0.1583	0.1542

,

Table 2. The evaluation results of the registered image of the sensed image 2 and the reference image. The bold text indicates the best performance.

Methods	Corr.	Feat	Control	HLMO	Ours
TRE	4.0155	2.7223	15.3362	2.1584	1.2083
CC	0.9523	0.9611	0.9415	0.9699	0.9715
SAM (radians)	0.1599	0.1581	0.1686	0.1401	0.1321

and

Table 3. The evaluation results of the registered image of the sensed image 3 and the reference image. The bold text indicates the best performance.

Methods	Corr	Feat	Control	HLMO	Ours
TRE	3.1533	2.0202	10.2546	1.5236	1.085
CC	0.9612	0.9795	0.9532	0.9802	0.9844
SAM (radians)	0.1403	0.1323	0.1541	0.1301	0.1204

. The physical dimension of TRE is considered as the number of pixels. Our method is optimal, with an error margin of less than two pixels.

The coherence coefficient (CC) is calculated for the part of the base image that completely coincides with the sensed image after registration, and the results are shown in the second row of Table 1, Table 2 and Table 3. Our algorithms also achieve the best results.

We evaluate the variation of the spectral angle between the reference image and the sensed image before and after registration to verify the registration accuracy. Before registration, the spectral angle between the reference image and the sensed image is 0.1885 radians. It is the average of the SAM between all overlapping pixels in the base and registered image. The third row of Table 1, Table 2 and Table 3 shows the spectral angles of registered images and sensed images under different algorithms. Our proposed algorithm demonstrates the best improvement in spectral correlation of the registered images.

The registration accuracy of the proposed algorithm is not affected by the number of feature points extracted from panoramic images. Block size is an important parameter because it involves local image feature extraction. Therefore, it is necessary to analyze the influence of different $N_b$ on the registration accuracy. It is set 60, 70, 80, 100, 110, 120, 160, 180, and 200, respectively, to calculate the coherence coefficient. If the block size is too small, for example less than 60, too few local features of the image block will be obtained, and it is difficult to match the features. Excessive block segmentation makes it difficult to ensure the registration accuracy due to various complex deformations such as stretching and shrinking existing in the block at the same time. CC is calculated by the part of the principal component fusion image and the reference image that are completely overlapped, and the corresponding results of block size and registration accuracy are shown in Figure 12. It can be seen from the figure that smaller block sizes achieve higher registration accuracy. However, if the block size is too small, it may not match the correct features, as reflected in Figure 12, where performance significantly declines when the size is less than 60.

Compared with the registration algorithm based on feature points, the proposed algorithm does not need too many feature points to achieve better registration results. Compared with the control point-based algorithm, the proposed algorithm is an automatic registration algorithm that does not require the boundary of control points. Compared with the deep learning model, the algorithm in this paper does not need to be trained, and can obtain good real-time performance, which is a great advantage for direct application to satellite ground application systems.

5. Conclusions

In summary, this paper proposes a new remote sensing hyperspectral image registration algorithm, which performs coarse registration through the image as a whole, divides the image into blocks at finer granularity to extract local features, and then uses the idea of image stitching to fuse the image after fine registration to obtain high-precision registration results. To verify the proposed algorithm, a simulated on-orbit push-broom imaging experiment was carried out to obtain hyperspectral images with local complex distortion under different lighting conditions. The simulation results confirm that the registration of the proposed remote sensing hyperspectral image is superior to the existing algorithms, including the registration algorithm based on feature points, the registration algorithm based on control points, and the registration algorithm based on cross-correlation. The advantages of the proposed algorithm in terms of registration accuracy and real-time performance make it have a broad prospect for application in satellite ground application systems.