Improvement of FAPAR Estimation Under the Presence of Non-Green Vegetation Considering Fractional Vegetation Coverage
Abstract
1. Introduction
2. Methodology
2.1. Data Collection and Preprocessing
2.2. Methods
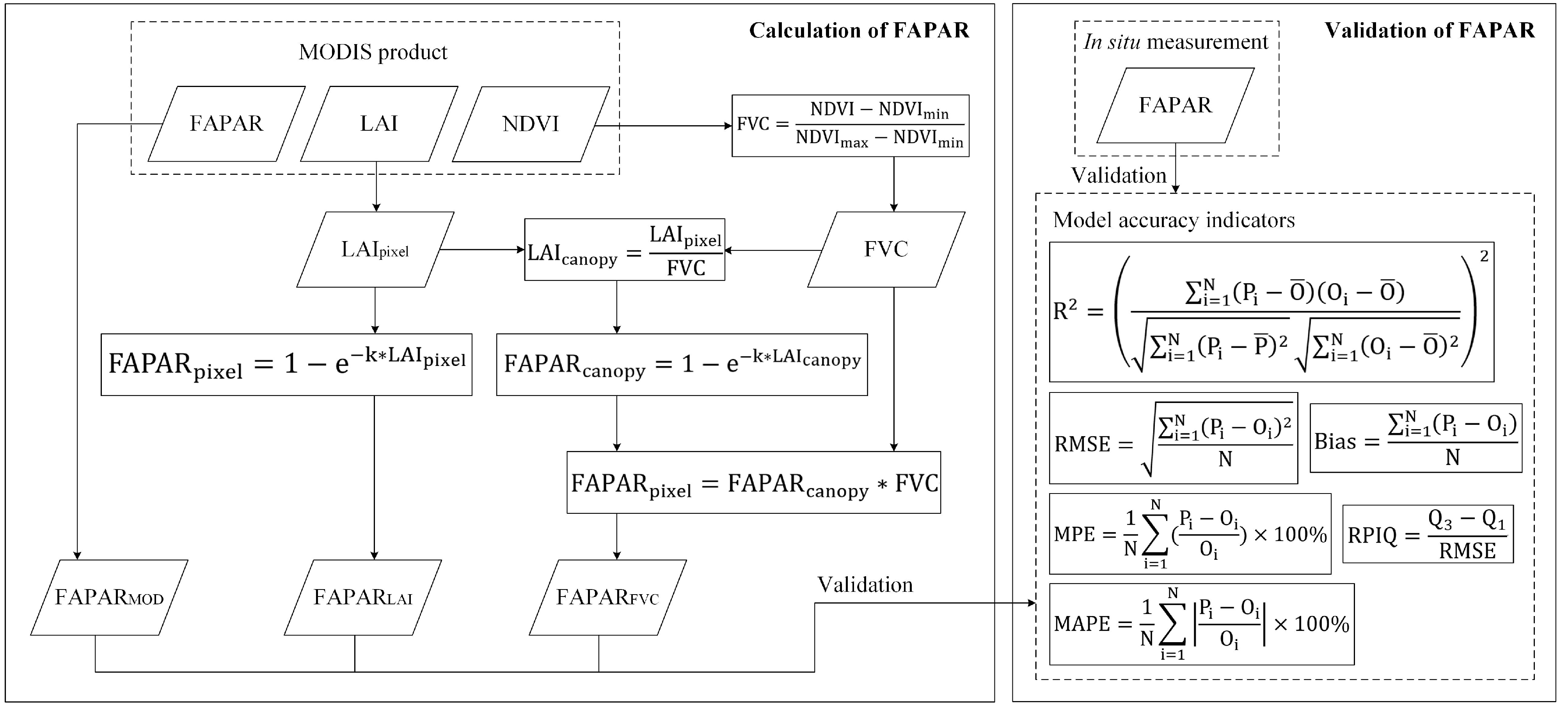
2.2.1. General Idea
2.2.2. Calculation of FAPAR
2.2.3. Validation of FAPAR
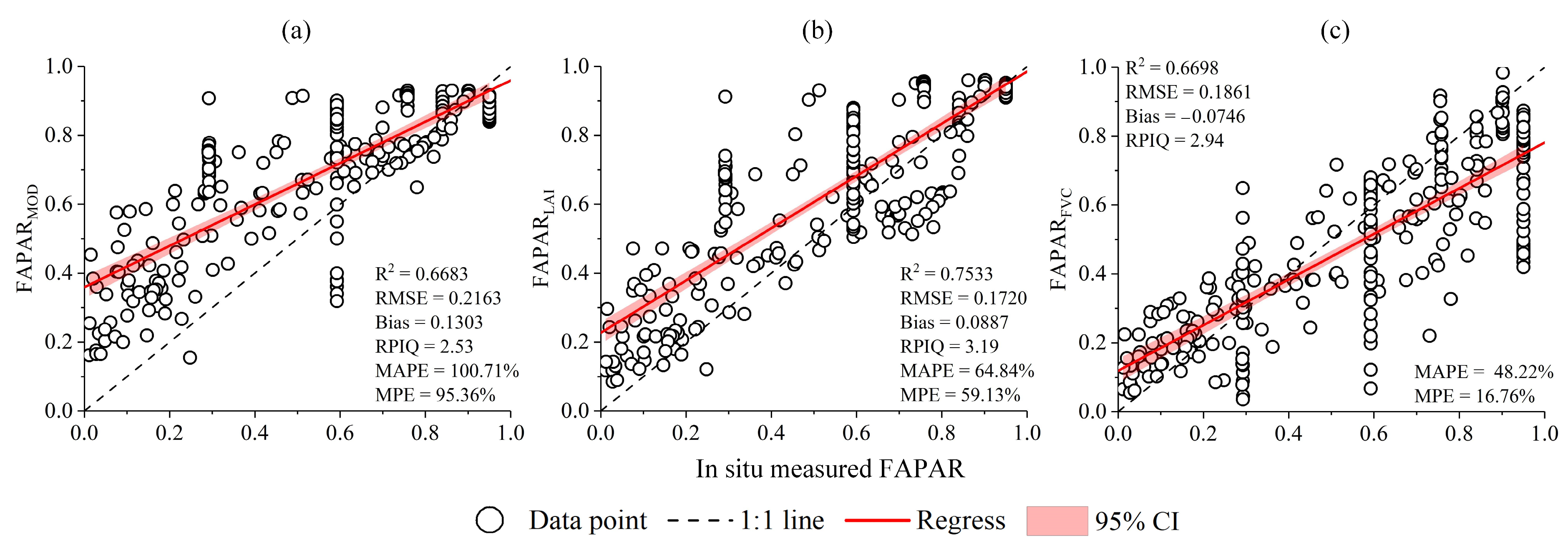
3. Results
3.1. Overall Situation of Model Accuracy
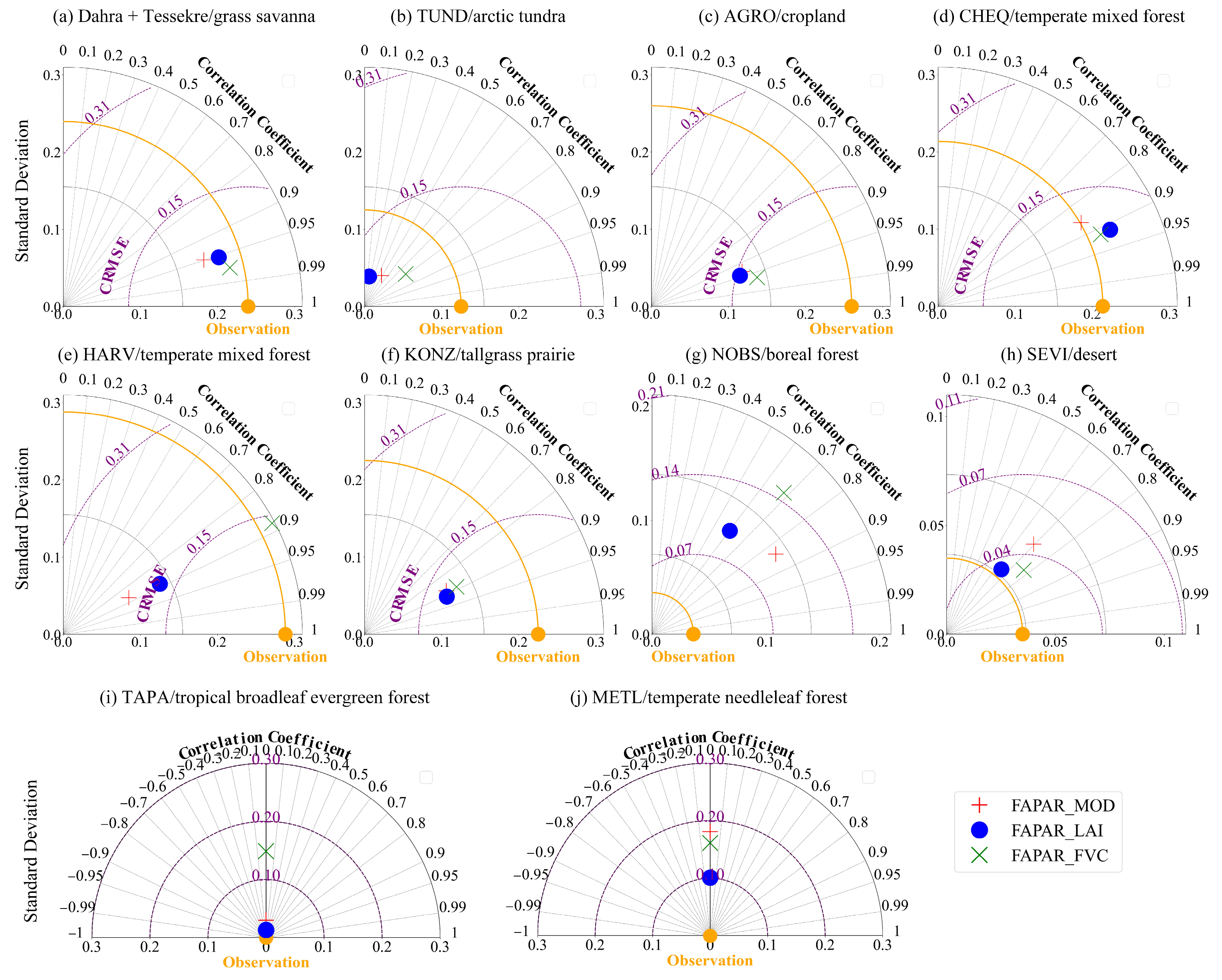
3.2. Differences in Model Accuracy Between Biome Types
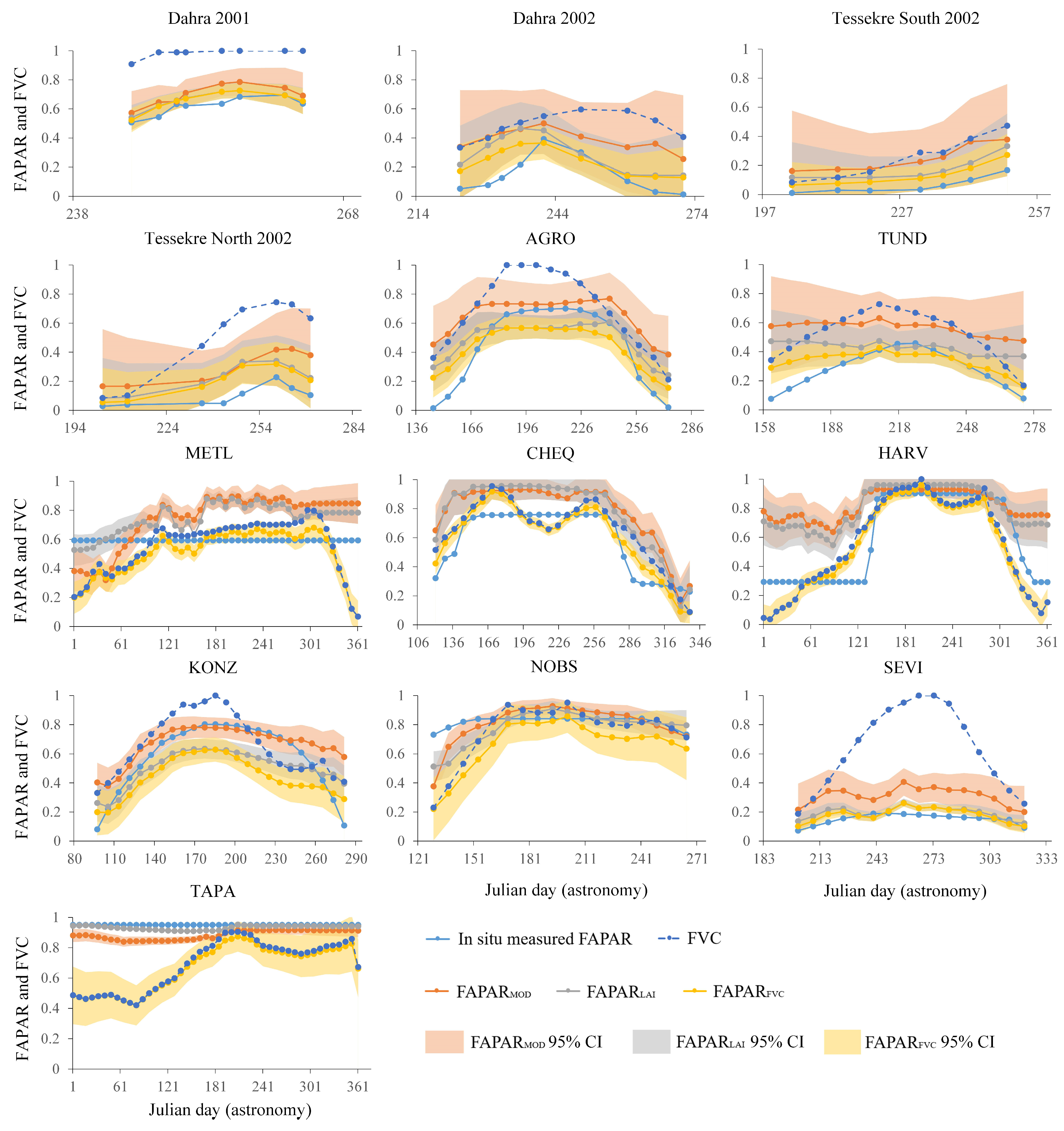
3.3. Differences in Model Accuracy in Temporal Changes
3.4. Model Accuracy and Fractional Vegetation Coverage
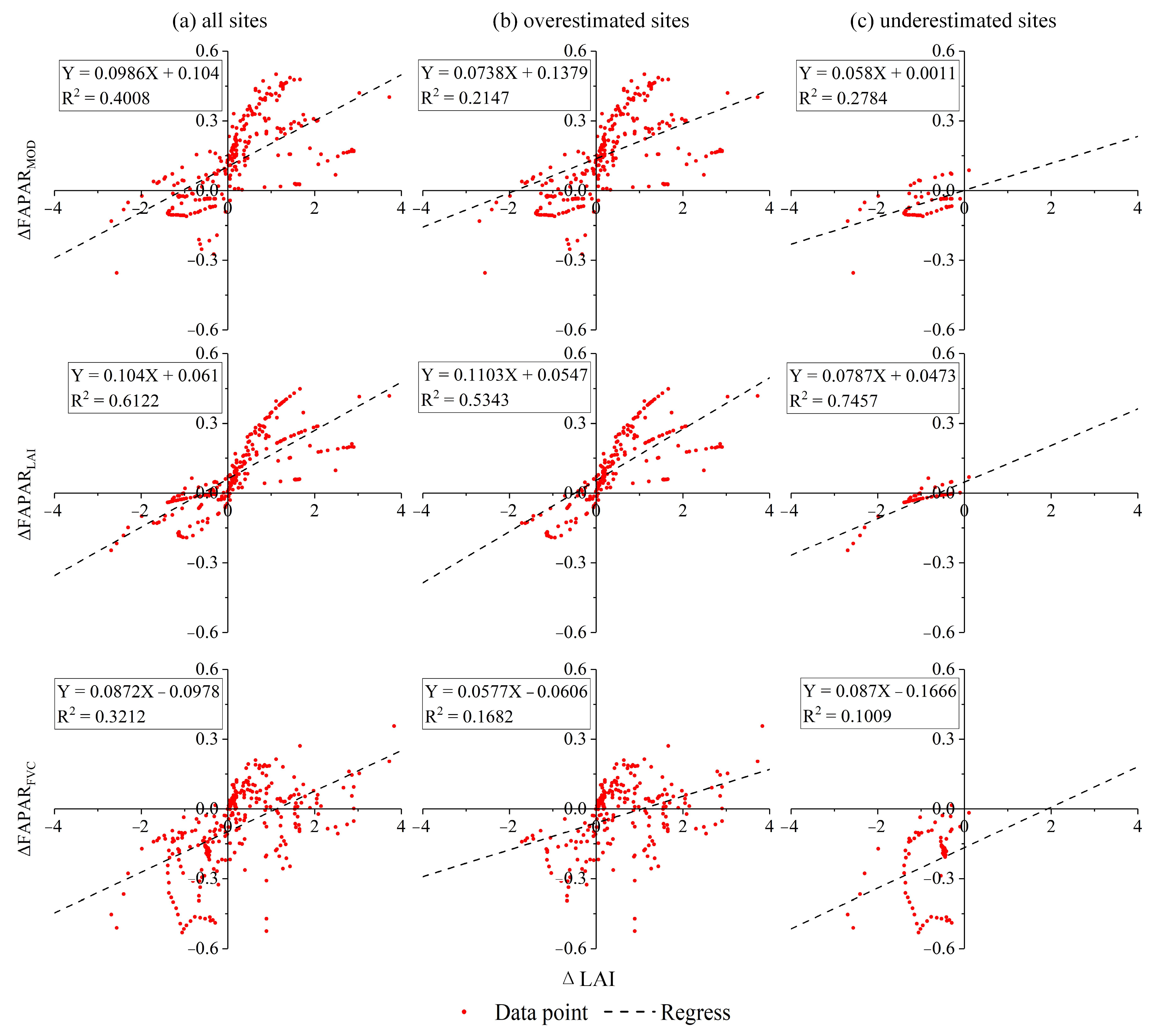
3.5. Relationship Between FAPAR Error and LAI Error
4. Discussion
4.1. Impact of Fractional Vegetation Coverage Estimation Errors on FAPARMOD
4.2. Effect of Presence in Non-Green Vegetation Canopy on FAPAR Estimation
4.3. Impact of MODIS LAI Errors on FAPAR Estimation
4.4. Research Uncertainties and Future Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Bias | Mean prediction error |
| CI | Confidence interval |
| FAPAR | Fraction of absorbed photosynthetically active radiation |
| FVC | Fractional vegetation coverage |
| GPP | Gross primary production |
| LAI | Leaf area index |
| LUE | Light use efficiency |
| MAPE | Mean absolute percentage error |
| MODIS | Moderate-resolution imaging spectroradiometer |
| MPE | Mean percentage error |
| NDVI | Normalized difference vegetation index |
| CRMSE | Centered root mean squared error |
| PAR | Photosynthetically active radiation |
| R | Correlation coefficient |
| R2 | Coefficient of determination |
| RMSE | Root mean squared error |
| RPIQ | Ratio of performance to interquartile range |
| SD | Standard deviation |
References
- Sabzchi-Dehkharghani, H.; Biswas, A.; Meshram, S.G.; Majnooni-Heris, A. Estimating gross and net primary productivities using earth observation products: A review. Environ. Model. Assess. 2024, 29, 179–200. [Google Scholar] [CrossRef]
- Pei, Y.Y.; Dong, J.W.; Zhang, Y.; Yuan, W.P.; Doughty, R.; Yang, J.L.; Zhou, D.C.; Zhang, L.X.; Xiao, X.M. Evolution of light use efficiency models: Improvement, uncertainties, and implications. Agric. For. Meteorol. 2022, 317, 108905. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Wulder, M.A.; Black, T.A.; Guy, R.D. The use of remote sensing in light use efficiency based models of gross primary production: A review of current status and future requirements. Sci. Total Environ. 2008, 404, 411–423. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.H.; Zhang, Q.; Li, J.; Yang, X.; Wu, Y.F.; Zhang, Z.Y.; Wang, S.H.; Wang, H.Z.; Zhang, Y.G. Solar-induced chlorophyll fluorescence and its link to canopy photosynthesis in maize from continuous ground measurements. Remote Sens. Environ. 2020, 236, 111420. [Google Scholar] [CrossRef]
- Goward, S.N.; Huemmrich, K.F. Vegetation canopy PAR absorptance and the normalized difference vegetation index: An assessment using the SAIL model. Remote Sens. Environ. 1992, 39, 119–140. [Google Scholar] [CrossRef]
- Hipps, L.E.; Asrar, G.; Kanemasu, E.T. Assessing the interception of photosynthetically active radiation in winter wheat. Agric. Meteorol. 1983, 28, 253–259. [Google Scholar] [CrossRef]
- Huemmrich, K.F.; Privette, J.L.; Mukelabai, M.; Myneni, R.B.; Knyazikhin, Y. Time-series validation of MODIS land biophysical products in a Kalahari woodland, Africa. Int. J. Remote Sens. 2005, 26, 4381–4398. [Google Scholar] [CrossRef]
- Yan, G.J.; Hu, R.H.; Luo, J.H.; Weiss, M.; Jiang, H.L.; Mu, X.H.; Xie, D.H.; Zhang, W.M. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B., III. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore, B., III; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; Baldocchi, D.D.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; Monson, R.K.; Schmid, H.P.; et al. Midday values of gross CO2 flux and light use efficiency during satellite overpasses can be used to directly estimate eight-day mean flux. Agric. For. Meteorol. 2005, 131, 1–12. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- He, M.; Ju, W.; Zhou, Y.; Chen, J.; He, H.; Wang, S.; Wang, H.; Guan, D.; Yan, J.; Li, Y.; et al. Development of a two-leaf light use efficiency model for improving the calculation of terrestrial gross primary productivity. Agric. For. Meteorol. 2013, 173, 28–39. [Google Scholar] [CrossRef]
- Guan, X.B.; Chen, J.M.; Shen, H.F.; Xie, X.Y. A modified two-leaf light use efficiency model for improving the simulation of GPP using a radiation scalar. Agric. For. Meteorol. 2021, 307, 108546. [Google Scholar] [CrossRef]
- Guan, X.B.; Chen, J.M.; Shen, H.F.; Xie, X.Y.; Tan, J.B. Comparison of big-leaf and two-leaf light use efficiency models for GPP simulation after considering a radiation scalar. Agric. For. Meteorol. 2022, 313, 108761. [Google Scholar] [CrossRef]
- Sun, Y.K.; Yuan, D.K.; Zheng, X.; Yang, S.S.; Zhang, S.; Zhang, J.H.; Bai, Y. Estimation of radiation scalar using deep learning for improved gross primary productivity estimation based on a light-use efficiency model. Int. J. Digit. Earth 2024, 17, 2402421. [Google Scholar] [CrossRef]
- Huang, L.X.; Yuan, W.P.; Zheng, Y.; Zhou, Y.L.; He, M.Z.; Jin, J.X.; Huang, X.J.; Chen, S.Y.; Liu, M.; Guan, X.B.; et al. A dynamic-leaf light use efficiency model for improving gross primary production estimation. Environ. Res. Lett. 2024, 19, 014066. [Google Scholar] [CrossRef]
- Verhoef, W. Light-scattering by leaf layers with application to canopy reflectance modeling—The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F.; Andrieu, B.; Danson, F.M.; Jaggard, K. Extraction of vegetation biophysical parameters by inversion of the PROSPECT + SAIL models on sugar beet canopy reflectance data. Application to TM and AVIRIS sensors. Remote Sens. Environ. 1995, 52, 163–172. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Rasmussen, M.S. Evaluation of MODIS LAI, fAPAR and the relation between fAPAR and NDVI in a semi-arid environment using in situ measurements. Remote Sens. Environ. 2004, 91, 490–507. [Google Scholar] [CrossRef]
- Steinberg, D.C.; Goetz, S.J.; Hyer, E.J. Validation of MODIS FPAR products in boreal forests of Alaska. IEEE Trans. Geosci. Remote. Sens. 2006, 44, 1818–1828. [Google Scholar] [CrossRef]
- D’Odorico, P.; Gonsamo, A.; Pinty, B.; Gobron, N.; Coops, N.; Mendez, E.; Schaepman, M.E. Intercomparison of fraction of absorbed photosynthetically active radiation products derived from satellite data over Europe. Remote Sens. Environ. 2014, 142, 141–154. [Google Scholar] [CrossRef]
- Chernetskiy, M.; Gómez-Dans, J.; Gobron, N.; Morgan, O.; Lewis, P.; Truckenbrodt, S.; Schmullius, C. Estimation of FAPAR over croplands using MISR data and the earth observation land data assimilation system (EO-LDAS). Remote Sens. 2017, 9, 656. [Google Scholar] [CrossRef]
- Stocker, B.D.; Wang, H.; Smith, N.G.; Harrison, S.P.; Keenan, T.F.; Sandoval, D.; Davis, T.; Prentice, I.C. P-model v1.0: An optimality-based light use efficiency model for simulating ecosystem gross primary production. Geosci. Model Dev. 2020, 13, 1545–1581. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Xiao, Z.Q.; Li, J.; Yang, H.; Song, J.L. Evaluation of global fraction of absorbed photosynthetically active radiation (FAPAR) products at 500 m spatial resolution. Remote Sens. 2022, 14, 3304. [Google Scholar] [CrossRef]
- Lai, P.Y.; Marshall, M.; Darvishzadeh, R.; Nelson, A. Crop productivity under heat stress: A structural analysis of light use efficiency models. Agric. For. Meteorol. 2025, 362, 110376. [Google Scholar] [CrossRef]
- Liang, S.Z.; Hou, X.H.; Sui, X.Y.; Wang, M. Deciduous broadleaf forests green FPAR and its relationship with spectral vegetation indices. In Proceedings of the 2017 10th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Shanghai, China, 14–16 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Majasalmi, T.; Stenberg, P.; Rautiainen, M. Comparison of ground and satellite-based methods for estimating stand-level fPAR in a boreal forest. Agric. For. Meteorol. 2017, 232, 422–432. [Google Scholar] [CrossRef]
- Tan, C.W.; Wang, D.L.; Zhou, J.; Du, Y.; Luo, M.; Zhang, Y.J.; Guo, W.S. Remotely assessing fraction of photosynthetically active radiation (FPAR) for wheat canopies based on hyperspectral vegetation indexes. Front. Plant Sci. 2018, 9, 776. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, S.H.; He, Z.; Liu, Y.H.; Su, Z.H. Synergistic inversion of rice FPAR based on optical and radar remote sensing data. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 1943–1946. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Frederic, B.; Guyot, G.; Major, D. TSAVI: A vegetation index which minimizes soil brightness effects on LAI and APAR estimation. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; pp. 1355–1358. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Ruimy, A.; Kergoat, L.; Bondeau, A. Comparing global models of terrestrial net primary productivity (NPP): Analysis of differences in light absorption and light-use efficiency. Glob. Change Biol. 1999, 5, 56–64. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Hu, Z.W.; Fang, H.L.; Gao, X.; Wang, J.Z.; Wu, G.F. Estimation of daily FAPAR from MODIS instantaneous observations at forest sites. Agric. For. Meteorol. 2023, 331, 109336. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, T.; Jiang, B. Retrieval of leaf area index (LAI) and fraction of absorbed photosynthetically active radiation (FAPAR) from VIIRS time-series data. Remote Sens. 2016, 8, 351. [Google Scholar] [CrossRef]
- Zhu, H.; Lin, A.; Wang, L.; Xia, Y.; Zou, L. Evaluation of MODIS gross primary production across multiple biomes in China using eddy covariance flux data. Remote Sens. 2016, 8, 395. [Google Scholar] [CrossRef]
- Florakis, K.; Trevezas, S.; Letort, V. Predicting tomato water consumption in a hydroponic greenhouse: Contribution of light interception models. Front. Plant Sci. 2023, 14, 1264915. [Google Scholar] [CrossRef] [PubMed]
- Shabanov, N.; Gastellu-Etchegorry, J.-P. The stochastic Beer–Lambert–Bouguer law for discontinuous vegetation canopies. J. Quant. Spectrosc. Radiat. Transf. 2018, 214, 18–32. [Google Scholar] [CrossRef]
- Ponce de León, M.A.; Bailey, B.N. Evaluating the use of Beer’s law for estimating light interception in canopy architectures with varying heterogeneity and anisotropy. Ecol. Model. 2019, 406, 133–143. [Google Scholar] [CrossRef]
- Nilson, T. A theoretical analysis of the frequency of gaps in plant stands. Agric. Meteorol. 1971, 8, 25–38. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Gregory, M. BigFoot GPP and NPP summary, 2000–2004. 2006. Available online: https://daac.ornl.gov/BIGFOOT_VAL/gpp_npp_summaries.html (accessed on 16 October 2024).
- Goulden, M.L.; Daube, B.C.; Fan, S.-M.; Sutton, D.J.; Bazzaz, A.; Munger, J.W.; Wofsy, S.C. Physiological responses of a black spruce forest to weather. J. Geophys. Res. Atmos. 1997, 102, 28987–28996. [Google Scholar] [CrossRef]
- Meyers, T.P.; Hollinger, S.E. An assessment of storage terms in the surface energy balance of maize and soybean. Agric. For. Meteorol. 2004, 125, 105–115. [Google Scholar] [CrossRef]
- Wofsy, S.C.; Goulden, M.L.; Munger, J.W.; Fan, S.M.; Bakwin, P.S.; Daube, B.C.; Bassow, S.L.; Bazzaz, F.A. Net exchange of CO2 in a mid-latitude forest. Science 1993, 260, 1314–1317. [Google Scholar] [CrossRef]
- Kurc, S.A.; Small, E.E. Dynamics of evapotranspiration in semiarid grassland and shrubland ecosystems during the summer monsoon season, central New Mexico. Water Resour. Res. 2004, 40, W09305. [Google Scholar] [CrossRef]
- Anthoni, P.M.; Unsworth, M.H.; Law, B.E.; Irvine, J.R.; Baldocchi, D.D.; Tuyl, S.V.; Moore, D. Seasonal differences in carbon and water vapor exchange in young and old-growth ponderosa pine ecosystems. Agric. For. Meteorol. 2002, 111, 203–222. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Huete, A.R.; Chen, J.; Chen, Y.H.; Li, J.; Yan, G.J.; Zhang, X.Y. Analysis of NDVI and scaled difference vegetation index retrievals of vegetation fraction. Remote Sens. Environ. 2006, 101, 366–378. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Rochford, P.A. SkillMetrics: A Python Package for Calculating the Skill of Model Predictions Against Observations. 2016. Available online: http://github.com/PeterRochford/SkillMetrics (accessed on 29 January 2025).
- Shabanov, N.V.; Knyazikhin, Y.; Baret, F.; Myneni, R.B. Stochastic Modeling of Radiation Regime in Discontinuous Vegetation Canopies. Remote Sens. Environ. 2000, 74, 125–144. [Google Scholar] [CrossRef]
- Shabanov, N.V.; Huang, D.; Knjazikhin, Y.; Dickinson, R.E.; Myneni, R.B. Stochastic radiative transfer model for mixture of discontinuous vegetation canopies. J. Quant. Spectrosc. Radiat. Transf. 2007, 107, 236–262. [Google Scholar] [CrossRef][Green Version]
- Huang, D.; Knyazikhin, Y.; Wang, W.; Deering, D.W.; Stenberg, P.; Shabanov, N.; Tan, B.; Myneni, R.B. Stochastic transport theory for investigating the three-dimensional canopy structure from space measurements. Remote Sens. Environ. 2008, 112, 35–50. [Google Scholar] [CrossRef]
- Kanniah, K.D.; Beringer, J.; Hutley, L.B.; Tapper, N.J.; Zhu, X. Evaluation of Collections 4 and 5 of the MODIS Gross Primary Productivity product and algorithm improvement at a tropical savanna site in northern Australia. Remote Sens. Environ. 2009, 113, 1808–1822. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Martonchik, J.V.; Myneni, R.B.; Diner, D.J.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Maeirsperger, T.K.; Gower, S.T.; Kirschbaum, A.A.; Running, S.W.; Zhao, M.S.; Wofsy, S.C.; Dunn, A.L.; et al. Site-level evaluation of satellite-based global terrestrial gross primary production and net primary production monitoring. Glob. Change Biol. 2005, 11, 666–684. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Zhao, M.S.; Kurc, S.A.; Dunn, A.L.; Wofsy, S.C.; Small, E.E.; Running, S.W. Assessing interannual variation in MODIS-based estimates of gross primary production. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1899–1907. [Google Scholar] [CrossRef]
- Chen, B.Q.; Li, X.P.; Xiao, X.M.; Zhao, B.; Dong, J.W.; Kou, W.L.; Qin, Y.W.; Yang, C.; Wu, Z.X.; Sun, R.; et al. Mapping tropical forests and deciduous rubber plantations in Hainan Island, China by integrating PALSAR 25-m and multi-temporal Landsat images. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 117–130. [Google Scholar] [CrossRef]
- Gao, S.P.; Liu, X.L.; Bo, Y.C.; Shi, Z.T.; Zhou, H.M. Rubber identification based on blended high spatio-temporal resolution optical remote sensing data: A case study in Xishuangbanna. Remote Sens. 2019, 11, 496. [Google Scholar] [CrossRef]
- Jiao, J.N.; Shi, J.; Tian, Q.J.; Gao, L.; Xu, N.X. Research on multispectral-image-based NDVI shadow-effect-eliminating model. Natl. Remote Sens. Bull. 2020, 24, 53–66. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Glassy, J.; Privette, J.L.; Tian, Y.; Lotsch, A.; Zhang, Y.; Wang, Y.; Morisette, J.T.; Votava, P.; Myneni, R.B.; et al. MODIS Leaf Area Index (LAI) and Fraction of Photosynthetically Active Radiation Absorbed by Vegetation (FPAR) Product (MOD15) Algorithm Theoretical Basis Document. 1999. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod15.pdf (accessed on 29 January 2025).
- Huemmrich, K.F.; Goward, S.N. Vegetation canopy PAR absorptance and NDVI: An assessment for ten tree species with the SAIL model. Remote Sens. Environ. 1997, 61, 254–269. [Google Scholar] [CrossRef]
- Huemmrich, K.F. The GeoSail model: A simple addition to the SAIL model to describe discontinuous canopy reflectance. Remote Sens. Environ. 2001, 75, 423–431. [Google Scholar] [CrossRef]
- Ehleringer, J. Leaf absorptances of mohave and sonoran desert plants. Oecologia 1981, 49, 366–370. [Google Scholar] [CrossRef]
- Krall, J.P.; Edwards, G.E. Relationship between photosystem-II activity and CO2 fixation in leaves. Physiol. Plant. 1992, 86, 180–187. [Google Scholar] [CrossRef]
- Björkman, O.; Demmig, B. Photon yield of O2 evolution and chlorophyll fluorescence characteristics at 77 K among vascular plants of diverse origins. Planta 1987, 170, 489–504. [Google Scholar] [CrossRef]
- He, L.; He, X.P.; Bian, J.M.; Zhu, C.L.; Fu, J.R.; Wu, Y.; He, H.H. Application of mechanistic model of light-response of photosynthetic electron flow on photosynthetic characteristics in super late rice. J. South. Agric. 2019, 50, 1937–1944. [Google Scholar]
- Ye, Z.P.; Hu, W.H.; Yan, X.H.; Fan, D.Y.; Yin, J.H.; Duan, S.H.; Yan, X.H.; He, L.; Zhang, S.S. A mechanistic model of light-response of photosynthetic electron flow and its application. Chin. J. Plant Ecol. 2014, 38, 1241–1249. [Google Scholar] [CrossRef]
- Zheng, Y.Y.; Zhao, W.Q.; Chen, A.P.; Chen, Y.; Chen, J.N.; Zhu, Z.C. Vegetation canopy structure mediates the response of gross primary production to environmental drivers across multiple temporal scales. Sci. Total Environ. 2024, 917, 170439. [Google Scholar] [CrossRef]



| Site Name | Latitude | Longitude | Biome Types | Year | References |
|---|---|---|---|---|---|
| NOBS | 55.885 | 98.477 | boreal forest | 2002 | [44] |
| KONZ | 39.089 | −96.571 | tallgrass prairie | 2000 | [43] |
| AGRO | 40.007 | 88.292 | cropland (corn and soybean) | 2000 | [45] |
| HARV | 42.529 | −72.173 | temperate mixed forest | 2002 | [46] |
| TUND | 71.272 | −156.613 | arctic tundra | 2002 | [43] |
| SEVI | 34.351 | −106.690 | desert | 2002 | [47] |
| TAPA | 2.870 | −54.949 | tropical broadleaf evergreen forest | 2004 | [43] |
| METL | 44.451 | 121.573 | temperate needleleaf forest | 2002 | [48] |
| CHEQ | 45.945 | −90.272 | temperate mixed forest | 2000 | [43] |
| Dahra | 15.000 | −15.443 | grass savanna | 2001; 2002 | [20] |
| Tessekre North | 15.885 | −15.081 | grass savanna | 2002 | [20] |
| Tessekre South | 15.796 | −15.083 | grass savanna | 2002 | [20] |
| Vegetation Type | Site Name | Model | R2 | RMSE | Bias | RPIQ | MAPE (%) | MPE (%) |
|---|---|---|---|---|---|---|---|---|
| grass savanna | Dahra + Tessekre | FAPARMOD | 0.90 | 0.20 | 0.18 | 1.92 | 333.75 | 333.75 |
| FAPARLAI | 0.91 | 0.13 | 0.11 | 2.88 | 195.71 | 195.38 | ||
| FAPARFVC | 0.94 | 0.10 | 0.08 | 3.85 | 142.72 | 141.36 | ||
| arctic tundra | TUND | FAPARMOD | 0.23 | 0.30 | 0.28 | 0.68 | 168.30 | 168.30 |
| FAPARLAI | 0.02 | 0.19 | 0.14 | 1.07 | 109.16 | 107.56 | ||
| FAPARFVC | 0.61 | 0.10 | 0.05 | 2.10 | 50.52 | 45.24 | ||
| cropland (corn and soybean) | AGRO | FAPARMOD | 0.87 | 0.25 | 0.20 | 1.86 | 350.12 | 350.12 |
| FAPARLAI | 0.89 | 0.16 | 0.04 | 3.01 | 217.02 | 203.62 | ||
| FAPARFVC | 0.93 | 0.13 | −0.01 | 3.64 | 154.70 | 134.37 | ||
| temperate mixed forest | CHEQ | FAPARMOD | 0.75 | 0.22 | 0.19 | 1.97 | 43.99 | 41.30 |
| FAPARLAI | 0.83 | 0.21 | 0.19 | 2.08 | 39.97 | 36.32 | ||
| FAPARFVC | 0.84 | 0.10 | 0.03 | 4.55 | 19.19 | 4.36 | ||
| HARV | FAPARMOD | 0.76 | 0.31 | 0.23 | 1.96 | 73.19 | 72.91 | |
| FAPARLAI | 0.79 | 0.27 | 0.21 | 2.22 | 65.05 | 64.50 | ||
| FAPARFVC | 0.78 | 0.16 | −0.06 | 3.90 | 30.16 | −10.31 | ||
| tallgrass prairie | KONZ | FAPARMOD | 0.78 | 0.16 | 0.09 | 2.12 | 52.61 | 50.64 |
| FAPARLAI | 0.83 | 0.15 | −0.07 | 2.27 | 38.69 | 9.07 | ||
| FAPARFVC | 0.79 | 0.19 | −0.14 | 1.80 | 37.43 | −9.67 | ||
| boreal forest | NOBS | FAPARMOD | 0.71 | 0.10 | −0.01 | 0.20 | 8.53 | −1.92 |
| FAPARLAI | 0.36 | 0.10 | −0.04 | 0.20 | 8.88 | −4.65 | ||
| FAPARFVC | 0.47 | 0.21 | −0.15 | 0.10 | 19.31 | −19.10 | ||
| desert | SEVI | FAPARMOD | 0.48 | 0.16 | 0.16 | 0.21 | 111.18 | 111.18 |
| FAPARLAI | 0.42 | 0.05 | 0.04 | 0.66 | 34.01 | 31.16 | ||
| FAPARFVC | 0.59 | 0.04 | 0.03 | 0.84 | 24.16 | 19.66 | ||
| tropical broadleaf evergreen forest | TAPA | FAPARMOD | - | 0.07 | −0.07 | - | 6.91 | −6.91 |
| FAPARLAI | - | 0.02 | −0.02 | - | 1.86 | −1.85 | ||
| FAPARFVC | - | 0.32 | −0.28 | - | 29.48 | −29.48 | ||
| temperate needleleaf forest | METL | FAPARMOD | - | 0.23 | 0.15 | - | 37.75 | 25.10 |
| FAPARLAI | - | 0.18 | 0.15 | - | 27.28 | 25.43 | ||
| FAPARFVC | - | 0.18 | −0.09 | - | 22.17 | −14.99 |
| Model | Vegetation Growth Stage | RMSE | Bias | MAPE (%) | MPE (%) |
|---|---|---|---|---|---|
| FAPARMOD | off-peak growth period | 0.274 | 0.201 | 171.9 | 165.8 |
| peak growth period | 0.142 | 0.065 | 34.3 | 29.7 | |
| FAPARLAI | off-peak growth period | 0.216 | 0.149 | 110.6 | 106.2 |
| peak growth period | 0.117 | 0.032 | 22.2 | 15.3 | |
| FAPARFVC | off-peak growth period | 0.173 | −0.038 | 76.1 | 42.2 |
| peak growth period | 0.197 | −0.108 | 22.2 | −7.0 |
| FAPAR | FVC Range | RMSE | Bias | MAPE (%) | MPE (%) |
|---|---|---|---|---|---|
| FAPARMOD | 70–90% | 0.124 | 0.068 | 19.4 | 16.8 |
| 30–70% | 0.247 | 0.162 | 131.5 | 125.2 | |
| 0–30% | 0.314 | 0.221 | 255.8 | 244.9 | |
| FAPARLAI | 70–90% | 0.113 | 0.036 | 14.0 | 7.6 |
| 30–70% | 0.189 | 0.112 | 83.4 | 78.4 | |
| 0–30% | 0.248 | 0.177 | 164.4 | 158.2 | |
| FAPARFVC | 70–90% | 0.115 | −0.056 | 14.0 | −4.1 |
| 30–70% | 0.223 | −0.077 | 65.4 | 33.1 | |
| 0–30% | 0.221 | −0.129 | 97.9 | 25.4 |
| FAPARMOD | Biome Types | Site Name | N | Average FVC | Standard Deviation |
|---|---|---|---|---|---|
| Overestimation | arctic tundra | TUND | 15 | 0.523 | 0.163 |
| temperate needleleaf forest | METL | 46 | 0.557 | 0.186 | |
| temperate mixed forest | HARV | 46 | 0.559 | 0.320 | |
| grass savanna | Dahra + Tessekre | 32 | 0.564 | 0.304 | |
| desert | SEVI | 16 | 0.639 | 0.285 | |
| temperate mixed forest | CHEQ | 28 | 0.657 | 0.221 | |
| tallgrass prairie | KONZ | 24 | 0.665 | 0.210 | |
| cropland (corn and soybean) | AGRO | 17 | 0.696 | 0.260 | |
| Underestimation | tropical broadleaf evergreen forest | TAPA | 46 | 0.689 | 0.164 |
| boreal forest | NOBS | 18 | 0.757 | 0.193 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Li, B.; Yuan, Y.; Liu, W.; Zhu, J.; Qi, J.; Liu, H.; Ma, G.; Jiang, Y.; Li, Y.; et al. Improvement of FAPAR Estimation Under the Presence of Non-Green Vegetation Considering Fractional Vegetation Coverage. Remote Sens. 2025, 17, 603. https://doi.org/10.3390/rs17040603
Li R, Li B, Yuan Y, Liu W, Zhu J, Qi J, Liu H, Ma G, Jiang Y, Li Y, et al. Improvement of FAPAR Estimation Under the Presence of Non-Green Vegetation Considering Fractional Vegetation Coverage. Remote Sensing. 2025; 17(4):603. https://doi.org/10.3390/rs17040603
Chicago/Turabian StyleLi, Rui, Baolin Li, Yecheng Yuan, Wei Liu, Jie Zhu, Jiali Qi, Haijiang Liu, Guangwen Ma, Yuhao Jiang, Ying Li, and et al. 2025. "Improvement of FAPAR Estimation Under the Presence of Non-Green Vegetation Considering Fractional Vegetation Coverage" Remote Sensing 17, no. 4: 603. https://doi.org/10.3390/rs17040603
APA StyleLi, R., Li, B., Yuan, Y., Liu, W., Zhu, J., Qi, J., Liu, H., Ma, G., Jiang, Y., Li, Y., & Tan, Q. (2025). Improvement of FAPAR Estimation Under the Presence of Non-Green Vegetation Considering Fractional Vegetation Coverage. Remote Sensing, 17(4), 603. https://doi.org/10.3390/rs17040603






