From Graph Synchronization to Policy Learning: Angle-Synchronized Graph and Bilevel Policy Network for Remote Sensing Object Detection

Highlights

What are the main findings?

• We proposed the ASBPNet framework that significantly improves oriented object detection through geometric alignment and policy adaptation.
• We achieved breakthrough performance: 68.10% mAP on DIOR-R, 98.20% mAP (12) on HRSC2016, and 79.60% mAP on DOTA-v1.0.

What is the implication of the main finding?

• The framework improves geometric stability and localization accuracy while remaining lightweight, achieving a balanced, efficient solution for high-density small object detection.

Abstract

Detection of rotating targets in complex remote sensing scenarios often suffers from angular inconsistencies and boundary jitter, especially for small-to-medium objects with rapid pose changes or indistinct boundaries in dense environments. To address this, we propose ASBPNet, a unified framework coupling geometric alignment with policy adaptation. It features the following: (1) Angle-Synchronized Graph (ASG), which injects angle–alignment relationships and residual-based boundary refinement to improve rotational consistency and reduce boundary errors for small objects; (2) Bilevel Policy Optimization (BPO), which unifies control over rotation enhancement, sample allocation, block scanning, and rotational NMS for cross-stage policy coordination and improved recall. Together, ASG and BPO form a tightly coupled pipeline in which geometric alignment directly reinforces policy optimization, yielding mutually enhanced rotation robustness, boundary stability, and detection recall across densely distributed remote sensing scenes. We conducted systematic evaluations on datasets including DIOR-R, HRSC2016, and DOTAv1.0: compared to baselines, overall accuracy achieved significant improvement on DIOR-R, with performance reaching 98.2% on HRSC2016. Simultaneously, enhanced robustness and boundary stability were demonstrated in complex backgrounds and dense small-object scenarios, validating the synergistic value of geometric alignment and policy adaptation.

1. Introduction

Remote sensing object detection refers to the automatic identification, localization, and extraction of targets of interest using observation images from satellites, drones, airborne platforms, or ground sensors [1,2,3]. Such images usually present a large-scale span, complex backgrounds, and diverse target morphology [4]. There are significant differences in spatial distribution and texture features between targets, and the background is often messy and dynamic, making it more difficult to distinguish the foreground from the background [5,6]. The targets themselves are also rich in morphological variations, from geometrically regular ships to complex industrial facilities, all of which put forward higher requirements on the feature characterization and generalization ability of the detection model [7,8]. Consequently, remote sensing object detection demands that models not only capture high-resolution details but also achieve robust contextual modeling and discrimination in complex environments [9]. In order to cope with these challenges, existing remote sensing object detection methods have played an important role in remote sensing interpretation and intelligent monitoring by means of feature pyramids [10,11,12], attention mechanisms [13,14], and multi-task learning [15,16] to continuously improve accuracy and robustness. However, the current methods are still prone to the problems of angular inconsistency and boundary jitter in directional target detection, and the strategies of rotational enhancement, sample allocation, block scanning, and Non-Maximum Suppression (NMS) involved in the training and inference process are often fragmented and optimized, which leads to the difficulty of balancing accuracy and delay. Thus, current remote sensing object detection models face the following limitations:

• The dual constraints of limited training efficiency and lack of small-target recall. Although multi-strategy combinations can improve the performance of the model in different scenarios, the traditional detection process often splits the execution of enhancement, assignment, cropping, and post-processing strategies, and the lack of global synergy and dynamic adaptation mechanisms between strategies leads to slow convergence of training and weak generalization ability of strategy migration. At the same time, the existing strategies are often insufficient to model the distribution and scale sensitivity of small targets, which makes it difficult to effectively improve the edge-detection capability and small-target recall rate, and ultimately affects the overall robustness and consistency of precision.
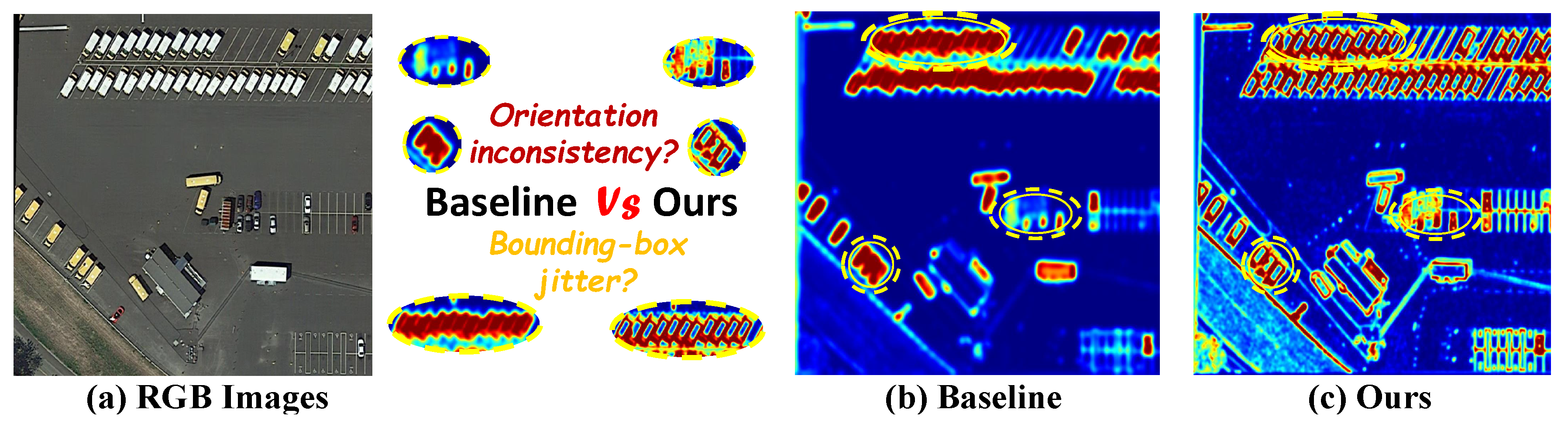
• Boundary fitting and angular consistency bottlenecks for rotating small targets. Small- and medium-scale targets in remote sensing images often show the characteristics of tiny size, changing attitude, and fuzzy boundary, which makes the rotation detection task face double challenges in returning to the frame boundary and maintaining the angular stability. Traditional methods often ignore the rotational correlation between candidate frames, and it is difficult to achieve the synergistic optimization of angular alignment and boundary correction, resulting in target edge drift and rotational angle jitter, which is especially obvious in multi-target dense scenarios.

In order to improve the accuracy of rotation detection and boundary fitting for small targets in remote sensing images, existing methods commonly use strategies such as rotating frame regression [17,18], angle classification [19,20], and direction-sensitive feature extraction [21] for modeling [22], while boundary refinement is performed through post-processing modules. These methods mitigate the localization error caused by target rotation to a certain extent, but due to the lack of modeling constraints on spatial geometric isotropy, it is often difficult to maintain stable consistency between the angle prediction and the edge contour. In addition, the boundary optimization process mostly relies on a fixed structure or heuristic design, with limited generalization capability, and is prone to problems such as jitter and trailing in high-density or complex backgrounds, leading to unstable performance in small-target detection.

To overcome these issues, we propose ASBPNet, a unified framework that concurrently addresses geometric instability and strategic fragmentation through two synergistic components: the Angle-Synchronized Graph (ASG) and the Bilevel Policy Optimization (BPO). The ASG establishes explicit geometric constraints among candidate boxes via graph message passing with SE(2)-equivariance, directly reducing angular jitter and improving boundary fitting. The BPO introduces a key innovation through its structured bilevel architecture, which formally separates strategy learning from execution. In this design, an upper-level reinforcement learning agent learns to coordinate all strategies, while a lower-level detector executes under these optimized strategies. This separation can uniformly optimize various non-differentiable strategies, including expansion, label assignment, and NMS, so as to jointly adapt under delay constraints.

A critical aspect of this design is the closed-loop interaction between these components: the stable geometric features from ASG provide a reliable basis for BPO’s policy evaluation, while the strategies optimized by BPO (like sample assignment) directly govern the learning process of ASG. This ensures that gains in one component consistently benefit the other, leading to aligned and robust performance across both training and inference.

The innovative contributions of this study are summarized as follows:

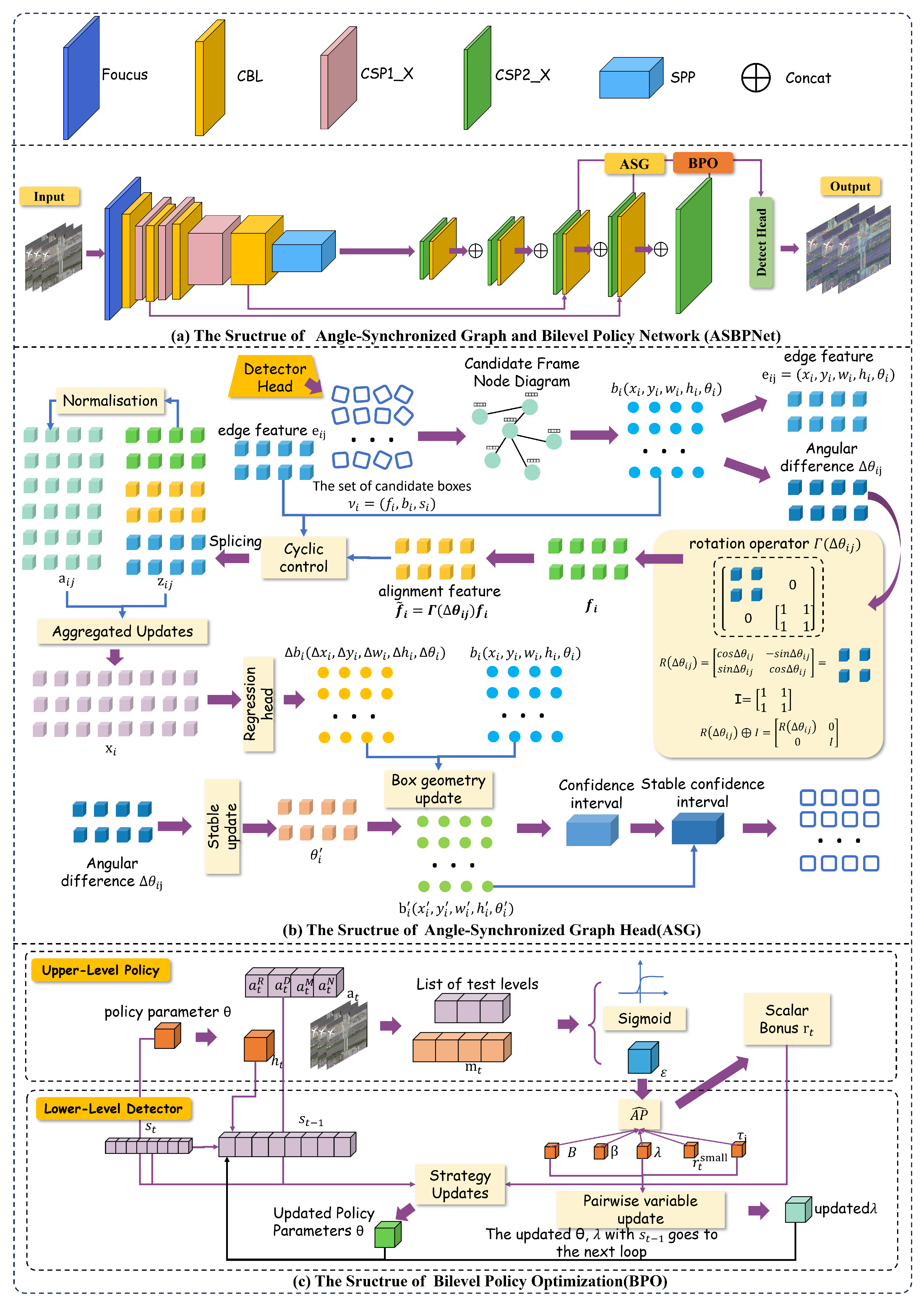
• We propose a deeply integrated approach that unifies graph-based geometric modeling and reinforcement learning-based policy optimization. This is achieved by synergizing an Angle-Synchronized Graph Head (ASG), which solves angular inconsistency and boundary jitter through equivariant message passing, and a Bilevel Policy Optimization (BPO) module, which overcomes the fragmentation of non-differentiable strategies in training and inference.
• To solve the problems of boundary instability and poor rotational robustness in the detection of remotely sensed targets at arbitrary angles, we propose the Angle-Synchronized Graph Head (ASG). Inspired by geometric equivariance and residual learning, this module enhances the angular consistency by introducing synapse-level equivariance constraints, and achieves the boundary refinement of candidate frames with the help of the micro-residual gating mechanism. It significantly improves the angle prediction accuracy and boundary alignment effect for small targets and dense structures.
• To alleviate the problem of training–inference inconsistency and delayed feedback during multi-strategy decision-making, we propose the Bilevel Policy Optimization (BPO). This module achieves consistent modeling of training and inference policies through a two-layer optimization framework combining microagentable metrics with a delayed pairing mechanism to improve the generalization and model robustness of detection policies.
• We conducted systematic evaluations on DIOR-R, HRSC2016, and DOTAv1.0. On the DIOR-R dataset, ASBPNet improves the mAP of the baseline from 63.40% to 68.10% with only a slight increase in parameters and computation; on the HRSC2016 dataset, it achieves 98.2% mAP (12), which is a new performance for similar models. Meanwhile, the heatmap visualization demonstrates that this method has stronger target-focusing and interference-suppression ability, which significantly reduces the misdetection rate in complex backgrounds and is especially suitable for high-density and small-target scenarios in the field of remote sensing.

2. Related Work

2.1. Graph Neural Network in Remote Sensing Object Detection

With the continuous development of graph representation learning, graph neural networks (GNN) have been explored in remote sensing object detection, with the advantage of being able to model complex relationships between targets and between targets and scenes [23]. By explicitly capturing topologies such as road networks, building layouts, or target co-occurrences, GNN methods effectively improve the detection performance of small, dense, and occluded targets, and make up for the shortcomings of traditional convolutional networks or Transformers in spatial relationship modeling [24,25]. According to different research focuses, GNN methods in remote sensing object detection can be broadly classified into three categories: relational inference [26,27], context-aware [28], and hierarchical graph modeling [29]; these show unique advantages in terms of accuracy and robustness, but still face the challenges of relying on the a priori for the composition of the graph, over-smoothing of the features, insufficient adaptation to multi-scale, and limited integration with the detection framework, which constrain the further development of GNNs in remote sensing object detection. The further development of GNN in remote sensing object detection is constrained.

Among them, relational inference-based models have been widely used in remote sensing image processing in recent years. These models mainly rely on the structure of graph neural networks to capture spatial and semantic relationships by constructing topological maps between targets, which is especially suitable for small-target detection tasks in complex scenes. The RelaDet [30] and GCN-based Detector [31] are the most representative models among them. RelaDet can model the contextual dependency between targets through relational embedding, which is especially suitable for the detection of densely distributed aircraft and ships; while GCN-based Detector introduces the mechanism of adjacency matrix propagation, which greatly enhances the structural sensing ability between targets, and is especially suitable for the scenes with occlusion or background interference. Although these models can effectively improve the detection accuracy and context-modeling capability, they still have limitations in applications. Relational embedding and neighbor propagation mechanisms usually rely on predefined topological graphs, lack adaptivity to dynamic scenes, and are prone to introduce noise when the distribution of targets is complex or the structure is ambiguous; meanwhile, graph convolution may lead to over-smoothing of features in multi-layer propagation, making it difficult to distinguish between neighboring but semantically significantly different targets, which can lead to confusing or redundant detection. In addition, relational modeling puts more emphasis on global consistency, with insufficient discriminative support for small-scale targets, limiting its further use in high-resolution remote sensing scenarios.

Complementary to this direction, context-aware models focus on utilising global and local contextual information in remote sensing images to aid target detection. Classical context-aware models, such as Contextual Graph Detector [26], extract image features through graph convolutional propagation and mask-attention mechanisms, and are able to effectively capture the contextual dependencies between multi-scale targets and explicitly model them. Hierarchical GNN [32], by introducing a hierarchical context-modeling mechanism, can solve the common problems of background interference and target obfuscation in remote sensing images, and is especially suitable for dealing with scenes with dense targets and large-scale differences. The advantage of these context-aware models is that they can significantly enhance the robustness of detection and adaptability to complex backgrounds, especially in large-scale remote sensing images. However, such approaches still have limitations in the modeling process. The graph convolution and attention mechanism mostly relies on neighborhood or super-pixel aggregation, which can capture the context but lacks the constraint of rotational invariance, and is prone to cause angular inconsistency and boundary jitter in directional targets; at the same time, context propagation emphasizes global consistency but may weaken the discriminative features of individual targets, leading to over-smoothing and redundancy detection; the hierarchical graph structure is also prone to introducing noise when aggregating across scales, making targets with large-scale differences underperform in boundary refinement.

In remote sensing object detection, hierarchical graph modeling approaches are gradually becoming an important direction by fusing local and global features by constructing graph structures at different levels. Representative models include PolyRoof [33] and HNS-GNN [34]. PolyRoof adopts the Attention U-Net backbone and vertex-level graph modeling in the roof polygonization task, which upgrades the pixel features into a vector structure, but relies on fixed adjacency connections in vertex relationship reasoning, which is prone to introducing misconnections in complex geometrical patterns, leading to discontinuities in local boundaries. HNS-GNN introduces structure-aware graph reasoning in road detection. GNN introduces a structure-aware graph inference module in road detection with simultaneous multi-task learning of regions and boundaries, but its hierarchical aggregation process overemphasizes boundary consistency, which may weaken the discriminative nature of fine-grained textures and easily cause pseudo-edge or false detection in scenes with strong background noise. Overall, this type of method effectively enhances multi-scale context perception capability through hierarchical graph structure, but there are still problems of noise propagation and insufficient feature refinement in the graph construction and hierarchical aggregation process, which limits its performance in large-scale complex remote sensing scenarios.

Compared with the existing methods, the ASBPNet framework proposed in this paper is more targeted at the graph neural network level. By constructing the graph structure between candidate frames through ASG and introducing SE(2) equivariant constraints in the message-passing process, we are able to maintain the feature consistency under rotation and translation, so as to realize the angular alignment and boundary refinement of candidate frames, and effectively alleviate the problems of angular inconsistency and boundary jitter that are prone to occur in previous methods for directional targeting. On this basis, we further design a residual boundary optimization mechanism, so that the nodes can predict the boundary residuals based on the neighborhood information, which significantly improves the geometric stability and positioning accuracy of the oriented frames. Meanwhile, this paper combines BPO to incorporate multiple policy decisions in training and inference into a unified optimization framework, which achieves a dynamic balance between detection accuracy and efficiency under the delay constraint. Overall, this design of combining the geometric modeling capability of graph neural networks and the adaptive optimization of reinforcement learning enables this paper’s method to achieve better accuracy, robustness, and efficiency than existing methods in remote sensing object detection.

2.2. Intensive Learning in Remote Sensing Object Detection

As the scale and complexity of remote sensing imagery increase, reinforcement learning (RL) has been progressively introduced into remote sensing object detection tasks to address challenges posed by small-scale targets, dense distributions, and multi-directional rotations [35,36,37]. RL models adaptively optimize the detection process through a state-action-reward mechanism, demonstrating advantages in candidate region selection, scale adjustment, rotation angle prediction, and redundancy suppression. Depending on methodological focus and application scenarios, RL approaches in remote sensing object detection can be categorized into region search and bounding box localization [38,39], rotation and scale modeling [40], and policy and fusion optimization [41], each exhibiting distinct capabilities. However, they also face challenges such as complex state spaces, reward function design sensitivity, and insufficient deep coupling with detectors.

Among them, reinforcement learning-based region search and candidate box localization have been widely used in remote sensing image processing in recent years. These methods model the detection problem of large-size remote sensing images as a sequential decision-making process of states, actions, and rewards, which enables the agent to gradually focus on potential target regions in a huge candidate space, thus significantly reducing the dependence on the whole high-resolution image. DeepRL-Detector [42] and RL-CNN [43] are the most representative models among them. The former learns whether to sample candidate regions at high resolution through a dual-layer network of coarse-grained and fine-grained strategies, which reduces redundant computation while maintaining detection accuracy, but is prone to missing fine-grained targets at the boundary due to the reliance on fixed grids for region delineation. The latter uses a reinforcement learning agent to gradually locate aircraft targets and verifies the detection results with a CNN, breaking through the limitation that traditional methods can only detect a fixed number of targets, but its action space is designed to gradually reduce the search area, which may trigger excessive search and localization conflicts in dense multi-target scenarios, thus affecting efficiency and accuracy. These methods have significant advantages in improving the computational efficiency and positioning accuracy of remote sensing object detection, but the inherent limitations of the candidate region delineation and action design make them still face certain challenges in scenes with complex target distribution or dense multi-targets.

Complementary to this direction, rotation and scale modeling approaches use reinforcement learning to dynamically adjust the angle and scale of candidate frames in remote sensing object detection to cope with multi-directional and multi-scale targets. Representative models such as FFPN-RL [44] achieve ship orientation prediction through feature pyramid fusion and iterative rotational actions, but the discrete action design is prone to slow convergence or error accumulation. These methods have advantages in rotational modeling and scale adaptation, but the limitations of action design and feature structure still affect their performance in complex scenes.

The strategy and fusion optimization approach emphasizes modeling the target detection process as a strategy selection and fusion learning problem, and realizing multi-link adaptive regulation by means of reinforcement learning. Representative models include Reinforcement Learning of Object Detection Strategies [45] and the HRL Saliency Model [46], which learn fusion strategies from different perspectives and information sources through Q-learning, combine PCA and RBF networks for appearance modeling, and then use Bayesian methods to improve detection confidence. The former uses Q-learning to learn the fusion strategy of different views and information sources, combines PCA and RBF network for appearance modeling, and then uses Bayesian method to improve the detection confidence, which significantly improves the detection efficiency in specific tasks, but due to the dependence of strategy learning on a predefined appearance-modeling module, it is easy to suffer from insufficient generalization in complex and diverse remote sensing images. The latter uses hierarchical reinforcement learning to generate saliency maps, fuses the bottom-layer color features with the top-layer line density features step by step, and judges the target saliency with the help of the thematic model to adaptively control the learning depth, which is able to effectively inhibit the background interference in airport detection. However, the inverse transfer of saliency maps between the layers is prone to introducing erroneous feedback when the features are weakened or the interference is enhanced, which leads to the insufficiently fine boundary delineation. Overall, such methods enhance the adaptability and robustness of detection through strategy optimization and fusion learning, but there are still structural limitations in appearance-modeling dependency and hierarchical feedback mechanisms.

In contrast, our ASBPNet framework introduces a structured bilevel optimization architecture. An upper-level policy learns to coordinate all key strategies including rotation augmentation, sample assignment, multi-tile scanning, and rotated NMS within a unified space. A lower-level detector then executes the actual detection task under these optimized strategies. This clear separation enables direct optimization of accuracy–efficiency trade-offs under latency constraints through dual variable updates, while differentiable performance proxies ensure stable policy learning. By addressing fundamental limitations in existing reinforcement learning methods, particularly in state space complexity and reward sensitivity, our bilevel design achieves significant improvements in small-target recall, angular consistency, and inference stability.

The analyses in Section 2.1 and Section 2.2 reveal complementary yet unaddressed challenges in existing approaches. While GNN-based methods improve relational modeling, they typically fail to enforce rotational equivariance, leading to persistent angular inconsistency in oriented object detection. Concurrently, RL-based methods provide adaptive policy optimization but remain insufficiently coupled with the geometric refinement process, resulting in fragmented strategy coordination. To address these interconnected limitations, we propose ASBPNet—a unified framework that systematically integrates equivariant graph modeling with Bilevel Policy Optimization. The methodology detailed next builds upon this coordinated design to simultaneously advance geometric stability and strategic coherence.

Relevant work summaries are presented in

Table 1. Summary of related methods.

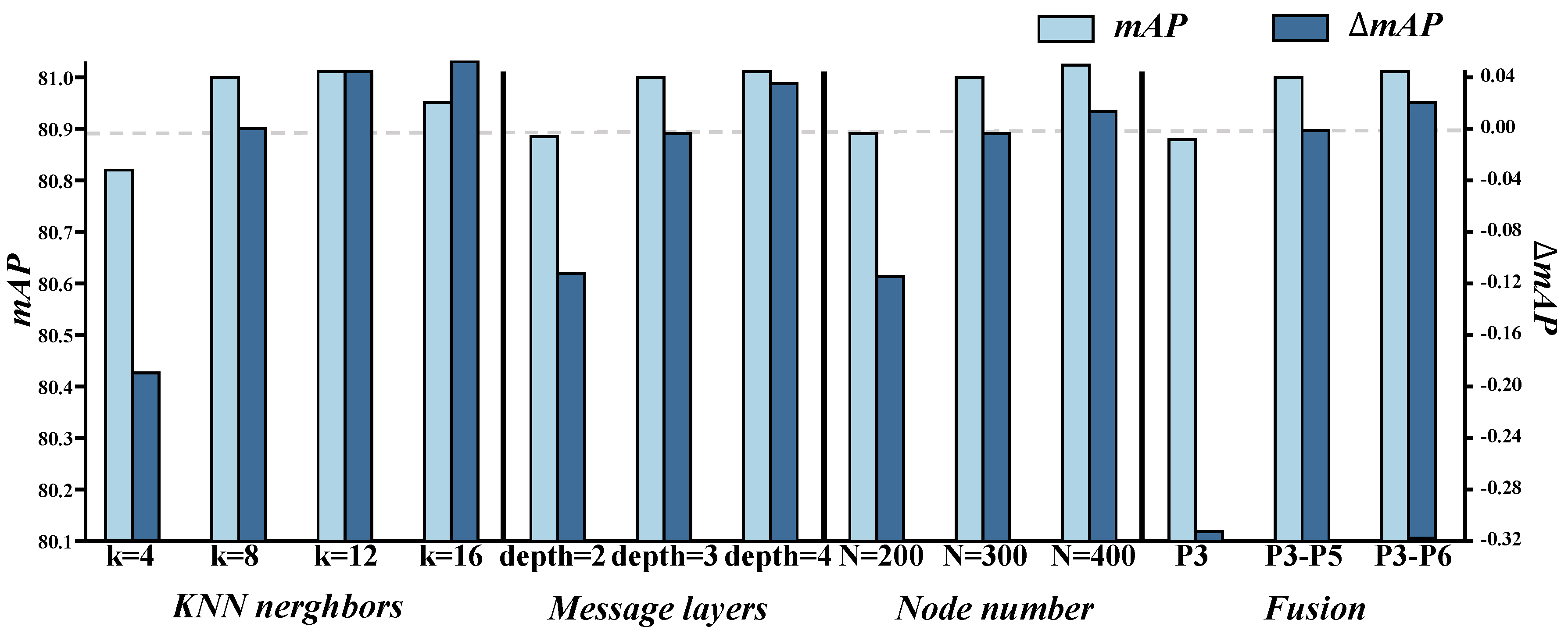
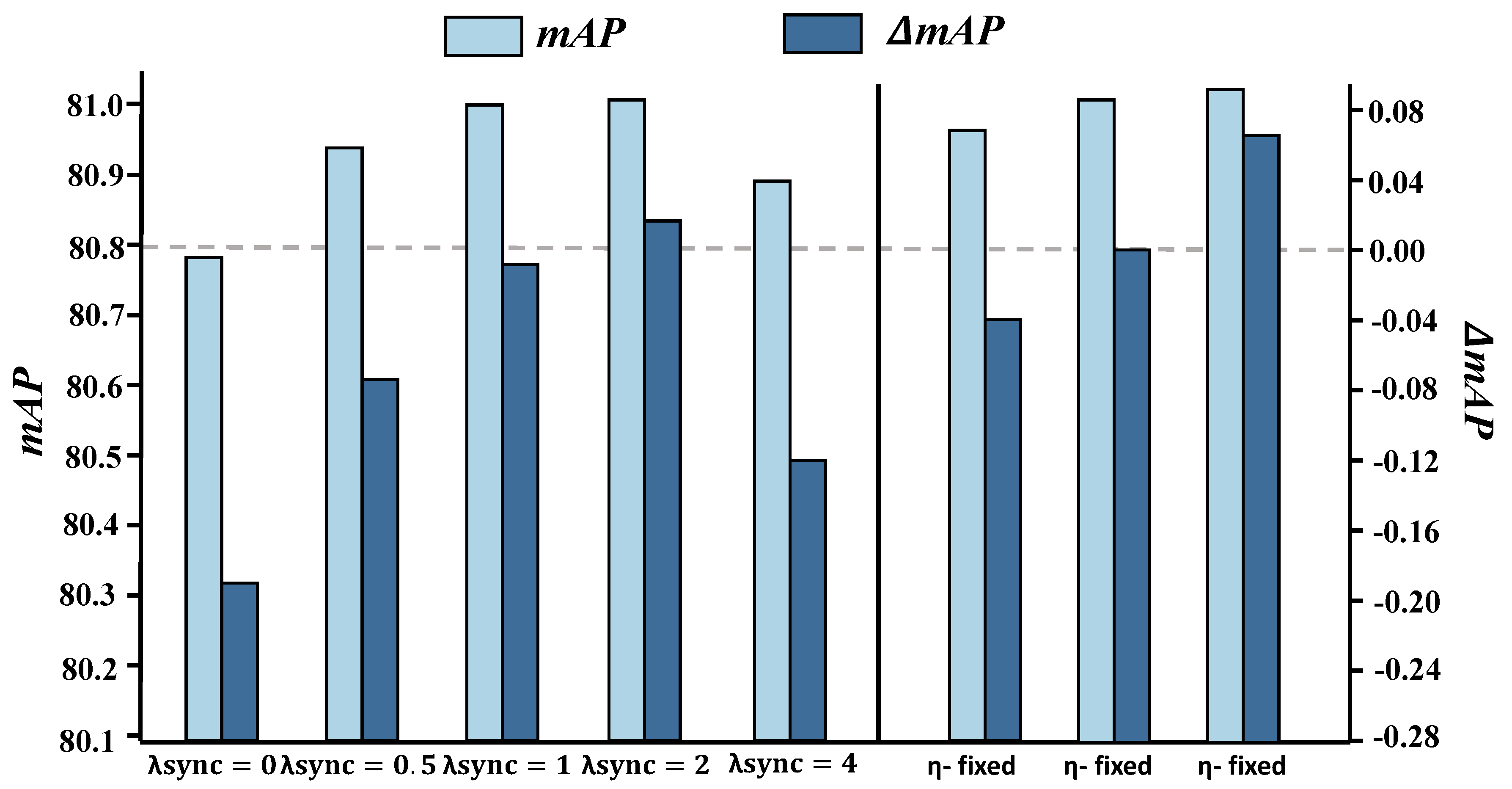
Method Category	Core Idea	Representative Models	Advantages	Limitations
GNN Methods
Relational Inference	Model contextual dependencies by constructing topological graphs between objects.	RelaDet; GCN-based Detector	Strong for dense and occluded objects; enhanced contextual reasoning.	Requires predefined graph structures; potential over-smoothing.
Context-Aware Modeling	Capture multi-scale contextual cues using graph convolution or attention.	Contextual Graph Detector; Hierarchical GNN	Robust under complex backgrounds; suitable for large-scale RS scenes.	Lacks rotational invariance; may introduce angular inconsistency.
Hierarchical Graph Fusion	Fuse local and global information using multi-level graph structures.	PolyRoof; HNS-GNN	Improved multi-scale representation.	Cross-level noise propagation; insufficient refinement.
RL Methods
Region Search	Model detection as a sequential decision process progressively focusing on candidate regions.	DeepRL-Detector; RLCNN	Efficient localization; reduced HR image computation.	Fixed search grids; action conflicts in dense scenes.
Rotation and Scale Adjustment	Learn actions that dynamically adjust bounding box orientation and scale.	FFPN-RL	Effective for multi-oriented, multi-scale objects.	Discrete actions cause error accumulation; slow convergence.
Policy Fusion and Optimization	Fuse multiple decision strategies to enhance adaptability and robustness.	Strategy Learning; HRL Saliency Model	Strong adaptability across scenes.	Depends on predefined modules; hierarchical feedback errors.

.

3. Methodology

ASBPNet is a unified framework where the Angle-Synchronized Graph (ASG) and Bilevel Policy Optimization (BPO) modules interact in a tightly coupled manner. Figure 1 illustrates the overall architecture and data flow. The pipeline commences with the backbone and neck networks extracting multi-scale features from the input image, subsequently generating an initial set of oriented candidate boxes. These candidate boxes and their associated features form the primary input to the ASG module.The code will be released at https://github.com/westneverlost/Angle-Synchronized-Graph-and-Bilevel-Policy-Network (accessed on 30 August 2025).

The ASG module then constructs a graph over these candidates and performs angle-synchronized message passing. Its output is a refined set of candidate boxes with significantly improved angular consistency and boundary precision. This geometrically stable set of detections is crucial for the subsequent stages.

Concurrently, the BPO module governs the strategic flow throughout the pipeline. During training, BPO observes performance proxies (e.g., IoU, recall) from the detector’s current state and outputs a set of optimized strategy parameters. These parameters control the data augmentation and sample assignment for the entire model, thereby influencing the feature learning in the backbone and the candidate boxes presented to the ASG. During inference, BPO’s learned policies directly configure the multi-tile scanning and rotated NMS procedures, which take the refined boxes from ASG as their input. The final output is produced by applying these optimized post-processing strategies to the stable geometries generated by ASG.

3.1. Baseline: YOLOv5-OBB

YOLOv5 with Oriented Bounding Box is an important detection framework in the field of remote sensing object detection, which is centered on extending the classical YOLOv5 architecture to the rotating box detection task in order to cope with the orientation diversity and scale inhomogeneity that are prevalent in remote sensing images. Architecturally, YOLOv5-OBB retains the end-to-end detection paradigm of YOLOv5, including input pre-processing, backbone feature extraction, feature fusion necking, and multi-scale prediction header.

Unlike the traditional horizontal frame detection pipeline, YOLOv5-OBB introduces a rotated frame parametric design in the prediction header section. Specifically, each candidate frame additionally outputs the rotation angle of the target in addition to the predicted center coordinates and width–height, enabling the model to directly regress to bounding boxes of arbitrary directions. This enables the network to perform more robustly when facing targets with significant directionality such as ships, aircraft, and buildings.

YOLOv5-OBB relies on the CSPDarknet backbone for multi-layer convolutional feature extraction in feature learning, and enhances multi-scale feature interactions through Path Aggregation Network (PANet) to ensure consistent modeling of large and small targets in high-resolution remote sensing scenes. Residual concatenation and cross-layer fusion further alleviate the gradient-vanishing problem and accelerate the convergence process under the rotation detection task.

In addition, YOLOv5-OBB adopts a rotating frame-specific label assignment and loss function design. To ensure the accuracy of detection, it combines IoU-based regression loss with angular regression loss to effectively suppress problems such as angular blurring and unstable bounding box regression.

Practical remote sensing missions often face challenges such as target orientation diversity, boundary jitter, and scale differences. Meanwhile, remote sensing images not only have a large number of invalid regions but also often contain complex texture patterns and non-homogeneous backgrounds, which require the model to have good geometric adaptability and contextual modeling capabilities while guaranteeing accuracy. YOLOv5-OBB adopts an end-to-end rotated frame detection architecture, which is equipped with fast prediction and rotationally invariant modeling capabilities, and is able to more adequately retain the orientation information in remote sensing images. For information in remote sensing images, in the detection head, the parametric design of the rotating frame of YOLOv5-OBB facilitates the capture of angular changes, which helps to achieve stable regression and fine alignment of candidate frames, and provides a natural advantage and strong support for mitigating the problems of orientation inconsistency and boundary instability.

Therefore, YOLOv5-OBB is chosen as the structural baseline in this paper, which not only considers target orientation diversity and boundary refinement but also has the ability to maintain detection stability under complex strategy space. YOLOv5-OBB has good generalization ability in remote sensing tasks, and it is especially suitable for multi-directional and multi-scale target-detection scenarios. However, YOLOv5-OBB is based on the rotating frame structure of horizontal frame extension, which is prone to boundary jitter in the dense target region, and has the problem where the strategy selection relies on manual experience, which is prone to the contradiction of delay increase and accuracy decrease in practical reasoning. If it can be optimized by combining the geometric constraints of remote sensing images with the task-adaptive structure, the performance of the model under orientation-consistent modeling and delay-constrained optimization will be significantly improved.

3.2. Angle-Synchronized Graph Head (ASG)

Accurate oriented object detection requires the predicted bounding boxes to maintain consistent angles and precise boundaries with the underlying targets. However, in dense or complex scenes, candidate boxes generated by a standard detector are often processed in isolation, lacking explicit constraints on their mutual rotational relationships. This isolation is a fundamental cause of angle inconsistency and boundary jitter, as the regression of each box fails to benefit from the collective geometric context. To address this core limitation, we introduce the Angle-Synchronized Graph Head (ASG). This module explicitly models the interdependencies between candidate boxes by constructing a graph where nodes represent boxes and edges encode their geometric relations. It then performs synchronized message passing that inherently respects rotational equivariance, allowing each node to refine its parameters based on coherent information from its neighbors. This process directly enforces angular alignment and enables collaborative boundary refinement, thereby overcoming the inherent instability of processing candidate boxes independently.

Each candidate box is regarded as a node i, whose feature is defined as

$$v_i=(f_i,b_i,s_i),$$

(1)

where $f_i\in {\mathbb{R}}^C$ is the RoI feature of candidate i extracted from the detector backbone, $b_i=(x_i,y_i,w_i,h_i,{\theta }_i)$ represents the oriented bounding box parameters with $(x_i,y_i)$ as the center coordinates, $(w_i,h_i)$ as width and height, ${\theta }_i$ as the rotation angle, and $s_i\in [0,1]$ denotes the confidence score of the candidate. The edge feature between nodes i and j is defined as

$$e_{ij}=\left[\parallel c_i-c_j{\parallel }_2,log\frac{min(w_i,h_i)}{min(w_j,h_j)},cos({\theta }_i-{\theta }_j),sin({\theta }_i-{\theta }_j)\right],$$

(2)

where $c_i=(x_i,y_i)$ and $c_j=(x_j,y_j)$ are the centers of nodes i and j, the first two terms represent the distance and scale ratio between nodes, and the last two terms encode the cosine and sine of the relative rotation angle for geometric constraints during message passing.

To ensure isometry under rotational transformations during message passing, we explicitly align features from neighboring nodes prior to aggregation. Since candidate boxes from different orientations encode features within their respective local coordinate systems, directly aggregating these unaligned features would compromise angular consistency. Therefore, we employ the relative rotation angle $\Delta {\theta }_{ij}={\theta }_j-{\theta }_i$ to rotate features from neighboring node j into the coordinate system of central node i. This rotation is achieved via the SE(2) rotation operator $\Gamma (\Delta {\theta }_{ij})$, which applies a 2D rotation matrix to the spatial dimensions of the features while preserving other feature channels. This operation ensures all features participating in message passing are geometrically aligned, enabling the network to learn transformation-invariant representations. The specific procedure is as follows:

$${\tilde{f}}_j=\Gamma (\Delta {\theta }_{ij})f_j,$$

(3)

with the SE(2) rotation operator defined as

$$\Gamma (\Delta \theta )=\left[\begin{array}{cc}cos\Delta \theta & -sin\Delta \theta \\ sin\Delta \theta & cos\Delta \theta \end{array}\right]\oplus I_{C-2},$$

(4)

where ${\tilde{f}}_j$ is the rotated feature used for message passing and $\oplus I_{C-2}$ indicates that the remaining feature channels are kept unchanged.

The node feature $x_i^{\left(l\right)}$ is updated through multiple layers of message passing:

$$x_i^{(l+1)}=x_i^{\left(l\right)}+\sum _{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}\Phi \left([x_i^{\left(l\right)},{\tilde{f}}_j,e_{ij}]\right),$$

(5)

where $x_i^{\left(l\right)}$ is the feature of node i at layer l; initialized as $x_i^{\left(0\right)}=f_i$, $\mathcal{N}\left(i\right)$ is the neighborhood of node i, $\Phi (·)$ is a learnable message function, and ${\alpha }_{ij}$ is the attention coefficient:

$${\alpha }_{ij}=\mathrm{softmax}\left(a^{\top }\sigma \left(W[x_i^{\left(l\right)},{\tilde{f}}_j,e_{ij}]\right)\right),$$

(6)

This aggregated message, refined by the attention gate, is used to predict a set of micro-residuals $\Delta b_i$. These residuals represent precise corrections to the original box parameters, computed through a linear layer that transforms the node’s updated feature. The key advantage of this residual formulation is that it decomposes the complex task of direct coordinate regression into learning smaller, more stable adjustments. This allows the model to specialize in refining initial detections by making targeted modifications to existing box coordinates. The final refined box is then obtained by applying these residuals:

$$\Delta b_i=[\Delta x_i,\Delta y_i,\Delta w_i,\Delta h_i,\Delta sin{\theta }_i,\Delta cos{\theta }_i],$$

(7)

which is applied to update the box as

$$b_i^{\prime }=\mathrm{Apply}(b_i,\Delta b_i),{\theta }_i^{\prime }=\mathrm{atan}2(sin{\theta }_i+\Delta sin{\theta }_i,cos{\theta }_i+\Delta cos{\theta }_i),$$

(8)

where $b_i^{\prime }$ is the refined oriented bounding box, ${\theta }_i^{\prime }$ is the refined rotation angle, and $\mathrm{Apply}(·)$ denotes applying the residual to the original box, with residuals derived from neighbor-informed message aggregation.

The final output set of ASG is

$${\mathcal{B}}^{\prime }=\{(b_i^{\prime },s_i^{\prime })\mid i=1,\dots ,N\},$$

(9)

where $b_i^{\prime }$ is the refined OBB computed from the original $b_i$ and residual $\Delta b_i$, and $s_i^{\prime }$ is the updated confidence score from the message-passed features. Compared to the original set $\{b_i,s_i\}$, ${\mathcal{B}}^{\prime }$ achieves better angular consistency, boundary precision, and redundancy suppression.

3.3. Bilevel Policy Optimization (BPO)

In rotated-object detection, multiple non-differentiable and coupled strategy decisions exist in both training and inference, including rotation augmentation, positive or negative sample assignment, multi-tile scanning, and rotated NMS. To jointly optimize these strategies under latency constraints, we propose a Bilevel Policy Optimization (BPO) framework. BPO formulates a bilevel optimization problem, where an upper-level policy decides strategy parameters and a lower-level detector evaluates the performance under those strategies.

The Bilevel Policy Optimization (BPO) framework is formally structured into two distinct layers with clearly separated responsibilities:

• Upper-Level Policy: This acts as the strategic planner, implemented as a reinforcement learning agent. It observes the detection system’s performance metrics and latency status, then outputs optimized parameters for the four core strategies: rotation augmentation, sample assignment, multi-tile scanning, and rotated NMS. This policy is trained to maximize a compound reward that balances accuracy improvements against computational costs, with an adaptive dual variable enforcing the latency constraint through projected ascent updates.
• Lower-Level Detector: This serves as the tactical executor, comprising the core detection network including the ASG module. It receives strategy configurations from the upper level as fixed hyperparameters, executes the detection task, and returns performance measurements. A key component is its differentiable performance surrogate that enables effective policy learning by approximating non-differentiable evaluation metrics.

This formal separation creates a coherent optimization cycle where the upper level learns what strategies to apply while the lower level specializes in executing detection under those strategies, with performance feedback closing the loop.

We define the environment state at time step t as

$${\mathbf{s}}_t=\left[{\overline{\rho }}_{0.5,t},{\overline{\rho }}_{0.75,t},r_t^{\mathrm{small}},p_t,{\mathbf{h}}_{t-1},{\tau }_{t-1}\right],$$

(10)

where ${\overline{\rho }}_{0.5,t}$ and ${\overline{\rho }}_{0.75,t}$ denote the mean rotated IoU at thresholds 0.5 and 0.75 for the mini-batch, $r_t^{\mathrm{small}}$ is the recall for small objects, $p_t$ is the precision, ${\mathbf{h}}_{t-1}$ encodes the previous strategy action in one-hot form, and ${\tau }_{t-1}$ is the latency observed in the previous step.

The LC-BPO policy outputs an action vector that configures the four strategy knobs:

$${\mathbf{a}}_t=\left[a_t^R,a_t^D,a_t^M,a_t^N\right],$$

(11)

where $a_t^R$ selects the rotation augmentation angle and probability, $a_t^D$ sets thresholds for positive/negative assignment, $a_t^M$ chooses multi-tile scanning parameters (tile size, stride, overlap, rotation switch), and $a_t^N$ determines rotated NMS thresholds.

Given ${\mathbf{a}}_t$, the lower-level detector evaluates its effect on the current mini-batch and returns proxy statistics:

$${\mathbf{m}}_t=f_{\mathrm{detector}}({\mathbf{X}}_t;{\mathbf{a}}_t),$$

(12)

where ${\mathbf{X}}_t$ is the mini-batch input and ${\mathbf{m}}_t$ summarizes approximated rotated IoU, recall, and precision.

The standard average precision (AP) metric relies on a non-differentiable Heaviside step function for determining true positives based on IoU thresholds:

$$H\left(x\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}x\ge 0\hfill \\ 0\hfill & \mathrm{if}x<0\hfill \end{array}\right.$$

(13)

where $x={\mathrm{rioU}}_i-{\tau }_i$. This discontinuity prevents gradient-based optimization. Therefore, to obtain a differentiable surrogate, we adopt a smoothed AP proxy via Heaviside relaxation by approximating $H\left(x\right)$ with a scaled sigmoid function:

$${\widehat{\mathrm{AP}}}_t={\displaystyle \frac{1}{M}}\sum _{i=1}^M\sigma \left({\displaystyle \frac{{\mathrm{rIoU}}_i-{\tau }_i}{ϵ}}\right)p_i,$$

(14)

where M is the number of detections, ${\mathrm{rIoU}}_i$ is the rotated IoU of detection i, ${\tau }_i$ is the threshold, $p_i$ is the confidence score, $ϵ$ is a smoothing factor, and $\sigma (·)$ is the sigmoid function.

The step-wise reward balances accuracy gains and latency penalties under a budget:

$$r_t=\left({\widehat{\mathrm{AP}}}_t-{\widehat{\mathrm{AP}}}_{t-1}\right)+\beta \left(r_t^{\mathrm{small}}-r_{t-1}^{\mathrm{small}}\right)-\lambda max(0,{\tau }_t-B),$$

(15)

where $\beta$ tunes the emphasis on small-object recall, $\lambda$ is a Lagrangian multiplier, and B is the latency budget.

The upper-level policy ${\pi }_{\theta }$ is optimized using a policy gradient method (e.g., PPO):

$$\theta \leftarrow \theta +\eta {\nabla }_{\theta }{\mathbb{E}}_{{\pi }_{\theta }}\left[\sum _t{r}_t\right],$$

(16)

where $\eta$ is the learning rate and $\theta$ denotes policy parameters.

To enforce the latency constraint, the dual variable $\lambda$ is updated by projected ascent. This update is central to our framework’s ability to balance accuracy and efficiency, as it dynamically adjusts the penalty weight based on constraint violation, steering policy learning toward latency-compliant solutions.

$$\lambda \leftarrow max\left(0,\lambda +\gamma ({\tau }_t-B)\right),$$

(17)

where $\gamma$ is the dual ascent step size.

After convergence, the framework yields an optimized strategy set for training and inference:

$${\mathcal{A}}^{*}=\{{\mathbf{a}}_1^{*},{\mathbf{a}}_2^{*},\dots ,{\mathbf{a}}_T^{*}\},$$

(18)

which, when deployed, produces the final latency-compliant rotated detection results:

$${\mathcal{D}}^{\prime }=\{(d_k^{\prime },s_k^{\prime })\mid k=1,\dots ,N\},$$

(19)

where $d_k^{\prime }$ are the refined oriented bounding boxes and $s_k^{\prime }$ are the updated confidence scores.

4. Experiments

4.1. Datasets

DOTAv1.0 is one of the largest rotating frame detection datasets currently available, containing 2806 frames with resolutions up to 4000 × 4000 remote sensing images with 188,282 instances of 15 types of targets: aircraft (PL), baseball diamonds (BD), bridges (BR), surface runways (GTF), small vehicles (SV), large vehicles (LV), ships (SH), tennis courts (TC), basketball courts (BC), storage tanks (ST), football fields (SBF), roundabouts (RA), harbors (HA), swimming pools (SP), and helicopters (HC).

HRSC2016 focuses on ship detection and contains 1061 high-resolution shoreline images with a total of 2976 labeled ship instances. With extreme target aspect ratios and large-scale spans, HRSC2016 is a classic dataset for evaluating the detection performance of elongated targets.

DIOR-R is a rotating frame extension of the DIOR dataset, providing 23,463 multi-source remote sensing images covering 20 common categories (e.g., aircraft, vehicles, ports, tanks, etc.), with a total of about 190 k directionally labeled instances.

4.2. Experiments Settings

To ensure comparability with mainstream methods, we maintained consistency in data pre-processing: DOTA-v1.0 employed single-scale training and testing; FAIR1M-v1.0 employs a multi-scale approach, where images are first scaled to three scales (0.5×, 1.0×, 1.5×), then cropped into 1024 × 1024 patches with 500-pixel overlap; HRSC2016 maintains aspect ratios while uniformly resizing the longer side to 800 pixels. All remote sensing object detection experiments were conducted on four RTX 4090 GPUs with a batch size of 8, learning rate of 0.00005, and 12 training epochs. Results are reported across the DOTA-v1.0, HRSC2016, and FAIR1M-v1.0 datasets.

5. Results in Classic Datasets

Figure 2 provides a visual comparison of feature attribution heatmaps between the baseline method and our proposed approach, offering analytical insights into the geometric stability of our framework. In the baseline heatmap, the elliptical region highlights critical issues with small rotating objects: the activation areas exhibit diffuse boundaries and significant background interference. This visual pattern correlates directly with the baseline’s tendency for boundary jitter and angular inconsistency, as the model fails to focus precisely on target contours.

In contrast, our ASBPNet generates markedly more concentrated activations with sharply defined boundaries in the same region. This cleaner visual manifestation demonstrates the effectiveness of our geometric modeling: the Angle-Synchronized Graph (ASG) head successfully enforces spatial coherence through its equivariant message passing, while the Bilevel Policy Optimization (BPO) module contributes by optimizing feature learning through improved sample assignment. The significantly reduced background activation further confirms our model’s enhanced discrimination capability, validating that our unified framework effectively addresses both boundary instability and background distraction in rotated object detection.

As shown in

Table 2. Comparison with SOTA methods on DIOR-R datasets.

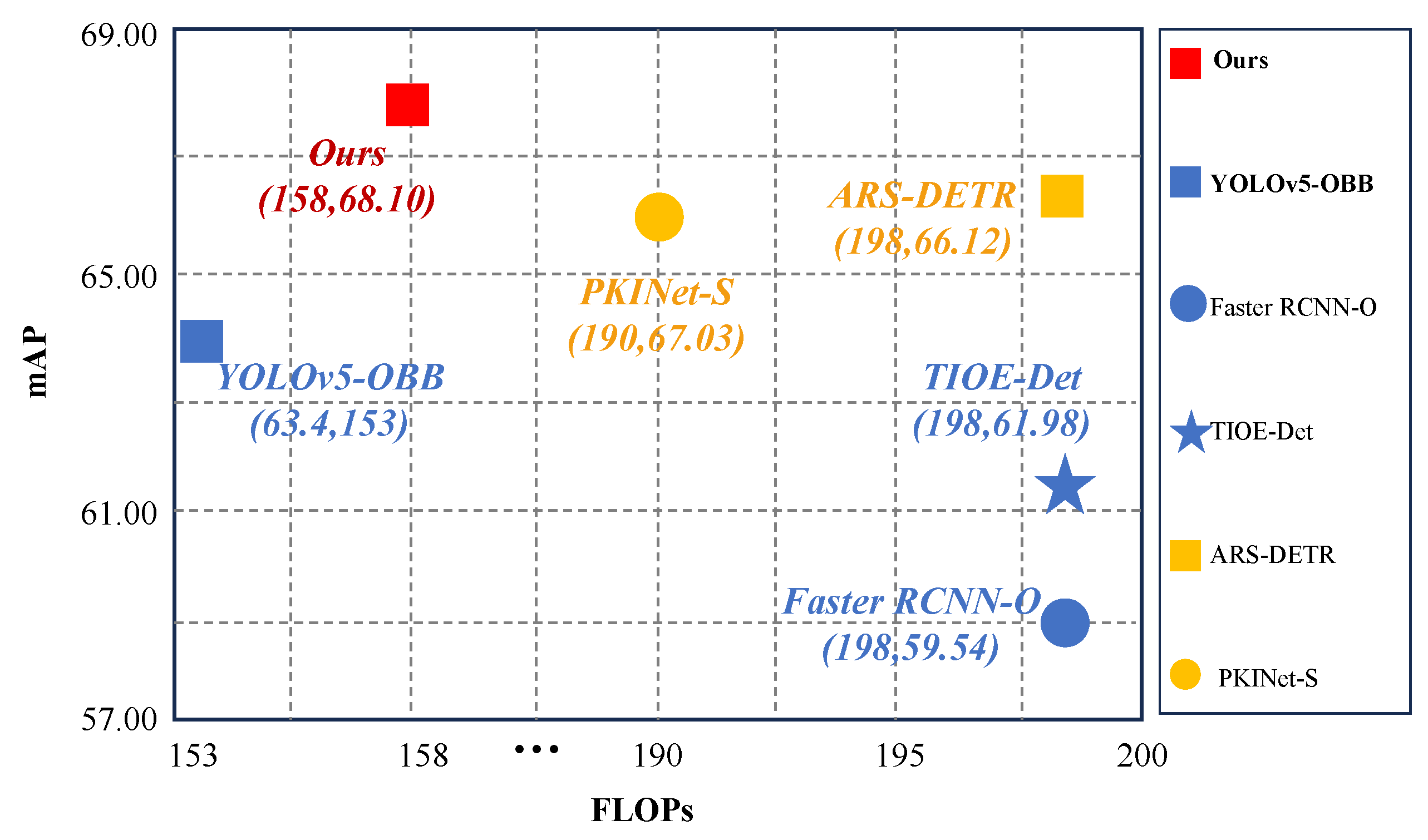
Method	Pre-Training	#P	FLOPs	FPS	mAP (%)
RetinaNet-O	IN	–	–	23.0	57.55
Faster RCNN-O	IN	41.1 M	198 G	19.0	59.54
TIOE-Det	IN	41.1 M	198 G	–	61.98
ARS-DETR	IN	41.1 M	198 G	12	66.12
O-RepPoints	IN	36.6 M	–	29	66.71
DCFL	IN	–	–	29	66.80
LSKNet-S	IN	31.0 M	161 G	–	65.90
PKINet-S	IN	30.8 M	190 G	5.2	67.03
YOLOv5m-OBB (baseline)	IN	21.2 M	153 G	62.3	63.40
ASBPNet	CO	22.1 M	158 G	61.1	68.10

The red values represent the best (optimal) performance, while the blue values indicate the second-best (suboptimal) performance.

and Figure 3, on the DIOR-R dataset, ASBPNet achieves a mAP of 68.10, which is 8.56 and 6.12 percentage points higher compared to the mainstream two-stage methods Faster RCNN-O and TIOE-Det, respectively, and also outperforms the Transformer architectures ARS-DETR and PKINet-S, demonstrating a stronger generalized detection capability. In particular, compared with our baseline YOLOv5m-OBB, mAP improves by 4.7 percentage points with only 0.9M increase in the number of parameters and 5G increase in the number of FLOPs, which fully demonstrates the significant performance gain of this architecture in efficiency-constrained scenarios.

Table 3. Comparison with SOTA methods on HRSC2016 datasets.

Method	Pre-Training	mAP (07)	mAP (12)	#P	FLOPs	FPS
DRN	IN	–	92.70	–	–	–
CenterMap	IN	–	92.80	41.1 M	198 G	–
RoI Trans.	IN	86.20	–	55.1 M	200G	6.0
G.V.	IN	88.20	–	41.1 M	198 G	–
R3Det	IN	89.26	96.01	41.9 M	336 G	12.0
DAL	IN	89.77	–	36.4 M	216 G	–
GWD	IN	89.85	97.37	47.4 M	456 G	–
S2ANet	IN	90.17	95.01	38.6 M	198 G	14.3
AOPG	IN	90.34	96.22	–	–	–
ReDet	IN	90.46	97.63	31.6 M	–	24.7
O-RCNN	IN	90.50	97.60	41.1 M	199 G	32.0
RTMDet	CO	90.60	97.10	52.3 M	205 G	–
YOLOv5m-OBB (baseline)	IN	88.50	96.80	21.2 M	153 G	62.6
ASBPNet	CO	90.60	98.20	22.1 M	158 G	61.7

The red values represent the best (optimal) performance, while the blue values indicate the second-best (suboptimal) performance.

shows that in the HRSC2016 dataset, ASBPNet achieves 90.60 on mAP (07), which is 2.1 percentage points higher than the 88.50 of the baseline YOLOv5m-OBB. This effect comes from the angle-aware adaptive grouping mechanism we introduce, which enables the model to be more accurate in feature extraction for rotating targets. On mAP (12), ASBPNet further achieves 98.20, an improvement of 1.4 from the baseline 96.80, thanks to the stable enhancement of the bounding box regression process by the delayed pairwise optimization strategy, which effectively reduces the localization error caused by the angular point offset of the long bar target. In terms of the number of parameters, ASBPNet is controlled at 22.1 M, which is only 0.9 M more than the baseline, but achieves higher detection accuracy, and this coordination between accuracy improvement and lightweight parameter scale indicates that the boundary perception module we designed has extremely strong feature enhancement capability and computational utilization. FLOPs increase slightly from 153 G to 158 G, but while maintaining very high inference efficiency, the FLOPs increase slightly from 153 G to 158 G, but maintain the high inference efficiency while significantly enhancing the sensitivity to the target’s rotational state, which is especially suitable for the vessel targets with high aspect ratios and variable orientations in HRSC2016. These results demonstrate that ASBPNet achieves high-precision modeling of angle-sensitive regions without substantially increasing model complexity, and its rotational robustness and boundary regression stability provide a reliable guarantee for the detection of complex attitude remote sensing targets.

Table 4. Per-class mAP comparison with mAP moved before class columns.

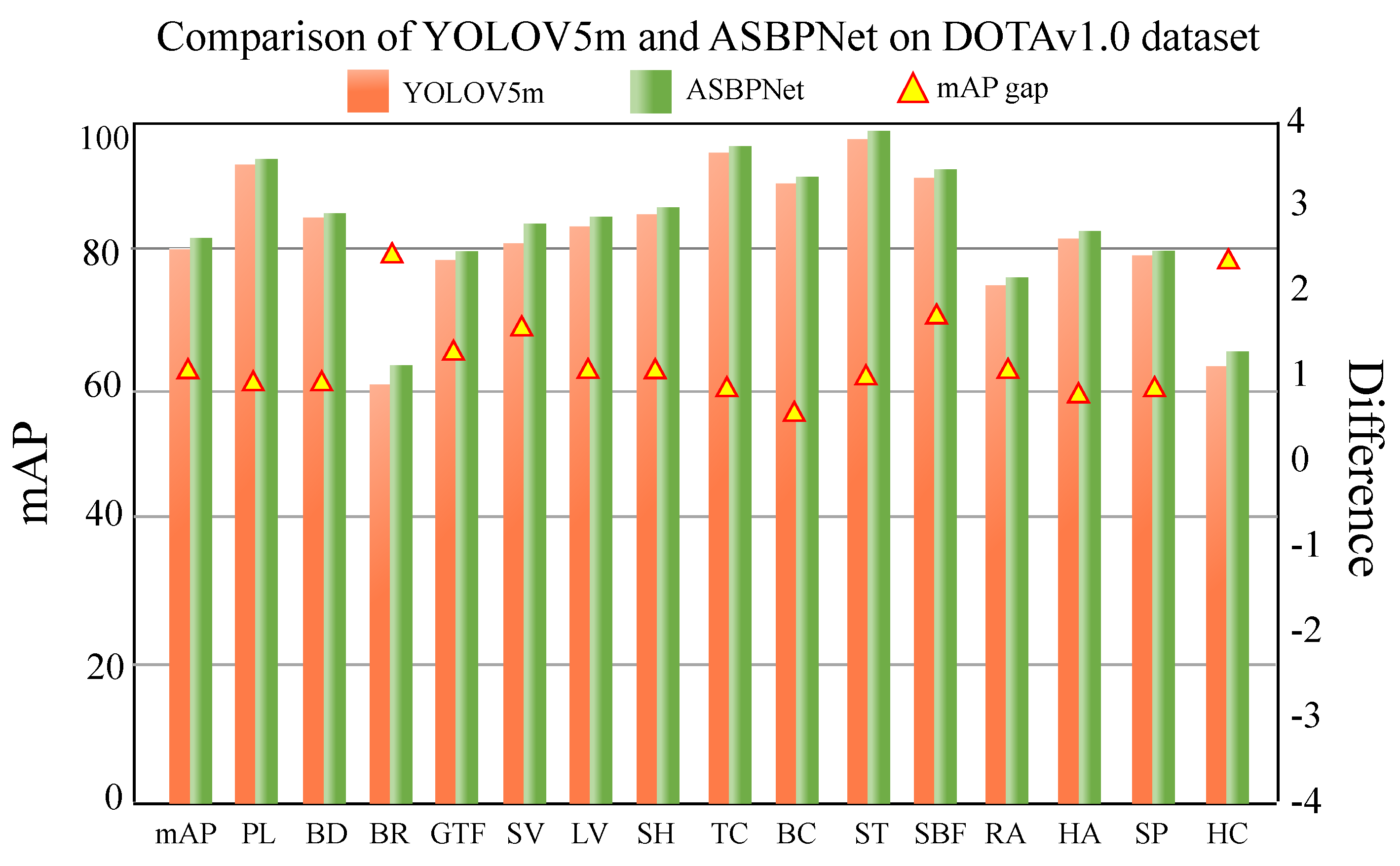
Method	mAP↑	PL	BD	BR	GTF	SV	LV	SH	TC	BC	ST	SBF	RA	HA	SP	HC
Single-Scale
EMO2-DETR [47]	70.91	87.99	79.46	45.74	66.64	78.90	73.90	73.30	90.40	80.55	85.89	55.19	63.62	51.83	70.15	60.04
CenterMap [48]	71.59	89.02	80.56	49.41	61.98	77.99	74.19	83.74	89.44	78.01	83.52	47.64	65.93	63.68	67.07	61.59
AO2-DETR [49]	72.15	86.01	75.92	46.02	66.65	79.70	79.93	89.17	90.44	81.19	76.00	56.91	62.45	64.22	65.80	58.96
SCRDet [50]	72.61	89.98	80.65	52.09	68.36	68.36	60.32	72.41	90.85	87.94	86.86	65.02	66.68	66.25	68.24	65.21
R3Det [51]	73.70	89.50	81.20	50.50	66.10	70.90	78.70	78.20	90.80	85.30	84.20	61.80	63.80	68.20	69.80	67.20
RoI Trans. [52]	74.05	89.01	77.48	51.64	72.07	74.43	77.55	87.76	90.81	79.71	85.27	58.36	64.11	76.50	71.99	54.06
S2ANet [53]	74.12	89.11	82.84	48.37	71.11	78.11	78.39	87.25	90.83	84.90	85.64	60.36	62.60	65.26	69.13	57.94
SASM [54]	74.92	86.42	78.97	52.47	69.84	77.30	75.99	86.72	90.89	82.63	85.66	60.13	68.25	73.98	72.22	62.37
G.V. [55]	75.02	89.64	85.00	52.26	77.34	73.01	73.14	86.82	90.74	79.02	86.81	59.55	70.91	72.94	70.86	57.32
O-RCNN [56]	75.87	89.46	82.12	54.78	70.86	78.93	83.00	88.20	90.90	87.50	84.68	63.97	67.69	74.64	84.93	52.28
ReDet [57]	76.25	88.79	82.64	53.97	74.00	78.13	84.06	88.04	90.89	87.78	85.75	61.76	60.39	75.96	68.07	63.59
R3Det-GWD [58]	76.34	88.82	82.94	55.63	72.75	78.52	83.10	87.46	90.21	86.36	85.44	64.70	61.41	73.46	76.94	57.38
R3Det-KLD [59]	77.36	88.90	84.17	55.80	69.35	78.72	84.08	87.00	89.75	84.32	85.73	64.74	61.80	76.62	78.49	70.89
ARC [60]	77.35	89.40	82.48	55.33	73.88	79.37	84.05	88.06	90.90	86.44	84.83	63.63	70.32	74.29	71.91	65.43
LSKNet-S [61]	77.49	89.66	85.52	57.72	75.70	74.95	78.69	88.24	90.88	86.79	86.38	66.92	63.77	77.77	74.47	64.82
PKINet-S [62]	78.39	89.72	84.20	55.81	77.63	80.25	84.45	88.12	90.88	87.57	86.07	66.86	70.23	77.47	73.62	62.94
O2DNet [63]	71.01	89.36	82.18	47.31	61.24	71.33	74.02	78.64	90.81	82.23	81.42	60.90	60.22	58.21	67.02	61.04
CFC-Net [64]	73.52	89.13	80.44	52.41	70.04	76.31	78.14	87.23	90.92	84.54	85.61	60.51	61.53	67.82	68.01	50.15
CBDA-Net [65]	75.74	89.24	85.94	50.32	65.01	77.71	82.33	87.93	90.52	86.51	85.90	66.92	66.51	67.43	71.32	62.91
CoF-Net [66]	77.21	89.60	83.12	48.31	73.64	78.23	83.04	86.72	90.24	82.32	86.61	67.61	64.63	74.70	71.32	78.42
MTP [67]	79.03	89.87	85.09	58.27	71.70	81.70	87.10	88.98	91.44	85.41	86.45	57.44	68.47	78.42	82.97	71.71
YOLOv5m-OBB (baseline) [68]	77.30	89.90	81.50	58.80	75.50	76.90	79.30	81.30	89.70	83.00	87.10	67.10	72.00	79.50	77.00	60.90
ASBPNet	79.60	91.50	83.00	64.40	77.70	80.80	81.30	83.10	90.90	84.60	89.10	69.10	73.90	81.00	78.70	64.90
Multi-Scale
CSL [69]	76.17	90.25	85.53	54.64	75.31	70.44	73.51	77.62	90.84	86.15	86.69	69.60	68.04	73.83	71.10	68.93
CFA [70]	76.67	89.08	83.20	54.37	66.87	81.23	80.96	87.17	90.21	84.32	86.09	52.34	69.94	75.52	80.76	67.96
DAFNeT [71]	76.95	89.40	86.27	53.70	60.51	82.04	81.17	88.66	90.37	83.81	87.27	53.93	69.38	75.61	81.26	70.86
DODet [72]	80.62	89.96	85.52	58.01	81.22	78.71	85.46	88.59	90.89	87.12	87.80	70.50	71.54	82.06	77.43	74.47
AOPG [73]	80.66	89.88	85.57	60.90	81.51	78.70	85.29	88.85	90.89	87.60	87.65	71.66	68.69	82.31	77.32	73.10
KFIoU [74]	80.93	89.44	84.41	62.22	82.51	80.10	86.07	88.68	90.90	87.32	88.38	72.80	71.95	78.96	74.95	75.27
RTMDet-RKFIoU [75]	81.33	88.01	86.17	58.54	82.44	81.30	84.82	88.71	90.89	88.77	87.37	71.96	71.18	81.23	81.40	77.13
Multi-Scale
RVSA [76]	81.24	88.97	85.76	61.46	81.27	79.98	85.31	88.30	90.84	85.06	87.50	66.77	73.11	84.75	81.88	77.58
LSKNet-S [61]	81.64	89.57	86.34	63.13	83.67	82.20	86.10	88.66	90.89	88.41	87.42	71.72	69.58	78.88	81.77	76.52
FR-O [77]	54.11	79.42	77.13	17.72	64.14	35.32	38.01	37.26	89.43	69.62	59.34	50.30	52.93	47.91	47.43	46.31
CAD-Net [78]	69.96	87.82	82.41	49.43	73.51	71.13	63.52	76.62	90.91	79.23	73.33	48.44	60.92	62.03	67.01	62.24
APE [79]	75.81	90.01	83.65	53.43	76.02	74.01	77.27	79.53	90.82	87.27	84.51	67.72	60.31	74.60	71.84	65.62
SCRDet [80]	72.63	90.01	80.71	52.14	68.43	68.42	60.32	72.44	90.92	87.94	86.96	65.02	66.73	66.31	68.23	65.21
YOLOv5m-OBB (baseline)	80.20	92.50	84.00	61.50	78.50	80.50	82.00	84.50	93.00	86.00	90.50	70.00	74.00	82.00	79.00	65.00
ASBPNet	81.50	93.40	84.90	64.10	79.90	82.30	83.20	85.60	93.30	86.80	91.50	71.80	75.30	82.90	79.90	67.60

The red values represent the best (optimal) performance, while the blue values indicate the second-best (suboptimal) performance.

and Figure 4 shows that ASBPNet achieves an mAP of 79.60 at a single scale, significantly outperforming YOLOv5m OBB’s 77.30 and surpassing the strongest competitor in the same group, MTP, with 79.03. At the multi-scale level, ASBPNet achieves an mAP of 81.50, slightly below LSKNet S’s 81.64 but securing top or second-place performance across most categories with greater overall stability. Category-by-category comparisons reveal improvements primarily in direction-sensitive and densely populated small-target categories like bridges, helicopters, and cars. This demonstrates the method’s effectiveness in suppressing angular inconsistencies and boundary jitter, yielding cleaner suppression results. This effect stems from enhanced consistency through geometric alignment at the candidate level and graph message passing, while also benefiting from the strategy layer’s joint adaptation of rotation enhancement, positive–negative assignment, tile scanning, and rotation NMS. Categories with relatively smaller gains, such as trucks and swimming pools, are more constrained by scale and texture representation, tending to rely on stronger backbone or multi-scale feature supplementation. Overall, ASBPNet achieves steady-state gains across all classes without modifying the backbone or neck architecture.

Ablation Study

Validation of the effectiveness of geometric modeling and strategy optimization for collaborative enhancement.

Table 5. Ablation study of ASG and BPO on YOLOv5m-OBB.

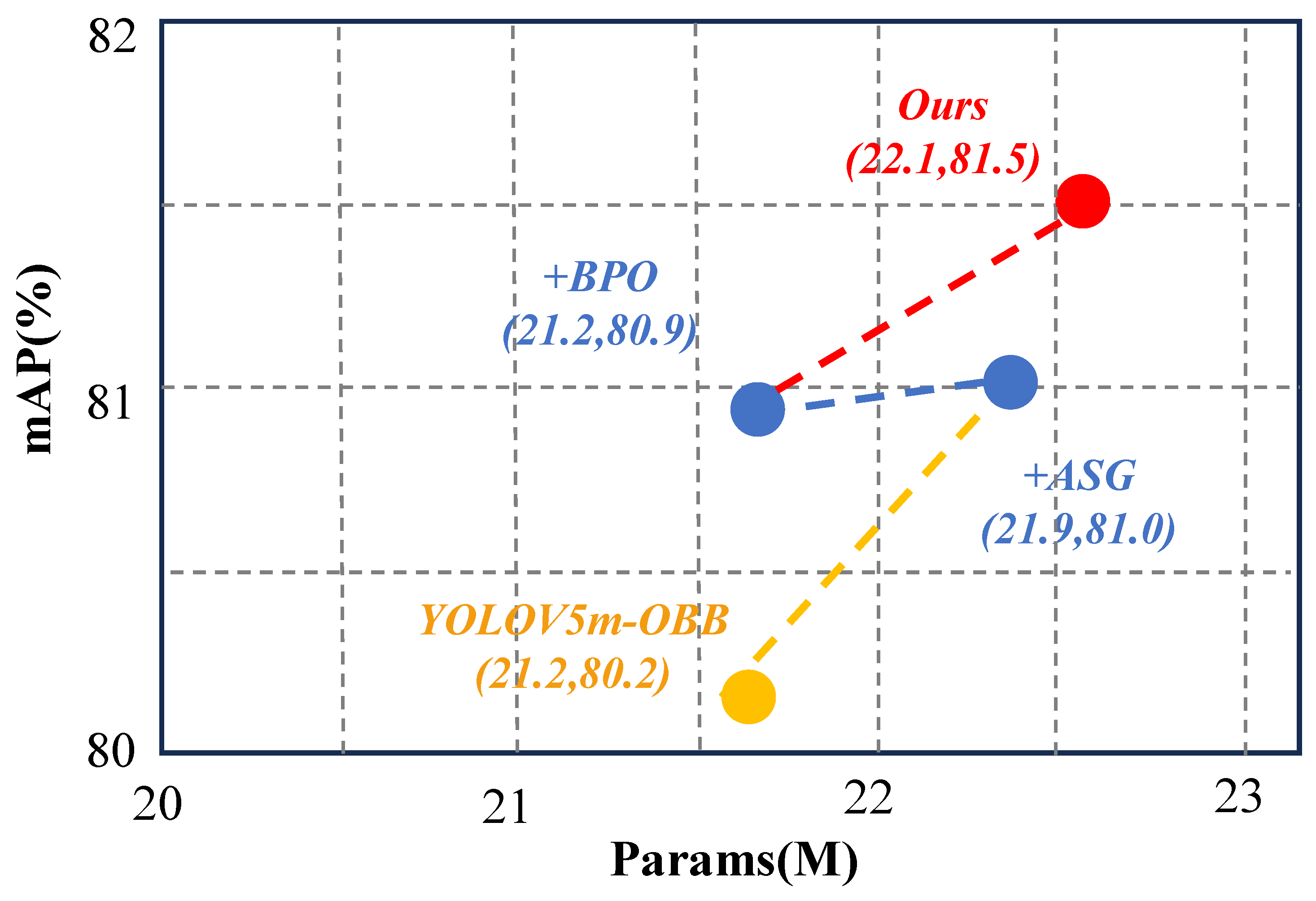
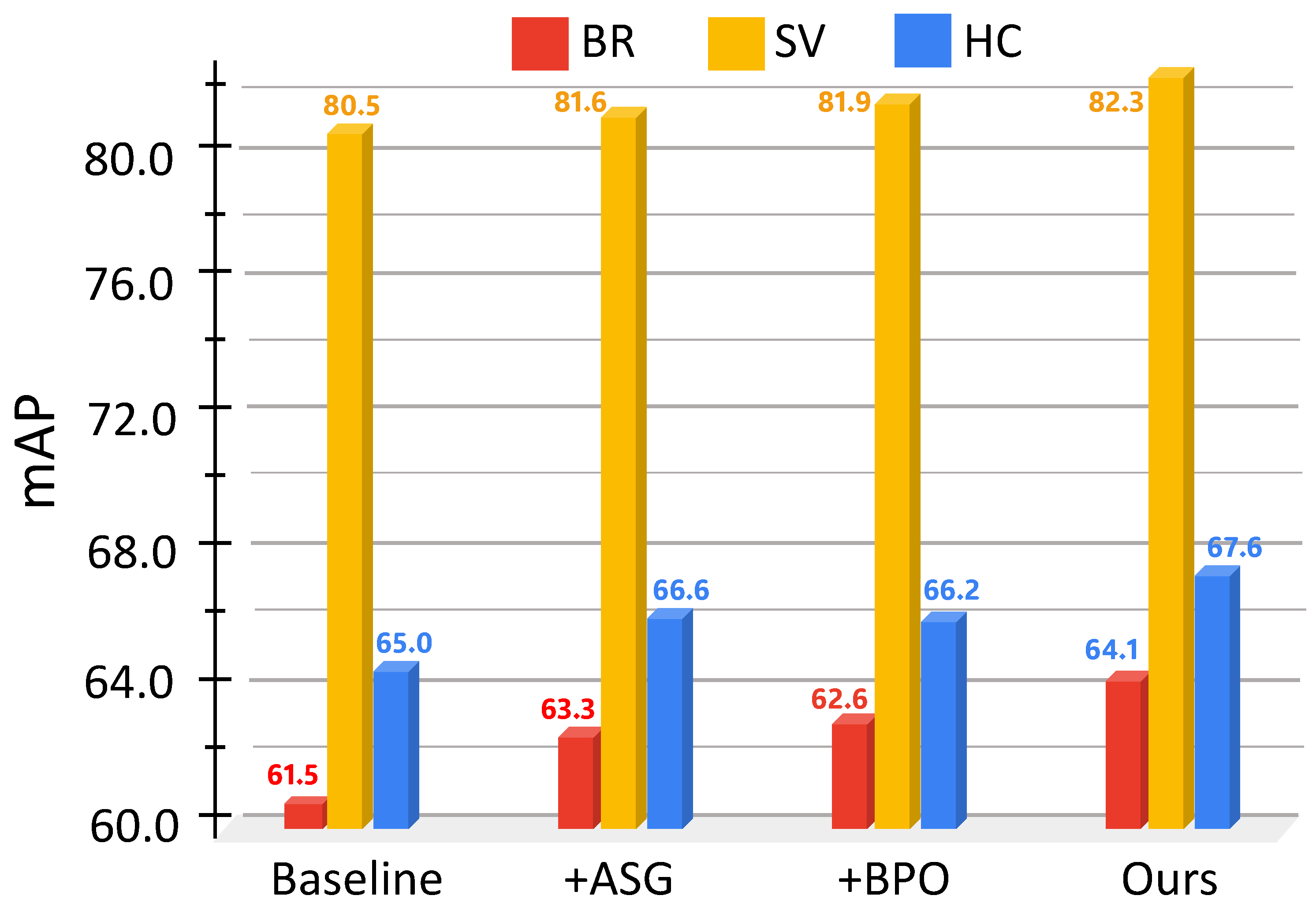
Setting	Description	mAP	ΔmAP	#Params	FLOPs (G)
A	YOLOv5m-OBB	80.20	–	21.2 M	153
B	+ASG	81.00	+0.80	21.9 M	156
C	+BPO	80.90	+0.70	21.2 M	153
D	ASG + BPO (Ours)	81.50	+1.30	22.1 M	158

and Figure 5 show that the introduction of the SE2-ASG module alone leads to a +0.8 mAP improvement, mainly due to the fact that the module maintains the angular consistency of the candidate frames through rotated iso-graph messaging, which significantly mitigates the boundary jitter problem. LC-BPO alone also delivers +0.7 mAP, indicating that the two-layer policy optimization under the delay constraint can stabilize the consistency in the training–inference phase and improve the recall of small targets. The largest improvement (+1.3) is achieved when combining the two, suggesting that geometric modeling and strategy optimization are complementary: the former improves the spatial consistency of the candidate frames, while the latter improves the adaptability of the multi-stage strategy, and the synergistic effect is significantly better than that of the separate modules.

The synergy between ASG and BPO originates from their interaction in feature regularization and adaptive optimization. ASG enhances spatial coherence and structural stability within feature maps, producing cleaner geometric priors for detection. BPO then leverages these priors to adaptively adjust anchor assignment and suppression strategies, improving the balance between precision and recall. In turn, BPO’s adaptive weighting further emphasizes features refined by ASG, forming a mutually reinforcing loop. This cooperative mechanism enables the combined model to achieve a +1.3 mAP gain, demonstrating that geometry-aware feature alignment and adaptive strategy optimization jointly contribute to more stable and discriminative detection performance.

While ASBPNet employs COCO pre-training compared to the ImageNet initialization of YOLOv5m-OBB baseline, this difference does not compromise the fairness of comparison. In remote sensing detection, both COCO and ImageNet serve primarily as general visual priors, whose influence is largely normalized after fine-tuning on large-scale domain-specific datasets like DIOR-R. Importantly, our experimental setup aligns with standard practices in the field, where numerous state-of-the-art methods, such as LSKNet [61] and PKINet [62], typically employ ImageNet pre-training before fine-tuning on remote sensing benchmarks including DIOR and DOTA. The +4.7 mAP improvement achieved with minimal parameter and FLOPs increase (+0.9M, +5G) strongly suggests that the performance gain originates primarily from our proposed ASG and BPO modules rather than pre-training bias. The architectural innovations enable more effective utilization of the feature representations regardless of the initial pre-training source.

Comparative analysis of angular synchronization and graphical information modeling.

Table 6. B-1: Variants with different message-passing, alignment, and synchronization strategies.

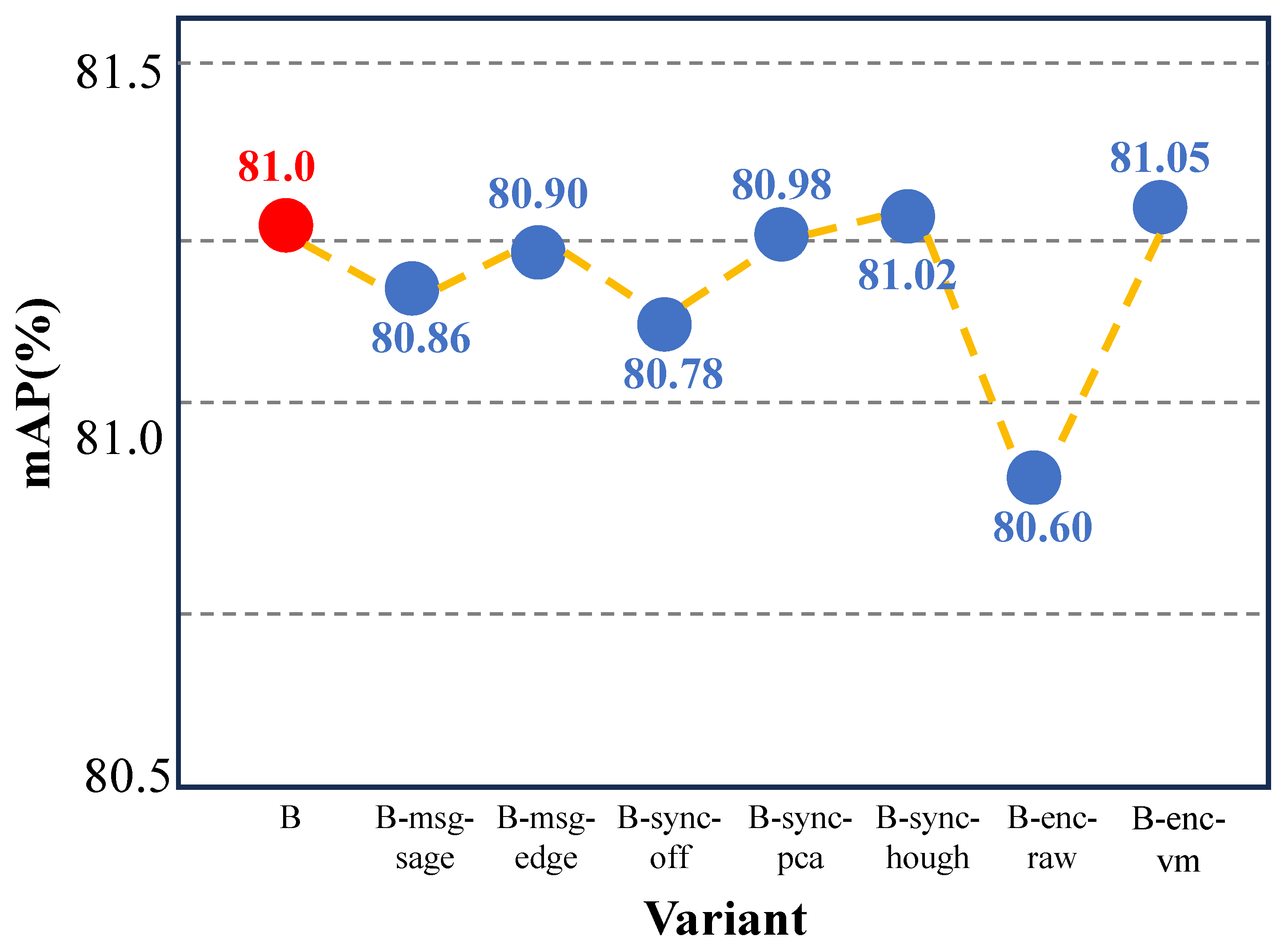
Variant	Description	mAP
B (default)	GATv2 message + SE(2) equivariant alignment + Angle Sync	81.00
B-msg-sage	GraphSAGE message passing	80.86
B-msg-edge	EdgeConv-style message passing	80.90
B-sync-off	Disable Angle Sync regularization	80.78
B-sync-pca	Sync prior: local PCA principal direction	80.98
B-sync-hough	Sync prior: Hough line direction	81.02
B-enc-rawθ	Angle encoding: raw $\theta$ (no sin/cos)	80.60
B-enc-vm	Angle encoding: sin/cos + von Mises embedding	81.05

and Figure 6 compare the different messaging and synchronization strategies. The results show that the Angle Sync constraint is indispensable, and the mAP decreases to 80.78 (−0.22) after removal, suggesting that angle alignment is crucial for rotational target stability. Meanwhile, the angle encoding embedded in von Mises performs the best (81.05), which is better than using the original angle directly (80.60), proving that the periodic modeling is more suitable for the rotational geometry property. In terms of message-passing methods, GATv2 maintains the best balance, and GraphSAGE and EdgeConv are slightly degraded but the difference is limited, indicating that the module is robust to message functions.

Structural perceptual analysis for boundary modeling.

Table 7. B-2: Variants on neighborhood size, message-passing depth, Top-N selection, and feature hierarchy.

Variant	Configuration	mAP	ΔmAP
k-4	kNN neighbors $k=4$	80.82	−0.18
k-8 (default)	$k=8$	81.00	–
k-12	$k=12$	81.04	+0.04
k-16	$k=16$	80.95	−0.05
depth-2	Message layers = 2	80.89	−0.11
depth-3 (default)	Message layers = 3	81.00	–
depth-4	Message layers = 4	81.03	+0.03
TopN-200	Node number $N=200$	80.90	−0.10
TopN-300 (default)	$N=300$	81.00	–
TopN-400	$N=400$	81.01	+0.01
P3-only	P3 RoI only	80.70	−0.30
P3–P5 (default)	Fusion of P3–P5	81.00	–
P3–P6	Fusion of P3–P6	81.02	+0.02

and Figure 7 shows that there is a “moderate optimality” between the neighborhood size and the number of layers on the performance; k = 8 and three layers have the best message delivery. Too small a neighborhood results in insufficient information (80.82), and too large a neighborhood or too deep a layer has limited benefits (81.04/81.03), indicating that excessive aggregation introduces noise. In terms of feature levels, P3 alone decreases significantly (−0.3), while multi-layer fusion (P3–P6) can be slightly improved, reflecting the role of cross-layer feature integration for boundary modeling of complex targets.

Sensitivity analysis of weights and steps.

Table 8. B-3: Variants on loss weighting ${\lambda }_{\mathrm{sync}}$ and step-size $\eta$.

Variant	Configuration	mAP	ΔmAP
${\lambda }_{\mathrm{sync}}=0$	Remove synchronization term	80.78	−0.22
${\lambda }_{\mathrm{sync}}=0.5$	Sync weight = 0.5	80.94	−0.06
${\mathit{\lambda }}_{\mathrm{sync}}=\mathbf{1}.\mathbf{0}$ (default)	Default sync weight	81.00	–
${\lambda }_{\mathrm{sync}}=2.0$	Sync weight = 2.0	81.02	+0.02
${\lambda }_{\mathrm{sync}}=4.0$	Sync weight = 4.0	80.88	−0.12
$\eta$-fixed	Fixed step size $\eta =1.0$	80.96	−0.04
$\mathit{\eta }$-learn (default)	Lightweight MLP predicts $\eta \in (0,1]$	81.00	–
$\eta$-linesearch	Line-search single-step backtracking	81.06	+0.06

and Figure 8 show that both excessively small and large values of the synchronization loss of weight ${\lambda }_{\mathrm{sync}}$ degrade performance, with the optimal range falling between 1 and 2, reflecting the moderate constraining effect of angle regularization. Adaptive prediction (81.00) and linear search (81.06) for the step size $\eta$ yield the best results, while a fixed step size leads to degradation, indicating that this module benefits from adaptive strategies during iterative updates.

An analysis of the advantages of strategy collaboration in reinforcement learning.

Table 9. B-3: RL refinement ablation on top of setting C.

Variant	Action Space	mAP	Latency Change
C1 R-Aug only	Learn rotation augmentation angle distribution	80.56	0%
C2 DNMS only	Learn rNMS threshold (class/scale adaptive)	80.48	0%
C3 AMTS only	Learn slice size/stride/overlap/rotation	80.42	+4%
C4 DPA only	Learn rIoU positive/negative thresholds	80.32	0%
C (default)	R-Aug + DNMS + AMTS (with budget)	80.90	+2%

shows that a single action space cannot steadily improve the precision, but instead both show a decrease (−0.34 to −0.58). In particular, DPA alone optimization tends to lead to an imbalance between recall and precision. In contrast, the joint optimization (C) obtains the best mAP (80.90) while ensuring the delay is controllable, indicating that multi-strategy coupling can compensate the limitations with each other, which is the key to RL optimization.

DNMS threshold adjustment and scale sensitivity.

Table 10. C-1: DNMS ablation with scale-specific rNMS IoU thresholds.

Small	Medium	Large	mAP	ΔmAP	Latency
0.35	0.45	0.55	80.72	−0.18	0%
0.40	0.50	0.55 (default)	80.90	–	+2%
0.45	0.55	0.60	81.00	+0.10	+2%
0.50	0.60	0.65	80.84	−0.06	+2%

demonstrates the performance of delay-constrained non-maximal suppression (DNMS) under different scale thresholds. The results show that moderately increasing the IoU thresholds (0.45/0.55/0.60) for medium and large targets can effectively suppress the redundant frames, and the mAP improves to 81.00. The reason is that the adaptive strategy of BPO retains the recall of small targets at higher IoUs and enhances the discriminative power of large targets at the same time. And when the threshold is too high (0.50/0.60/0.65), the discrimination of small targets is weakened, resulting in the overall precision falling back. This indicates that DNMS needs to dynamically balance overlap suppression and small-target retention in multi-scale targets, which is tightly coupled with the delayed budget-scheduling mechanism of BPO.

Interaction of slicing strategy with rotation enhancement.

Table 11. C-2: AMTS ablation with different tile/stride/overlap/rotation settings.

Tile/Stride/Overlap/Rotation	mAP	ΔmAP	Latency
768/256/33%/ON	80.96	+0.06	+6%
1024/384/25%/ON (default)	80.90	–	+2%
1024/384/25%/OFF	80.85	−0.05	+1%
1280/512/20%/ON	80.88	−0.02	−3%

compares the effect of different slicing configurations on accuracy and latency. A smaller tile (768/256/33%) leads to a slight accuracy improvement (80.96) with denser spatial coverage, but a significant increase in inference latency (+6%). In contrast, large tiles (1280/512/20%) reduce redundant computation but result in a slight decrease in mAP due to an increase in misdetection. Turning off rotational enhancement (OFF) resulted in a performance degradation (−0.05), verifying that rotational enhancement is critical for the angular alignment of aerial-type targets (e.g., aircraft, ships). Overall, the design of the AMTS plays a key role in the accuracy–delay trade-off by dynamically selecting the tile scale and rotation switch in the BPO framework.

Rotation enhancement distributions and a priori matching.

Table 12. C-3: R-Aug ablation with different rotation augmentation distributions.

Distribution	Angle/Probability Scheme	mAP	ΔmAP
Uniform	$U[0^{\circ },{180}^{\circ }]$	80.82	−0.08
Bimodal	High weights at $\pm {15}^{\circ }$/$\pm {30}^{\circ }$	81.02	+0.12
Tri-modal (default)	Mix of $0^{\circ }$, $\pm {30}^{\circ }$, and uniform	80.90	–

shows that different rotation enhancement distributions significantly affect model performance. The uniform distribution (Uniform) introduced too many invalid rotations with full angular coverage, leading to a decrease in mAP (80.82). In contrast, the Bimodal distribution (±15°/±30°) has the highest accuracy (81.02) because it is more consistent with the orientation prior (e.g., runway, road, boat direction) in the remote sensing scene. This suggests that LC-BPO can better optimize the angular inconsistency problem and improve the rotational robustness of the model if it is combined with the data distribution prior when learning the enhancement strategy.

Impact of positive and negative sample segmentation on boundary learning.

Table 13. C-4: DPA ablation with different positive/negative rIoU thresholds.

(IoUpos, IoUneg)	mAP	ΔmAP
(0.4, 0.2)	80.60	−0.30
(0.5, 0.3) (default)	80.90	–
(0.6, 0.3)	80.96	+0.06
(0.6, 0.4)	80.88	−0.02

explores the impact of positive and negative thresholds in Dynamic Sample Allocation (DPA) on the results. Looser thresholds (0.4, 0.2) lead to too many mis-matched samples and a significant decrease in mAP (80.60). When the positive threshold is increased to 0.6, the mAP reaches its highest (80.96), suggesting that a stricter definition of positive samples can improve the boundary fitting accuracy. However, if the negative sample threshold is increased to 0.4 at the same time, some of the fuzzy boundary targets are misclassified as negative examples, recall decreases, and the overall performance is not as good as the default setting. This verifies the key role of BPO in threshold scheduling, i.e., dynamic balance between precision and recall.

Robustness of policy optimization with delay budget effect.

Table 14. C-5: Sensitivity analysis of training algorithm, reward weights, and latency budget.

Hyperparameter	Setting	mAP	Latency
Algorithm	PPO (default)	80.90	+2%
	SAC	80.88	+2%
Budget B	10.0 ms	80.70	≤10 ms
	12.5 ms (default)	80.90	≤12.5 ms
	15.0 ms	81.05	≤15 ms
Small-object weight $\beta$	0.0	80.78	+1%
	0.2 (default)	80.90	+2%
	0.5	81.00	+3%
AP surrogate $ϵ$	0.05	80.82	+2%
	0.10 (default)	80.90	+2%
	0.20	80.84	+2%

shows that both PPO and SAC converge stably, verifying the robustness of the reinforcement learning framework. More importantly, the delay budget B has a significant effect on the performance: when relaxed to 15 ms, the mAP improves to 81.05, indicating that the policy space can be more fully explored when resources allow. The mAP reaches 81.00 for small-target weight $\beta =0.5$, indicating that increasing the reward signal for small targets is effective in mitigating the lack of recall. Experiments with the AP agent smoothing factor $ϵ$ show that values either too small or too large can lead to instability, while the default value of 0.1 is optimal. These results demonstrate that BPO can maintain a balance between computational resources, reward design, and convergence stability.

Advantages of module complementarity on complex categories:Figure 9 compares the results for the three most challenging target categories (bridge BR, vessel SV, and helicopter HC). The results show that SE2-ASG alone (B) improves significantly on the geometrically sensitive BR category (+1.8), while LC-BPO alone (C) improves even more on the dynamically distributed SV category (+1.4). The complete scheme (D) combines the two and significantly improves all three classes to 64.1/82.3/67.6. This suggests that angular equivariance modeling with graph neural networks and strategy optimization with reinforcement learning complement each other, with the former addressing angular consistency and boundary stability, and the latter improving the robustness of small targets and complex scenarios, and the synergy is particularly prominent in the complex target classes.

6. Discussion

To qualitatively evaluate ASBPNet’s boundary stability and feature-focusing capability in rotating-object detection, we selected eight representative remote sensing scenes from the DOTA dataset for visual analysis. We selected both conventional conditions (Figure 10) and complex conditions (Figure 11) to discuss the detection performance of both methods. For each scenario, we present the detection results alongside their corresponding attention heatmaps.

In both regular and complex scenes, the activation range of the baseline model YOLOv5-OBB thermogram is relatively diffuse, and many background areas such as water surface and open space show large highlight responses, resulting in the boundaries and contours of the foreground targets not being clear enough, and the detection frame Angular drift and boundary jitter occur, reflecting the model’s deficiencies in rotational consistency and feature focusing. In contrast, the activation distribution of the ASBPNet heatmap is obviously more focused on the actual buildings and dock structures, with clear boundaries, target contours, and geometries being better portrayed, while the responses from the water surface and other irrelevant areas are effectively suppressed. The effectiveness of the proposed BPO method in suppressing irrelevant surface texture and background shadows is verified.

The resulting detection frames are highly consistent with the orientation and geometry of the real target, which fully demonstrates the robust detection and focusing capability of the model on regular small targets and boundary-sensitive targets. Comparing the detection result plots of the two methods, some of the detection frames generated by the baseline method fail to achieve accurate wrapping of the target, and there is a slight boundary jitter. Taking the aircraft in the first row of Figure 10 as an example, the detection frame of the baseline method has a large offset from the real boundary in the left wing region, while ASBPNet is able to achieve a highly consistent fit with the contour of the airframe. In the second and third rows of vehicle detection, the detection frame generated by the baseline method does not fit well with the vehicle boundary, and the tail of some vehicles still maintains a certain distance from the detection frame, while ASBPNet is able to achieve complete coverage of the target. In the tennis court detection task in the fourth row, the detection frame of the baseline method has obvious deviation between the left boundary and the real field, while ASBPNet shows significant advantages in boundary fitting and achieves a high degree of consistency with the target contour.

7. Conclusions

In this paper, we propose a unified detection framework that combines geometric perception and policy optimization to address the key problems of remote sensing object detection, such as insufficient small-target recall, unstable boundary fitting, and inference delay due to multi-policy coupling. The core of the method includes two innovative modules, Angle-Synchronized Graph Head (ASG) and Bilevel Policy Optimization (BPO). The former achieves angular consistency modeling and boundary residual optimization by constructing graph structures between candidate frames and introducing rotational equivariant messaging, thus significantly mitigating the boundary jitter and angular deviation problems of rotating small targets. The latter unifies multiple non-differentiation strategies in the training and inference phases into a reinforcement learning optimization framework through the modules of rotational augmentation, sample allocation, multi-block scanning, and rotational NMS, which enables the detector to achieve dynamic accuracy–efficiency trade-offs under delay constraints.

In the experimental part, this paper performs systematic validation on several remote sensing rotating frame detection datasets such as DIOR-R, HRSC2016, and DOTA-v1.0. The results show that the method outperforms the baseline YOLOv5-OBB in terms of overall accuracy and achieves significant performance improvement on complex categories such as bridges, ships and helicopters. Meanwhile, ablation experiments further validate the complementary nature of the two modules: while ASG mainly improves angular consistency and geometric stability, BPO effectively improves small-target recall and multi-strategy adaptivity, and the combination of the two can achieve optimal performance.

Overall, the framework proposed in this paper breaks through the bottleneck of existing methods in rotational consistency modeling and delay constraint optimization while maintaining lightweight and real-time performance. It not only provides a new solution for rotating target detection in remote sensing under complex background but also provides a useful exploration for the deep integration of graph neural networks and reinforcement learning in remote sensing visual tasks.

For future work, we aim to explore several research directions that further leverage the unique synergy between geometry-aware representation and policy optimization in ASBPNet. One direction is cross-modal adaptation. We will extend ASG to align geometric cues across optical, SAR, and multispectral inputs and couple this with a policy module that selects modality-specific scanning and suppression strategies. Another direction is efficient large-model migration. We will study adapter-style modules, low-rank adaptation and policy-conditioned fine-tuning to transfer pretrained backbones while keeping ASG’s structural priors intact and maintaining low FLOPs. We will also investigate temporal and multi-resolution designs so that ASG can aggregate spatio-temporal geometry and BPO can schedule computation dynamically across frames and scales. We will validate these extensions through transfer experiments, per-class robustness tests, and deployment-aware latency–accuracy trade-off analysis.