Correcting Atmospheric Temperature and Vapor Density Profiles of Ground-Based Microwave Radiometer in Diverse Skies by Regression Model and Artificial Neural Network Methods
Highlights
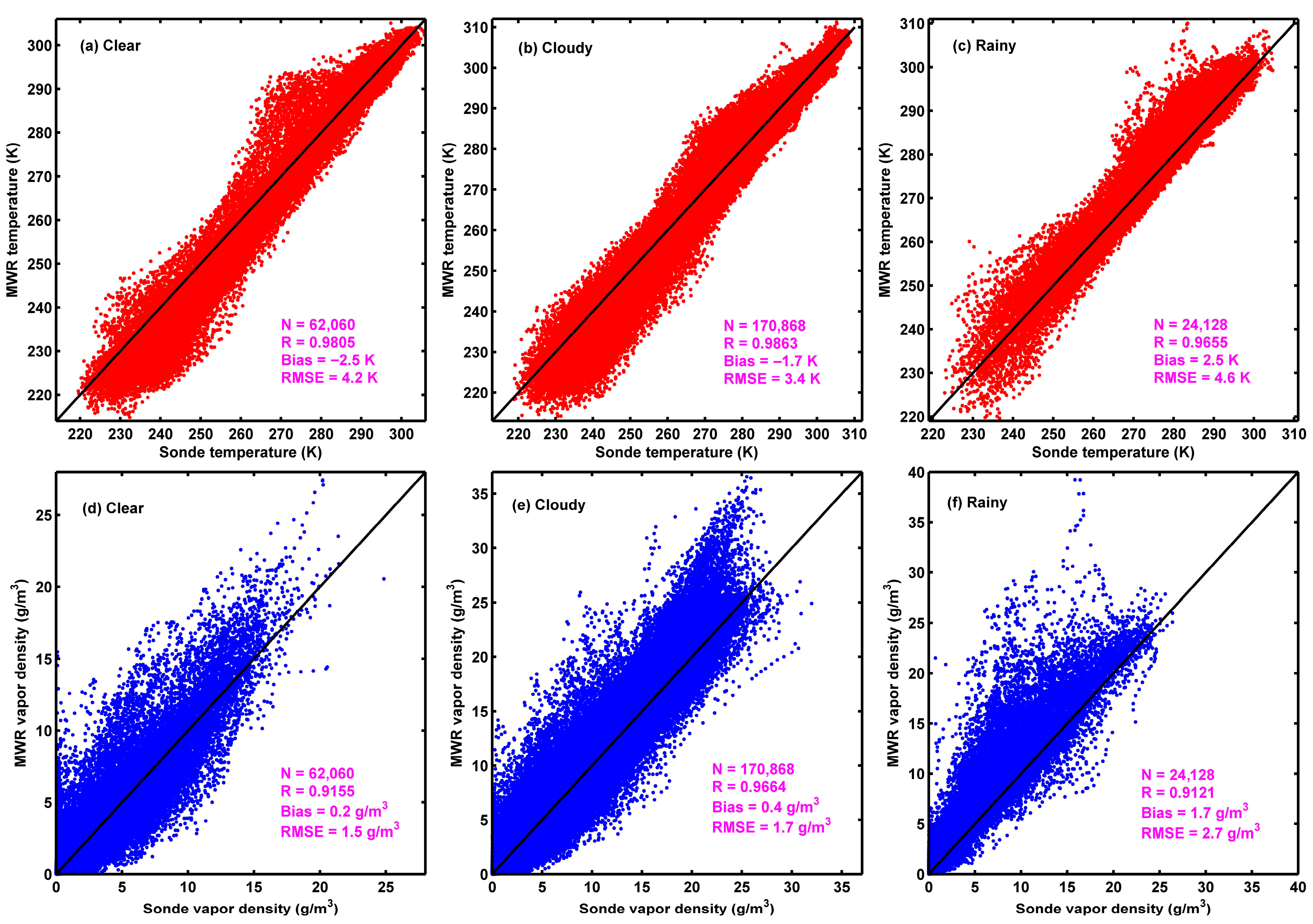
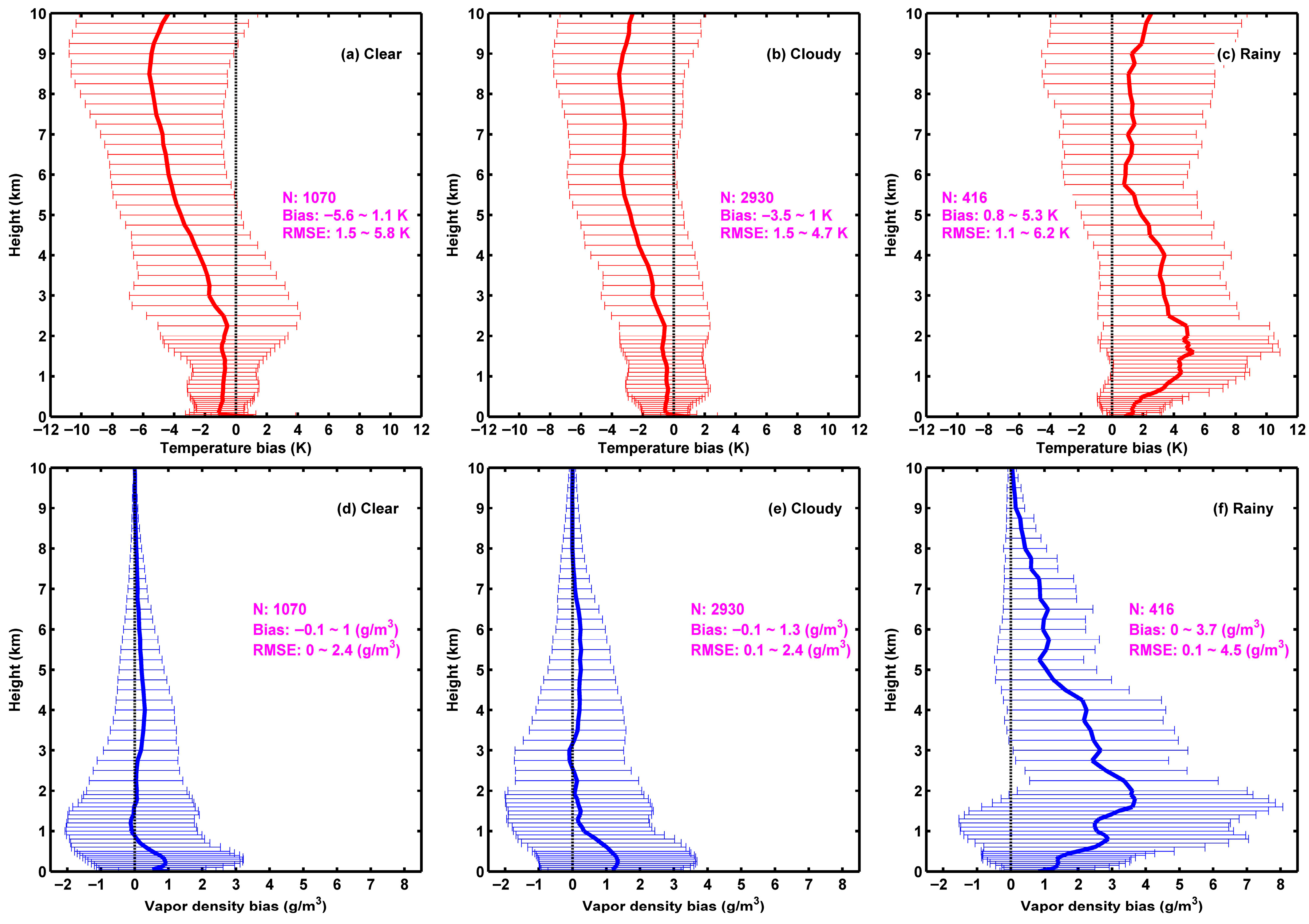
- Radiosonde temperature has a positive bias, while the humidity has a dry bias due to solar heating, and this leads to MWR temperature being colder and MWR vapor density being wetter than radiosondes in clear and cloudy skies. But, in rainy skies, the impact of raindrops results in a pseudo-high brightness temperature, which consequently leads to MWR temperature becoming warmer than radiosondes, while the wet MWR vapor density becomes more significant.
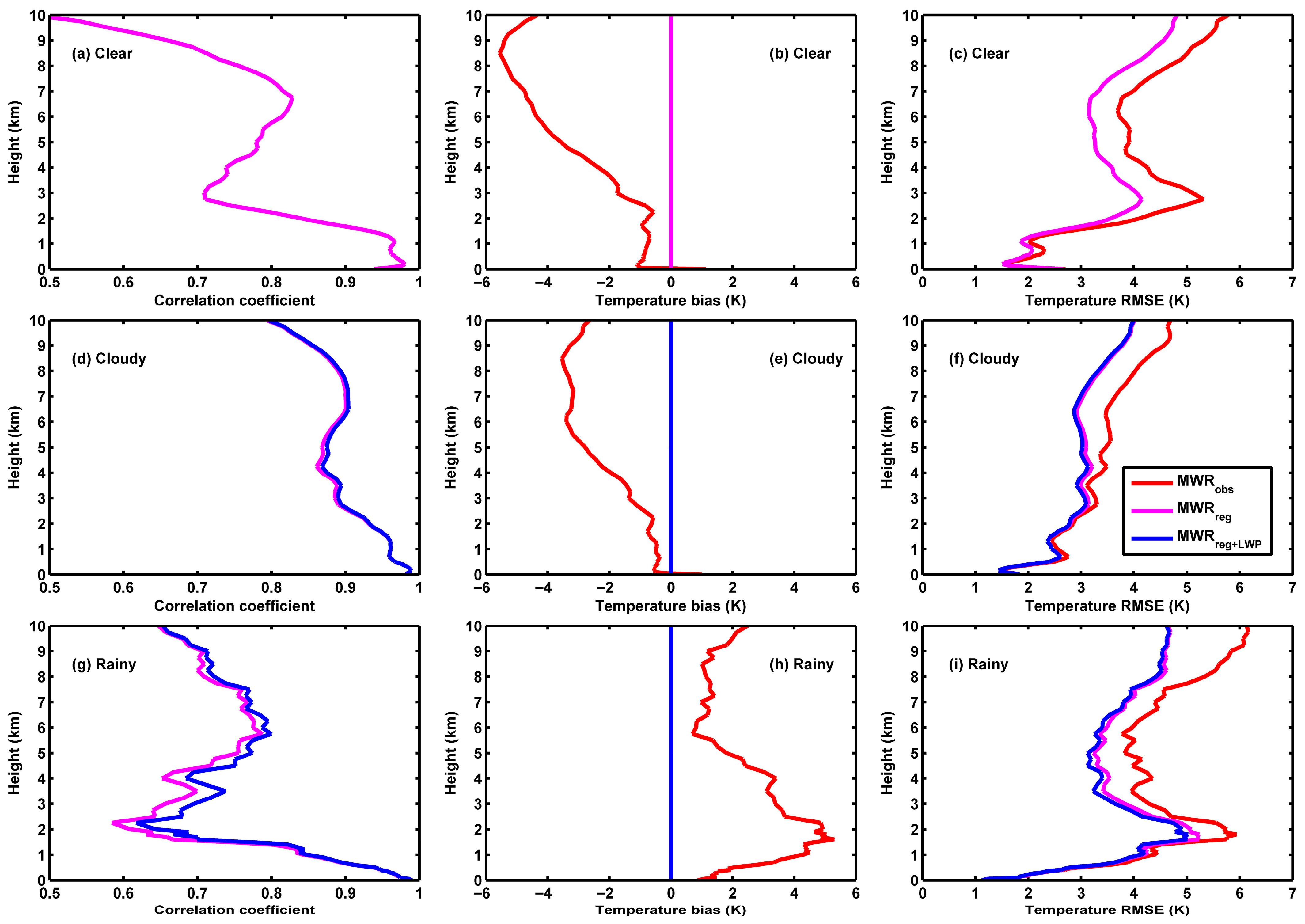
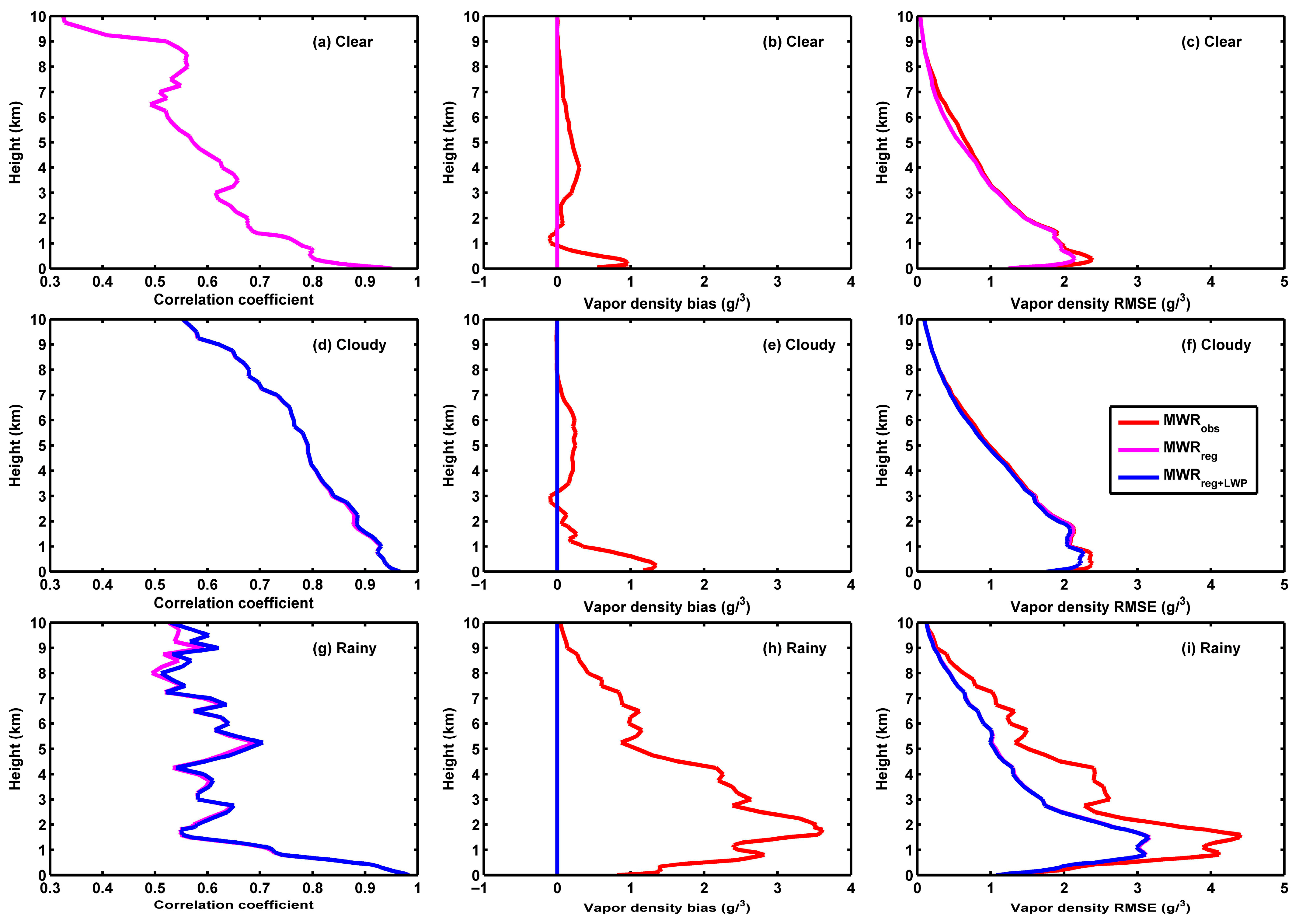
- Both regression and ANN models can reduce the biases of MWR temperature and vapor density against radiosondes to around zero in diverse skies. Moreover, after correcting using a regression model, the RMSEs of MWR temperature (vapor density) in clear, cloudy, and rainy skies decline by 14% (7%), 7% (4%), and 12% (29%), respectively, and the correction effect of the ANN model is slightly better than the regression model, with corresponding decreases of 19% (8%), 10% (8%), and 12% (30%), respectively.
- The deviation of MWR retrievals from radiosonde measurements is caused by various factors, many of which depend on atmospheric conditions, and this results in different characteristics of MWR retrieval deviation in diverse skies. Therefore, correcting MWR retrieval deviation may require different methods.
- Regression and ANN models have a reasonable ability to correct MWR retrieval deviation in diverse skies. However, there is remaining room for further improvement in MWR retrieval accuracy, especially in rainy skies.
Abstract
1. Introduction
2. Materials and Methods
3. Results
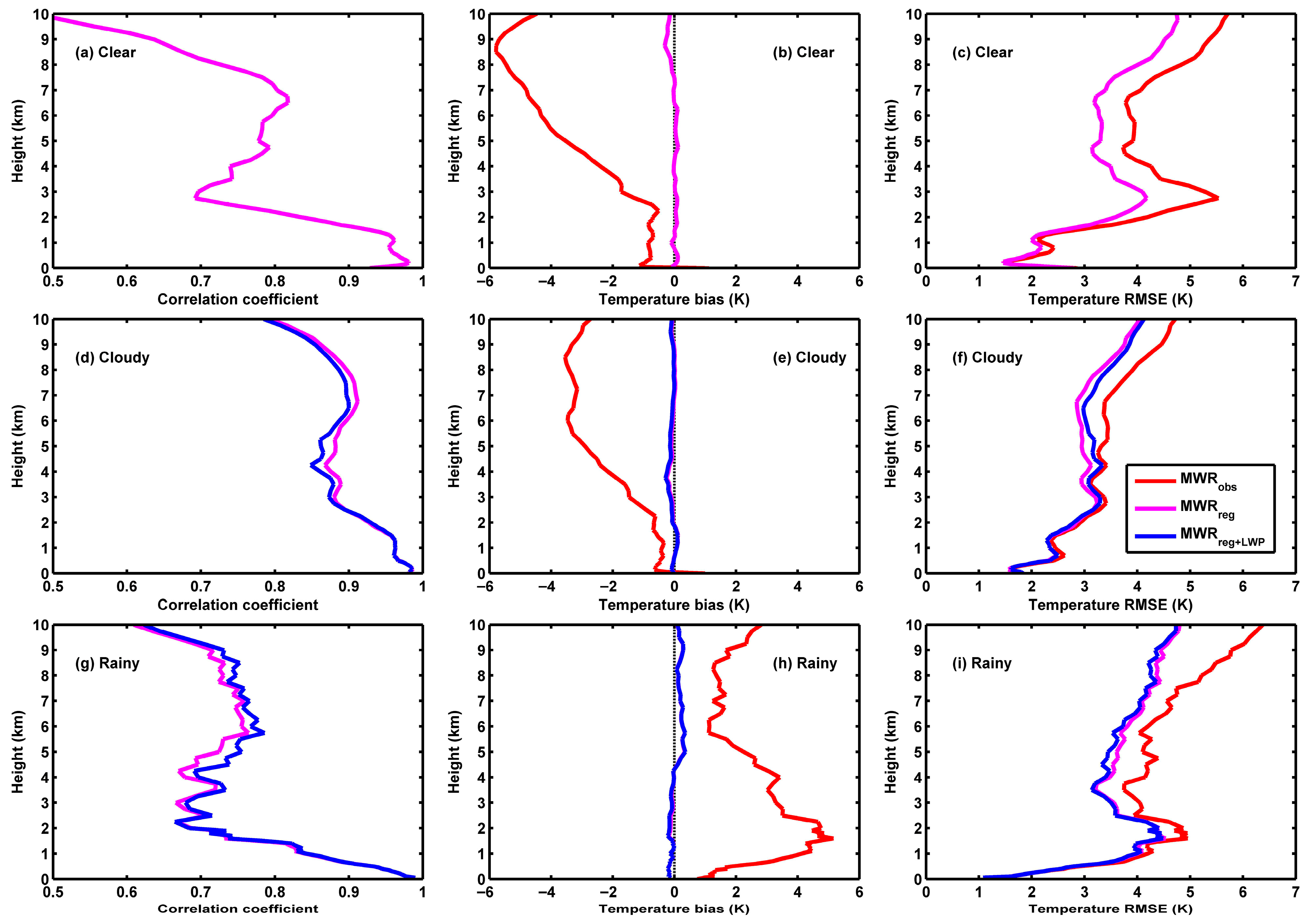
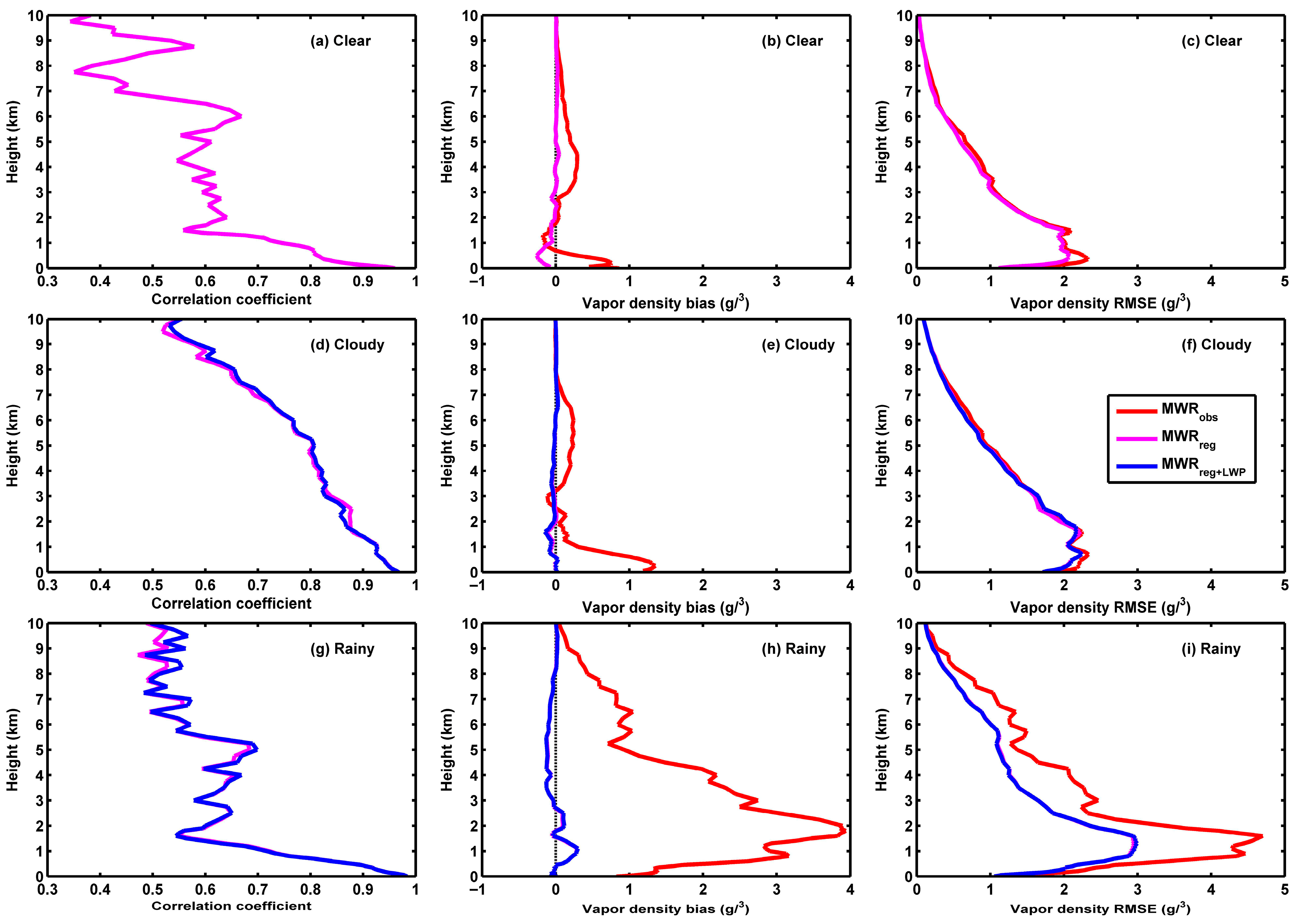
3.1. Deviations of MWR Temperature and Vapor Density in Diverse Skies
3.2. Correction of MWR Temperature and Vapor Density by Regression Model Method
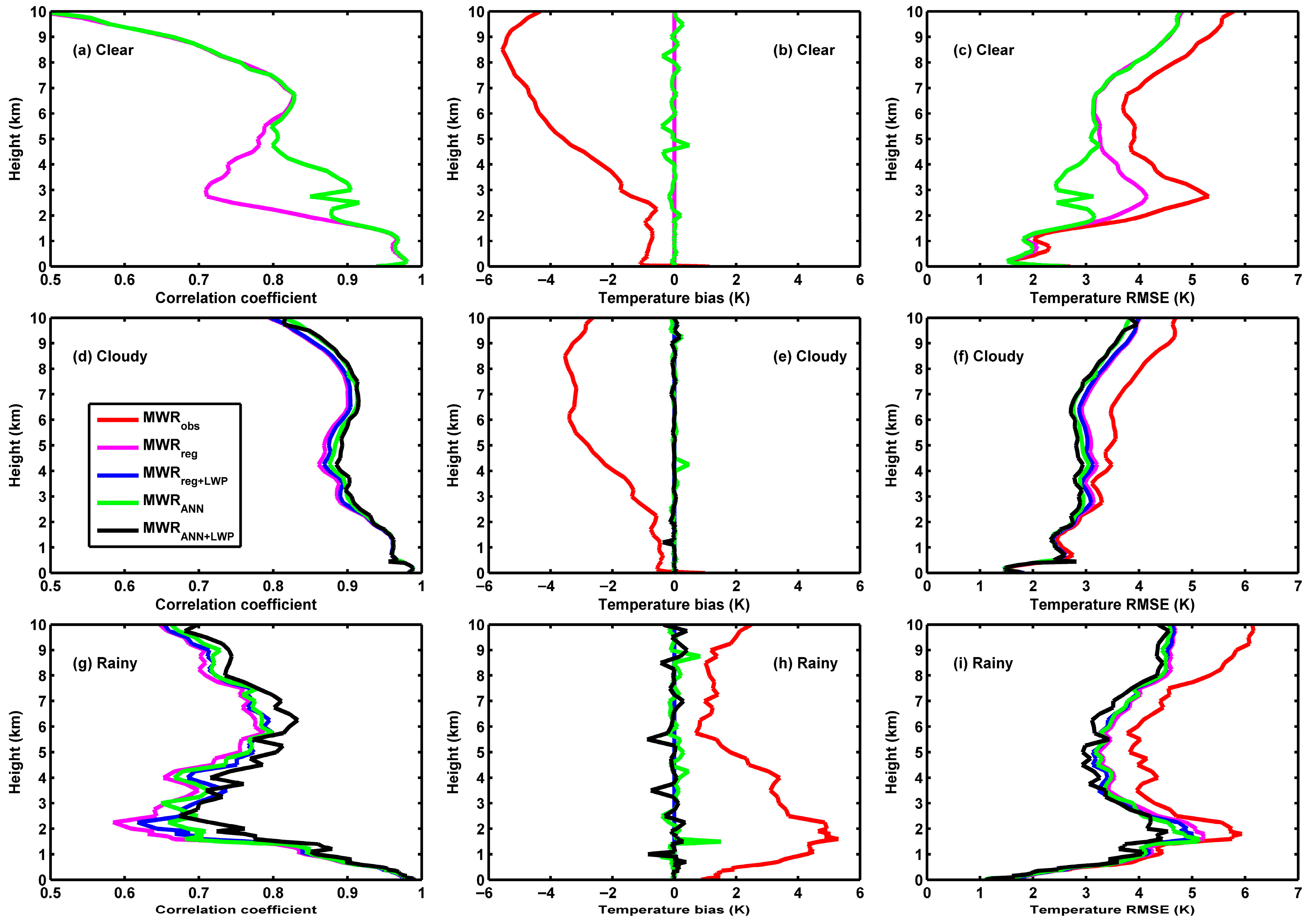
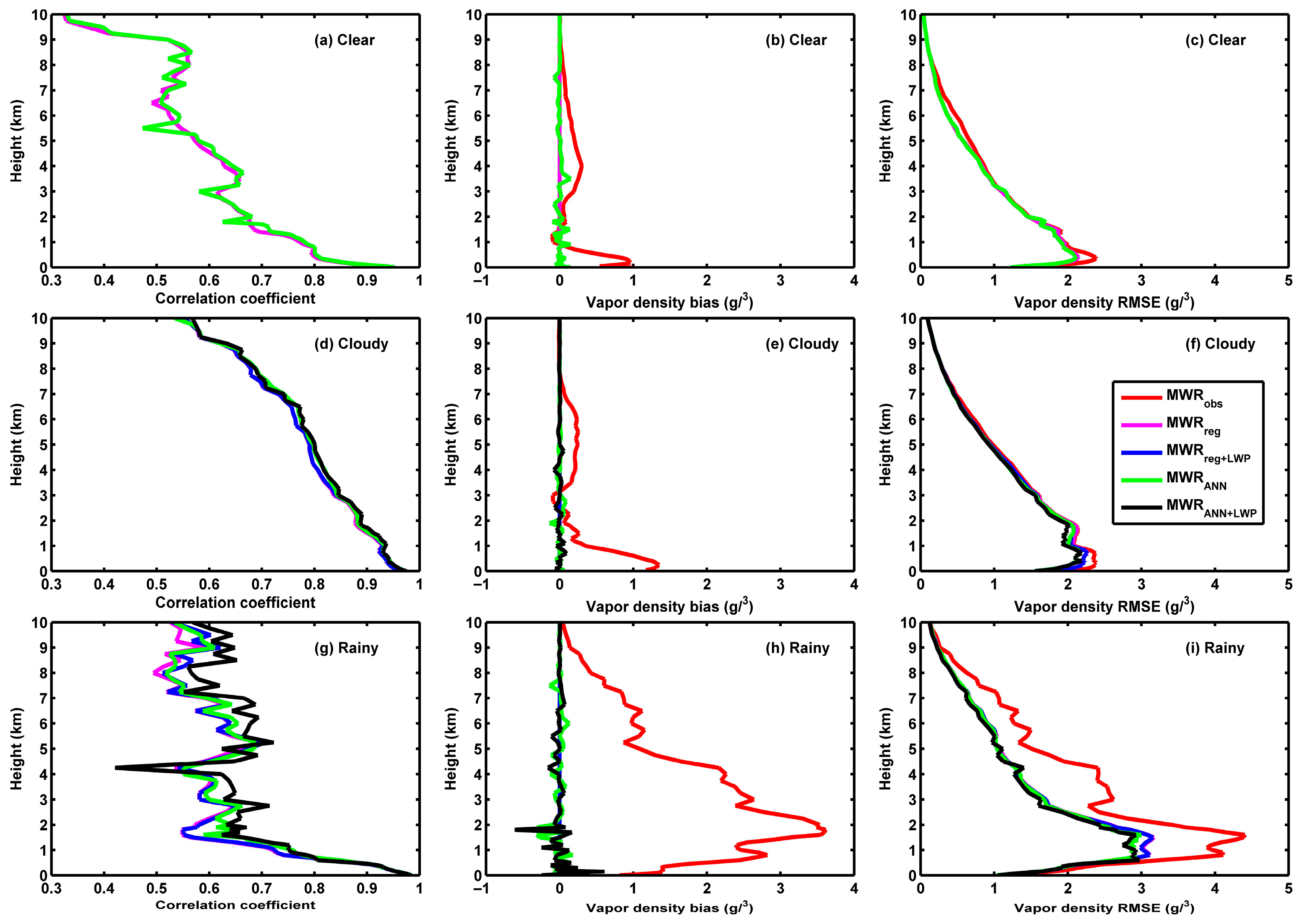
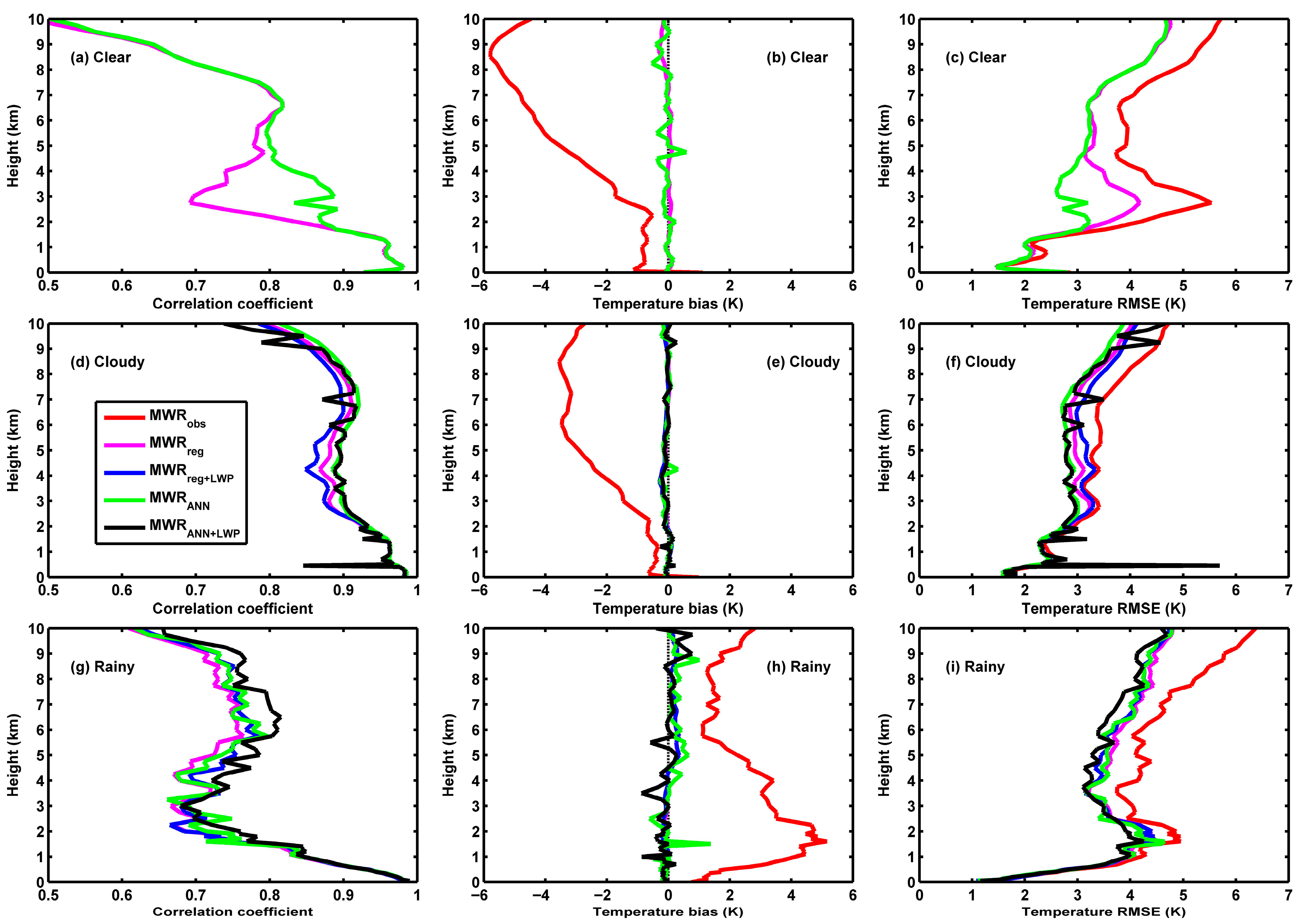
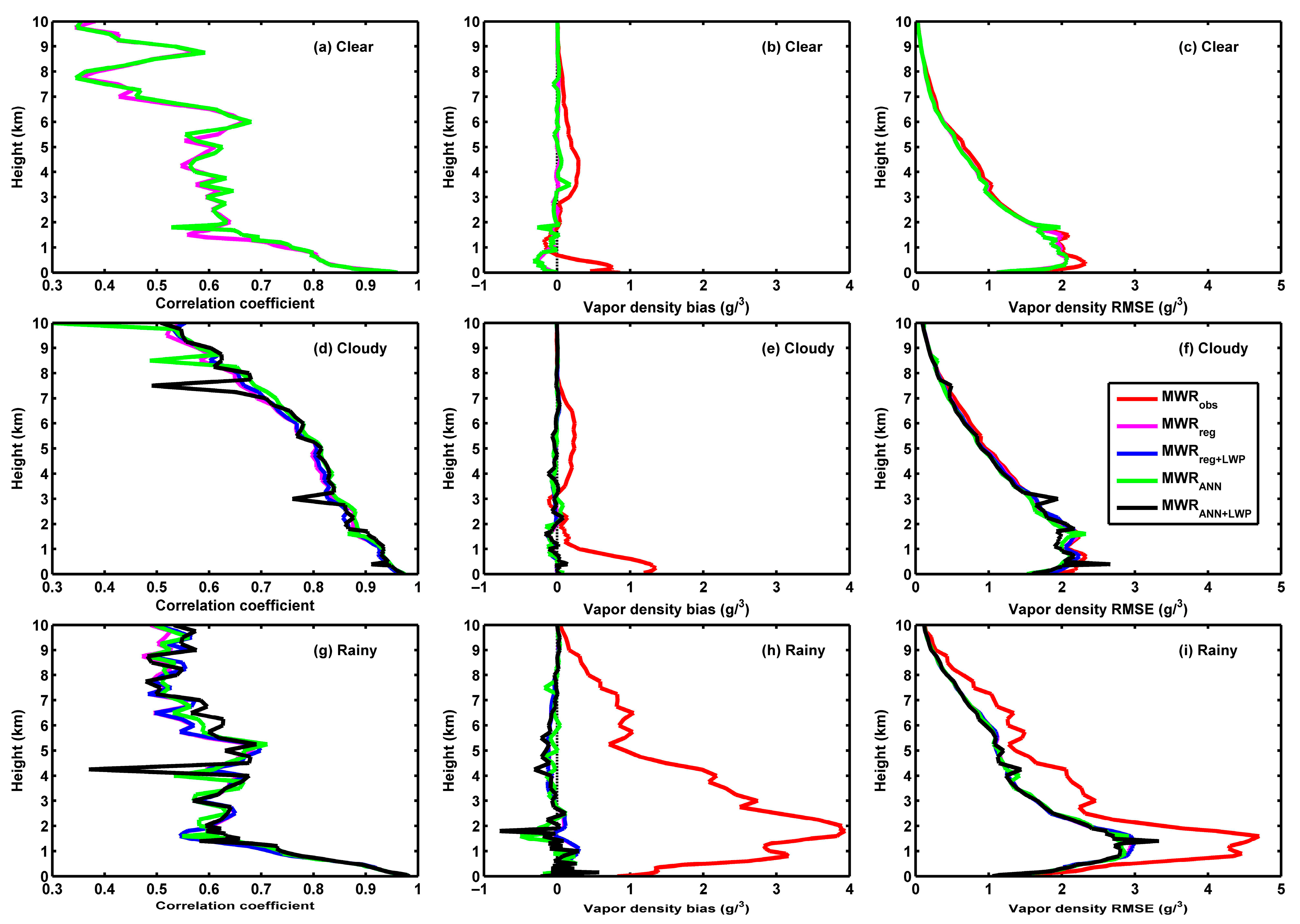
3.3. Correction of MWR Temperature and Vapor Density Through ANN Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MWR | Microwave radiometer |
| LWC | Liquid water content |
| IWV | Integrated water vapor |
| LWP | Liquid water path |
| ANN | Artificial neural network |
| IRT | Infrared thermometer |
| CBH | Cloud base height |
| RMSE | Root mean square error |
| MWRobs | Observed MWR retrievals |
| MWRreg | MWR retrievals recalculated with regression model |
| MWRreg+LWP | MWR retrievals recalculated with regression model, adding LWP as an input |
| MWRANN | MWR retrievals recalculated with ANN model |
| MWRANN+LWP | MWR retrievals recalculated with ANN model, adding LWP as an input |
References
- Wang, J.; Rossow, W.B. Determination of cloud vertical structure from upper-air observations. J. Appl. Meteor. 1995, 34, 2243–2258. [Google Scholar] [CrossRef]
- Thorne, P.W.; Parker, D.E.; Christy, J.R.; Mears, C.A. Uncertainties in climate trends: Lessons from upper-air temperature records. Bull. Am. Meteor. Soc. 2005, 86, 1437–1442. [Google Scholar] [CrossRef]
- Illingworth, A.; Cimini, D.; Haefele, A.; Haeffelin, M.; Hervo, M.; Kotthaus, S.; Löhnert, U.; Martinet, P.; Mattis, I.; O’Connor, E.; et al. How can existing ground-based profiling instruments improve European weather forecast? Bull. Am. Meteor. Soc. 2019, 100, 605–619. [Google Scholar] [CrossRef]
- Tang, Y.; Xu, G.; Wan, R.; Wang, X.; Wang, J.; Li, P. Atmospheric thermal and dynamic vertical structures of summer hourly precipitation in Jiulong of the Tibetan Plateau. Atmosphere 2021, 12, 505. [Google Scholar] [CrossRef]
- Angell, J.K. Variations and trends in tropospheric and stratospheric global temperatures, 1958–1987. J. Clim. 1998, 1, 1296–1313. [Google Scholar] [CrossRef]
- Thompson, D.W.J.; Solomon, S. Recent stratospheric climate trends as evidenced in radiosonde data: Global structure and tropospheric linkages. J. Clim. 2005, 18, 4785–4794. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Schreiner, W.S.; Wang, J.; Rossiter, D.L.; Zhang, Y. Comparison of GPS radio occultation soundings with radiosondes. Geophys. Res. Lett. 2005, 32, L05817. [Google Scholar] [CrossRef]
- Xu, G.; Yue, X.; Zhang, W.; Wan, X. Assessment of atmospheric wet profiles obtained from COSMIC radio occultation observations over China. Atmosphere 2017, 8, 208. [Google Scholar] [CrossRef]
- Xue, Q.; Guan, L.; Shi, X. One-dimensional variational retrieval of temperature and humidity profiles from the FY4A GIIRS. Adv. Atmos. Sci. 2022, 39, 471–486. [Google Scholar] [CrossRef]
- Cui, C.G.; Zhou, W.; Yang, H.; Wang, X.K.; Deng, Y.; Wang, X.F.; Xu, G.R.; Wang, J.Y. Analysis of the characteristics of the low-level jets in the middle reaches of the Yangtze River during the Mei-yu season. Adv. Atmos. Sci. 2023, 40, 711–724. [Google Scholar] [CrossRef]
- Ware, R.; Carpenter, R.; Güldner, J.; Liljegren, J.; Nehrkorn, T.; Solheim, F.; Vandenberghe, F. A multi-channel radiometric profiler of temperature, humidity and cloud liquid. Radio Sci. 2003, 38, 8079. [Google Scholar] [CrossRef]
- Westwater, E.R.; Crewell, S.; Mätzler, C. A review of surfaced-based microwave and millimeter-wave radiometric remote sensing of the Troposphere. Radio Sci. Bull. 2004, 310, 59–80. [Google Scholar] [CrossRef]
- Güldner, J.; Spänkuch, D. Remote sensing of the thermodynamic state of the atmospheric boundary layer by ground-based microwave radiometry. J. Atmos. Ocean. Technol. 2001, 18, 925–933. [Google Scholar] [CrossRef]
- Ware, R.; Cimini, D.; Campos, E.; Giuliani, G.; Albers, S.; Nelson, M.; Koch, S.E.; Joe, P.; Cober, S. Thermodynamic and liquid profiling during the 2010 Winter Olympics. Atmos. Res. 2013, 132–133, 278–290. [Google Scholar] [CrossRef]
- Madhulatha, A.; Rajeevan, M.; Ratnam, M.V.; Bhate, J.; Naidu, C.V. Nowcasting severe convective activity over southeast India using ground-based microwave radiometer observations. J. Geophys. Res. Atmos. 2013, 118, 1–13. [Google Scholar] [CrossRef]
- Cimini, D.; Nelson, M.; Güldner, J.; Ware, R. Forecast indices from a ground-based microwave radiometer for operational meteorology. Atmos. Meas. Technol. 2015, 8, 315–333. [Google Scholar] [CrossRef]
- Xu, G. A review of remote sensing of atmospheric profiles and cloud properties by ground-based microwave radiometers in central China. Remote Sens. 2024, 16, 966. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, C.; Li, Y.; Sun, J.; Chen, Z.; Li, L. Concurrence of temperature and humidity inversions in winter in Qingdao, China. Geophys. Res. Lett. 2024, 51, e2024GL108350. [Google Scholar] [CrossRef]
- Wei, J.; Shi, Y.; Ren, Y.; Li, Q.; Qiao, Z.; Cao, J.; Ayantobo, O.O.; Yin, J.; Wang, G. Application of ground-based microwave radiometer in retrieving meteorological characteristics of Tibet Plateau. Remote Sens. 2021, 13, 2527. [Google Scholar] [CrossRef]
- Wang, W.; Hocke, K. Atmospheric effects and precursors of rainfall over the Swiss Plateau. Remote Sens. 2022, 14, 2938. [Google Scholar] [CrossRef]
- Cheng, X.; Xu, X.; Bai, G.; Wang, R.; Ma, J.; Su, D.; Chen, B.; Ma, S.; Hu, C.; Zhang, S.; et al. Mobile observation field experiment of atmospheric vertical structure and its application in precipitation forecasts over the Tibetan Plateau. J. Geophys. Res. Atmos. 2024, 129, e2024JD042467. [Google Scholar] [CrossRef]
- Askne, J.I.H.; Westwater, E.R. A review of ground-based remote sensing of temperature and moisture by passive microwave radiometers. IEEE Trans. Geosci. Remote Sens. 1986, GE-24, 340–352. [Google Scholar] [CrossRef]
- Xu, G.; Xi, B.; Zhang, W.; Cui, C.; Dong, X.; Liu, Y.; Yan, G. Comparison of atmospheric profiles between microwave radiometer retrievals and radiosonde soundings. J. Geophys. Res. Atmos. 2015, 120, 10313–10323. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, X.; Mao, J.; Wang, Z. Comparison analysis on detection performance of ground-based microwave radiometers under different weather conditions. J. Appl. Meteorol. Sci. 2018, 29, 282–295. (In Chinese) [Google Scholar] [CrossRef]
- Wu, M.; Bao, Y.; Mao, J.; Zhang, H.; Li, W. Research on bias analysis and correction of temperature and humidity data with ground-based microwave radiometer. Torrential Rain Disasters 2023, 42, 467–478. (In Chinese) [Google Scholar] [CrossRef]
- Xu, G.; Ware, R.; Zhang, W.; Feng, G.; Liao, K.; Liu, Y. Effect of off-zenith observations on reducing the impact of precipitation on ground-based microwave radiometer measurement accuracy. Atmos. Res. 2014, 140–141, 85–94. [Google Scholar] [CrossRef]
- Chan, P.W. Performance and application of a multi-wavelength, ground-based microwave radiometer in intense convective weather. Meteorol. Z. 2009, 18, 253–265. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, F.; Xu, G.; Li, D.; Yuan, Z.; Xiong, J. Comparative analysis of the zenith and off-zenith retrieved results from microwave radiometer in rain and snow weather conditions. Torrential Rain Disasters 2015, 34, 375–383. (In Chinese) [Google Scholar] [CrossRef]
- Foth, A.; Lochmann, M.; Garfias, P.S.; Kalesse-Los, H. Determination of low-level temperature profiles from microwave radiometer observations during rain. Atmos. Meas. Technol. 2024, 17, 7169–7181. [Google Scholar] [CrossRef]
- Li, Q.; Wei, M.; Wang, Z.; Chu, Y. Evaluation and improvement of the quality of ground-based microwave radiometer clear-sky data. Atmosphere 2021, 12, 435. [Google Scholar] [CrossRef]
- Li, Q.; Wei, M.; Wang, Z.; Jiang, S.; Chu, Y. Improving the retrieval of cloudy atmospheric profiles from brightness temperatures observed with a ground-based microwave radiometer. Atmosphere 2021, 12, 648. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, D.; Yan, H. An improved retrieval method of atmospheric parameter profiles based on the BP neural network. Atmos. Res. 2018, 213, 389–397. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhou, D.; Liu, C.; Wu, P.; Li, L.; Zhang, L.; Cheng, W. Numerical correction of atmospheric temperature profiles in clear and cloudy days. Atmos. Res. 2019, 217, 49–56. [Google Scholar] [CrossRef]
- Vömel, H.; Selkirk, H.; Miloshevich, L.; Valverde-Canossa, J.; Valdes, J.; Kyro, E.; Kivi, R.; Stolz, W.; Peng, G.; Diaz, J. Radiation dry bias of the Vaisala RS92 humidity sensor. J. Atmos. Ocean. Technol. 2007, 24, 953–963. [Google Scholar] [CrossRef]
- Yoneyama, K.; Fujita, M.; Sato, N.; Fujiwara, M.; Inai, Y.; Hasebe, F. Correction for radiation dry bias found in RS(@ radiosonde data during the MISMO field experiment. SOLA 2008, 4, 13–16. [Google Scholar] [CrossRef]
- Bian, J.; Chen, H.; Vömel, H.; Duan, Y.; Xuan, Y.; Lü, D. Intercomparison of humidity and temperature sensors: GTS1, Vaisala RS80, and CFH. Adv. Atmos. Sci. 2011, 28, 139–146. [Google Scholar] [CrossRef]
- Mao, J.; Zhang, X.; Wang, Z.; Yang, R.; Pan, X.; Ji, C.; Guo, R. Comparison of brightness temperature of multi-type ground-based microwave radiometers. J. Appl. Meteorol. Sci. 2018, 29, 724–736. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, H.; Wu, P.; Zhou, D. Linear correction method for improved atmospheric vertical profile retrieval based on ground-based microwave radiometer. Atmos. Res. 2020, 232, 104678. [Google Scholar] [CrossRef]

| Analysis Parameters 1 | Sky Conditions | Sample Number | Correlation Coefficient | Confidence Level |
|---|---|---|---|---|
| Tbias vs. R1 | rainy | 416 | 0.2016 | >99% |
| TRMSE vs. R1 | rainy | 416 | 0.0217 | 34% |
| VDbias vs. R1 | rainy | 416 | 0.3183 | >99% |
| VDRMSE vs. R1 | rainy | 416 | 0.2910 | >99% |
| Tbias vs. LWP | rainy | 416 | 0.4412 | >99% |
| TRMSE vs. LWP | rainy | 416 | 0.1910 | >99% |
| VDbias vs. LWP | rainy | 416 | 0.4914 | >99% |
| VDRMSE vs. LWP | rainy | 416 | 0.3392 | >99% |
| Tbias vs. LWP | cloudy | 2930 | 0.2139 | >99% |
| TRMSE vs. LWP | cloudy | 2930 | −0.0123 | 49% |
| VDbias vs. LWP | cloudy | 2930 | 0.2031 | >99% |
| VDRMSE vs. LWP | cloudy | 2930 | 0.0548 | >99% |
| Sky Conditions | Temperature Dataset | Sample Size | R | Bias (K) | RMSE (K) |
|---|---|---|---|---|---|
| Clear | MWRobs | 214 | 0.8237 | −2.5 | 3.6 |
| Clear | MWRreg | 214 | 0.8237 | 0 | 3.1 |
| Cloudy | MWRobs | 586 | 0.9192 | −1.7 | 3.0 |
| Cloudy | MWRreg | 586 | 0.9192 | 0 | 2.8 |
| Cloudy | MWRreg+LWP | 586 | 0.9136 | −0.1 | 2.8 |
| Rainy | MWRobs | 83 | 0.7822 | 2.6 | 4.1 |
| Rainy | MWRreg | 83 | 0.7822 | 0 | 3.6 |
| Rainy | MWRreg+LWP | 83 | 0.7915 | 0 | 3.6 |
| Sky Conditions | Vapor Density Dataset | Sample Size | R | Bias (g/m3) | RMSE (g/m3) |
|---|---|---|---|---|---|
| Clear | MWRobs | 214 | 0.6355 | 0.17 | 1.17 |
| Clear | MWRreg | 214 | 0.6355 | −0.05 | 1.09 |
| Cloudy | MWRobs | 586 | 0.8125 | 0.37 | 1.41 |
| Cloudy | MWRreg | 586 | 0.8125 | −0.02 | 1.35 |
| Cloudy | MWRreg+LWP | 586 | 0.8146 | −0.02 | 1.36 |
| Rainy | MWRobs | 83 | 0.6631 | 1.76 | 2.20 |
| Rainy | MWRreg | 83 | 0.6631 | 0.01 | 1.56 |
| Rainy | MWRreg+LWP | 83 | 0.6673 | 0.01 | 1.57 |
| Sky Conditions | Temperature Dataset | Sample Size | R | Bias (K) | RMSE (K) |
|---|---|---|---|---|---|
| Clear | MWRobs | 214 | 0.8237 | −2.5 | 3.6 |
| Clear | MWRreg | 214 | 0.8237 | 0 | 3.1 |
| Clear | MWRANN | 214 | 0.8474 | 0 | 2.9 |
| Cloudy | MWRobs | 586 | 0.9192 | −1.7 | 3.0 |
| Cloudy | MWRreg | 586 | 0.9192 | 0 | 2.8 |
| Cloudy | MWRreg+LWP | 586 | 0.9136 | −0.1 | 2.8 |
| Cloudy | MWRANN | 586 | 0.9267 | 0 | 2.7 |
| Cloudy | MWRANN+LWP | 586 | 0.9175 | 0 | 2.8 |
| Rainy | MWRobs | 83 | 0.7822 | 2.6 | 4.1 |
| Rainy | MWRreg | 83 | 0.7822 | 0 | 3.6 |
| Rainy | MWRreg+LWP | 83 | 0.7915 | 0 | 3.6 |
| Rainy | MWRANN | 83 | 0.7931 | 0.1 | 3.6 |
| Rainy | MWRANN+LWP | 83 | 0.8111 | −0.1 | 3.4 |
| Sky Conditions | Vapor Density Dataset | Sample Size | R | Bias (g/m3) | RMSE (g/m3) |
|---|---|---|---|---|---|
| Clear | MWRobs | 214 | 0.6355 | 0.17 | 1.17 |
| Clear | MWRreg | 214 | 0.6355 | −0.05 | 1.09 |
| Clear | MWRANN | 214 | 0.6415 | −0.05 | 1.08 |
| Cloudy | MWRobs | 586 | 0.8125 | 0.37 | 1.41 |
| Cloudy | MWRreg | 586 | 0.8125 | −0.02 | 1.35 |
| Cloudy | MWRreg+LWP | 586 | 0.8146 | −0.02 | 1.36 |
| Cloudy | MWRANN | 586 | 0.8172 | −0.02 | 1.30 |
| Cloudy | MWRANN+LWP | 586 | 0.8155 | −0.01 | 1.33 |
| Rainy | MWRobs | 83 | 0.6631 | 1.76 | 2.20 |
| Rainy | MWRreg | 83 | 0.6631 | 0.01 | 1.56 |
| Rainy | MWRreg+LWP | 83 | 0.6673 | 0.01 | 1.57 |
| Rainy | MWRANN | 83 | 0.6701 | −0.03 | 1.55 |
| Rainy | MWRANN+LWP | 83 | 0.6772 | −0.03 | 1.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Tang, Y.; Gou, A.; Wang, Y.; Yang, W.; Yan, J. Correcting Atmospheric Temperature and Vapor Density Profiles of Ground-Based Microwave Radiometer in Diverse Skies by Regression Model and Artificial Neural Network Methods. Remote Sens. 2025, 17, 3819. https://doi.org/10.3390/rs17233819
Xu G, Tang Y, Gou A, Wang Y, Yang W, Yan J. Correcting Atmospheric Temperature and Vapor Density Profiles of Ground-Based Microwave Radiometer in Diverse Skies by Regression Model and Artificial Neural Network Methods. Remote Sensing. 2025; 17(23):3819. https://doi.org/10.3390/rs17233819
Chicago/Turabian StyleXu, Guirong, Yonglan Tang, Aning Gou, Yiqin Wang, Weifa Yang, and Jing Yan. 2025. "Correcting Atmospheric Temperature and Vapor Density Profiles of Ground-Based Microwave Radiometer in Diverse Skies by Regression Model and Artificial Neural Network Methods" Remote Sensing 17, no. 23: 3819. https://doi.org/10.3390/rs17233819
APA StyleXu, G., Tang, Y., Gou, A., Wang, Y., Yang, W., & Yan, J. (2025). Correcting Atmospheric Temperature and Vapor Density Profiles of Ground-Based Microwave Radiometer in Diverse Skies by Regression Model and Artificial Neural Network Methods. Remote Sensing, 17(23), 3819. https://doi.org/10.3390/rs17233819






