Evaluating Airborne Thermal Infrared Hyperspectral Data for Leaf Area Index Retrieval in Temperate Forests
Highlights
- TIR narrowband indices demonstrated poor performance in estimating LAI.
- Wavebands located at 8.1 µm, 9.1 µm, 9.85–9.95 µm, and 9.99–10.27 µm domains are effective in predicting LAI.
- The ANN approach using the Levenberg–Marquardt algorithm outperformed the PLSR model in retrieving LAI using TIR hyperspectral data.
- The main implication of our findings is that TIR hyperspectral data can reliably be used for LAI estimation in real-world fields and airborne conditions, not just in controlled laboratory experiments.
- Equally important is the discovery that specific TIR wavebands (8.1 µm, 9.1 µm, 9.85–9.95 µm, and 9.99–10.27 µm) consistently perform well across different environments and measurement setups. This suggests these wavebands are robust predictors of LAI, making them particularly valuable for operational monitoring.
- From a practical standpoint, the findings have direct implications for scaling up LAI estimation to regional and global levels, since these wavebands overlap with the capabilities of next-generation thermal satellite missions. This means that LAI monitoring could be integrated into future Earth observation programs, expanding the role of TIR data in vegetation and ecosystem monitoring.
Abstract
1. Introduction
2. Materials and Methods
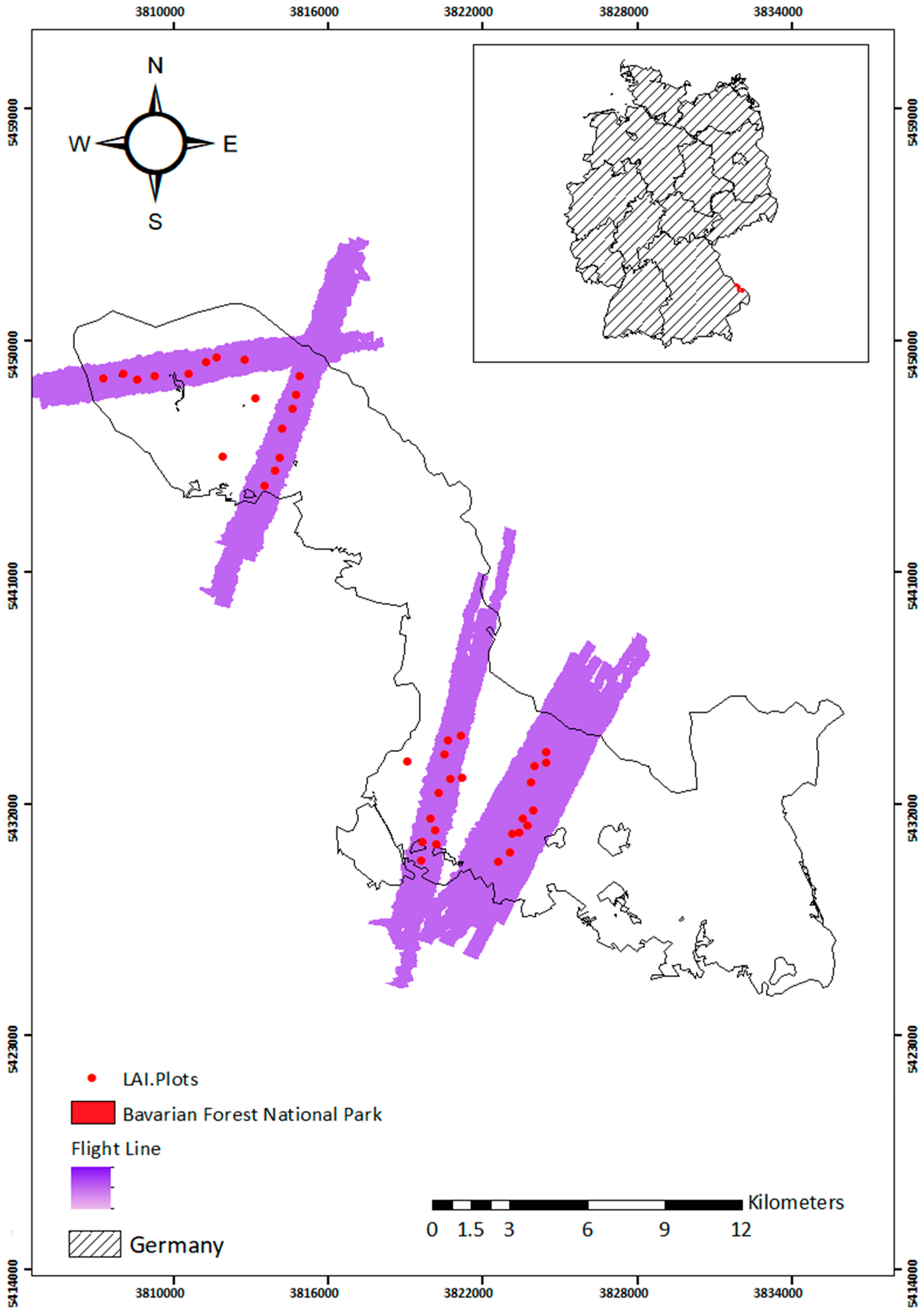
2.1. Study Area
2.2. In Situ Measurement

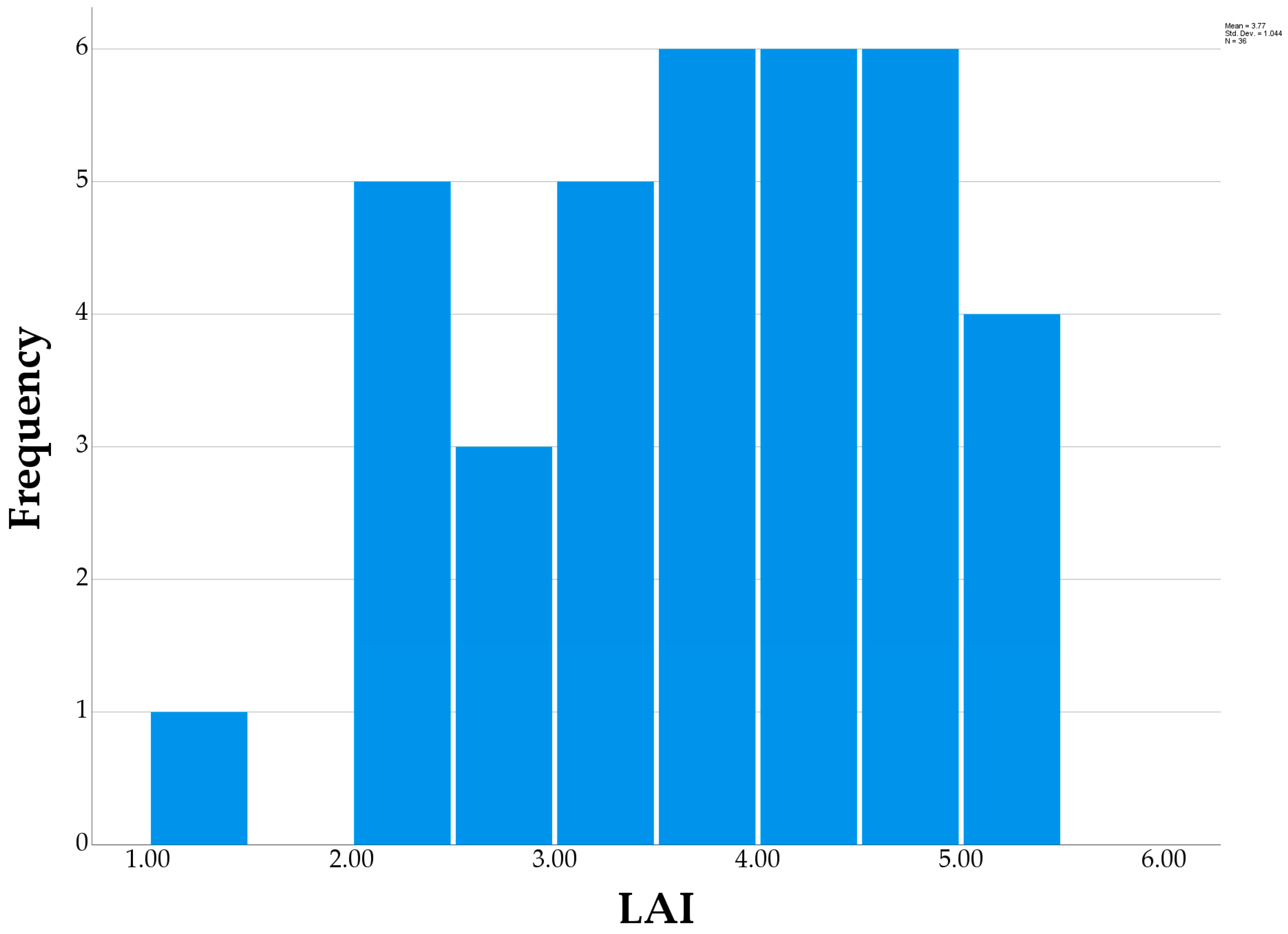
2.3. Leaf Area Index Measurement
2.4. Airborne Thermal Infrared Hyperspectral Data and Data Pre-Processing
2.5. Prediction of Leaf Area Index
2.5.1. Narrowband Vegetation Indices
2.5.2. Partial Least Squares Regression
2.5.3. Artificial Neural Network
3. Results
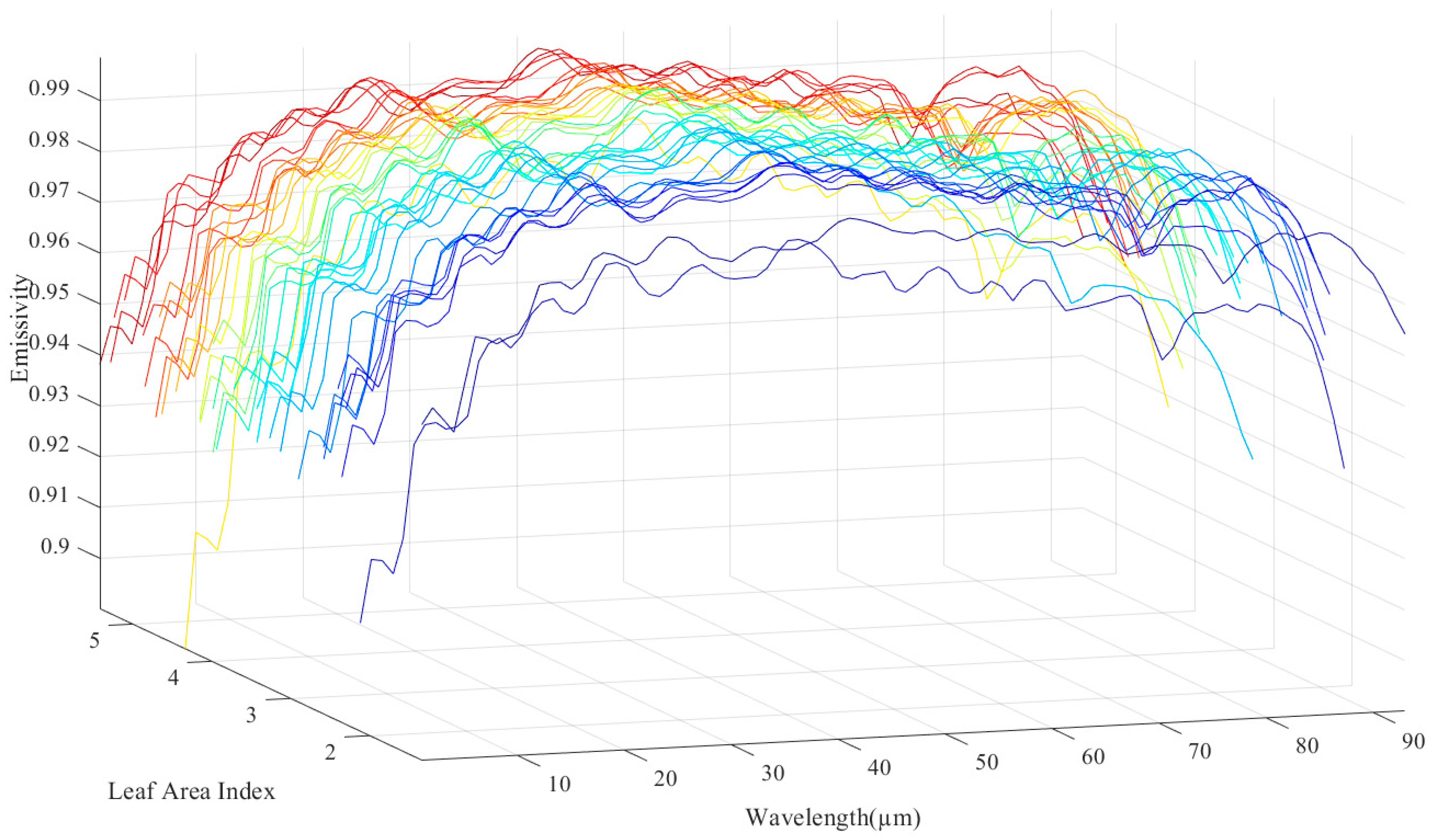
3.1. Narrowband Indices for Leaf Area Index Estimation
3.2. Estimation of Leaf Area Index Using Partial Least Squares Regression
3.3. Retrieval of Leaf Area Index Using an Artificial Neural Network
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BFNP | Bavarian Forest National Park |
| ITC | Faculty of Geo-Information Science and Earth Observation |
| LAI | Leaf Area Index |
| LM | Levenberg–Marquardt |
| PLSR | Partial Least Squares Regression |
| R2 | Coefficients of Determination |
| RMSE | Root Mean Squared Error |
| RMSECV | Cross-Validation Root Mean Squared Error |
| RS | Remote Sensing |
| SCG | Scaled Conjugate Gradient |
| TIR | Thermal infrared |
| UAV | Unmanned Aerial Vehicle |
| VIs | Vegetation Indices |
| VIS-SWIR | Visible-Short Wave Infrared |
References
- Fang, H.; Baret, F.; Plummer, S.; SchaepmanÔÇÉStrub, G. An overview of global leaf area index (LAI): Methods, products, validation, and applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Tripathi, A.M.; Pohanková, E.; Fischer, M.; Orság, M.; Trnka, M.; Klem, K.; Marek, M.V. The evaluation of radiation use efficiency and leaf area index development for the estimation of biomass accumulation in short rotation poplar and annual field crops. Forests 2018, 9, 168. [Google Scholar] [CrossRef]
- Taugourdeau, S.; Le Maire, G.; Avelino, J.; Jones, J.R.; Ramirez, L.G.; Quesada, M.J.; Charbonnier, F.; Gómez-Delgado, F.; Harmand, J.-M.; Rapidel, B. Leaf area index as an indicator of ecosystem services and management practices: An application for coffee agroforestry. Agric. Ecosyst. Environ. 2014, 192, 19–37. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The concept of essential climate variables in support of climate research, applications, and policy. Bull. Am. Meteorol. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- Skidmore, A.K.; Coops, N.C.; Neinavaz, E.; Ali, A.; Schaepman, M.E.; Paganini, M.; Kissling, W.D.; Vihervaara, P.; Darvishzadeh, R.; Feilhauer, H.; et al. Priority list of biodiversity metrics to observe from space. Nat. Ecol. Evol. 2021, 5, 896–906. [Google Scholar] [CrossRef]
- Skidmore, A.K.; Pettorelli, N.; Coops, N.C.; Geller, G.N.; Hansen, M.; Lucas, R.; Mücher, C.A.; O’Connor, B.; Paganini, M.; Pereira, H.M.; et al. Environmental science: Agree on biodiversity metrics to track from space. Nature 2015, 523, 403–405. [Google Scholar] [CrossRef] [PubMed]
- Clevers, J.G.; Kooistra, L.; Schaepman, M.E. Estimating canopy water content using hyperspectral remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 119–125. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Wang, L.; Qu, J.J.; Hao, X. Remote sensing of fuel moisture content from canopy water indices and normalized dry matter index. J. Appl. Remote Sens. 2012, 6, 061705. [Google Scholar] [CrossRef]
- Yebra, M.; Dennison, P.E.; Chuvieco, E.; Riaño, D.; Zylstra, P.; Hunt, E.R., Jr.; Danson, F.M.; Qi, Y.; Jurdao, S. A global review of remote sensing of live fuel moisture content for fire danger assessment: Moving towards operational products. Remote Sens. Environ. 2013, 136, 455–468. [Google Scholar] [CrossRef]
- Simic, A.; Fernandes, R.; Wang, S. Assessing the impact of leaf area index on evapotranspiration and groundwater recharge across a shallow water region for diverse land cover and soil properties. J. Water Resour. Hydraul. Eng 2014, 3, 60–73. [Google Scholar]
- Liu, Y.; Xiao, J.; Ju, W.; Zhu, G.; Wu, X.; Fan, W.; Li, D.; Zhou, Y. Satellite-derived LAI products exhibit large discrepancies and can lead to substantial uncertainty in simulated carbon and water fluxes. Remote Sens. Environ. 2018, 206, 174–188. [Google Scholar] [CrossRef]
- Kang, Y.; Ozdogan, M.; Gao, F.; Anderson, M.C.; White, W.A.; Yang, Y.; Yang, Y.; Erickson, T.A. A data-driven approach to estimate leaf area index for Landsat images over the contiguous US. Remote Sens. Environ. 2021, 258, 112383. [Google Scholar] [CrossRef]
- Pu, R.; Landry, S. Evaluating seasonal effect on forest leaf area index mapping using multi-seasonal high resolution satellite pléiades imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 268–279. [Google Scholar] [CrossRef]
- Tillack, A.; Clasen, A.; Kleinschmit, B.; Förster, M. Estimation of the seasonal leaf area index in an alluvial forest using high-resolution satellite-based vegetation indices. Remote Sens. Environ. 2014, 141, 52–63. [Google Scholar] [CrossRef]
- Xie, R.; Darvishzadeh, R.; Skidmore, A.K.; Heurich, M.; Holzwarth, S.; Gara, T.W.; Reusen, I. Mapping leaf area index in a mixed temperate forest using Fenix airborne hyperspectral data and Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2021, 95, 102242. [Google Scholar] [CrossRef]
- Xie, Q.; Huang, W.; Liang, D.; Chen, P.; Wu, C.; Yang, G.; Zhang, J.; Huang, L.; Zhang, D. Leaf area index estimation using vegetation indices derived from airborne hyperspectral images in winter wheat. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3586–3594. [Google Scholar] [CrossRef]
- Qi, H.; Zhu, B.; Wu, Z.; Liang, Y.; Li, J.; Wang, L.; Chen, T.; Lan, Y.; Zhang, L. Estimation of peanut leaf area index from unmanned aerial vehicle multispectral images. Sensors 2020, 20, 6732. [Google Scholar] [CrossRef] [PubMed]
- Stobbelaar, P.; Neinavaz, E.; Nyktas, P. Prediction of leaf area index using thermal infrared data acquired by UAS over a mixed temperate forest. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103049. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of sentinel-2 red-edge bands for empirical estimation of green LAI and chlorophyll content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef]
- Atzberger, C.; Richter, K. Spatially constrained inversion of radiative transfer models for improved LAI mapping from future Sentinel-2 imagery. Remote Sens. Environ. 2012, 120, 208–218. [Google Scholar] [CrossRef]
- Laurent, V.C.; Schaepman, M.E.; Verhoef, W.; Weyermann, J.; Chávez, R.O. Bayesian object-based estimation of LAI and chlorophyll from a simulated Sentinel-2 top-of-atmosphere radiance image. Remote Sens. Environ. 2014, 140, 318–329. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods–A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Ribeiro da Luz, B.; Crowley, J.K. Identification of plant species by using high spatial and spectral resolution thermal infrared (8.0–13.5 μm) imagery. Remote Sens. Environ. 2010, 114, 404–413. [Google Scholar] [CrossRef]
- Ribeiro da Luz, B.; Crowley, J.K. Spectral reflectance and emissivity features of broad leaf plants: Prospects for remote sensing in the thermal infrared (8.0–14.0 μm). Remote Sens. Environ. 2007, 109, 393–405. [Google Scholar] [CrossRef]
- Neinavaz, E.; Schlerf, M.; Darvishzadeh, R.; Gerhards, M.; Skidmore, A.K. Thermal infrared remote sensing of vegetation: Current status and perspectives. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102415. [Google Scholar] [CrossRef]
- Neinavaz, E.; Darvishzadeh, R.; Skidmore, A.K.; Abdullah, H. Integration of Landsat-8 Thermal and Visible-Short Wave Infrared Data for Improving Prediction Accuracy of Forest Leaf Area Index. Remote Sens. 2019, 11, 390. [Google Scholar] [CrossRef]
- Neinavaz, E.; Darvishzadeh, R.; Skidmore, A.K.; Groen, T.A. Measuring the response of canopy emissivity spectra to leaf area index variation using thermal hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 40–47. [Google Scholar] [CrossRef]
- Heurich, M.; Beudert, B.; Rall, H.; Křenová, Z. Long-Term Ecological Research; Springer: Berlin/Heidelberg, Germany, 2010; pp. 327–344. [Google Scholar]
- Huber, C. Long lasting nitrate leaching after bark beetle attack in the highlands of the Bavarian Forest National Park. J. Environ. Qual. 2005, 34, 1772–1779. [Google Scholar] [CrossRef] [PubMed]
- Gara, T.W.; Darvishzadeh, R.; Skidmore, A.K.; Wang, T.; Heurich, M. Accurate modelling of canopy traits from seasonal Sentinel-2 imagery based on the vertical distribution of leaf traits. ISPRS J. Photogramm. Remote Sens. 2019, 157, 108–123. [Google Scholar] [CrossRef]
- Silveyra Gonzalez, R.; Latifi, H.; Weinacker, H.; Dees, M.; Koch, B.; Heurich, M. Integrating LiDAR and high-resolution imagery for object-based mapping of forest habitats in a heterogeneous temperate forest landscape. Int. J. Remote Sens. 2018, 39, 8859–8884. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Liu, C.; Xu, R.; Xie, F.; Jin, J.; Yuan, L.; Lv, G.; Wang, Y.; Li, C.; Wang, J. New airborne thermal-infrared hyperspectral imager system: Initial validation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4149–4165. [Google Scholar] [CrossRef]
- Harris, L.; Warren, M.; Grant, M.; Llewellyn, G.M. Spectral characterization of the AisaOWL. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2751–2756. [Google Scholar] [CrossRef]
- Harris, L.J.; Warren, M.; Clewley, D.; Taylor, B.; Llewellyn, G.; Maclellan, C.; Mata, A.; Goult, S.; Grant, M.; Groom, S. NERC-ARSF-DAN Thermal Hyperspectral Data Quality Report 2015, 2016.
- Wolosin, M.; Harris, N. Tropical Forests and Climate Change: The Latest Science; World Resources Institute: Washington, DC, USA, 2018. [Google Scholar]
- Manolakis, D.; Pieper, M.; Truslow, E.; Lockwood, R.; Weisner, A.; Jacobson, J.; Cooley, T. Longwave infrared hyperspectral imaging: Principles, progress, and challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 72–100. [Google Scholar] [CrossRef]
- Minkina, W.; Dudzik, S. Infrared Thermography: Errors and Uncertainties; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Vollmer, M. Computer Vision: A Reference Guide; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–4. [Google Scholar]
- Borel, C.C. Iterative Retrieval of Surface Emissivity and Temperature for a Hyperspectral Sensor; Los Alamos National Lab. (LANL): Los Alamos, NM, USA, 1997. [Google Scholar]
- Realmuto, V. Separating the effects of temperature amd emissivity: Emissivity spectrum normalization. In Proceedings of the Second Thermal Infrared Multispectral Scanner (TIMS) Workshop, Reston, Virginia, 29–30 October 1985; pp. 31–35. [Google Scholar]
- Young, S.J.; Johnson, B.R.; Hackwell, J.A. An in-scene method for atmospheric compensation of thermal hyperspectral data. J. Geophys. Res. Atmos. 2002, 107, 4774. [Google Scholar] [CrossRef]
- Norman, J.M.; Divakarla, M.; Goel, N.S. Algorithms for extracting information from remote thermal-IR observations of the earth’s surface. Remote Sens. Environ. 1995, 51, 157–168. [Google Scholar] [CrossRef]
- Norman, J.M.; Becker, F. Terminology in thermal infrared remote sensing of natural surfaces. Agric. For. Meteorol. 1995, 77, 153–166. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Atzberger, C.; Skidmore, A.; Schlerf, M. Mapping grassland leaf area index with airborne hyperspectral imagery: A comparison study of statistical approaches and inversion of radiative transfer models. ISPRS J. Photogramm. Remote Sens. 2011, 66, 894–906. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Retrieving leaf area index of boreal conifer forests using Landsat TM images. Remote Sens. Environ. 1996, 55, 153–162. [Google Scholar] [CrossRef]
- Viña, A.; Bearer, S.; Zhang, H.; Ouyang, Z.; Liu, J. Evaluating MODIS data for mapping wildlife habitat distribution. Remote Sens. Environ. 2008, 112, 2160–2169. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Breon, F.-M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sens. Environ. 1995, 51, 375–384. [Google Scholar] [CrossRef]
- Paltridge, G.; Barber, J. Monitoring grassland dryness and fire potential in Australia with NOAA/AVHRR data. Remote Sens. Environ. 1988, 25, 381–394. [Google Scholar] [CrossRef]
- Rouse, J.; Haas, R.; Schell, J.; Deering, D.; Harlan, J. Monitoring the Vernal Advancements and Retrogradation of Natural Vegetation; NASA/GSFC Final Report; NASA: Greenbelt MD USA, 1974; pp. 1–137. [Google Scholar]
- Cho, M.A.; Skidmore, A.; Corsi, F.; Van Wieren, S.E.; Sobhan, I. Estimation of green grass/herb biomass from airborne hyperspectral imagery using spectral indices and partial least squares regression. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 414–424. [Google Scholar] [CrossRef]
- Neinavaz, E.; Skidmore, A.K.; Darvishzadeh, R.; Groen, T.A. Retrieval of leaf area index in different plant species using thermal hyperspectral data. ISPRS J. Photogramm. Remote Sens. 2016, 119, 390–401. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E. Pattern classification and scene analysis. A Wiley-Interscience Publication; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Haaland, D.M.; Thomas, E.V. Partial least-squares methods for spectral analyses. 1. Relation to other quantitative calibration methods and the extraction of qualitative information. Anal. Chem. 1988, 60, 1193–1202. [Google Scholar] [CrossRef]
- Chai, L.; Qu, Y.; Zhang, L.; Liang, S.; Wang, J. Estimating time-series leaf area index based on recurrent nonlinear autoregressive neural networks with exogenous inputs. Int. J. Remote Sens. 2012, 33, 5712–5731. [Google Scholar] [CrossRef]
- Johnson, D.M.; Smith, W.K.; Vogelmann, T.C.; Brodersen, C.R. Leaf architecture and direction of incident light influence mesophyll fluorescence profiles. Am. J. Bot. 2005, 92, 1425–1431. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, Z.; Wang, Q.; Jin, W.; Meng, K.; Wang, C.; Yin, G.; Xu, B.; Shi, Z. Estimating rice leaf area index at multiple growth stages with Sentinel-2 data: An evaluation of different retrieval algorithms. Eur. J. Agron. 2024, 161, 127362. [Google Scholar] [CrossRef]
- Wang, T.; Xiao, Z.; Liu, Z. Performance evaluation of machine learning methods for leaf area index retrieval from time-series MODIS reflectance data. Sensors 2017, 17, 81. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, P.M.; Tatnall, A.R. Introduction neural networks in remote sensing. Int. J. Remote Sens. 1997, 18, 699–709. [Google Scholar] [CrossRef]
- Nowlan, S.J.; Hinton, G.E. Simplifying neural networks by soft weight-sharing. Neural Comput. 1992, 4, 473–493. [Google Scholar] [CrossRef]
- Boeriu, C.G.; Bravo, D.; Gosselink, R.J.; van Dam, J.E. Characterisation of structure-dependent functional properties of lignin with infrared spectroscopy. Ind. Crops Prod. 2004, 20, 205–218. [Google Scholar] [CrossRef]
- Socrates, G. Infrared and Raman Characteristic Group Frequencies: Tables and Charts; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Elvidge, C.D. Thermal infrared reflectance of dry plant materials: 2.5–20.0 μm. Remote Sens. Environ. 1988, 26, 265–285. [Google Scholar] [CrossRef]
- Mayo, D.W.; Miller, F.A.; Hannah, R.W. Course Notes on the Interpretation of Infrared and Raman Spectra; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Ribeiro da Luz, B. Attenuated total reflectance spectroscopy of plant leaves: A tool for ecological and botanical studies. New Phytol. 2006, 172, 305–318. [Google Scholar] [CrossRef]
- Stewart, D.; Yahiaoui, N.; McDougall, G.J.; Myton, K.; Marque, C.ę.; Boudet, A.M.; Haigh, J. Fourier-transform infrared and Raman spectroscopic evidence for the incorporation of cinnamaldehydes into the lignin of transgenic tobacco (Nicotiana tabacum L.) plants with reduced expression of cinnamyl alcohol dehydrogenase. Planta 1997, 201, 311–318. [Google Scholar] [CrossRef]
- Ullah, S.; Skidmore, A.K.; Naeem, M.; Schlerf, M. An accurate retrieval of leaf water content from mid to thermal infrared spectra using continuous wavelet analysis. Sci. Total Environ. 2012, 437, 145–152. [Google Scholar] [CrossRef] [PubMed]
- Buitrago, M.F.; Groen, T.A.; Hecker, C.A.; Skidmore, A.K. Changes in thermal infrared spectra of plants caused by temperature and water stress. ISPRS J. Photogramm. Remote Sens. 2016, 111, 22–31. [Google Scholar] [CrossRef]
- Richardson, A.D.; Aubrecht, D.M.; Basler, D.; Hufkens, K.; Muir, C.D.; Hanssen, L. Developmental changes in the reflectance spectra of temperate deciduous tree leaves and implications for thermal emissivity and leaf temperature. New Phytol. 2021, 229, 791–804. [Google Scholar] [CrossRef]
- Rock, G.; Gerhards, M.; Schlerf, M.; Hecker, C.; Udelhoven, T. Plant species discrimination using emissive thermal infrared imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 16–26. [Google Scholar] [CrossRef]
- Kirkland, L.; Herr, K.; Keim, E.; Adams, P.; Salisbury, J.; Hackwell, J.; Treiman, A. First use of an airborne thermal infrared hyperspectral scanner for compositional mapping. Remote Sens. Environ. 2002, 80, 447–459. [Google Scholar] [CrossRef]
- Fabre, S.; Lesaignoux, A.; Olioso, A.; Briottet, X. Influence of Water Content on Spectral Reflectance of Leaves in the 3–15. IEEE Geosci. Remote Sens. Lett. 2011, 8, 143–147. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Kerr, Y.H.; Brunet, Y. An experimental study of angular effects on surface temperature for various plant canopies and bare soils. Agric. For. Meteorol. 1995, 77, 167–190. [Google Scholar] [CrossRef]
- Still, C.; Powell, R.; Aubrecht, D.; Kim, Y.; Helliker, B.; Roberts, D.; Richardson, A.; Goulden, M. Thermal imaging in plant and ecosystem ecology: Applications and challenges. Ecosphere 2019, 10, e02768. [Google Scholar] [CrossRef]
- Cheng, J.-H.; Sun, D.-W. Partial least squares regression (PLSR) applied to NIR and HSI spectral data modeling to predict chemical properties of fish muscle. Food Eng. Rev. 2017, 9, 36–49. [Google Scholar] [CrossRef]
- Tran, T.N.; Afanador, N.L.; Buydens, L.M.; Blanchet, L. Interpretation of variable importance in partial least squares with significance multivariate correlation (sMC). Chemom. Intell. Lab. Syst. 2014, 138, 153–160. [Google Scholar] [CrossRef]
- Vega, J.; Reynoso, R.; Calvet, H.C. Effect of signal noise on the learning capability of an artificial neural network. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 606, 693–699. [Google Scholar] [CrossRef]

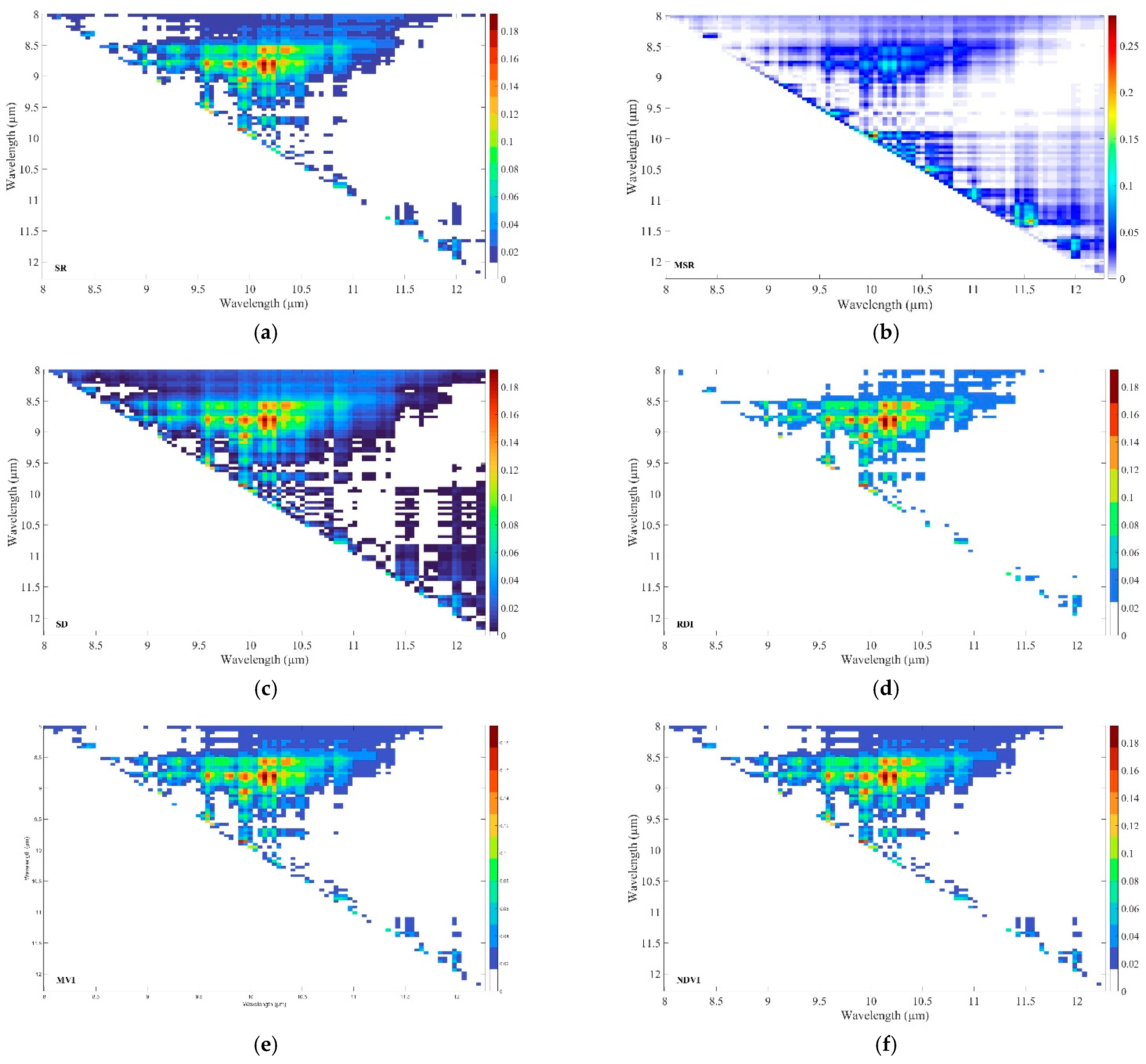



| Vegetation Index | Acronym | Initial Equation | Implemented Equation | Reference |
|---|---|---|---|---|
| Simple Ratio | SR | * | ** | [50] |
| Modified Simple Ratio | MSR | [51] | ||
| Difference Vegetation Index | SD | [52] | ||
| Re-normalized Difference Index | RDI | [53] | ||
| Modified Vegetation Index | MVI | [54] | ||
| Normalized Difference Vegetation Index | NDVI | [55] |
| Index | Most Sensitive Wavebands Combination | R2 | RMSECV |
|---|---|---|---|
| SR | 9.95 µm and 9.99 µm | 0.19 | 0.003 |
| MSR | 9.95 µm and 9.99 µm | 0.28 | 0.002 |
| SD | 8.75 µm and 10.13 µm | 0.19 | 0.001 |
| RDI | 8.79 µm and 10.13 µm | 0.19 | 0.009 |
| MVI | 8.79 µm and 10.13 µm | 0.19 | 0.007 |
| NDVI | 8.79 µm and 10.13 µm | 0.19 | 0.007 |
| Important Wavebands (µm) | Associated Biochemical Properties | Reference | |
|---|---|---|---|
| Neinavaz, et al. [57] | Current Study | ||
| - | 8.01 | Cutin | Ribeiro da Luz and Crowley [24] |
| - | 8.06 | Cutin | Ribeiro da Luz and Crowley [24] |
| 8.1 | 8.10 | - | - |
| - | 8.15 | - | - |
| - | 8.19 | Lignin | Boeriu, et al. [67] |
| 8.4 | - | Lignin | Socrates [68] |
| 8.5 | - | Cellulose, Cutin | Ribeiro da Luz and Crowley [24] |
| 8.8 | - | Cellulose | |
| 9.0 | - | Cellulose | [24,69] |
| 9.1 | 9.12 | Silica, Sulphate anion | [24], Mayo et al. [70] |
| 9.2 | - | Cellulose | Elvidge [69] |
| - | 9.35 | Cellulose | Elvidge [69] |
| - | 9.49 | Cellulose | Ribeiro da Luz and Crowley [24] |
| - | 9.53 | - | - |
| - | 9.58 | - | - |
| - | 9.62 | Hemicellulose xylan | Ribeiro da Luz and Crowley [24] |
| 9.7–10.02 | 9.85–9.95 | Oleanolic acid | Ribeiro da Luz [71] |
| 9.9–10.2 | 9.99–10.27 | Oleanolic acid | Ribeiro da Luz and Crowley [24] |
| - | 10.31–10.96 | Cellulose, Hollocellulose, Ester | Elvidge [69], Stewart et al. [72] |
| - | 11.103 | - | - |
| - | 11.195 | - | - |
| 11.86–11.94 | - | Lignin | Boeriu, et al. [67], Elvidge [69] |
| 12.0 | - | Cutin | Ribeiro da Luz and Crowley [24] |
| 12.1 | - | Cutin | Ribeiro da Luz and Crowley [24] |
| - | 12.210 | - | - |
| - | 12.256 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neinavaz, E.; Darvishzadeh, R.; Skidmore, A.K.; Heurich, M.; Zhu, X. Evaluating Airborne Thermal Infrared Hyperspectral Data for Leaf Area Index Retrieval in Temperate Forests. Remote Sens. 2025, 17, 3820. https://doi.org/10.3390/rs17233820
Neinavaz E, Darvishzadeh R, Skidmore AK, Heurich M, Zhu X. Evaluating Airborne Thermal Infrared Hyperspectral Data for Leaf Area Index Retrieval in Temperate Forests. Remote Sensing. 2025; 17(23):3820. https://doi.org/10.3390/rs17233820
Chicago/Turabian StyleNeinavaz, Elnaz, Roshanak Darvishzadeh, Andrew K. Skidmore, Marco Heurich, and Xi Zhu. 2025. "Evaluating Airborne Thermal Infrared Hyperspectral Data for Leaf Area Index Retrieval in Temperate Forests" Remote Sensing 17, no. 23: 3820. https://doi.org/10.3390/rs17233820
APA StyleNeinavaz, E., Darvishzadeh, R., Skidmore, A. K., Heurich, M., & Zhu, X. (2025). Evaluating Airborne Thermal Infrared Hyperspectral Data for Leaf Area Index Retrieval in Temperate Forests. Remote Sensing, 17(23), 3820. https://doi.org/10.3390/rs17233820










