Machine Learning Approaches to Phytoplankton Identification and Classification Using GCOM-C/SGLI Imagery
Highlights
- Machine learning approaches were developed to classify phytoplankton types, including coccolithophores, diatoms, and dinoflagellates, using GCOM-C/SGLI satellite imagery.
- Random Forest (RF) and Gradient Tree Boosting (GTB) models outperformed other tested algorithms, achieving high accuracy of classification results.
- The developed machine learning models enable scalable monitoring of phytoplankton blooms, supporting both regional and global ocean observation.
- Combining remote sensing with artificial intelligence can be used as an alternative approach to monitor the marine ecosystem.
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Selection and Rationale
2.2. GCOM-C/SGLI Data Acquisition and Extraction
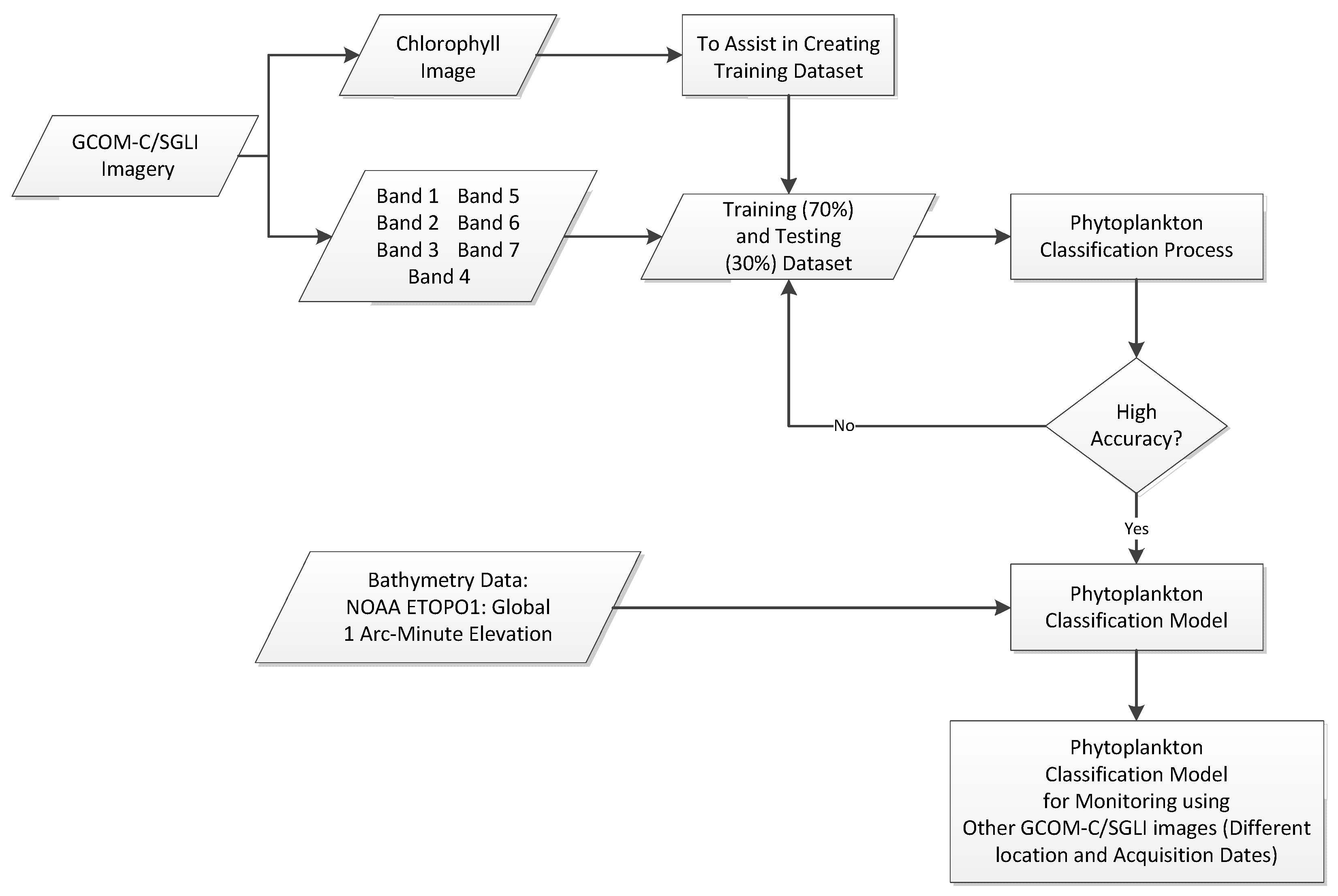
2.3. Machine Learning Approach to Phytoplankton Identification and Classification
2.4. Assessment of the Results
3. Results
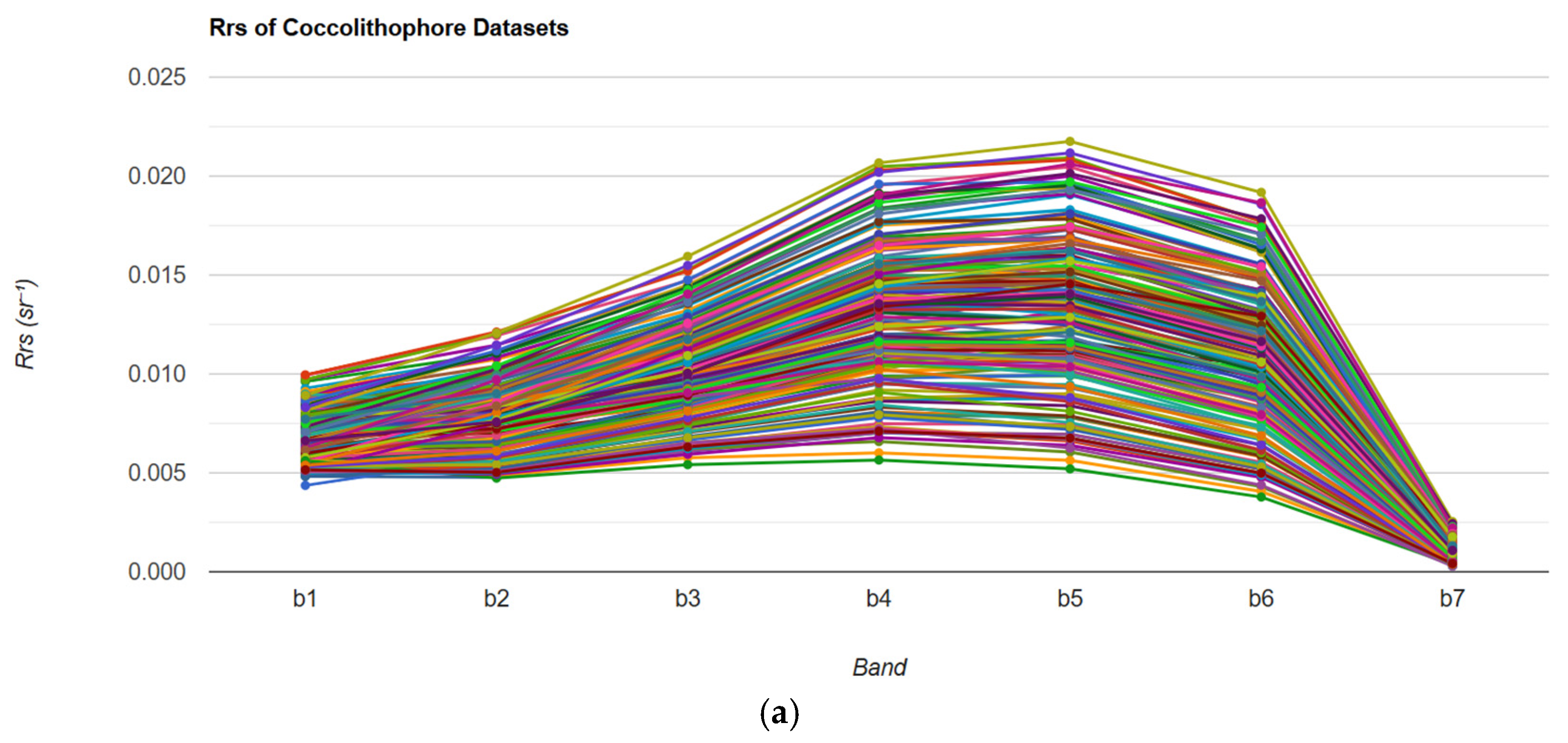
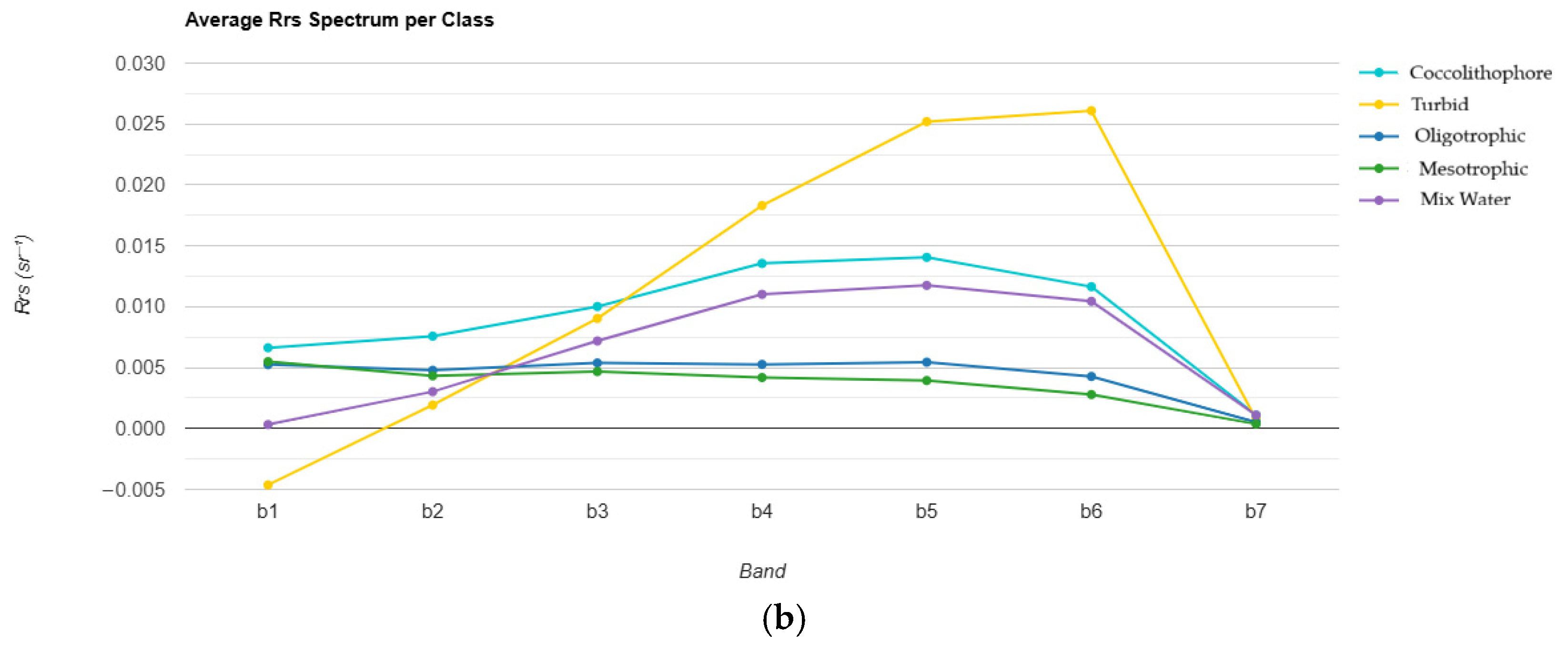
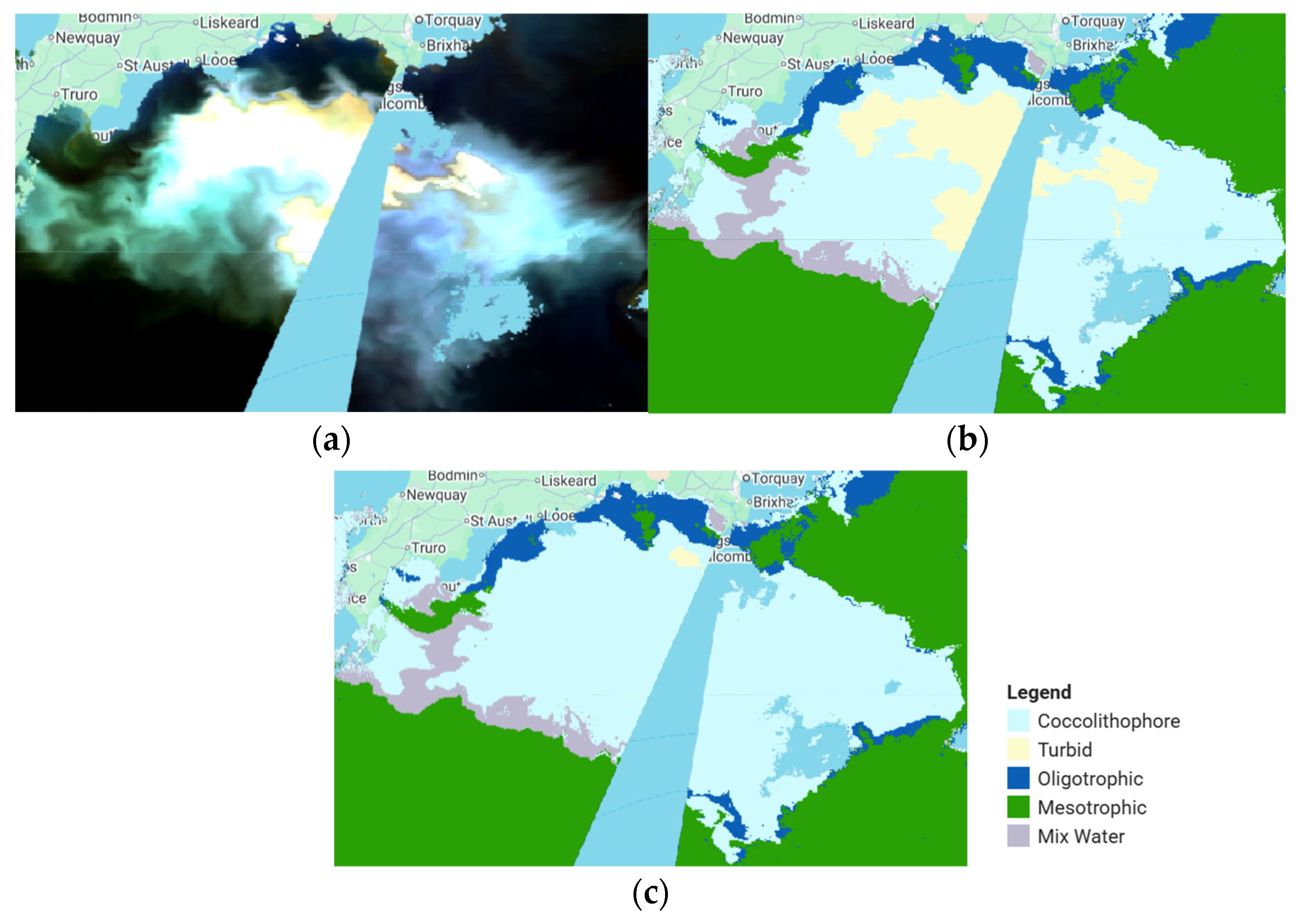
3.1. Coccolithophore Blooms Identification and Classification
3.2. Diatom Blooms Identification and Classification
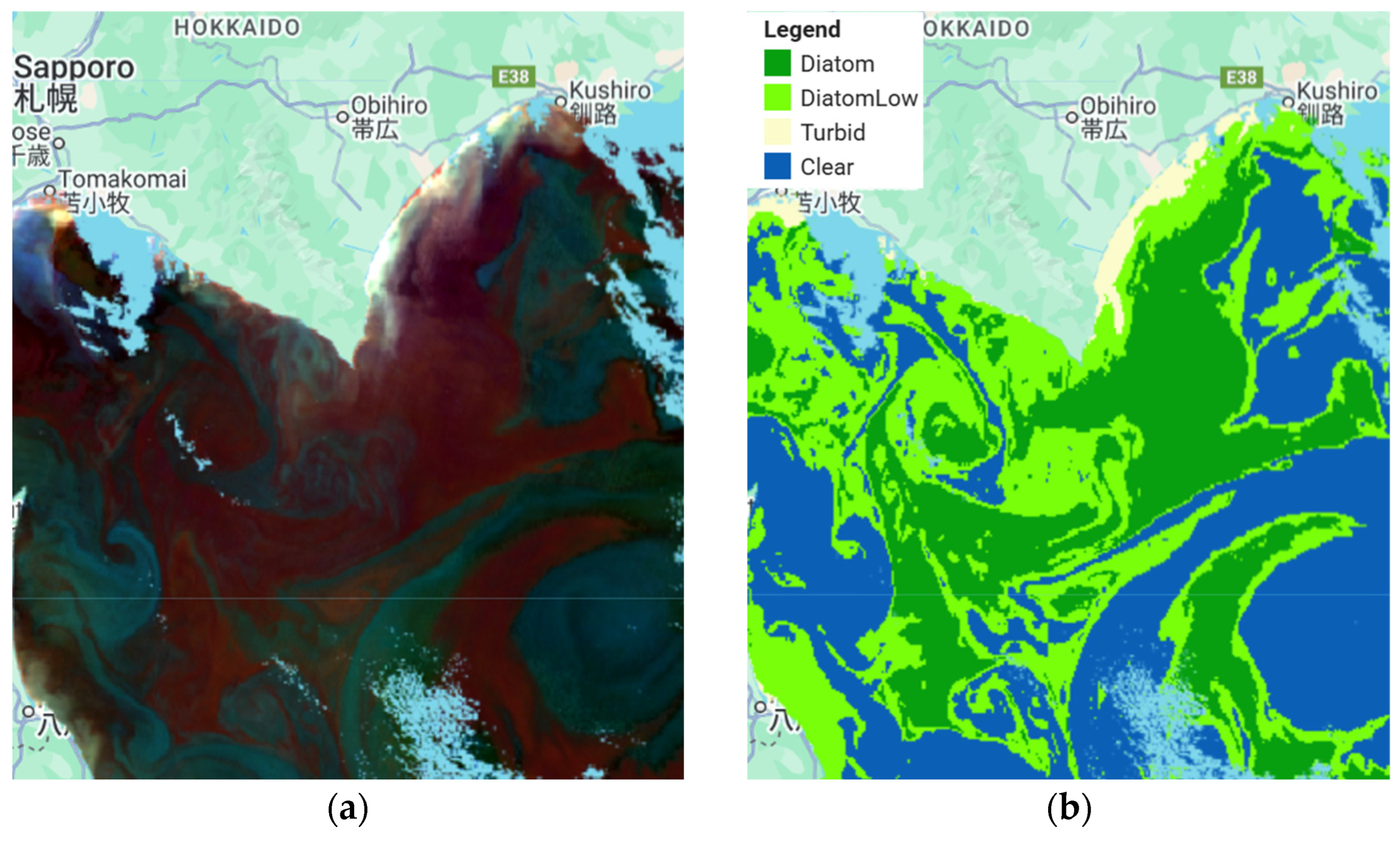
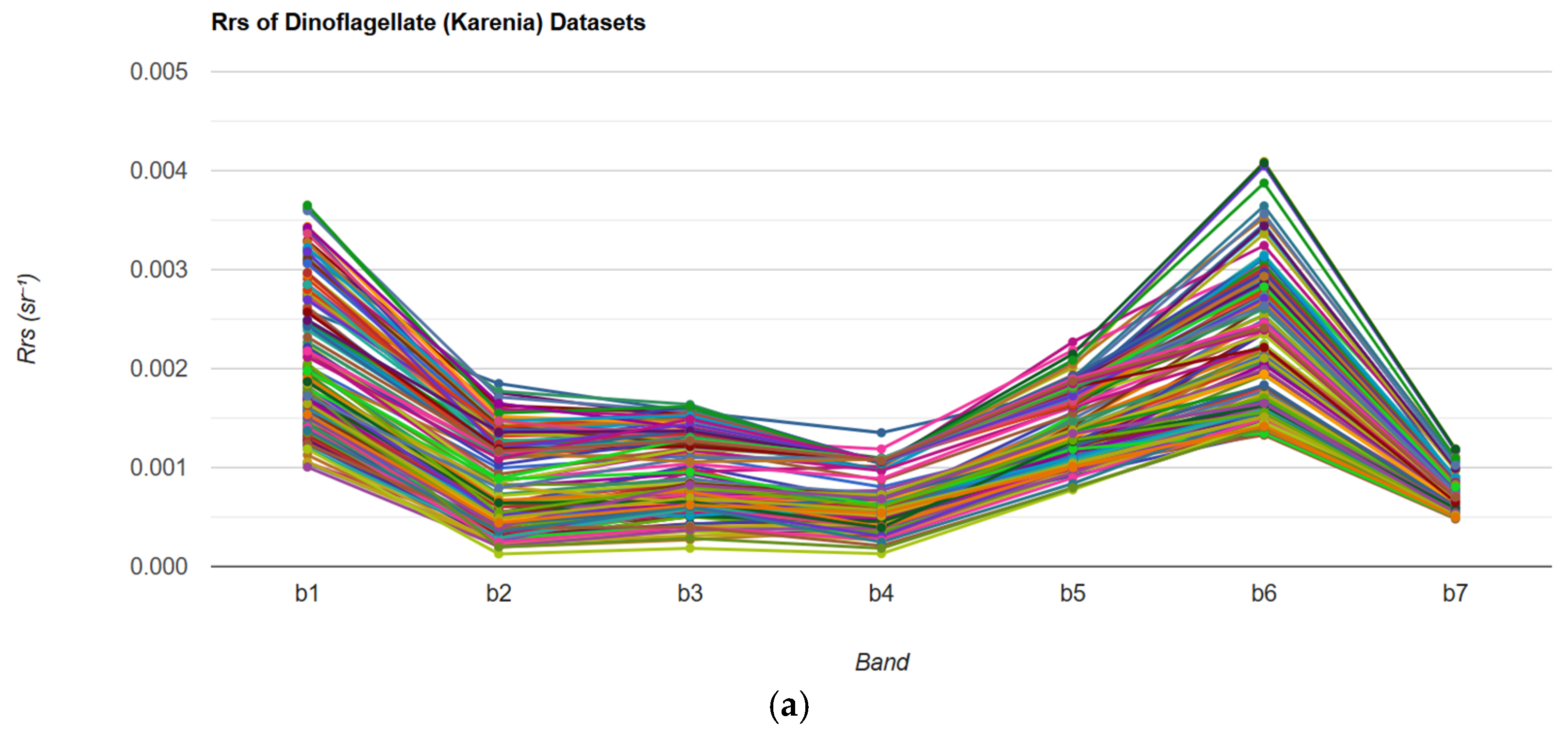
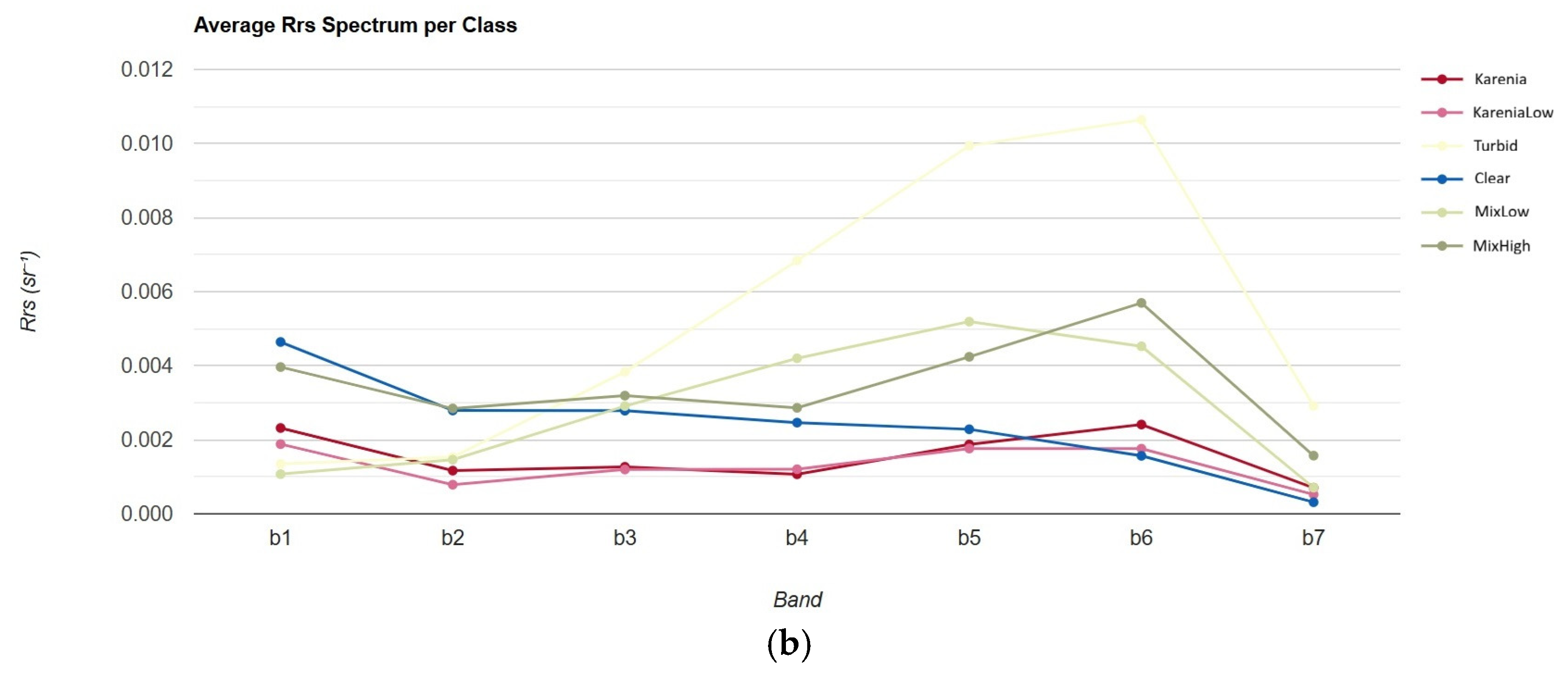
3.3. Dinoflagellate Blooms Identification and Classification
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ryan-Keogh, T.J.; Thomalla, S.J.; Chang, N.; Moalusi, T. A new global oceanic multi-model net primary productivity data product. Earth Syst. Sci. Data 2023, 15, 4829–4848. [Google Scholar] [CrossRef]
- Silsbe, G.M.; Fox, J.; Westberry, T.K.; Halsey, K.H. Global declines in net primary production in the ocean color era. Nat. Commun. 2025, 16, 5821. [Google Scholar] [CrossRef]
- Litchman, E.; de Tezanos Pinto, P.; Edwards, K.F.; Klausmeier, C.A.; Kremer, C.T.; Thomas, M.K. Global biogeochemical impacts of phytoplankton: A trait-based perspective. J. Ecol. 2015, 103, 1384–1396. [Google Scholar] [CrossRef]
- Moore, T.; Dowell, M.; Franz, B. Detection of coccolithophore blooms in ocean color satellite imagery: A generalized approach for use with multiple sensors. Remote Sens. Environ. 2011, 117, 249–263. [Google Scholar] [CrossRef]
- Anderson, S.I.; Barton, A.D.; Clayton, S.; Dutkiewicz, S.; Rynearson, T.A. Marine phytoplankton functional types exhibit diverse responses to thermal change. Nat. Commun. 2021, 12, 6413. [Google Scholar] [CrossRef] [PubMed]
- El Hourany, R.; Karlusich, J.P.; Zinger, L.; Loisel, H.; Levy, M.; Bowler, C. Linking satellites to genes with machine learning to estimate phytoplankton community structure from space. Ocean Sci. 2024, 20, 217–239. [Google Scholar] [CrossRef]
- Balch, W.M.; Bowler, B.C.; Drapeau, D.T.; Lubelczyk, L.C.; Lyczkowski, E. Vertical Distributions of Coccolithophores, PIC, POC, Biogenic Silica, and Chlorophyll a Throughout the Global Ocean. Global Biogeochem. Cycles 2018, 32, 2–17. [Google Scholar] [CrossRef] [PubMed]
- Balch, W.M.; Mitchell, C. Remote sensing algorithms for particulate inorganic carbon (PIC) and the global cycle of PIC. Earth Sci. Rev. 2023, 239, 104363. [Google Scholar] [CrossRef]
- Grubb, A.; Johns, C.; Hayden, M.; Subhas, A.; Thamatrakoln, K.; Bidle, K. Calcification increases carbon supply, photosynthesis, and growth in a globally distributed coccolithophore. Limnol. Oceanogr. 2024, 69, 2152–2166. [Google Scholar] [CrossRef]
- Neukermans, G.; Fournier, G. Optical Modeling of Spectral Backscattering and Remote Sensing Reflectance from Emiliania huxleyi Blooms. Front. Mar. Sci. 2018, 5, 146. [Google Scholar] [CrossRef]
- Cetinić, I.; Rousseaux, C.S.; Carroll, I.T.; Chase, A.P.; Kramer, S.J.; Werdell, P.J.; Siegel, D.A.; Dierssen, H.M.; Catlett, D.; Neeley, A.; et al. Phytoplankton composition from sPACE: Requirements, opportunities, and challenges. Remote Sens. Environ. 2024, 302, 113964. [Google Scholar] [CrossRef]
- Williams, J.R.; Giering, S.L.C.; Baker, C.A.; Pabortsava, K.; Briggs, N.; East, H.; Espinola, B.; Blackbird, S.; Le Moigne, F.A.C.; Villa-Alfageme, M.; et al. Inefficient transfer of diatoms through the subpolar Southern Ocean twilight zone. Nat. Geosci. 2025, 18, 72–77. [Google Scholar] [CrossRef] [PubMed]
- Abrantes, F.; Cermeno, P.; Lopes, C.; Romero, O.; Matos, L.; Van Iperen, J.; Rufino, M.; Magalhães, V. Diatoms Si uptake capacity drives carbon export in coastal upwelling systems. Biogeosciences 2016, 13, 4099–4109. [Google Scholar] [CrossRef]
- Zúñiga, D.; Sanchez-Vidal, A.; Flexas, M.M.; Carroll, D.; Rufino, M.M.; Spreen, G.; Calafat, A.; Abrantes, F. Sinking Diatom Assemblages as a Key Driver for Deep Carbon and Silicon Export in the Scotia Sea (Southern Ocean). Front. Earth Sci. 2021, 9, 579198. [Google Scholar] [CrossRef]
- Larsson, M.E.; Bramucci, A.R.; Collins, S.; Hallegraeff, G.; Kahlke, T.; Raina, J.-B.; Seymour, J.R.; Doblin, M.A. Mucospheres produced by a mixotrophic protist impact ocean carbon cycling. Nat. Commun. 2022, 13, 1301. [Google Scholar] [CrossRef]
- Möller, K.; Thoms, S.; Tillmann, U.; Krock, B.; Koch, F.; Peeken, I.; Meunier, C.L. Effects of bottom-up factors on growth and toxin content of a harmful algae bloom dinoflagellate. Limnol. Oceanogr. 2024, 69, 1335–1349. [Google Scholar] [CrossRef]
- Mulholland, M.R.; Morse, R.; Egerton, T.; Bernhardt, P.W.; Filippino, K.C. Blooms of Dinoflagellate Mixotrophs in a Lower Chesapeake Bay Tributary: Carbon and Nitrogen Uptake over Diurnal, Seasonal, and Interannual Timescales. Estuaries Coasts 2018, 41, 1744–1765. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef]
- Blondeau-Patissier, D.; Gower, J.F.R.; Dekker, A.G.; Phinn, S.R.; Brando, V.E. A review of ocean color remote sensing methods and statistical techniques for the detection, mapping and analysis of phytoplankton blooms in coastal and open oceans. Prog. Oceanogr. 2014, 123, 123–144. [Google Scholar] [CrossRef]
- Groom, S.; Sathyendranath, S.; Ban, Y.; Bernard, S.; Brewin, R.; Brotas, V.; Brockmann, C.; Chauhan, P.; Choi, J.-K.; Chuprin, A.; et al. Satellite Ocean Colour: Current Status and Future Perspective. Front. Mar. Sci. 2019, 6, 485. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, F.; Zhao, H.; Sun, X.; Zhu, Q.; Li, M. Optical distinguishability of phytoplankton species and its implications for hyperspectral remote sensing discrimination potential. J. Sea Res. 2024, 202, 102540. [Google Scholar] [CrossRef]
- Ansper-Toomsalu, A.; Uusõue, M.; Kangro, K.; Hieronymi, M.; Alikas, K. Suitability of different in-water algorithms for eutrophic and absorbing waters applied to Sentinel-2 MSI and Sentinel-3 OLCI data. Front. Remote Sens. 2024, 5, 1423332. [Google Scholar] [CrossRef]
- Bi, S.; Hieronymi, M. Holistic optical water type classification for ocean, coastal, and inland waters. Limnol. Oceanogr. 2024, 69, 1547–1561. [Google Scholar] [CrossRef]
- Wu, Z.; Pang, J.; Li, J.; Wang, Y.; Ruan, J.; Zhang, X.; Yang, L.; Pang, Y.; Gao, Y. A review of remote sensing-based water quality monitoring in turbid coastal waters. Intell. Mar. Technol. Syst. 2025, 3, 24. [Google Scholar] [CrossRef]
- Bachimanchi, H.; Pinder, M.I.M.; Robert, C.; De Wit, P.; Havenhand, J.; Kinnby, A.; Midtvedt, D.; Selander, E.; Volpe, G. Deep-learning-powered data analysis in plankton ecology. Limnol. Oceanogr. Lett. 2024, 9, 324–339. [Google Scholar] [CrossRef]
- Li, Z.; Yang, W.; Matsushita, B.; Kondoh, A. Remote estimation of phytoplankton primary production in clear to turbid waters by integrating a semi-analytical model with a machine learning algorithm. Remote Sens. Environ. 2022, 275, 113027. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, P.; Zhang, S.; Huang, H.; Pan, Y.; Pan, D. A Review of Machine Learning Applications in Ocean Color Remote Sensing. Remote Sens. 2025, 17, 1776. [Google Scholar] [CrossRef]
- Fasnacht, Z.; Joiner, J.; Haffner, D.; Qin, W.; Vasilkov, A.; Castellanos, P.; Krotkov, N. Using Machine Learning for Timely Estimates of Ocean Color Information from Hyperspectral Satellite Measurements in the Presence of Clouds, Aerosols, and Sunglint. Front. Remote Sens. 2022, 3, 846174. [Google Scholar] [CrossRef]
- Li, X.; Liu, B.; Zheng, G.; Ren, Y.; Zhang, S.; Liu, Y.; Gao, L.; Liu, Y.; Zhang, B.; Wang, F. Deep learning-based information mining from ocean remote sensing imagery. Natl. Sci. Rev. 2020, 7, 1584–1605. [Google Scholar] [CrossRef]
- Hadjal, M.; Medina-Lopez, E.; Ren, J.; Gallego, A.; McKee, D. An Artificial Neural Network Algorithm to Retrieve Chlorophyll a for Northwest European Shelf Seas from Top of Atmosphere Ocean Colour Reflectance. Remote Sens. 2022, 14, 3353. [Google Scholar] [CrossRef]
- Hu, S.; Liu, H.; Zhao, W.; Shi, T.; Hu, Z.; Li, Q.; Wu, G. Comparison of Machine Learning Techniques in Inferring Phytoplankton Size Classes. Remote Sens. 2018, 10, 191. [Google Scholar] [CrossRef]
- Nakajima, T.Y.; Ishida, H.; Nagao, T.M.; Hori, M.; Letu, H.; Higuchi, R.; Tamaru, N.; Imoto, N.; Yamazaki, A. Theoretical basis of the algorithms and early phase results of the GCOM-C (Shikisai) SGLI cloud products. Prog. Earth Planet. Sci. 2019, 6, 52. [Google Scholar] [CrossRef]
- Zheng, L.; Lee, Z.; Wang, Y.; Yu, X.; Lai, W.; Shang, S. Evaluation of near-blue UV remote sensing reflectance over the global ocean from SNPP VIIRS, PACE OCI, and GCOM-C SGLI. Opt. Express 2025, 33, 40465–40488. [Google Scholar] [CrossRef]
- Salem, S.I.; Toratani, M.; Higa, H.; Son, S.; Siswanto, E.; Ishizaka, J. Long-Term Evaluation of GCOM-C/SGLI Reflectance and Water Quality Products: Variability Among JAXA G-Portal and JASMES. Remote Sens. 2025, 17, 221. [Google Scholar] [CrossRef]
- Yano, K.; Takayama, Y.; Shimode, S.; Toratani, M.; Murakami, H.; Kuwahara, V.S. Observation of a coccolithophore Gephyrocapsa oceanica bloom in the temperate coastal waters of Sagami Bay, Japan. Plankton Benthos Res. 2024, 19, 37–50. [Google Scholar] [CrossRef]
- Siswanto, E.; Luang-on, J.; Ogata, K.; Higa, H.; Toratani, M. Observations of water optical properties during red tide outbreaks off southeast Hokkaido by GCOM-C/SGLI: Implications for the development of red tide algorithms. Remote Sens. Lett. 2024, 15, 121–132. [Google Scholar] [CrossRef]
- Kuroda, H.; Taniuchi, Y.; Watanabe, T.; Azumaya, T.; Hasegawa, N. Distribution of Harmful Algae (Karenia spp.) in October 2021 Off Southeast Hokkaido, Japan. Front. Mar. Sci. 2022, 9, 841364. [Google Scholar] [CrossRef]
- Murakami, H.; Antoine, D.; Vellucci, V.; Frouin, R. System vicarious calibration of GCOM-C/SGLI visible and near-infrared channels. J. Oceanogr. 2022, 78, 245–261. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Belgiu, M.; Draguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.; Ghimire, B.; Rogan, J.; Chica, M.; Rigol-Sanchez, J. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Fernandez-Delgado, M.; Cernadas, E.; Barro, S.; Amorim, D. Do we Need Hundreds of Classifiers to Solve Real World Classification Problems? J. Mach. Learn. Res. 2014, 15, 3133–3181. [Google Scholar]
- Breimanvol, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Loh, W.-Y. Classification and Regression Trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Friedman, J. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2000, 29, 1189–1232. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Song, W.; Dolan, J.M.; Cline, D.; Xiong, G. Learning-Based Algal Bloom Event Recognition for Oceanographic Decision Support System Using Remote Sensing Data. Remote Sens. 2015, 7, 13564–13585. [Google Scholar] [CrossRef]
- Joshi, N.; Park, J.; Zhao, K.; Londo, A.; Khanal, S. Monitoring Harmful Algal Blooms and Water Quality Using Sentinel-3 OLCI Satellite Imagery with Machine Learning. Remote Sens. 2024, 16, 2444. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, D.; Lin, J.; Peng, Q.; Lei, X.; Jin, T.; Wang, J.; Yuan, R. Prediction of phytoplankton biomass and identification of key influencing factors using interpretable machine learning models. Ecol. Indic. 2024, 158, 111320. [Google Scholar] [CrossRef]
- Orynbaikyzy, A.; Gessner, U.; Conrad, C. Spatial Transferability of Random Forest Models for Crop Type Classification Using Sentinel-1 and Sentinel-2. Remote Sens. 2022, 14, 1493. [Google Scholar] [CrossRef]
- Rubin, H.J.; Lutz, D.A.; Steele, B.G.; Cottingham, K.L.; Weathers, K.C.; Ducey, M.J.; Palace, M.; Johnson, K.M.; Chipman, J.W. Remote Sensing of Lake Water Clarity: Performance and Transferability of Both Historical Algorithms and Machine Learning. Remote Sens. 2021, 13, 1434. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, W.; Chen, J.; Yao, J.; Liao, Y.; Liu, J. Heterogeneous transfer learning considering feature representation and environmental consistency for landslide spatial prediction. GISci. Remote Sens. 2024, 61, 2349343. [Google Scholar] [CrossRef]
- Feng, C.; Zhu, Y.; Shen, A.; Li, C.; Song, Q.; Tao, B.; Zeng, J. Assessment of GCOM-C Satellite Imagery in Bloom Detection: A Case Study in the East China Sea. Remote Sens. 2023, 15, 691. [Google Scholar] [CrossRef]
- Luang-On, J.; Siswanto, E.; Ogata, K.; Toratani, M.; Buranapratheprat, A.; Leenawarat, D.; Ishizaka, J. Enhancing the reliability of GCOM-C/SGLI data for red tide detection in the upper Gulf of Thailand. Remote Sens. Lett. 2024, 15, 1096–1106. [Google Scholar] [CrossRef]
- Fan, Y.; Li, W.; Chen, N.; Ahn, J.-H.; Park, Y.-J.; Kratzer, S.; Schroeder, T.; Ishizaka, J.; Chang, R.; Stamnes, K. OC-SMART: A machine learning based data analysis platform for satellite ocean color sensors. Remote Sens. Environ. 2021, 253, 112236. [Google Scholar] [CrossRef]
- Adhikary, S.; Tiwari, S.P.; Banerjee, S.; Dwivedi, A.; Rahman, S.M. Global marine phytoplankton dynamics analysis with machine learning and reanalyzed remote sensing. PeerJ 2024, 12, e17361. [Google Scholar] [CrossRef]


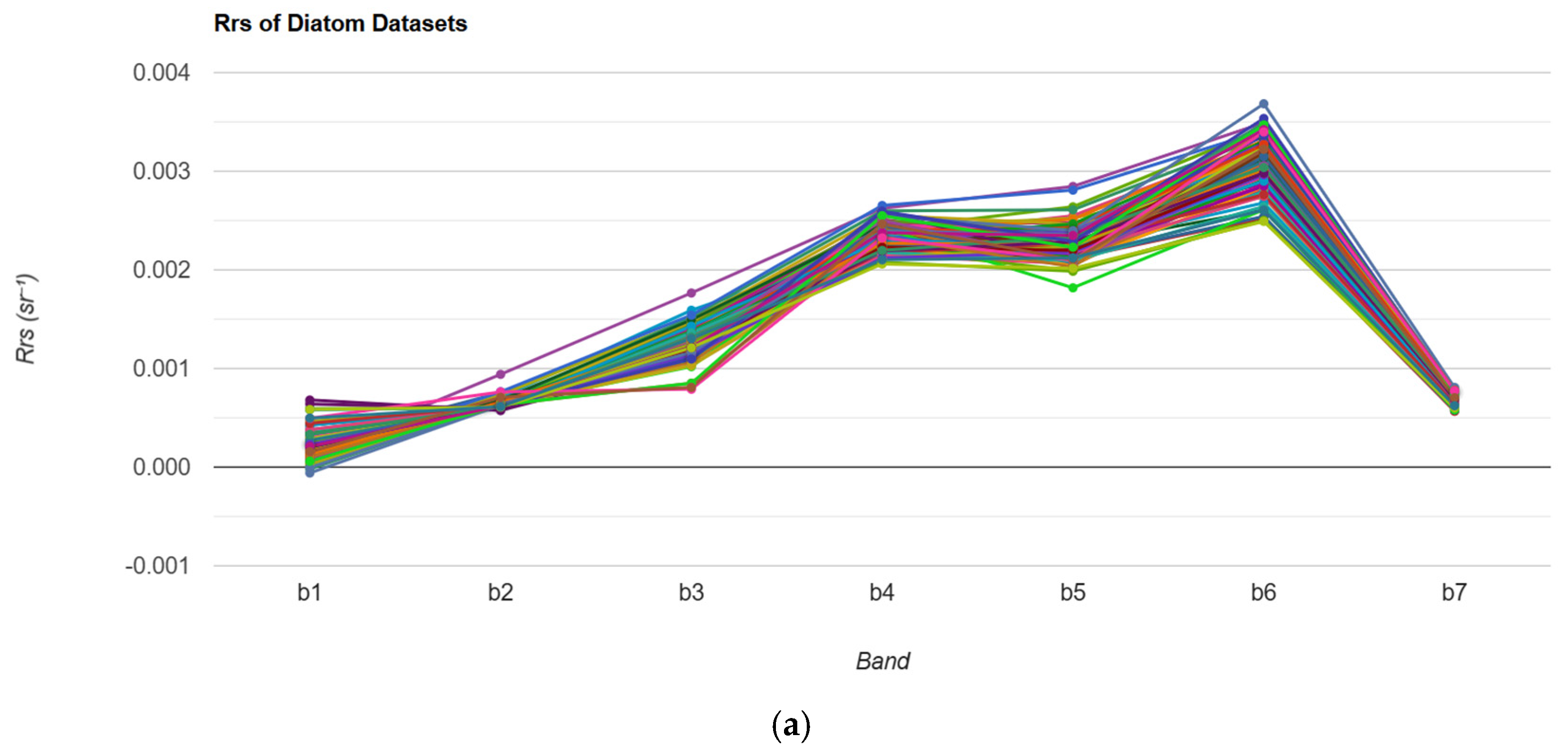
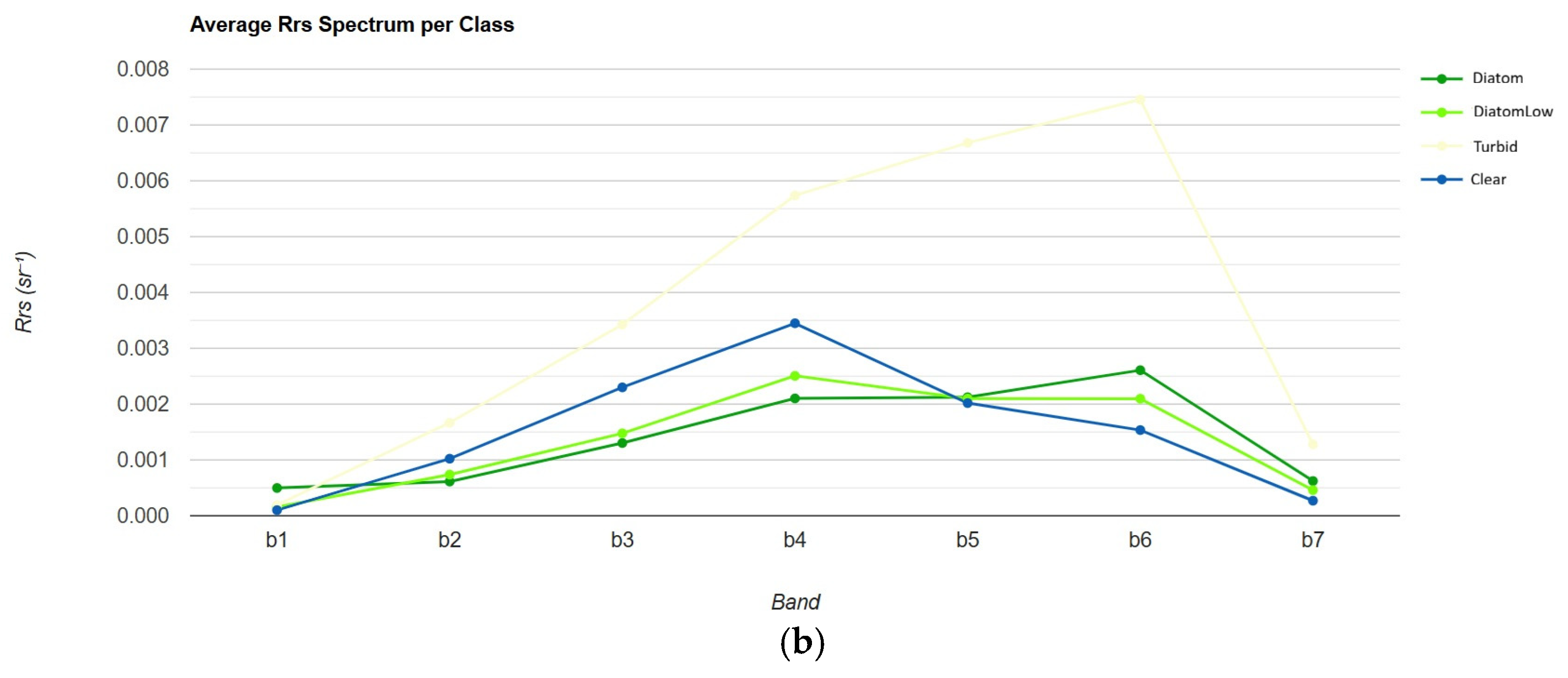
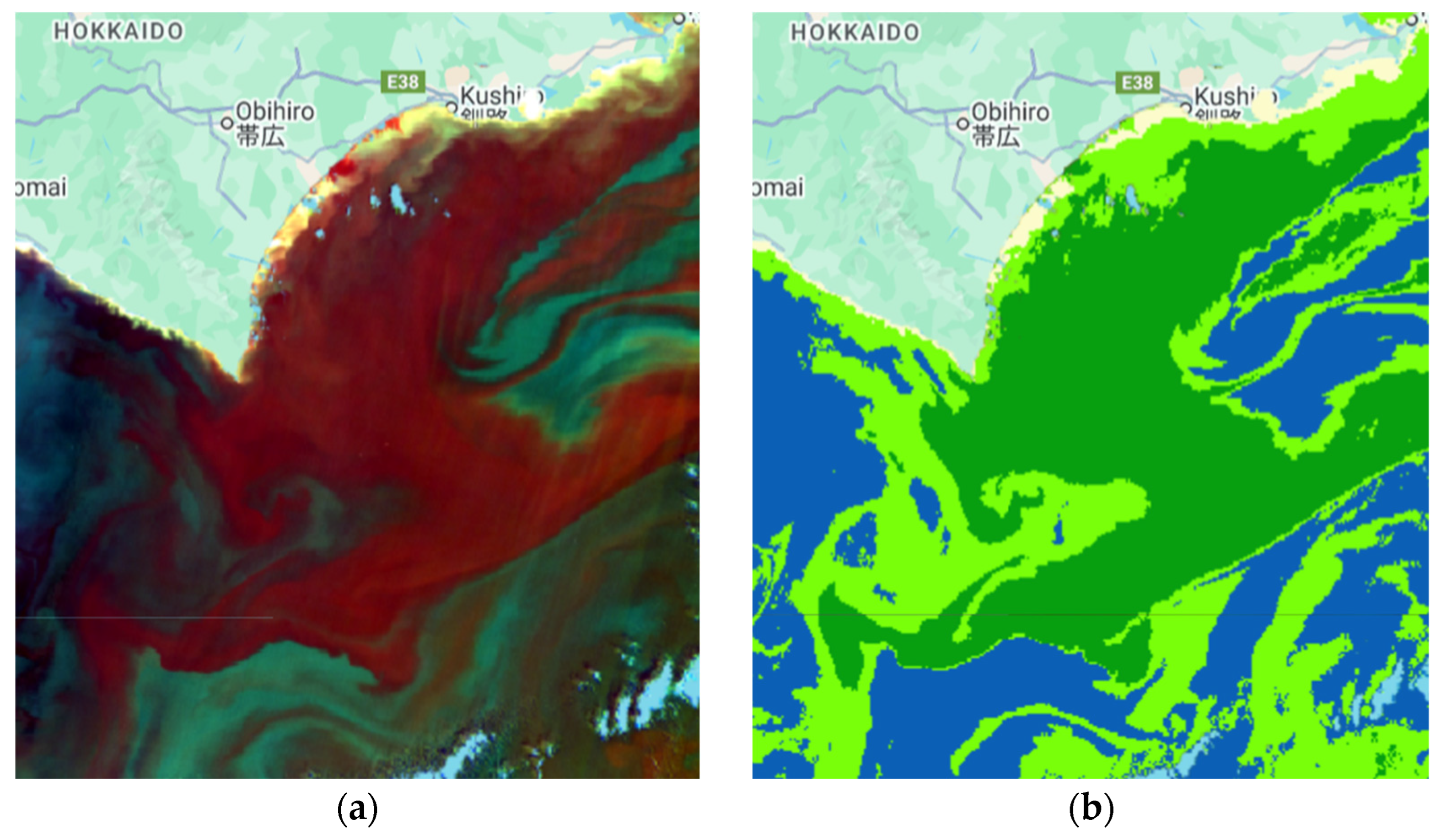
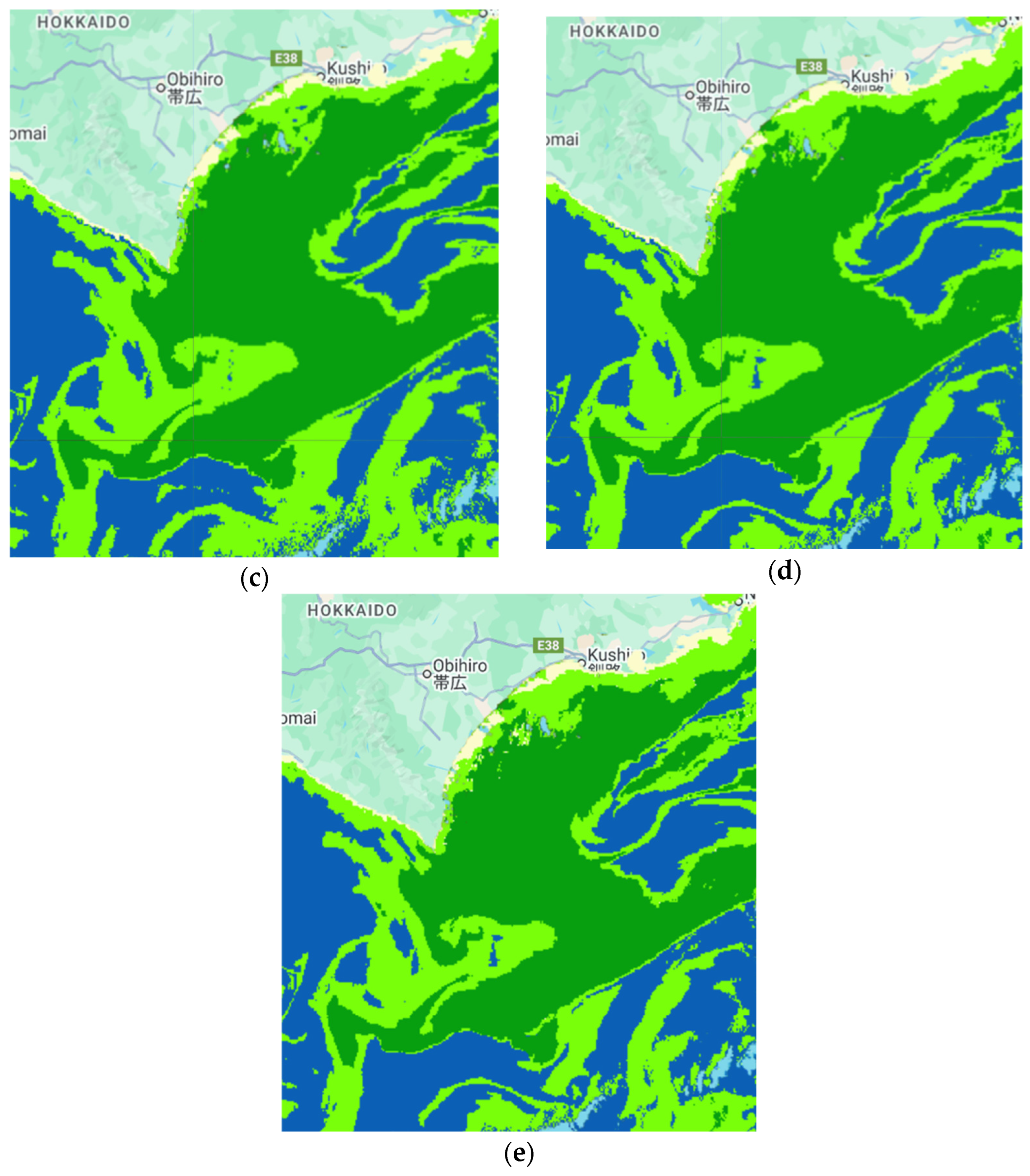

| Sub-Region | Observation Date | Consideration/Confirmation |
|---|---|---|
| Sagami Bay | 17 May 2020 | Confirmed phytoplankton coccolithophore bloom [35] |
| Waters of Southeast Hokkaido | 13 October 2021 | Confirmed red tide caused by phytoplankton from the dinoflagellate group [36,37] |
| 8 May 2022 | Expected to be seasonal blooms of phytoplankton diatoms | |
| 7 May 2022 | Expected to be seasonal blooms of phytoplankton diatoms |
| Absolute Magnitude of Correlation Coefficient | Interpretation |
|---|---|
| 0.00–0.10 | Negligible correlation |
| 0.10–0.39 | Weak correlation |
| 0.40–0.69 | Moderate correlation |
| 0.70–0.89 | Strong correlation |
| 0.90–1.00 | Very strong correlation |
| Scenario | Overall Accuracy | Kappa Coefficient | Pearson Correlation Coefficient | Determination Coefficient (R2) |
|---|---|---|---|---|
| RF with seven bands | 0.976 | 0.962 | 0.977 | 0.954 |
| RF with six bands | 0.939 | 0.911 | 0.931 | 0.861 |
| CART with seven bands | 0.967 | 0.950 | 0.956 | 0.908 |
| GTB with seven bands | 0.984 | 0.975 | 0.987 | 0.974 |
| Scenario | Overall Accuracy | Kappa Coefficient | Pearson Correlation Coefficient | Determination Coefficient (R2) |
|---|---|---|---|---|
| RF with seven bands | 0.978 | 0.969 | 0.970 | 0.940 |
| RF with six bands | 0.988 | 0.983 | 0.996 | 0.991 |
| CART with seven bands | 0.966 | 0.953 | 0.966 | 0.933 |
| GTB with seven bands | 0.978 | 0.969 | 0.970 | 0.940 |
| Scenario | Overall Accuracy | Kappa Coefficient | Pearson Correlation Coefficient | Determination Coefficient (R2) |
|---|---|---|---|---|
| RF with seven bands | 0.988 | 0.982 | 0.997 | 0.994 |
| RF with six bands | 0.922 | 0.888 | 0.928 | 0.846 |
| CART with seven bands | 0.988 | 0.982 | 0.997 | 0.994 |
| GTB with seven bands | 0.976 | 0.963 | 0.994 | 0.987 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Candra, D.S.; Siswanto, E. Machine Learning Approaches to Phytoplankton Identification and Classification Using GCOM-C/SGLI Imagery. Remote Sens. 2025, 17, 3759. https://doi.org/10.3390/rs17223759
Candra DS, Siswanto E. Machine Learning Approaches to Phytoplankton Identification and Classification Using GCOM-C/SGLI Imagery. Remote Sensing. 2025; 17(22):3759. https://doi.org/10.3390/rs17223759
Chicago/Turabian StyleCandra, Danang Surya, and Eko Siswanto. 2025. "Machine Learning Approaches to Phytoplankton Identification and Classification Using GCOM-C/SGLI Imagery" Remote Sensing 17, no. 22: 3759. https://doi.org/10.3390/rs17223759
APA StyleCandra, D. S., & Siswanto, E. (2025). Machine Learning Approaches to Phytoplankton Identification and Classification Using GCOM-C/SGLI Imagery. Remote Sensing, 17(22), 3759. https://doi.org/10.3390/rs17223759





