Construction and Visualization of Levels of Detail for High-Resolution LiDAR-Derived Digital Outcrop Models

Highlights

What are the main findings?

• Proposed an automated and adaptive workflow for constructing multi-scale LOD models from high-resolution LiDAR-derived digital outcrops, integrating model segmentation, pseudo-quadtree tiling, and feature-preserving simplification.
• Enhanced the traditional QEM simplification algorithm with vertex sharpness constraint and boundary-freezing and fallback strategies to maintain geometric continuity and preserve key geological structures.
• Developed a dynamic multi-scale visualization framework using an LOD index and the OSG PagedLOD mechanism, achieving real-time, view-dependent rendering of massive outcrop models on standard hardware.

What are the implications of the main findings?

• Provide a practical and efficient solution for managing and visualizing large-scale LiDAR-derived outcrop models, effectively addressing rendering bottlenecks in geological applications.
• Enable smooth, interactive, and scalable visualization, supporting detailed multi-scale geological interpretation and paving the way for future web-based collaborative analysis platforms.

Abstract

High-resolution LiDAR-derived three-dimensional (3D) digital outcrop models are crucial for detailed geological analysis. However, their massive data volumes often exceed the rendering and memory capacities of standard computer systems, posing significant visualization challenges. Although Level of Detail (LOD) techniques are well-established in Geographic Information Systems (GISs) and computer graphics, they still require customized design to address the unique characteristics of geological outcrops. This paper presents an automated method for constructing and visualizing LOD models specifically tailored to high-resolution LiDAR outcrops. The workflow begins with segmenting the single-body model based on texture coverage, followed by building an adaptive LOD tile pyramid for each segment using a pseudo-quadtree approach. The proposed LOD construction method incorporates several innovative components: segmentation based on texture coverage, an adaptive LOD tile pyramid using a pseudo-quadtree, and a feature-preserving mesh simplification algorithm that includes vertex sharpness constraint and boundary freezing strategy to maintain critical geological features. For visualization, a dynamic multi-scale loading and rendering mechanism is implemented using an LOD index with the OpenSceneGraph (OSG) engine. The results demonstrate that the proposed method effectively addresses the bottleneck of rendering massive outcrop models. The models loading time and average memory usage were reduced by more than 90%, while the average display frame rate reached around 60 FPS. It enables smooth, interactive visualization and provides a robust foundation for multi-scale geological interpretation.

1. Introduction

Geological outcrops are important research objects in geological research [1,2,3]. Traditional outcrop studies mainly rely on field investigations, which are limited by terrain and thus cannot effectively survey outcrops located in high or hazardous areas. The emergence of digital outcrop technology has provided new technical means for geological outcrop research [4].

Light Detection and Ranging (LiDAR), as one of the most precise and commonly used digital outcrop acquisition techniques, enables rapid and large-scale collection of high-resolution point cloud data of geological outcrops, with scanning accuracy reaching up to 1 mm [5]. Based on these data, high-resolution 3D digital outcrop mesh models with photographic textures can be constructed, allowing for detailed digital representation and analysis of outcrops [6]. Using such high-resolution LiDAR-derived digital outcrop models, geoscientists can conduct lithological and mineral identification [7,8], structural surface interpretation [9], fracture and cavity extraction [10,11], sedimentary feature description [12], and rock joint measurement and characterization [13] directly at the desktop, thereby greatly improving research efficiency and reducing the cost and intensity of geological exploration. However, as data sources continue to diversify and collection accuracy increases, the data volume of high-resolution digital outcrop models grows exponentially, placing significant pressure on model storage, transmission, and real-time visualization.

Level of Detail (LOD) technology is an effective solution to the problem of visualizing large-scale 3D models [14]. In this framework, each node represents a mesh model at a specific resolution and spatial extent, enabling real-time rendering of massive 3D scenes through efficient data scheduling between memory and external storage [15,16]. However, current LOD technologies are mainly targeted at fields such as computer vision [17,18,19], GIS and remote sensing [20,21,22], and urban and landscape modeling [23,24]. Their application in digital outcrop modeling still faces three significant challenges: (1) Unsuitable data partitioning for irregular, elongated outcrop shapes; (2) loss of key geological features during model simplification; and (3) inefficient rendering of massive, high-resolution outcrop data.

To address these challenges, this paper presents an automated Level of Detail (LOD) method tailored for high-resolution LiDAR outcrops. The main contributions of this work are threefold:

• A specialized LOD workflow that uses texture-based segmentation and a pseudo-quadtree to generate an adaptive tile pyramid, effectively handling the elongated morphology of outcrops.
• A feature-preserving simplification algorithm that introduces a vertex sharpness constraint and a boundary freezing strategy to retain critical geological features during aggressive mesh reduction.
• A dynamic visualization framework that leverages an LOD index and the OSG engine to achieve real-time, view-dependent loading and rendering, enabling interactive exploration of massive models on standard hardware.

The proposed approach effectively overcomes the rendering bottleneck, significantly reducing loading time and memory usage while maintaining a high frame rate, thus providing a robust foundation for multi-scale geological interpretation.

2. Literature Review

2.1. Digital Outcrops

Digital outcrops, also known as virtual outcrops, represent a key component of the emerging field of digital geology [25]. A digital outcrop refers to a 3D model of a rock exposure that preserves realistic spatial coordinates and texture information, generated through technologies such as remote sensing, photogrammetry, and laser scanning. Since Bryant et al. (2000) systematically elaborated its scientific value, this technology has undergone more than two decades of rapid development and has become an indispensable data foundation in geological modeling, reservoir characterization, and related fields [4]. Their work laid the foundation for subsequent digital geological modeling frameworks.

Among various modeling approaches, LiDAR has consistently maintained a leading position in spatial accuracy, enabling the acquisition of dense point cloud data with millimeter-level precision. In 2005, Bellian et al. first introduced LiDAR systems into geological outcrop investigations and established a complete workflow encompassing data acquisition, processing, and visualization [5]. Building upon this foundation, subsequent studies have enhanced scanning precision, improved point cloud registration algorithms, and developed automated methods for lithological and structural feature extraction [25,26,27]. Over the past two decades, LiDAR-based digital outcrop techniques have matured substantially, achieving accuracies of up to 1 mm. The steadily increasing level of detail and scale of reconstructed models has made LiDAR the most precise and widely adopted approach in digital outcrop research [8,28].

In parallel, photogrammetry-based modeling techniques have developed rapidly. In 2012, Westoby et al. introduced the Structure from Motion (SfM) approach to digital outcrop reconstruction, providing a cost-effective alternative to LiDAR [29]. By matching multiple overlapping images, SfM reconstructs 3D structures efficiently. With the widespread availability of unmanned aerial vehicles (UAVs), it has become possible to capture centimeter-scale detail and achieve full-coverage reconstructions of complex outcrops. Comparative analyses conducted in 2016 confirmed the high consistency between SfM-derived models and terrestrial laser scanning results [30]. Since then, the integration of UAV-based oblique photogrammetry has further enriched digital outcrop workflows, leading to a mature technical framework and a growing number of successful applications [31,32,33,34].

More recently, digital outcrop modeling has entered a phase of multi-source data integration. This integration leverages LiDAR geometry, UAV-SfM texture richness, and satellite-based contextual information. The high geometric accuracy of LiDAR and the rich texture information captured by photogrammetry offer complementary advantages. The integration of these multi-source data is crucial for the determination of 3D roughness of rock joints based on profile slices [35]. Furthermore, the incorporation of additional data sources such as Global Positioning System (GPS) measurements and remote sensing imagery has transformed digital outcrops from isolated 3D models into comprehensive geospatial information platforms [36,37]. This fusion enables multi-scale geological feature recognition and extends the application of digital outcrops to structural interpretation, reservoir modeling, fracture characterization, and lithological or mineral identification [6,7,8,9,10,11,12,38,39].

However, as data volumes continue to grow, efficient data organization and hierarchical indexing have become critical challenges. Achieving a balance between geological accuracy and interactive visualization performance is essential for supporting large-scale analysis and interpretation. In this context, LOD-based data structuring and visualization are essential for scalable and interactive geological interpretation.

2.2. Level of Detail

The concept of Level of Detail (LOD), initially proposed by Clark (1976), aims to reduce the computational overhead of real-time rendering and transformation through multi-resolution geometric representations [14]. Although originally developed for computer graphics, the concept has since become central to geospatial data management. Early research primarily focused on geometric simplification algorithms within computer graphics, such as edge-collapse-based progressive meshes [40] and hierarchical structures built upon quadtrees or octrees [41]. These methods facilitated multi-level representations and dynamic switching between resolutions based on viewing distance.

In recent years, LOD research has expanded to encompass dense geospatial datasets like point clouds and DTMs [19,20,21]. Techniques such as mipmap-based multiresolution texture mapping and GPU-driven dynamic detail scheduling have significantly enhanced rendering efficiency for large-scale and complex scenes [42]. Despite these advancements in large-scale scene visualization, their generalized data organization methods (e.g., regular tile pyramids) and geometric simplification algorithms (e.g., curvature-based uniform simplification) still face challenges [15,16]. When geological outcrops exhibit significant anisotropy (e.g., being elongated, overhanging) or contain multi-scale structures (from regional tectonics to microscopic fractures), existing methods struggle to preserve visual coherence while adaptively maintaining their structural integrity and geological significance.

Particularly in the field of 3D city modeling, the LOD concept has been redefined; for instance, the CityGML standard classifies urban objects into five discrete levels (LOD0–LOD4) [43,44,45]. However, such LOD paradigms derived from urban modeling show significant limitations when dealing with irregular, feature-rich geological surfaces like cliffs. The discrete classification in CityGML relies on regularized geometric abstractions (e.g., prismatic blocks in LOD2, regularized texture models in LOD3), making it difficult to effectively represent the highly heterogeneous and complex geometric forms of geological outcrops.

Although LOD technology is crucial for visualizing large-scale digital outcrops, the vast majority of existing techniques are not tailored for them. Previous research on digital outcrops has primarily emphasized data acquisition and geological interpretation [46,47,48,49], while comparatively less attention has been given to LOD organization or hierarchical design strategies aligned with the distinctive characteristics of geological data [34,50]. Currently, there is no standardized scheme specifically designed for the characteristics of outcrop models (such as their spatial layout, scale, and observation perspectives) for customizing LOD hierarchy division or tile pyramid construction. Furthermore, during the LOD construction process, critical geological features are prone to being over-smoothed or culled, leading to the loss of associated semantic information. Consequently, there is a pressing need to develop simplification algorithms that prioritize the preservation of detailed geological structures within digital outcrop models.

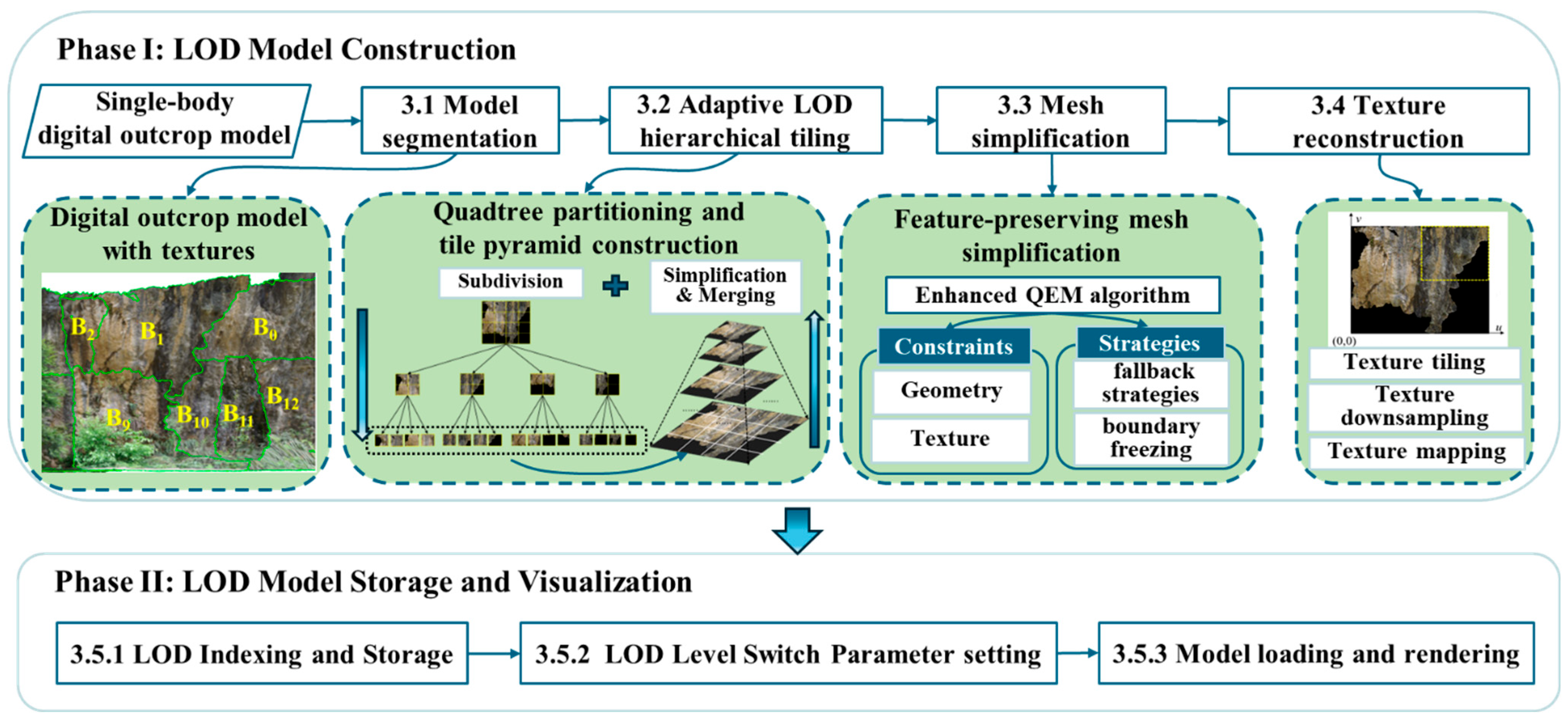
3. Methods

To achieve the construction and visualization of LOD models for high-resolution LiDAR-based digital outcrops, we propose an automated solution that integrates model simplification, LOD index construction, and multi-scale rendering. As illustrated in Figure 1, the entire workflow comprises seven sequential steps, organized into two primary phases:

Phase I: LOD Model Construction

• Single-body Model Segmentation (Section 3.1): Import the high-resolution, large-scale LiDAR-derived single-body digital outcrop model, then partition it into multiple sub-models according to the coverage area of each texture image.
• Adaptive LOD Hierarchical Tiling (Section 3.2): For each sub-model, construct a multi-level LOD tile structure using a pseudo-quadtree partitioning approach, forming a tile pyramid through iterative subdivision, simplification, and merging processes.
• Mesh Simplification (Section 3.3): Apply a feature-preserving QEM algorithm to simplify each tile across all LOD levels, incorporating constraints for geometry and texture preservation along with strategies such as fallback tactics and boundary freezing.
• Texture Reconstruction (Section 3.4): Reconstruct texture images and their corresponding coordinates for tiles at each LOD level, involving texture tiling, downsampling, and remapping operations.

Phase II: LOD Model Storage and Visualization

• LOD Indexing and Storage (Section 3.5.1): Establish an LOD index file for the entire model, storing geometric data, texture information, and other parameters of each constructed tile in OSGB format.
• Display Parameter Setting (Section 3.5.2): Configure model display parameters based on the texture image size of each tile to optimize visualization quality.
• Model Loading and Rendering (Section 3.5.3): Implement multi-scale loading and rendering of the LOD digital outcrop model using the OSG engine, enabling efficient visualization across different detail levels.

In summary, this solution realizes the construction and visualization of LOD for high-resolution LiDAR-derived digital outcrop models through seven steps in two phases, and the following will elaborate on the specific implementation methods and technical details of each step.

3.1. Single-Body Model Segmentation

The original model used for LOD construction is a LiDAR-derived single-body digital outcrop model. LiDAR technology acquires high-density point cloud data from outcrop surfaces, which are triangulated to generate a high-resolution mesh. High-resolution photographic images are then applied through texture mapping to produce a photorealistic 3D model (Figure 2a). A single-body digital outcrop model generally consists of two core components: (1) geometric data: three-dimensional meshes generated by triangulating laser-scanned point clouds to accurately represent outcrop morphology (Figure 2c); and (2) texture data: high-resolution images captured by digital cameras and mapped onto the mesh surface to provide realistic visualization (Figure 2b).

To preserve the integrity of the original texture mapping, the digital outcrop model is first subdivided into multiple sub-models B = {B₀, B₁, B₂, …} based on the coverage of texture images on the model surface (Figure 2a). Subsequently, a quadtree-based tile pyramid is built for each sub-model, resulting in a multi-scale LOD tiled structure described in the following sections. This method ensures geometric accuracy and texture fidelity while reducing the complexity of texture reconstruction during LOD construction.

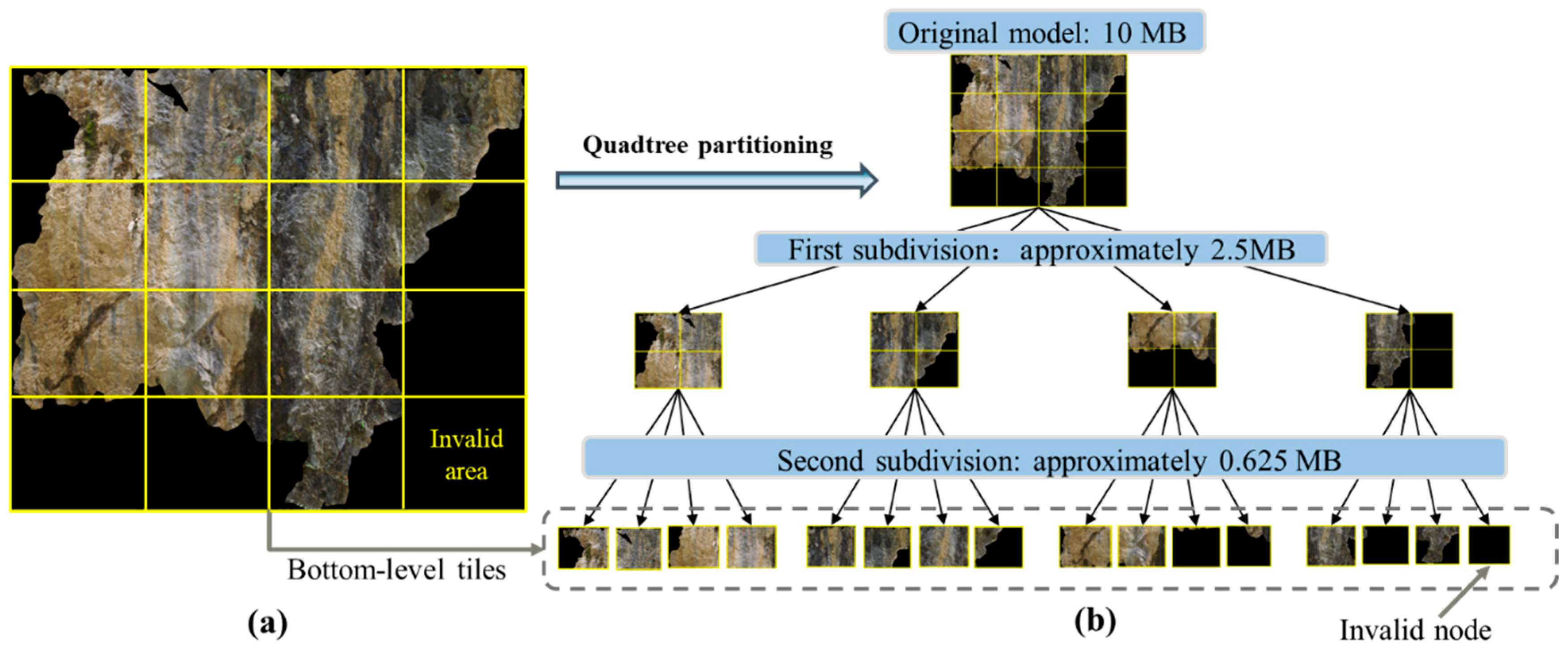
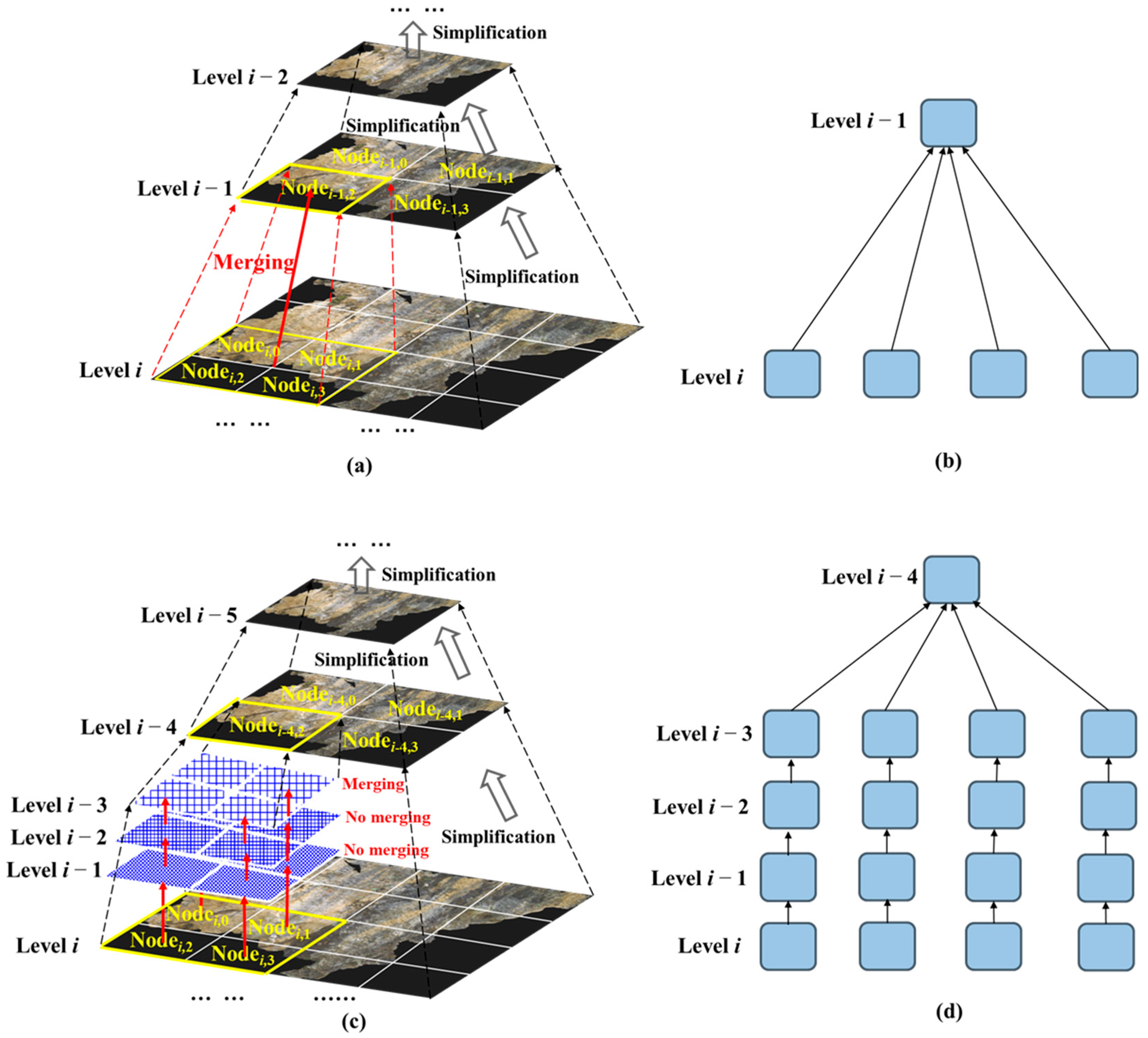
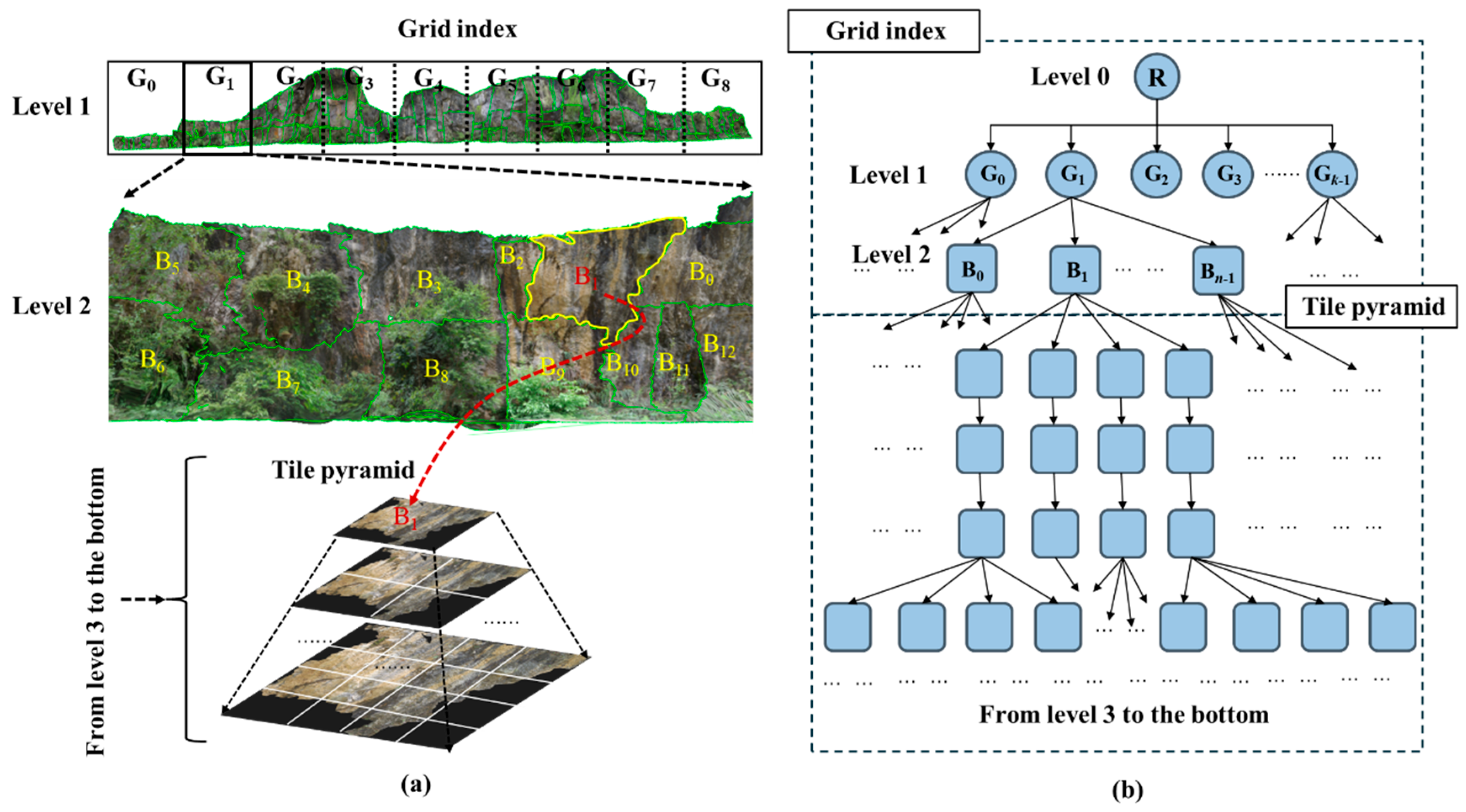
3.2. Adaptive LOD Hierarchical Tiling

To achieve efficient multi-scale organization of complex outcrop models, this section proposes an adaptive LOD tiling strategy that integrates a bottom-up simplification process with quadtree-based hierarchical partitioning. The process first applies quadtree subdivision in texture space to generate fine-grained bottom-level tiles, and then progressively simplifies and merges them to construct upper-level LOD nodes. It is important to note that this approach is best suited for outcrop models with relatively planar or gently curved geometries, such as typical cliff faces and fault walls. Its performance may be suboptimal for structures with extreme geometric complexity, as discussed in Section 5.1.

3.2.1. Bottom-Level Tile Generation Based on Quadtree Partitioning

The quadtree index was first proposed by Tayeb in 1998 [51]. Its basic principle is to recursively divide a rectangular region into four subregions until the number of elements in each subregion does not exceed a specified capacity. In this study, the sub-models are partitioned in the 2D texture coordinate space using a quadtree structure, resulting in a multi-level, hierarchically refined tile pyramid. A key question is how many levels of subdivision are appropriate for each sub-model. Here, we adopt the data volume of a single tile node as the criterion for further subdivision. Since each subdivision divides one tile into four child tiles, under the assumption of uniform data distribution, the data volume of each child tile is approximately one quarter of its parent. We define a threshold V_t (e.g., 1.0 MB) such that the data volume of each node in the constructed LOD structure is close to this threshold, enabling efficient loading and network transmission during rendering. Subdivision is terminated once the data volume of a single tile falls below V_t. Accordingly, the number of quadtree subdivision levels can be estimated as:

$$n=⌊l{og}_4(V_0/V_t)⌋+1$$

(1)

where V₀ denotes the data volume of the original sub-model, V_t is the predefined data volume threshold for a single tile, and n is the estimated number of subdivision levels in the quadtree.

Based on the above idea, performing n quadtree subdivisions on a given sub-model yields the bottom-level tile data, whose resolution remains consistent with the original model without any simplification (see Figure 3). Obviously, the valid part of a texture image is not necessarily a regular rectangle, and the black regions represent invalid areas. If a tile’s coverage falls entirely within an invalid area, that tile will be treated as an invalid node and ignored in subsequent processing.

3.2.2. Simplification and Merging Strategies for Bottom-Up Tile Generation

After the above quadtree subdivisions, we have obtained the bottom-level tiles of the LOD model. Next, the remaining tiles at higher levels of the LOD model are generated gradually using a bottom-up strategy that simplifies and merges tiles simultaneously. The simplification ratio θ is defined as the ratio of the face count in the simplified mesh to that in the original mesh (e.g., θ = 0.8 indicates retaining 80% of the original faces). Suppose the simplification ratio between two adjacent levels from bottom to top in the LOD model is θ. According to the previously proposed simplification algorithm, each tile’s mesh is simplified individually, while its texture image is also correspondingly downsampled. Figure 4 demonstrates how the simplification and merging operations are flexibly applied according to data size thresholds when generating higher-level tiles in a bottom-up LOD construction. Consider four tiles at level i that belong to the same parent node in the previous quadtree subdivision (Node_i,0, Node_i,1, Node_i,2, Node_i,3). First, the total data size for the simplified level i − 1 is estimated as:

$$V_{i-1}=\left(V_i^0+V_i^1+V_i^2+V_i^3\right) \times \theta$$

(2)

where $V_i^0$, $V_i^1$, $V_i^2$, and $V_i^3$ are the data size of the four tiles at level i, θ is the simplification ratio.

If V_i−1 < V_t, four corresponding simplified tiles at the upper level are merged into a single parent node (see Figure 4a); otherwise, they remain unmerged and are preserved as four separate upper-level nodes, each corresponding to a lower-level node (see Figure 4c). During this process, the correspondence between nodes in adjacent levels is also established, forming either one-to-one or one-to-four relationships (see Figure 4b,d).

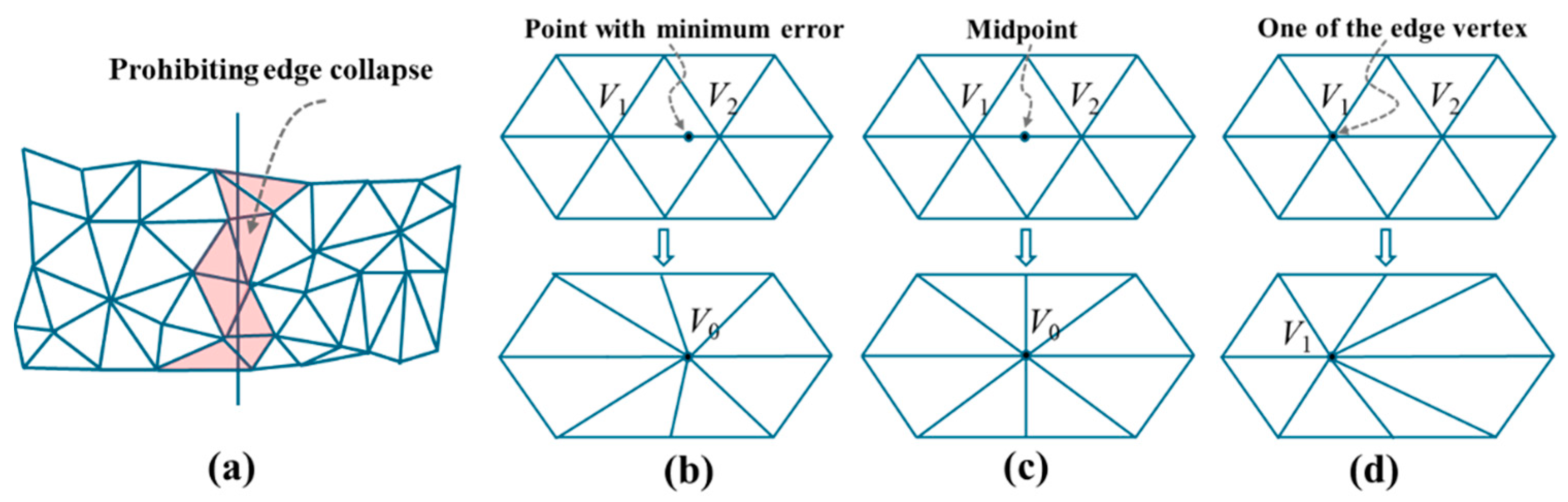
3.3. Feature-Preserving Mesh Simplification

In the construction of the tile pyramid, model simplification is a critical step, as each tile consists of both geometric (mesh) and texture components. During the hierarchical simplification process, it is essential to preserve these geometric and texture features as much as possible. For textured mesh simplification, Garland et al. introduced an edge-collapse algorithm based on QEM, which is computationally efficient and produces simplified models of good quality [52]. However, when applied to the construction of LOD models for digital outcrops, additional optimization and customization are necessary. To this end, we propose a feature-preserving QEM simplification algorithm, which incorporates tailored constraints to simultaneously preserve geometric and texture features of digital outcrop models. Specifically, for texture preservation, we extend the QEM framework by integrating texture coordinates; for geometric preservation, we introduce a vertex sharpness constraint to retain fine surface details; and under specific conditions, we further design dedicated edge-collapse strategies to better maintain detailed features in the simplified model.

3.3.1. QEM Simplification Algorithm

The QEM algorithm is an edge collapse simplification algorithm. In mesh simplification via the edge collapse method, an edge (V₁, V₂) is considered the basic operation unit, and its vertices V₁ and V₂ are contracted to a single point v₀ (see Figure 1). It calculates the sum of squared distances from the new vertex V₀ in space to each triangular face in the one-ring neighborhood of the original edge (V₁, V₂) as the error metric for edge collapse, thereby optimizing the selection of edges to collapse. However, for the simplification of textured mesh models, the optimization of texture coordinates at the new vertex after collapse must also be considered. To address this, Garland et al. extended the foundational QEM algorithm by incorporating attribute features such as texture coordinates (u, v) alongside the three-dimensional coordinates (x, y, z) of the vertices [52]. This constructs a multidimensional space for the model and calculates the quadratic error of vertices within this multidimensional space. Through the minimization of the quadratic error matrix, the optimal spatial coordinates and texture coordinates for each vertex in the abstract multidimensional space are determined. In the described multidimensional space, a quadratic error matrix Q_i can be calculated for each triangular face within the one-ring neighborhood of any vertex V_i. Consequently, the error of collapsing an edge (V₁, V₂) is expressed as:

E(V₀) = V₀^T(Q₁ + Q₂)V₀

(3)

where V₀ = [ x₀, y₀, z₀, u₀, v₀, 1]^T is the high-dimensional homogeneous coordinate of the new vertex. Q₁ and Q₂ are the error matrices of V₁ and V₂, respectively. E(V₀) is determined by the position of the new vertex.

3.3.2. Vertex Sharpness Constraint

Compared to the smooth parts of the model, the concave and convex parts represent significant geometric structural features and should be preserved as much as possible during simplification. To enhance the algorithm’s sensitivity to these concave and convex regions, ensuring that more detailed features are retained even under high simplification ratios, we introduce vertex sharpness α as a constraint factor for modeling geometric detail characteristics. As illustrated in Figure 5, the calculation involves, for any vertex in the model, iterating through its one-ring neighborhood to compute the angles (in radians) between the normal vectors of every pair of adjacent triangular faces. The sum of these angles is then weighted and averaged using the corresponding triangle areas to measure the vertex’s sharpness. We define α as the vertex sharpness of a point in the mesh, and the corresponding calculation formula is shown in Equation (4).

$$\alpha =\sum _{i=1}^{n-1}{\displaystyle \frac{\left(\left(S_i+S_{i+1}\right)\times <N_i,N_{i+1}>+\left(S_i+S_{i+2}\right)\times <N_i,N_{i+2}>+\cdots +\left(S_i+S_n\right)\times <N_i,N_n>\right)}{2S_{sum}}}$$

(4)

where α is the vertex sharpness, n is the number of triangles in the one-ring neighborhood of the vertex, S_sum is the total area of these triangles, S_i represents the area of the i-th triangle, and N_i represents the normal vector of this triangle.

Integrating the fundamental QEM error function from Section 3.2.1 with the vertex sharpness constraint factor, we propose a new error function as shown in Equation (5):

E(V₀) = V₀^T(α₁Q₁ + α₂Q₂)V₀

(5)

where α₁ and α₂ are the vertex sharpness of V₁ and V₂, respectively. The meanings of other parameters are the same as those in Equation (3). Our goal is to find the V₀ that minimizes the E(V₀). This is a classic quadratic optimization problem. The error function E(V₀) is a quadratic function with respect to V₀. To find its minimum, we take its gradient and set it to zero:

∇E(V₀) = 2(α₁Q₁ + α₂Q₂) V₀ = 0

(6)

Letting Q = α₁Q₁ + α₂Q₂, the problem reduces to solving the linear system:

QV₀ = 0

(7)

However, the matrix Q may be singular (non-invertible), for example, when all associated planes are coplanar or collinear. In such cases, the algorithm needs to adopt a fallback strategy.

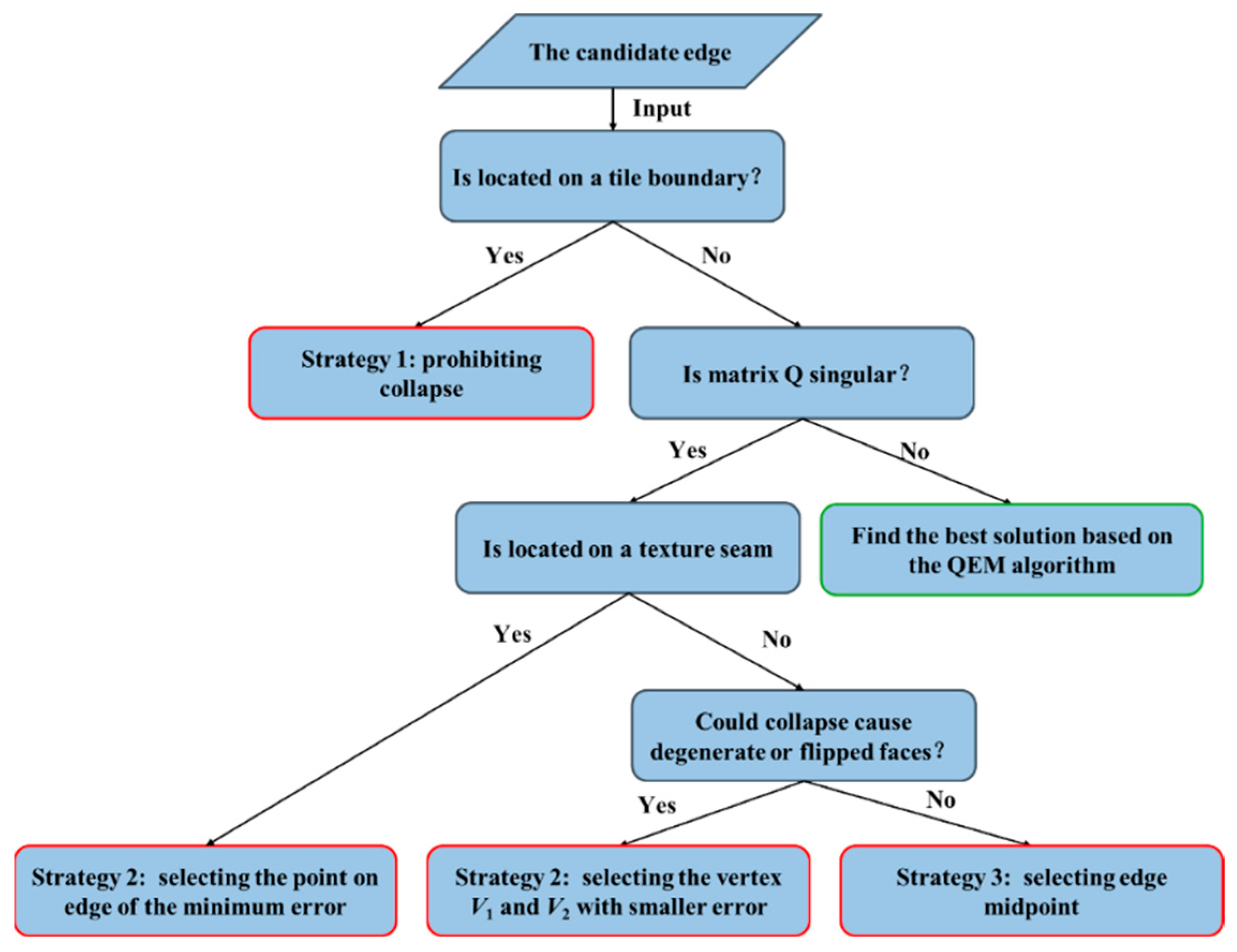
3.3.3. Strategies for Specific Cases

Since our simplification algorithm is specifically designed for constructing LOD models—where the model is divided into tiles during LOD structure creation—we introduce a tile boundary freezing strategy (Strategy 1) to maintain topological and texture continuity between adjacent tiles. Meanwhile, when the Q matrix in the error function is singular, the equation QV₀ = 0 has no solution or no unique solution. In such cases, three fallback strategies (Strategies 2–4) can be employed. In summary, the following four strategies are applied depending on the situation:

• Strategy 1: Prohibiting edge collapse (Figure 6a);
• Strategy 2: Finding the point on the edge that minimizes the error (Figure 6b);
• Strategy 3: Selecting one of the edge vertices, V₁ or V₂ (Figure 6c);
• Strategy 4: Selecting the midpoint of the edge (Figure 6d).

The decision tree for selecting these strategies is illustrated in Figure 7. The process first checks if the candidate edge is located on a tile boundary—if true, it immediately applies Strategy 1 by assigning infinite collapse cost to prohibit collapse. For non-boundary edges, it then checks if matrix Q is singular; if not, it directly computes the optimal solution using V₀₌ = −Q⁻¹b. If Q is singular, a fallback strategy is triggered based on the edge properties. For texture seams, the point minimizing the error function along the edge is selected to preserve texture integrity (Strategy 2); for non-seam edges, the risk of generating degenerate or flipped faces is assessed—if high, the vertex with the smaller QEM error (V₁ or V₂) is chosen (Strategy 3), otherwise the edge midpoint is selected for stability (Strategy 4). Finally, the collapse error of the edge is calculated to update the simplification priority queue.

3.4. Tile Texture Downsampling and Remapping

During the construction of the tile pyramid, adaptive hierarchical partitioning is achieved through bottom-up tiles simplification and merging. In this process, texture images are simultaneously divided into smaller rectangular tiles, thereby disrupting the original texture mapping relationships. Consequently, for each tile unit, in addition to mesh simplification (see Section 3.3), texture downsampling and remapping must be performed in a bottom-up manner.

To ensure that the texture downsampling ratio corresponds to the degree of geometric simplification, the downsampling window size is set as the reciprocal of the simplification ratio (e.g., when the simplification ratio θ = 0.5, the downsampling window size is 2). As image downsampling is a mature technique, it is not further elaborated here. Texture coordinate remapping aims to establish a correspondence between the original global texture coordinate space and the local coordinate space of each tile (see Figure 8). For any tile at a given LOD level, the new texture coordinates of its vertices are computed as follows:

$$\left\{\begin{array}{c}{u}^{\prime }=(u-u_{min})/(u_{max}-u_{min})\\ v^{\prime }=(v-v_{min})/(v_{max}-v_{min})\end{array}\right.$$

(8)

where u and v represent the original texture coordinates of a vertex in the global texture space; u_min, v_min, u_max, and v_max define the bounding range of the texture region covered by the tile in the original global texture space; and u’ and v’ represent the transformed texture coordinates after remapping. They correspond to the local coordinate system of the tile’s cropped texture image, ensuring that the texture aligns correctly with the simplified mesh.

3.5. LOD Model Storage and Visualization

To ensure efficient management, storage, and visualization of large-scale outcrop models, a multi-level LOD structure must be systematically organized, stored, and rendered. This section introduces the design of the LOD indexing and storage structure, and the OSG-based visualization mechanism, including parameter settings and dynamic loading strategies.

3.5.1. LOD Indexing and Storage

After model partitioning and tile pyramid construction, the single-body model is decomposed into multi-level discrete sub-blocks (sub-models or tiles), which must be organized through an appropriate spatial index to enable the 3D visualization module to dynamically schedule and render them according to the viewport state.

As described in Section 3.1, the single-body model is divided into multiple sub-models, and then a tile pyramid is constructed for each sub-model (see Figure 9a). Given that the digital outcrop exhibits a banded façade, a regular grid is used to construct the top-level spatial index of the sub-models. The outcrop profile is partitioned along its major axis into several equally sized rectangular grids, and each sub-model Bi is assigned to the grids it overlaps or intersects, thereby forming the top-level grid index of the entire outcrop model. In practice, we traverse all sub-model data blocks, compute the centroid of each sub-model, and then assign the sub-model to the grid cell that contains its centroid.

As shown in Figure 9b, in this indexing structure, the node representing the entire model extent serves as the root node (Level 0). Each rectangular grid corresponds to a level 1 node, and the nodes associated with the sub-models linked to these grids are defined as level 2 nodes. From Level 2 downward, the nodes correspond to the tile pyramid generated by further subdivision of each sub-model. The logical structure of this pyramid has been described in detail in Section 3.2. To index these tiles, we construct a spatial index that approximates a quadtree, following the pyramid hierarchy from top to bottom. During the bottom-up tile generation process, parent–child relationships can be either one-to-four or one-to-one, resulting in a quadtree-like hierarchy. We therefore refer to this structure as a pseudo-quadtree. Unlike a standard quadtree, where each parent node has exactly four children, the pseudo-quadtree allows more flexible relationships between levels.

Following the multi-level indexing structure, the constructed LOD model is stored in the OSGB format. OSGB is a binary storage format that supports LOD structures. Typically, a single OSGB 3D model dataset contains multiple folders, and each folder includes several OSGB files. Each OSGB file contains one root node (Root), several intermediate-level nodes (of type Group or Geode), and the leaf nodes (of type Geode). The intermediate nodes store information such as geometry, textures, and parent–child relationships between hierarchical levels, while the leaf nodes only contain the geometric and texture information of the model. This design is fully compatible with the constructed LOD indexing structure and facilitates efficient visualization of LOD 3D models based on the OSG engine.

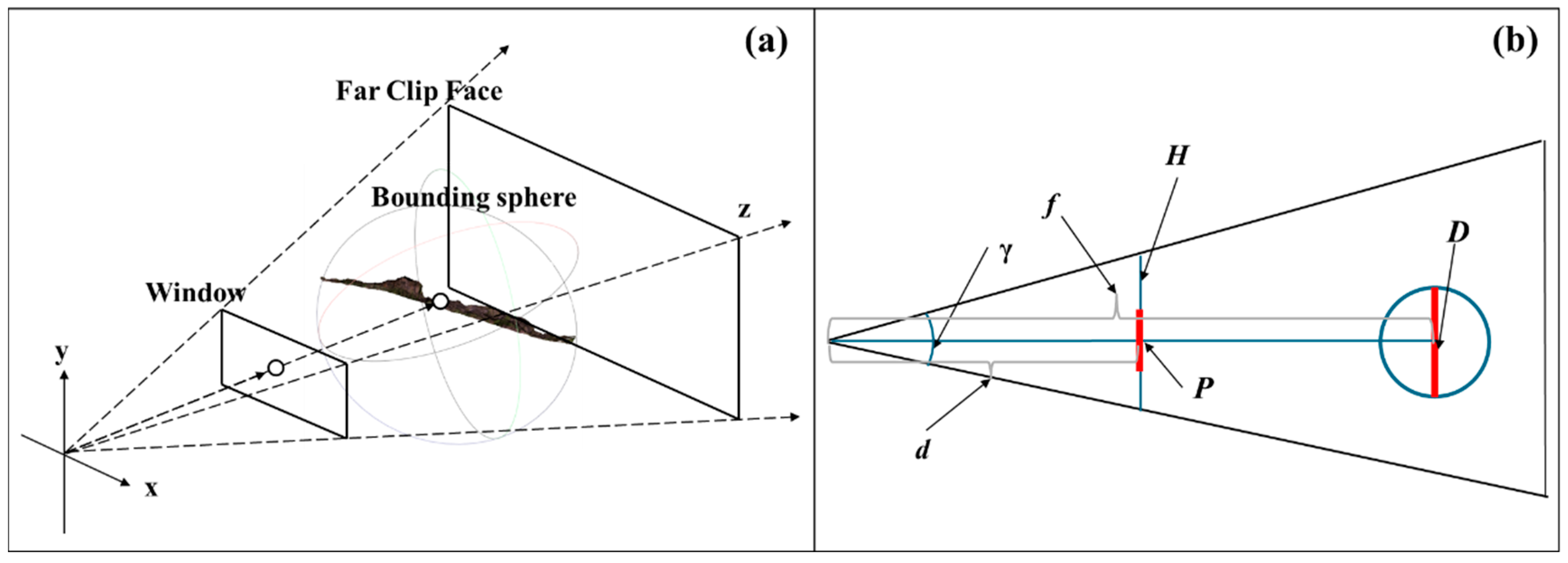
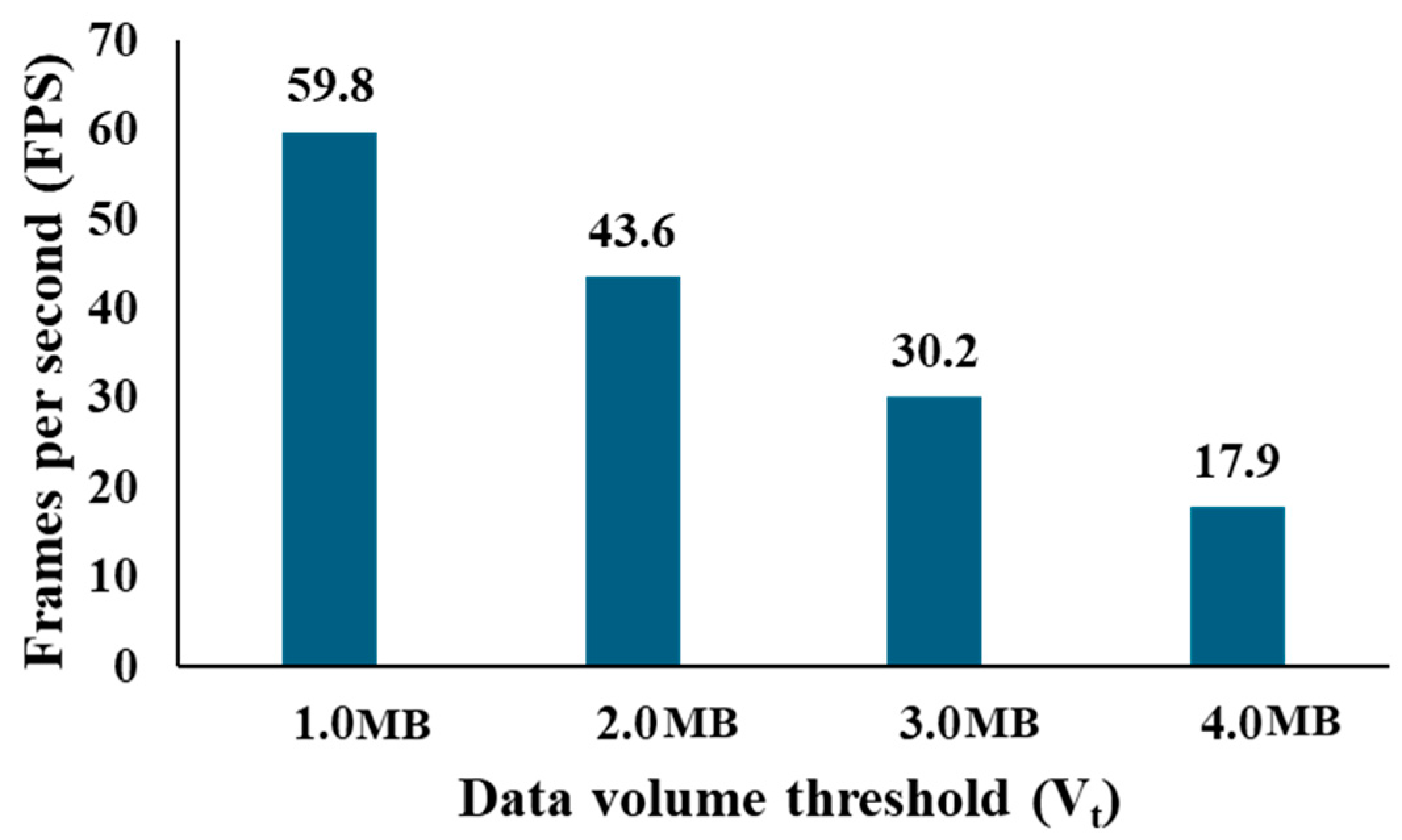
3.5.2. LOD Level Switch Parameter

In OSG, node switching follows the “near-large, far-small” principle of LOD visualization, controlled by the RangeList parameter. To improve adaptability, this study adopts the screen-pixel-based RangeMode, which determines LOD switching according to the model’s projected pixel size, avoiding the limitations of distance-based thresholds. Figure 10 illustrates the geometric basis for screen-pixel-based LOD switching used in this work: (a) the camera frustum, viewport and the model’s bounding sphere in 3D; (b) a 2D cross-section that shows the viewing angle, the distance d from the camera to the bounding-sphere center, and the viewport plane. Let D denote a representative model size (we use the bounding-sphere diameter) and let γ and H be the vertical field of view and the viewport height in pixels, respectively (see Figure 10b). The model’s projected height in pixels P can be expressed as

$$P={\displaystyle \frac{D·f}{d}},f={\displaystyle \frac{H}{2\mathrm{t}\mathrm{a}\mathrm{n}(\mathsf{\gamma }/2)}},$$

so that

$$P={\displaystyle \frac{DH}{2d\mathrm{t}\mathrm{a}\mathrm{n}(\mathsf{\gamma }/2)}}$$

(9)

In implementation, we compare P with the tile texture size S_t (in pixels) and set the RangeList threshold so that when P reaches the maximum allowable screen size (Pixelsize_max), the engine loads a higher-resolution sub-node. Practically, we take Pixelsize_max = S_t. Note that using the bounding sphere gives a conservative, inexpensive estimate; for irregular sub-models, one may alternatively use the projected diagonal of the bounding box or the nearest-point distance to avoid popping at close range.

3.5.3. LOD Model Loading and Rendering

This study utilizes the PagedLOD and DatabasePager classes in OSG to organize and schedule LOD models, supporting large-scale digital outcrop visualization in both desktop and web environments. The core idea is to display visible elements within the current view while preloading potentially visible elements and unloading those unlikely to be seen soon. This ensures limited in-memory data, preventing rendering lag or data loss during scene browsing.

As shown in Figure 11, PagedLOD dynamically loads model nodes (tiles or sub-models) of different detail levels based on the viewing range, enabling paged LOD rendering. Unlike static loading, the database loads or removes nodes dynamically as the viewpoint changes, significantly reducing memory and computation costs. The DatabasePager class manages node scheduling by unloading scene subtrees outside the current view and loading new ones entering the view. It maintains nodes through queues and supports separate threads for local and remote data. For network data, a cache path (OSG_FILE_CACHE) can be set to store downloaded models locally, further improving rendering efficiency and responsiveness.

4. Results

To verify the feasibility and effectiveness of the proposed LOD construction and visualization method, experiments and tests are conducted on the LOD construction tasks of two high-resolution point cloud outcrop models.

4.1. Experimental Dataset and Environment

Two outcrop profiles located in the Sichuan Basin, China, were selected as data sources for the experiments. They are the Gaojiashan outcrop profile of the Dengying Formation (Sinian System) and the Panlongdong outcrop profile of the Changxing Formation (Permian System):

Model 1: The Gaojiashan Dengying Formation outcrop is located approximately 0.5 km north of Gaojiashan Village, Hujia Town, Ningqiang County, Sanxi Province. It is distributed in a strip-like shape along the roadside, with a total length of about 0.85 km.

Model 2: The Panlongdong Changxing Formation outcrop is located beside the highway near Panlongdong in Jichang Town, northeastern Xuanhan County, Sichuan Province. It extends in a northeast–southwest direction along the river, with a profile length of about 0.75 km.

During data acquisition, a RIEGL VZ-400 terrestrial laser scanner (RIEGL Laser Measurement Systems GmbH, Horn, Austria) was used to capture high-resolution 3D point clouds of the outcrop surfaces, and a Pentax 645D high-resolution digital camera (Pentax Imaging Company, Tokyo, Japan) was used to obtain high-quality texture images. Subsequently, high-fidelity 3D digital outcrop models with realistic textures were generated through processes such as point cloud registration and thinning, triangular mesh construction, and texture mapping. The single-body models were stored in OBJ format. Figure 12 shows the visualization results of the two large-scale digital outcrop models used in the case study. The basic information of the two constructed single-body models is listed in

Table 1. The basic information of the single-body digital outcrop models.

Model	Number of Vertices	Number of Triangular Facets	Number of Texture Images	Amount of the Model (GB)
Model 1	592,473	1,145,853	103	1.16
Model 2	648,698	1,244,590	146	1.74

.

The constructed single-body digital outcrop models contain massive amounts of data, which can easily lead to issues such as insufficient memory, lagging performance, and visual artifacts like jumping or missing scenes during model loading and scene switching. Therefore, it is necessary to perform LOD reconstruction on the single-body models. The proposed LOD-based digital outcrop modeling method was implemented under the development environment of Windows 10, Visual Studio 2017, and OSG 3.6. A 3D visualization tool for digital outcrops was developed using visualization techniques to enable multi-scale loading and real-time browsing of LOD models, significantly improving computational efficiency. The hardware configuration of the computer used for the experiments is as follows: Intel Core i7-11700K @ 3.60 GHz processor, 16.0 GB RAM, and NVIDIA GeForce GTX 1650 graphics card. All algorithms and tools mentioned above were implemented based on the OSG 3D visualization open-source library and the C++ programming language. The detailed visualization results will be presented in the following sections.

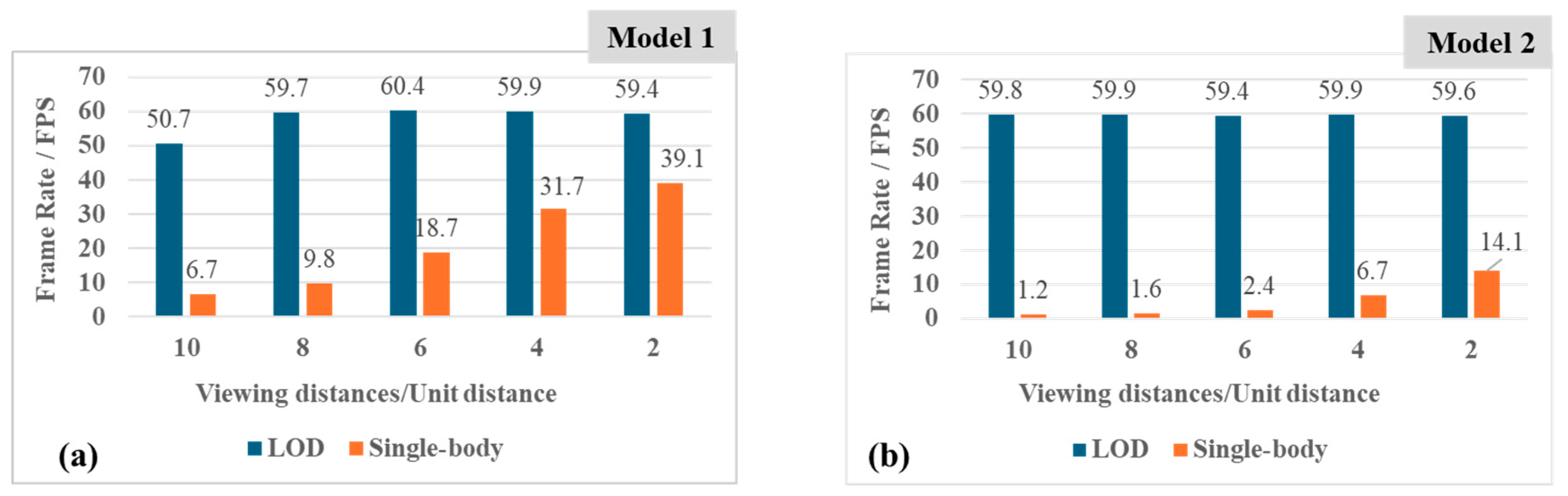
4.2. Results and Analysis of LOD Models Construction and Visualization

LOD structures were constructed for the two single-body models obtained during the data acquisition stage. In this experiment, the model simplification ratio θ was set to 0.8, and the tile data size threshold V_t was set to 1.0 MB. During the process, the computer’s performance was monitored, and the algorithm’s execution time (s), average memory usage (MB), and average CPU usage (%) were recorded. The experiment was repeated 5 times, and the results were averaged with standard deviations.

For Model 1, the generation time of the LOD model was 8421 s, with an average CPU utilization of approximately 9.6% and an average memory usage of about 2652.2 MB. For Model 2, the LOD model generation took 13,425 s, with an average CPU utilization of approximately 12.1% and an average memory usage of about 3354.1 MB. The basic information of the two constructed LOD models is summarized in

Table 2. The basic information of the two LOD models.

Model	Execution Time (s)	Memory Usage (MB)	CPU Usage (%)	Amount of the LOD Model (GB)
Model 1	8421 ± 12	2652.2 ± 42	9.6 ± 0.5	9.74
Model 2	13,425 + 26	3354.1 ± 47	12.1 ± 0.7	8.72

.

The purpose of constructing LOD models is to minimize the loading time and memory consumption of large-scale, high-resolution 3D digital outcrop models, thereby reducing the hardware requirements during visualization and improving rendering efficiency. To evaluate the effectiveness of this approach, the generated LOD models were imported into an OSG-based 3D visualization window. Key performance indicators were collected for the LOD models, including model loading time, memory usage after loading, display frame rate, and the number of stuttering occurrences during roaming. These indicators were then compared with those of the original single-body models. Based on this comparison, a comprehensive assessment of the LOD models’ visualization performance was conducted.

As shown in

Table 3. LOD model loading test data.

Model	CPU Usage (%)	Memory Usage (MB)	Loading Time (s)	Display Frame Rate (FPS)
Model 1 (LOD)	15 ± 1	187 ± 5	3.7 ± 0.1	57.7 ±0.3
Model 1 (single-body)	21 ± 1	3504 ± 15	118.1 ± 2.5	6.8 ± 0.1
Model 2 (LOD)	13.7 ± 0.7	111 ± 4	4.1 ± 0.1	58.8 ± 0.3
Model 2 (single-body)	20.1 ± 0.8	11,609 ± 50	551.2 ± 10	1.2 ± 0.1

, for Model 1, the LOD model had an average CPU usage of 15%, memory usage after loading of 187 MB, a loading time of 3.7 s, and a display frame rate of 57.7 FPS. In comparison, the original model had an average CPU usage of 21%, memory usage after loading of 3504 MB, a loading time of 118.1 s, and a display frame rate of 6.8 FPS. Compared with directly loading the full model, the LOD model reduced average CPU usage by 28.6%, memory usage by 94.7%, and loading time by 96.9%. For Model 2, the LOD model had an average CPU usage of 13.7%, memory usage after loading of 111 MB, a loading time of 4.1 s, and a display frame rate of 58.8 FPS. The original model had an average CPU usage of 20.1%, memory usage after loading of 11,609 MB, a loading time of 551.2 s, and a display frame rate of 1.2 FPS. Compared with directly loading the full model, the LOD model reduced average CPU usage by 31.8%, memory usage by 99.0%, and loading time by 99.3%. Overall, the models’ loading time was reduced by more than 95%, while the average display frame rate can reach around 60 FPS.

In addition, we measured and recorded the frame rate of the model at various camera distances. Here, the viewing distance refers to the distance between the camera and the model. The LOD model loading and scheduling mechanism dynamically adjusts the model’s level of detail according to the viewing distance. We divided the distance from the viewpoint to the model within the view frustum into 10 equal intervals, representing 10 discrete levels. Lower levels correspond to shorter distances, where the model is closer to the viewpoint and displays higher detail; conversely, higher levels correspond to greater distances, where the model is farther from the viewpoint and displays lower detail. Figure 13 presents the frame rate statistics of the model with and without LOD across these different viewing distances.

As shown in Figure 13, Model 1 with LOD exhibits higher frame rates, remaining at the screen refresh rate limit once the viewing distance decreases to 8. In contrast, the frame rates of the non-LOD model increase gradually as the viewing distance decreases, with stable values of 6.7 FPS, 9.8 FPS, 18.7 FPS, 31.7 FPS, and 39.1 FPS, respectively. Similarly, Model 2 with LOD maintains a high frame rate, around 60 FPS, whereas the frame rates of the non-LOD model rise gradually with decreasing viewing distance, with stable values of 1.2 FPS, 1.6 FPS, 2.4 FPS, 6.7 FPS, and 14.1 FPS, respectively. These results indicate that models with LOD achieve significantly higher frame rates across different viewing distances.

Furthermore, we present the actual rendering results of local regions of the LOD models at different viewing distances (see Figure 14 and Figure 15, from (a) to (e), with the viewpoint progressively approaching the model). It can be observed that across all viewing distances, the geometric structure of the model remains stable, tile seams are tightly aligned without gaps, and the visual transitions during multi-detail tile scheduling are smooth, resulting in consistently high visual quality.

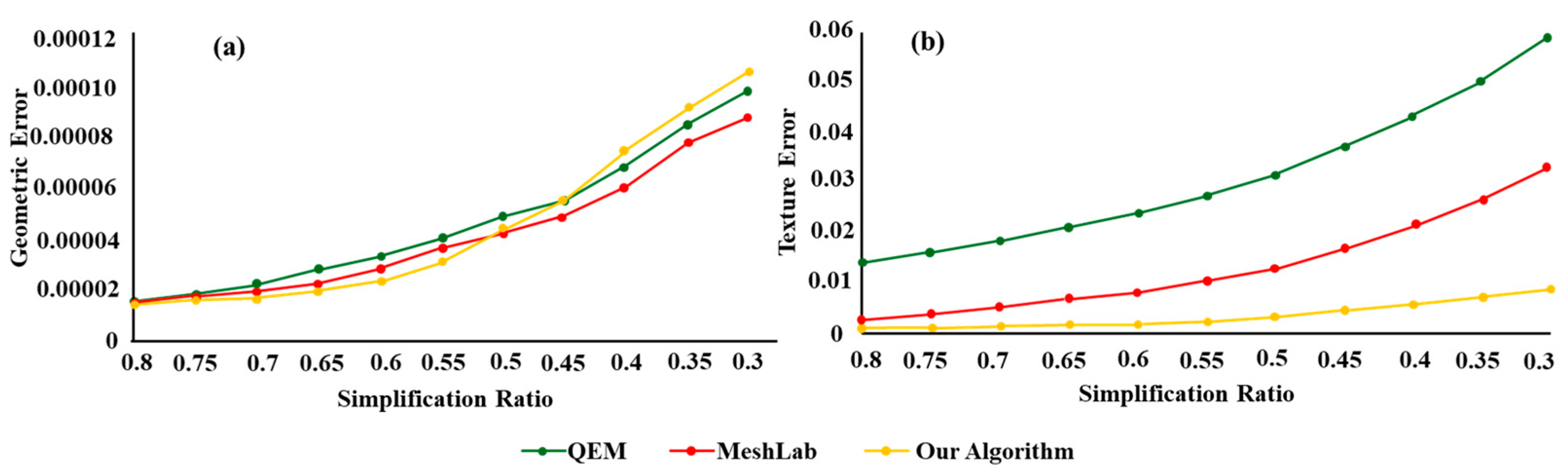
4.3. Comparative Analysis of Simplification Algorithm Results

While Section 4.2 demonstrated the visual results and scalability of our constructed LOD models, this section quantitatively validates the effectiveness of our proposed simplification algorithm. As the core component responsible for feature preservation and smooth visual transitions, the simplification algorithm’s performance is critical. We conducted a comparative experiment pitting our algorithm against two established methods: the foundational QEM [52] and the MeshLab QEM-based simplification [53].

The experiment tested ten different simplification rates for each algorithm on Model 2, evaluating their ability to preserve both geometric and textural features. The simplification error was measured using the following two criteria:

Geometric Error: The two-way Hausdorff distance was used to quantify the maximum geometric deviation between the original model M₁ and the simplified model M₂. It is defined as [20]:

$$\mathrm{H}\left(M_1,M_2\right)=max\left(\mathrm{h}\left(M_1,M_2\right),\mathrm{h}\left(M_2,M_1\right)\right)$$

(10)

where h(M₁, M₂) is the one-sided (or directed) Hausdorff distance from M₁ to M₂, and h(M₂, M₁) is the one-sided Hausdorff distance from M₂ to M₁.

Texture Error: Texture fidelity was assessed using the Structural Similarity Index (SSIM), a perceptually-motivated metric that more comprehensively captures image degradation by considering luminance, contrast, and structure [54]. For each model, we captured the images before and after simplification. The final texture error was then defined as:

$$TE=1-\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}(x,y)$$

(11)

where TE is the texture error, and SSIM(x, y) is the Structural Similarity Index between two images, x and y. The SSIM can be computed as:

$$\mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}(x,y)={\mathrm{I}(x,y)}^{\alpha }·{\mathrm{c}(x,y)}^{\beta }{·\mathrm{s}(x,y)}^{\gamma }$$

(12)

where I(x, y) is the luminance comparison function, c(x, y) is the contrast comparison function, and s(x, y) is the structure comparison function (see Reference [54] for details). The weighting parameters α, β and γ (all > 0) are all set to 1 in this study for simplicity.

The results of geometric and texture errors in model simplification are shown in Figure 16. In terms of geometric error testing, the geometric errors of all three simplification methods gradually increase with lower simplification ratios. When the simplification ratio falls below 0.5, the geometric error of our algorithm becomes slightly larger than the other two methods. This increased geometric error may be attributed to our algorithm’s consideration of more local detail features and texture characteristics, leading to a slight increase in global integration error. Regarding texture error testing, the texture errors of all three methods also increase with lower simplification ratios, but our algorithm achieves the smallest texture error, while the QEM algorithm exhibits the largest. This demonstrates the effectiveness of the constraints and strategies designed in our algorithm for texture protection.

We compared the visual effects of different simplification results, taking the simplified model with a 0.3 simplification ratio derived from experiments as an example. As shown in Figure 17, conventional QEM and MeshLab simplifications cause noticeable texture stretching and boundary cracks, whereas our method maintains coherent textures and intact geological features.

5. Discussion

5.1. Potential Limitations of the Tiling Method

The adaptive LOD hierarchical tiling method proposed in this study is primarily driven by partitioning in 2D texture space. While this approach offers significant advantages for preserving texture fidelity and streamlining the LOD generation pipeline for elongated, facade-like outcrop profiles, it inherently possesses limitations when dealing with highly complex 3D geometries, such as intensely folded structures or intersecting surfaces. The fundamental issue stems from the decoupling of the partitioning logic from the 3D geometric structure. Our method’s segmentation (Section 3.1) and quadtree subdivision (Section 3.2.1) are optimized for texture coherence rather than geometric homogeneity. This can lead to two specific problems in complex scenarios:

• Suboptimal Tile Boundaries on Complex Geometry: A single tile in 2D texture space may encompass disparate 3D regions with different geometric characteristics, such as the limb and hinge of a fold. During the tile-wise simplification (Section 3.2.2), the algorithm cannot adapt to intra-tile geometric variance, potentially leading to visual artifacts like over-simplification of high-curvature features or aliasing along sharp intersections.
• Inefficient Culling and Streaming: For self-intersecting or highly folded surfaces, multiple disjoint 3D regions can be mapped to a contiguous area in the 2D texture atlas. A quadtree partition in this 2D space will create tiles that combine these disjointed 3D elements. During rendering, this can frustrate view-frustum culling and lead to inefficient data streaming, as a single tile may be loaded to render several small, spatially separated parts of the model.

To address these limitations, future work will focus on developing a classification-driven, hybrid partitioning framework that dynamically balances texture and geometric constraints. We propose the following strategies:

• Geometric Feature Analysis: Prior to partitioning, the 3D mesh will be analyzed to compute key geometric attributes such as curvature, normal vector variation, and relief intensity [20]. This will identify regions of high geometric complexity (e.g., folds, fractures) versus relatively planar regions.
• Hybrid Quadtree-Octree Partitioning: Based on this analysis, an adaptive strategy can be implemented: for planar regions, the current texture-space quadtree partitioning remains highly efficient; for regions identified as highly complex, the method would switch to a 3D octree partitioning. An octree recursively subdivides 3D space, ensuring that tiles represent spatially coherent and geometrically homogeneous regions, allowing for more effective simplification and culling [20].
• Morphology-Based Classification: We will explore classifying outcrop profiles into different morphological types (e.g., planar facade, folded structure, and intersecting bedding). A classifier could then select the optimal partitioning strategy for each segment, ensuring robustness across a wider range of geological scenarios.

5.2. Empirical and Generalizability Concerns in Algorithm Parameters

The model simplification ratio and tile data volume threshold in the current method may rely on practical application requirements and manual experience. In our experiments, the simplification ratio was set to 0.8, and the tile data threshold was set to 1.0 MB. While these settings are relatively straightforward to implement, they may not optimally suit all scenarios. The current reliance on manually tuned settings may limit the method’s generalizability and automation across diverse scenarios. To address this, we have conducted supplementary experiments to analyze their sensitivity and, based on this, propose future automated strategies.

Data volume threshold (V_t) directly governs the balance between rendering performance and data granularity. y controlling the simplification ratio (θ = 0.8), we tested the influence of different V_t values on the average frame rate of Model 2. Considering common network bandwidth limitations, controlling individual tile data volume within 1.0 MB helps meet efficient data scheduling requirements in most standalone or network environments. When models don’t require loading and display in network environments, this threshold can be appropriately increased, for instance, set to 3.0 MB. Therefore, we used 1.0 MB as the minimum benchmark for testing and analysis. As shown in Figure 18, when V_t increases from 1.0 MB to 4.0 MB, rendering performance shows a sharp decline, with the frame rate for Model 2 dropping from a smooth 59.8 FPS to merely 17.9 FPS. This result indicates that the increase in single tile data volume imposes greater pressure on memory bandwidth and real-time rendering processing capabilities. Although smaller V_t values would generate more tiles, V_t = 1.0 MB achieves a good balance between data management overhead and the high rendering cost associated with larger tiles. Consequently, this parameter plays a crucial role in coordinating the fundamental trade-off between data granularity and rendering performance.

Simplification ratio (θ) determines the rate of data reduction between LOD levels and is crucial for balancing visual quality and storage overhead. We performed an in-depth analysis based on the quantitative experiments from Section 4.3 (Figure 16). As observed, when θ progressively decreases from 0.8 to 0.3, both the geometric error and texture error curves gradually rise with an accelerating upward trend. We set θ = 0.8 in our experiments to ensure that visual transitions between different LOD levels remain perceptually smooth.

To overcome the limitations of manual parameter tuning, we outline a data-driven framework for automated parameter selection as a core direction for future research. The threshold V_t should dynamically adapt to the user’s hardware and network environment. The simplification ratio θ should not be globally fixed but should vary based on the local characteristics of the model. For instance, we can incorporate additional constraint parameters such as geometric features, textural characteristics, and semantic importance. Based on these parameters, we partition the model into different regions. Each region is then assigned a locally optimal simplification ratio, ensuring mild simplification in visually sensitive areas and aggressive simplification in non-critical regions.

5.3. Analysis of Algorithmic Performance Bottlenecks and Optimization Directions

Although the LOD models constructed by our method enable efficient rendering of digital outcrop models, the processing time during the LOD construction phase (e.g., approximately 3.7 h for Model 2) indeed constitutes a bottleneck for practical applications. To address this, we have conducted a more in-depth analysis of the algorithm’s temporal cost.

We decomposed the execution time of the construction process for multiple models, and the results are shown in Figure 19. The data indicate that the total processing time varies between different models, primarily driven by the data scale of the original models (number of vertices/faces, texture resolution). By breaking down the different stages, we have clarified the composition of the algorithm’s temporal consumption:

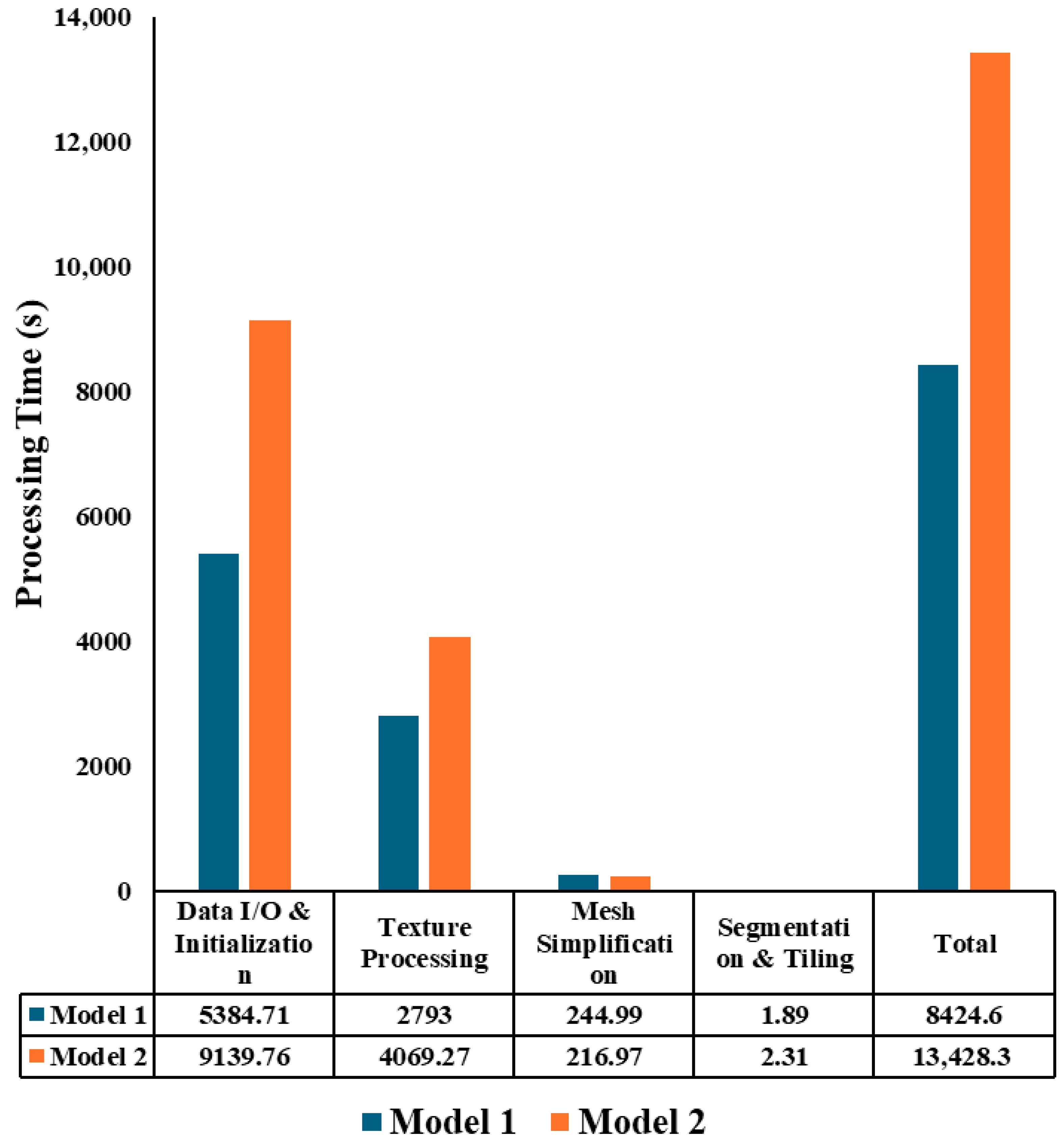
• Data I/O and Initialization: The model loading and data preparation stage (Data reading and copying) is one of the most time-consuming components, especially for very large-scale models. This stage involves reading high-resolution mesh and texture data from storage into memory and performing initial data structure conversions. This process is currently single-threaded and heavily constrained by storage I/O speed and memory copy bandwidth. For Model 1 and Model 2, this stage accounts for approximately 64% and 68% of the total time, respectively. Therefore, our primary optimization efforts should focus on efficient handling of the reading, writing, and initialization of massive datasets.
• Texture Processing: Texture reconstruction is another major bottleneck. This stage includes texture image partitioning, downsampling, and coordinate remapping. For models with high-resolution textures (such as Model 1 and Model 2), the time consumption in this stage is an order of magnitude higher than that of mesh simplification. Its computational complexity is directly related to the total number of pixels in the texture images, indicating that the efficiency of image processing operations (e.g., resampling) in the current implementation needs improvement. Parallelization of related operations will be a key direction for future enhancements.
• Mesh Simplification: The mesh simplification stage follows, with time consumption significantly lower than texture processing. The computational complexity of the QEM-based simplification algorithm is closely related to the number of vertices in the input model and involves extensive iterative calculations and local geometric queries. While its optimization approach is similar to that of texture processing and also requires parallelization, this component is not the primary focus of optimization.
• Segmentation and Tiling: Although it is the core of the algorithm, the data show that its time consumption is negligible compared to other components. The overhead of model segmentation and tiling is minimal, confirming that this stage is efficiently designed and does not constitute a bottleneck.

The above analysis indicates that the performance bottlenecks primarily stem from a highly serialized execution mode and inefficient handling of massive data. First, I/O and memory access optimization are crucial. For this, we can employ pipelining, designing the data reading, mesh simplification, and texture processing stages to overlap. While one portion of data is being simplified, the next portion can be loaded simultaneously, and the textures for another portion can be processed, thereby hiding I/O latency. Second, comprehensive parallelization of texture reconstruction and mesh simplification algorithms is essential [55]. The partitioning, downsampling, and remapping of texture images are highly parallelizable tasks typical of image processing. The texture processing for each tile can be executed as an independent GPU thread or thread block, potentially achieving speedups of several orders of magnitude. Furthermore, the existing QEM algorithm can be parallelized. Its vertex error calculations and edge collapse evaluations can run simultaneously on the GPU. We believe that through these improvements, the LOD construction time is expected to be reduced from several hours to several minutes or even seconds, thereby achieving high efficiency in the LOD model construction phase and meeting the requirements for rapid iteration and real-time preview in practical production environments.

6. Conclusions

This paper has presented a comprehensive LOD-based solution for the efficient visualization of large-scale, high-resolution LiDAR digital outcrop models. Addressing the rendering bottleneck caused by massive data volumes and complex geometries, the proposed approach integrates model segmentation, adaptive tiling, feature-preserving simplification, and dynamic visualization into a unified workflow.

First, we designed a tailored LOD construction pipeline that integrates model segmentation, pseudo-quadtree tiling, feature-preserving simplification, and texture reconstruction. This workflow effectively addresses the unique challenges posed by the elongated and vertical nature of digital outcrops, overcoming the limitations of conventional LOD methods designed for planar or large-area models. Second, we developed and integrated key algorithmic optimizations. The incorporation of boundary freezing and fallback strategies into the feature-preserving QEM algorithm ensured the protection of both geometric integrity at tile borders and critical geological features during aggressive mesh simplification. Finally, we established an efficient data organization and dynamic visualization framework. By employing an LOD index and OSG PagedLOD mechanism, we achieved real-time, view-dependent loading and seamless multi-scale rendering of high-resolution LiDAR-derived digital outcrop models on standard computer hardware.

Experimental results demonstrate that the proposed method achieves substantial reductions in loading time and memory usage while maintaining high visual fidelity. Overall, this research provides a practical and scalable solution for 3D geological model visualization, paving the way for advanced applications such as semantic attribute integration and web-based collaborative geological interpretation.

Notwithstanding these contributions, several limitations warrant consideration. The current LOD generation process is driven by 2D texture parameterization, which may not be optimal for highly complex 3D structures such as tightly folded geology. Furthermore, the approach relies on empirically tuned parameters, and the preprocessing stage, while a one-time cost, remains computationally intensive due to the sequential nature of the core algorithms. These limitations define clear pathways for future work. Our immediate efforts will focus on: (1) Developing automated parameter-tuning strategies; (2) implementing parallel and pipelined execution for key components of the LOD algorithm; and (3) extending the framework to better handle geometrically complex scenarios.