Reconstruction of SMAP Soil Moisture Data Based on Residual Autoencoder Network with Convolutional Feature Extraction
Highlights
- Developed TsSMNet, a residual autoencoder model that reconstructs gap-free 9 km SMAP soil moisture from 2016 to 2022 in China using multi-source remote sensing data and time-series statistical features.
- Demonstrates that combining 1D convolutional encoding across multi-source feature vectors with temporal descriptors effectively addresses spatial gaps and heterogeneity in satellite SSM data.
- Provides a continuous and reliable SSM dataset that can support large-scale hydrological, climatic, and ecological applications.
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.1.1. Study Area
2.1.2. Data Acquisition
2.1.3. Data Processing
2.2. Method
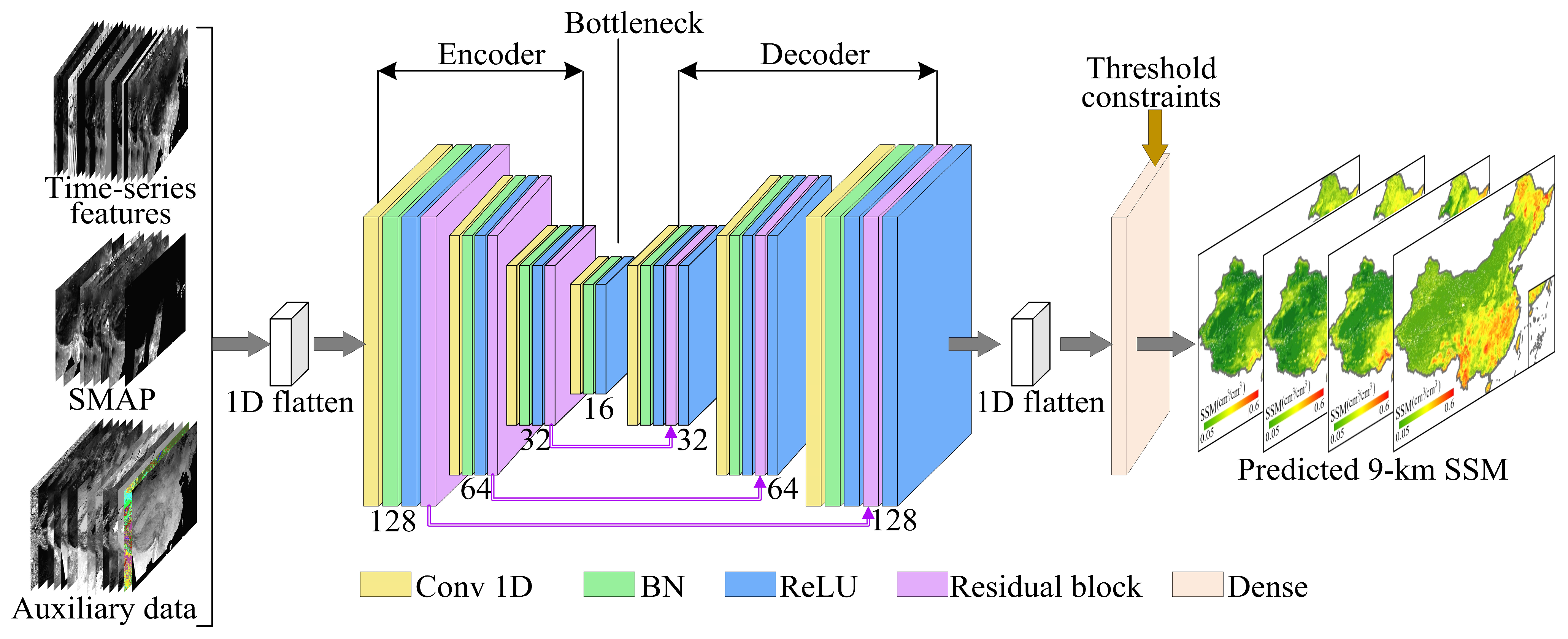
2.2.1. TsSMNet Model
2.2.2. Model Validation
2.2.3. SSM Reconstruction Strategy
3. Results
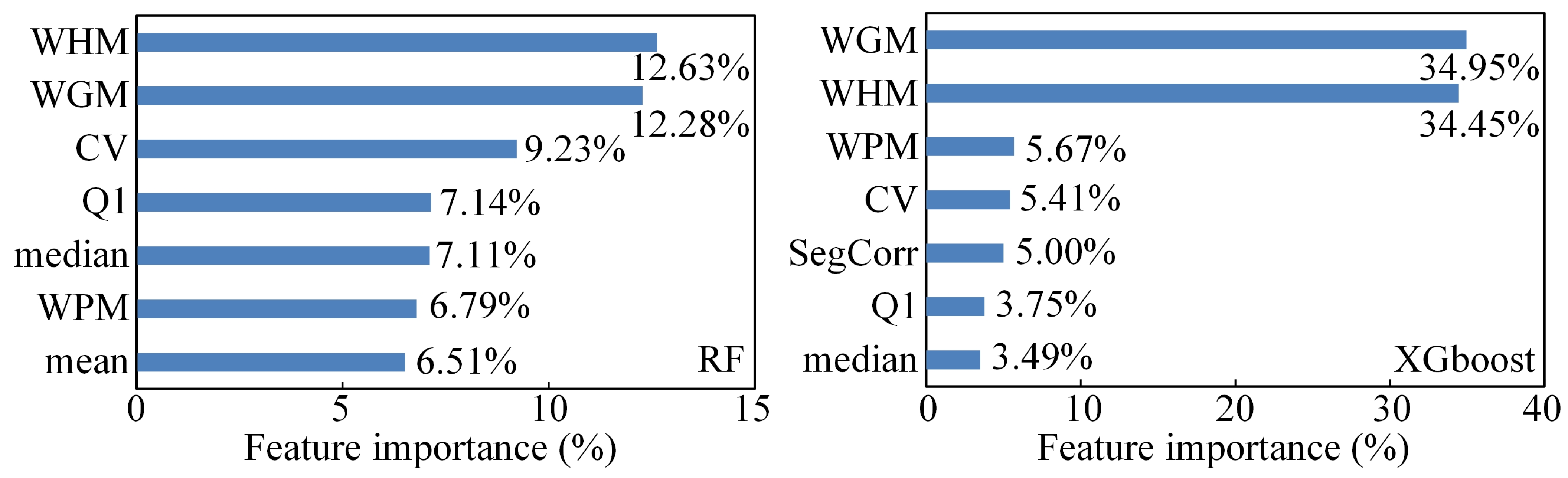
3.1. Training Performance and Feature Configuration Analysis of the TsSMNet Model
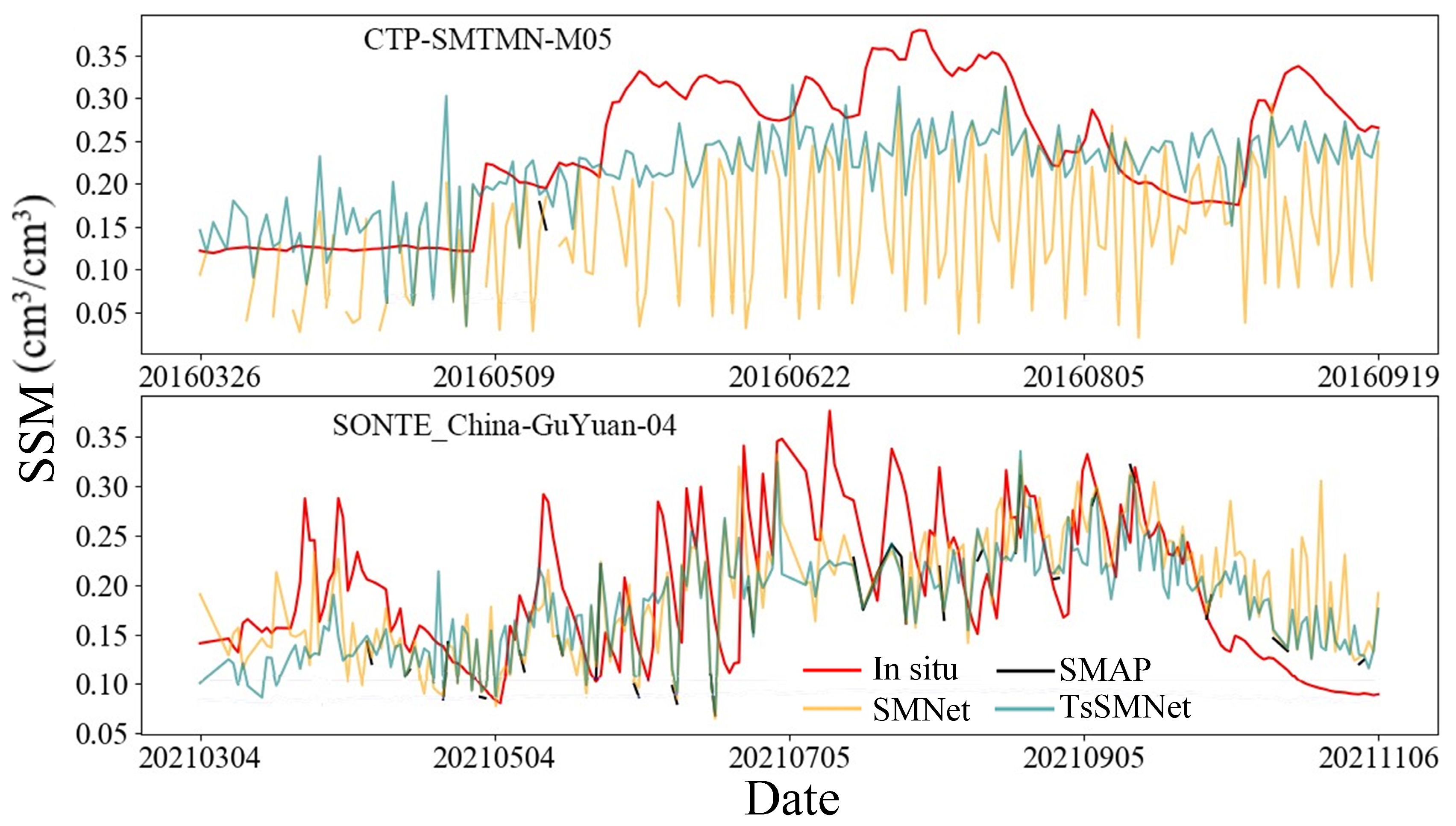
3.2. Reconstructed SSM Results
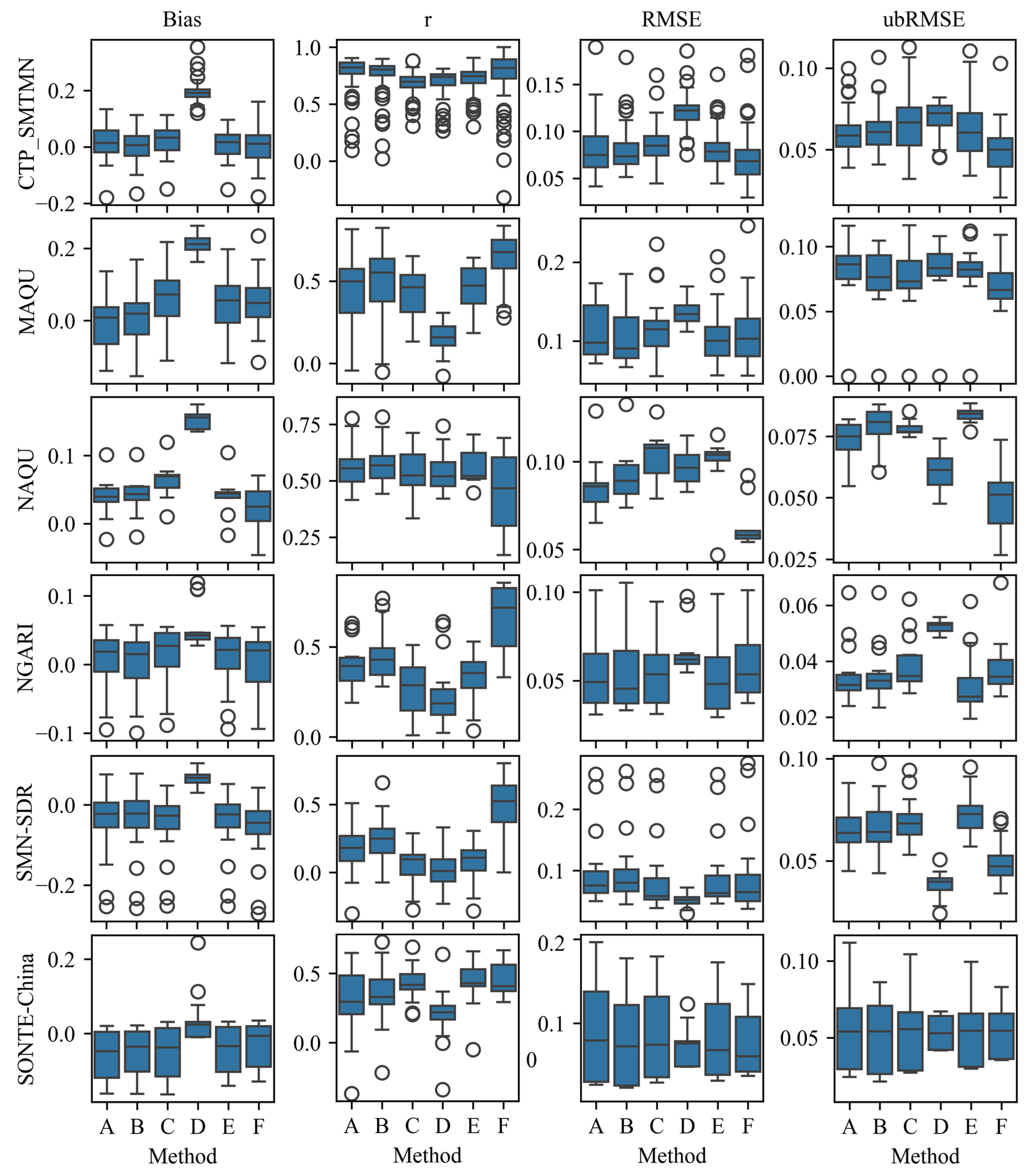
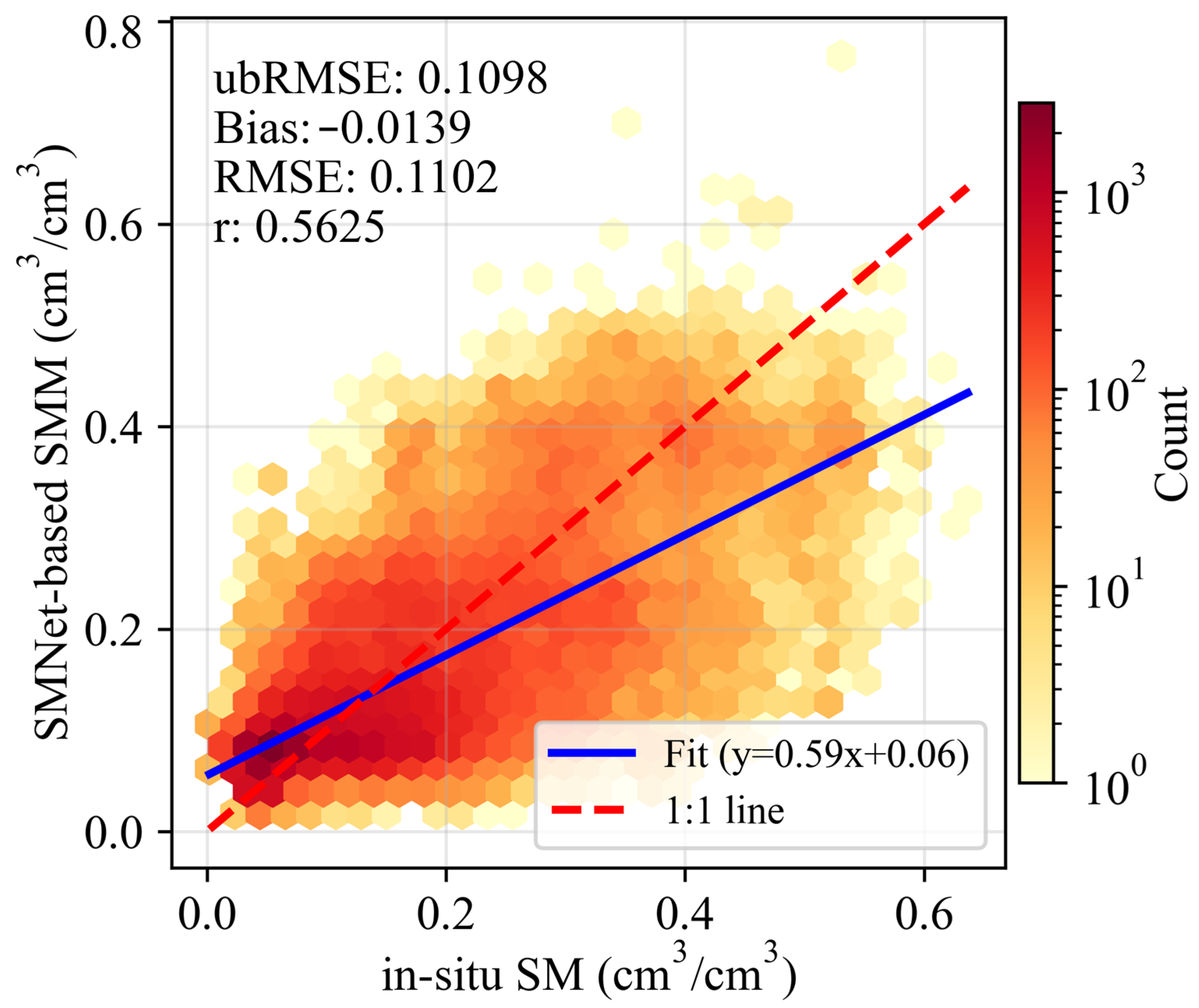
3.3. Validation Through In Situ Observation and ESA CCI SSM
4. Discussion
4.1. Importance and Selection of Temporal Features
4.2. Model Performance in the Absence of Temporal Features
4.3. Limitations and Research Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Category | Feature Name | Abbreviation | Definition/Calculation |
|---|---|---|---|
| Central tendency | Mean | Mean | Arithmetic average of the time series values |
| Median | Median | Middle value of the series | |
| Weighted harmonic mean | WHM | Harmonic mean weighted by observational weights | |
| Weighted geometric mean | WGM | Geometric mean weighted by observational weights | |
| Weighted power mean | WPM | Power mean with weighting | |
| Dispersion and variability | Standard deviation | Std | Square root of variance |
| Variance | Var | Mean squared deviation from mean | |
| Coefficient of variation | CV | Standard deviation divided by the mean | |
| Mean absolute deviation | MAD | Average absolute difference from the mean | |
| Median absolute deviation | MeAD | Median of absolute differences from the median | |
| Interquartile range | IQR | Difference between the third quartile (Q3) and the first quartile (Q1) | |
| Root mean square | RMS | Square root of the mean of squared values | |
| Extremes and distribution | Minimum | Min | Lowest observed value |
| Maximum | Max | Highest observed value | |
| Skewness | Skew | Measure of asymmetry of the distribution | |
| Kurtosis | Kurt | Measure of peakedness of the distribution | |
| First quartile | Q1 | 25th percentile of the series | |
| Sample entropy | SampEn | Quantifies irregularity and unpredictability by comparing repeated patterns | |
| Temporal dynamics | Mean of successive differences | MeanDiff | Mean of differences between consecutive values |
| Median of successive differences | MedDiff | Median of differences between consecutive values | |
| Mean absolute successive difference | MASD | Mean of absolute differences between consecutive values | |
| Median absolute successive difference | MeASD | Median of absolute differences between consecutive values | |
| Autocorrelation | ACF | Correlation of series with its lagged version | |
| Second central derivative mean | SecDerMean | Mean of the second-order central differences, used to characterize the curvature and acceleration of changes in the time series. | |
| Segment correlation | SegCorr | Correlation between non-overlapping segments of the series, reflecting structural similarity and stability over time. | |
| Peak-to-peak interval | P2P | Average interval between consecutive local maxima | |
| Magnitude and energy | Absolute energy | AbsE | Sum of squared values |
| Sum of values | Sum | Total sum of series values | |
| Sum of absolute differences | SAD | Sum of absolute differences between consecutive values | |
| Count-based | Count above mean | CAM | Number of observations greater than mean |
| Count below mean | CBM | Number of observations less than mean |

References
- Zhang, M.; Zhang, D.; Jin, Y.; Wan, X.; Ge, Y. Evolution of Soil Moisture Mapping from Statistical Models to Integrated Mechanistic and Geoscience-Aware Approaches. Inform. Geogr. 2025, 1, 100005. [Google Scholar] [CrossRef]
- Ge, Y.; Hu, S.; Song, Y.Z.; Zheng, H.; Liu, Y.S.; Ye, X.Y.; Ma, T.; Liu, M.X.; Zhou, C.H. Sustainable poverty reduction models for the coordinated development of the social economy and environment in China. Sci. Bull. 2023, 68, 2236–2246. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R.; Arnold, J.G.; Di Luzio, M. Estimation of Long-Term Soil Moisture Using a Distributed Pa-Rameter Hydrologic Model and Verification Using Remotely Sensed Data. Trans. ASAE 2005, 48, 1101–1113. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Bongiovanni, T.; Judge, J.; Nagarajan, K.; Principe, J.C. Downscaling Satellite-Based Soil Moisture in Heterogeneous Regions Using High-Resolution Remote Sensing Products and Information Theory: A Synthetic Study. IEEE Trans. Geosci. Remote Sens. 2015, 53, 85–101. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A Review of Spatial Downscaling of Satellite Remotely Sensed Soil Moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Zhao, W.; Wen, F.P.; Cai, J.F. Methods, Progresses, and Challenges of Passive Microwave Soil Moisture Spatial Downscaling. Nat. Remote Sens. Bull. 2022, 26, 1699–1722. [Google Scholar] [CrossRef]
- Yang, Z.; He, Q.; Miao, S.; Wei, F.; Yu, M. Surface Soil Moisture Retrieval of China Using Multi-Source Data and Ensemble Learning. Remote Sens. 2023, 15, 2786. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Dunbar, R.S.; Chaubell, M.J.; Colliander, A.; Yueh, S.; Jagdhuber, T.; Chen, F.; Crow, W.; O’Neill, P.E.; et al. The SMAP and Copernicus Sentinel 1A/B microwave active-passive high resolution surface soil moisture product. Remote Sens. Environ. 2019, 233, 111380. [Google Scholar] [CrossRef]
- Colliander, A.; Reichle, R.H.; Crow, W.T.; Cosh, M.H.; Chen, F.; Chan, S.; Das, N.N.; Bindlish, R.; Chaubell, J.; Kim, S.; et al. Validation of Soil Moisture Data Products from the NASA SMAP Mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 364–392. [Google Scholar] [CrossRef]
- Setti, P.T.; Tabibi, S. Enhancing Soil Moisture Estimates Through the Fusion of SMAP and GNSS-R Data at 3-Km Resolution for Daily Mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 5303–5316. [Google Scholar] [CrossRef]
- Xing, C.; Chen, N.; Zhang, X.; Gong, J. A Machine Learning Based Reconstruction Method for Satellite Remote Sensing of Soil Moisture Images with In Situ Observations. Remote Sens. 2017, 9, 484. [Google Scholar] [CrossRef]
- Usowicz, B.; Lipiec, J.; Łukowski, M.; Słomiński, J. Improvement of Spatial Interpolation of Precipitation Distribution Using Cokriging Incorporating Rain-Gauge and Satellite (SMOS) Soil Moisture Data. Remote Sens. 2021, 13, 1039. [Google Scholar] [CrossRef]
- Liu, C.Y.; Yao, L.; Jing, W.; Di, L.; Yang, J.; Li, Y. Comparison of Two Satellite-Based Soil Moisture Reconstruction Algorithms: A Case Study in the State of Oklahoma, USA. J. Hydrol. 2020, 590, 125406. [Google Scholar] [CrossRef]
- Cui, Y.; Chen, X.; Xiong, W.; He, L.; Lv, F.; Fan, W.; Luo, Z.; Hong, Y. A Soil Moisture Spatial and Temporal Resolution Improving Algorithm Based on Multi-Source Remote Sensing Data and GRNN Model. Remote Sens. 2020, 12, 455. [Google Scholar] [CrossRef]
- Xiao, Z.; Jiang, L.; Zhu, Z.; Wang, J.; Du, J. Spatially and Temporally Complete Satellite Soil Moisture Data Based on a Data Assimilation Method. Remote Sens. 2016, 8, 49. [Google Scholar] [CrossRef]
- Nadeem, A.A.; Zha, Y.; Shi, L.; Ali, S.; Wang, X.; Zafar, Z.; Afzal, Z.; Tariq, M.A.U.R. Spatial Downscaling and Gap-Filling of SMAP Soil Moisture to High Resolution Using MODIS Surface Variables and Machine Learning Approaches over ShanDian River Basin, China. Remote Sens. 2023, 15, 812. [Google Scholar] [CrossRef]
- Ding, T.; Zhao, W.; Yang, Y. Addressing spatial gaps in ESA CCI soil moisture product: A hierarchical reconstruction approach using deep learning model. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104003. [Google Scholar] [CrossRef]
- Llamas, R.M.; Guevara, M.; Rorabaugh, D.; Taufer, M.; Vargas, R. Spatial Gap-Filling of ESA CCI Satellite-Derived Soil Moisture Based on Geostatistical Techniques and Multiple Regression. Remote Sens. 2020, 12, 665. [Google Scholar] [CrossRef]
- Tong, C.; Wang, H.; Magagi, R.; Goita, K.; Wang, K. Spatial Gap-Filling of SMAP Soil Moisture Pixels over Tibetan Plateau via Machine Learning Versus Geostatistics. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9899–9912. [Google Scholar] [CrossRef]
- Sun, H.; Xu, Q. Evaluating Machine Learning and Geostatistical Methods for Spatial Gap-Filling of Monthly ESA CCI Soil Moisture in China. Remote Sens. 2021, 13, 2848. [Google Scholar] [CrossRef]
- Zhang, C.; Zeng, J.; Shi, P.; Ma, H.; Letu, H.; Zhang, X.; Wang, P.; Bi, H.; Rong, J. Global-Scale Gap Filling of Satellite Soil Moisture Products: Methods and Validation. J. Hydrol. 2025, 653, 132762. [Google Scholar] [CrossRef]
- Liu, K.; Li, X.; Wang, S.; Zhang, H. A Robust Gap-Filling Approach for European Space Agency Climate Change Initiative (ESA CCI) Soil Moisture Integrating Satellite Observations, Model-Driven Knowledge, and Spatiotemporal Machine Learning. Hydrol. Earth Syst. Sci. 2023, 27, 577–598. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Q. Reconstruction of a Spatially Seamless, Daily SMAP (SSD_SMAP) Surface Soil Moisture Dataset from 2015 to 2021. J. Hydrol. 2023, 621, 129579. [Google Scholar] [CrossRef]
- Shangguan, Y.; Min, X.; Shi, Z. Gap Filling of the ESA CCI Soil Moisture Data Using a Spatiotemporal Attention-Based Residual Deep Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 5344–5354. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, S.; Zhu, Z.; Ma, H.; He, T. Soil Moisture Content Retrieval from Landsat 8 Data Using Ensemble Learning. ISPRS J. Photogramm. Remote Sens. 2022, 185, 32–47. [Google Scholar] [CrossRef]
- Jia, Y.; Xiao, Z.; Jin, S.; Yan, Q.; Jin, Y.; Li, W. Improving CYGNSS-Based Soil Moisture Coverage through Autocorrelation and Machine Learning-Aided Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 12554–12566. [Google Scholar] [CrossRef]
- Hu, Z.; Chai, L.; Crow, W.T.; Liu, S.; Zhu, Z.; Zhou, J.; Qu, Y.; Liu, J.; Yang, S.; Lu, Z. Applying a Wavelet Transform Technique to Optimize General Fitting Models for SM Analysis: A Case Study in Downscaling over the Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 3063. [Google Scholar] [CrossRef]
- Xing, Z.; Fan, L.; Zhao, L.; De Lannoy, G.; Frappart, F.; Peng, J.; Li, X.; Zeng, J.; Al-Yaari, A.; Yang, K.; et al. A first assessment of satellite and reanalysis estimates of surface and root-zone soil moisture over the permafrost region of Qinghai-Tibet Plateau. Remote Sens. Environ. 2021, 265, 112666. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Q.; Ma, X.; Liu, W.; Liu, H. Digital Soil Mapping Based on Fine Temporal Resolution Landsat Data Produced by Spatiotemporal Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3905–3914. [Google Scholar] [CrossRef]
- Jiang, M.; Qiu, T.; Wang, T.; Zeng, C.; Zhang, B.; Shen, H. Seamless Global Daily Soil Moisture Mapping using Deep Learning Based Spatiotemporal Fusion. Int. J. Appl. Earth Obs. Geoinf. 2025, 139, 104517. [Google Scholar] [CrossRef]
- Li, Q.; Li, Z.; Shangguan, W.; Wang, X.; Li, L.; Yu, F. Improving Soil Moisture Prediction using a Novel Encoder-Decoder Model with Residual Learning. Comput. Electron. Agric. 2022, 195, 106816. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, Z.; Gui, H.; Chen, X.; Hu, S.; Gao, L.; Yang, H.; Qiu, J.; Xin, Q. A Meteorology-Driven Transformer Network to Predict Soil Moisture for Agriculture Drought Forecasting. IEEE Trans. Geosci. Remote Sens. 2025, 63, 4405818. [Google Scholar] [CrossRef]
- Gao, P.; Fang, J.; He, J.; Ma, S.; Wen, G.; Li, Z. GRU–Transformer Hybrid Model for GNSS/INS Integration in Orchard Environments. Agriculture 2025, 15, 1135. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, S.; Ma, H.; He, T.; Tian, F.; Zhang, G.; Xu, J. A Seamless Global Daily 5 km Soil Moisture Product from 1982 to 2021 using AVHRR Satellite Data and An Attention-Based Deep Learning Model. Earth Syst. Sci. Data Discuss 2025, 17, 1–39. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, Y.; Yin, C. A Transformer-Based Method to Simulate Multi-Scale Soil Moisture. J. Hydrol. 2025, 655, 132900. [Google Scholar] [CrossRef]
- Dabboor, M.; Atteia, G.; Meshoul, S.; Alayed, W. Deep Learning-Based Framework for Soil Moisture Content Retrieval of Bare Soil from Satellite Data. Remote Sens. 2023, 15, 1916. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, Z.; Xiong, S.; Zhang, W. Enhancing Global Surface Soil Moisture Estimation from ESA CCI and SMAP Product with Conditional Variational Auto-Encoder. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 9337–9359. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, W.; Qin, Q.; Long, Z. Downscaling Solar-Induced Chlorophyll Fluorescence Based on Convolutional Neural Network Method to Monitor Agricultural Drought. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1012–1028. [Google Scholar] [CrossRef]
- Hu, P.; Pan, X.; Yang, Y.; Dai, Y.; Chen, Y. A Two-Stage Hierarchical Spatiotemporal Fusion Network for Land Surface Temperature with Transformer. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5002320. [Google Scholar] [CrossRef]
- Ge, Y.; Zhang, L.; Han, Y.; Zhang, D.; Yang, W.J.; Feng, L.; Dong, J.W.; Wang, S.P.; Peng, S.M.; Fang, C.Y. Enhancing water security in lake basins through geographic intelligence technology. Sci. Bull. 2025, 70, 2047–2050. [Google Scholar] [CrossRef]
- Egeonu, D.; Jia, B. Performance Evaluation and Comparison of Deep Neural Network Models for African Soil Properties Prediction. Commun. Soil Sci. Plant Anal. 2024, 55, 2799–2820. [Google Scholar] [CrossRef]
- Liu, N.; Wan, L.; Zhang, Y.; Zhou, T.; Huo, H.; Fang, T. Exploiting Convolutional Neural Networks with Deeply Local Description for Remote Sensing Image Classification. IEEE Access 2018, 6, 11215–11228. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 15, 185–215. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A Practical Reanalysis Data and Thermal Infrared Remote Sensing Data Merging (RTM) Method for Reconstruction of a 1-Km All-Weather Land Surface Temperature. Remote Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Xia, L.; Song, X.; Leng, P.; Wang, Y.; Hao, Y.; Wang, Y. A Comparison of Two Methods for Estimating Surface Soil Moisture Based on the Triangle Model Using Optical/Thermal Infrared Remote Sensing over the Source Area of the Yellow River. Int. J. Remote Sens. 2018, 40, 2120–2137. [Google Scholar] [CrossRef]
- Hengl, T.; Consoli, D.; Tian, X.; Nauman, T.W.; Nussbaum, M.; Isik, M.S.; Parente, L.; Ho, Y.-F.; Simoes, R.; Gupta, S.; et al. OpenLandMap-SoilDB: Global Soil Information at 30 m Spatial Resolution for 2000–2022+ Based on Spatiotemporal Machine Learning and Harmonized Legacy Soil Samples and Observations. Earth Syst. Sci. Data Discuss. 2025, 2025, 1–66. [Google Scholar] [CrossRef]
- Dorigo, W.; Himmelbauer, I.; Aberer, D.; Schremmer, L.; Petrakovic, I.; Zappa, L. The International Soil Moisture Network: Serving Earth System Science for over a Decade. Hydrol. Earth Syst. Sci. 2021, 25, 5749–5804. [Google Scholar] [CrossRef]
- Cao, R.; Chen, Y.; Shen, M.; Chen, J.; Zhou, J.; Wang, C.; Yang, W. A Simple Method to Improve the Quality of NDVI Time-Series Data by Integrating Spatiotemporal Information with the Savitzky-Golay Filter. Remote Sens. Environ. 2018, 217, 244–257. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, G.; Ge, Y.; Xu, Z. Mapping Gridded Gross Domestic Product Distribution of China Using Deep Learning with Multiple Geospatial Big Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1791–1802. [Google Scholar] [CrossRef]
- Li, L.; Fang, Y.; Wu, J.; Wang, J.; Ge, Y. Encoder–Decoder Full Residual Deep Networks for Robust Regression and Spatio-temporal Estimation. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4217–4230. [Google Scholar] [CrossRef] [PubMed]
- Terven, J.; Cordova-Esparza, D.M.; Romero-González, J.A.; Ramírez-Pedraza, A.; Chávez-Urbiola, E.A. A Comprehensive Survey of Loss Functions and Metrics in Deep Learning. Artif. Intell. Rev. 2025, 58, 195. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Li, Z.-L.; Leng, P.; Zhou, C.; Chen, K.-S.; Zhou, F.-C.; Shang, G.-F. Soil Moisture Retrieval from Remote Sensing Measurements: Current Knowledge and Directions for the Future. Earth-Sci. Rev. 2021, 218, 103673. [Google Scholar] [CrossRef]
- Le, M.S.; Liou, Y.-A. Spatio-Temporal Assessment of Surface Moisture and Evapotranspiration Variability Using Remote Sensing Techniques. Remote Sens. 2021, 13, 1667. [Google Scholar] [CrossRef]
- Wang, Q.; You, Y.; Yang, H.; Xu, R.; Zhang, H.K.; Lu, P.; Tong, X. A TCN-Transformer Parallel Model for Reconstruction of a Global, Daily, Spatially Seamless FY-3B Soil Moisture Dataset. Remote Sens. Environ. 2025, 328, 114841. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Li, Q.; Zhu, J. Enhancing Soil Moisture Forecasting Accuracy with REDF-LSTM: Integrating Residual En-Decoding and Feature Attention Mechanisms. Water 2024, 16, 1376. [Google Scholar] [CrossRef]
- Li, L.; Dai, Y.J.; Wei, Z.W.; Wei, S.G.; Wei, N.; Zhang, Y.G.; Li, Q.L.; Li, X.X. Enhancing Deep Learning Soil Moisture Forecasting Models by Integrating Physics-based Models. Adv. Atmos. Sci. 2024, 41, 1326–1341. [Google Scholar] [CrossRef]

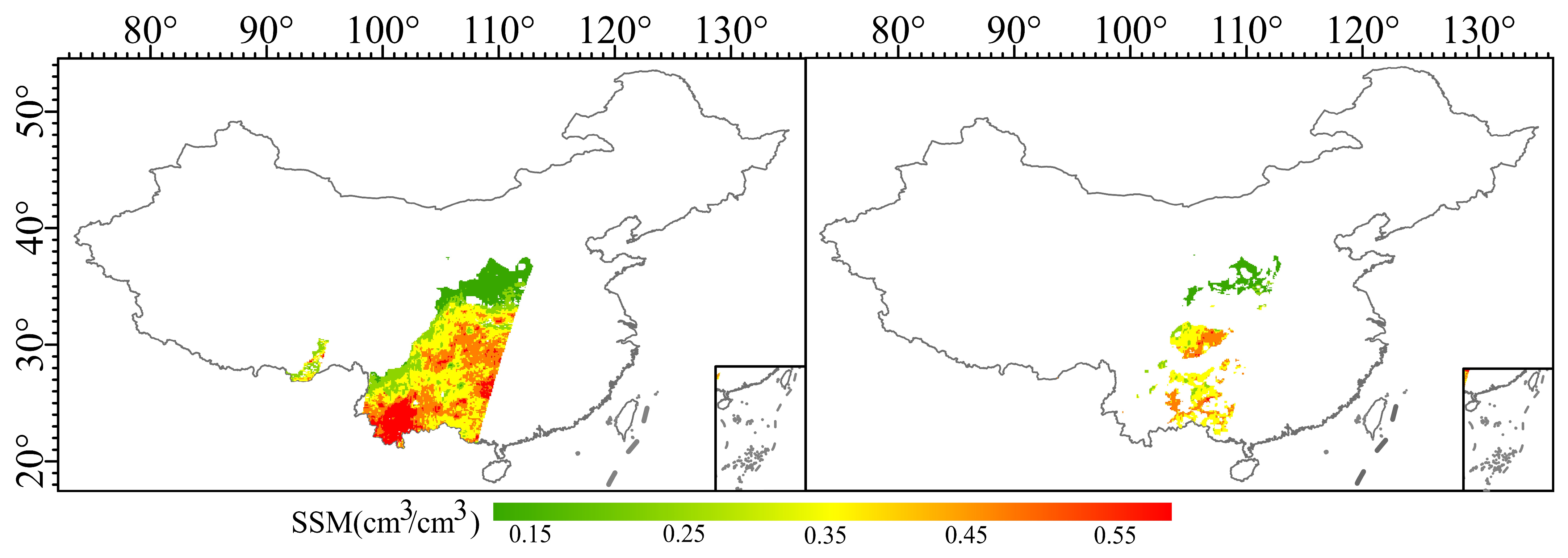




| Data Source | Variables | Resolution |
|---|---|---|
| MODIS | LST | Daily 1 km |
| EVI and NDVI | 16-day 1 km | |
| Land Cover | 500 m | |
| Calculated TVDI | Daily 9 km | |
| OpenLandMap | Soil classification, clay content, sand content, bulk density, organic carbon content, soil texture | 250 m |
| Copernicus DEM | DEM, Aspect, Slope | 30 m |
| ESA CCI | SSM | 0.25 degree |
| SMAP | SSM | Daily 9 km |
| 31 time series features from SMAP | 9 km |
| SSM Network | Site ID | Land Cover Type | Observation Period |
|---|---|---|---|
| SONTE-China | GuYuan01 to GuYuan10 | Shrubland | Mar 2021 to Nov 2021 |
| MinQin01 to MinQin10 | Mixed forest | Jan 2021 to Dec 2021 | |
| JingYueTan01 to JingYueTan10 | Cropland | Aug 2020 to Dec 2021 | |
| Hefei01 to Hefei10 | Grassland and sparse vegetation | Apr 2019 to Dec 2021 | |
| JiangShanJiao01 to JiangShanJiao10 | Grassland | Aug 2019 to Dec 2021 | |
| XiTianShan01 to XiTianShan10 | Shrubland | Aug 2019 to Dec 2021 | |
| HuLunBeiEr01 to HuLunBeiEr10 | Grassland | Aug 2019 to Dec 2021 | |
| XiLinHaoTe01 to XiLinHaoTe10 | Grassland | May 2019 to Dec 2021 | |
| QiYang01 to QiYang10 | Shrubland | Nov 2019 to Dec 2021 | |
| DongTingHu01 to DongTingHu10 | Cropland | Aug 2020 to Dec 2021 | |
| GuangZhou01 to GuangZhou10 | Grassland | Dec 2018 to Nov 2021 | |
| YuCheng01 to YuCheng10 | Cropland | Mar 2019 to Dec 2021 | |
| NanJing01 to NanJing10 | Cropland | Dec 2019 to Dec 2021 | |
| QingDao01 to QingDao10 | Shrubland and Grassland | Mar 2019 to Dec 2021 | |
| QianYanZhou01 to QianYanZhou10 | Shrubland | Nov 2019 to Dec 2021 | |
| NAQU | NQ1 to NQ4 | Shrubland | Aug 2016 to Sep 2019 |
| NQBJ and NQMS | Meadow | Feb 2016 to Sep 2019 | |
| NQKema | Meadow | Feb 2016 to Jul 2018 | |
| NQNorth | Meadow | Aug 2016 to Sep 2019 | |
| NQWest | Shrubland | Aug 2016 to Jul 2018 | |
| MAQU | CST03 to CST05 | Shrubland and meadow | Aug 2016 to May 2019 |
| NST01 to NST32 | Shrubland and mixed cropland | Feb 2016 to Jun 2019 | |
| SMN_SDR | L1 to L14 M1 to M12 | Mixed sparse vegetation, mixed cropland, grassland, mixed wetland | Sep 2018 to Nov 2019 |
| S1 to S8 | Grassland, mixed cropland | Jul 2018 to Aug 2019 | |
| CTP_SMTMN | L1 to L38 | Meadow | Jun 2016 to Aug 2016 |
| M1 to M20 | Meadow | Feb 2016 to Sep 2016 | |
| S2 to S7 | Meadow | May 2016 to Sep 2016 | |
| NGARI | ALI1 to ALI3 | Steppe, mixed forest | Feb 2016 to Aug 2018 |
| SQ1 to SQ20 | Steppe, shrubland, mixed forest, wetland | Feb 2016 to Sep 2019 |
| Model | Feature Configuration | Training LOSS | Training R2 | Validation Loss | Validation R2 | Training Duration (h) |
|---|---|---|---|---|---|---|
| TsSMNet | Full features | 0.0249 | 0.9746 | 0.0480 | 0.9508 | 29.25 |
| TsSMNet | Without collinearity features | 0.0214 | 0.9781 | 0.0431 | 0.9560 | 24.1 |
| SMNet | Without temporal features | 0.0587 | 0.9402 | 0.1056 | 0.8916 | 8.45 |
| ResAutoNet | Full features | 0.0587 | 0.9401 | 0.0465 | 0.9526 | 7.5 |
| ResAutoNet | Without collinearity features | 0.0599 | 0.9387 | 0.0476 | 0.9514 | 5.5 |
| Transformer | Without collinearity features | 0.0562 | 0.9510 | 0.0490 | 0.9504 | 24.6 |
| RF | Without collinearity features | 0.1797 | 0.8341 | 0.1824 | 0.8278 | 4.55 |
| XGBoost | Without collinearity features | 0.1105 | 0.8819 | 0.1234 | 0.8777 | 2.8 |
| SSM Data | Bias | r | RMSE | ubRMSE | Slope | Count |
|---|---|---|---|---|---|---|
| SMAP | 0.0085 | 0.73 | 0.089 | 0.088 | 0.754 | 14,265 |
| RF-derived SSM | 0.0007 | 0.64 | 0.094 | 0.094 | 0.565 | 60,591 |
| XGBoost-derived SSM | −0.0034 | 0.61 | 0.102 | 0.101 | 0.596 | 60,591 |
| Transformer-derived SSM | 0.1229 | 0.53 | 0.182 | 0.135 | 0.572 | 60,591 |
| ResAutoNet-derived SSM | −0.0118 | 0.64 | 0.096 | 0.095 | 0.567 | 60,591 |
| TsSMNet-derived SSM | −0.0115 | 0.66 | 0.093 | 0.093 | 0.605 | 60,591 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Fan, H.; Jin, Y.; Zhu, S. Reconstruction of SMAP Soil Moisture Data Based on Residual Autoencoder Network with Convolutional Feature Extraction. Remote Sens. 2025, 17, 3729. https://doi.org/10.3390/rs17223729
Liu Y, Fan H, Jin Y, Zhu S. Reconstruction of SMAP Soil Moisture Data Based on Residual Autoencoder Network with Convolutional Feature Extraction. Remote Sensing. 2025; 17(22):3729. https://doi.org/10.3390/rs17223729
Chicago/Turabian StyleLiu, Yaojie, Haoyu Fan, Yan Jin, and Shaonan Zhu. 2025. "Reconstruction of SMAP Soil Moisture Data Based on Residual Autoencoder Network with Convolutional Feature Extraction" Remote Sensing 17, no. 22: 3729. https://doi.org/10.3390/rs17223729
APA StyleLiu, Y., Fan, H., Jin, Y., & Zhu, S. (2025). Reconstruction of SMAP Soil Moisture Data Based on Residual Autoencoder Network with Convolutional Feature Extraction. Remote Sensing, 17(22), 3729. https://doi.org/10.3390/rs17223729








