Deep Line-Segment Detection-Driven Building Footprints Extraction from Backpack LiDAR Point Clouds for Urban Scene Reconstruction

Highlights

What are the main findings?

• A deep line-segment detection-driven framework is proposed for extracting complete and topologically consistent building footprints from backpack LiDAR point clouds.
• The method employs multi-layer accumulated projection and deep geometric feature learning to robustly identify continuous and topologically consistent structural boundaries in complex urban scenes.

What are the implications of the main findings?

• The proposed framework achieves robust, geometry-regularized, and orthogonally constrained footprints reconstruction, boosts building delineation completeness, and provides high-precision primitives for 3D reconstruction via remote sensing data.
• This work provides an extensible paradigm for the reconstruction of smart city scenes and digital twin modeling, demonstrating the potential of intelligent remote sensing methods in automated urban mapping, digital twin construction, and large-scale geographic spatial information extraction.

Abstract

Accurate and reliable extraction of building footprints from LiDAR point clouds is a fundamental task in remote sensing and urban scene reconstruction. Building footprints serve as essential geospatial products that support GIS database updating, land-use monitoring, disaster management, and digital twin development. Traditional image-based methods enable large-scale mapping but suffer from 2D perspective limitations and radiometric distortions, while airborne or vehicle-borne LiDAR systems often face single-viewpoint constraints that lead to incomplete or fragmented footprints. Recently, backpack mobile laser scanning (MLS) has emerged as a flexible platform for capturing dense urban geometry at the pedestrian level. However, the high noise, point sparsity, and structural complexity of MLS data make reliable footprints delineation particularly challenging. To address these issues, this study proposes a Deep Line-Segment Detection–Driven Building Footprints Extraction Framework that integrates multi-layer accumulated occupancy mapping, deep geometric feature learning, and structure-aware regularization. The accumulated occupancy maps aggregate stable wall features from multiple height slices to enhance contour continuity and suppress random noise. A deep line-segment detector is then employed to extract robust geometric cues from noisy projections, achieving accurate edge localization and reduced false responses. Finally, a structural chain-based completion and redundancy filtering strategy repairs fragmented contours and removes spurious lines, ensuring coherent and topologically consistent footprints reconstruction. Extensive experiments conducted on two campus scenes containing 102 buildings demonstrate that the proposed method achieves superior performance with an average Precision of 95.7%, Recall of 92.2%, F1-score of 93.9%, and IoU of 88.6%, outperforming existing baseline approaches by 4.5–7.8% in F1-score. These results highlight the strong potential of backpack LiDAR point clouds, when combined with deep line-segment detection and structural reasoning, to complement traditional remote sensing imagery and provide a reliable pathway for large-scale urban scene reconstruction and geospatial interpretation.

1. Introduction

Building footprints refer to the outline or shape of a building drawn on a map, aerial image, or 3D model, representing the ground-level perimeter of the structure. As an important mapping product, building footprints not only provide basic data for Geographic Information System (GIS) databases, but also offer significant support for tasks such as urban planning, environmental simulation, and autonomous driving navigation [1,2]. In the process of emergency response and post-disaster reconstruction, quickly obtaining high-precision building footprints can serve as an important reference for disaster assessment and rescue decision-making [3,4]. Therefore, the accurate extraction of building footprints is of great significance in fields such as urban modeling, land use investigation, 3D reconstruction, disaster assessment, and smart city construction, and it is a research hotspot in the fields of remote sensing and geoinformation science [5,6,7].

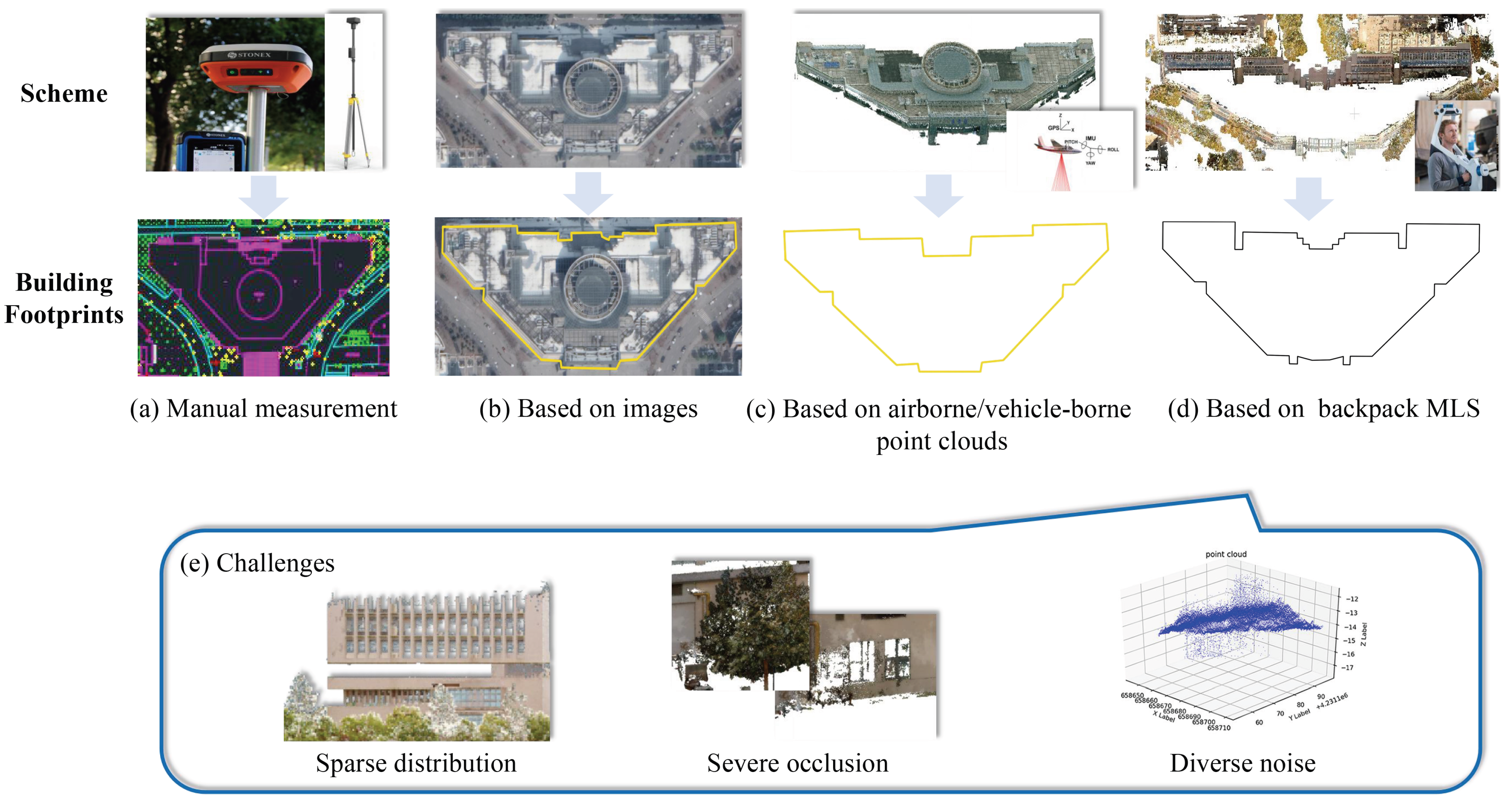
Figure 1a–d show the main schemes for extracting building footprints. Early building footprints extraction mainly relied on manual measurement and vectorization. Although these methods achieved high accuracy, they are time-consuming and labor-intensive, making them unsuitable for large-scale applications [8]. With the advent of high-resolution remote sensing imagery, approaches such as edge detection, morphological filtering, and object-based image analysis achieved initial success in extracting regular buildings [9,10]. Subsequently, convolutional neural networks (CNNs), U-Nets, and related variants sgreatly improved the accuracy of building footprints extraction [11,12,13]. However, image-based methods are inherently constrained by their 2D nature. In complex urban environments, shadows, occlusions, and illumination variations often degrade performance, making it difficult to accurately describe irregular or multi-layer structures.

To overcome the limitations of 2D imagery, the emergence of light detection and ranging (LiDAR) provided new opportunities for footprints extraction. Airborne laser scanning (ALS) provides generates large-scale, high-density 3D point clouds, from which preliminary building boundaries can be derived using filtering, clustering, alpha-shape, or convex hull algorithms [14,15,16]. More advanced approaches integrate RANSAC, Bayesian classification, and deep learning models to jointly extract roof planes and footprints, improving geometric representation to some extent [17,18,19,20]. Nevertheless, ALS primarily provides top-view information (housetop). As wall structures are poorly captured, results remain unsatisfactory for complex roof shapes or irregular buildings.

With the development of vehicle-borne laser scanning, research has gradually shifted to block-scale and near-field reconstruction, offering higher spatial resolution and more detailed geometric depiction [21,22,23]. However, fixed platforms suffer from limited viewpoints, making it difficult to acquire complete building information in narrow streets or dense urban areas.

Recently, backpack mobile laser scanning (backpack MLS) has emerged as a promising alternative [24,25]. Compared with airborne or vehicle-borne systems, backpack MLS offers greater mobility and flexibility, while capturing high-density and high-accuracy point clouds. Yet, the advantages of precision and density also bring new challenges (see Figure 1e). First, massive data volumes increase computational and storage burdens. Second, uneven point distributions caused by occlusions or local sparsity often lead to missing walls and broken boundaries in footprints. Third, random noise and multipath reflections introduce false points, which are easily misinterpreted as spurious contours or redundant structures. Finally, complex architectural forms such as overhead floors, corridors, and multi-layer superpositions frequently cause footprints breakage or misconnection. Overall, methods originally designed for airborne or vehicle-borne point clouds are difficult to directly apply to backpack MLS data, and specialized research on this type of complex dataset remains limited.

To this end, we propose an automatic method for extracting building footprints from backpack MLS point clouds. The method is designed to address contour loss and misjudgment caused by point cloud sparsity, noise, and the diversity of architectural forms. Unlike existing approaches that primarily target airborne or vehicle-borne point clouds, the proposed method is specifically tailored to the characteristics of backpack MLS data. By integrating projection enhancement, deep line-segment detection, and structural constraints, it enables high-precision and fully automated extraction of building footprints.

The main contributions of this work are summarized as follows:

• Occupancy map generation from point clouds based on multi-Layer accumulated projection (MLAP). By performing accumulated projection and superposition of point clouds across multiple height layers, the saliency of building footprints in the projection space is effectively enhanced, thereby mitigating the problem of footprints missing caused by sparse point clouds and local occlusions.
• Line segment detection based on a learning network. Combined with a deep line segment detection model, potential building structural lines are automatically identified and extracted from the occupancy map, improving the accuracy of line segment detection and the continuity of boundaries.
• Line segment optimization and regularization based on building features. Optimization strategies such as structural chain-based screening, directional extension, and orthogonal intersection constraints are proposed to further complete broken boundaries, eliminate redundant line segments, and achieve footprints regularization in terms of geometry and topology.

2. Related Work

2.1. Building Footprints Extraction Method on Images

Early-stage research on building footprints extraction mainly relies on image data, and its core idea is to identify building boundaries through 2D geometric and spectral features. Traditional geometry and rule-driven methods include rasterization, region growing, triangulated irregular network (TIN) reconstruction, and morphological filtering, which have achieved initial results in the extraction of regular buildings. In addition, the occupancy map, as a spatial representation method, is also gradually applied in the scenario of combining images and point clouds [26]. Its basic idea is to project 3D data onto a raster or pixel plane to establish the representation of space-occupied and free regions, thereby simplifying the transition process of 3D–2D footprints [27]. For example, in building detection, the planar occupancy information of buildings is often obtained through projection and spatial filtering [28]. Projection methods based on regular grids are simple to implement and fast, but the degree of footprints detail depiction is constrained by resolution.

With the development of deep learning, CNNs, U-Nets and their variants have been widely used in image segmentation tasks. These methods have significantly improved the accuracy of building segmentation and footprints extraction, but they still perform poorly in corners, broken lines, and small-scale details. In order to further optimize the boundaries, some studies have proposed methods that fuse CNNs with active contour models, which realize geometric regularization of boundaries through energy constraints on the basis of coarse segmentation [29,30]. Later, generative models are introduced into the extraction of building footprints. For example, generative adversarial networks (GANs) and variational autoencoders (VAEs) can directly generate building footprints or their probability maps from remote sensing images or rasterized point clouds, and then realize vector boundaries by combining morphological processing and graph optimization [31,32]. However, such methods may still have footprints fluctuations and pseudo-contours at irregular broken lines and corners, and their stability is limited.

Building footprints have significant geometric features of straight lines and polygons, so line segment detection methods have gradually attracted attention in recent years. Traditional line segment detection operators such as line segment detector (LSD) [33], enhanced line segment detector and descriptor (ELSD) [34], and Markov chain marginal line segment detector (MCMLSD) [35] can extract main straight line features in images. Deep learning methods have further expanded this idea. For example, by transforming line segment detection into vector field prediction, holistically attracted wireframe parsing (HAWP) improves robustness in vertex-edge joint modeling and graph consistency [36,37,38], while DeepLSD [39] significantly enhances the accuracy and stability of straight line detection by learning direction fields and distance fields. At the same time, researchers have also introduced geometric regularization operators, adding constraints such as orthogonality, parallelism, and collinearity at the vector level, thereby improving the geometric consistency after line segment combination and reducing burrs and broken boundaries [28,40].

2.2. Building Footprints Extraction Method on Point Cloud

Compared with image methods, LiDAR point clouds can directly provide 3D geometric information, thus gradually becoming an important data source for building footprints extraction. Airborne LiDAR provides large-scale point clouds, and early studies mostly adopt filtering, clustering, Alpha-shape or convex hull algorithms to realize preliminary footprints extraction. The Alpha-shape method [41] is widely used due to its variable radius adjustment ability, but it is sensitive to noise and prone to over-smoothing or gaps. The Hough transform [42] aided by ordered points enhances the stability and repeatability of voting in the Hough space through ordered point sequences, thereby detecting straight lines and corner points more reliably. The recursive convex hull method [43] enhances footprints integrity by combining signal regularization. The RANSAC-based method [19] achieves robust modeling through proportional segmentation, yet its performance in detail recovery is limited. Recent studies have shown that combining aerial image/aerial point clouds with laser point clouds to enhance the integrity and accuracy of contour extraction has become a common practice. For instance, an improved octree/block strategy is used to co-process images and LiDAR data to improve boundary connectivity and geometric restoration capabilities [44]. In addition, point-cloud slicing–based contour extraction has recently received increased attention [45,46]. These approaches discretize 3D point sets into layered slices and reconstruct footprints from slice-wise contours, and studies show that slice thickness, grid resolution and directional constraints strongly affect contour continuity and geometric fidelity [47]. To mitigate fragmentation and noise sensitivity, dynamic/adaptive slicing, cumulative projection, and contour-linking strategies have been proposed [48,49].

Later, PointNet/PointNet++ [50,51] pioneered point-level feature learning, and subsequent methods such as KPConv [52], RandLA-Net [53], and Point Transformer further improve the representation capability and efficiency of large-scale point clouds. Recently, advanced deep learning approaches have been applied to building footprints extraction from LiDAR data. Self-supervised and terrain-informed frameworks improve generalization with limited annotations [54], end-to-end contour learning enhances geometric regularity [55], and attention-based architectures further strengthen robustness in complex urban environments [56]. However, deep learning methods often require large-scale annotated samples and substantial computational costs, and the generalization ability of trained models is easily affected by different data sources and scenarios [54,57]. Advanced point cloud processing + machine learning technologies are gradually being applied to the extraction of building structures and geometric features, but the problems of boundary breaks caused by sparsity, local notches and noise have not been systematically solved yet [58]. Vehicle-borne LiDAR then promotes fine modeling of block-scale and close-range buildings, improving spatial resolution and detail characterization capabilities. Such methods typically generate building footprints through roof plane segmentation and line fitting, which are suitable for extracting regular buildings. Nevertheless, in cases of complex topology, local occlusion, and polygonal buildings, problems such as footprints breakage or adhesion still tend to occur.

In summary, building footprints extraction methods have evolved from image-based to point cloud-based approaches, achieving notable progress in geometric representation and accuracy. However, most studies focus on airborne or vehicle-borne LiDAR data, with algorithms and application settings tailored to the characteristics of these platforms. By contrast, backpack MLS systems offer flexible mobility and high precision, making them well suited for fine-scale modeling in dense urban environments and narrow spaces. Yet, research specifically addressing this data type remains limited. Current methods have not effectively reconciled the high density and complexity of backpack MLS data with the need for regularized footprints representation.

To address this gap, we propose a method that integrates multi-layer cumulative projection occupancy maps, network-based line segment detection, and structural chain completion with geometric regularization. This approach leverages the feature extraction advantages of deep learning while incorporating structural priors of buildings, thereby improving the continuity, integrity, and geometric consistency of extracted footprints.

3. Methodology

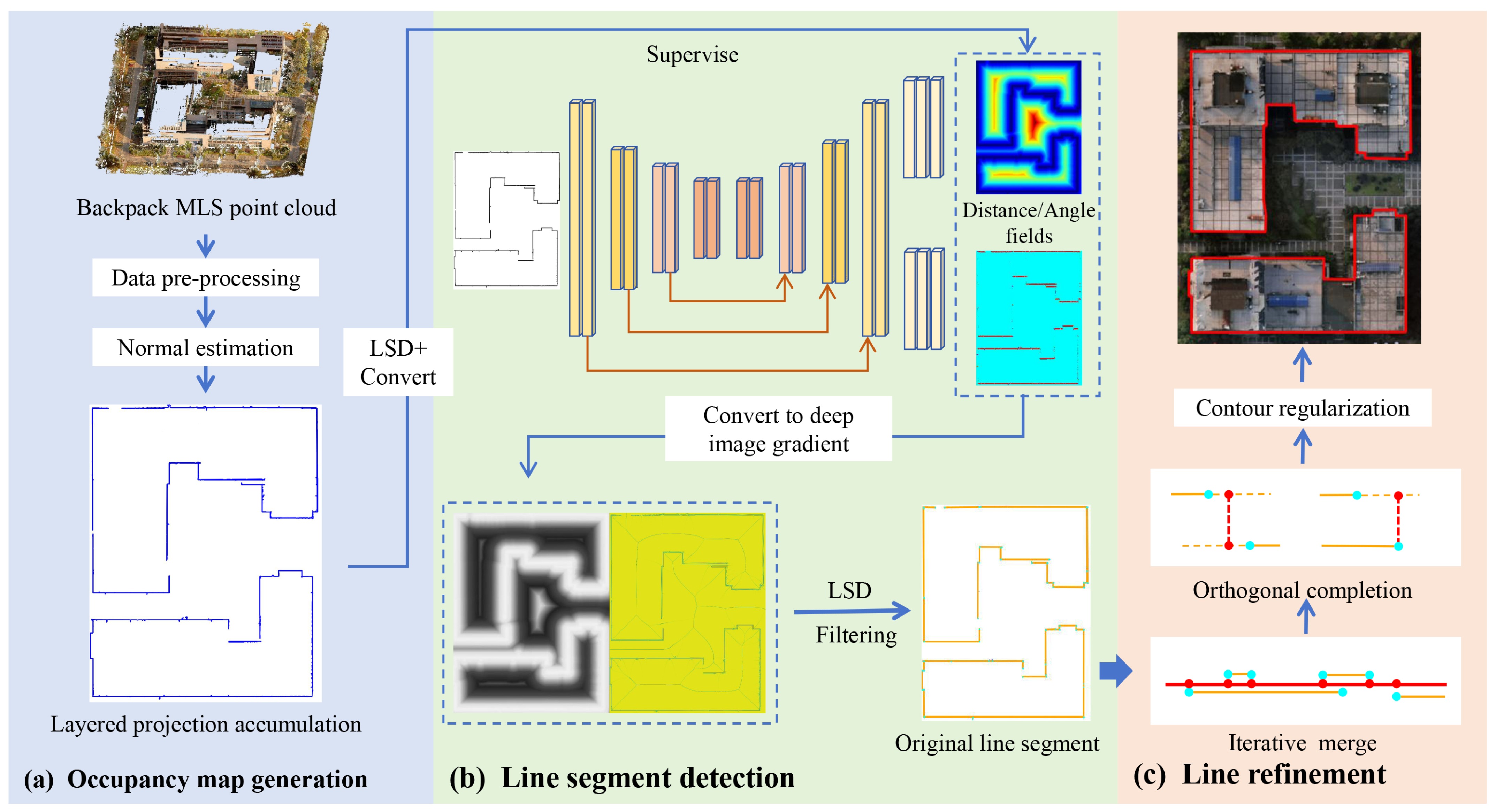
We propose a three-stage method for the automatic extraction of building footprints from backpack MLS. The overall workflow, shown in Figure 2, consists of occupancy map generation, line segment detection, and structural optimization with geometric regularization. By incorporating prior spatial and geometric knowledge of building structures, the method substantially improves the robustness and accuracy of footprints extraction, even from sparse or noisy point clouds.

3.1. Multi-Layer Occupancy Map Generation

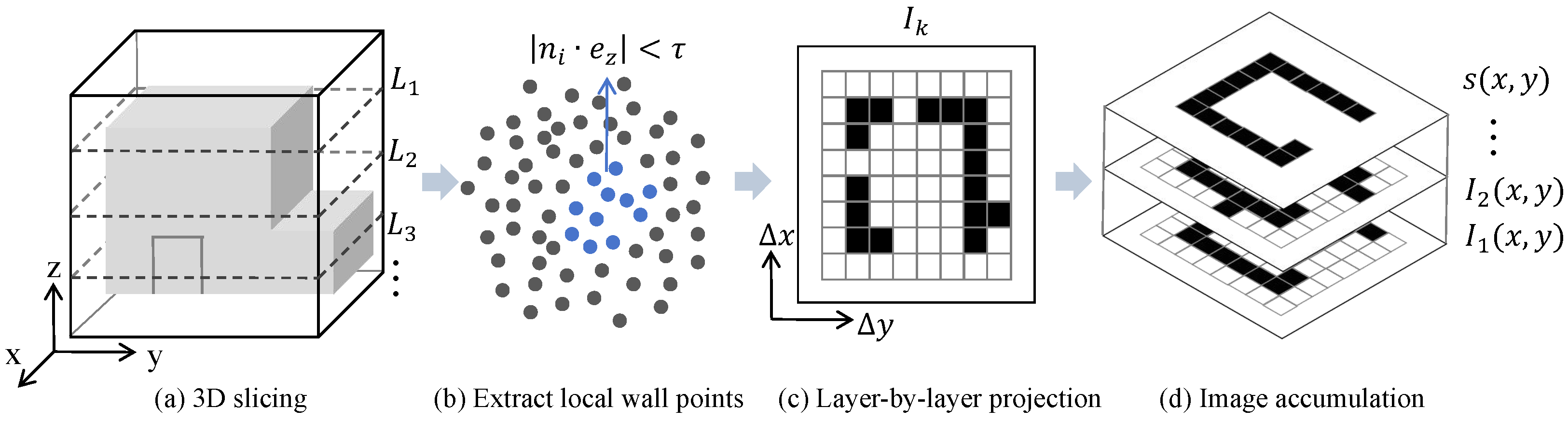
We propose an occupancy grid generation strategy based on MLAP, which integrates local normal features and height information from point clouds. By accumulating stable projections of wall structures, the method enhances the completeness and robustness of building façade representations, as illustrated in Figure 3. This approach not only eliminates noise from isolated points but also accurately reconstructs the footprints of buildings in 2D images, serving as a foundational input for subsequent line segment detection and optimization modules.

The MLAP method slices the point cloud into several height intervals and independently extracts wall projections at each layer. All resulting images are then combined through pixel-wise accumulation to form a more stable and precise structural representation. The core idea of the method is as follows: The point cloud is divided at equal intervals along the z-axis, resulting in a sequence of overlapping height slices $L_k$:

$$L_k=\{P_i\mid z_{min}+k·\Delta z\le z_i<z_{min}+(k+1)·\Delta z\}$$

(1)

Neighborhood PCA is applied to estimate normals for the point cloud. In each layer, only the points with approximately vertical normal directions (representing walls) are retained—i.e., points that satisfy $|n_i·e_z|<\tau$ (where $e_z\in (0,1)$). In practice, building wall structures exhibit strong continuity across multiple height layers. For each $L_k$ layer, the extracted wall points are projected onto a 2D plane using their x,y coordinates, mapping them to pixel positions in a 2D image:

$$x_{\mathrm{idx}}=\left[{\displaystyle \frac{x_i-x_{min}}{s}}\right],y_{\mathrm{idx}}=\left[{\displaystyle \frac{y_i-y_{min}}{s}}\right]$$

(2)

here, s denotes the grid spacing, which determines the level of detail in the output image. We define the 2D image generated from each layer as $I_k(x,y)\in (0,1)$, and the accumulated support map is:

$$S(x,y)=\sum _{k=1}^K{I}_k(x,y)$$

(3)

where $S(x,y)\in N$ indicates the number of layers in which the pixel is hit by the wall projection. Compared with single-layer projection, cumulative images can more effectively distinguish architectural structures from accidental projections. Similar studies have also pointed out that the structural signals at sparse or locally missing areas can be enhanced through hierarchical/regionalized projections or octree blocking, thereby improving boundary connectivity and noise resistance performance [59]. This mechanism not only compensates for sparse point distributions that cause local gaps, but also filters out isolated noise points that only appear in a single slice, thereby enhancing both robustness and continuity of structural contours.

Considering sensor errors and the influence of isolated points, only pixels that appear in multiple layers are retained as valid structural points. The lower limit of the supporting layers is set to n, and a mask image is constructed:

$$M(x,y)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}S(x,y)\ge n\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(4)

where the value of threshold n depends on the point cloud density and building height, increasing it appropriately in high-rise buildings or dense areas can reduce redundant interference. To further improve reproducibility, we introduce a quantitative rule to guide the adaptive selection of n based on building height ($H_b$) and average point cloud density (${\rho }_p$). Specifically, n can be determined as:

$$n=\mathrm{clip}\left(2+\alpha ·{\displaystyle \frac{H_b}{10}}+\beta ·{\displaystyle \frac{{\rho }_p}{500}},2,6\right)$$

(5)

where $\alpha =0.4$ and $\beta =0.2$ are empirically determined coefficients, and the function $\mathrm{clip}(·)$ constrains n within [2, 6]. This adaptive rule ensures that higher buildings or denser point clouds result in a slightly larger n, enhancing inter-layer stability, whereas low or sparse structures use smaller n to retain sharper boundaries.

Morphological closing operation is applied to the obtained mask image M, this processing step eliminates small voids and connects adjacent wall structures, resulting in an image with clear connectivity and structural boundaries. Finally, the $findContours$ function from OpenCV is used to extract edge contours from the morphological image $M^{\prime }$, retaining only the outermost contours. To avoid preserving noisy regions, an area threshold $A_{min}$ is further applied, keeping only closed contours larger than the specified value. The final output is the resulting occupancy map $I_{outline}$, where only the contour lines are marked as 1, and their shape closely matches the building’s planar projection.

The core rationale of the MLAP module lies in enhancing the structural continuity of building footprints by aggregating multi-height geometric evidence. Instead of relying on a single horizontal slice that may be affected by local occlusion or sparse sampling, MLAP performs cumulative projection across multiple elevation layers. By integrating height-layer accumulation with occupancy voting, the resulting 2D map captures both the persistence and spatial confidence of structural points, providing a noise-resistant and geometrically consistent foundation for subsequent line detection.

3.2. Line Segment Detection

After obtaining a clear and structurally stable occupancy map, the next step is to automatically extract raw line segments of the building footprints from this map to establish a foundation for subsequent optimization and structural reasoning. Traditional image edge detection methods (e.g., Canny, LSD [33], ELSD [34]), while computationally efficient, often suffer from issues such as structural drift, excessive fragmentation, or false edge detection when dealing with occlusions, discontinuities, and blurred boundaries in architectural structures.

We introduce an end-to-end deep learning-based line segment detection method. The input is a single-channel grayscale occupancy map, and the process involves three progressive steps: ground truth generation, feature field prediction, and line segment extraction and filtering. The final output is a set of raw line segments.

3.2.1. Ground Truth Generation

We employ the homography adaptation method to generate ground truth for line segment feature fields without relying on manually annotated line segment data. For the input occupancy map, N random homography matrices $H_i$ are generated, producing N warped images through homography transformation $I_i$. The LSD algorithm (known for its high accuracy in noise-free scenarios) is used to detect line segments in each warped image $I_i$. These line segments are then mapped back to the original image coordinate system via the inverse transformation $H_i^{-1}$, yielding N sets of line segments $L_i$. Each set of line segments is subsequently converted into corresponding distance fields $D_i$ (the Euclidean distance from a pixel to the nearest line segment) and angle fields $A_i$ (the orientation angle of the nearest line segment). Median aggregation is applied to eliminate noise interference:

$$\left\{\begin{array}{c}D(u,v)={\mathrm{median}}_{i\in [1,N]} D_i(u,v)\hfill \\ A(u,v)={\mathrm{median}}_{i\in [1,N]} A_i(u,v)\hfill \end{array}\right.$$

(6)

3.2.2. Line Segment Feature Field Prediction

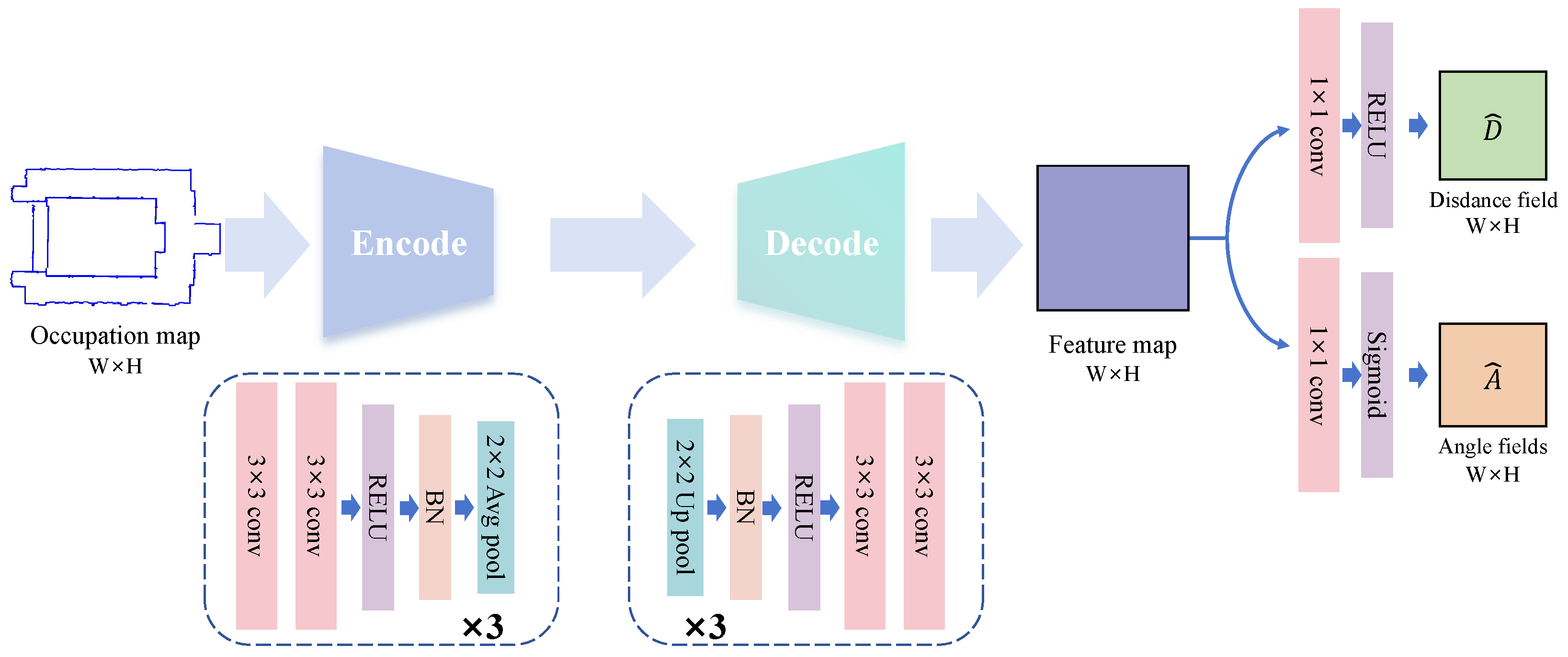
The detection network constructed in this paper adopts a lightweight fully convolutional encoder-decoding structure, referring to the U-Net framework, and balances local details and global context information through feature fusion on the encoder-decoder path, as illustrated in Figure 4. Specifically, the network takes an occupancy map (single-channel and size of H × W) as input and progressively extracts high-level features in the encoder stage (downsampling path). The encoder consists of three consecutive downsampling blocks with channel dimensions of 32, 64, and 128, respectively. Each block comprises two 3 × 3 convolutional layers, batch normalization, and a ReLU activation function, followed by a 2 × 2 average pooling layer for 2× downsampling, which reduces the feature map size to one-eighth of the input. This reduces the feature map size to 1/8 of the input. The decoder stage gradually restores resolution through three upsampling modules. Each module first employs bilinear interpolation to upsample the feature map by 2×, then concatenates it with the corresponding encoder feature map of the same scale via skip connections, followed by two 3 × 3 convolutional layers for feature integration. The decoder channels are symmetrically configured as 128, 64, and 32, and all convolution kernels use a size of 3 × 3 without employing dilated convolution. The output layer splits the final feature map into two parallel branches to predict the distance field $\widehat{D}$ and angle field $\widehat{A}$, ensuring the output size matches the input occupancy map.

To enhance prediction accuracy for pixels near line segments, a specialized normalization strategy is applied to the distance field. The normalized distance field ${\widehat{D}}_n$ from the branch is mapped to the actual distance via an exponential transformation:

$$\widehat{D}=r·e^{-{\widehat{D}}_n}$$

(7)

where r is a predefined effective radius, ensuring higher resolution in regions closer to line segments ($\widehat{D}<r$). For the angle field branch, a sigmoid activation function maps the output to the interval $(0,\pi )$, accommodating the periodic nature of line segment orientations ($\widehat{A}\equiv \widehat{A}+\pi ·mod\pi$).

3.2.3. Line Segment Detection Based on Pseudo-Gradient

The distance field and angle field output by the network are converted into pseudo-gradient features interpretable by traditional line segment detection algorithms. By incorporating geometric constraints, line segment detection and noise filtering are achieved, ultimately yielding high-quality initial line segments.

To meet the input requirements of the conventional LSD algorithm, the feature fields are converted into gradient-like feature pairs, primarily including gradient magnitude M and gradient direction $\theta$. The gradient magnitude M, which mainly reflects the confidence of a pixel belonging to a line segment edge, is defined as:

$$M=max\left(0,y-\widehat{D}\right)$$

(8)

Specifically, pixels near line segments ($\widehat{D}<r$) exhibit high magnitude values, while regions far from line segments have zero magnitude. The gradient direction $\theta$ is derived from the angle field, with the line segment orientation being perpendicular to the gradient direction. The conversion is formulated as:

$$\theta =\widehat{A}-\pi /2·mod\pi$$

(9)

In practical scenarios, the presence of double-line edges requires direction correction by verifying the consistency between $\theta$ and the local gradient direction in the occupancy map. If the deviation exceeds $\pi /2$, the direction is adjusted to $\theta -\pi$ to ensure the gradient direction conforms to the intensity variation pattern of edges.

The line segment detection process proceeds as follows: The pseudo-gradient features are fed into the LSD algorithm, where seed points are first selected via gradient magnitude thresholding ($M>3$). These seeds are then clustered by gradient direction to grow line segment regions, with minimum bounding rectangles fitted to determine the endpoints ($s_x,s_y$) and ($e_x,e_y$). This generates an initial line segment set S. The LSD algorithm was adopted in this study due to its superior balance between detection precision and computational efficiency. Unlike probabilistic or voting-based approaches, which require iterative parameter tuning and are sensitive to noise, LSD directly operates on gradient fields through region growing, achieving sub-pixel localization without the need for threshold-heavy voting. Compared with EDLines, which emphasizes real-time performance, LSD provides higher robustness for complex, dense edge distributions, making it more suitable for pseudo-gradient features derived from neural network predictions. These characteristics align well with the requirements of the proposed framework, ensuring accurate and efficient extraction of dense structural line segments in complex urban scenes. To make this process more explicit, Algorithm 1 summarizes the full pipeline for converting predicted feature fields into initial line segments, including pseudo-gradient restoration, LSD-based detection, and line-growth refinement.

Algorithm 1: Line Segment Detection from Predicted Feature Fields

3.3. Line Segment Optimization and Regularization

The initial line segment detection results often exhibit intermingled segments from different buildings, along with issues such as noise and fragmentation, making it difficult to directly form complete building footprints. To address this, we propose a regularization method that integrates pruning optimization and completion strategies, leveraging the spatial topological relationships and geometric features of buildings to achieve precise line segment optimization. The refinement process follows two main principles: geometric regularization and topological reasoning. The former merges and aligns line segments based on angular and distance consistency to restore the dominant orthogonal and parallel structures of buildings, while the latter infers missing connections among endpoints to reconstruct continuous and complete contours. Together, these steps ensure that fragmented and noisy segments are transformed into regular, topologically coherent building footprints.

First, for the presence of line segments with consistent orientations and spatial proximity in the original segment set, an iterative merging strategy is employed to reduce over-fragmented line representations and enhance the expression of main structures. The specific strategy includes: for any two line segments $l_i$ and $l_j$, their principal direction angle difference $\Delta \theta$ and shortest distance d are calculated. When $\Delta \theta <{\theta }_{thresh}$ and $d<d_{thresh}$, they are identified as mergeable. The endpoints of the two segments are projected onto the principal direction vector, and the minimum and maximum points of the projected range are extracted as the endpoints of the newly merged segment. This operation is iteratively repeated until no new mergeable pairs are found, resulting in a preliminary regularized structure.

For gaps, openings, and fragmented regions in building footprints, relying solely on line segment merging often fails to achieve automatic restoration. Therefore, We propose a line segment completion mechanism based on directional extension and structural constraints to address broken segments and typical gap types.

During the completion phase, all endpoints $p_i$ from existing segments are extracted, and every endpoint pair ($p_i,p_j$) is enumerated. Candidate completion segments are generated by evaluating their euclidean distance $d_{ij}=\left||p_i-p_j\right||$ and directional consistency ${\alpha }_{ij}$ (the angle between the connecting line and nearby segments). Pairs satisfying $d_{min}<d_{ij}<d_{max}$ and ${\alpha }_{ij}<{\alpha }_{thresh}$ are retained as valid candidates. For typical gap types, for U-shaped gaps, a perpendicular line is drawn from the endpoint of the longer segment to the opposing short segment’s line, with the foot of the perpendicular serving as the new endpoint, forming an orthogonal completion segment to close the unilateral gap; for N-shaped gaps, perpendicular lines are drawn from both endpoints to the opposing segment, and the midpoint of the two perpendicular lines is used to construct an orthogonal completion segment, achieving bilateral gap closure.

Additionally, to avoid redundant segments caused by erroneous completions, redundancy filtering is performed. This step is particularly effective in discarding segments generated from noisy points, ensuring that the final footprints are both continuous and noise-free. The specific method involves screening candidate segments based on endpoint frequency: constructing an endpoint connection frequency map $C\left(p\right)$ to count the occurrence of each endpoint in the merged segment set; identifying potential break endpoints, where candidate segments connecting two structural ends are considered valid structural extensions, thereby screening effective completions; and iteratively updating the connection map to avoid duplicate completions.

4. Experiment and Analysis

4.1. Dataset Preparation

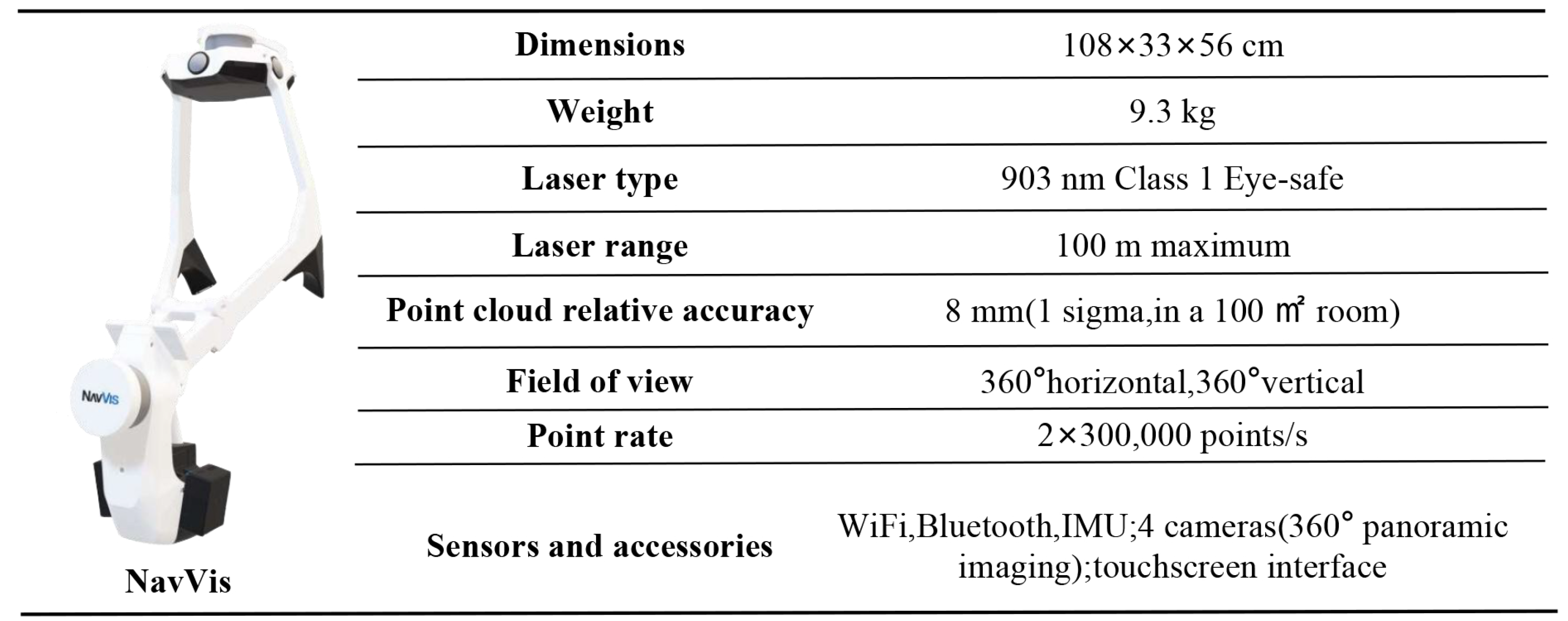
The data used in this study were collected in situ by our team at Hohai University, utilizing the NavVis VLX backpack-mounted mobile laser scanning system. Full-coverage surveys were conducted across two of the university’s campuses, namely the Jiangning campus and the Jintan campus, with a total covered area of approximately 2.1 km². During the data collection process, a total survey route of about 18 km is traversed, the cumulative collection time exceeded 20 h, the acquired point cloud data volume reached approximately 1.5 billion points, and the original data size exceeded 500 GB. The NavVis VLX is a high-precision wearable 3D mapping device designed for the engineering and architecture industries (see Figure 5), equipped with dual multi-layer LiDAR sensors. Combined with the simultaneous localization and mapping (SLAM) algorithm, it enables rapid acquisition of high-quality 3D point cloud data in indoor and outdoor built environments. The survey routes covered sidewalks and building exteriors across multiple blocks, ensuring full coverage of building footprints and high surveying accuracy. The raw point clouds output by the device are processed using official post-processing software, including SLAM optimization, dynamic object removal, and color mapping, ultimately generating high-precision 3D point cloud data with realistic textures.

The entire dataset contains approximately 102 buildings, covering various types such as teaching buildings, dormitory buildings, laboratory buildings, libraries, and stadiums. The building morphologies include not only regular rectangular structures but also buildings with hollow courtyard structures and complex polygonal footprints, which fully cover building features under different scenarios, as shown in Figure 6. The overall average density of the point cloud is approximately 1800 points/m², and the average number of points per building is about 12 million, ensuring the complete representation of building footprints. In the data preprocessing stage, the raw point clouds are subjected to noise removal, coordinate unification, ground point segmentation, and normalization to obtain building point clouds with clear structures, suitable for footprints extraction. After processing the entire dataset using the proposed method, the overall reconstruction rate of building footprints reached 96.3%, which can relatively completely restore the actual distribution of the campus building complex.

In this work, the ground truth building footprints are manually vectorized from the original backpack LiDAR point clouds. Experienced annotators delineated footprints boundaries directly on the high-density point cloud projections, ensuring geometric fidelity to the measured data. Although these ground truths are not obtained from total station measurements, they originate from accurately georeferenced point clouds, and their spatial precision is therefore consistent with the LiDAR measurement accuracy. To more intuitively analyze the performance of the method under different building morphologies, four typical regions are selected from the entire campus for detailed experiments and visualization: a multi-story single building with a regular outer footprint (Region 1), multi-story adjacent buildings with regular outer footprints (Region 2), a building with hollowed areas (Region 3), and a polygonal building with an irregular shape (Region 4) (see Figure 7). The point cloud of each sample region covers the full perimeter of the building, generated at a point cloud density corresponding to an acquisition rate of approximately 600,000 points per second, with a spatial point spacing of about 3–5 cm. This ensures the complete representation of the planar footprints details of the building, providing a reliable data foundation for subsequent occupancy map generation, line segment detection, and footprints extraction.

4.2. Experimental Settings

4.2.1. Method Parameters

All module parameters in this study can be adaptively adjusted according to point cloud density, building scale, and scene complexity, ensuring applicability across different data conditions and practical requirements. The experimental parameters in this work were determined through cross-experiments and sensitivity tests based on experience. To guarantee the comparability and reproducibility of experimental results, a unified set of parameter configurations is applied to all samples.

In the occupancy grid generation stage, the vertical slicing interval is set to 0.5 m, and the grid resolution is fixed at 0.1 m/pixel to preserve sufficient contour details. The support-layer threshold n is determined based on the slicing interval and the overall building height, ranging between 2 and 6. Pixels projected by building walls in no fewer than n slices are retained. A morphological closing operation is performed with a 3 × 3 pixel structural element. During contour extraction, closed regions with an area smaller than 1 m² are removed to suppress small noise objects.

In the line segment detection stage, the input resolution is kept unchanged. For ground-truth generation, the number of homography transformations N is set to 100, and the default threshold of the LSD algorithm is adopted. The effective radius of the distance field is set to 5 pixels to enhance prediction resolution near line segments. The angle field is normalized, followed by orientation correction during pseudo-gradient generation. A gradient magnitude threshold of 3 is applied to select seed points.

In the line segment optimization and regularization stage, two line segments are merged if their orientation difference is within 10° and their shortest distance did not exceed 20 pixels. A new completion line segment is generated when the distance between endpoints is below 150 pixels and the orientation difference is less than 35°; for orthogonal completions, the angular deviation tolerance is 10°. Completion line segments are further filtered using a “structural chain” strategy, retaining only those consistent with the building’s topological structure. To avoid over-completion, each endpoint is allowed to connect with at most two completion segments, and redundant candidates are discarded.

4.2.2. Comparison Methods

To validate the effectiveness and superiority of the proposed method in building footprints extraction, 6 representative existing approaches are selected as baselines. These cover a broad spectrum of techniques, ranging from traditional geometry-based rules to point-cloud geometric processing and deep learning models. Specifically, the baselines include: (1) a geometric detection method that leverages ordered-point-assisted Hough Transform for line detection and footprints generation (OP-HT) [42]; (2) a Bayesian–RANSAC method that integrates Naïve Bayes classification with RANSAC fitting for proportionally guided segmentation (NB-RANSAC) [19]; (3) a gridding-based method that projects point clouds onto a regular grid and directly extracts footprints based on grid features (Grid) [28]; (4) a recursive convex hull combined with signal-based regularization approach, which constructs an initial footprint via recursive convex hulls and refines it with signal-constrained footprints smoothing (RCH-SR) [43]; (5) a deep learning method based on generative adversarial networks for automatic extraction of building footprints from point clouds (GAN) [18]; and (6) an improved Alpha-shape method with variable-radius adaptation to accommodate building structures of different scales (AlphaS) [60]. Among these, the GAN-based approach [18] represents a deep learning framework that employs a generative adversarial network to learn the distribution of building boundary features from LiDAR-derived occupancy maps. This method captures nonlinear spatial patterns and serves as a representative learning-based baseline, ensuring that our comparative evaluation includes both traditional geometric algorithms and modern deep learning approaches.

Together, these methods span a wide range of technical paradigms, from rule-based geometric construction to data-driven prediction, thereby providing a comprehensive benchmark for assessing the proposed method in terms of geometric accuracy, contour completeness, and robustness against noise.

4.2.3. Running Platforms

All experiments in this study are implemented using the PyTorch 1.12 deep learning framework with cuDNN 11.1.1 for GPU acceleration. The software dependencies included torchvision, numpy, matplotlib, opencv-python, shapely, scikit-image, and h5py. The hardware platform consisted of an Intel(R) Xeon(R) CPU E5-2673 v4 processor and an NVIDIA GeForce RTX 3090 GPU with 24 GB of memory. All training and testing procedures are conducted on an Ubuntu 20.04 operating system, with both model inference and training accelerated by the GPU.

4.2.4. Evaluation Metrics

To comprehensively evaluate the performance of the proposed method in building footprints extraction, multiple evaluation metrics are adopted, covering three key aspects: accuracy, completeness, and overall contour quality. These metrics ensure that the evaluation reflects both the geometric precision and the structural fidelity of the extracted footprints.

Line segment detection precision (P) and recall (R): Given the set of detected line segments and the ground-truth annotations, precision is defined as the ratio of correctly detected line segments to the total number of detected line segments, while recall is defined as the ratio of correctly detected line segments to the total number of ground-truth line segments. A detected line segment is considered correct if its average endpoint distance to a ground-truth segment is below a predefined threshold and its orientation difference falls within an angular tolerance.

F1-score: To balance precision and recall, the F1-score is employed as a comprehensive measure, defined as:

$$F1={\displaystyle \frac{2\times P\times R}{P+R}}$$

(10)

Contour similarity: For building footprints represented as closed polygons, the Intersection-over-Union (IoU) is computed between the predicted footprints and the ground truth:

$$IoU={\displaystyle \frac{A_{pred}\cap A_{gt}}{A_{pred}\cup A_{gt}}}$$

(11)

where $A_{pred}$ and $A_{gt}$ denote the areas enclosed by the predicted and ground-truth polygons, respectively. This metric directly reflects the degree of overlap between the predicted and actual building shapes.

Contour completeness: The predicted and ground-truth footprints are uniformly sampled along their boundaries, and the proportion of matched points is calculated. Missing segments are penalized proportionally, thereby measuring the algorithm’s ability to recover structural continuity under fragmentation and occlusion conditions.

4.3. Training Configuration

This work adopts an algorithmic ground truth generation process: First, traditional LSD combined with multiple homography transformations is applied to the occupancy maps to obtain robust line segment candidates, which are then converted into pixel-level distance fields and angle fields as pseudo-ground truth. This approach avoids manual annotation costs while ensuring the stability of supervision signals. Considering that the data are derived from two campuses containing 102 buildings, we generated several overlapping/patched occupancy map samples from MLAP, eventually constructing approximately 800 occupancy map samples. These samples are divided into training, validation, and testing sets in a ratio of 7:2:1. The split was performed at the building level, ensuring that all occupancy maps from the same building were assigned to a single subset. In this way, the test set exclusively contains unseen buildings, enhancing the reliability and independence of the evaluation. All images are uniformly scaled to 512 × 512, with data augmentation techniques such as rotation, cropping, and noise addition applied. The network employs a lightweight encoder-decoder structure, regressing both distance fields and angle fields simultaneously, and is optimized using weighted MSE/cosine loss. The training process utilizes the Adam optimizer with an initial learning rate of 1 × 10⁻⁴, a batch size of 16, and a total of 100 training epochs. During inference, the predicted fields are restored to pseudo-gradients, and initial line segments are generated by combining LSD and other line segment growth operators. These segments then proceed to subsequent structural chain completion and regularization modules to obtain the final continuous and consistent building footprints.

4.4. Comparison and Analysis

To comprehensively evaluate the performance of the proposed method, it is compared with 6 representative building footprints extraction approaches, including the OP-HT, NB-RANSAC, Grid, RCH-SR, GAN, Alphas. The qualitative visual comparison results are shown in Figure 8, while the results of quantitative indicators are shown in

Table 1. Performance comparison of different methods in building footprints extraction task for different regions.

Dataset	Method	Precision (%)	Recall (%)	F1-Score (%)	IoU (%)
Region 1	OP-HT (2019) [42]	94.0	91.9	92.9	90.7
	NB-RANSAC (2020) [19]	94.3	92.0	93.1	90.1
	Grid (2022) [28]	93.5	91.3	92.4	87.9
	RCH-SR (2022) [43]	94.7	92.5	93.6	89.1
	GAN (2022) [18]	95.0	93.1	94.0	88.8
	Alphas (2024) [60]	94.2	91.8	93.0	90.2
	Ours	96.2	94.4	95.3	90.9
Region 2	OP-HT (2019) [42]	93.0	91.4	92.2	85.4
	NB-RANSAC (2020) [19]	93.4	91.7	92.5	85.9
	Grid (2022) [28]	92.7	91.0	91.8	84.7
	RCH-SR (2022) [43]	93.8	92.0	92.9	86.4
	GAN (2022) [18]	94.2	92.8	93.5	87.4
	Alphas (2024) [60]	93.1	91.5	92.3	85.6
	Ours	95.4	93.7	94.5	89.1
Region 3	OP-HT (2019) [42]	89.0	85.2	87.1	82.5
	NB-RANSAC (2020) [19]	89.8	85.9	87.8	78.3
	Grid (2022) [28]	88.9	85.0	86.9	87.1
	RCH-SR (2022) [43]	90.2	86.7	88.4	79.0
	GAN (2022) [18]	91.1	87.3	89.2	80.1
	Alphas (2024) [60]	89.4	85.8	87.6	86.9
	Ours	92.8	89.4	91.1	88.5
Region 4	OP-HT (2019) [42]	91.0	87.9	89.4	80.8
	NB-RANSAC (2020) [19]	91.4	88.2	89.8	81.3
	Grid (2022) [28]	90.7	87.6	89.1	80.3
	RCH-SR (2022) [43]	91.9	88.8	90.3	81.9
	GAN (2022) [18]	92.5	89.1	90.8	82.5
	Alphas (2024) [60]	91.3	88.1	89.7	81.0
	Ours	94.1	91.2	92.6	85.9

.

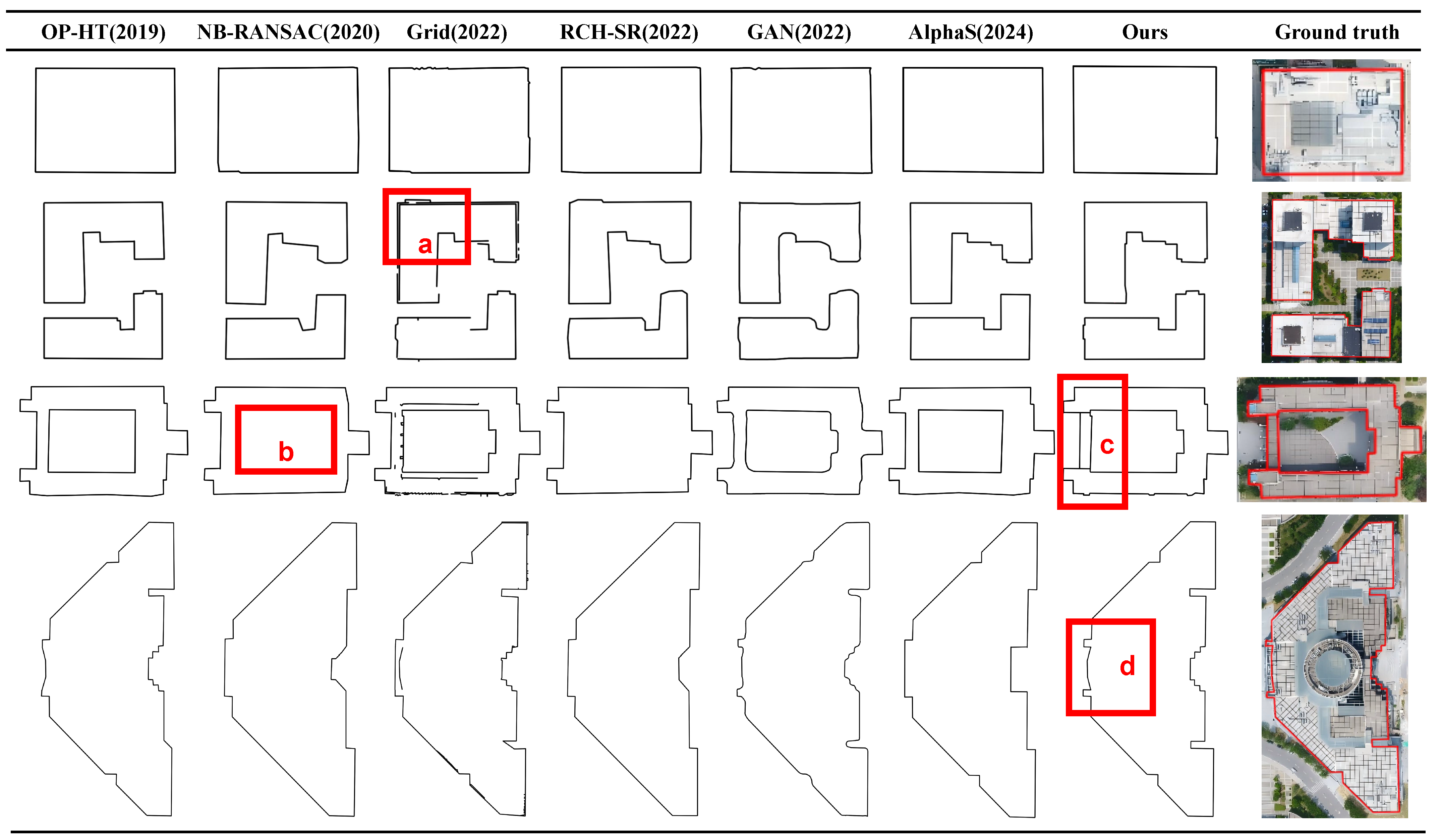
In rectangular buildings with regular footprints (Region 1 and Region 2), AlphaS and RCH-SR perform well in large-scale footprints extraction and can maintain the overall shape relatively well. However, they tend to undergo excessive smoothing when depicting corners and details, leading to a decline in local geometric accuracy. The GAN method is relatively close to the ground truth in terms of footprints morphology, but there are local fluctuations and irregular jitters of boundaries in some areas. OP-HT and NB-RANSAC can detect the main structure well, but they are insufficient in restoring small-scale gaps and detailed connections. The Grid method is limited by grid resolution, so its detail depiction ability is limited, and stepped serrations are prone to appear at footprints, as shown in part a of the Figure 8. In contrast, the method proposed in this work is superior to other methods in footprints continuity, corner accuracy, and detail restoration, and can accurately restore the geometric features of regular buildings while maintaining the stability of the overall structure.

In buildings with hollow areas and corridor structures (Region 3), RCH-SR and NB-RANSAC not only misclassify atrium or hollow areas as building entity areas, resulting in the failure to detect hollow structures (as shown in part b of the Figure 8), but also overfit the connection area between the corridor and the main building into a continuous entity, making it impossible to identify the independent contour of the corridor. Although the GAN method retains the hollow shape to a certain extent, the corridor footprints fluctuate unstably and connection nodes are blurred and adhered. OP-HT has difficulty capturing the slender straight-line features of the corridor and is prone to misclassifying them as noise. Grid confuses the corridor and hollow boundaries due to resolution limitations.

Relying on the deep line segment detection and structural chain completion strategy, the method in this work can accurately identify the corridor and clearly distinguish its footprints from that of the main building. While maintaining the integrity of the outer footprints, it accurately retains the structural features of the hollow area and the corridor (as shown in part c of the Figure 8).

In polygonal buildings with irregular shapes and hollow protrusions (Region 4), most methods have deformation or missing parts at folded-line corners and edge mutations. GAN and NB-RANSAC also cause unreal footprints bending locally or mistakenly include occluded areas into the main contour due to the occlusion of protruding parts. Although AlphaS and RCH-SR can maintain the general contour of the polygon, they are insufficient in adapting to high-frequency folded-line changes and cannot handle the sharp corners and hollow topology at the root of the protruding part. OP-HT is prone to incomplete line segment detection due to occlusion, and Grid produces stepped distortion at occluded edges. The method in this work combines direction extension and orthogonal intersection detection, which can extend along the direction of unoccluded line segments to locate occluded endpoints, eliminate noise line segments generated by occlusion, effectively repair the fracture and missing of irregular boundaries, eliminate the influence of occlusion by protruding parts, make the overall shape of the extraction result highly consistent with the ground truth, and completely retain the geometric features and detailed structures of polygonal buildings, as shown in part d of the Figure 8.

Overall, the proposed method achieved significant improvements in average Precision, Recall, F1-score, and IoU: average Precision increased by 1–2% compared with the best-performing baseline; average Recall exceeded traditional methods by 2–4%, also outperforming other mainstream approaches; the F1-score, reflecting the balance between precision and recall, improved by 1–3% over the second-best method and surpassed most baselines by more than 3%; in terms of overall contour similarity measured by IoU, the proposed method achieved notably higher values, exceeding similar methods by 3–5%. Specifically, the MLAP strengthens boundary saliency in sparse or occluded regions, thereby boosting Recall, while the structure-aware optimization effectively filters noise-induced spurious edges, leading to higher Precision. Together, these modules ensure that the final footprints remain both complete and geometrically consistent, resulting in substantial gains across all metrics.

4.5. Building Footprints Extraction Analysis

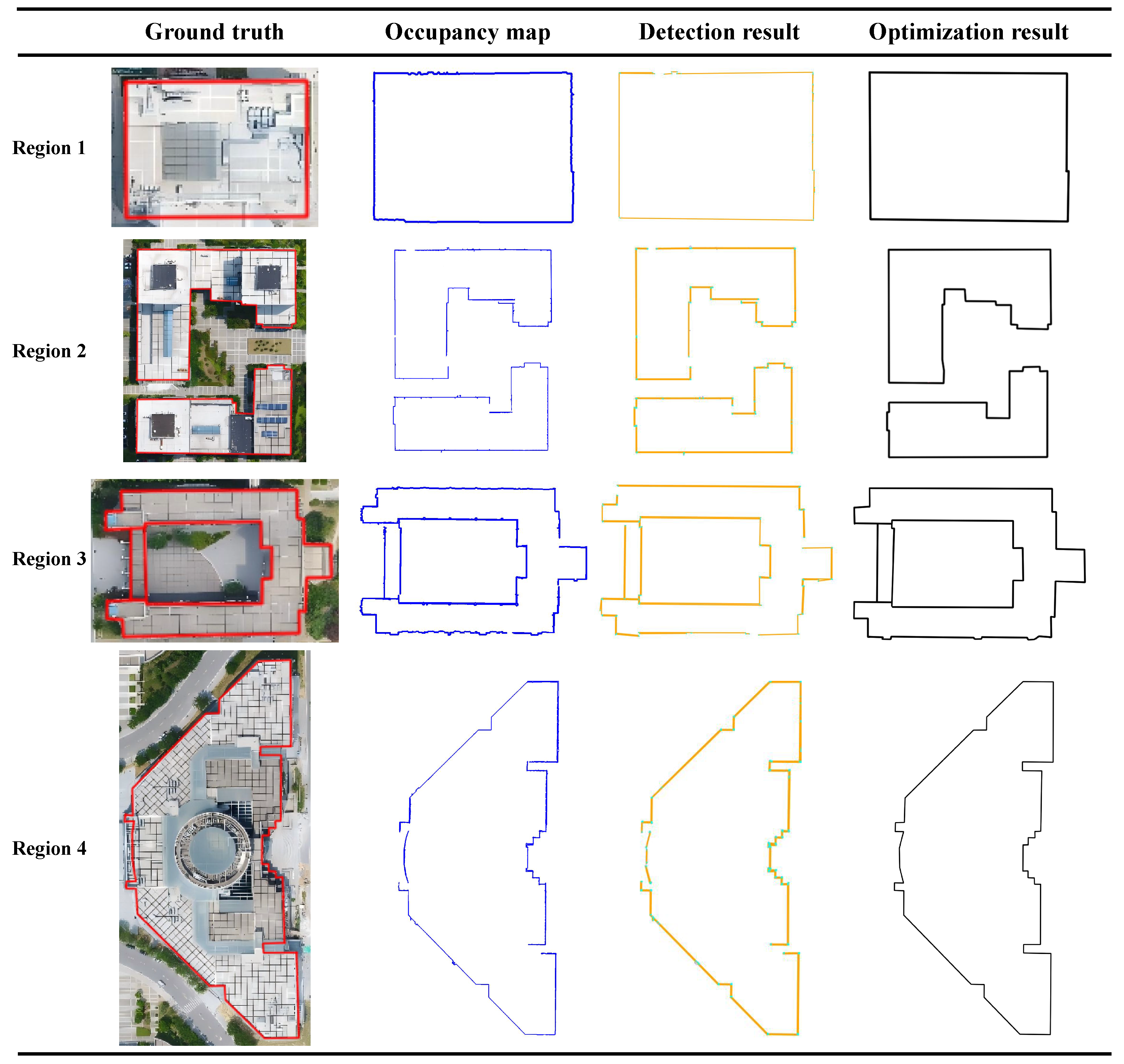
To comprehensively verify the effectiveness of the proposed method, this section presents the step-by-step result evolution at each stage and the experimental outcomes in different regions (see Figure 9). From the perspective of the processing workflow, in the point cloud occupancy map stage, the overall footprints of the building only appears as a vague density footprints. Affected by noise and point cloud sparsity, some boundaries have fractures or gaps. After line segment detection based on the learning network, the main structural lines of the building are well extracted, but incompleteness still exists at corners, small footprints, and complex geometric shapes. Subsequently, through the line segment optimization and completion process, the structural chain connection and directional extension mechanism are used to effectively repair footprints fractures and eliminate redundant line segments, making the footprints more coherent and complete. Finally, in the regularization stage, the building footprints further gain geometric consistency and stability, realizing the evolution from the initial vague footprints to a clear and complete building footprints.

In the experiments on typical regions, the proposed method shows good performance in four types of representative building scenarios. For a regular rectangular single building (Region 1), the method can fully depict the rectangular outer footprints and maintain high geometric accuracy at the corners. In the case of regular adjacent buildings (Region 2), it effectively distinguishes the shared boundaries of adjacent buildings and avoids footprints adhesion and misjudgment. For buildings with hollowed areas (Region 3), the method not only maintains the integrity of the outer footprints but also accurately retains the hollow area of the atrium, avoiding common filling errors. In the case of polygonal buildings with irregular shapes (Region 4), the method also shows stable performance at complex polylines and acute angles, and the overall shape is highly consistent with the ground truth, highlighting its robustness under complex geometric conditions.

Furthermore, to further verify the applicability of the method in large-scale scenarios, a vectorization reconstruction experiment is conducted on the data of two complete campus areas (see Figure 10 and Figure 11). The results show that the proposed method can not only maintain footprints continuity and geometric accuracy in local areas but also keep stable performance in large-scale scenarios. The building vectorization results of the two campuses show that the method still has a high degree of automation and robustness when processing hundreds of buildings, avoiding problems such as fragmentation, footprints adhesion, and unstable vectorization that are common in traditional methods during large-scale data processing.

Table 2. This table presents the statistical results of the quantitative performance indicators of the proposed method in the building footprints extraction task. Rect. (38) represents 38 regular rectangular buildings, Adj. (26) represents 26 adjacent and joined buildings, Irreg. (31) represents 31 irregular polygonal buildings, Courtyard (17) represents 17 hollowed-out/atrium buildings, and Overall (112) represents the quantitative index of the overall average.

Dataset	Precision (%)	Recall (%)	F1-Score (%)	IoU (%)
Rect. (38)	95.6	94.1	94.8	91.3
Adj. (26)	94.2	93.0	93.6	90.1
Irreg. (31)	92.3	90.1	91.2	87.0
Courtyard (17)	90.7	88.9	89.7	85.4
Overall (112)	93.7	92.5	93.1	89.6

presents the quantitative indicators of the proposed method in different building types and typical regions, including Precision, Recall, F1-score, and IoU. The results show that the proposed method performs best in regular rectangular and adjacent multi-story buildings, with F1-scores reaching 94.8% and 93.6%, respectively; in irregular polygonal buildings and buildings with hollows/atriums, despite complex factors such as sparse point clouds and occlusions, the method still achieves F1-scores of 91.2% and 89.7%, with IoU remaining above 85%. Overall, the average Precision, Recall, F1-score, and IoU of the proposed method on 112 buildings are 93.7%, 92.5%, 93.1%, and 89.6%, respectively, which fully proves the robustness and generalization ability of the method in diverse scenarios.

4.6. Ablation Study

To verify the core roles of MLAP, the deep learning network, and the structural optimization strategy in our method, we conducted experiments by removing each module: Scheme 1 (without MLAP), Scheme 2 (without deep learning network), and Scheme 3 (without optimization and regularization), and compared their performance with the complete method across four regions. The results are shown in the

Table 3. Table of performance indicators for each scheme of the ablation experiment in four regions. Scheme 1 is the experiment without the cumulative occupancy map, Scheme 2 is the experiment without the deep learning network, and Scheme 3 is the experiment without structural optimization.

Scheme	Precision (%)	Recall (%)	F1-Score (%)	IoU (%)
Ours	96.2	94.4	95.3	90.9
	95.4	93.7	94.5	89.1
	92.8	89.4	91.1	88.5
	94.1	91.2	92.6	85.9
Scheme 1	91.5	88.5	90.1	85.2
	90.2	87.3	88.6	83.4
	86.3	81.5	83.8	78.9
	88.7	84.5	86.6	79.6
Scheme 2	89.3	86.5	87.9	83.9
	88.6	85.1	86.8	82.0
	84.7	79.2	81.9	78.2
	86.5	82.3	84.3	77.5
Scheme 3	93.8	90.2	92.0	87.5
	92.5	89.8	91.1	85.8
	89.6	85.3	87.4	83.2
	91.3	87.6	89.4	82.4

, and the specific analysis is as follows:

Without MLAP, the occupancy map is directly exposed to single-point noise and locally sparse point clouds, causing the average Precision and Recall of line segment detection to decrease by 4–6%. In scenarios with hollow areas and occlusions, single-layer projection fails to distinguish stable walls from noisy points, leading to the most significant drop in Recall (7.9%) and a simultaneous 8.9% decrease in IoU. This indicates that MLAP, through pixel-level aggregation, strengthens the spatial continuity of building structures and serves as a core module for resisting noise and sparse point cloud interference. This clearly indicates that MLAP alleviates the problem of point cloud sparsity by aggregating information from multiple height layers and suppresses isolated noise responses that only appear in single slices, thereby strengthening spatial continuity and robustness of building structures.

When the deep learning feature field prediction is replaced by the traditional LSD algorithm, line segment breakage and false detections increase significantly in complex scenes, such as occluded boundaries and sharp corners. Precision decreases by 6–8% on average, Recall drops by 5–7%, and for irregular polygonal contours, the network’s precise angle field prediction constrains directional deviation, whereas LSD alone cannot adapt to high-frequency angle changes, resulting in an 8.3% decrease in F1-score. This validates that feature field prediction can compensate for the generalization shortcomings of traditional algorithms.

Without line segment optimization and regularization, the original segments are fragmented and discontinuous. In narrow gaps between adjacent buildings or occluded regions, the absence of the completion mechanism leads to a 3–5% drop in Recall and an average 3–4% reduction in F1-score; incomplete contours also cause a 3–5% decrease in IoU. This demonstrates that the structural optimization strategy, through topological constraints, repairs broken boundaries and is a key factor in ensuring contour integrity and improving modeling accuracy in complex scenarios. This demonstrates that the structural optimization strategy not only repairs fragmented boundaries caused by sparse sampling but also filters out spurious line segments generated by noise points. By enforcing topological and orthogonal constraints, the optimization module ensures contour integrity and significantly improves modeling accuracy in complex urban scenarios.

To further enhance the transparency of parameter settings and validate their empirical rationale, we additionally analyze the key hyperparameters used in MLAP and line-segment optimization.

Table 4. Parameter ablation results of the main hyperparameters in the proposed method.

Parameter	Value	Precision (%)	Recall (%)	F1-Score (%)
$\Delta z$ (m)	0.25	94.8	91.9	93.3
	0.5 (ours)	95.7	92.2	93.9
	1.0	94.2	90.1	92.1
r (m)	0.05	95.6	92.0	93.7
	0.1 (ours)	95.7	92.2	93.9
	0.2	93.8	90.5	92.1
${\theta }_t$ (°)	5	95.1	91.7	93.3
	10 (ours)	95.7	92.2	93.9
	15	94.6	90.3	92.4
$d_t$ (m)	0.2	95.3	91.1	93.1
	0.3 (ours)	95.7	92.2	93.9
	0.5	94.0	89.7	91.8

summarizes the parameter ablation experiments. The slice thickness $\Delta z$, grid resolution r, and support-layer threshold n were adjusted to evaluate their effects on detection accuracy, while the optimization thresholds (${\theta }_t$, $d_t$) control geometric regularity. The results demonstrate that $\Delta z$ = 0.5 m and r = 0.1 m achieve the best balance between structural completeness and noise suppression, and ${\theta }_t$ = 10° with $d_t$ = 0.3 m ensures orthogonal continuity without over-connection.

The parameter ablation results indicate that the proposed configuration yields stable performance under moderate variations. Most parameters are empirically determined through repeated validation experiments rather than adopted directly from prior literature, ensuring reproducibility and robustness across different building scenes.

In addition to the above accuracy analysis, we further evaluated the computational efficiency of the proposed framework to verify its practicality for large-scale backpack MLS data. Under the same hardware environment, the complete pipeline processes each building footprints within approximately 8–12 s on average, with peak memory usage below 2 GB. Compared with the traditional LSD-based baseline, our method achieves similar runtime but yields significantly more complete and regularized footprints, while being faster than the geometry-heavy RANSAC-based approach. Although the MLAP stage introduces moderate preprocessing overhead due to multi-layer accumulation, the lightweight network inference and parallel regularization ensure that the overall computational cost remains efficient.

4.7. Limitations

It should be noted that the proposed method still has certain limitations for curved or circular buildings: line segment detection tends to approximate curved boundaries as a large number of short line segments, thereby reducing the overall geometric smoothness (see Figure 12). Future research will consider introducing a hybrid modeling strategy combining straight lines and circular arcs to further improve the geometric expression capability for circular or curved buildings. In addition, the proposed method assumes that building facades are approximately vertical when generating the occupancy map. As a result, facades with significant tilts or non-vertical orientations cannot be fully represented, limiting its applicability to such structures. Future work will explore a slope-aware occupancy modeling mechanism that analyzes gradient continuity across adjacent height slices to detect inclined surfaces and adaptively adjust projection weighting, thereby extending the method’s capability to slanted facades and improving its generalization to diverse architectural forms.

5. Conclusions

We propose a method that integrates multi-layer accumulated projection occupancy maps, deep learning-based line segment detection, and feature-driven regularization. Through a three-stage process, this method achieves stable extraction of building footprints from complex backpack MLS: (1) Generating a point cloud occupancy map using MLAP to enhance the geometric expression capability of point clouds in the 2D plane; (2) Realizing line segment detection based on a learning-based network to effectively obtain high-confidence building footprints candidates; (3) Implementing a line segment optimization and regularization strategy that integrates building geometric features to ensure the continuity and integrity of footprints.

In the experimental section, the proposed method demonstrates high accuracy and robustness across typical building regions with varying scales, morphologies, and environmental conditions. Particularly for buildings with regular outer footprints, it could accurately restore footprints geometric features; for buildings with hollowed structures and complex configurations, it also maintains local details well. Compared with multiple comparative methods, the proposed method achieves advantages in metrics including Precision, Recall, F1-score, and IoU, verifying its effectiveness in mobile-mapped point cloud scenarios. While the proposed method demonstrates strong robustness, it is still limited in handling buildings with tilted or curved facades. Future work will focus on adaptive slicing and hybrid line-arc modeling to better represent such complex geometries and enhance footprints continuity.

In summary, through MLAP, deep line detection, and structural regularization, the method effectively alleviates the negative impact of point cloud sparsity and random noise, ensuring that the extracted footprints remain continuous, geometrically consistent, and robust in complex urban scenarios. In practical terms, the extracted building footprints can serve as precise and lightweight geometric primitives for various downstream applications, such as cadastral mapping, large-scale urban reconstruction, and city-scale visualization for planning and management. By automatically generating consistent and topologically complete footprints from backpack LiDAR data, the proposed method substantially reduces the dependence on manual vectorization, which is often time-consuming and labor-intensive in traditional workflows. This capability enables more efficient urban modeling pipelines, accelerates 3D reconstruction and semantic mapping processes, and provides a reliable foundation for digital twin construction and dynamic city monitoring.