Near-Real-Time Turbidity Monitoring at Global Scale Using Sentinel-2 Data and Machine Learning Techniques
Highlights
- We have developed a machine-learning algorithm able to quantify high-turbid environments.
- We use open-source and free databases to train the model and open-source and free tools to develop it, which makes it easily replicable and transferable.
- The social impact of our work implies improved monitoring of areas with high turbidity, which can lead to a better understanding and use of forecasting.
- Ocean color and water quality communities can take advantage of the lessons learned for developing new products or services.
Abstract
1. Introduction
2. Materials and Methods
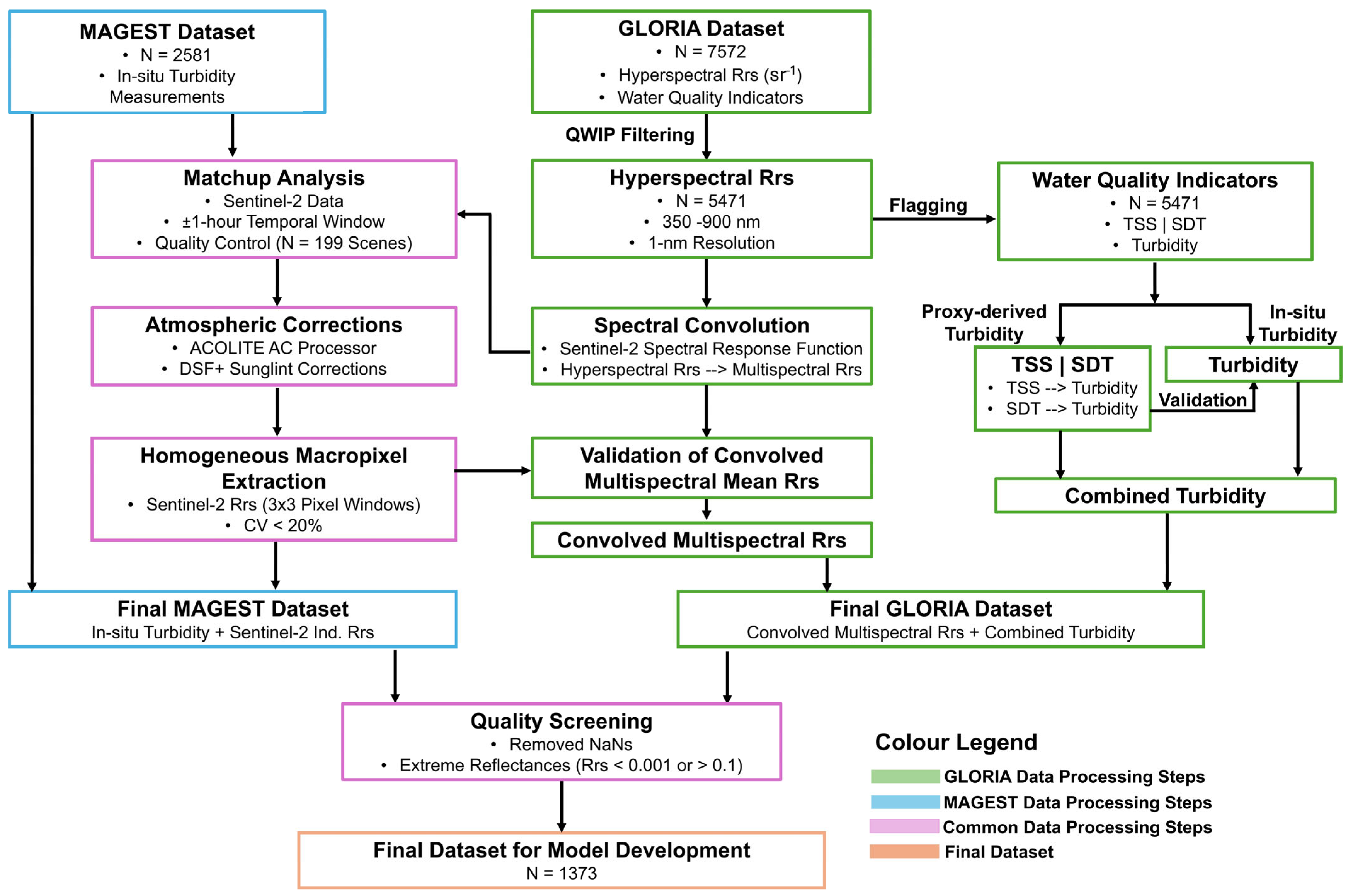
2.1. Dataset Integration and Quality Control
2.2. Hyperspectral to Multispectral Conversion
2.3. Satellite Data Processing
2.4. Machine Learning Framework
2.4.1. Algorithm Selection and Configuration
2.4.2. Model Evaluation and Interpretability
2.4.3. Uncertainty Quantification
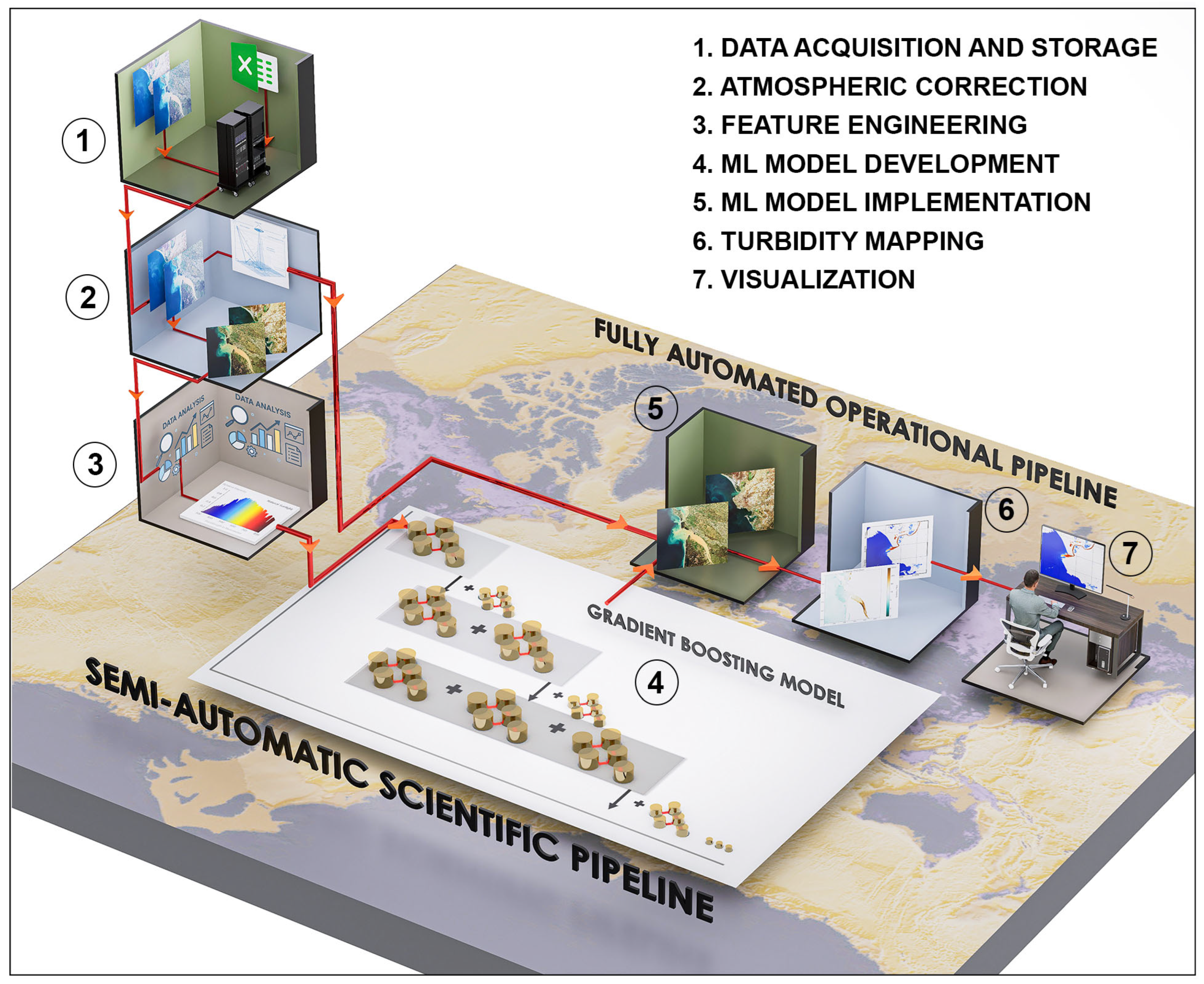
2.5. Automated Processing Pipelines
3. Results
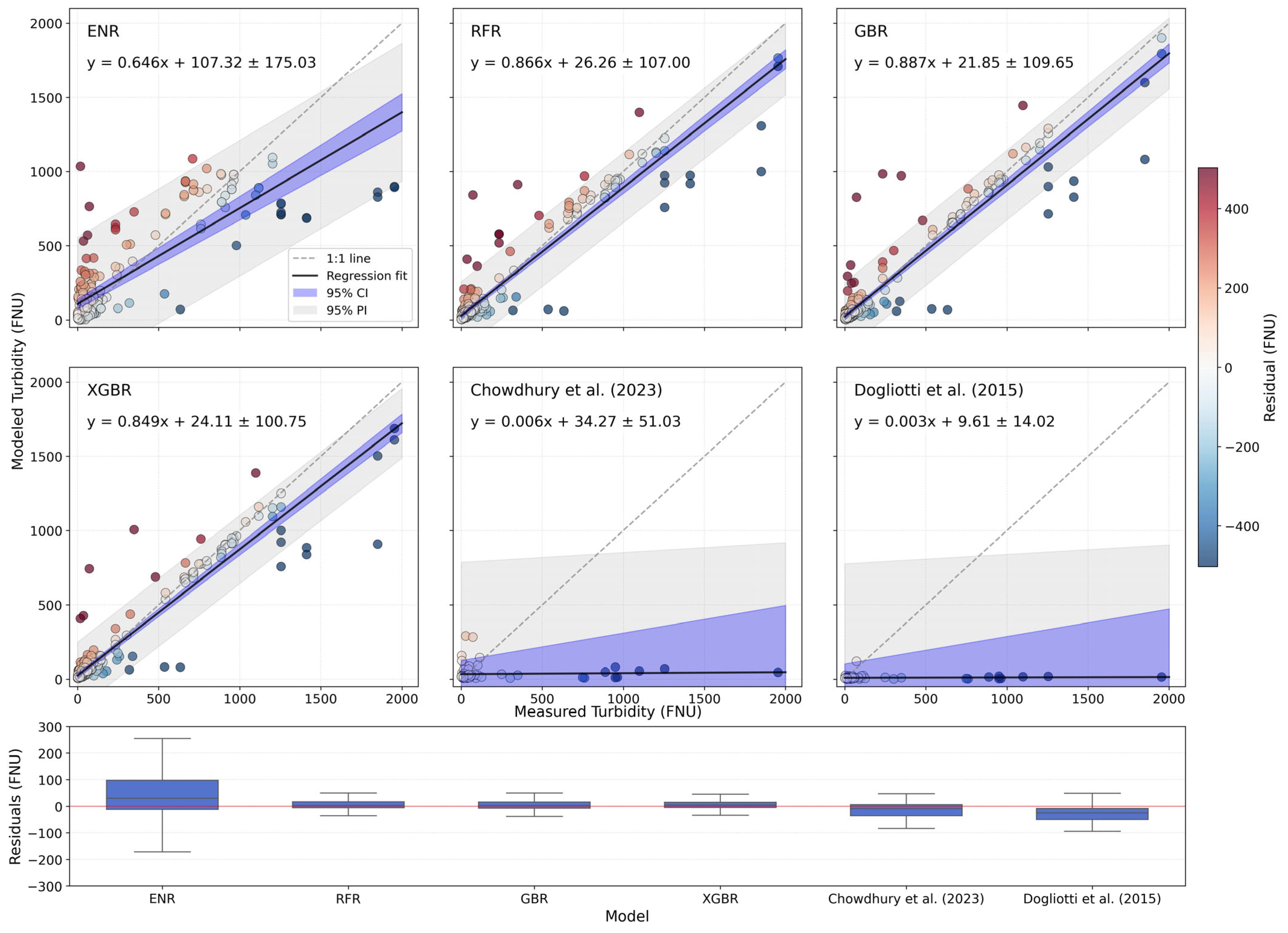
3.1. Model’s Performance Evaluation
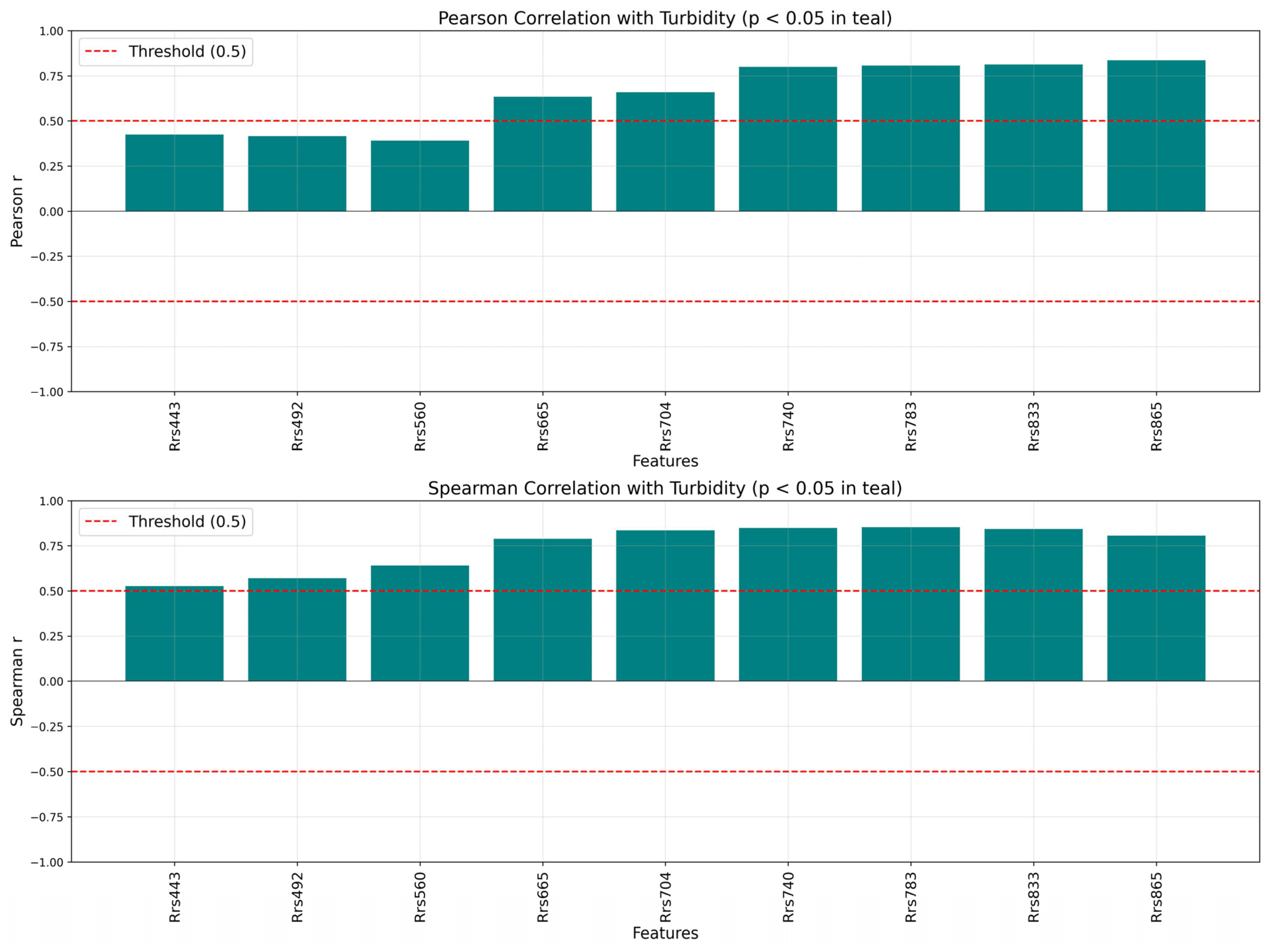
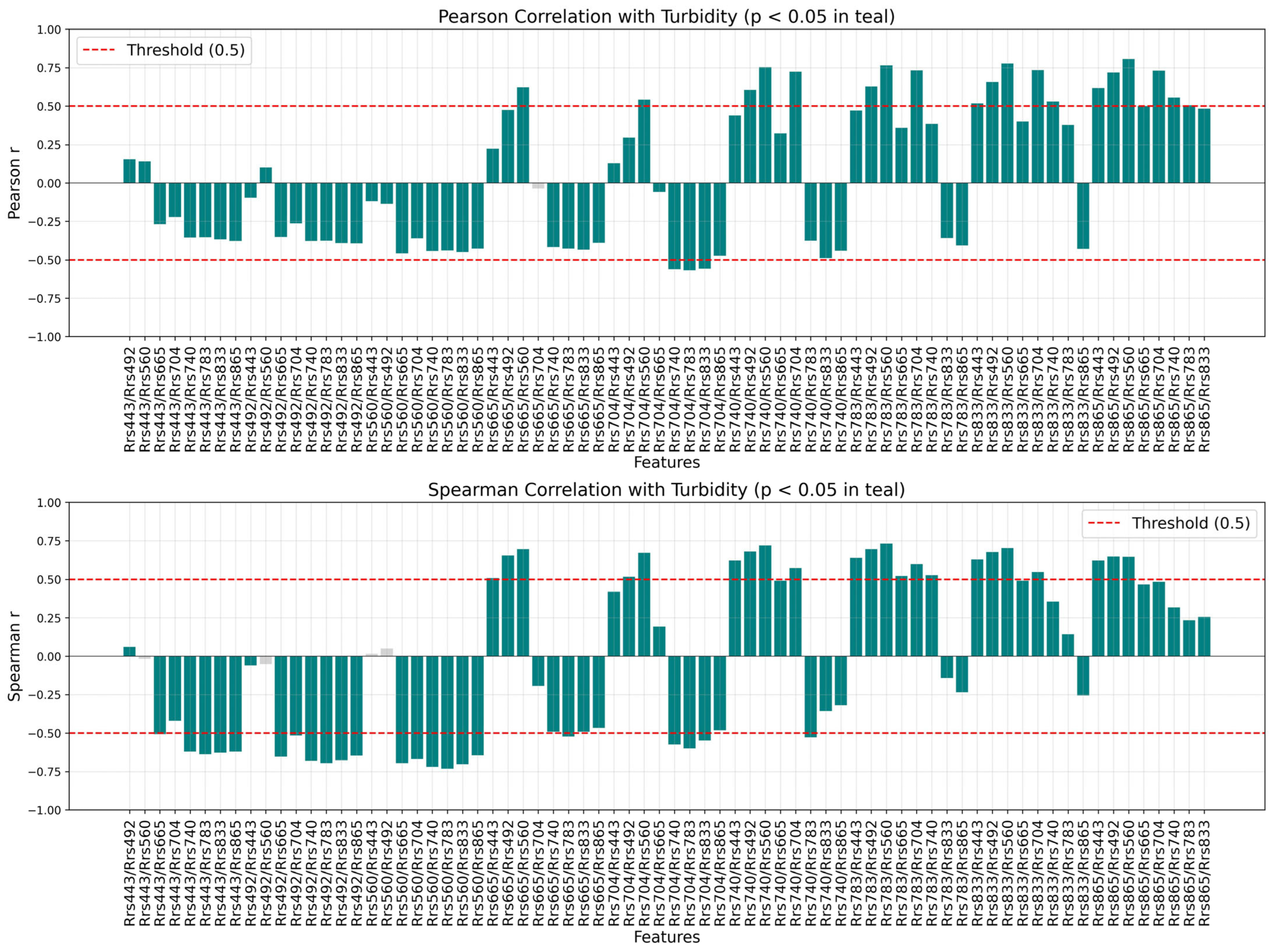
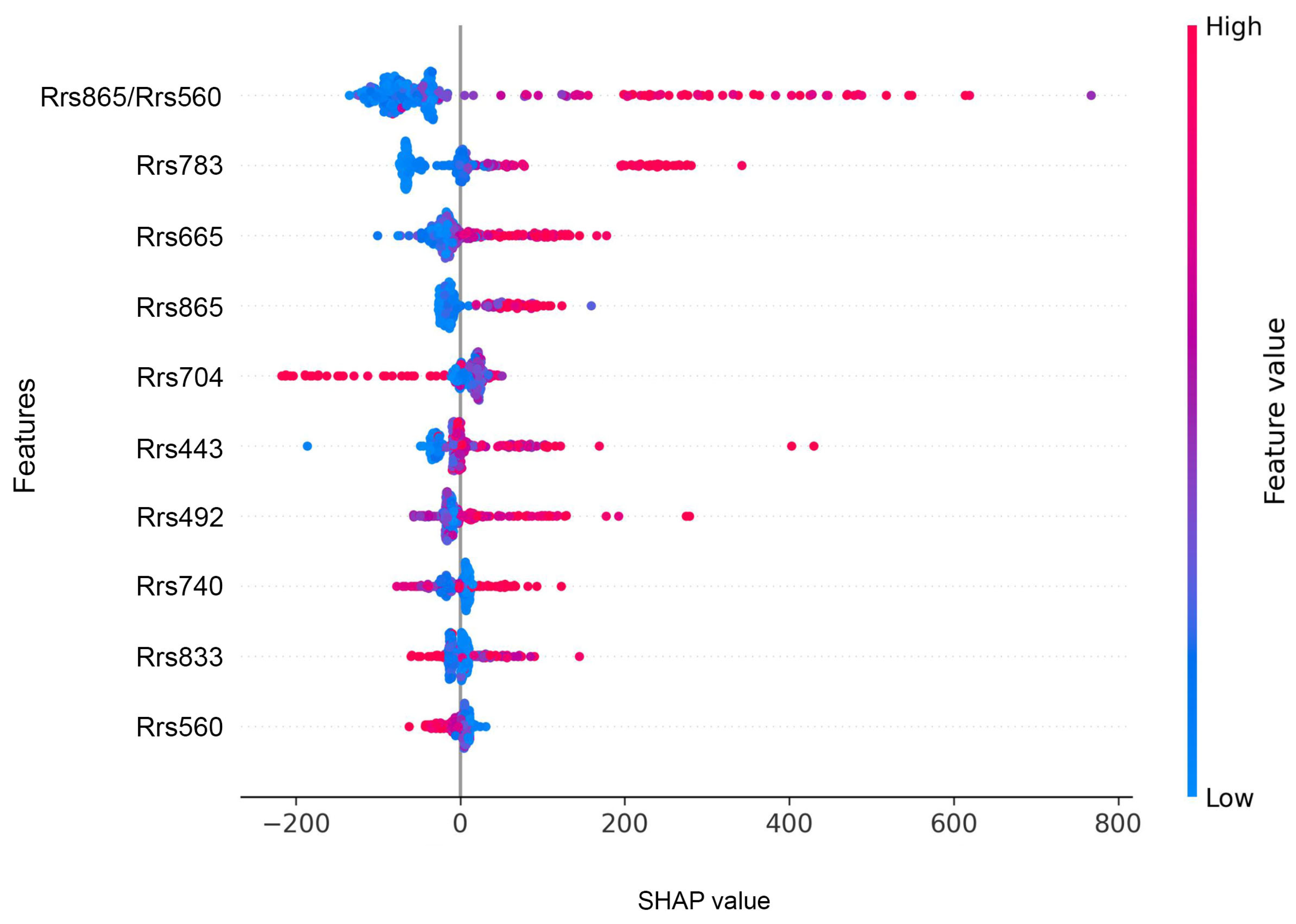
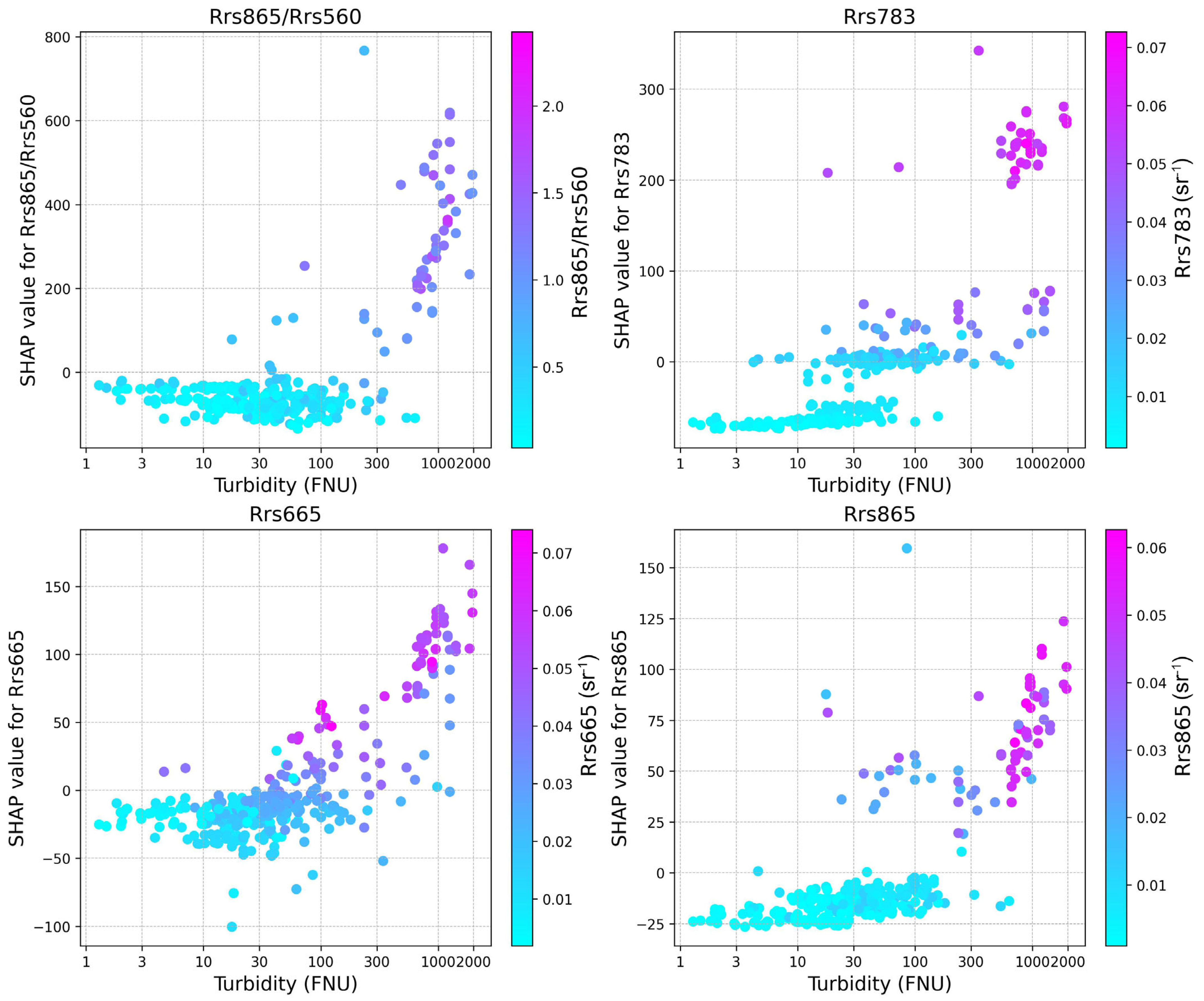
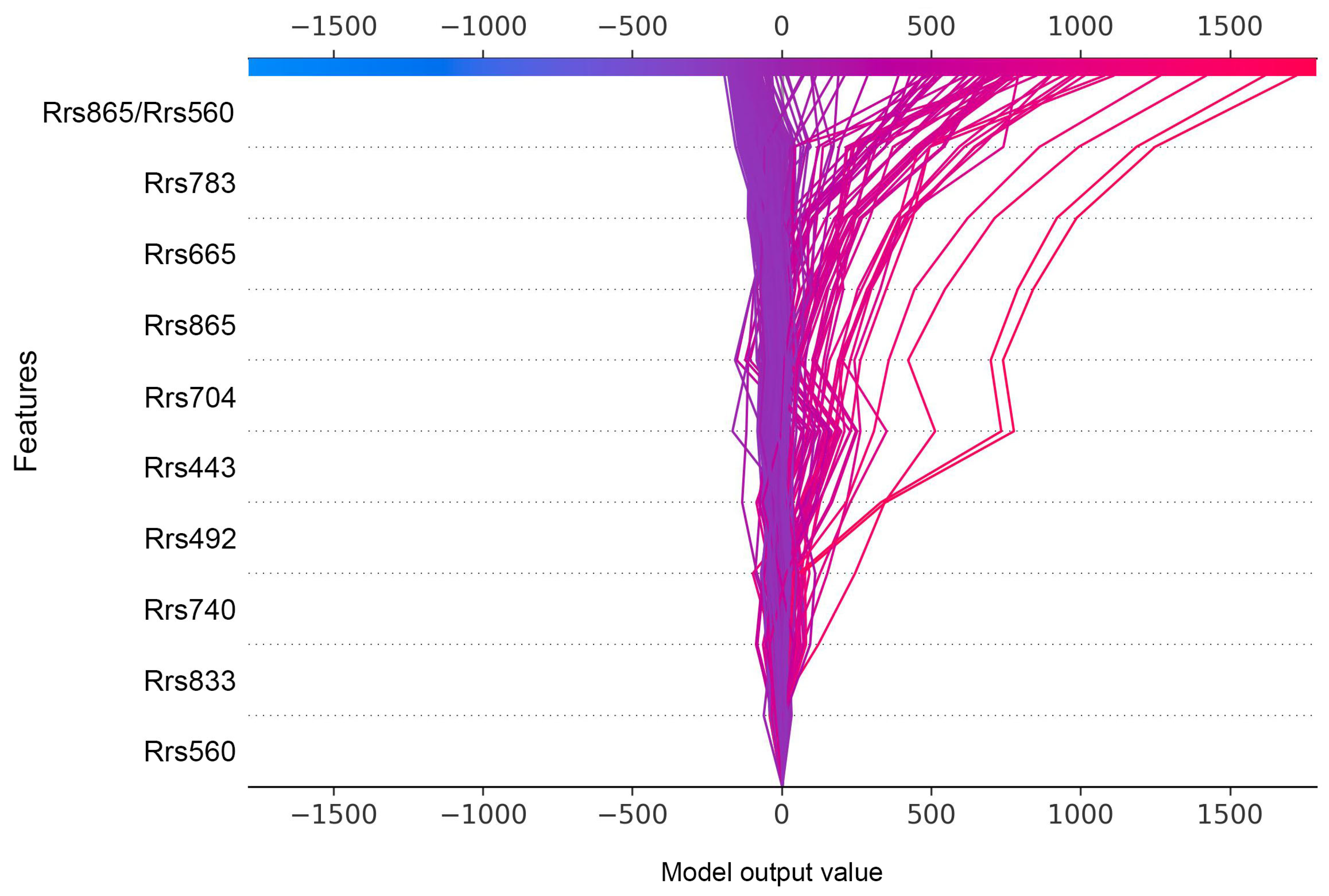
3.2. Model Interpretation
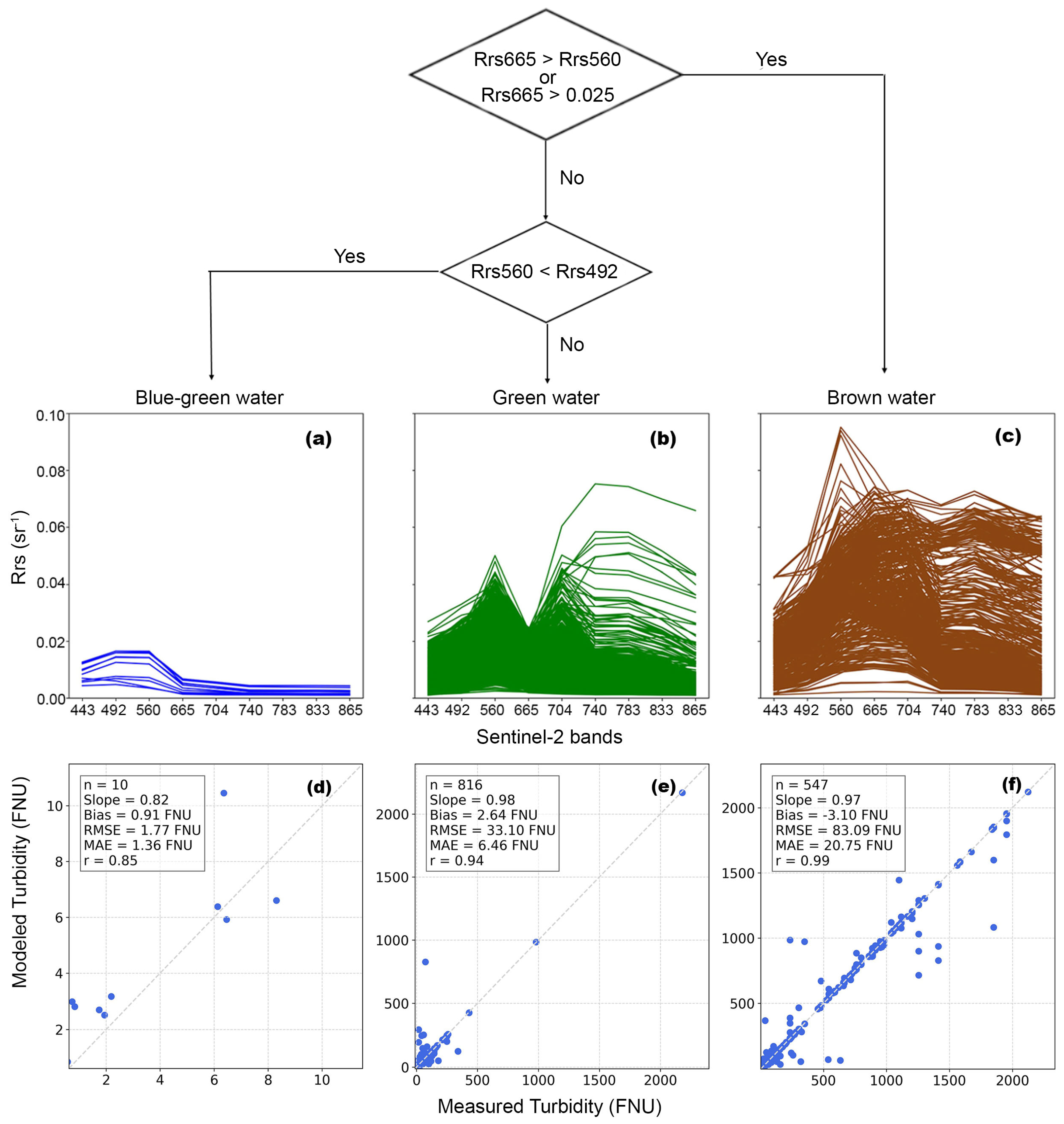
3.3. Model Performance Across Optical Water Types
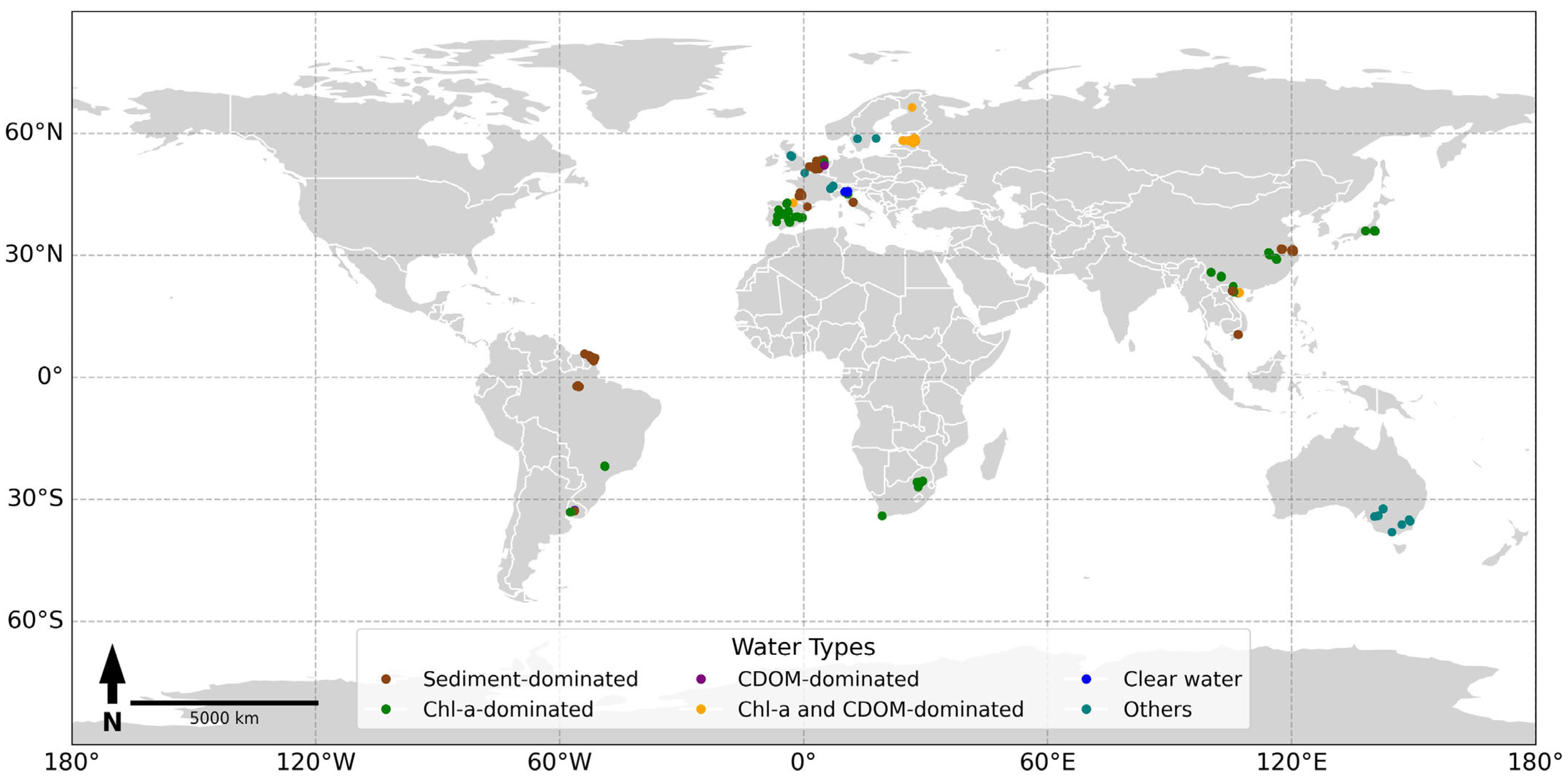
3.4. Model Application Across Diverse Geographic Settings
3.5. Model Validation in an Independent Site
3.6. Performance of Automated Pipelines
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SeaWiFS | Sea-Viewing Wide Field-of-view Sensor |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| MERIS | Medium Resolution Imaging Spectrometer |
| MSI | MultiSpectral Instrument |
| ML | Machine-learning |
| FNU | Formazin Nephelometric Units |
| GLORIA | GLObal Reflectance community dataset for Imaging and optical sensing of Aquatic environments |
| MAGEST | Monitoring the water quality of the Gironde Estuary |
| SHAP | SHapley Additive exPlanations |
| AI | Artificial Intelligence |
| Chl-a | Chlorophyll-a |
| Rrs | Remote Sensing Reflectance |
| TSS | Total Suspended Solids |
| SDT | Secchi-depth Transparency |
| QWIP | Quality Water Index Polynomial |
| RMSE | Root Mean Squared Error |
| MAE | Mean Absolute Error |
| r | Correlation Coefficient |
| SRF | Spectral Response Function |
| API | Application Programming Interface |
| DSF | Dark Spectrum Fitting |
| CV | Coefficient of Variation |
| CDOM | Colored Dissolved Organic Matter |
| ENR | Elastic Net |
| RFR | Random Forest |
| GBR | Gradient Boosting |
| XGBR | Extreme Gradient Boosting |
| VNIR | Visible and Near-Infrared |
| CI | Confidence Intervals |
| PI | Prediction Intervals |
| SEP | Scientific Exploitation Platform |
| SIMBAD | Sentinel Imagery Multiband Analysis and Dissemination |
Appendix A
| Country | Site Name | Water Body Type | Water Type | No. of Samples | Turbidity Range (FNU) |
|---|---|---|---|---|---|
| Australia | |||||
| Australia | Burrinjuck Dam | Lake | Others | 1 | 11.49–11.49 |
| Australia | Lake Burley Griffin | Lake | Others | 2 | 10.23–13.67 |
| Australia | Lake Hume | Lake | Others | 1 | 21.92–21.92 |
| Australia | Lake Pamamaroo | Lake | Others | 7 | 102.56–151.02 |
| Australia | Lake Victoria | Lake | Others | 2 | 17.49–22.85 |
| Australia | Wachtels Lagoon | Lake | Others | 3 | 32.40–36.76 |
| Australia | Western Treatment Plant | Others | Others | 1 | 51.52–51.52 |
| Belgium | |||||
| Belgium | English Channel | Coastal ocean | Sediment-dominated | 12 | 4.58–46.74 |
| Brazil | |||||
| Brazil | Curuai Lake | Lake | Sediment-dominated | 14 | 3.92–37.90 |
| Brazil | Ibitinga Reservoir | Lake | Chl-a-dominated | 15 | 3.23–50.60 |
| China | |||||
| China | Chaohu | Lake | Sediment-dominated | 40 | 12.52–339.40 |
| China | Dianchi | Lake | Chl-a-dominated | 63 | 19.84–158.76 |
| China | Erhai | Lake | Chl-a-dominated | 3 | 6.00–8.30 |
| China | Hou Lake | Lake | Chl-a-dominated | 22 | 18.40–102.50 |
| China | Liangzi Lake | Lake | Chl-a-dominated | 33 | 9.14–108.00 |
| China | Poyang Lake | Lake | Chl-a-dominated | 12 | 7.18–30.60 |
| China | Taihu | Lake | Sediment-dominated | 165 | 1.89–212.09 |
| China | Wuhan East Lake | Lake | Chl-a-dominated | 20 | 3.13–37.55 |
| Estonia | |||||
| Estonia | Lake Holstre | Lake | Chl-a and CDOM-dominated | 1 | 9.73–9.73 |
| Estonia | Lake Kaiavere | Lake | Chl-a and CDOM-dominated | 1 | 9.66–9.66 |
| Estonia | Lake Kooraste Linajarv | Lake | Chl-a and CDOM-dominated | 1 | 16.65–16.65 |
| Estonia | Lake Nohipalu Valgjarv | Lake | Chl-a and CDOM-dominated | 1 | 2.20–2.20 |
| Estonia | Lake Pangodi | Lake | Chl-a and CDOM-dominated | 1 | 4.07–4.07 |
| Estonia | Lake Peipsi | Lake | Chl-a and CDOM-dominated | 21 | 1.13–22.85 |
| Estonia | Lake Rouge Suurjarv | Lake | Chl-a and CDOM-dominated | 2 | 2.57–3.92 |
| Estonia | Lake Vortsjarv | Lake | Chl-a and CDOM-dominated | 7 | 11.09–17.69 |
| Estonia | Parnu Bay | Estuary | Chl-a and CDOM-dominated | 4 | 12.87–17.34 |
| Finland | |||||
| Finland | Lake Vanttausjarvi | Lake | Chl-a and CDOM-dominated | 1 | 2.37–2.37 |
| France | |||||
| France | Arcachon Bay | Coastal ocean | Sediment-dominated | 17 | 1.64–1562.04 |
| France | Arcachon Bay | Coastal ocean | Others | 1 | 1.42–1.42 |
| France | English Channel | Coastal ocean | Others | 1 | 0.84–0.84 |
| France | Gironde River | Estuary | Sediment-dominated | 31 | 7.48–2124.59 |
| France | Gironde River | River | Sediment-dominated | 296 | 21.70–1953.84 |
| France | Guiana | Coastal ocean | Sediment-dominated | 126 | 2.70–1673.86 |
| France | Guiana | Coastal ocean | Others | 2 | 30.12–32.21 |
| France | Guiana | Coastal ocean | Others | 2 | 32.31–69.19 |
| France | Guiana | Coastal ocean | Chl-a-dominated | 7 | 10.28–258.20 |
| Italy | |||||
| Italy | Garda | Lake | Clear water | 2 | 0.57–5.00 |
| Italy | Iseo | Lake | Clear water | 4 | 2.04–3.49 |
| Italy | Mantova | Lake | Chl-a-dominated | 15 | 4.97–15.11 |
| Italy | Trasimeno | Lake | Sediment-dominated | 7 | 3.92–24.57 |
| Japan | |||||
| Japan | Lake Kasumigaura | Lake | Chl-a-dominated | 84 | 8.87–42.67 |
| Japan | Shirakaba | Lake | Chl-a-dominated | 1 | 8.28–8.28 |
| Japan | Suwa | Lake | Chl-a-dominated | 3 | 7.56–8.75 |
| Netherlands | |||||
| Netherlands (the) | English Channel | Coastal ocean | Sediment-dominated | 12 | 1.92–58.40 |
| Netherlands (the) | Ijsselmeer De Oude Zeug | Lake | Chl-a-dominated | 1 | 21.07–21.07 |
| Netherlands (the) | Loosdtrechtse plassen nr5 | Lake | CDOM-dominated | 1 | 14.68–14.68 |
| Netherlands (the) | North Sea | Coastal ocean | Sediment-dominated | 24 | 1.45–21.09 |
| South Africa | |||||
| South Africa | Bronkhorstspruit | Lake | Chl-a-dominated | 4 | 7.02–11.66 |
| South Africa | Hartbeespoort | Lake | Chl-a-dominated | 11 | 4.78–2179.62 |
| South Africa | Loskop | Lake | Chl-a-dominated | 8 | 15.02–23.62 |
| South Africa | Roodeplaat | Lake | Chl-a-dominated | 9 | 3.92–50.80 |
| South Africa | Theewaterskloof | Lake | Chl-a-dominated | 10 | 8.90–25.53 |
| South Africa | Vaal | Lake | Chl-a-dominated | 5 | 4.61–72.74 |
| Spain | |||||
| Spain | Aguilar | Lake | Chl-a-dominated | 1 | 8.54–8.54 |
| Spain | Alarcón | Lake | Chl-a-dominated | 1 | 5.57–5.57 |
| Spain | Albufera | Lake | Chl-a-dominated | 19 | 26.91–93.45 |
| Spain | Alcántara | Lake | Chl-a-dominated | 6 | 4.22–18.06 |
| Spain | Almendra | Lake | Chl-a-dominated | 1 | 4.80–4.80 |
| Spain | Brovales | Lake | Chl-a-dominated | 1 | 14.37–14.37 |
| Spain | Contreras | Lake | Chl-a-dominated | 1 | 3.88–3.88 |
| Spain | Cortes | Lake | Chl-a-dominated | 1 | 2.19–2.19 |
| Spain | Ebro | Lake | Chl-a-dominated | 3 | 4.94–17.46 |
| Spain | Giribaile | Lake | Chl-a-dominated | 1 | 3.86–3.86 |
| Spain | Guadalén | Lake | Chl-a-dominated | 1 | 8.71–8.71 |
| Spain | Navalcán | Lake | Chl-a-dominated | 3 | 12.54–18.17 |
| Spain | Pinilla | Lake | Chl-a-dominated | 3 | 4.44–8.15 |
| Spain | Rosarito | Lake | Chl-a-dominated | 30 | 1.82–25.39 |
| Spain | Santa Teresa | Lake | Chl-a-dominated | 1 | 3.85–3.85 |
| Spain | Santillana | Lake | Chl-a-dominated | 1 | 8.98–8.98 |
| Spain | Terradets | Lake | Sediment-dominated | 2 | 10.47–29.56 |
| Spain | Ullívarri | Lake | Chl-a and CDOM-dominated | 1 | 1.90–1.90 |
| Spain | Valuengo | Lake | Chl-a-dominated | 2 | 12.37–20.70 |
| Spain | Vega de Jabalón | Lake | Chl-a-dominated | 1 | 13.92–13.92 |
| Sweden | |||||
| Sweden | Baltic Sea | Coastal ocean | Others | 1 | 1.06–1.06 |
| Sweden | Lake Vänern | Lake | Others | 2 | 1.25–1.29 |
| Sweden | Lake Vanern | Lake | Chl-a-dominated | 1 | 2.31–2.31 |
| Switzerland | |||||
| Switzerland | Lake Biel | Lake | Others | 3 | 2.19–2.95 |
| Switzerland | Lake Geneva | Lake | Others | 3 | 0.74–2.89 |
| United Kingdom | |||||
| United Kingdom of Great Britain and Northern Ireland (the) | Bassenthwaite Lake | Lake | Others | 1 | 1.49–1.49 |
| United Kingdom of Great Britain and Northern Ireland (the) | English Channel | Coastal ocean | Sediment-dominated | 9 | 1.74–102.27 |
| United Kingdom of Great Britain and Northern Ireland (the) | Windermere | Lake | Others | 2 | 1.98–5.51 |
| Uruguay | |||||
| Uruguay | Embalse de Paso del Palmar | Lake | Chl-a-dominated | 24 | 12.70–100.00 |
| Uruguay | Embalse de Paso del Palmar | Lake | Sediment-dominated | 9 | 12.20–19.00 |
| Uruguay | Lago Rincon del Bonete | Lake | Sediment-dominated | 10 | 1.90–15.00 |
| Uruguay | Lago Rincon del Bonete | Lake | Clear water | 1 | 14.20–14.20 |
| Viet Nam | |||||
| Viet Nam | Ba Be Lake | Lake | Chl-a-dominated | 2 | 13.38–15.19 |
| Viet Nam | Gulf of Tonkin | Coastal ocean | Sediment-dominated | 23 | 21.71–127.52 |
| Viet Nam | Ha Long Bay, Quang Ninh Province | Coastal ocean | Chl-a and CDOM-dominated | 7 | 12.01–14.29 |
| Viet Nam | Red River | River | Sediment-dominated | 34 | 36.95–115.40 |
| Viet Nam | Soai Rap River | Coastal ocean | Sediment-dominated | 6 | 35.97–207.05 |
| Viet Nam | West Lake, Hanoi | Lake | Chl-a-dominated | 15 | 20.95–70.37 |
References
- Cloern, J.E. Turbidity as a Control on Phytoplankton Biomass and Productivity in Estuaries. Cont. Shelf Res. 1987, 7, 1367–1381. [Google Scholar] [CrossRef]
- Doan, P.T.K.; Némery, J.; Schmid, M.; Gratiot, N. Eutrophication of Turbid Tropical Reservoirs: Scenarios of Evolution of the Reservoir of Cointzio, Mexico. Ecol. Inform. 2015, 29, 192–205. [Google Scholar] [CrossRef]
- Neukermans, G.; Ruddick, K.G.; Greenwood, N. Diurnal Variability of Turbidity and Light Attenuation in the Southern North Sea from the SEVIRI Geostationary Sensor. Remote Sens. Environ. 2012, 124, 564–580. [Google Scholar] [CrossRef]
- Potes, M.; Costa, M.J.; Salgado, R. Satellite Remote Sensing of Water Turbidity in Alqueva Reservoir and Implications on Lake Modelling. Hydrol. Earth Syst. Sci. Discuss. 2012, 16, 1623–1633. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, H.; Lin, J.; Zhu, J.; Zhang, W.; Li, C. Phytoplankton Blooms off a High Turbidity Estuary: A Case Study in the Changjiang River Estuary. J. Geophys. Res. Ocean. 2019, 124, 8036–8059. [Google Scholar] [CrossRef]
- Lee, H.W.; Kim, E.J.; Park, S.S.; Choi, J.H. Effects of Climate Change on the Movement of Turbidity Flow in a Stratified Reservoir. Water Resour Manag. 2015, 29, 4095–4110. [Google Scholar] [CrossRef]
- Mi, H.; Fagherazzi, S.; Qiao, G.; Hong, Y.; Fichot, C.G. Climate Change Leads to a Doubling of Turbidity in a Rapidly Expanding Tibetan Lake. Sci. Total Environ. 2019, 688, 952–959. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency. Climate Adaptation and Erosion & Sedimentation. Available online: https://www.epa.gov/arc-x/climate-adaptation-and-erosion-sedimentation (accessed on 2 May 2025).
- Vergara, I.; Garreaud, R.; Ayala, Á. Sharp Increase of Extreme Turbidity Events Due to Deglaciation in the Subtropical Andes. J. Geophys. Res. Earth Surf. 2022, 127, e2021JF006584. [Google Scholar] [CrossRef]
- León-Muñoz, J.; Aguayo, R.; Corredor-Acosta, A.; Tapia, F.J.; Iriarte, J.L.; Reid, B.; Soto, D. Hydrographic Shifts in Coastal Waters Reflect Climate-Driven Changes in Hydrological Regimes across Northwestern Patagonia. Sci. Rep. 2024, 14, 20632. [Google Scholar] [CrossRef]
- Hou, X.; Feng, L.; Duan, H.; Chen, X.; Sun, D.; Shi, K. Fifteen-Year Monitoring of the Turbidity Dynamics in Large Lakes and Reservoirs in the Middle and Lower Basin of the Yangtze River, China. Remote Sens. Environ. 2017, 190, 107–121. [Google Scholar] [CrossRef]
- Nechad, B.; Ruddick, K.G.; Park, Y. Calibration and Validation of a Generic Multisensor Algorithm for Mapping of Total Suspended Matter in Turbid Waters. Remote Sens. Environ. 2010, 114, 854–866. [Google Scholar] [CrossRef]
- Dogliotti, A.I.; Ruddick, K.G.; Nechad, B.; Doxaran, D.; Knaeps, E. A Single Algorithm to Retrieve Turbidity from Remotely-Sensed Data in All Coastal and Estuarine Waters. Remote Sens. Environ. 2015, 156, 157–168. [Google Scholar] [CrossRef]
- van der Woerd, H.; Pasterkamp, R. Mapping of the North Sea Turbid Coastal Waters Using SeaWiFS Data. Can. J. Remote Sens. 2004, 30, 44–53. [Google Scholar] [CrossRef]
- Magrì, S.; Ottaviani, E.; Prampolini, E.; Besio, G.; Fabiano, B.; Federici, B. Application of Machine Learning Techniques to Derive Sea Water Turbidity from Sentinel-2 Imagery. Remote Sens. Appl. Soc. Environ. 2023, 30, 100951. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, C.; Tian, B.; Wu, W.; Zhou, Y. Mapping Intertidal Topographic Changes in a Highly Turbid Estuary Using Dense Sentinel-2 Time Series with Deep Learning. ISPRS J. Photogramm. Remote Sens. 2023, 205, 1–16. [Google Scholar] [CrossRef]
- Chowdhury, M.; Vilas, C.; VanBergeijk, S.; Navarro, G.; Laiz, I.; Caballero, I. Monitoring Turbidity in a Highly Variable Estuary Using Sentinel 2-A/B for Ecosystem Management Applications. Front. Mar. Sci. 2023, 10, 1186441. [Google Scholar] [CrossRef]
- Jiang, D.; Matsushita, B.; Pahlevan, N.; Gurlin, D.; Fichot, C.G.; Harringmeyer, J.; Sent, G.; Brito, A.C.; Brotas, V.; Werther, M.; et al. Estimating the Concentration of Total Suspended Solids in Inland and Coastal Waters from Sentinel-2 MSI: A Semi-Analytical Approach. ISPRS J. Photogramm. Remote Sens. 2023, 204, 362–377. [Google Scholar] [CrossRef]
- Sebastiá-Frasquet, M.-T.; Aguilar-Maldonado, J.A.; Santamaría-Del-Ángel, E.; Estornell, J. Sentinel 2 Analysis of Turbidity Patterns in a Coastal Lagoon. Remote Sens. 2019, 11, 2926. [Google Scholar] [CrossRef]
- Zeng, F.; Song, C.; Cao, Z.; Xue, K.; Lu, S.; Chen, T.; Liu, K. Monitoring Inland Water via Sentinel Satellite Constellation: A Review and Perspective. ISPRS J. Photogramm. Remote Sens. 2023, 204, 340–361. [Google Scholar] [CrossRef]
- Luo, Y.; Doxaran, D.; Vanhellemont, Q. Retrieval and Validation of Water Turbidity at Metre-Scale Using Pléiades Satellite Data: A Case Study in the Gironde Estuary. Remote Sens. 2020, 12, 946. [Google Scholar] [CrossRef]
- Bid, S.; Siddique, G. Identification of Seasonal Variation of Water Turbidity Using NDTI Method in Panchet Hill Dam, India. Model. Earth Syst. Environ. 2019, 5, 1179–1200. [Google Scholar] [CrossRef]
- Yang, Z.; Gong, C.; Lu, Z.; Wu, E.; Huai, H.; Hu, Y.; Li, L.; Dong, L. Combined Retrievals of Turbidity from Sentinel-2A/B and Landsat-8/9 in the Taihu Lake through Machine Learning. Remote Sens. 2023, 15, 4333. [Google Scholar] [CrossRef]
- Bustamante, J.; Pacios, F.; Díaz-Delgado, R.; Aragonés, D. Predictive Models of Turbidity and Water Depth in the Doñana Marshes Using Landsat TM and ETM+ Images. J. Environ. Manag. 2009, 90, 2219–2225. [Google Scholar] [CrossRef] [PubMed]
- CMEMS. CMEMS Copernicus Marine Service to Deliver High-Resolution Ocean Colour Products Using Sentinel-2. Available online: https://marine.copernicus.eu/news/copernicus-marine-service-deliver-high-resolution-ocean-colour-products-using-sentinel-2 (accessed on 27 June 2025).
- Cao, Z.; Ma, R.; Duan, H.; Pahlevan, N.; Melack, J.; Shen, M.; Xue, K. A Machine Learning Approach to Estimate Chlorophyll-a from Landsat-8 Measurements in Inland Lakes. Remote Sens. Environ. 2020, 248, 111974. [Google Scholar] [CrossRef]
- Ruescas, A.B.; Hieronymi, M.; Mateo-Garcia, G.; Koponen, S.; Kallio, K.; Camps-Valls, G. Machine Learning Regression Approaches for Colored Dissolved Organic Matter (CDOM) Retrieval with S2-MSI and S3-OLCI Simulated Data. Remote Sens. 2018, 10, 786. [Google Scholar] [CrossRef]
- Lehmann, M.K.; Gurlin, D.; Pahlevan, N.; Alikas, K.; Anstee, J.M.; Balasubramanian, S.V.; Barbosa, C.C.F.; Binding, C.; Bracher, A.; Bresciani, M.; et al. GLORIA—A Global Dataset of Remote Sensing Reflectance and Water Quality from Inland and Coastal Waters [dataset]. PANGAEA 2022. [Google Scholar] [CrossRef]
- MAGEST. MAGEST Network. Available online: https://magest.oasu.u-bordeaux.fr/index.php (accessed on 19 August 2024).
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.-I. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Vandermeulen, R.A.; Barnes, B.B.; Castagna, A.; Knaeps, E.; Vanhellemont, Q. QWIP: A Quantitative Metric for Quality Control of Aquatic Reflectance Spectral Shape Using the Apparent Visible Wavelength. Front. Remote Sens. 2022, 3, 869611. [Google Scholar] [CrossRef]
- Hern, T.; Lai, S.; Ibrahim, S.; Nik Sulaiman, N.M.; Sharifi, M.; Abe, S. Impact of Fine Sediment on TSS and Turbidity in Retention Structure. J. Geosci. Environ. Prot. 2014, 2, 1–8. [Google Scholar] [CrossRef]
- Baughman, C.; Jones, B.; Bartz, K.; Young, D.; Zimmerman, C. Reconstructing Turbidity in a Glacially Influenced Lake Using the Landsat TM and ETM+ Surface Reflectance Climate Data Record Archive, Lake Clark, Alaska. Remote Sens. 2015, 7, 13692–13710. [Google Scholar] [CrossRef]
- ESA. Sentinel-2 Spectral Response Functions (S2-SRF). Available online: https://sentinels.copernicus.eu/-/copernicus-sentinel-2c-spectral-response-functions (accessed on 18 March 2024).
- Vanhellemont, Q. Adaptation of the Dark Spectrum Fitting Atmospheric Correction for Aquatic Applications of the Landsat and Sentinel-2 Archives. Remote Sens. Environ. 2019, 225, 175–192. [Google Scholar] [CrossRef]
- EUMETSAT. Algorithm Theoretical Baseline Document for Matchup Generation; EUMETSAT: Darmstadt, Germany, 2021. [Google Scholar]
- Zou, H.; Hastie, T. Regularization and Variable Selection Via the Elastic Net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Qiu, J. An Analysis of Model Evaluation with Cross-Validation: Techniques, Applications, and Recent Advances. Adv. Econ. Manag. Political Sci. 2024, 99, 69–72. [Google Scholar] [CrossRef]
- Chowdhury, M. Mapping and Monitoring Valencia Flood 2024 Using Sentinel-2 MSI Data and Machine-Learning-Based Turbidity Models. In Proceedings of the ESA Living Planet Symosium 2025, Vienna, Austria, 23–27 June 2025. [Google Scholar]
- Shapley, L.S. A Value for n-Person Games. In Contributions to the Theory of Games; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 2016; Volume 2, pp. 307–318. ISBN 978-1-4008-8197-0. [Google Scholar]
- Cook, R.D.; Weisberg, S. Residuals and Influence in Regression; Chapman and Hall: New York, NY, USA, 1982; ISBN 978-0-412-24280-9. [Google Scholar]
- Kutner, M.H. Applied Linear Statistical Models; McGraw-Hill Irwin: Boston, MA, USA, 2005; ISBN 978-0-07-238688-2. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1998; ISBN 978-0-471-17082-2. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 978-0-470-54281-1. [Google Scholar]
- Chatterjee, S.; Hadi, A.S. Regression Analysis by Example; John Wiley & Sons: Hoboken, NJ, USA, 2013; ISBN 978-1-118-45624-8. [Google Scholar]
- Chowdhury, M.; Martínez-Sansigre, A.; Mole, M.; Alonso-Peleato, E.; Basos, N.; Blanco, J.M.; Ramirez-Nicolas, M.; Caballero, I.; de la Calle, I. AI-Driven Remote Sensing Enhances Mediterranean Seagrass Monitoring and Conservation to Combat Climate Change and Anthropogenic Impacts. Sci. Rep. 2024, 14, 8360. [Google Scholar] [CrossRef]
- Qin, B.; Zhu, G.; Gao, G.; Zhang, Y.; Li, W.; Paerl, H.W.; Carmichael, W.W. A Drinking Water Crisis in Lake Taihu, China: Linkage to Climatic Variability and Lake Management. Environ. Manag. 2010, 45, 105–112. [Google Scholar] [CrossRef]
- Le, T.P.Q.; Garnier, J.; Gilles, B.; Sylvain, T.; Van Minh, C. The Changing Flow Regime and Sediment Load of the Red River, Viet Nam. J. Hydrol. 2007, 334, 199–214. [Google Scholar] [CrossRef]
- Martinez, J.M.; Guyot, J.L.; Filizola, N.; Sondag, F. Increase in Suspended Sediment Discharge of the Amazon River Assessed by Monitoring Network and Satellite Data. CATENA 2009, 79, 257–264. [Google Scholar] [CrossRef]
- Sottolichio, A.; Castaing, P. A Synthesis on Seasonal Dynamics of Highly-Concentrated Structures in the Gironde Estuary. Comptes Rendus L’académie Sci.-Ser. IIA-Earth Planet. Sci. 1999, 329, 795–800. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Qin, B.Q.; Liu, M.L. Temporal–Spatial Variations of Chlorophyll a and Primary Production in Meiliang Bay, Lake Taihu, China from 1995 to 2003. J. Plankton Res. 2007, 29, 707–719. [Google Scholar] [CrossRef]
- Allen, G.P.; Salomon, J.C.; Bassoullet, P.; Du Penhoat, Y.; de Grandpré, C. Effects of Tides on Mixing and Suspended Sediment Transport in Macrotidal Estuaries. Sediment. Geol. 1980, 26, 69–90. [Google Scholar] [CrossRef]
- Froidefond, J.-M.; Gardel, L.; Guiral, D.; Parra, M.; Ternon, J.-F. Spectral Remote Sensing Reflectances of Coastal Waters in French Guiana under the Amazon Influence. Remote Sens. Environ. 2002, 80, 225–232. [Google Scholar] [CrossRef]
- Woo Kim, Y.; Kim, T.; Shin, J.; Lee, D.-S.; Park, Y.-S.; Kim, Y.; Cha, Y. Validity Evaluation of a Machine-Learning Model for Chlorophyll a Retrieval Using Sentinel-2 from Inland and Coastal Waters. Ecol. Indic. 2022, 137, 108737. [Google Scholar] [CrossRef]
- Emami, S.; Martínez-Muñoz, G. Condensed-Gradient Boosting. Int. J. Mach. Learn. Cyber. 2025, 16, 687–701. [Google Scholar] [CrossRef]
- Maciel, D.A.; Barbosa, C.C.F.; Novo, E.M.L.d.M.; Flores Júnior, R.; Begliomini, F.N. Water Clarity in Brazilian Water Assessed Using Sentinel-2 and Machine Learning Methods. ISPRS J. Photogramm. Remote Sens. 2021, 182, 134–152. [Google Scholar] [CrossRef]
- Chen, J.; Cui, T.; Qiu, Z.; Lin, C. A Three-Band Semi-Analytical Model for Deriving Total Suspended Sediment Concentration from HJ-1A/CCD Data in Turbid Coastal Waters. ISPRS J. Photogramm. Remote Sens. 2014, 93, 1–13. [Google Scholar] [CrossRef]
- Chen, S.; Han, L.; Chen, X.; Li, D.; Sun, L.; Li, Y. Estimating Wide Range Total Suspended Solids Concentrations from MODIS 250-m Imageries: An Improved Method. ISPRS J. Photogramm. Remote Sens. 2015, 99, 58–69. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.-M.; Castaing, P. Remote-Sensing Reflectance of Turbid Sediment-Dominated Waters. Reduction of Sediment Type Variations and Changing Illumination Conditions Effects by Use of Reflectance Ratios. Appl. Opt. 2003, 42, 2623–2634. [Google Scholar] [CrossRef] [PubMed]
- Ouillon, S.; Douillet, P.; Petrenko, A.; Neveux, J.; Dupouy, C.; Froidefond, J.-M.; Andréfouët, S.; Muñoz-Caravaca, A. Optical Algorithms at Satellite Wavelengths for Total Suspended Matter in Tropical Coastal Waters. Sensors 2008, 8, 4165–4185. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Zhou, C.; Zhou, X.; Duan, M.; Yan, Y.; Wang, J.; Wang, L.; Jia, K.; Sun, Y.; Wang, D.; et al. A Universal Method to Recognize Global Big Rivers Estuarine Turbidity Maximum from Remote Sensing. ISPRS J. Photogramm. Remote Sens. 2025, 220, 509–523. [Google Scholar] [CrossRef]
- Güttler, F.N.; Niculescu, S.; Gohin, F. Turbidity Retrieval and Monitoring of Danube Delta Waters Using Multi-Sensor Optical Remote Sensing Data: An Integrated View from the Delta Plain Lakes to the Western–Northwestern Black Sea Coastal Zone. Remote Sens. Environ. 2013, 132, 86–101. [Google Scholar] [CrossRef]
- Martín, M.; Hernández-Crespo, C.; Andrés-Doménech, I.; Benedito-Durá, V. Fifty Years of Eutrophication in the Albufera Lake (Valencia, Spain): Causes, Evolution and Remediation Strategies. Ecol. Eng. 2020, 155, 105932. [Google Scholar] [CrossRef]
- Xue, K.; Ma, R.; Duan, H.; Shen, M.; Boss, E.; Cao, Z. Inversion of Inherent Optical Properties in Optically Complex Waters Using Sentinel-3A/OLCI Images: A Case Study Using China’s Three Largest Freshwater Lakes. Remote Sens. Environ. 2019, 225, 328–346. [Google Scholar] [CrossRef]



| Algorithms | Study Region | Satellites/Sensors (Operational Period) | Turbidity Levels |
|---|---|---|---|
| Semi-empirical single-band algorithm using Rrs859 for high turbidity, and Rrs645 for medium to low turbidity [13] | Southern North Sea, French Guyana, Scheldt, Gironde, Rio Plata | MERIS (2002–2012), MODIS (1999–Present), SeaWiFS (1997–2010) | 1–1000 FNU * |
| Single band algorithm using Rrs842 and Rrs665 [21] | Gironde Estuary, France | Pléiades (2011–Present) | 200–900 FNU |
| Multi-conditional algorithm using Rrs665 and Rrs704 [17] | Guadalquivir Estuary, Spain | Sentinel-2 (2015–Present) | 0–600 FNU |
| Normalized difference turbidity index [22] | Panchet Hill Dam, India | Landsat 5 (1984–2013), Landsat 8 (2013–Present) | <700 FNU |
| Machine learning [15,23] | Taihu Lake, China; North Tyrrhenian Sea, Italy |
Sentinel-2 (2015–Present), Landsat 8/9 (2013–Present) |
0–200; 0–30 FNU |
| Generalized additive models [24] | Doñana Marshes, Spain | Landsat 5 (1984–2013), Landsat 7 (1999–Present) | 1–500 FNU |
| CMEMS [25] | European Seas | Sentinel-2 (2015–Present) | - |
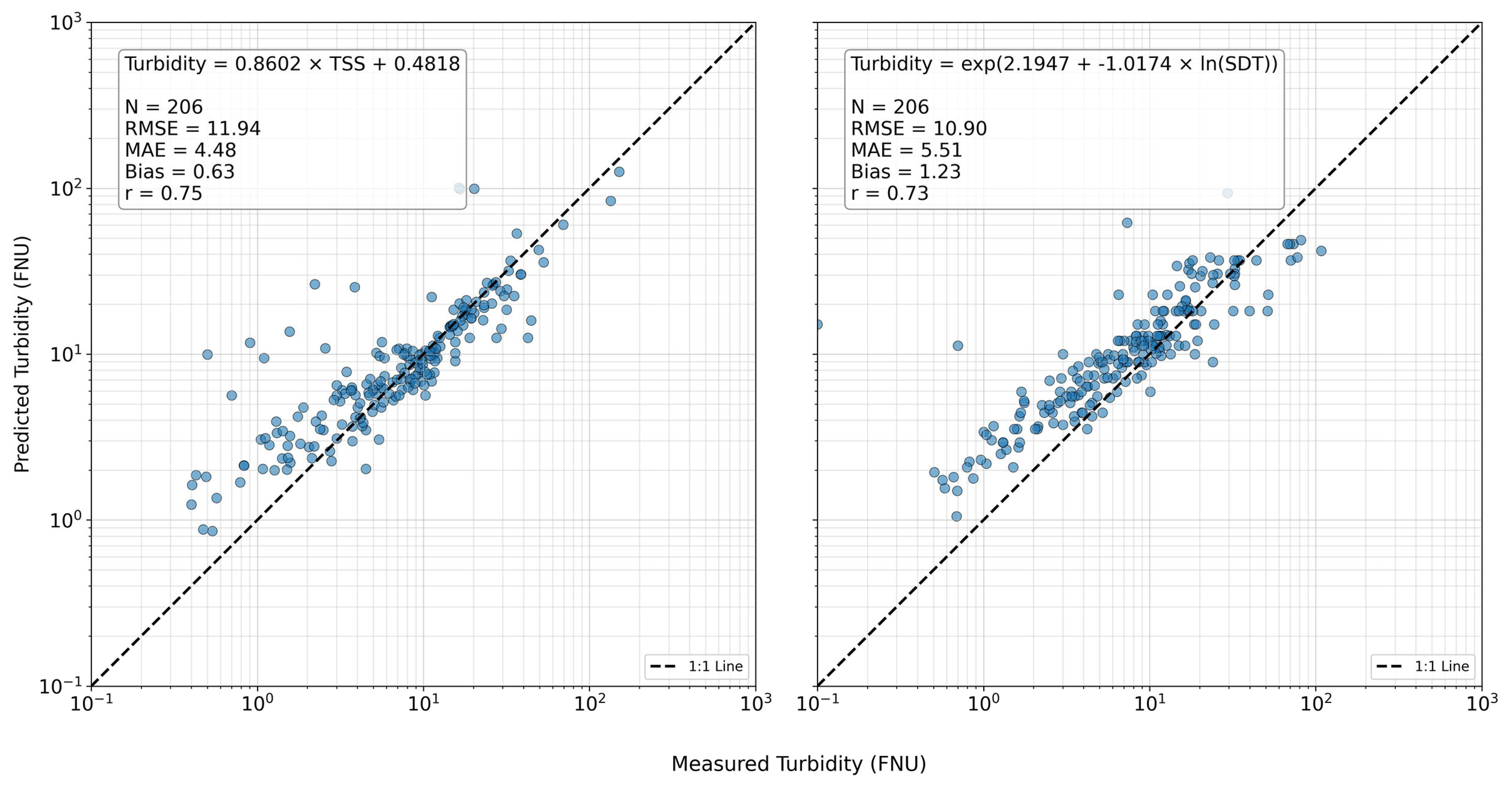
| Model | Equation | Root Mean Squared Error (RMSE), FNU | Mean Absolute Error (MAE), FNU | Bias FNU | Correlation Coefficient (r) |
|---|---|---|---|---|---|
| TurbidityTSS | y = 0.86x + 0.48 | 11.94 | 4.48 | 0.63 | 0.75 |
| TurbiditySDT | y = exp(2.19 − 1.02ln(x)) | 10.90 | 5.51 | 1.23 | 0.73 |
| Model | r | R2 | RMSE (FNU) | MAE (FNU) | Bias (FNU) |
|---|---|---|---|---|---|
| ENR | 0.83 | 0.69 | 226.56 | 127.11 | 21.19 |
| RFR | 0.95 | 0.89 | 117.12 | 47.10 | 1.86 |
| GBR | 0.95 | 0.90 | 116.62 | 43.24 | 1.32 |
| XGBR | 0.95 | 0.90 | 114.21 | 41.56 | −3.29 |
| Chowdhury et al., 2023 [17] | 0.05 | −0.13 | 369.92 | 152.61 | −123.81 |
| Dogliotti et al., 2015 [13] | 0.06 | −0.18 | 377.29 | 151.79 | −149.11 |
| Processing Steps | Description | Avg. Runtime |
|---|---|---|
| Satellite data download | Fetching Sentinel-2 imagery from defined sources | ~30–45 min/100 images |
| Atmospheric correction | DSF-based correction using ACOLITE | ~10–45 min/image |
| Feature extraction, and model implementation | Preparing input feature variables, and applying the pre-trained model to produce turbidity maps | Few min to <1 h |
| Validation and diagnostics | Comparing predictions with observations, computing accuracy metrics, etc. | Few min/image |
| Output logging | Saving trained model, metadata, and logs | Few s/image |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, M.; de la Calle, I.; Laiz, I.; Ruescas, A.B. Near-Real-Time Turbidity Monitoring at Global Scale Using Sentinel-2 Data and Machine Learning Techniques. Remote Sens. 2025, 17, 3716. https://doi.org/10.3390/rs17223716
Chowdhury M, de la Calle I, Laiz I, Ruescas AB. Near-Real-Time Turbidity Monitoring at Global Scale Using Sentinel-2 Data and Machine Learning Techniques. Remote Sensing. 2025; 17(22):3716. https://doi.org/10.3390/rs17223716
Chicago/Turabian StyleChowdhury, Masuma, Ignacio de la Calle, Irene Laiz, and Ana B. Ruescas. 2025. "Near-Real-Time Turbidity Monitoring at Global Scale Using Sentinel-2 Data and Machine Learning Techniques" Remote Sensing 17, no. 22: 3716. https://doi.org/10.3390/rs17223716
APA StyleChowdhury, M., de la Calle, I., Laiz, I., & Ruescas, A. B. (2025). Near-Real-Time Turbidity Monitoring at Global Scale Using Sentinel-2 Data and Machine Learning Techniques. Remote Sensing, 17(22), 3716. https://doi.org/10.3390/rs17223716







