Probabilistic Forecasting Model for Tropical Cyclone Intensity Based on Diffusion Model
Highlights
- This study proposes a novel conditional diffusion model (TCDM), representing the first probabilistic generative framework for tropical cyclone (TC) intensity forecasting capable of integrating multimodal data to generate the full future intensity probability distribution.
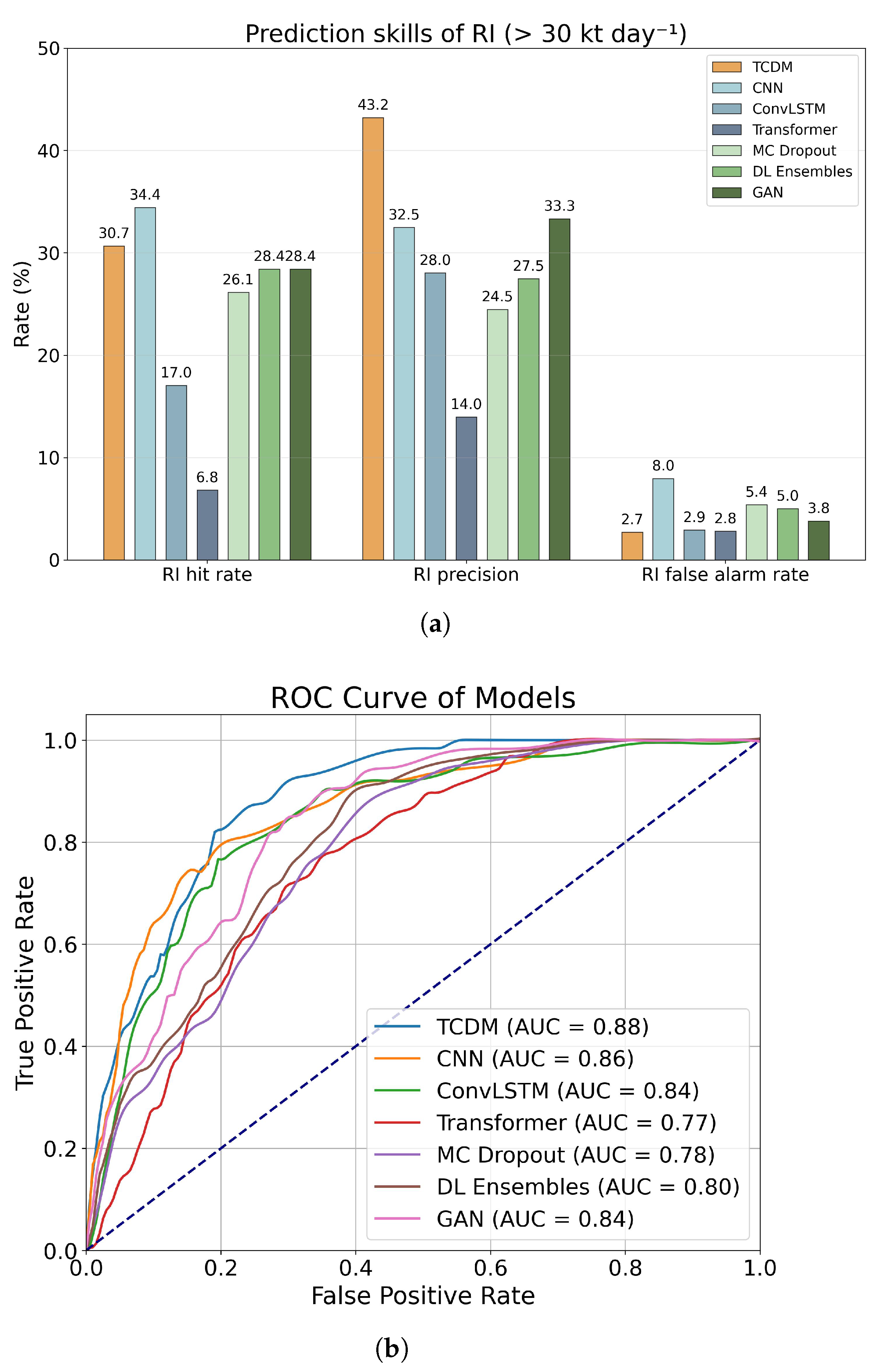
- Compared with mainstream baseline models, TCDM demonstrates a substantial improvement in forecasting rapid intensification (RI) events, achieving the highest hit rate (30.7%) and precision (43.2%) and the lowest false alarm rate (2.7%) in the testing experiments.
- The TCDM framework is capable of generating high-quality and highly reliable probabilistic forecasts, providing more effective decision support for meteorological agencies in tropical cyclone risk assessment and disaster preparedness.
- This study demonstrates the strong potential of diffusion models in simulating and forecasting the uncertainty of extreme weather events, opening new avenues for developing more intelligent and reliable meteorological disaster forecasting systems.
Abstract
1. Introduction
2. Data and Methodology
2.1. Data
2.1.1. Satellite Imagery Data
2.1.2. SHIPS Development Database
2.1.3. Data Preprocessing and Alignment
2.2. TCDM Model for Probabilistic Forecasting of Tropical Cyclone Intensity
2.2.1. Feature Encoder
2.2.2. Condition Fusion
2.2.3. Diffusion Model Framework
- Forward diffusion process: In the forward process, the model gradually adds noise to the true intensity information until it becomes pure noise. Assuming the initial true intensity, noise is added at each time step to obtain the noisy intensity, and this process can be represented asIn this context, denotes the Gaussian distribution, serves as the noise attenuation factor that evolves with the time step t, and I denotes the identity matrix, which characterizes the variance of the noise.
- Reverse process: The reverse denoising process aims to recover the true signal intensity from noise by progressively removing noise through the prediction of the noise component at each step, ultimately resulting in the final intensity estimate. This reverse denoising procedure can be mathematically described by the following formula:Here, represents the denoised estimate predicted based on the current noisy state and the time step t, while denotes the variance of the noise, characterizing the uncertainty in the denoising process.
2.2.4. Conditional Diffusion Mechanism
2.2.5. Probabilistic Forecast Generation via Diffusion Sampling
2.2.6. Loss Function
2.2.7. Training Details
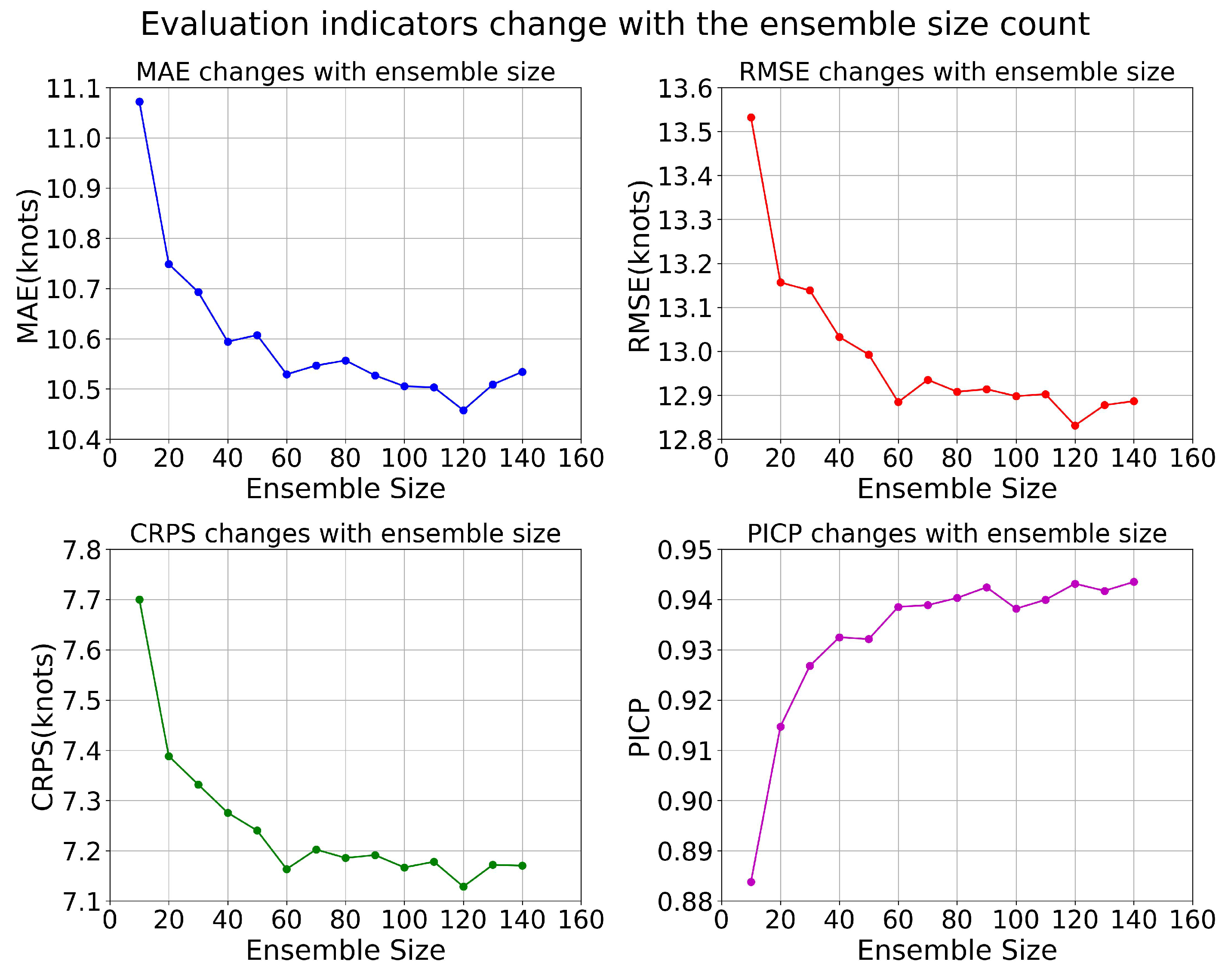
2.3. Evaluation Methods
3. Results
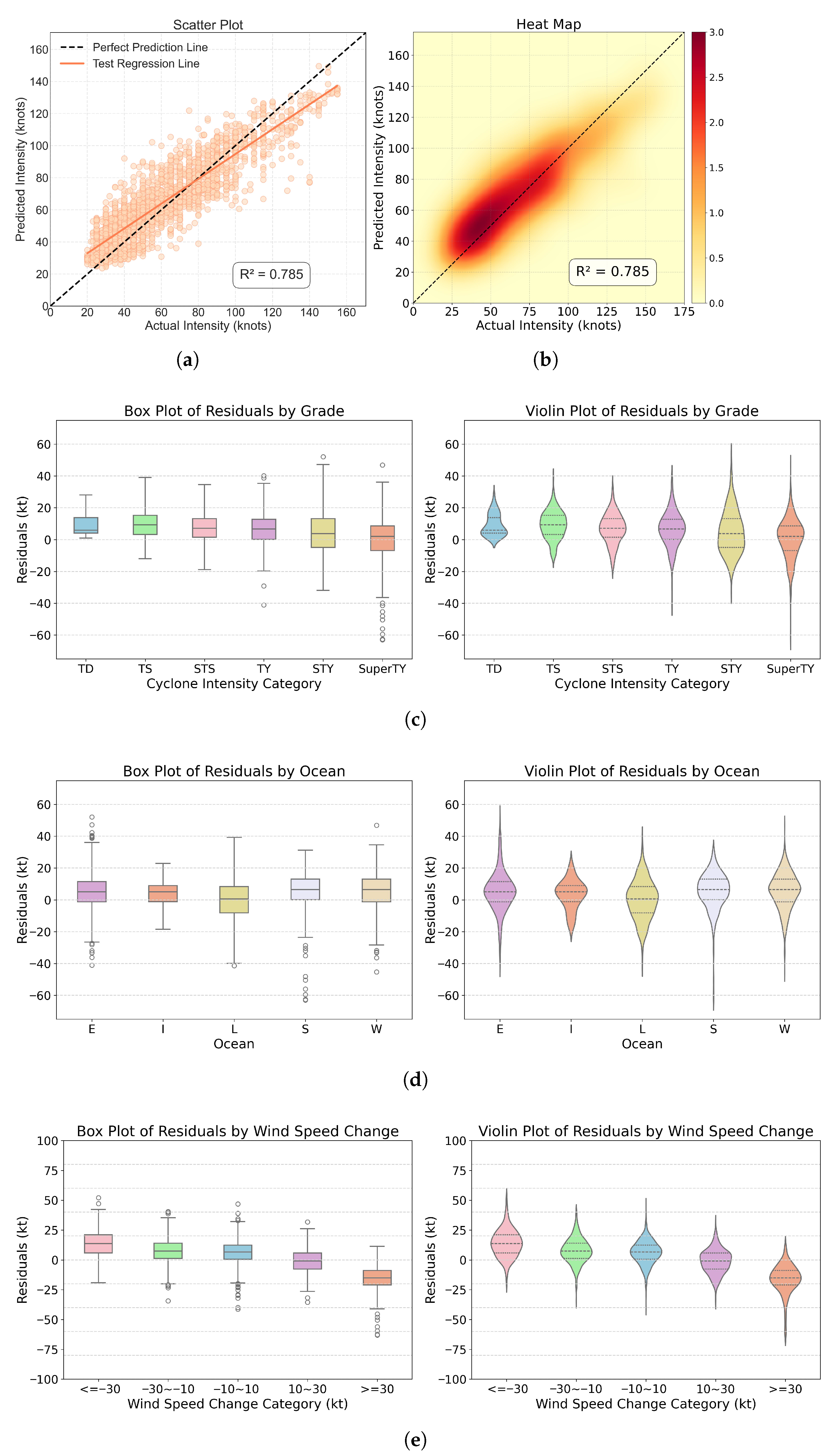
3.1. Model Performance
3.2. Comparison Model
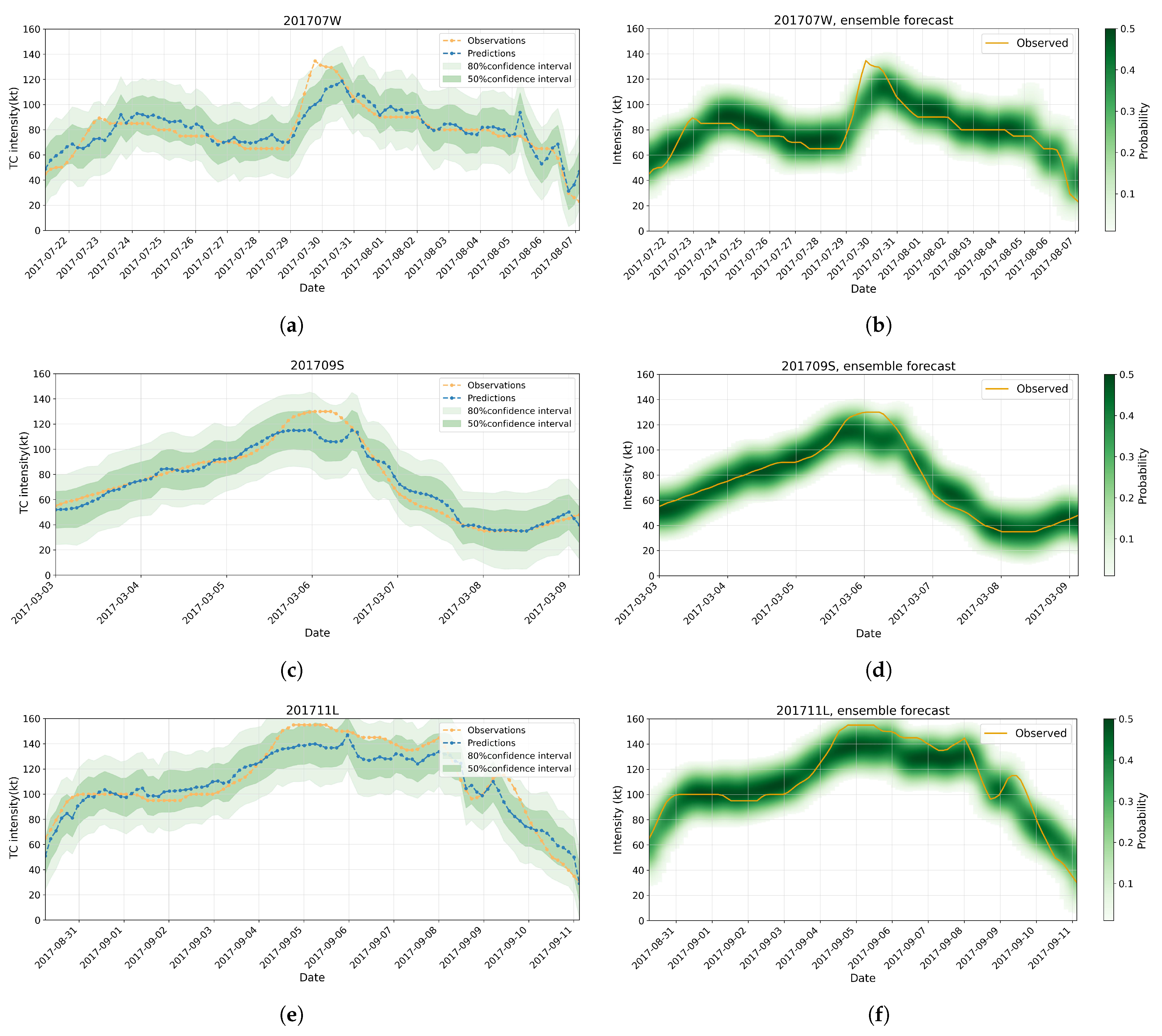
3.3. Case Study
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Meteorological Organization. Rising Risks. 2022. Available online: https://public.wmo.int/en/resources/world-meteorological-day/world-meteorological-day-2022-early-warning-early-action/risking-risks (accessed on 4 September 2025).
- Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef]
- Patricola, C.M.; Wehner, M.F. Anthropogenic increase in Atlantic hurricane intensities. Science 2018, 359, eaao6757. [Google Scholar]
- Chen, B.-F.; Kuo, Y.-T.; Huang, T.-S. A deep learning ensemble approach for predicting tropical cyclone rapid intensification. Atmos. Sci. Lett. 2023, 24, e1151. [Google Scholar] [CrossRef]
- Kaplan, J.; DeMaria, M. Large-scale characteristics of rapidly intensifying tropical cyclones in the North Atlantic basin. Weather Forecast. 2003, 18, 1033–1046. [Google Scholar] [CrossRef]
- DeMaria, M.; Mainelli, M.; Shay, L.K.; Knaff, J.A.; Kaplan, J. The Hurricane Weather Research and Forecasting (HWRF) model. Mon. Weather Rev. 2005, 133, 1801–1816. [Google Scholar]
- Cangialosi, J.P.; Blake, E.; DeMaria, M.; Penny, A.; Latto, A.; Rappaport, E.; Tallapragada, V. Recent progress in tropical cyclone intensity forecasting at the national hurricane center. Weather Forecast. 2020, 35, 1913–1922. [Google Scholar] [CrossRef]
- DeMaria, M.; Knaff, J.A.; Sampson, C.R.; Musgrave, K.D.; Kaplan, J. Advances in tropical cyclone intensity forecasting. Weather Forecast. 2014, 29, 523–549. [Google Scholar]
- Rogers, R.; Aberson, S.; Aksoy, A.; Annane, B.; Black, M.; Cione, J.; Dorst, N.; Dunion, J.; Gamache, J.; Goldenberg, S.; et al. NOAA’s hurricane intensity forecasting experiment: A progress report. Bull. Am. Meteorol. Soc. 2013, 94, 859–882. [Google Scholar] [CrossRef]
- DeMaria, M.; Kaplan, J. A statistical hurricane intensity prediction scheme (SHIPS) for the Atlantic basin. Weather Forecast. 1994, 9, 209–220. [Google Scholar] [CrossRef]
- DeMaria, M.; Kaplan, J. An updated statistical hurricane intensity prediction scheme (SHIPS) for the Atlantic and eastern North Pacific basins. Weather Forecast. 1999, 14, 326–337. [Google Scholar] [CrossRef]
- Roy, C.; Kovordanyi, R. Tropical cyclone track forecasting techniques—A review. Atmos. Res. 2012, 104, 40–69. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Weather forecasting with ensemble methods. Science 2005, 310, 248–249. [Google Scholar] [CrossRef]
- Hazelton, A.T. Improved Tropical Cyclone Rapid Intensification Forecasts in the Operational HAFS. Weather Forecast. 2023, 38, 1335–1354. [Google Scholar]
- Zhang, J.A.; Marks, F.D. Progress and challenges in understanding and forecasting tropical cyclone rapid intensification. Trop. Cyclone Res. Rev. 2021, 10, 1–13. [Google Scholar]
- Haupt, S.E.; Pasini, A. (Eds.) Artificial Intelligence Methods in the Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for self-explaining earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Ham, Y.-G.; Kim, J.-H.; Luo, J.-J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Espeholt, L.; Agrawal, S.; Sønderby, C.; Kumar, M.; Heek, J.; Bromberg, C.; Gazen, C.; Hickey, J.; Bell, A.; Kalchbrenner, N. Skillful twelve hour precipitation forecasts using large context neural networks. Nature 2022, 609, 503–508. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the NIPS’15: Proceedings of the 29th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Chen, R.; Zhang, W.; Wang, X. Machine learning in tropical cyclone forecast modeling: A review. Atmosphere 2020, 11, 676. [Google Scholar] [CrossRef]
- Xu, W.; Balaguru, K.; August, A.; Lalo, N.; Hodas, N.; DeMaria, M.; Judi, D. Deep learning experiments for tropical cyclone intensity forecasts. Weather Forecast. 2021, 36, 1453–1470. [Google Scholar] [CrossRef]
- Wimmers, A.; Velden, C.; Cossuth, J.H. Using deep learning to estimate tropical cyclone intensity from satellite passive microwave imagery. Mon. Weather Rev. 2019, 147, 2261–2282. [Google Scholar] [CrossRef]
- Cloud, K.; Rozoff, C.; Lewis, W.; Wimmers, A.; Velden, C.; Kossin, J. A deep learning model for rapid intensification of Atlantic hurricanes. Weather Forecast. 2019, 34, 1745–1761. [Google Scholar]
- Su, H.; Wu, L.; Jiang, J.H.; Pai, C.-W.; Zhai, A.; Fovell, R.G. Applying satellite observations of tropical cyclone internal structures to rapid intensification forecast with machine learning. Geophys. Res. Lett. 2020, 47, e2020GL089102. [Google Scholar] [CrossRef]
- Yang, Q.; Lee, C.Y.; Tippett, M.K. A long short-term memory model for global rapid intensification prediction. Weather Forecast. 2020, 35, 1203–1220. [Google Scholar] [CrossRef]
- Meng, F.; Yang, K.; Yao, Y.; Wang, Z.; Song, T. Tropical Cyclone Intensity Probabilistic Forecasting System Based on Deep Learning. Int. J. Intell. Syst. 2023, 3569538. [Google Scholar] [CrossRef]
- Meng, F.; Yao, Y.; Wang, Z.; Peng, S.; Xu, D.; Song, T. Probabilistic forecasting of tropical cyclones intensity using machine learning model. Environ. Res. Lett. 2023, 18, 044042. [Google Scholar] [CrossRef]
- Berner, J.; Achatz, U.; Batté, L.; De La Cámara, A.; Christensen, H.M.; Colangeli, M.; Colangeli, M.; Coleman, D.R.B.; Crommelin, D.; Dolaptchiev, S.I.; et al. Stochastic parameterization: Toward a new view of weather and climate models. Bull. Am. Meteorol. Soc. 2017, 98, 565–588. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Probabilistic forecasts, calibration and sharpness. J. R. Stat. Soc. Ser. Stat. Methodol. 2007, 69, 243–268. [Google Scholar] [CrossRef]
- Price, I.; Sanchez-Gonzalez, A.; Alet, F.; Andersson, T.R.; El-Kadi, A.; Masters, D.; Ewalds, T.; Stott, J.; Mohamed, S.; Battaglia, P.; et al. Probabilistic weather forecasting with machine learning. Nature 2025, 637, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Taillardat, M.; Mestre, O.; Zamo, M.; Naveau, P. Calibrated ensemble forecasts using quantile regression forests and ensemble model output statistics. Mon. Weather Rev. 2016, 144, 2375–2393. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. In Proceedings of the NIPS’20: Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; pp. 6840–6851. [Google Scholar]
- Sohl-Dickstein, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2256–2265. [Google Scholar]
- Song, Y.; Ermon, S. Improved techniques for training score-based generative models. In Proceedings of the NIPS’20: Proceedings of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–12 December 2020; pp. 12438–12448. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21–24 June 2022; pp. 10684–10695. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational Bayes. In Proceedings of the 2nd International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Chen, B.; Chen, B.-F.; Lin, H.-T. Rotation-blended CNNs on a new open dataset for tropical cyclone image-to-intensity regression. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), London, UK, 19–23 August 2018. [Google Scholar]
- hariwal, P.; Nichol, A. Diffusion models beat GANs on image synthesis. In NIPS’21: Proceedings of the 35th International Conference on Neural Information Processing System, Virtual, 6–14 December 2021. [Google Scholar]
- Ravuri, S.; Lenc, K.; Willson, M.; Kangin, D.; Lam, R.; Mirowski, P.; Fitzsimons, M.; Athanassiadou, M.; Kashem, S.; Madge, S.; et al. Skilful precipitation nowcasting using deep generative models of radar. Nature 2021, 597, 672–677. [Google Scholar] [CrossRef] [PubMed]
- Beusch, L.; Rasp, S.; Dueben, P.D. Physics-constrained deep learning postprocessing of temperature and humidity. Geophys. Res. Lett. 2023, 50, e2023GL103582. [Google Scholar]
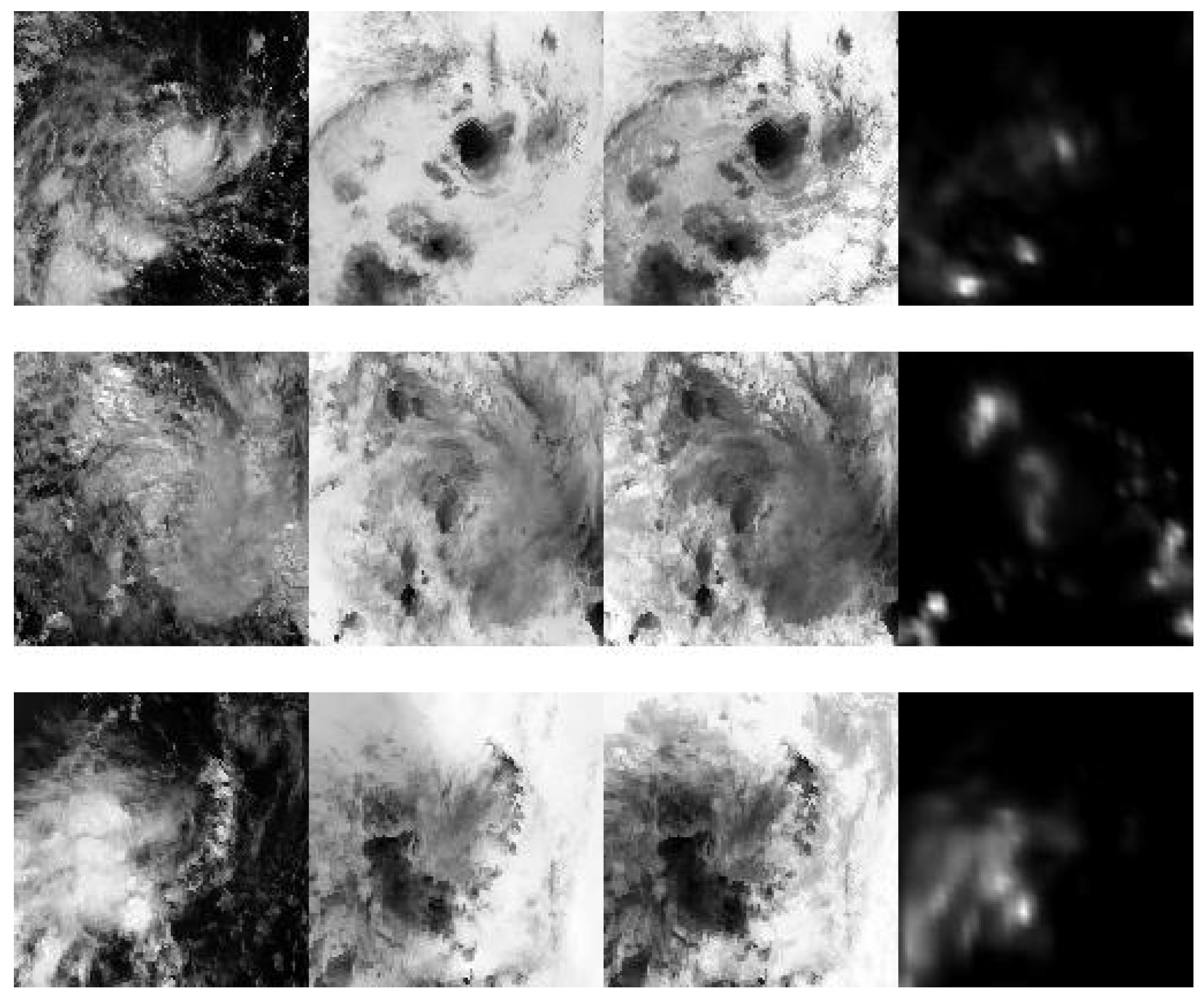

| Combination | MAE | RMSE | R2 | CRPS | PICP |
|---|---|---|---|---|---|
| IR | 15.20 | 19.50 | 0.60 | 14.50 | 0.60 |
| VIS | 16.50 | 20.50 | 0.50 | 16.00 | 0.55 |
| PMW | 13.90 | 17.50 | 0.66 | 12.60 | 0.68 |
| WV | 14.80 | 18.00 | 0.57 | 14.80 | 0.61 |
| IR + VIS | 13.50 | 17.20 | 0.67 | 13.50 | 0.66 |
| IR + PMW | 11.80 | 15.00 | 0.75 | 8.80 | 0.82 |
| IR + WV | 13.20 | 16.70 | 0.68 | 11.90 | 0.70 |
| VIS + PMW | 14.20 | 17.80 | 0.64 | 12.20 | 0.69 |
| VIS + WV | 15.20 | 18.80 | 0.59 | 13.60 | 0.64 |
| PMW + WV | 13.60 | 17.20 | 0.70 | 9.80 | 0.75 |
| IR + VIS + PMW | 11.10 | 13.70 | 0.77 | 7.90 | 0.84 |
| IR + VIS + WV | 12.90 | 16.00 | 0.68 | 11.00 | 0.72 |
| IR + PMW + WV | 10.20 | 12.90 | 0.77 | 7.10 | 0.91 |
| VIS + PMW + WV | 11.20 | 14.20 | 0.72 | 8.50 | 0.86 |
| IR + VIS + PMW + WV | 10.50 | 12.80 | 0.76 | 7.40 | 0.90 |
| IR + PMW + WV + SHIPS | 10.04 | 12.73 | 0.78 | 7.17 | 0.93 |
| MAE | RMSE | R2 | CRPS | PICP | |
|---|---|---|---|---|---|
| CNN | 13.17 | 17.33 | 0.62 | \ | \ |
| ConvLSTM | 11.87 | 15.69 | 0.68 | \ | \ |
| Transformer | 11.71 | 14.93 | 0.71 | \ | \ |
| MC Dropout | 12.46 | 15.82 | 0.64 | 11.93 | 0.78 |
| Deep Ensemble | 12.11 | 15.78 | 0.66 | 9.34 | 0.81 |
| GAN | 11.21 | 14.24 | 0.73 | 7.98 | 0.86 |
| TCDM | 10.04 | 12.73 | 0.78 | 7.17 | 0.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, J.; Yang, P.; Meng, F. Probabilistic Forecasting Model for Tropical Cyclone Intensity Based on Diffusion Model. Remote Sens. 2025, 17, 3600. https://doi.org/10.3390/rs17213600
Luo J, Yang P, Meng F. Probabilistic Forecasting Model for Tropical Cyclone Intensity Based on Diffusion Model. Remote Sensing. 2025; 17(21):3600. https://doi.org/10.3390/rs17213600
Chicago/Turabian StyleLuo, Jingjia, Peng Yang, and Fan Meng. 2025. "Probabilistic Forecasting Model for Tropical Cyclone Intensity Based on Diffusion Model" Remote Sensing 17, no. 21: 3600. https://doi.org/10.3390/rs17213600
APA StyleLuo, J., Yang, P., & Meng, F. (2025). Probabilistic Forecasting Model for Tropical Cyclone Intensity Based on Diffusion Model. Remote Sensing, 17(21), 3600. https://doi.org/10.3390/rs17213600





