RMCMamba: A Multi-Factor High-Speed Railway Bridge Pier Settlement Prediction Method Based on RevIN and MARSHead
Highlights
- We propose the RMCMamba model, which innovatively integrates RevIN and MARSHead modules. It effectively captures long-range dependencies in settlement time series and mitigates distribution shift issues.
- RMCMamba significantly outperforms comparative methods in multi-factor scenarios, attaining an MAE of 0.049 mm and an RMSE of 0.077 mm, which corresponds to a 4.8% reduction in MAE compared to the second-best performing method.
- The study provides a reliable technical framework (from E-PS-InSAR monitoring to multi-source data fusion and prediction) for high-precision health monitoring of critical transportation infrastructure like high-speed railways.
- The open-sourced dataset and code serve as a valuable benchmark for future research in settlement prediction and relevant time series forecasting domains, promoting reproducibility and further development.
Abstract
1. Introduction
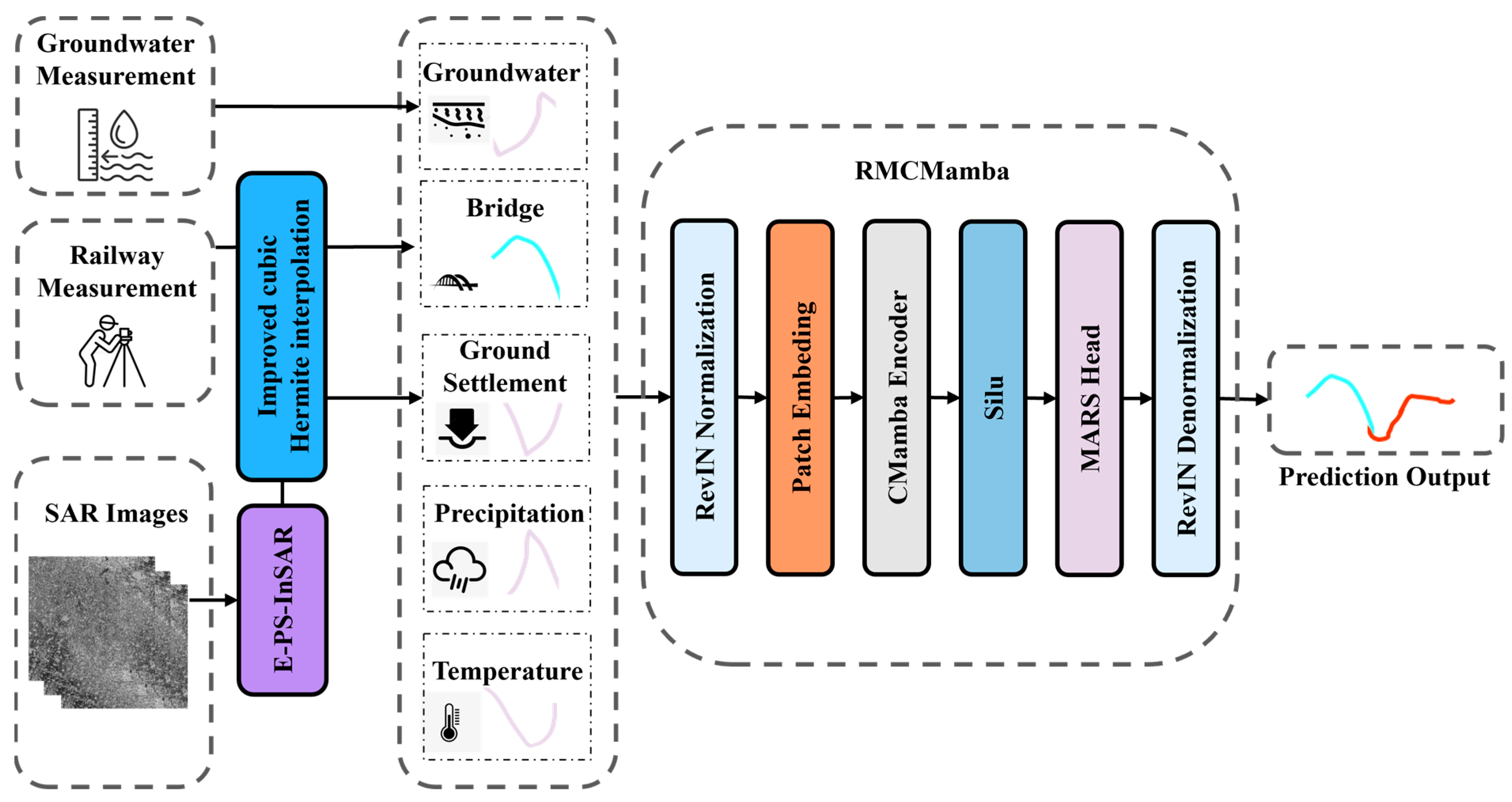
- A machine learning framework for HSR-BP settlement prediction: Firstly, sub-centimeter-level monitoring accuracy of land subsidence along the high-speed railway is realized using E-PS-InSAR technology. Secondly, the improved cubic Hermite interpolation algorithm is utilized to solve the problem of missing time series data. Then, the geological and environmental parameters are integrated with pier settlement data, and a multi-source time series dataset is constructed. Finally, the RMCMamba model proposed in this paper realizes high-precision prediction of pier settlement.
- Multi-Scale Adaptive Resolution Stream Head (MARSHead): Construct a three-branch parallel convolution architecture, unify the sequence length through the adaptive pooling layer, introduce learnable branch weight parameters to achieve dynamic weighting across time granularity, and finally perform timing alignment to complete feature dimensions unification.
- RevIN-based distribution calibration enhancement mechanism: The reversible instance normalization module is used to integrate into the time series prediction framework and combined with the state space modeling capability of the CMamba encoder, which alleviates the distribution shift of multi-factor sequences. This module can significantly alleviate the distribution shift of multi-factor time series and improve the robustness of CMamba’s state space modeling.
2. Methodology
- Land subsidence monitoring: This paper uses E-PS-InSAR (Enhanced PS-InSAR) technology to obtain high-quality land subsidence data along high-speed railways.
- Data enhancement: The improved cubic Hermite interpolation method is used for timing sequence interpolation of the land subsidence and HSR-BP settlement. The traditional cubic Hermite interpolation method is an approximate curve interpolation method. In this paper, the cubic fitting polynomial is obtained by weighted least squares fitting, and the derivative is obtained by deriving the cubic fitting polynomial. The derivative replaces the original slope estimation method. The specific formula is:In the formula, and are interpolation basis functions, , is the interpolation node. are the new parameters obtained by using the least squares method.
- Dataset establishment: The time series dataset is established by five kinds of data of HSR-BP settlement, land subsidence, groundwater, temperature, and precipitation.
- HSR-BP settlement prediction: The RMCMamba model is used to complete the settlement prediction of HSR-BPs.
2.1. The Enhanced PS-InSAR Technology
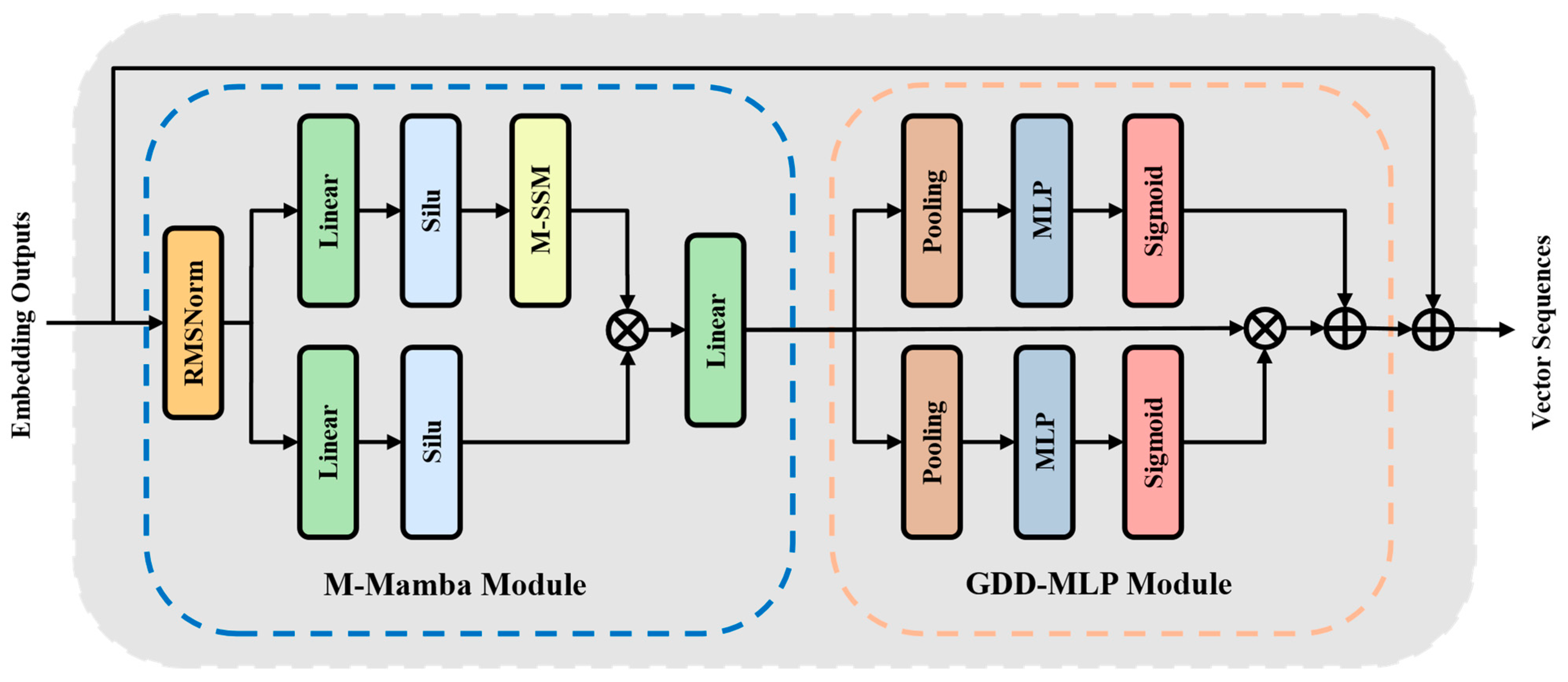
2.2. CMamba Encoder
2.3. The Proposed Multi-Scale Adaptive Resolution Stream Head
2.4. Reversible Instance Normalization Module
3. Experimental Design
3.1. Study Area and Data
3.2. Experimental Settings
3.3. Evaluation Metrics
4. Experimental Results and Analysis
4.1. E-PS-InSAR Land Subsidence Monitoring Result
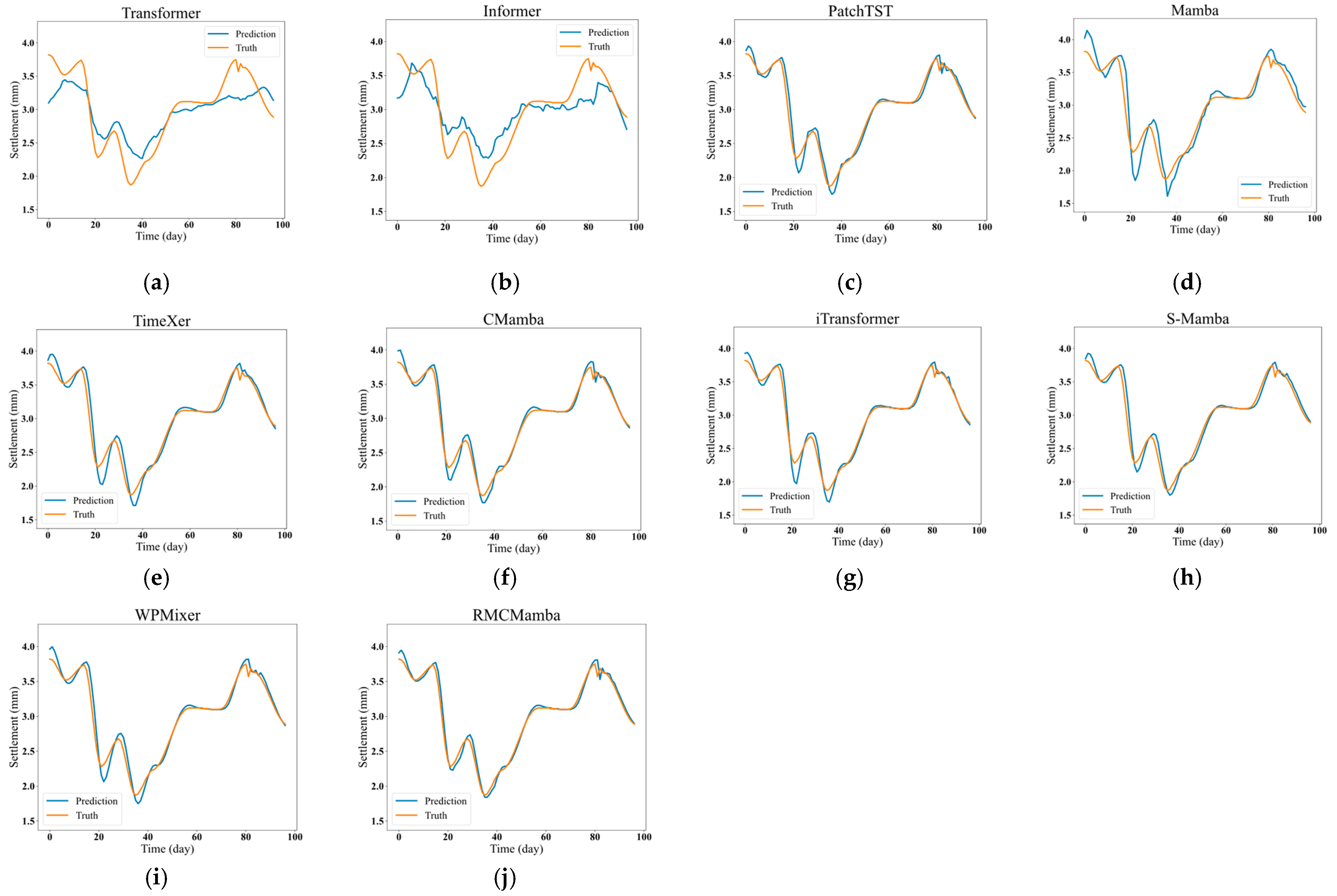
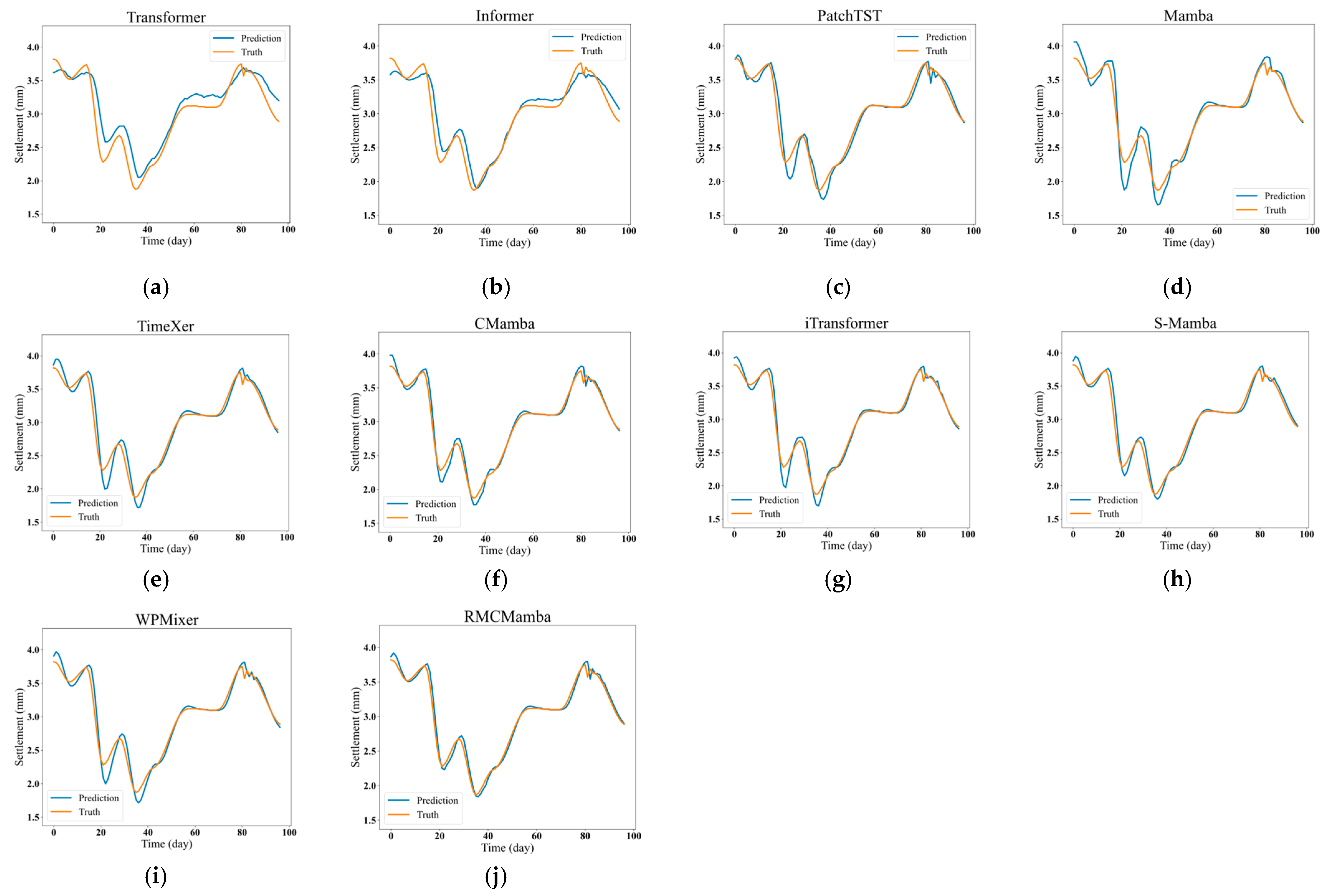
4.2. Prediction Results and Analysis of HSR-BP Settlement
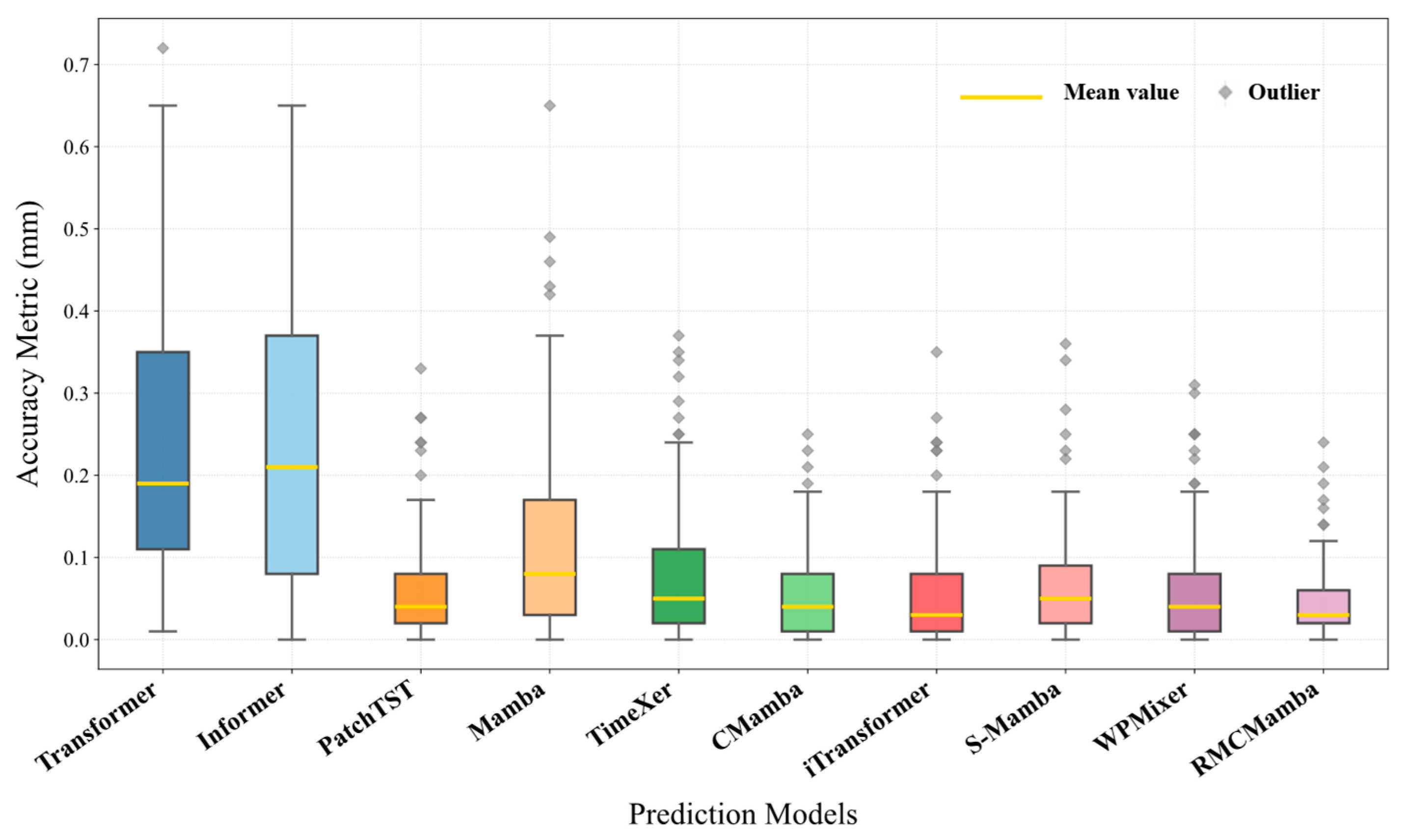
4.2.1. Statistical Results and Analysis of Multi-Factor HSR-BP Settlement
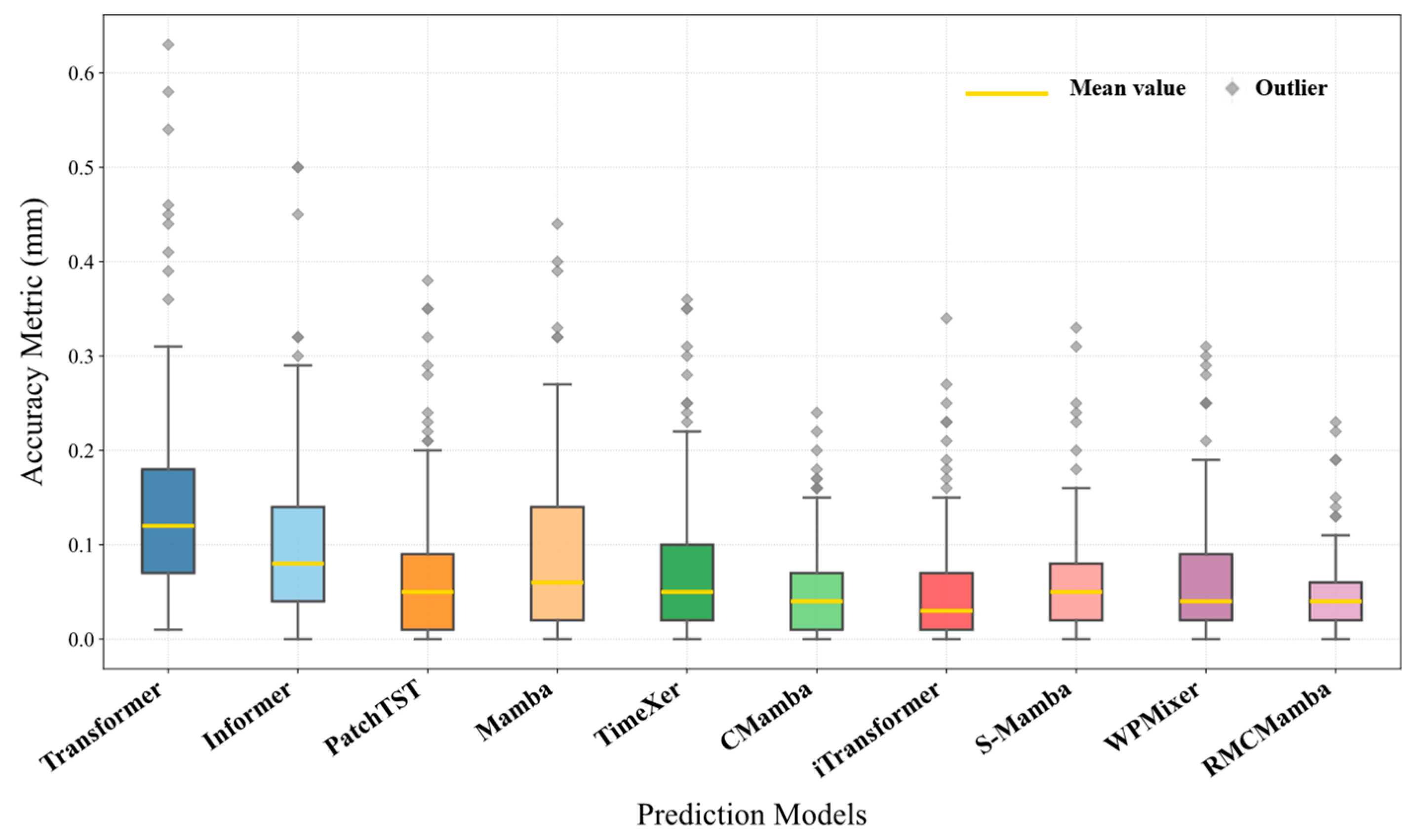
4.2.2. Statistical Results and Analysis of HSR-BP Single-Factor Prediction
4.2.3. Comparative Analysis of the Performance of Multi-Factor and Single-Factor HSR-BP Prediction
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, X.; Chen, X.; Hu, H.; Zhou, X.; Cheng, M.; Sun, L.; Li, X. Energy Dissipation and Seismic Response Reduction System for High-Speed Railway Bridges Based on Multiple Performance Requirements. Eng. Struct. 2024, 307, 117919. [Google Scholar] [CrossRef]
- Chen, Z.; Fang, H. Influence of Pier Settlement on Contact Behavior between CRTS II Track and Bridge in High-Speed Railways. Eng. Struct. 2021, 235, 112007. [Google Scholar] [CrossRef]
- He, Y.; Li, Y.; Xu, L. An Integrated Multisource and Multiscale Monitoring Technique for Assessing the Health Status of High-Speed Railway Subgrade. Remote Sens. 2024, 16, 1972. [Google Scholar] [CrossRef]
- Wei, B.; Zheng, X.; Jiang, L.; Lai, Z.; Zhang, R.; Chen, J.; Yang, Z. Seismic response prediction and fragility assessment of high-speed railway bridges using machine learning technology. Structures 2024, 66, 106845. [Google Scholar] [CrossRef]
- Yao, J.; Lan, H.; Li, L.; Cao, Y.; Wu, Y.; Zhang, Y.; Zhou, C. Characteristics of a Rapid Landsliding Area along Jinsha River Revealed by Multi-Temporal Remote Sensing and Its Risks to Sichuan-Tibet Railway. Landslides 2022, 19, 703–718. [Google Scholar] [CrossRef]
- Chen, B.; Gong, H.; Chen, Y.; Lei, K.; Zhou, C.; Si, Y.; Li, X.; Pan, Y.; Gao, M. Investigating Land Subsidence and Its Causes along Beijing High-Speed Railway Using Multi-Platform InSAR and a Maximum Entropy Model. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102284. [Google Scholar] [CrossRef]
- Gong, X.; Li, Z. Robust Weighted Total Least Squares Based on IGG Weighting Function. Acta Geod. Cartogr. Sin. 2014, 43, 888–894. [Google Scholar] [CrossRef]
- Zhao, H.; Wei, B.; Zhang, P.; Guo, P.; Shao, Z.; Xu, S.; Jiang, L.; Hu, H.; Zeng, Y.; Xiang, P. Safety analysis of high-speed trains on bridges under earthquakes using a LSTM-RNN-based surrogate model. Comput. Struct. 2024, 294, 107274. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Dănişor, C.; Pauciullo, A.; Reale, D.; Fornaro, G. Detection of Distributed Scatterers in Multitemporal SAR Interferometry: A Comparison Between CAESAR and SqueeSAR Detectors. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5220415. [Google Scholar] [CrossRef]
- Zhou, C.; Cao, Y.; Gan, L.; Wang, Y.; Motagh, M.; Roessner, S.; Hu, X.; Yin, K. A Novel Framework for Landslide Displacement Prediction Using MT-InSAR and Machine Learning Techniques. Eng. Geol. 2024, 334, 107497. [Google Scholar] [CrossRef]
- Li, Y.; Zuo, X.; Yang, F.; Bu, J.; Wu, W.; Liu, X. Effectiveness Evaluation of DS-InSAR Method Fused PS Points in Surface Deformation Monitoring: A Case Study of Hongta District, Yuxi City, China. Geomat. Nat. Hazards Risk 2023, 14, 2176011. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Shan, X.; Wang, Z.; Gong, W.; Zhang, G. Deep Learning for Automatic Detection of Volcanic and Earthquake-Related InSAR Deformation. Remote Sens. 2025, 17, 686. [Google Scholar] [CrossRef]
- Cheng, Y.; Pang, H.; Li, Y.; Fan, L.; Wei, S.; Yuan, Z.; Fang, Y. Applications and Advancements of Spaceborne InSAR in Landslide Monitoring and Susceptibility Mapping: A Systematic Review. Remote Sens. 2025, 17, 999. [Google Scholar] [CrossRef]
- Du, Y.-N.; Feng, D.-C.; Wu, G. InSAR-Based Rapid Damage Assessment of Urban Building Portfolios Following the 2023 Turkey Earthquake. Int. J. Disaster Risk Reduct. 2024, 103, 104317. [Google Scholar] [CrossRef]
- Hu, J.; Motagh, M.; Guo, J.; Haghighi, M.H.; Li, T.; Qin, F.; Wu, W. Inferring Subsidence Characteristics in Wuhan (China) through Multitemporal InSAR and Hydrogeological Analysis. Eng. Geol. 2022, 297, 106530. [Google Scholar] [CrossRef]
- Zhang, B.; Liao, X.; Zhang, J.; Xiong, S.; Wang, C.; Wu, S.; Zhu, C.; Zhu, J.; Qin, X.; Li, Q. Megalopolitan-Scale Ground Deformation along Metro Lines in the Guangdong-Hong Kong-Macao Greater Bay Area, China, Revealed by MT-InSAR. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103432. [Google Scholar] [CrossRef]
- Luo, Q.; Li, J.; Zhang, Y. Monitoring Subsidence over the Planned Jakarta–Bandung (Indonesia) High-Speed Railway Using Sentinel-1 Multi-Temporal InSAR Data. Remote Sens. 2022, 14, 4138. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, W.; Cheng, Y.; Li, Z. Landslide Detection in the Linzhi–Ya’an Section along the Sichuan–Tibet Railway Based on InSAR and Hot Spot Analysis Methods. Remote Sens. 2021, 13, 3566. [Google Scholar] [CrossRef]
- China Railway Corporation. Observation and Evaluation Specification for Settlement Deformation of Railway Engineering; Q/CR 9230-2016; China Railway Corporation: Beijing, China, 2016. [Google Scholar]
- Gong, X.; Li, Z. Bridge Pier Settlement Prediction in High-Speed Railway via Autoregressive Model Based on Robust Weighted Total Least-Squares. Surv. Rev. 2018, 50, 147–154. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, H.; Huang, J.; Wen, T.; Ma, J.; Zhang, J. A Comparative Study of Different Machine Learning Methods for Reservoir Landslide Displacement Prediction. Eng. Geol. 2022, 298, 106544. [Google Scholar] [CrossRef]
- Huang, W.; Liao, W.; Li, J.; Qiao, X.; Yusan, S.; Yasen, A.; Li, X.; Zhang, S. The Long-Term Surface Deformation Monitoring and Prediction of Hutubi Gas Storage Reservoir in Xinjiang Based on InSAR and the GWO-VMD-GRU Model. Remote Sens. 2025, 17, 2480. [Google Scholar] [CrossRef]
- Xue, Y.-A.; Zou, Y.-F.; Li, H.-Y.; Zhang, W.-Z. Regional Subsidence Monitoring and Prediction along High-Speed Railways Based on PS-InSAR and LSTM. Sci. Rep. 2024, 14, 24622. [Google Scholar] [CrossRef] [PubMed]
- Gong, X.; Wang, H.; Lu, T.; You, W. A General Progressive Decomposition Long-Term Prediction Network Model for High-Speed Railway Bridge Pier Settlement. Acta Geod. Cartogr. Sin. 2024, 53, 1113. [Google Scholar] [CrossRef]
- Gong, X.; Wang, H.; Lu, T.; You, W.; Zhang, R. Combined Prediction Model for High-Speed Railway Bridge Pier Settlement Based on Robust Weighted Total Least-Squares Autoregression and Adaptive Dynamic Cubic Exponential Smoothing. J. Surv. Eng. 2023, 149, 04023001. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6000–6010. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Kitaev, N.; Kaiser, L.; Levskaya, A. Reformer: The Efficient Transformer. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. iTransformer: Inverted Transformers Are Effective for Time Series Forecasting. In Proceedings of the Twelfth International Conference on Learning Representations, ICLR 2024, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Zhang, Y.; Yan, J. Crossformer: Transformer Utilizing Cross-Dimension Dependency for Multivariate Time Series Forecasting. In Proceedings of the Eleventh International Conference on Learning Representations, Windsor Great Park, UK, 29 September 2022. [Google Scholar]
- Wang, Z.; Kong, F.; Feng, S.; Wang, M.; Yang, X.; Zhao, H.; Wang, D.; Zhang, Y. Is Mamba Effective for Time Series Forecasting? Neurocomputing 2025, 619, 129178. [Google Scholar] [CrossRef]
- Zeng, C.; Liu, Z.; Zheng, G.; Kong, L. CMamba: Channel Correlation Enhanced State Space Models for Multivariate Time Series Forecasting. 2024. Available online: https://arxiv.org/abs/2406.05316 (accessed on 12 January 2025).
- Kim, T.; Kim, J.; Tae, Y.; Park, C.; Choi, J.-H.; Choo, J. Reversible Instance Normalization for Accurate Time-Series Forecasting against Distribution Shift. In Proceedings of the International Conference on Learning Representations, Virtually, 6 October 2021. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-Time Sequence Modeling with Selective State Spaces. In Proceedings of the First Conference on Language Modeling, Philadelphia, PA, USA, 26 August 2024. [Google Scholar]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A Time Series Is Worth 64 Words: Long-Term Forecasting with Transformers. In Proceedings of the Eleventh International Conference on Learning Representations, ICLR 2023, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Wang, Y.; Wu, H.; Dong, J.; Qin, G.; Zhang, H.; Liu, Y.; Qiu, Y.; Wang, J.; Long, M. TimeXer: Empowering Transformers for Time Series Forecasting with Exogenous Variables. In Proceedings of the Advances in Neural Information Processing Systems 38: Annual Conference on Neural Information Processing Systems 2024, NeurIPS 2024, Vancouver, BC, Canada, 10–15 December 2024. [Google Scholar]
- Murad, M.M.N.; Aktukmak, M.; Yilmaz, Y. WPMixer: Efficient Multi-Resolution Mixing for Long-Term Time Series Forecasting. In Proceedings of the AAAI-25, Sponsored by the Association for the Advancement of Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Walsh, T., Shah, J., Kolter, Z., Eds.; AAAI Press: Palo Alto, CA, USA, 2025; pp. 19581–19588. [Google Scholar]
- Pan, G.; Wang, X.; Zhang, J.; Liu, G.; Wang, J.; Hou, Z.; Li, B. Interpretation and Analysis of Multi-Source Remote Sensing Fault Structure in Taiyangshan Fault Zone and Surrounding Areas. J. Geod. Geodyn. 2021, 41, 754–758. [Google Scholar]
- Liu, X.; Xing, X.; Wen, D.; Chen, L.; Yuan, Z.; Liu, B.; Tan, J. Mining-Induced Time-Series Deformation Investigation Based on SBAS-InSAR Technique: A Case Study of Drilling Water Solution Rock Salt Mine. Sensors 2019, 19, 5511. [Google Scholar] [CrossRef]


| Monitoring Point | Start Date (yyyy/mm/dd) | End Date (yyyy/mm/dd) | Total Measurement Days | Average Settlement Rate (mm/year) | Number of Measurement Periods |
|---|---|---|---|---|---|
| 1 | 2020/07/15 | 2021/12/27 | 530 | 2.066 | 37 |
| 2 | 2020/09/30 | 2021/12/27 | 453 | 2.264 | 32 |
| 3 | 2021/02/28 | 2021/12/19 | 294 | 3.017 | 136 |
| 4 | 2020/10/24 | 2021/12/19 | 421 | 2.211 | 84 |
| 5 | 2020/10/24 | 2021/12/19 | 421 | 1.543 | 32 |
| 6 | 2020/09/09 | 2021/12/20 | 487 | 1.432 | 34 |
| 7 | 2020/08/18 | 2021/12/20 | 489 | 2.157 | 36 |
| 8 | 2020/10/02 | 2021/12/06 | 430 | 2.122 | 109 |
| 9 | 2020/07/16 | 2021/12/20 | 522 | 0.762 | 36 |
| 10 | 2020/08/13 | 2021/12/05 | 479 | 1.676 | 69 |
| Settlement Rate (mm/year) | Number of Monitoring Points | Proportion of Total |
|---|---|---|
| x < −5.00 | 4940 | 0.270% |
| −5.00 ≤ x < −2.00 | 64,656 | 3.535% |
| −2.00 ≤ x < −1.00 | 183,084 | 10.011% |
| −1.00 ≤ x < −0.50 | 238,330 | 13.032% |
| −0.50 ≤ x < 0.50 | 774,831 | 42.368% |
| 0.50 ≤ x < 1.00 | 290,439 | 15.881% |
| 1.00 ≤ x < 2.00 | 235,767 | 12.892% |
| 2.00 ≤ x < 5.00 | 36,597 | 2.001% |
| ≥5.00 | 151 | 0.008% |
| Model | Multi-Factor | ||
|---|---|---|---|
| MAE/mm | RMSE/mm | MAPE | |
| Transformer [22] | 0.48586 | 0.54525 | 28.398% |
| Informer [23] | 0.47114 | 0.53077 | 25.430% |
| PatchTST [31] | 0.05165 | 0.07919 | 5.427% |
| Mamba [30] | 0.09438 | 0.13917 | 9.497% |
| TimeXer [32] | 0.05881 | 0.09126 | 5.996% |
| CMamba [28] | 0.05222 | 0.08253 | 5.429% |
| iTransformer [25] | 0.05697 | 0.08930 | 6.604% |
| S-Mamba [27] | 0.05856 | 0.08936 | 6.569% |
| WPMixer [33] | 0.06006 | 0.09175 | 6.251% |
| RMCMamba | 0.04918 | 0.07718 | 5.022% |
| Model | Single-Factor | ||
|---|---|---|---|
| MAE/mm | RMSE/mm | MAPE | |
| Autoregressive Model | 0.99326 | 1.15223 | 50.677% |
| Grey Models | 46.20070 | 50.53772 | 1933.847% |
| Back Propagation | 1.57358 | 1.70844 | 175.677% |
| Transformer [22] | 0.29114 | 0.35578 | 16.737% |
| Informer [23] | 0.30361 | 0.36864 | 16.685% |
| PatchTST [31] | 0.06357 | 0.09639 | 6.189% |
| Mamba [30] | 0.05889 | 0.08949 | 6.396% |
| TimeXer [32] | 0.06011 | 0.08627 | 6.087% |
| CMamba [28] | 0.05172 | 0.08149 | 5.635% |
| iTransformer [25] | 0.05853 | 0.09127 | 6.472% |
| S-Mamba [27] | 0.05625 | 0.08420 | 6.431% |
| WPMixer [33] | 0.06046 | 0.09202 | 6.043% |
| RMCMamba | 0.04945 | 0.07796 | 5.015% |
| Method | Multi-Factor | Single-Factor | ||||
|---|---|---|---|---|---|---|
| MAE/mm | RMSE/mm | MAPE | MAE/mm | RMSE/mm | MAPE | |
| Variant 1 | 0.05222 | 0.08253 | 5.429% | 0.05172 | 0.08149 | 5.635% |
| Variant 2 | 0.05142 | 0.08027 | 5.276% | 0.05089 | 0.07978 | 5.304% |
| Variant 3 | 0.05223 | 0.08253 | 5.416% | 0.05171 | 0.08148 | 5.635% |
| Variant 4 | 0.04918 | 0.07718 | 5.022% | 0.04945 | 0.07796 | 5.015% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Gong, X.; Liang, Q.; Chen, Z.; Lu, T.; Zhang, R.; Mao, W. RMCMamba: A Multi-Factor High-Speed Railway Bridge Pier Settlement Prediction Method Based on RevIN and MARSHead. Remote Sens. 2025, 17, 3596. https://doi.org/10.3390/rs17213596
Liu J, Gong X, Liang Q, Chen Z, Lu T, Zhang R, Mao W. RMCMamba: A Multi-Factor High-Speed Railway Bridge Pier Settlement Prediction Method Based on RevIN and MARSHead. Remote Sensing. 2025; 17(21):3596. https://doi.org/10.3390/rs17213596
Chicago/Turabian StyleLiu, Junjie, Xunqiang Gong, Qi Liang, Zhiping Chen, Tieding Lu, Rui Zhang, and Wenfei Mao. 2025. "RMCMamba: A Multi-Factor High-Speed Railway Bridge Pier Settlement Prediction Method Based on RevIN and MARSHead" Remote Sensing 17, no. 21: 3596. https://doi.org/10.3390/rs17213596
APA StyleLiu, J., Gong, X., Liang, Q., Chen, Z., Lu, T., Zhang, R., & Mao, W. (2025). RMCMamba: A Multi-Factor High-Speed Railway Bridge Pier Settlement Prediction Method Based on RevIN and MARSHead. Remote Sensing, 17(21), 3596. https://doi.org/10.3390/rs17213596






