Enhanced Detection of Permafrost Deformation with Machine Learning and Interferometric SAR Along the Qinghai–Tibet Engineering Corridor
Abstract
1. Introduction
2. Study Area and Datasets
2.1. Study Area
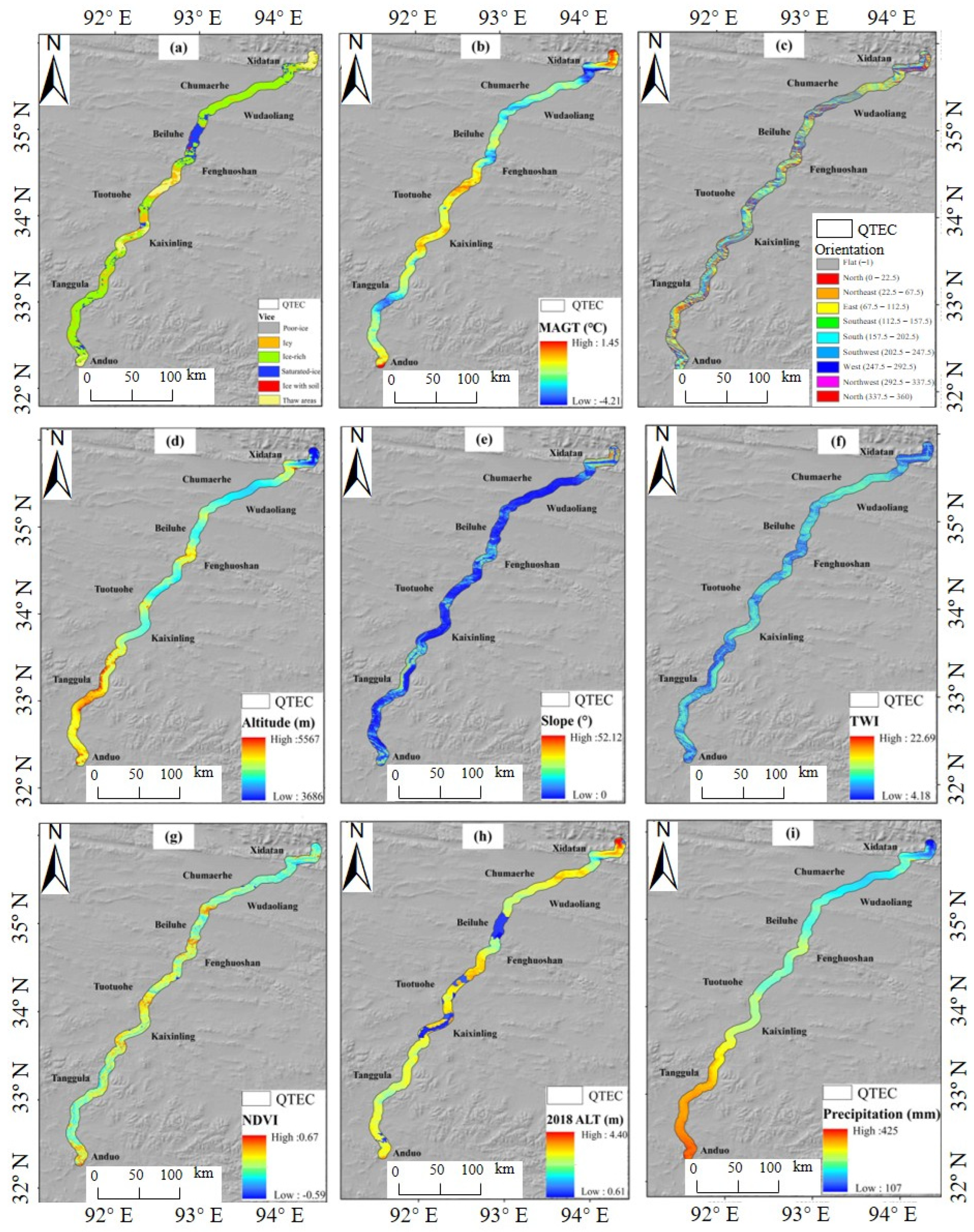
2.2. Dataset
2.2.1. SAR Datasets
2.2.2. Factors Driving Permafrost Thaw Settlement
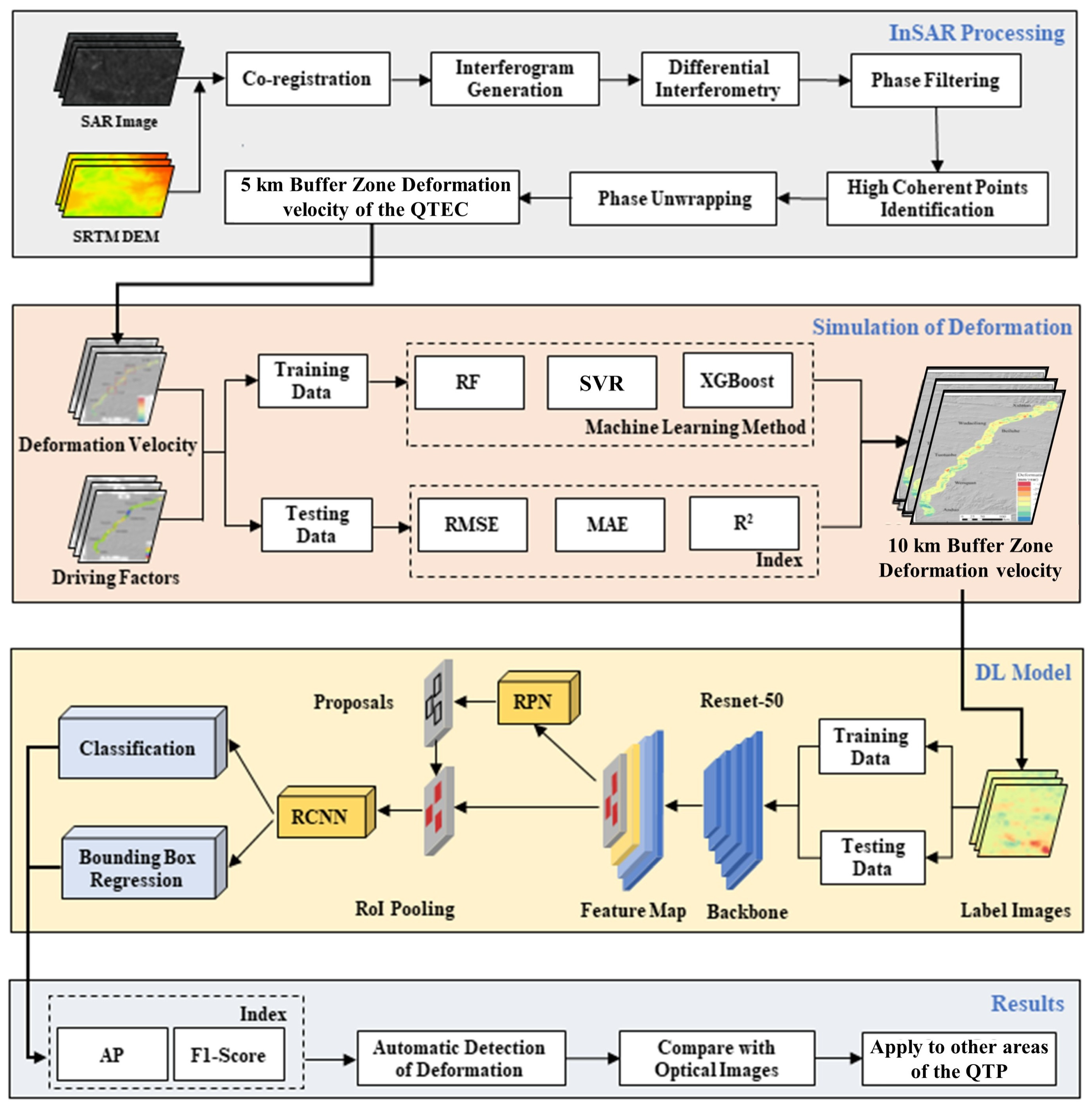
3. Method
3.1. Deformation Estimation Using InSAR
3.2. Deformation Simulation Using Machine Learning
3.2.1. Random Forest
3.2.2. Support Vector Regression
3.2.3. Extreme Gradient Boosting
3.2.4. Training and Testing Samples
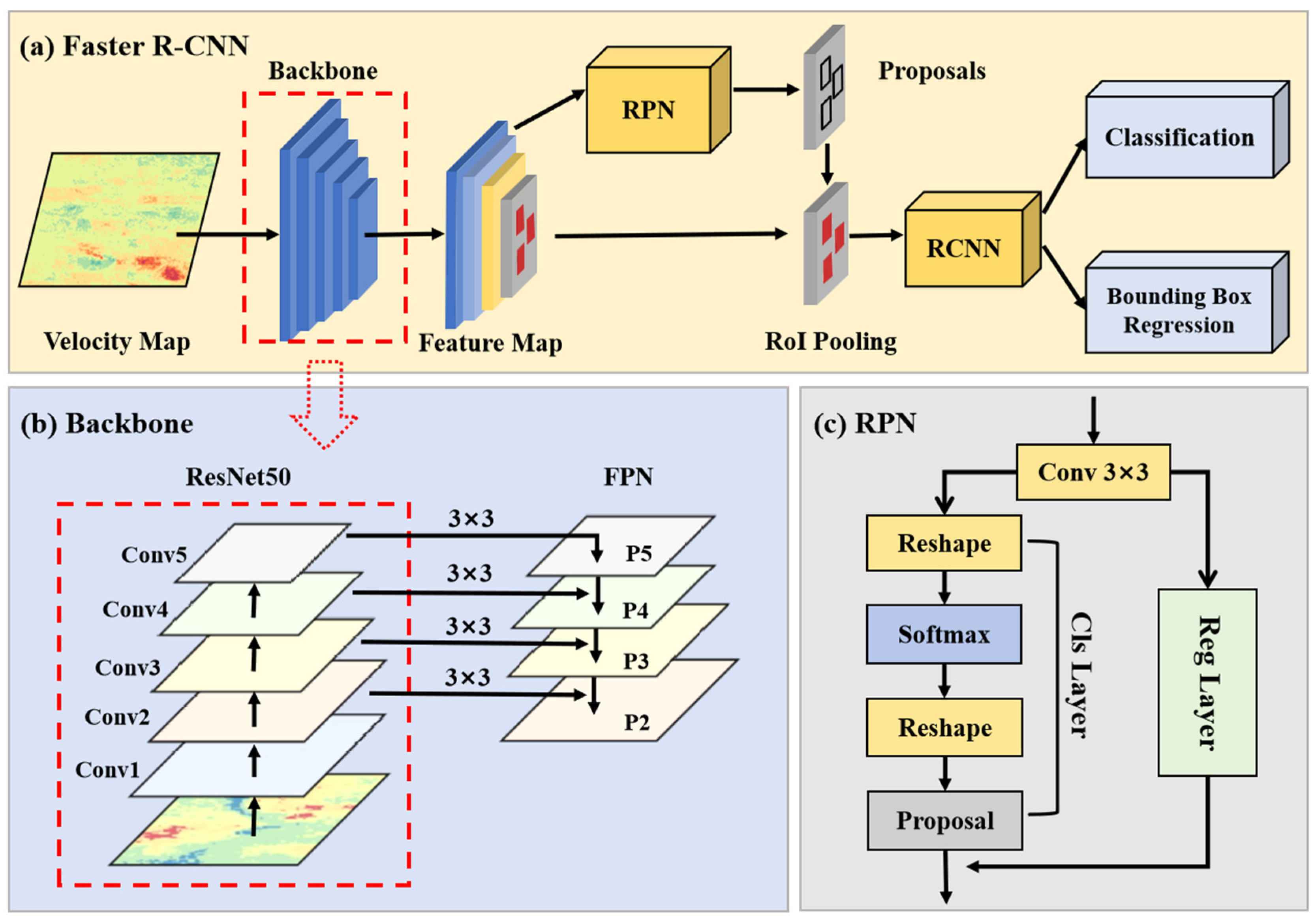
3.3. Deformation Automatic Detection Using DL
3.3.1. Automatic Detection Model
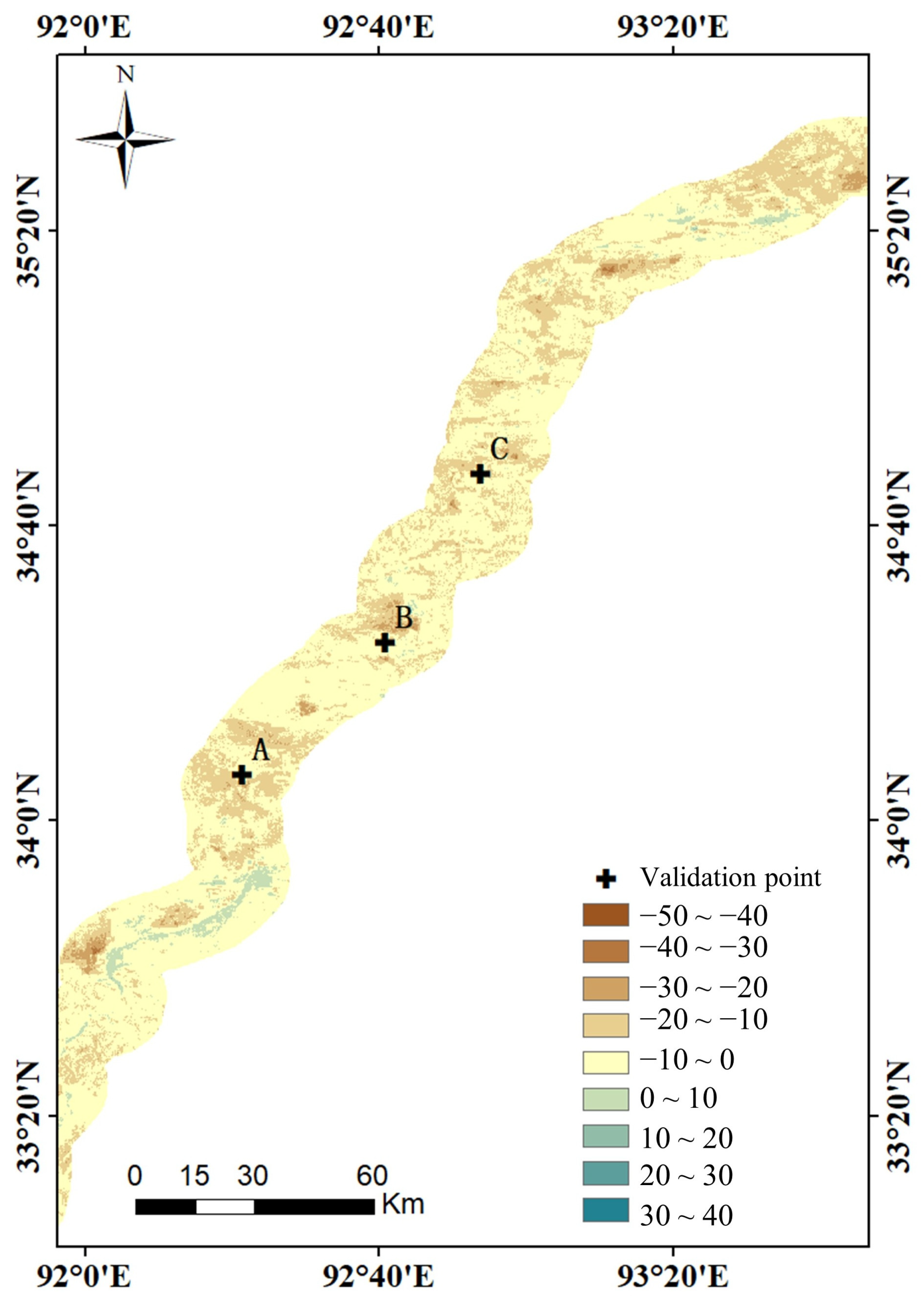
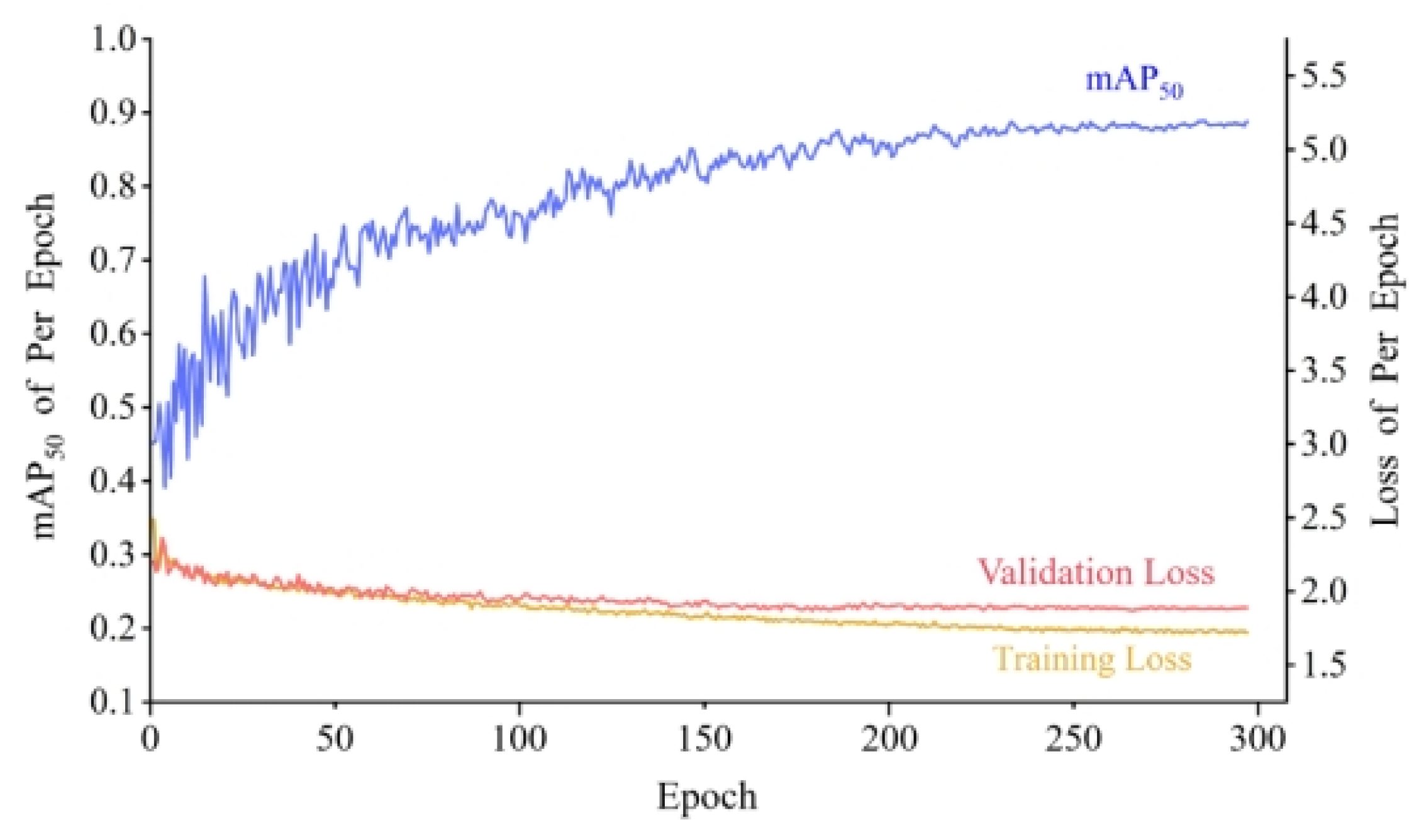
3.3.2. Training Settings and Accuracy Verification
4. Experimental Results
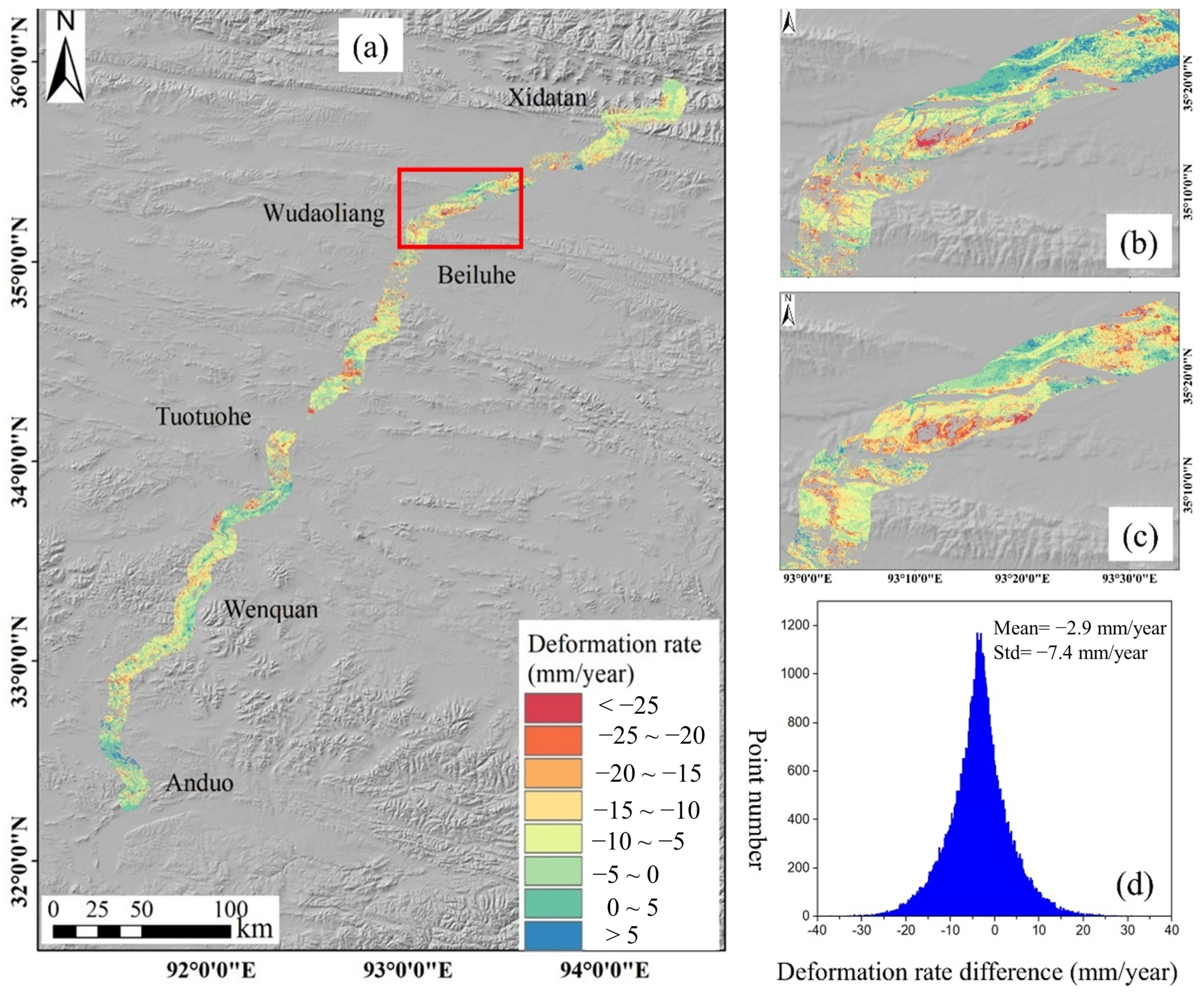
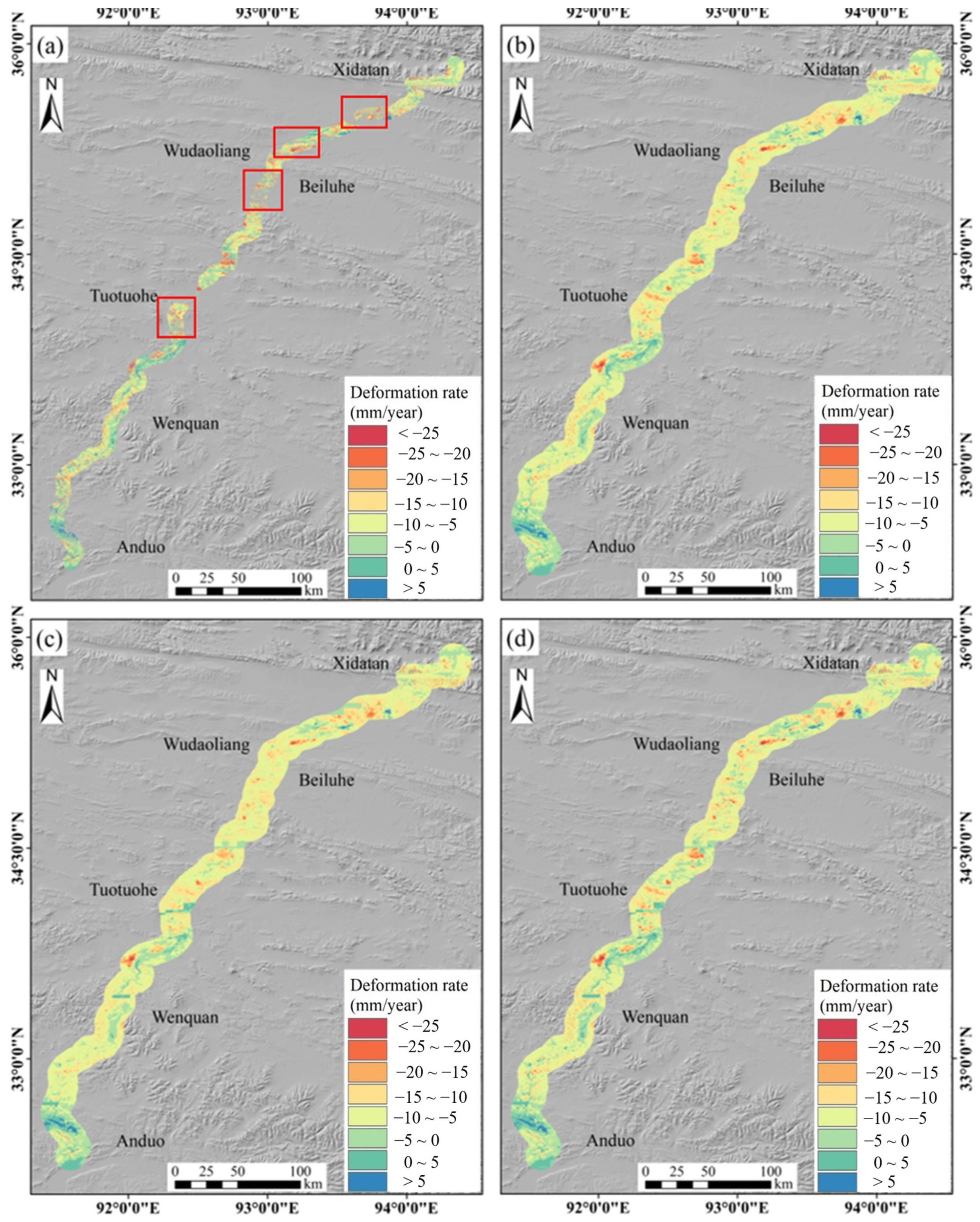
4.1. InSAR Results
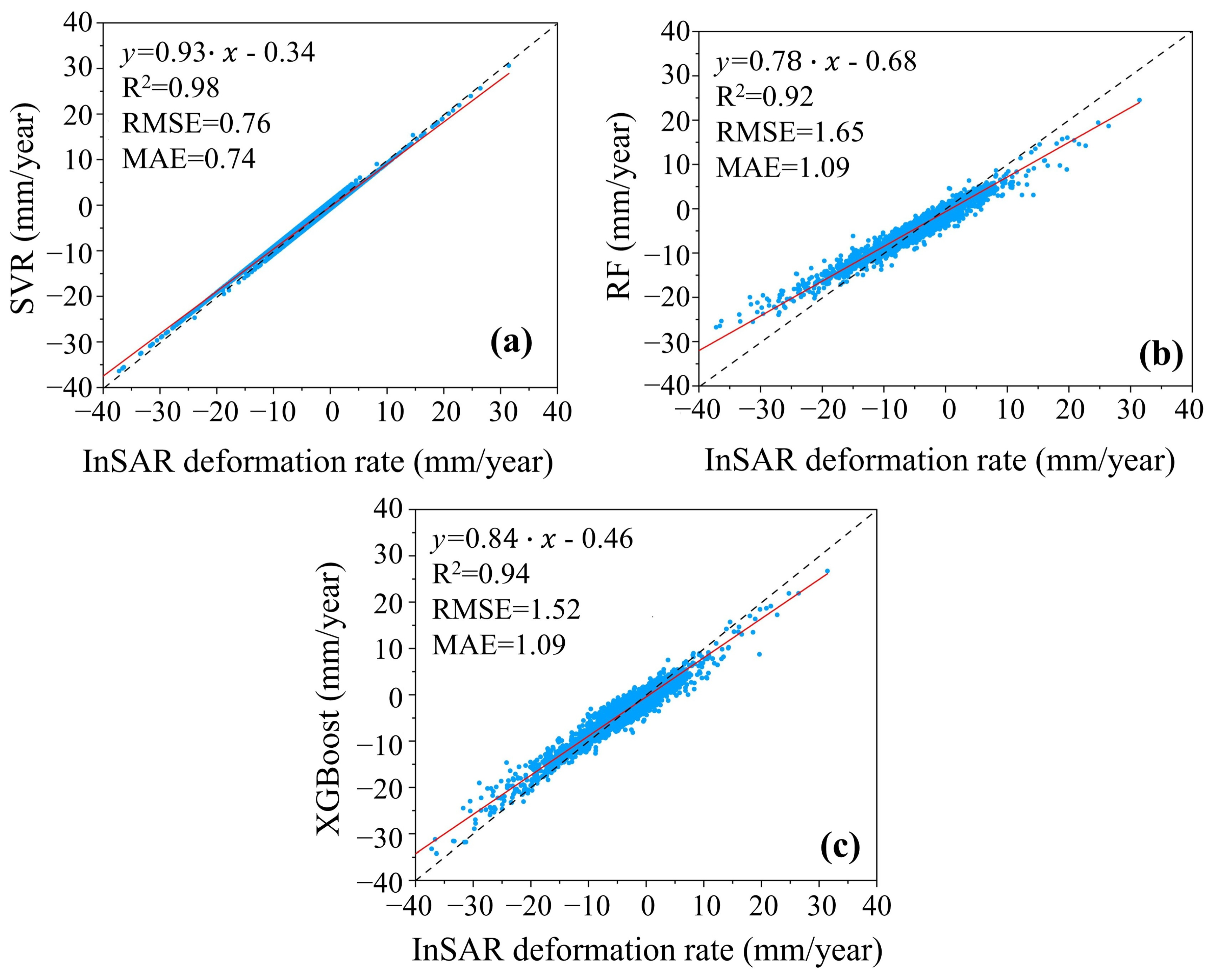
4.2. Performance of the Three Machine Learning Models
4.3. Correlation and Importance Analysis of Various Factors
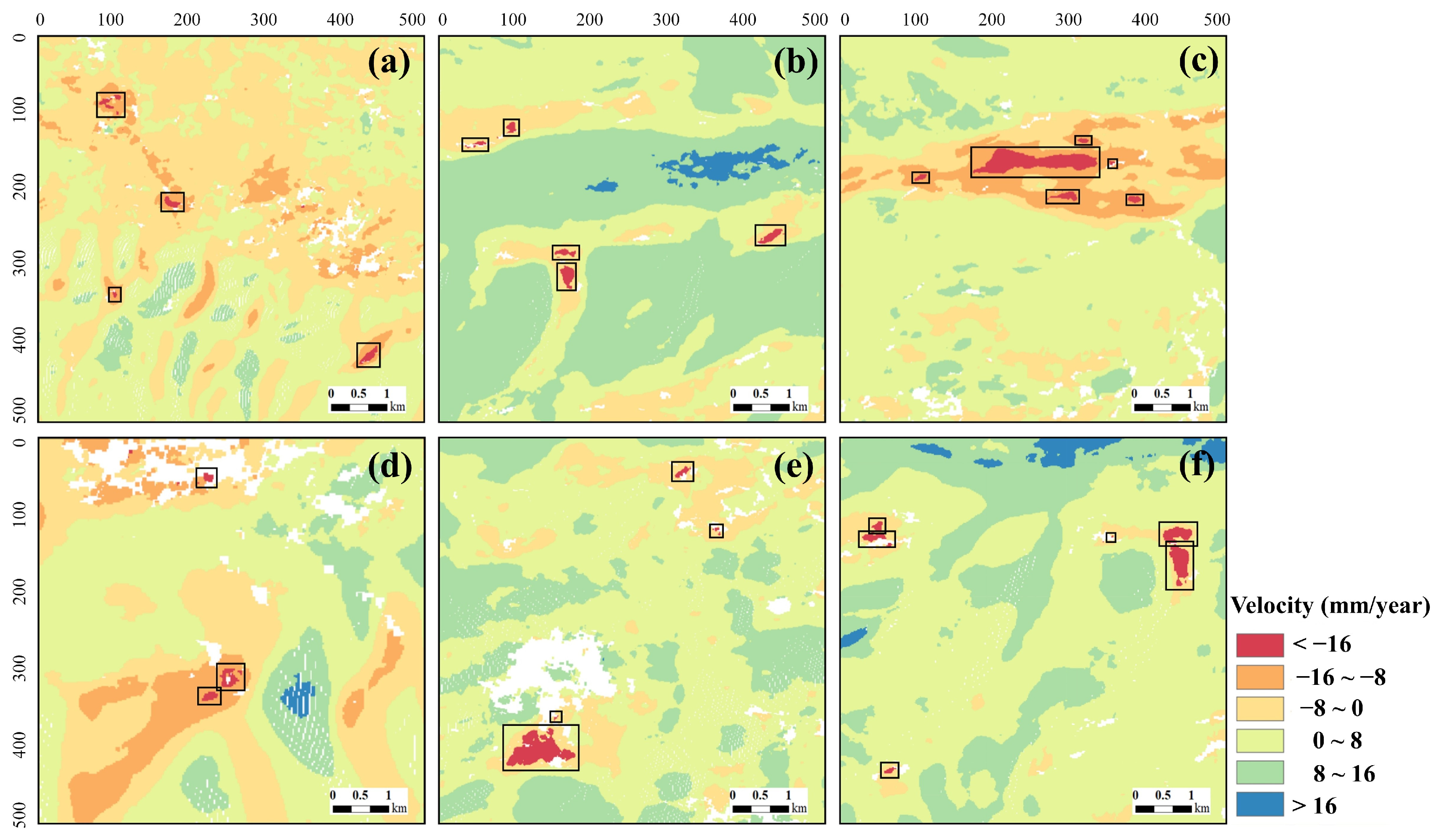
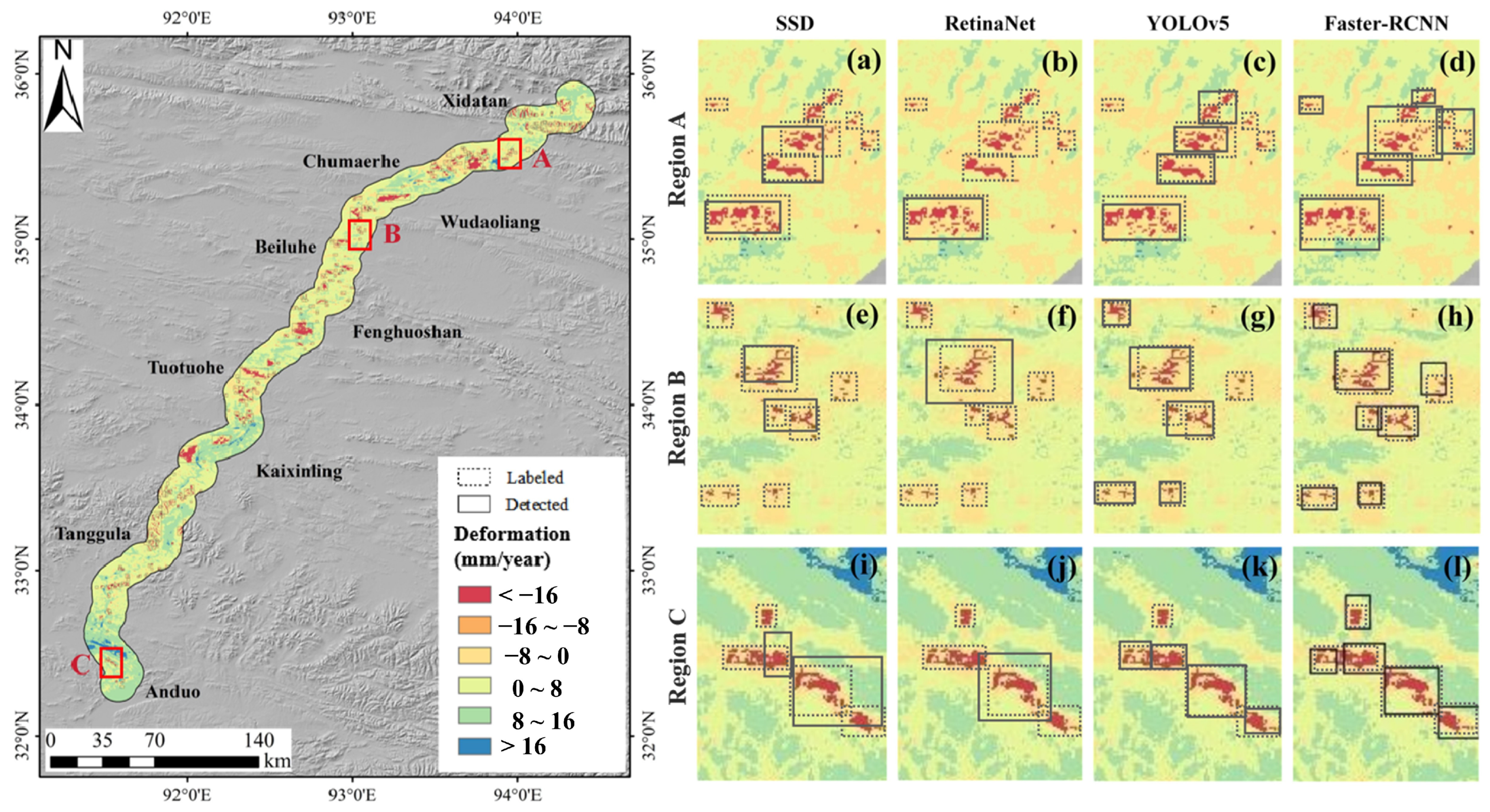
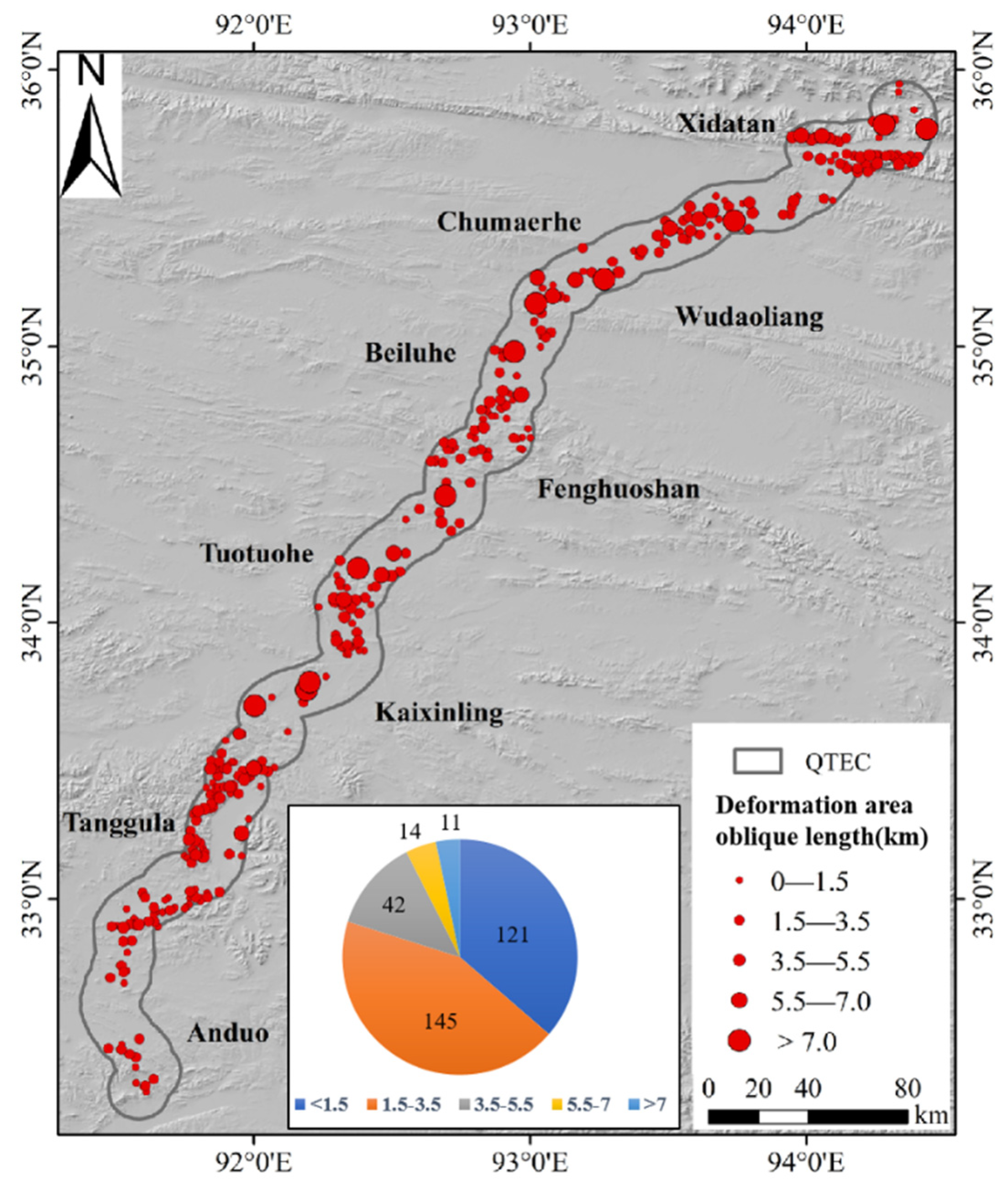
4.4. Detection of Permafrost Deformation Regions
5. Discussion
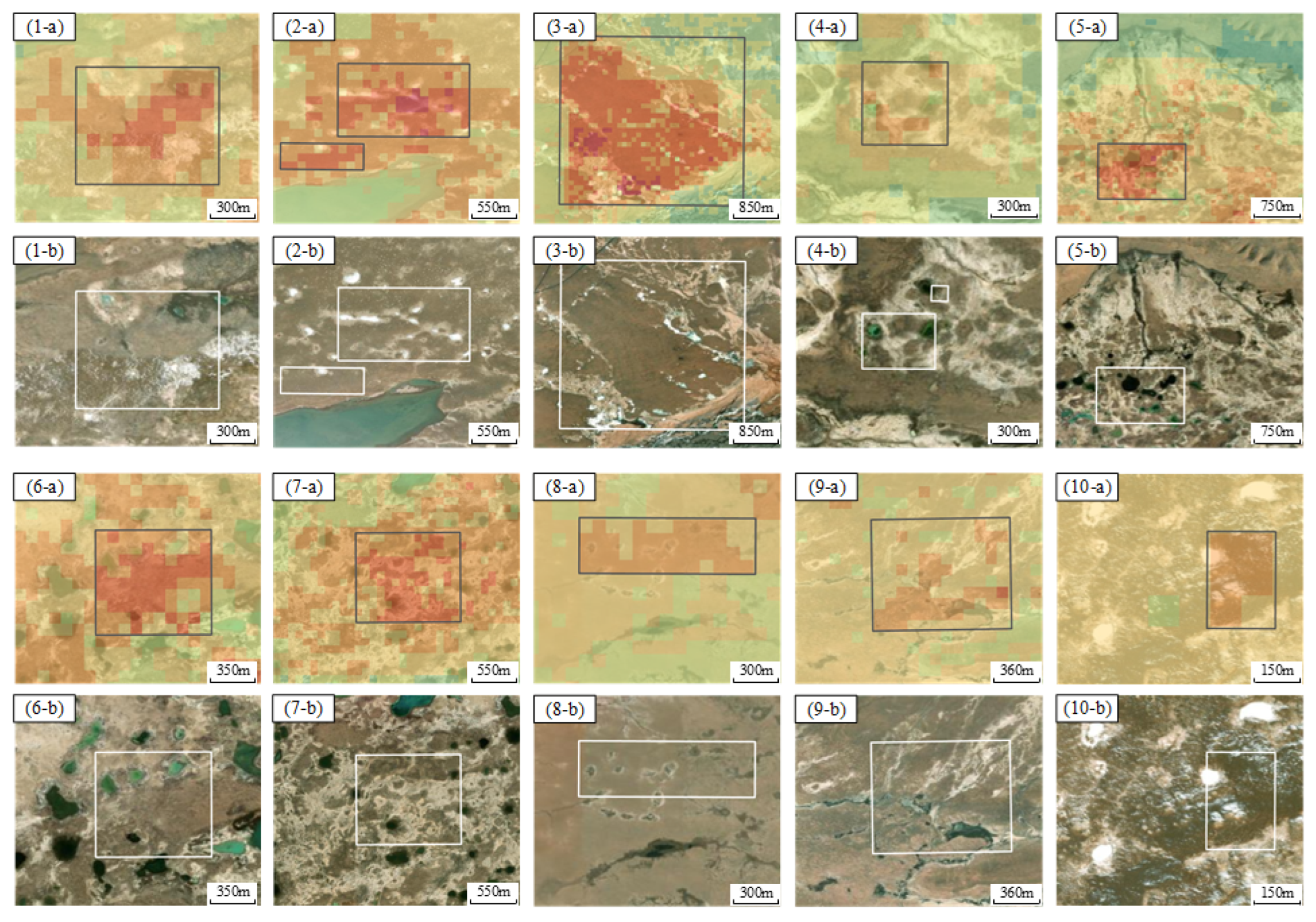
5.1. Detection of Obvious Settlement Regions Along the QTEC
5.2. Generalization Ability of Deep Learning Models
5.3. Limitations
- (1)
- For areas with significant incoherence, we relied on machine learning-based deformation simulation results for deformation area detection. Despite the relatively high accuracy of machine learning simulations, some errors in the simulations may lead to bias in the subsequent extraction results. In areas where the deformation values are close to the detection threshold, the underestimation of the results based on machine learning may lead to inaccuracies in the detection outcomes. In regions characterized by high coherence values, employing direct deep learning monitoring rather than machine learning simulations can mitigate errors induced by simulation processes.
- (2)
- During subsidence area detection, this study only considered deformation information and neglected environmental factors, such as geological conditions, water storage, and vegetation cover, which are crucial for deformation area monitoring [65,66]. In future work, we will integrate deformation and other environmental factors for permafrost thawing region detection.
- (3)
- Since there are no InSAR results available for other permafrost regions, the proposed method has only been applied in the Zonag Lake Basin. Future testing in other plateau regions will be necessary to validate the effectiveness of the method. This may require a more extensive set of training samples to accommodate the varied demands of different scenarios.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| InSAR | interferometric synthetic aperture radar |
| QTEC | Qinghai–Tibet Engineering Corridor |
| SVR | support vector regression |
| QTP | Qinghai–Tibet Plateau |
| GNSS | Global Navigation Satellite System |
| RTSs | retrogressive thaw slumps |
| NDVI | normalized difference vegetation index |
| DL | deep learning |
| MAGT | mean annual ground temperature |
| ESA | European Space Agency |
| TWI | topographic wetness index |
| VIC | volumetric ice content |
| ALT | active layer thickness |
| SRTM | Shuttle Radar Topography Mission |
| DEM | digital elevation model |
| ECMWF | European Center for Medium-Range Weather Forecasts |
| SBAS-InSAR | small baseline subset-InSAR |
| ESD | enhanced spectral diversity |
| MCF | minimum cost flow |
| LOS | light of sight |
| RF | random forest |
| GBDT | gradient boosting decision tree |
| FPN | feature-pyramid network |
| RPN | region proposal network |
| RoI | Region of Interest |
| AP | average precision |
| IoU | intersection over union |
Appendix A
| Soil | Type | Silt clay | Silt loam | Clay | Sand | NPCR * |
| Model value | 34 | 20 | 27 | 14 | 0 | |
| NDVI | Type | >0.7 | 0.5~0.7 | 0.3~0.5 | 0.1~0.3 | <0.1 |
| Model value | 28 | 23 | 18 | 13 | 8 | |
| Slope | Type | <4 | 4~8 | 8~16 | 16~25 | >25 |
| Model value | 18 | 23 | 13 | 8 | 5 | |
| MAGT | Type | <−5 | −5~−3 | −3~−1.5 | −1.5~−0.5 | 0.5~0 |
| Model value | 8 | 10 | 13 | 11 | 5 |
| Ice Content Type | Poor-Ice | Icy | Ice-Rich | Saturated-Ice | Ice with Soil |
|---|---|---|---|---|---|
| Model value | <48 | 48–58 | 58–68 | 68–80 | 80–100 |
References
- Hjort, J.; Streletskiy, D.; Doré, G.; Wu, Q.; Bjella, K.; Luoto, M. Impacts of permafrost degradation on infrastructure. Nat. Rev. Earth Environ. 2022, 3, 24–38. [Google Scholar] [CrossRef]
- Ran, Y.; Cheng, G.; Dong, Y.; Hjort, J.; Lovecraft, A.L.; Kang, S.; Li, X. Permafrost degradation increases risk and large future costs of infrastructure on the Third Pole. Commun. Earth Environ. 2022, 3, 238. [Google Scholar] [CrossRef]
- Hjort, J.; Karjalainen, O.; Aalto, J.; Westermann, S.; Romanovsky, V.E.; Nelson, F.E.; Etzelmüller, B.; Luoto, M. Degrading permafrost puts Arctic infrastructure at risk by mid-century. Nat. Commun. 2018, 9, 5147. [Google Scholar] [CrossRef]
- Chen, F.; Lin, H.; Li, Z.; Chen, Q.; Zhou, J. Interaction between permafrost and infrastructure along the Qinghai–Tibet Railway detected via jointly analysis of C-and L-band small baseline SAR interferometry. Remote Sens. Environ. 2012, 123, 532–540. [Google Scholar] [CrossRef]
- Wu, Q.B.; Cheng, G.D.; Ma, W.; Niu, F.; Sun, Z.Z. Technical approaches on permafrost thermal stability for Qinghai–Tibet Railway. Geomech. Geoengin. Int. J. 2006, 1, 119–127. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, T.; Wahr, J. InSAR measurements of surface deformation over permafrost on the North Slope of Alaska. J. Geophys. Res. Earth Surf. 2010, 115, F0302. [Google Scholar] [CrossRef]
- Du, Y.; Feng, G.; Peng, X.; Li, Z. Subsidence evolution of the Leizhou Peninsula, China, Based on InSAR observation from 1992 to 2010. Appl. Sci. 2017, 7, 466. [Google Scholar] [CrossRef]
- Shi, X.; Wang, J.; Jiang, M.; Zhang, S.; Wu, Y.; Zhong, Y. Extreme rainfall-related accelerations in landslides in Danba County, Sichuan Province, as detected by InSAR. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103109. [Google Scholar] [CrossRef]
- Rykhus, R.P.; Lu, Z. InSAR detects possible thaw settlement in the Alaskan Arctic Coastal Plain. Can. J. Remote Sens. 2008, 34, 100–112. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, Z.; Chen, Q.; Guo, Z.; Zhang, H.; Wang, M.; Gao, W.; Liu, X. Integrating remote sensing, GIS, and multi-criteria decision making for assessing PV potential in mountainous regions. Renew. Energy 2025, 241, 122340. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, H.; Wang, M.; Liu, X.; Chen, Q.; Wang, C.; Zhang, H. A review of satellite synthetic aperture radar interferometry applications in permafrost regions: Current status, challenges, and trends. IEEE Geosci. Remote Sens. Mag. 2022, 10, 93–114. [Google Scholar] [CrossRef]
- Ahmed, R.; Siqueira, P.; Hensley, S.; Chapman, B.; Bergen, K. A survey of temporal decorrelation from spaceborne L-Band repeat-pass InSAR. Remote Sens. Environ. 2011, 115, 2887–2896. [Google Scholar] [CrossRef]
- Duan, M.; Xu, B.; Li, Z.; Wu, W.; Cao, Y.; Liu, J.; Wang, G.; Hou, J. A new weighting method by considering the physical characteristics of atmospheric turbulence and decorrelation noise in SBAS-InSAR. Remote Sens. 2020, 12, 2557. [Google Scholar] [CrossRef]
- Chen, C.W. A spectral model for multilook InSAR phase noise due to geometric decorrelation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5207611. [Google Scholar] [CrossRef]
- Del Soldato, M.; Confuorto, P.; Bianchini, S.; Sbarra, P.; Casagli, N. Review of works combining GNSS and InSAR in Europe. Remote Sens. 2021, 13, 1684. [Google Scholar] [CrossRef]
- Fabris, M.; Battaglia, M.; Chen, X.; Menin, A.; Monego, M.; Floris, M. An integrated InSAR and GNSS approach to monitor land subsidence in the Po River Delta (Italy). Remote Sens. 2022, 14, 5578. [Google Scholar] [CrossRef]
- Jiao, Z.; Xu, Z.; Guo, R.; Zhou, Z.; Jiang, L. Potential of Multi-temporal InSAR for Detecting Retrogressive Thaw Slumps: A Case of the Beiluhe Region of the Tibetan Plateau. Int. J. Disaster Risk Sci. 2023, 14, 523–538. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Zhang, J.; Luo, J.; Yin, G. Automatic Identification of Thaw Slumps Based on Neural Network Methods and Thaw Slumping Susceptibility. Int. J. Disaster Risk Sci. 2023, 14, 539–548. [Google Scholar] [CrossRef]
- Huang, L.; Liu, L.; Luo, J.; Lin, Z.; Niu, F. Automatically quantifying evolution of retrogressive thaw slumps in Beiluhe (Tibetan Plateau) from multi-temporal CubeSat images. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102399. [Google Scholar] [CrossRef]
- Xia, Z.; Huang, L.; Fan, C.; Jia, S.; Lin, Z.; Liu, L.; Zhang, T. Retrogressive thaw slumps along the Qinghai–Tibet Engineering Corridor: A comprehensive inventory and their distribution characteristics. Earth Syst. Sci. Data 2022, 14, 3875–3887. [Google Scholar] [CrossRef]
- Witharana, C.; Udawalpola, M.R.; Liljedahl, A.K.; Jones, M.K.W.; Jones, B.M.; Hasan, A.; Manos, E. Automated Detection of Retrogressive Thaw Slumps in the High Arctic Using High-Resolution Satellite Imagery. Remote Sens. 2022, 14, 4132. [Google Scholar] [CrossRef]
- Huang, L.; Luo, J.; Lin, Z.; Niu, F.; Liu, L. Using deep learning to map retrogressive thaw slumps in the Beiluhe region (Tibetan Plateau) from CubeSat images. Remote Sens. Environ. 2020, 237, 111534. [Google Scholar] [CrossRef]
- Yang, Y.; Rogers, B.M.; Fiske, G.; Watts, J.; Potter, S.; Windholz, T.; Natali, S.M. Mapping retrogressive thaw slumps using deep neural networks. Remote Sens. Environ. 2023, 288, 113495. [Google Scholar] [CrossRef]
- Anantrasirichai, N.; Biggs, J.; Albino, F.; Bull, D. A deep learning approach to detecting volcano deformation from satellite imagery using synthetic datasets. Remote Sens. Environ. 2019, 230, 111179. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, L.; Dong, J.; Guo, J.; Wang, Y.; Liao, M. Automatic identification of active landslides over wide areas from time-series InSAR measurements using Faster RCNN. Int. J. Appl. Earth Obs. Geoinf. 2023, 124, 103516. [Google Scholar] [CrossRef]
- Wu, Z.; Ma, P.; Zheng, Y.; Gu, F.; Liu, L.; Lin, H. Automatic detection and classification of land subsidence in deltaic metropolitan areas using distributed scatterer InSAR and Oriented R-CNN. Remote Sens. Environ. 2023, 290, 113545. [Google Scholar] [CrossRef]
- Xi, N.; Mei, G.; Liu, Z.; Xu, N. Automatic identification of mining-induced subsidence using deep convolutional networks based on time-series InSAR data: A case study of Huodong mining area in Shanxi Province, China. Bull. Eng. Geol. Environ. 2023, 82, 78. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, C.; Zhang, H.; Tang, Y.; Zhang, B.; Li, L. Inversion of seismic source parameters from satellite InSAR data based on deep learning. Tectonophysics 2021, 821, 229140. [Google Scholar] [CrossRef]
- Luo, L.; Ma, W.; Zhuang, Y.; Zhang, Y.; Yi, S.; Xu, J.; Zhang, Z. The impacts of climate change and human activities on alpine vegetation and permafrost in the Qinghai-Tibet Engineering Corridor. Ecol. Indic. 2018, 93, 24–35. [Google Scholar] [CrossRef]
- Ma, W.; Mu, Y.; Zhang, J.; Yu, W.; Zhou, Z.; Chen, T. Lateral thermal influences of roadway and railway embankments in permafrost zones along the Qinghai-Tibet Engineering Corridor. Transp. Geotech. 2019, 21, 100285. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, M.; Liu, X.; Wang, C.; Zhang, H. Map and quantify the ground deformation around salt lake in Hoh Xil, Qinghai-Tibet Plateau using time-series InSAR from 2006 to 2018. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 858–869. [Google Scholar] [CrossRef]
- Zhongqiong, Z.; Qingbai, W.; Guanli, J.; Siru, G.; Ji, C.; Yongzhi, L. Changes in the permafrost temperatures from 2003 to 2015 in the Qinghai-Tibet Plateau. Cold Reg. Sci. Technol. 2020, 169, 102904. [Google Scholar] [CrossRef]
- Lu, H.L.; Li, F.F.; Gong, T.L.; Gao, Y.H.; Li, J.F.; Qiu, J. Reasons behind seasonal and monthly precipitation variability in the Qinghai-Tibet Plateau and its surrounding areas during 1979~2017. J. Hydrol. 2023, 619, 129329. [Google Scholar] [CrossRef]
- Niu, F.; Yin, G.; Luo, J.; Lin, Z.; Liu, M. Permafrost distribution along the Qinghai-Tibet Engineering Corridor, China using high-resolution statistical mapping and modeling integrated with remote sensing and GIS. Remote Sens. 2018, 10, 215. [Google Scholar] [CrossRef]
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Cheng, G. A new map of permafrost distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G.; Nan, Z.; Che, J.; Sheng, Y.; Wu, X. Mapping the permafrost stability on the Tibetan Plateau for 2005–2015. Sci. China Earth Sci. 2021, 64, 62–79. [Google Scholar] [CrossRef]
- Ni, J.; Wu, T.; Zhu, X.; Wu, X.; Pang, Q.; Zou, D.; Qiao, Y. Risk assessment of potential thaw settlement hazard in the permafrost regions of Qinghai-Tibet Plateau. Sci. Total Environ. 2021, 776, 145855. [Google Scholar] [CrossRef]
- Li, R.; Zhang, M.; Konstantinov, P.; Pei, W.; Tregubov, O.; Li, G. Permafrost degradation induced thaw settlement susceptibility research and potential risk analysis in the Qinghai-Tibet Plateau. CATENA 2022, 214, 106239. [Google Scholar] [CrossRef]
- Wu, Q.B.; Dong, X.F.; Liu, Y.Z. Spatial Distribution Model of High Ice Content Frozen Soil along Qinghai-Tibetan Highway—A GIS-aided model. J. Glaciol. Geocryol. 2004, 26, 137–141. [Google Scholar]
- Pan, X.; Li, Y.; Yu, Q.; Shi, X.; Yang, D.; Roth, K. Effects of stratified active layers on high-altitude permafrost warming: A case study on the Qinghai–Tibet Plateau. Cryosphere 2016, 10, 1591–1603. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Zhang, Z.; Jin, Q.; Liu, L.; Wang, M.; Zhang, X. Improved ALT retrieval in the Yellow River source region using time-series InSAR and multilayer soil moisture modeling. J. Hydrol. 2025, 654, 132847. [Google Scholar] [CrossRef]
- Wang, L.; Marzahn, P.; Bernier, M.; Charbonneau, F.; Zhang, Y. Sentinel-1 InSAR measurements of deformation over discontinuous permafrost terrain, Northern Quebec, Canada. Remote Sens. Environ. 2020, 248, 111965. [Google Scholar] [CrossRef]
- Rouyet, L.; Lauknes, T.R.; Christiansen, H.H.; Strand, S.M.; Larsen, Y. Seasonal dynamics of a permafrost landscape, Adventdalen, Svalbard, investigated by InSAR. Remote Sens. Environ. 2019, 231, 111236. [Google Scholar] [CrossRef]
- Fattahi, H.; Agram, P.; Simons, M. A network-based enhanced spectral diversity approach for TOPS time-series analysis. IEEE Trans. Geosci. Remote Sens. 2016, 55, 777–786. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorquí, J.J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Khodaei, B.; Hashemi, H. An integrated InSAR-machine learning approach for ground deformation rate modeling in arid areas. J. Hydrol. 2022, 608, 127627. [Google Scholar] [CrossRef]
- Chen, J.; Lin, X.; Wu, T.; Hao, J.; Wu, X.; Zou, D.; Zhu, X.; Hu, G.; Qiao, Y.; Wang, D.; et al. Predicting seasonal deformation using InSAR and machine learning in the permafrost regions of the Yangtze River source region. Water Resour. Res. 2024, 60, e2023WR036700. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Saravi, M.M. Land-subsidence spatial modeling using the random forest data-mining technique. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 147–159. [Google Scholar]
- Mohammady, M.; Pourghasemi, H.R.; Amiri, M. Land subsidence susceptibility assessment using random forest machine learning algorithm. Environ. Earth Sci. 2019, 78, 92. [Google Scholar] [CrossRef]
- Chen, B.Q.; Deng, K.Z. Integration of D-InSAR technology and PSO-SVR algorithm for time series monitoring and dynamic prediction of coal mining subsidence. Surv. Rev. 2014, 46, 392–400. [Google Scholar] [CrossRef]
- Mitchell, R.; Frank, E. Accelerating the XGBoost algorithm using GPU computing. PeerJ Comput. Sci. 2017, 3, e127. [Google Scholar] [CrossRef]
- Gu, Z.; Cao, M.; Wang, C.; Liu, J.; He, B. Research on mining maximum subsidence prediction based on genetic algorithm combined with XGBoost model. Sustainability 2022, 14, 10421. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Khosravi, K.; Bui, D.T.; Dholakia, M.B. A comparison of Support Vector Machines and Bayesian algorithms for landslide susceptibility modelling. Geocarto Int. 2019, 34, 1385–1407. [Google Scholar] [CrossRef]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.; Berg, A. SSD: Single shot multibox detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; pp. 21–37. [Google Scholar]
- Zhu, X.; Lyu, S.; Wang, X.; Zhao, Q. TPH-YOLOv5: Improved YOLOv5 based on transformer prediction head for object detection on drone-captured scenarios. In Proceedings of the IEEE/CVF International Conference on Computer Vision 2021, Montreal, QC, Canada, 11–17 October 2021; pp. 2778–2788. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision 2017, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Wu, Q.B.; Zhang, T.J. Recent permafrost warming on the Qinghai-Tibetan Plateau. J. Geophys. Res. Atmos. 2008, 113, D1310. [Google Scholar] [CrossRef]
- Han, J.P.; Lu, P. Retrieving surface deformation of the Qinghai-Tibet railway across permafrost areas from InSAR. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar]
- Wang, J.; Wang, C.; Zhang, H.; Tang, Y.; Duan, W.; Dong, L. Freeze-thaw deformation cycles and temporal-spatial distribution of permafrost along the Qinghai-Tibet Railway using multitrack InSAR processing. Remote Sens. 2021, 13, 4744. [Google Scholar] [CrossRef]
- Hong, Z.; Jin, S. Permafrost deformation in Qinghai-Tibet Plateau time-series PS-InSAR. Bull. Surv. Mapp. 2021, 1, 35–40. [Google Scholar]
- Mu, M.; Mu, C.; Chen, X. The distribution data of thermokarst lakes along the Qinghai-Tibet Highway (1991–2020); National Tibetan Plateau/Third Pole Environment Data Center: Beijing, China, 2023. [Google Scholar] [CrossRef]
- Xu, G.; Wu, Y.; Liu, S.; Cheng, S.; Zhang, Y.; Pan, Y.; Nkwazema, O.C. How 2022 extreme drought influences the spatiotemporal variations of terrestrial water storage in the Yangtze River Catchment: Insights from GRACE-based drought severity index and in-situ measurements. J. Hydrol. 2023, 626, 130245. [Google Scholar] [CrossRef]
- Wang, R.; Wang, M.; Ren, C.; Chen, G.; Mills, G.; Ching, J. Mapping local climate zones and its applications at the global scale: A systematic review of the last decade of progress and trend. Urban Climate 2024, 57, 102129. [Google Scholar] [CrossRef]

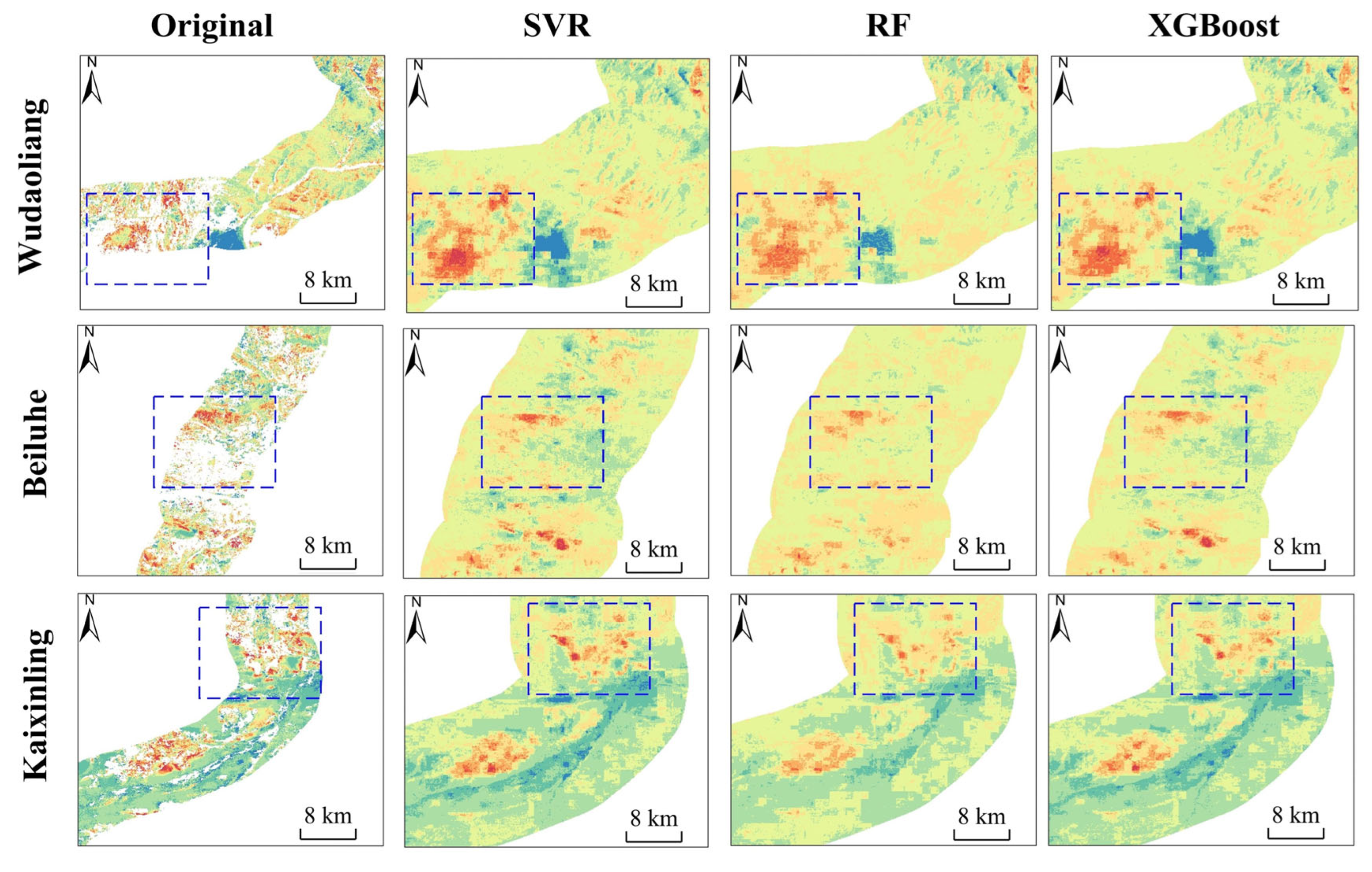
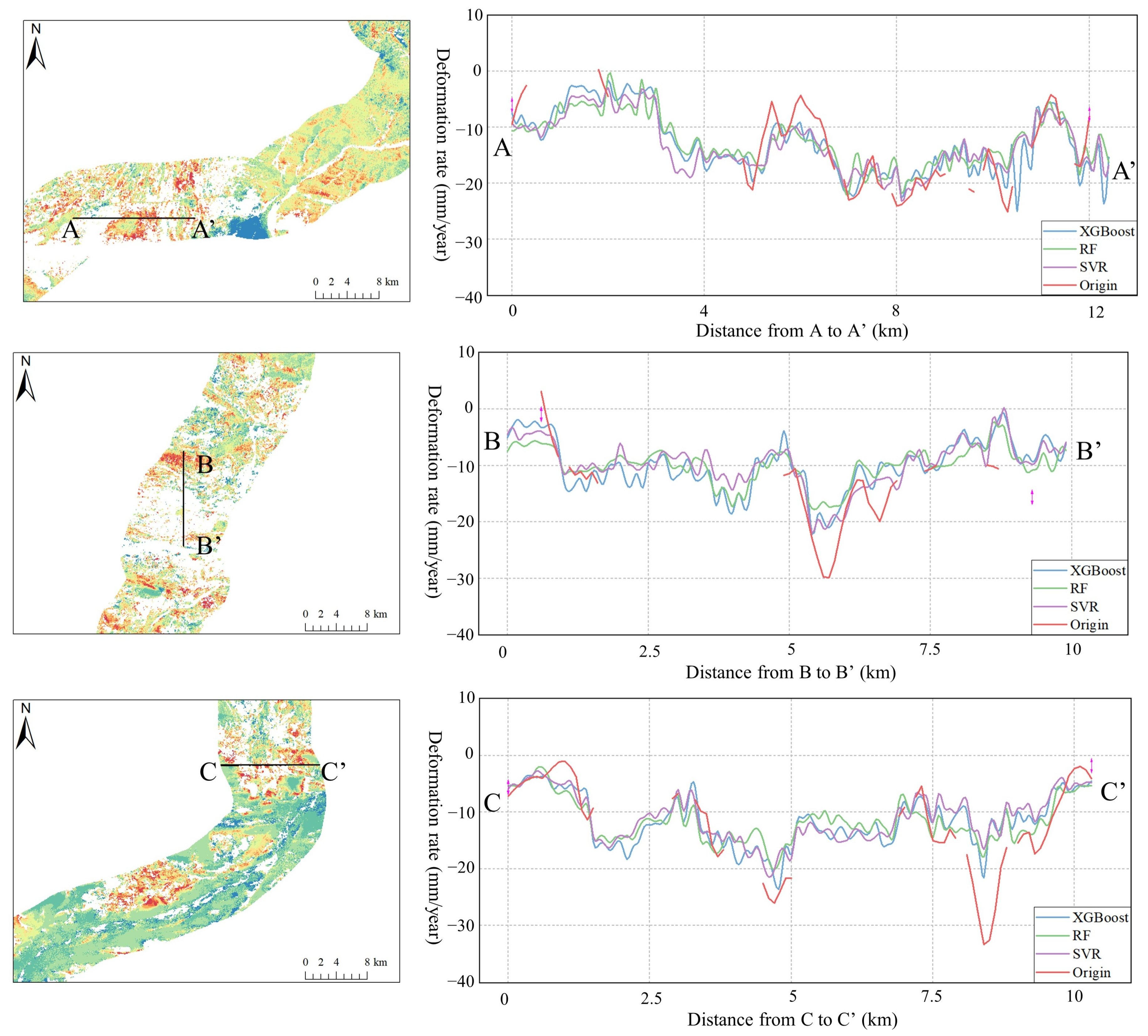
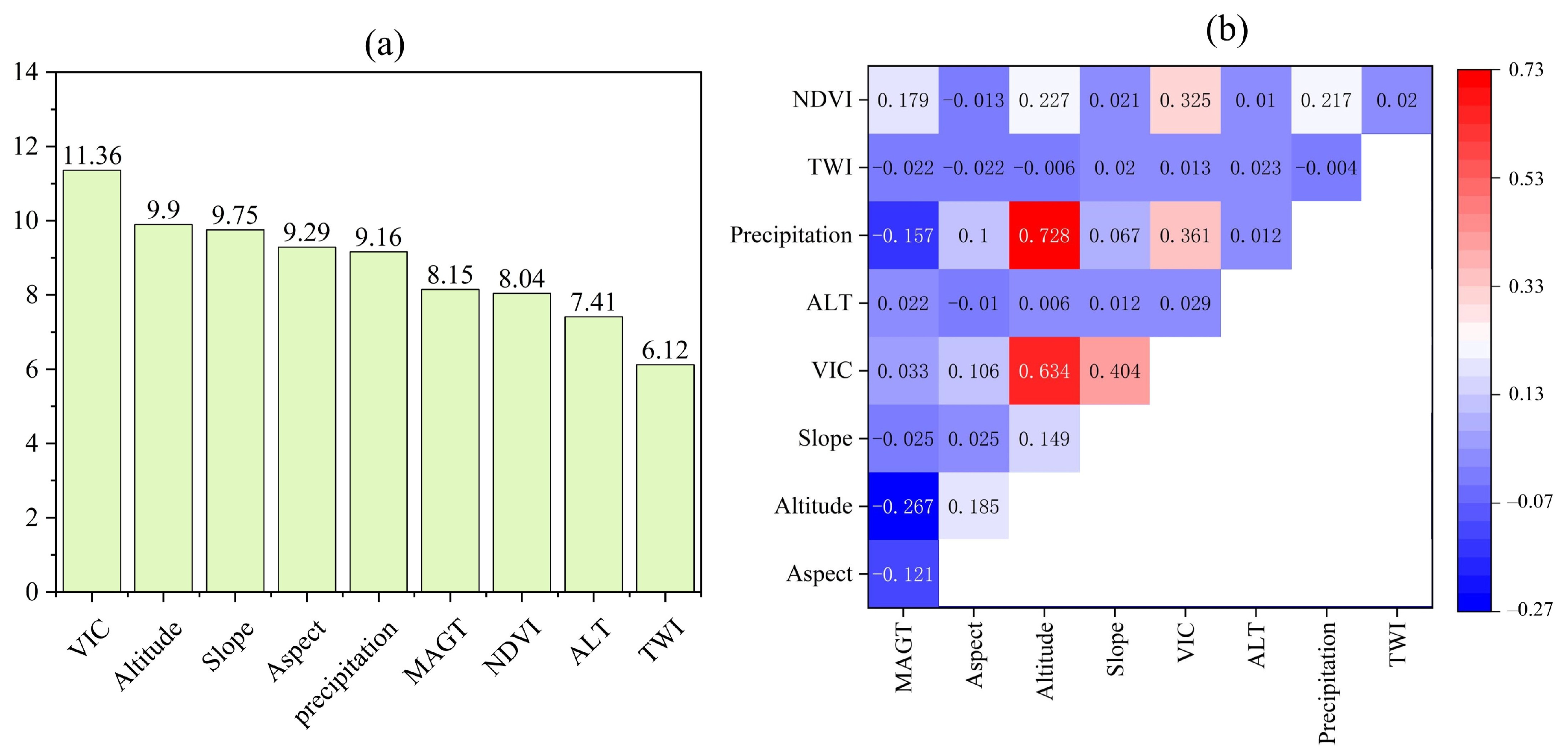
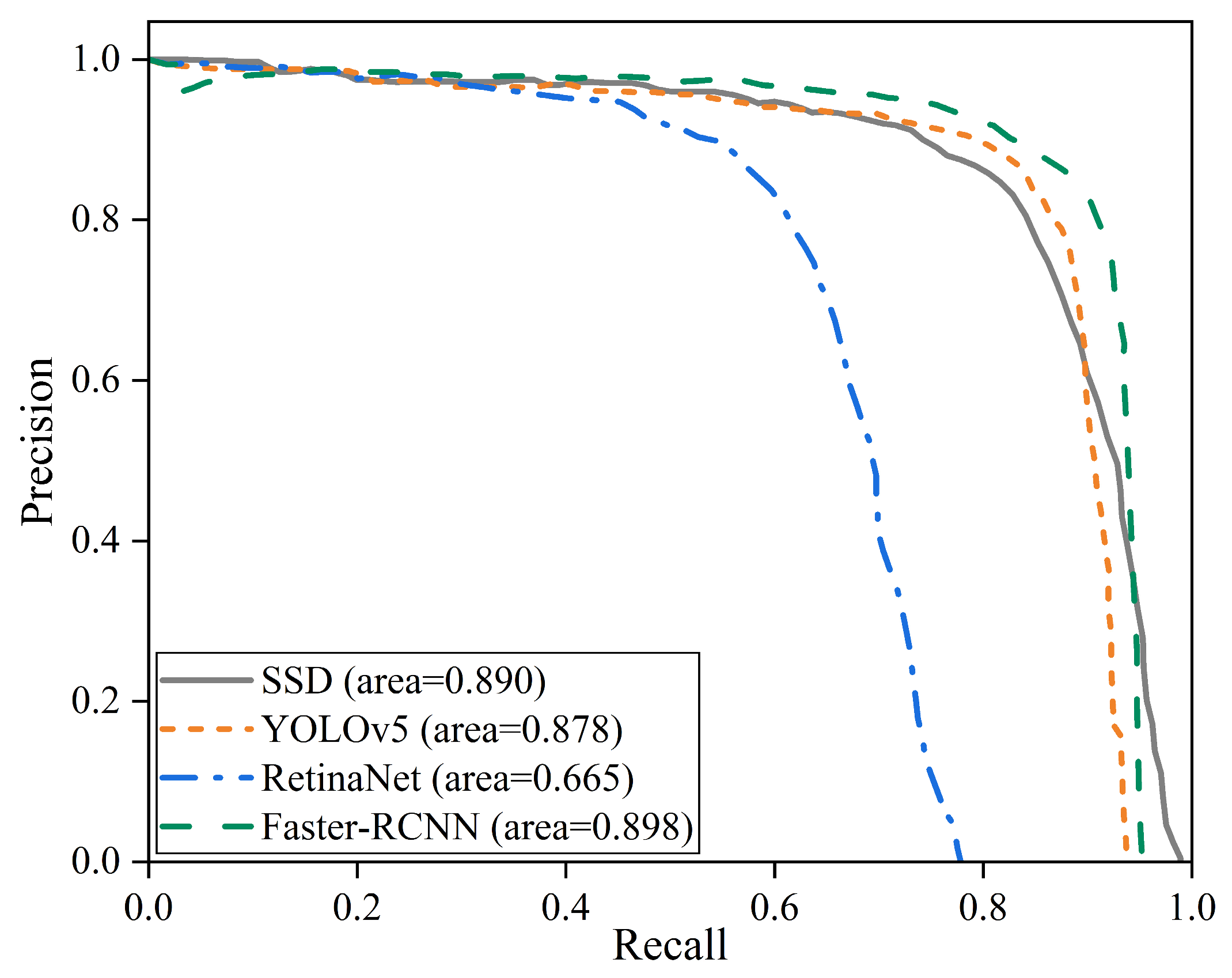
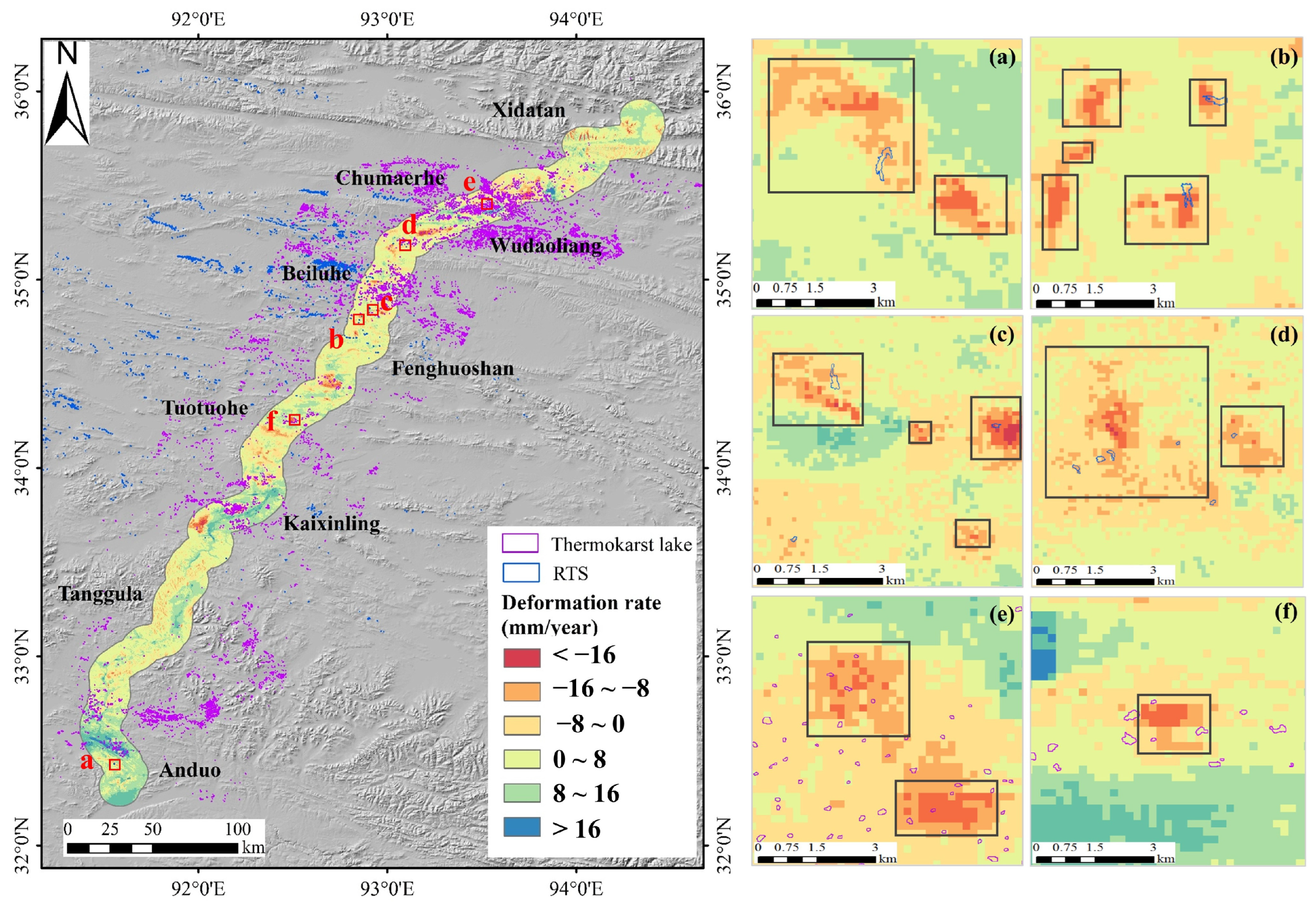
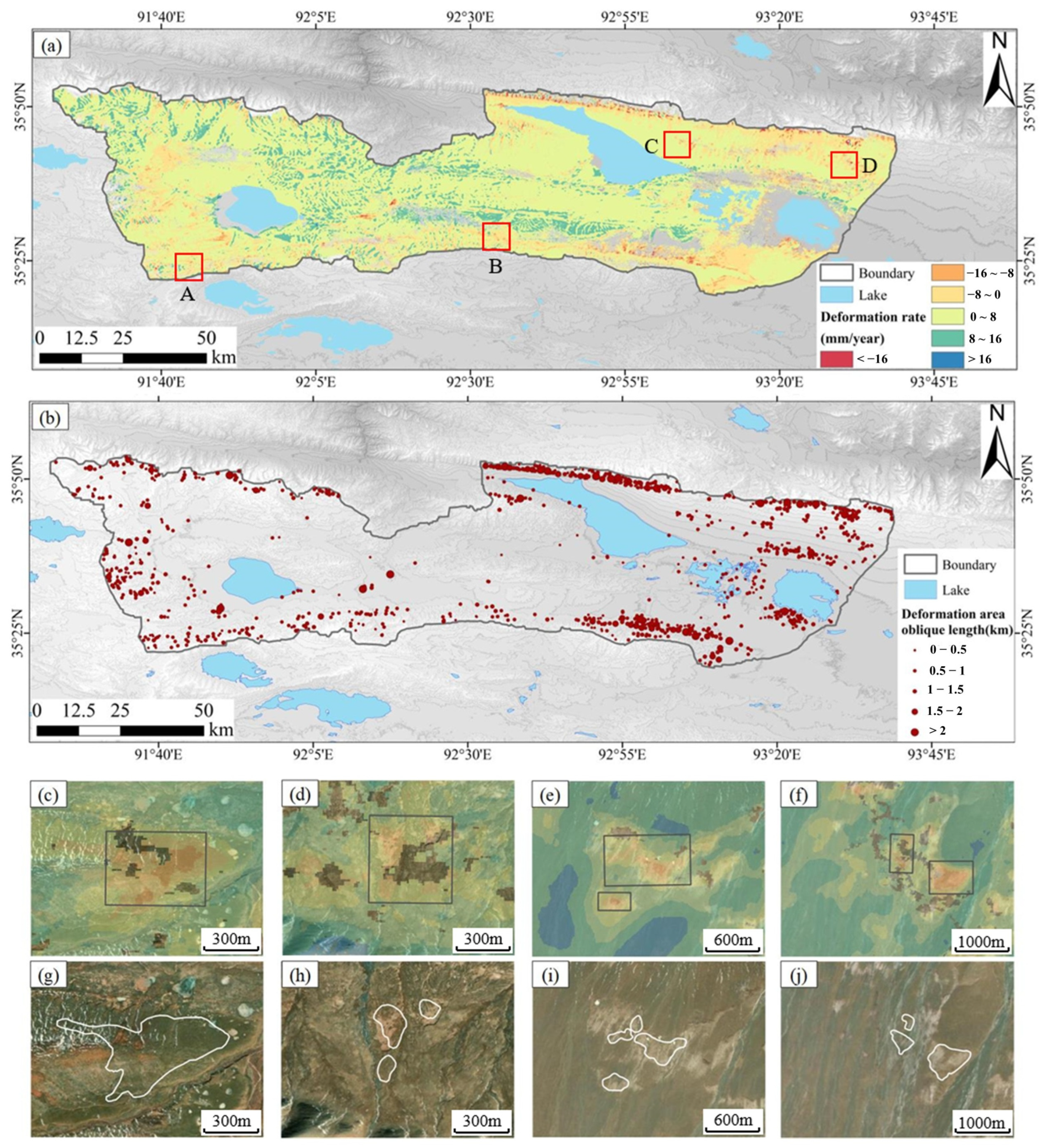
| Deformation Rate (mm/year) | −5~0 | −10~−5 | −15~−10 | −20~−15 | −25~−20 | <−25 |
|---|---|---|---|---|---|---|
| SVR | 0.3 | 1.0 | 3.8 | 18.2 | 53.4 | 23.3 |
| RF | 0.2 | 0.7 | 3.5 | 21.4 | 55.8 | 18.5 |
| XGBoost | 0.4 | 1.10 | 4.1 | 17.8 | 51.6 | 24.9 |
| Method | Backbone | F1-Score | AP50 (%) | AP50-95 (%) |
|---|---|---|---|---|
| SSD | VGG | 0.82 | 87.8 | 51.4 |
| YOLOv5 | CSPDarknet | 0.82 | 89.0 | 53.2 |
| RetinaNet | ResNet50 | 0.66 | 66.5 | 41.2 |
| Faster R-CNN | ResNet50 | 0.85 | 89.8 | 54.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, P.; Lin, H.; Zhang, Z.; Deng, H. Enhanced Detection of Permafrost Deformation with Machine Learning and Interferometric SAR Along the Qinghai–Tibet Engineering Corridor. Remote Sens. 2025, 17, 2231. https://doi.org/10.3390/rs17132231
Fan P, Lin H, Zhang Z, Deng H. Enhanced Detection of Permafrost Deformation with Machine Learning and Interferometric SAR Along the Qinghai–Tibet Engineering Corridor. Remote Sensing. 2025; 17(13):2231. https://doi.org/10.3390/rs17132231
Chicago/Turabian StyleFan, Peng, Hong Lin, Zhengjia Zhang, and Heming Deng. 2025. "Enhanced Detection of Permafrost Deformation with Machine Learning and Interferometric SAR Along the Qinghai–Tibet Engineering Corridor" Remote Sensing 17, no. 13: 2231. https://doi.org/10.3390/rs17132231
APA StyleFan, P., Lin, H., Zhang, Z., & Deng, H. (2025). Enhanced Detection of Permafrost Deformation with Machine Learning and Interferometric SAR Along the Qinghai–Tibet Engineering Corridor. Remote Sensing, 17(13), 2231. https://doi.org/10.3390/rs17132231







