Multi-Pattern Scanning Mamba for Cloud Removal
Highlights
- Designed a Multi-Pattern Scanning Mamba block with a dynamic, path-aware mechanism to effectively capture 2D spatial dependencies.
- Built a U-Net based framework with multi-scale supervision for cloud removal.
- Achieved state-of-the-art performance on RICE1, RICE2, and T-CLOUD datasets.
- Provided an efficient and effective solution for remote-sensing cloud removal.
Abstract
1. Introduction
- We propose a multi-pattern scanning Mamba (MPSM) block that adapts the 1D Mamba architecture for 2D images to comprehensively model the complex long-range spatial dependencies crucial for cloud removal.
- We introduce a dynamic path-aware (DPA) mechanism within the MPSM block to recalibrate feature contributions from diverse paths, enhancing the model’s spatial awareness.
- We propose a multi-pattern scanning Mamba framework with multi-scale supervision, which enables the model to attend to both coarse global structures and local fine details.
2. Related Works
2.1. Convolutional Neural Networks-Based Cloud Removal Algorithms
2.2. Transformer-Based Cloud Removal Algorithms
2.3. State Space Model-Based Algorithms
3. Method
3.1. Preliminaries
3.1.1. State Space Models
3.1.2. Mamba
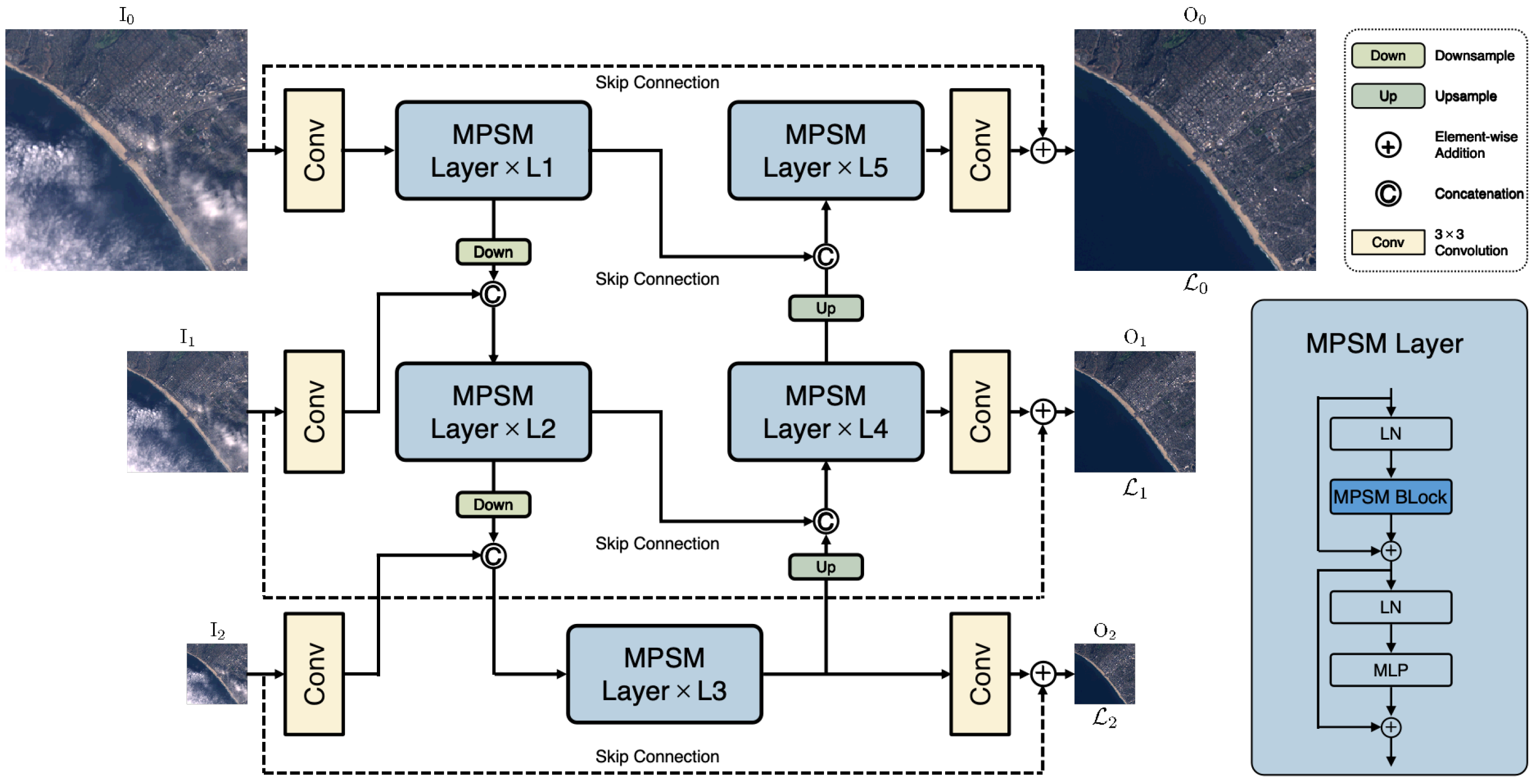
3.2. Overall Framework
3.2.1. Network Architecture
3.2.2. MPSM Layer
3.2.3. Multi-Scale Loss Function
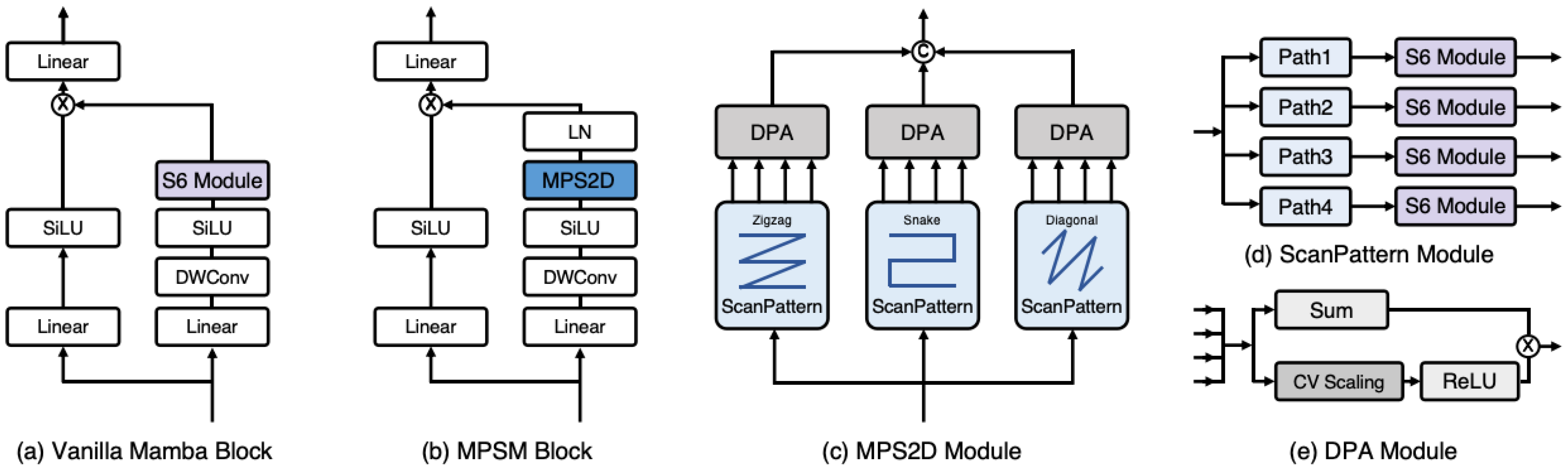
3.3. Multi-Pattern Scanning Mamba Block
3.3.1. Multi-Pattern Scanning 2D Module
3.3.2. ScanPattern Module
3.3.3. Dynamic Path-Aware Module
| Algorithm 1 Pseudo-Code for Multi-Pattern Scanning 2D (MPS2D) module |
Input: , a feature map of shape (batch size, height, width, channel); m, number of heads; k, number of traversal paths. Output: , result of MPS2D module with shape .
|
4. Results
4.1. Experimental Setting
4.1.1. Datasets
4.1.2. Evaluation Metrics
4.1.3. Implementation Details
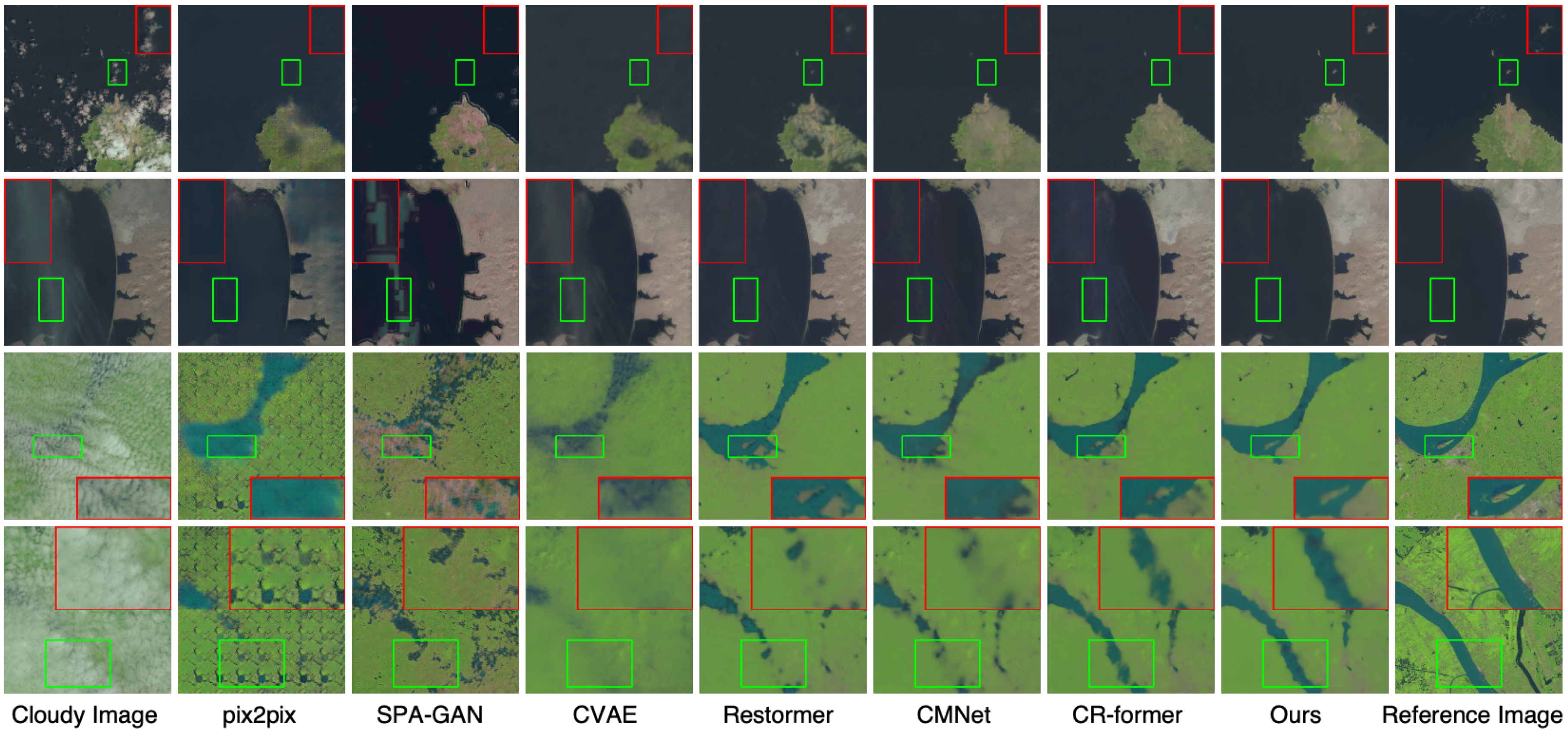
4.2. Comparison with State-of-the-Art Methods
4.3. Evaluation on the Multi-Modal SEN12MS-CR Dataset
5. Discussion
5.1. Architecture-Level Ablations
5.2. Comparison Under Varying Cloud and Surface Conditions
5.3. Efficiency and Scalability
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Azimi, S.M.; Vig, E.; Bahmanyar, R.; Körner, M.; Reinartz, P. Towards multi-class object detection in unconstrained remote sensing imagery. In Proceedings of the Asian Conference on Computer Vision, Perth, Australia, 2–6 December 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 150–165. [Google Scholar]
- Wang, P.; Sun, X.; Diao, W.; Fu, K. FMSSD: Feature-merged single-shot detection for multiscale objects in large-scale remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2019, 58, 3377–3390. [Google Scholar] [CrossRef]
- Carranza-García, M.; García-Gutiérrez, J.; Riquelme, J.C. A framework for evaluating land use and land cover classification using convolutional neural networks. Remote Sens. 2019, 11, 274. [Google Scholar] [CrossRef]
- Tong, X.Y.; Xia, G.S.; Lu, Q.; Shen, H.; Li, S.; You, S.; Zhang, L. Land-cover classification with high-resolution remote sensing images using transferable deep models. Remote Sens. Environ. 2020, 237, 111322. [Google Scholar] [CrossRef]
- Stumpf, F.; Schneider, M.K.; Keller, A.; Mayr, A.; Rentschler, T.; Meuli, R.G.; Schaepman, M.; Liebisch, F. Spatial monitoring of grassland management using multi-temporal satellite imagery. Ecol. Indic. 2020, 113, 106201. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, B.; Zhang, W.; Hong, D.; Zhao, B.; Li, Z. Cloud removal with SAR-optical data fusion using a unified spatial–spectral residual network. IEEE Trans. Geosci. Remote Sens. 2023, 62, 5600820. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Malek, S.; Melgani, F.; Bazi, Y.; Alajlan, N. Reconstructing cloud-contaminated multispectral images with contextualized autoencoder neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 56, 2270–2282. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Chen, D.; Chan, J.C.W. Thin cloud removal with residual symmetrical concatenation network. ISPRS J. Photogramm. Remote Sens. 2019, 153, 137–150. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, X.; Pun, M.O. Cloud removal in optical remote sensing imagery using multiscale distortion-aware networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5512605. [Google Scholar] [CrossRef]
- Ding, H.; Zi, Y.; Xie, F. Uncertainty-based thin cloud-removal network via conditional variational autoencoders. In Proceedings of the Asian Conference on Computer Vision, Macao, China, 4–8 December 2022; pp. 469–485. [Google Scholar]
- Wu, P.; Pan, Z.; Tang, H.; Hu, Y. Cloudformer: A cloud-removal network combining self-attention mechanism and convolution. Remote Sens. 2022, 14, 6132. [Google Scholar] [CrossRef]
- Zhao, B.; Zhou, J.; Xu, H.; Feng, X.; Sun, Y. PM-LSMN: A Physical-Model-based Lightweight Self-attention Multiscale Net For Thin Cloud Removal. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5003405. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Xu, F.; Shi, Y.; Ebel, P.; Yu, L.; Xia, G.S.; Yang, W.; Zhu, X.X. GLF-CR: SAR-enhanced cloud removal with global–local fusion. ISPRS J. Photogramm. Remote Sens. 2022, 192, 268–278. [Google Scholar] [CrossRef]
- Chi, K.; Yuan, Y.; Wang, Q. Trinity-Net: Gradient-guided Swin transformer-based remote sensing image dehazing and beyond. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4702914. [Google Scholar] [CrossRef]
- Liu, J.; Pan, B.; Shi, Z. Cascaded Memory Network for Optical Remote Sensing Imagery Cloud Removal. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5613611. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Online, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient transformer for high-resolution image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5728–5739. [Google Scholar]
- Wu, Y.; Deng, Y.; Zhou, S.; Liu, Y.; Huang, W.; Wang, J. CR-former: Single Image Cloud Removal with Focused Taylor Attention. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5651614. [Google Scholar] [CrossRef]
- Gu, A.; Goel, K.; Ré, C. Efficiently modeling long sequences with structured state spaces. arXiv 2021, arXiv:2111.00396. [Google Scholar]
- Gu, A.; Johnson, I.; Goel, K.; Saab, K.; Dao, T.; Rudra, A.; Ré, C. Combining recurrent, convolutional, and continuous-time models with linear state space layers. Adv. Neural Inf. Process. Syst. 2021, 34, 572–585. [Google Scholar]
- Smith, J.T.; Warrington, A.; Linderman, S.W. Simplified state space layers for sequence modeling. arXiv 2022, arXiv:2208.04933. [Google Scholar]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar] [CrossRef]
- Wen, X.; Pan, Z.; Hu, Y.; Liu, J. An Effective Network Integrating Residual Learning and Channel Attention Mechanism for Thin Cloud Removal. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 6507605. [Google Scholar] [CrossRef]
- Pan, H. Cloud removal for remote sensing imagery via spatial attention generative adversarial network. arXiv 2020, arXiv:2009.13015. [Google Scholar] [CrossRef]
- Singh, P.; Komodakis, N. Cloud-gan: Cloud removal for sentinel-2 imagery using a cyclic consistent generative adversarial networks. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1772–1775. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2223–2232. [Google Scholar]
- Ma, X.; Huang, Y.; Zhang, X.; Pun, M.O.; Huang, B. Cloud-egan: Rethinking cyclegan from a feature enhancement perspective for cloud removal by combining cnn and transformer. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 4999–5012. [Google Scholar] [CrossRef]
- Mao, R.; Li, H.; Ren, G.; Yin, Z. Cloud removal based on SAR-optical remote sensing data fusion via a two-flow network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7677–7686. [Google Scholar] [CrossRef]
- Anandakrishnan, J.; Sundaram, V.M.; Paneer, P. CERMF-Net: A SAR-Optical feature fusion for cloud elimination from Sentinel-2 imagery using residual multiscale dilated network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 11741–11749. [Google Scholar] [CrossRef]
- Wen, X.; Pan, Z.; Hu, Y.; Liu, J. Generative adversarial learning in YUV color space for thin cloud removal on satellite imagery. Remote Sens. 2021, 13, 1079. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Gu, J.; Kong, L.; Yang, X.; Yu, F. Dual aggregation transformer for image super-resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 12312–12321. [Google Scholar]
- Li, Y.; Fan, Y.; Xiang, X.; Demandolx, D.; Ranjan, R.; Timofte, R.; Van Gool, L. Efficient and explicit modelling of image hierarchies for image restoration. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Paris, France, 2–6 October 2023; pp. 18278–18289. [Google Scholar]
- Xu, M.; Deng, F.; Jia, S.; Jia, X.; Plaza, A.J. Attention mechanism-based generative adversarial networks for cloud removal in Landsat images. Remote Sens. Environ. 2022, 271, 112902. [Google Scholar] [CrossRef]
- Liu, H.; Huang, J.; Nie, J.; Xie, J.; Chen, L.; Zhou, X. Density Guided and Frequency Modulation Dehazing Network for Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 9533–9545. [Google Scholar] [CrossRef]
- Mehta, H.; Gupta, A.; Cutkosky, A.; Neyshabur, B. Long range language modeling via gated state spaces. arXiv 2022, arXiv:2206.13947. [Google Scholar] [CrossRef]
- Fu, D.Y.; Dao, T.; Saab, K.K.; Thomas, A.W.; Rudra, A.; Ré, C. Hungry hungry hippos: Towards language modeling with state space models. arXiv 2022, arXiv:2212.14052. [Google Scholar]
- Liu, Y.; Tian, Y.; Zhao, Y.; Yu, H.; Xie, L.; Wang, Y.; Ye, Q.; Jiao, J.; Liu, Y. Vmamba: Visual state space model. Adv. Neural Inf. Process. Syst. 2024, 37, 103031–103063. [Google Scholar]
- Guo, H.; Li, J.; Dai, T.; Ouyang, Z.; Ren, X.; Xia, S.T. Mambair: A simple baseline for image restoration with state-space model. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 222–241. [Google Scholar]
- Zhang, C.; Wang, F.; Zhang, X.; Wang, M.; Wu, X.; Dang, S. Mamba-CR: A state-space model for remote sensing image cloud removal. IEEE Trans. Geosci. Remote Sens. 2024, 63, 5601913. [Google Scholar] [CrossRef]
- Liu, J.; Pan, B.; Shi, Z. CR-Famba: A frequency-domain assisted mamba for thin cloud removal in optical remote sensing imagery. IEEE Trans. Multimed. 2025, 27, 5659–5668. [Google Scholar] [CrossRef]
- Martin, E.; Cundy, C. Parallelizing linear recurrent neural nets over sequence length. arXiv 2017, arXiv:1709.04057. [Google Scholar]
- Wang, J.; Zhu, W.; Wang, P.; Yu, X.; Liu, L.; Omar, M.; Hamid, R. Selective structured state-spaces for long-form video understanding. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 6387–6397. [Google Scholar]
- Li, K.; Li, X.; Wang, Y.; He, Y.; Wang, Y.; Wang, L.; Qiao, Y. Videomamba: State space model for efficient video understanding. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 237–255. [Google Scholar]
- Ma, J.; Li, F.; Wang, B. U-mamba: Enhancing long-range dependency for biomedical image segmentation. arXiv 2024, arXiv:2401.04722. [Google Scholar]
- Islam, M.M.; Hasan, M.; Athrey, K.S.; Braskich, T.; Bertasius, G. Efficient movie scene detection using state-space transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 18749–18758. [Google Scholar]
- Nguyen, E.; Goel, K.; Gu, A.; Downs, G.; Shah, P.; Dao, T.; Baccus, S.; Ré, C. S4nd: Modeling images and videos as multidimensional signals with state spaces. Adv. Neural Inf. Process. Syst. 2022, 35, 2846–2861. [Google Scholar]
- Qiao, Y.; Yu, Z.; Guo, L.; Chen, S.; Zhao, Z.; Sun, M.; Wu, Q.; Liu, J. Vl-mamba: Exploring state space models for multimodal learning. arXiv 2024, arXiv:2403.13600. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015. Proceedings, Part III 18. pp. 234–241. [Google Scholar]
- Lin, D.; Xu, G.; Wang, X.; Wang, Y.; Sun, X.; Fu, K. A remote sensing image dataset for cloud removal. arXiv 2019, arXiv:1901.00600. [Google Scholar] [CrossRef]
- Ebel, P.; Meraner, A.; Schmitt, M.; Zhu, X.X. Multisensor data fusion for cloud removal in global and all-season sentinel-2 imagery. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5866–5878. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Korhonen, J.; You, J. Peak signal-to-noise ratio revisited: Is simple beautiful? In Proceedings of the 2012 Fourth International Workshop on Quality of Multimedia Experience, Melbourne, Australia, 5–7 July 2012; pp. 37–38. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.; Barloon, P.; Goetz, A.F. The spectral image processing system (SIPS)—interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Meraner, A.; Ebel, P.; Zhu, X.X.; Schmitt, M. Cloud removal in Sentinel-2 imagery using a deep residual neural network and SAR-optical data fusion. ISPRS J. Photogramm. Remote Sens. 2020, 166, 333–346. [Google Scholar] [CrossRef]
- Ebel, P.; Garnot, V.S.F.; Schmitt, M.; Wegner, J.D.; Zhu, X.X. UnCRtainTS: Uncertainty quantification for cloud removal in optical satellite time series. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 2086–2096. [Google Scholar]




| Stage | Operation | In Size | Out Size | K/S |
|---|---|---|---|---|
| Conv | 3/1 | |||
| MPSM Layer × 1 | 3/1 | |||
| Inp, Conv, Cat | 3,1/1 | |||
| Conv | 3/1 | |||
| MPSM Layer × 2 | 3/1 | |||
| Inp, Conv, Cat | 3,1/1 | |||
| Conv | 3/1 | |||
| MPSM Layer × 8 | 3/1 | |||
| Conv, Add | 3/1 | |||
| Conv, Cat | 3/1 | |||
| MPSM Layer × 2 | 3/1 | |||
| Conv, Add | 3/1 | |||
| Conv, Cat | 3/1 | |||
| MPSM Layer × 1 | 3/1 | |||
| Conv, Add | 3/1 |
| Dataset | Source | Size | Training | Testing |
|---|---|---|---|---|
| RICE1 [51] | Google Earth | 512 × 512 | 400 | 100 |
| RICE2 [51] | Landsat 8 | 512 × 512 | 588 | 147 |
| T-CLOUD [11] | Landsat 8 | 256 × 256 | 2351 | 588 |
| SEN12MS-CR [52] | Sentinel series satellites | 256 × 256 | 114,325 | 7893 |
| Method | Backbone | RICE1 | Overhead | ||||
|---|---|---|---|---|---|---|---|
| MAE↓ | SAM↓ | PSNR↑ | SSIM↑ | Param (M) | FLOPs (G) | ||
| pix2pix [7] | CNN | 0.0253 | 4.11 | 31.97 | 0.9161 | 54.41 | 6.1 |
| SPA-GAN [26] | 0.0372 | 2.25 | 28.89 | 0.9144 | 0.21 | 15.2 | |
| RCA-Net [25] | 0.0906 | 5.26 | 23.02 | 0.9001 | 3.09 | 402.3 | |
| CVAE [11] | Transformer | 0.0198 | 1.11 | 33.70 | 0.9562 | 15.42 | 37.1 |
| Restormer [19] | 0.0176 | 1.01 | 35.42 | 0.9617 | 26.13 | 155.0 | |
| Trinity-Net [16] | 0.0305 | 2.20 | 30.12 | 0.9605 | 20.24 | 17.6 | |
| CMNet [17] | 0.0144 | 0.99 | 36.20 | 0.9619 | 16.51 | 236.0 | |
| CR-former [20] | 0.0141 | 0.95 | 36.56 | 0.9620 | 17.18 | 60.89 | |
| CR-Famba [42] | Mamba | 0.0325 | 1.64 | 30.91 | 0.9142 | 174.94 | 165.0 |
| Ours | 0.0140 | 0.92 | 36.65 | 0.9625 | 4.27 | 32.6 | |
| Method | Backbone | RICE2 | Overhead | ||||
|---|---|---|---|---|---|---|---|
| MAE↓ | SAM↓ | PSNR↑ | SSIM↑ | Params (M) | FLOPs (G) | ||
| pix2pix [7] | CNN | 0.0327 | 5.08 | 29.45 | 0.8473 | 54.41 | 6.1 |
| SPA-GAN [26] | 0.0403 | 3.36 | 27.51 | 0.8177 | 0.21 | 15.2 | |
| RCA-Net [25] | 0.1374 | 10.28 | 16.48 | 0.7942 | 3.09 | 402.3 | |
| CVAE [11] | Transformer | 0.0216 | 1.69 | 33.62 | 0.9079 | 15.42 | 37.1 |
| Restormer [19] | 0.0163 | 1.27 | 36.05 | 0.9155 | 26.13 | 155.0 | |
| Trinity-Net [16] | 0.0295 | 2.63 | 30.09 | 0.8771 | 20.24 | 17.6 | |
| CMNet [17] | 0.0167 | 1.29 | 35.82 | 0.9151 | 16.51 | 236.0 | |
| CR-former [20] | 0.0161 | 1.28 | 36.21 | 0.9151 | 17.18 | 60.89 | |
| CR-Famba [25] | Mamba | 0.0252 | 2.23 | 31.90 | 0.8495 | 174.94 | 165.0 |
| Ours | 0.0156 | 1.21 | 36.38 | 0.9168 | 4.27 | 32.6 | |
| Method | Backbone | T-CLOUD | Overhead | ||||
|---|---|---|---|---|---|---|---|
| MAE↓ | SAM↓ | PSNR↑ | SSIM↑ | Params (M) | FLOPs (G) | ||
| pix2pix [7] | CNN | 0.0449 | 10.01 | 25.64 | 0.7563 | 54.41 | 6.1 |
| SPA-GAN [26] | 0.0419 | 4.09 | 26.14 | 0.7954 | 0.21 | 15.2 | |
| RCA-Net [25] | 0.0692 | 3.90 | 23.38 | 0.8155 | 3.09 | 402.3 | |
| CVAE [11] | Transformer | 0.0342 | 2.95 | 28.19 | 0.8613 | 15.42 | 37.1 |
| Restormer [19] | 0.0248 | 2.46 | 30.49 | 0.8851 | 26.13 | 155.0 | |
| Trinity-Net [16] | 0.0365 | 3.67 | 27.33 | 0.8410 | 20.24 | 17.6 | |
| CMNet [17] | 0.0251 | 2.49 | 30.32 | 0.8823 | 16.51 | 236.0 | |
| CR-former [20] | 0.0242 | 2.46 | 30.60 | 0.8838 | 17.18 | 60.89 | |
| CR-Famba [42] | Mamba | 0.0262 | 2.48 | 30.10 | 0.8810 | 174.94 | 165.0 |
| Ours | 0.0237 | 2.36 | 30.82 | 0.8887 | 4.27 | 32.6 | |
| Model | MAE↓ | SAM↓ | PSNR↑ | SSIM↑ | Param (M) | FLOPs (G) |
|---|---|---|---|---|---|---|
| pix2pix [7] | 0.031 | 10.784 | 27.60 | 0.864 | 54.41 | 6.1 |
| SPA-GAN [26] | 0.045 | 18.085 | 24.78 | 0.754 | 0.21 | 15.2 |
| DSen2-CR [58] | 0.031 | 9.472 | 27.76 | 0.874 | 18.92 | 1240.2 |
| GLF-CR [15] | 0.028 | 8.981 | 28.64 | 0.885 | 14.82 | 250.0 |
| UnCRtainTS [59] | 0.027 | 8.320 | 28.90 | 0.880 | 0.56 | 37.1 |
| Ours | 0.026 | 8.220 | 29.59 | 0.893 | 4.27 | 32.6 |
| Components | RICE2 | Overhead | ||||||
|---|---|---|---|---|---|---|---|---|
| Zigzag | Snake | Diagonal | MAE↓ | SAM↓ | PSNR↑ | SSIM↑ | Param (M) | FLOPs (G) |
| ✓ | × | × | 0.0162 | 1.28 | 35.87 | 0.9159 | 4.38 | 33.45 |
| × | ✓ | × | 0.0165 | 1.25 | 35.94 | 0.9159 | 4.38 | 33.45 |
| × | × | ✓ | 0.0166 | 1.26 | 35.75 | 0.9155 | 4.38 | 33.45 |
| ✓ | ✓ | × | 0.0160 | 1.25 | 36.02 | 0.9166 | 4.30 | 32.82 |
| × | ✓ | ✓ | 0.0164 | 1.29 | 35.87 | 0.9153 | 4.30 | 32.82 |
| ✓ | × | ✓ | 0.0162 | 1.27 | 35.97 | 0.9152 | 4.30 | 32.82 |
| ✓ | ✓ | ✓ | 0.0157 | 1.25 | 36.07 | 0.9175 | 4.27 | 32.60 |
| Models | Components | RICE2 | Overhead | ||||
|---|---|---|---|---|---|---|---|
| MAE↓ | SAM↓ | PSNR↑ | SSIM↑ | Param (M) | FLOPs (G) | ||
| U-Net (Vanilla Mamba) | - | 0.0162 | 1.28 | 35.87 | 0.9159 | 4.38 | 33.45 |
| w/o DPA | 0.0157 | 1.25 | 36.07 | 0.9175 | 4.27 | 32.60 | |
| U-Net (MPSM) | w/o | 0.0159 | 1.24 | 36.25 | 0.9159 | 4.26 | 32.53 |
| full | 0.0156 | 1.21 | 36.38 | 0.9168 | 4.27 | 32.60 | |
| Model | Backbone | Param (M) | FLOPs (G) | Time (ms) | Memory (MB) |
|---|---|---|---|---|---|
| pix2pix [7] | CNN | 54.41 | 6.1 | 4.60 | 3357 |
| SPA-GAN [26] | 0.21 | 15.2 | 26.00 | 3749 | |
| CVAE [11] | Transformer | 15.42 | 37.1 | 15.10 | 1097 |
| Restormer [19] | 26.13 | 155.0 | 112.30 | 1629 | |
| CMNet [17] | 16.51 | 236.0 | 197.00 | 1607 | |
| CR-Former [20] | 17.18 | 60.8 | 72.88 | 1561 | |
| CR-Famba [42] | Mamba | 174.94 | 165.0 | 119.54 | 1716 |
| Ours | 4.27 | 32.6 | 75.78 | 1094 |
| Image Resolution | MAE↓ | SAM↓ | PSNR↑ | SSIM↑ | Param (M) | FLOPs (G) | Time (ms) | GPU Memory (MB) |
|---|---|---|---|---|---|---|---|---|
| 2048 × 2048 | 0.0239 | 1.58 | 33.27 | 0.9643 | 4.27 | 2117.63 | 6675.43 | 37154 |
| 1024 × 1024 | 0.0188 | 1.34 | 35.19 | 0.9472 | 4.27 | 534.53 | 1128.41 | 9664 |
| 768 × 768 | 0.0167 | 1.25 | 35.98 | 0.9393 | 4.27 | 300.03 | 522.97 | 5666 |
| 512 × 512 | 0.0157 | 1.25 | 36.07 | 0.9175 | 4.27 | 133.12 | 191.86 | 2798 |
| 384 × 384 | 0.0152 | 1.20 | 36.56 | 0.9186 | 4.27 | 73.34 | 105.05 | 1802 |
| 256 × 256 | 0.0157 | 1.26 | 36.24 | 0.9046 | 4.27 | 32.60 | 75.78 | 1094 |
| 128 × 128 | 0.0188 | 1.15 | 34.62 | 0.8696 | 4.27 | 8.15 | 65.10 | 704 |
| 64 × 64 | 0.0249 | 1.89 | 32.18 | 0.8406 | 4.27 | 2.03 | 62.53 | 644 |
| 32 × 32 | 0.0354 | 2.59 | 28.56 | 0.8098 | 4.27 | 0.51 | 54.72 | 510 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, X.; Deng, Y.; Huang, W.; Wu, Y.; Fang, J.; Wang, J. Multi-Pattern Scanning Mamba for Cloud Removal. Remote Sens. 2025, 17, 3593. https://doi.org/10.3390/rs17213593
Xin X, Deng Y, Huang W, Wu Y, Fang J, Wang J. Multi-Pattern Scanning Mamba for Cloud Removal. Remote Sensing. 2025; 17(21):3593. https://doi.org/10.3390/rs17213593
Chicago/Turabian StyleXin, Xiaomeng, Ye Deng, Wenli Huang, Yang Wu, Jie Fang, and Jinjun Wang. 2025. "Multi-Pattern Scanning Mamba for Cloud Removal" Remote Sensing 17, no. 21: 3593. https://doi.org/10.3390/rs17213593
APA StyleXin, X., Deng, Y., Huang, W., Wu, Y., Fang, J., & Wang, J. (2025). Multi-Pattern Scanning Mamba for Cloud Removal. Remote Sensing, 17(21), 3593. https://doi.org/10.3390/rs17213593






