JSPSR: Joint Spatial Propagation Super-Resolution Networks for Enhancement of Bare-Earth Digital Elevation Models from Global Data
Highlights
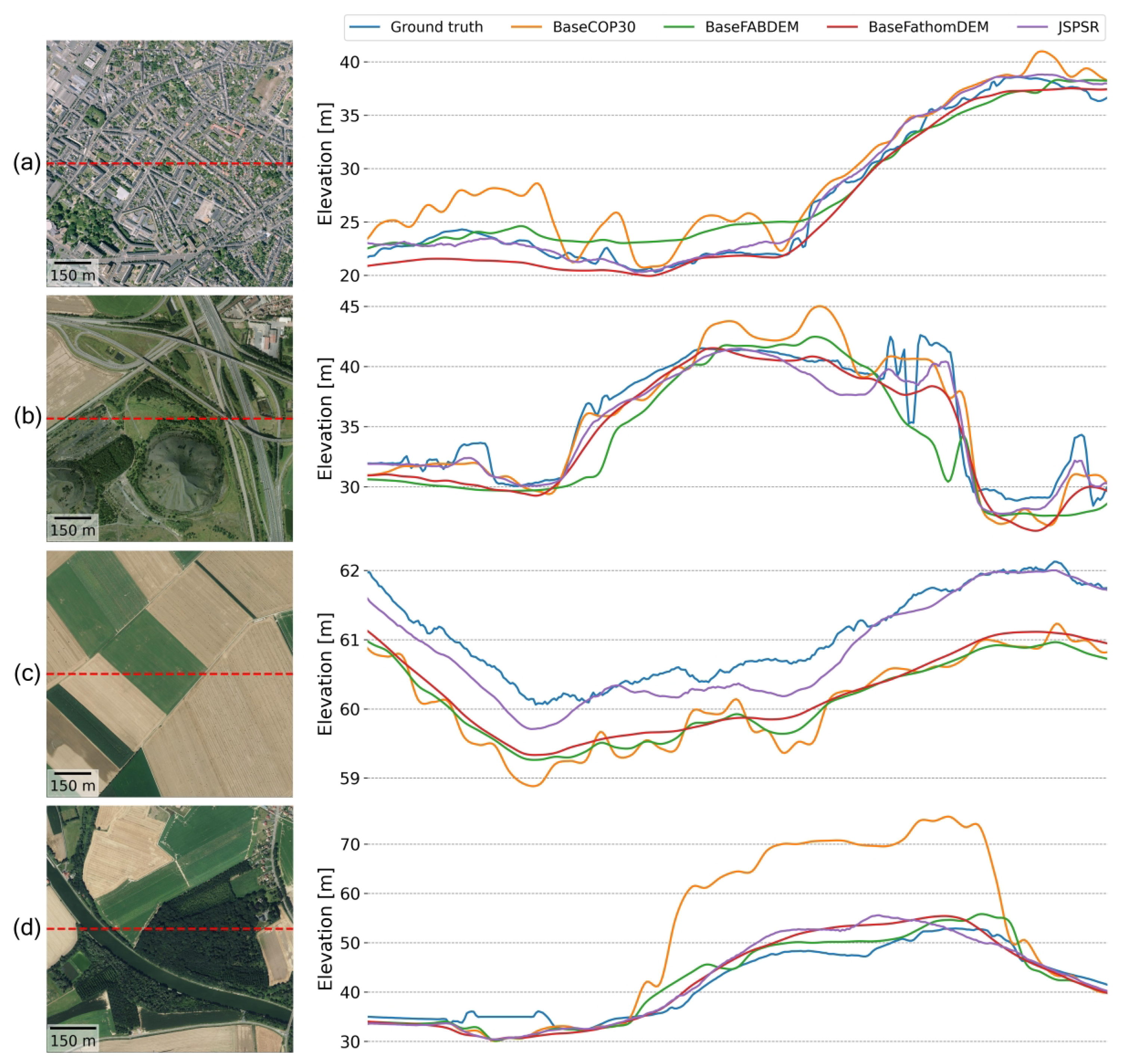
- We introduce JSPSR, a depth completion approach for real-world digital elevation model (DEM) super-resolution problems, and demonstrated that it is able to enhance global DEMs by accurately predicting ground terrain elevation at fine spatial resolution, including correction for surface features.
- JSPSR was used to predict elevation at 3 m and 8 m spatial resolution from globally-available 30 m Copernicus GLO-30 DEM data and aerial guidance imagery, achieving superior performance to other methods (∼1.05 m RMSE, up to a ∼72% improvement on GLO30 and ∼18% improvement on FathomDEM), at lower computational cost (over 4× faster than EDSR).
- Studies which require high-accuracy ground terrain elevation, e.g., flood risk assessment, may utilise JSPSR to enhance global elevation data such as the Copernicus GLO30 DEM, especially where airborne data such as LiDAR are unavailable.
- The high accuracy and low computational cost of JSPSR opens the possibility to create an open-access fine spatial resolution global elevation model with good accuracy.
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
3.1. Dataset Development
- Guidance information degradation: Remote sensing images (or other auxiliary spatial data) lose detail at lower resolutions. Considering road width, tree canopy radius, and residential property size, an 8 m resolution is an appropriate threshold. If the resolution is coarser than 8 m, ground features (e.g., narrow roads, individual trees, and small houses) may be lost during downsampling to the target resolution from high-resolution data.
- Network input limitation: JSPSR only allows input tensors with shapes that are multiples of 8 (e.g., 128 × 128, 144 × 144, etc.). The input shape of 128 × 128 pixels is the minimal adequate size for feature extraction in networks, equivalent to ∼8 m resolution.
- Computational efficiency: training with very high resolution (e.g., 1 m resolution) data is expensive due to the vast amount of data for training, which will slow the experiment progress.
3.2. Elevation Data Scaling
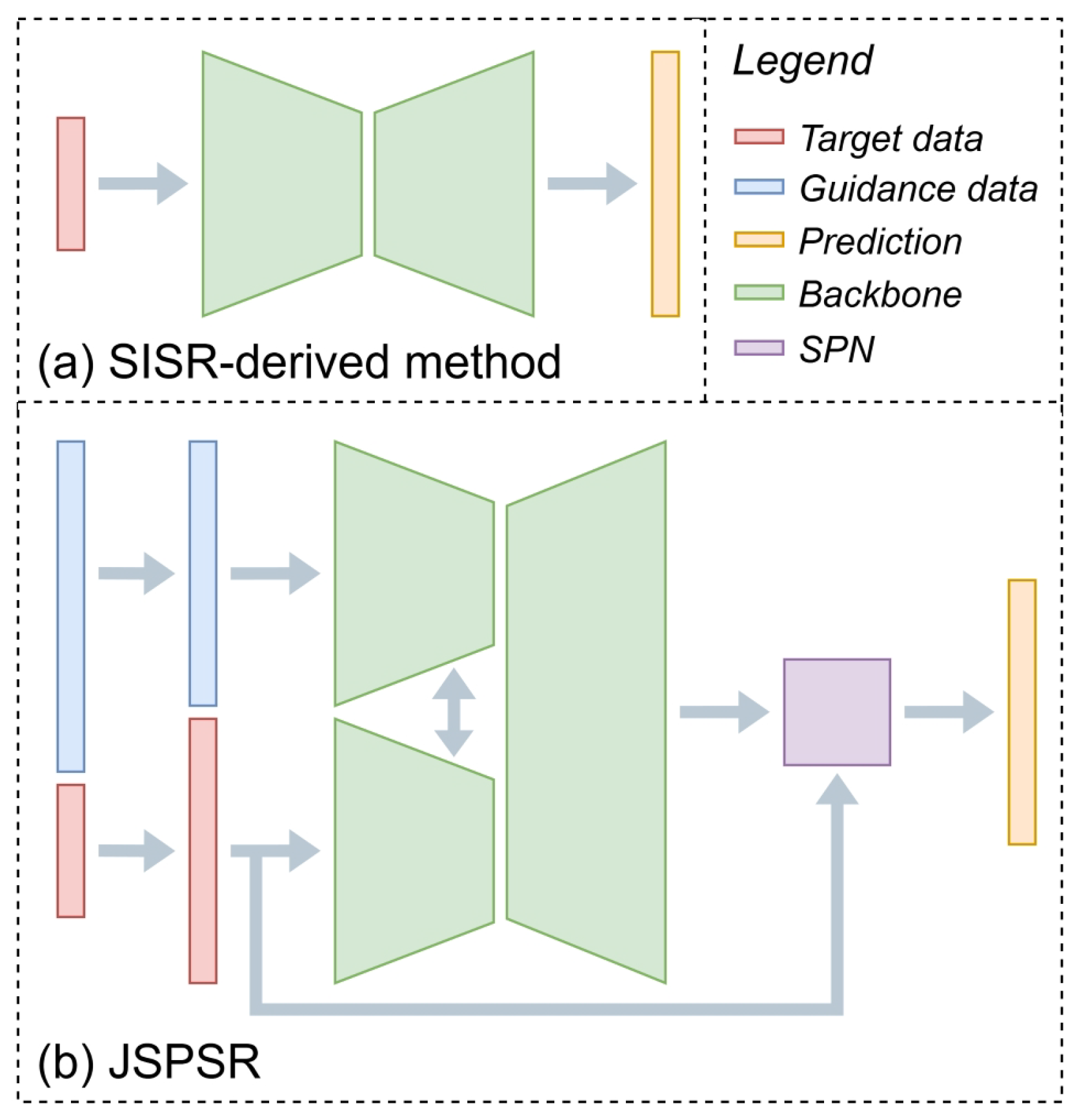
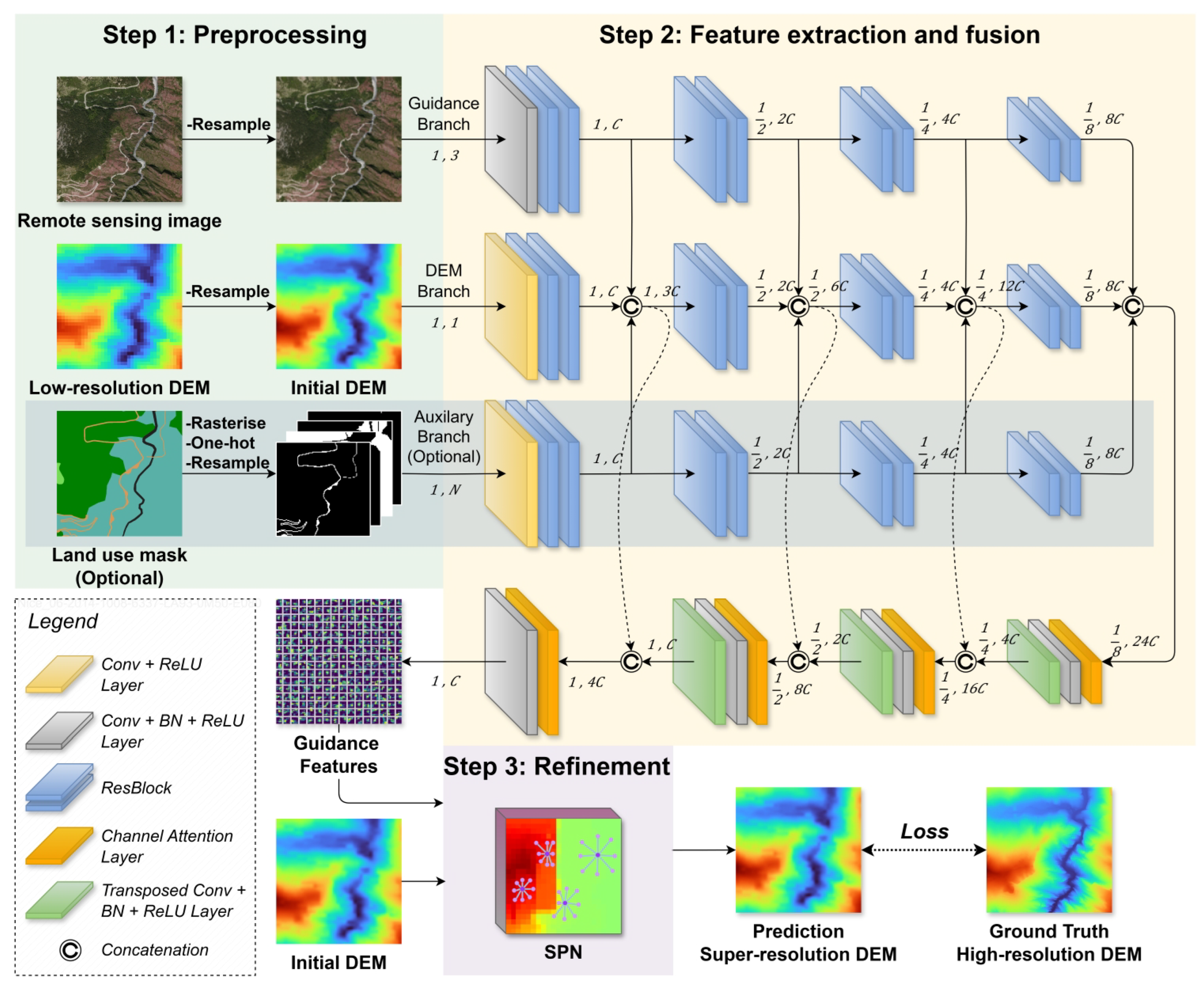
3.3. Joint Spatial Propagation Super-Resolution Networks Design
3.3.1. Guided Image Filtering
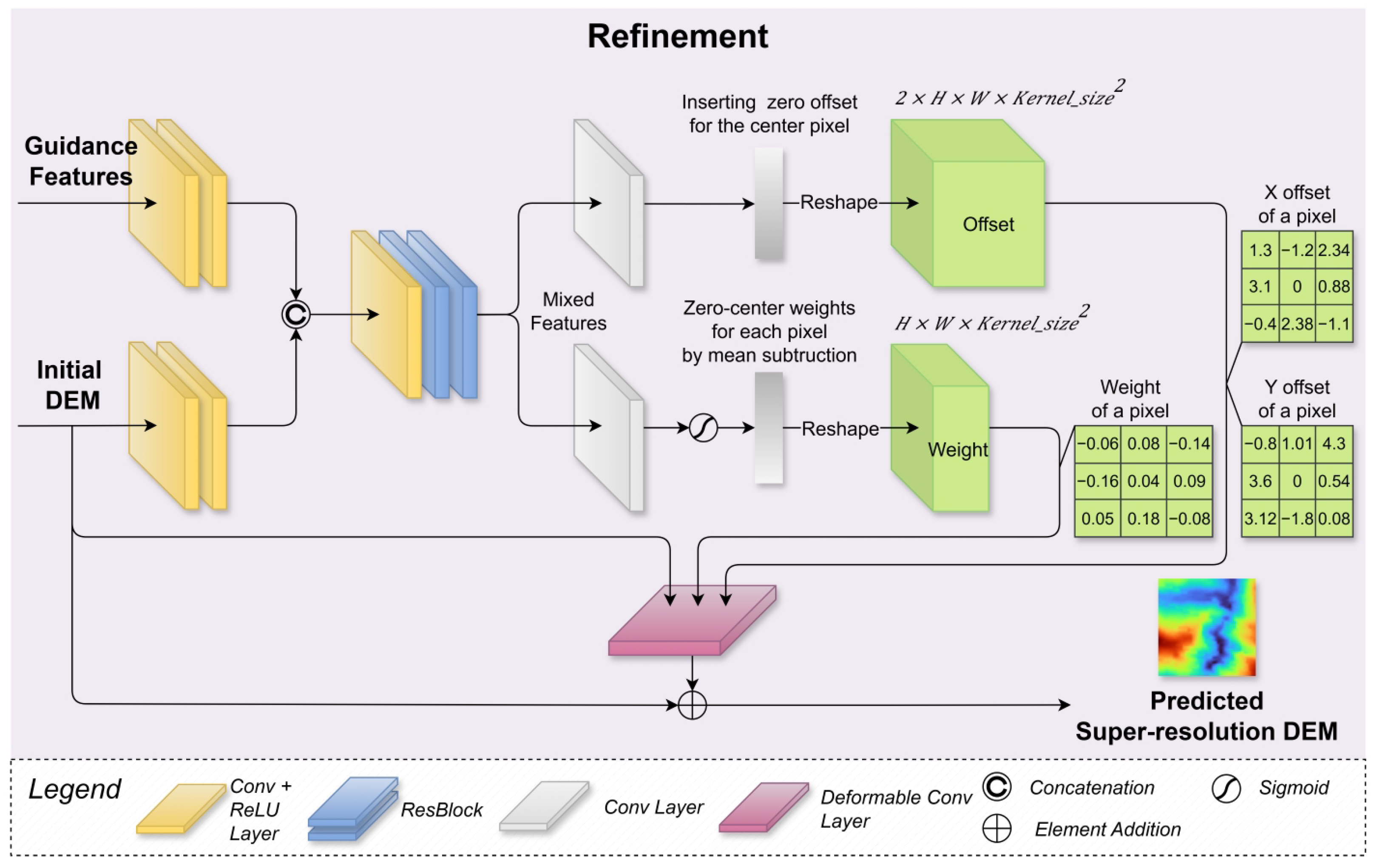
3.3.2. Spatial Propagation Network
- Less computing cost: our refinement module runs once per batch during training and inference, while the previous works need to run iterations per batch;
- Optimised high-frequency information: our refinement module directly uses initial DEMs as one of the inputs, and it does not contain a batch normalisation layer, which gains access to more high-frequency information to contribute to the DEM reconstruction quality.
3.3.3. Implementation
3.4. Other Methods for Comparison
4. Results
4.1. Experimental Setup
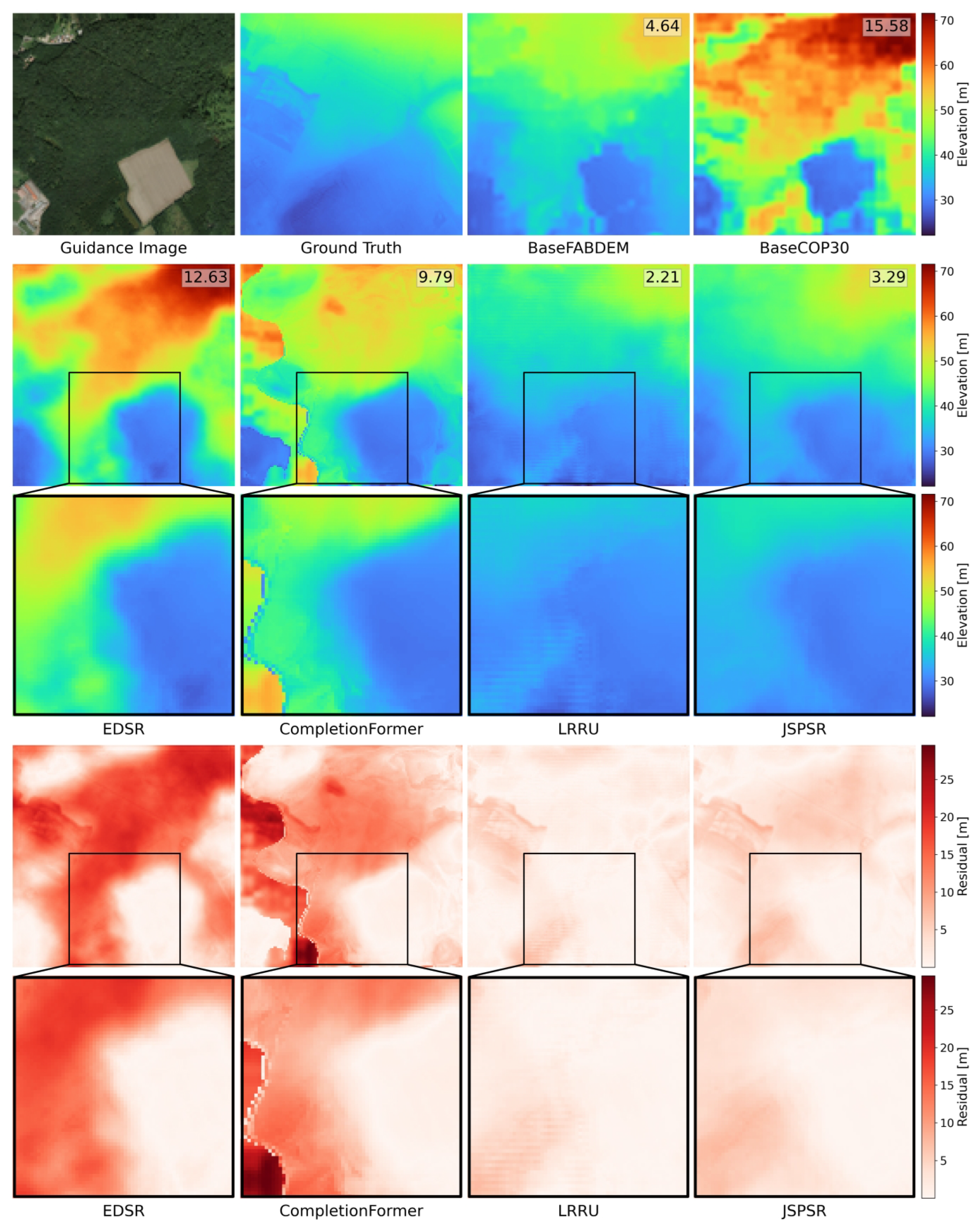
4.2. Experimental Results
4.3. Ablation Studies
4.3.1. Effectiveness of Proposed Data Scale Method
4.3.2. Effectiveness of Guidance Data
4.3.3. Comparison of Data Fusion Operations for Guided Image Filtering (GIF)
4.3.4. Effectiveness of Refinement Module
4.3.5. Generalisation
4.4. Assessment of JSPSR Predictions by Topographic Context
4.4.1. Vertical Accuracy by Slope
4.4.2. Vertical Accuracy by Land Use Mask Categories
4.4.3. Vertical Accuracy for DSM to DTM
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Supplementary Methods
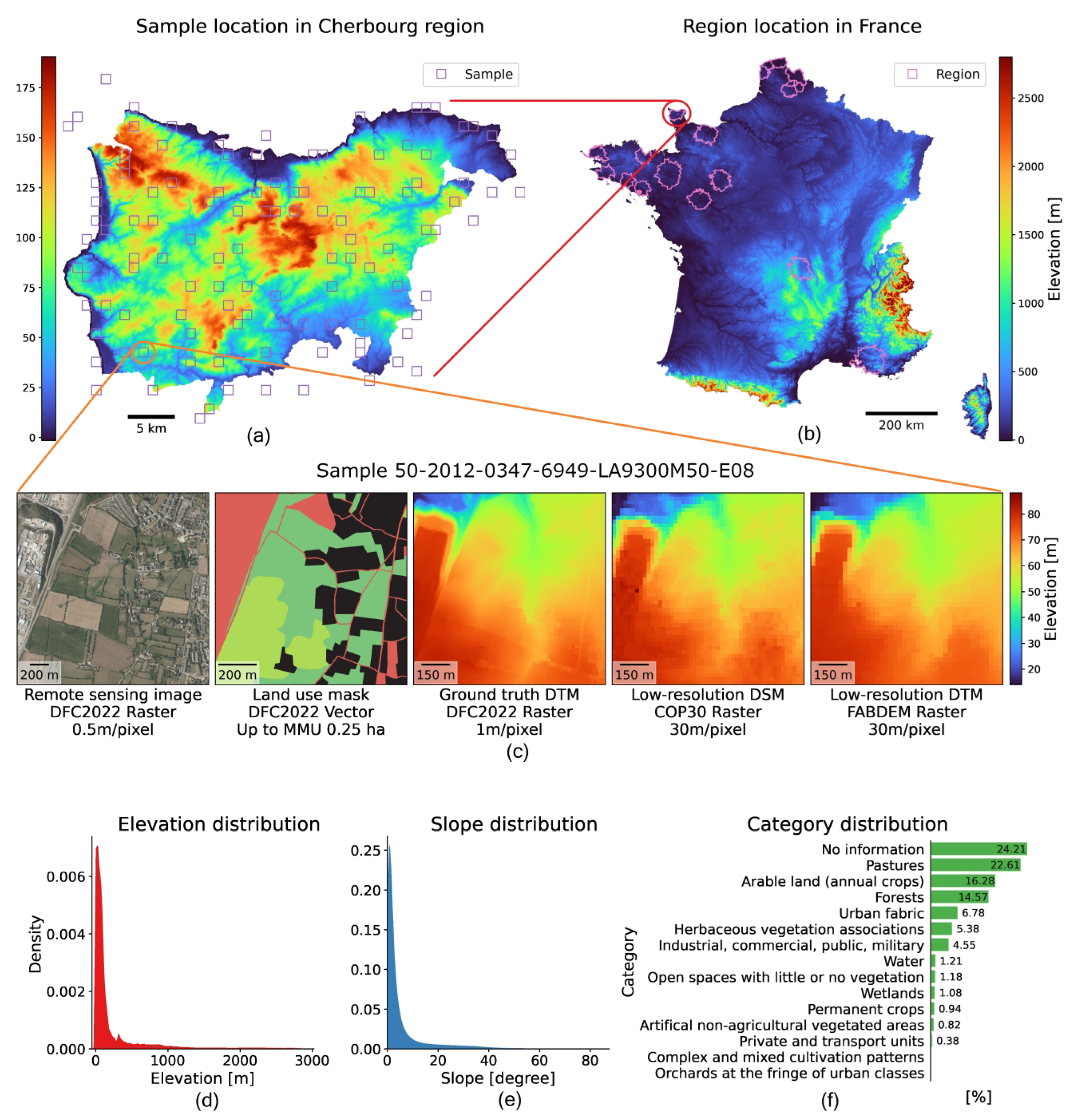
Appendix A.1. Data Assembly
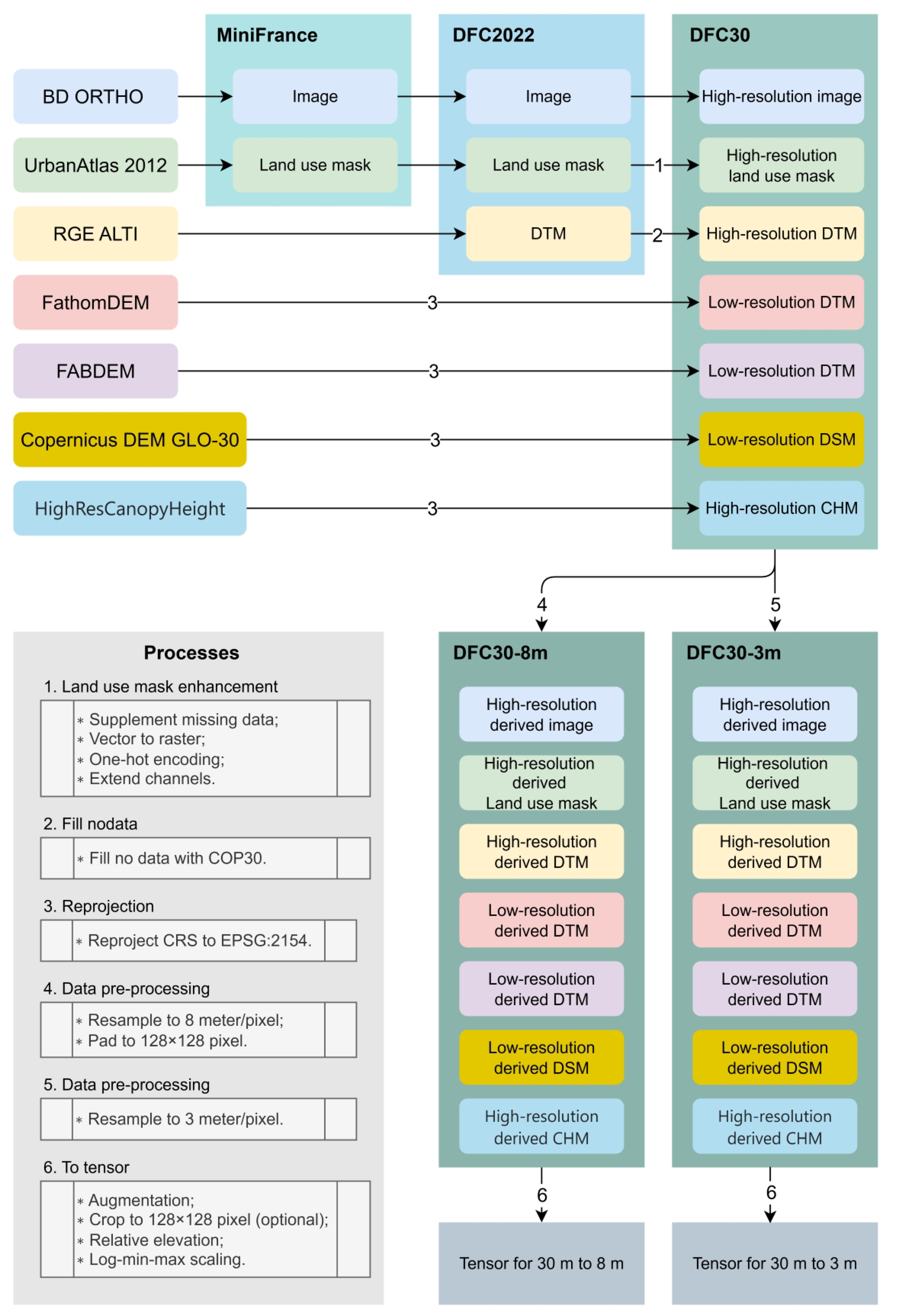
Appendix A.2. Metric Calculation Details
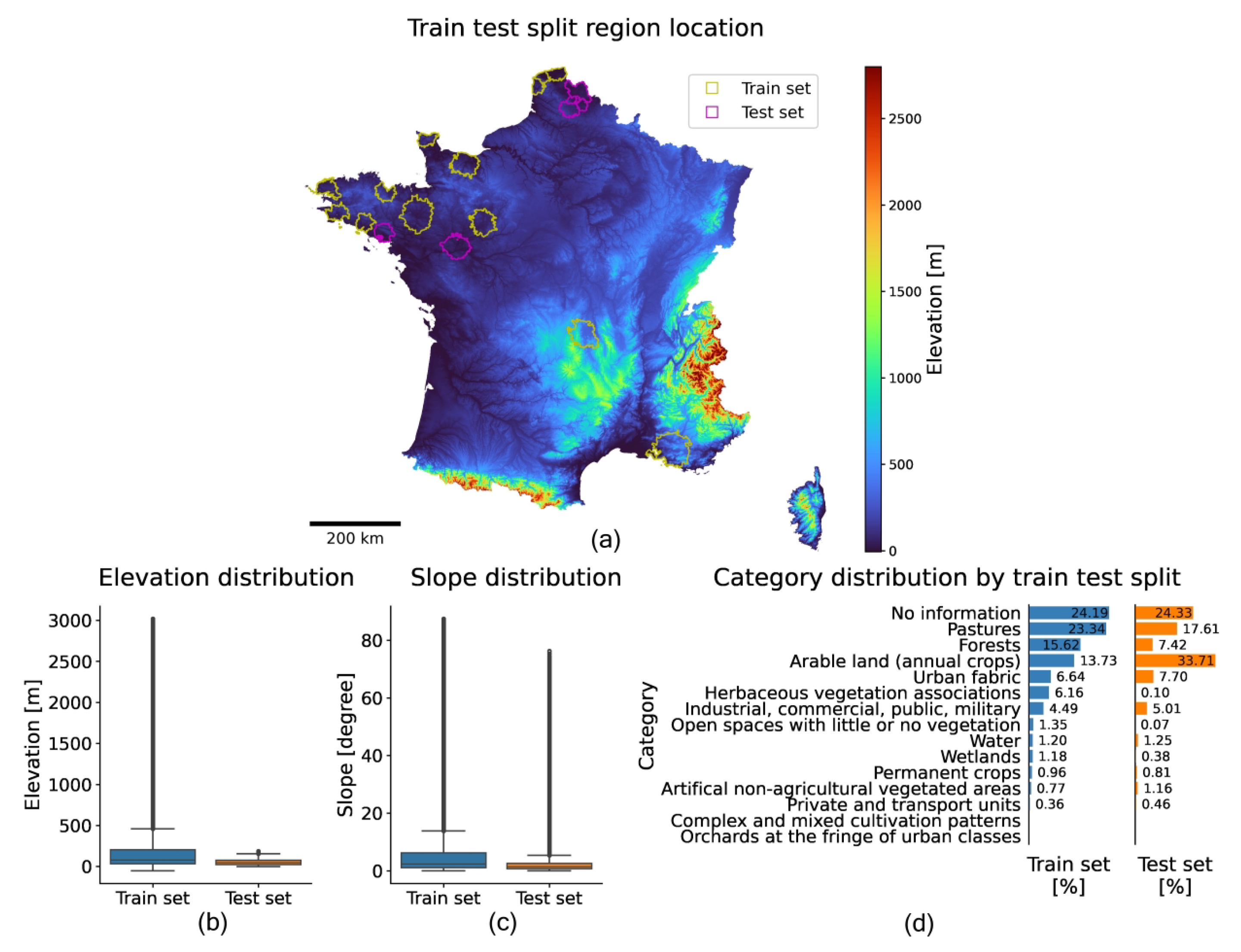
Appendix A.3. Training Set and Test Set Splitting
References
- Rocha, J.; Duarte, A.; Silva, M.; Fabres, S.; Vasques, J.; Revilla-Romero, B.; Quintela, A. The importance of high resolution digital elevation models for improved hydrological simulations of a mediterranean forested catchment. Remote Sens. 2020, 12, 3287. [Google Scholar] [CrossRef]
- Wechsler, S. Uncertainties associated with digital elevation models for hydrologic applications: A review. Hydrol. Earth Syst. Sci. 2007, 11, 1481–1500. [Google Scholar] [CrossRef]
- McClean, F.; Dawson, R.; Kilsby, C. Implications of using global digital elevation models for flood risk analysis in cities. Water Resour. Res. 2020, 56, e2020WR028241. [Google Scholar] [CrossRef]
- Nandam, V.; Patel, P. A framework to assess suitability of global digital elevation models for hydrodynamic modelling in data scarce regions. J. Hydrol. 2024, 630, 130654. [Google Scholar] [CrossRef]
- Zandsalimi, Z.; Feizabadi, S.; Yazdi, J.; Salehi Neyshabouri, S.A.A. Evaluating the Impact of Digital Elevation Models on Urban Flood Modeling: A Comprehensive Analysis of Flood Inundation, Hazard Mapping, and Damage Estimation. Water Resour. Manag. 2024, 38, 4243–4268. [Google Scholar] [CrossRef]
- Meadows, M.; Jones, S.; Reinke, K. Vertical accuracy assessment of freely available global DEMs (FABDEM, Copernicus DEM, NASADEM, AW3D30 and SRTM) in flood-prone environments. Int. J. Digit. Earth 2024, 17, 2308734. [Google Scholar] [CrossRef]
- Guth, P.L.; Van Niekerk, A.; Grohmann, C.H.; Muller, J.P.; Hawker, L.; Florinsky, I.V.; Gesch, D.; Reuter, H.I.; Herrera-Cruz, V.; Riazanoff, S.; et al. Digital elevation models: Terminology and definitions. Remote Sens. 2021, 13, 3581. [Google Scholar] [CrossRef]
- Dolloff, J.; Theiss, H.; Bollin, B. Assessment, specification, and validation of a geolocation system’s accuracy and predicted accuracy. Photogramm. Eng. Remote Sens. 2024, 90, 157–168. [Google Scholar] [CrossRef]
- Elaksher, A.; Ali, T.; Alharthy, A. A quantitative assessment of LiDAR data accuracy. Remote Sens. 2023, 15, 442. [Google Scholar] [CrossRef]
- Ho, Y.F.; Grohmann, C.H.; Lindsay, J.; Reuter, H.I.; Parente, L.; Witjes, M.; Hengl, T. GEDTM30: Global ensemble digital terrain model at 30 m and derived multiscale terrain variables. PeerJ 2025, 13, e19673. [Google Scholar] [CrossRef]
- Bielski, C.; López-Vázquez, C.; Grohmann, C.H.; Guth, P.L.; Hawker, L.; Gesch, D.; Trevisani, S.; Herrera-Cruz, V.; Riazanoff, S.; Corseaux, A.; et al. Novel approach for ranking dems: Copernicus DEM improves one arc second open global topography. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4503922. [Google Scholar] [CrossRef]
- European Space Agency. Copernicus DEM—Global and European Digital Elevation Model; Copernicus Data Space Ecosystem: Zaventem, Belgium, 2022. [Google Scholar] [CrossRef]
- Hawker, L.; Uhe, P.; Paulo, L.; Sosa, J.; Savage, J.; Sampson, C.; Neal, J. A 30 m global map of elevation with forests and buildings removed. Environ. Res. Lett. 2022, 17, 024016. [Google Scholar] [CrossRef]
- Uhe, P.; Lucas, C.; Hawker, L.; Brine, M.; Wilkinson, H.; Cooper, A.; Saoulis, A.A.; Savage, J.; Sampson, C. FathomDEM: An improved global terrain map using a hybrid vision transformer model. Environ. Res. Lett. 2025, 20, 034002. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Wing, O.E.J.; Bates, P.D.; Quinn, N.D.; Savage, J.T.S.; Uhe, P.F.; Cooper, A.; Collings, T.P.; Addor, N.; Lord, N.S.; Hatchard, S.; et al. A 30 m global flood inundation model for any climate scenario. Water Resour. Res. 2024, 60, e2023WR036460. [Google Scholar] [CrossRef]
- Schumann, G.J.P.; Bates, P.D. The Need for a High-Accuracy, Open-Access Global DEM. Front. Earth Sci. 2018, 6, 225. [Google Scholar] [CrossRef]
- Fisher, P.F.; Tate, N.J. Causes and consequences of error in digital elevation models. Prog. Phys. Geogr. 2006, 30, 467–489. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 184–199. [Google Scholar]
- Zhang, Y.; Yu, W.; Zhu, D. Terrain feature-aware deep learning network for digital elevation model superresolution. ISPRS J. Photogramm. Remote Sens. 2022, 189, 143–162. [Google Scholar] [CrossRef]
- Jiang, Y.; Xiong, L.; Huang, X.; Li, S.; Shen, W. Super-resolution for terrain modeling using deep learning in high mountain Asia. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103296. [Google Scholar] [CrossRef]
- Han, X.; Zhou, C.; Sun, S.; Lyu, C.; Gao, M.; He, X. An ensemble learning framework for generating high-resolution regional DEMs considering geographical zoning. ISPRS J. Photogramm. Remote Sens. 2025, 221, 363–383. [Google Scholar] [CrossRef]
- Wu, Z.; Zhao, Z.; Ma, P.; Huang, B. Real-world DEM super-resolution based on generative adversarial networks for improving InSAR topographic phase simulation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8373–8385. [Google Scholar] [CrossRef]
- Zhang, Y.; Funkhouser, T. Deep Depth Completion of a Single RGB-D Image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Habib, M. Evaluation of DEM interpolation techniques for characterizing terrain roughness. Catena 2021, 198, 105072. [Google Scholar] [CrossRef]
- Tsai, R.Y.; Huang, T.S. Multiframe image restoration and registration. Multiframe Image Restor. Regist. 1984, 1, 317–339. [Google Scholar]
- Hu, J.; Bao, C.; Ozay, M.; Fan, C.; Gao, Q.; Liu, H.; Lam, T.L. Deep depth completion from extremely sparse data: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 8244–8264. [Google Scholar] [CrossRef]
- Rajan, D.; Chaudhuri, S. Generalized interpolation and its application in super-resolution imaging. Image Vis. Comput. 2001, 19, 957–969. [Google Scholar] [CrossRef]
- Zhao, X.; Su, Y.; Dong, Y.; Wang, J.; Zhai, L. Kind of super-resolution method of CCD image based on wavelet and bicubic interpolation. Appl. Res. Comput. 2009, 26, 2365–2367. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Mu Lee, K. Enhanced deep residual networks for single image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision And Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Chen, Z.; Wang, X.; Xu, Z.; Hou, W. Convolutional neural network based dem super resolution. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 247–250. [Google Scholar] [CrossRef]
- Zhang, R.; Bian, S.; Li, H. RSPCN: Super-resolution of digital elevation model based on recursive sub-pixel convolutional neural networks. ISPRS Int. J. Geo-Inf. 2021, 10, 501. [Google Scholar] [CrossRef]
- Zhou, A.; Chen, Y.; Wilson, J.P.; Su, H.; Xiong, Z.; Cheng, Q. An enhanced double-filter deep residual neural network for generating super resolution DEMs. Remote Sens. 2021, 13, 3089. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, W. Comparison of DEM super-resolution methods based on interpolation and neural networks. Sensors 2022, 22, 745. [Google Scholar] [CrossRef] [PubMed]
- Demiray, B.Z.; Sit, M.; Demir, I. D-SRGAN: DEM super-resolution with generative adversarial networks. SN Comput. Sci. 2021, 2, 48. [Google Scholar] [CrossRef]
- Argudo, O.; Chica, A.; Andujar, C. Terrain super-resolution through aerial imagery and fully convolutional networks. Comput. Graph. Forum 2018, 37, 101–110. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, Z.; Yi, W.; Gui, Q.; Hou, W.; Ding, M. Deep gradient prior network for DEM super-resolution: Transfer learning from image to DEM. ISPRS J. Photogramm. Remote Sens. 2019, 150, 80–90. [Google Scholar] [CrossRef]
- Sun, G.; Chen, Y.; Huang, J.; Ma, Q.; Ge, Y. Digital Surface Model Super-Resolution by Integrating High-Resolution Remote Sensing Imagery Using Generative Adversarial Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 10636–10647. [Google Scholar] [CrossRef]
- Zhou, A.; Chen, Y.; Wilson, J.P.; Chen, G.; Min, W.; Xu, R. A multi-terrain feature-based deep convolutional neural network for constructing super-resolution DEMs. Int. J. Appl. Earth Obs. Geoinf. 2023, 120, 103338. [Google Scholar] [CrossRef]
- Tang, J.; Tian, F.P.; Feng, W.; Li, J.; Tan, P. Learning guided convolutional network for depth completion. IEEE Trans. Image Process. 2020, 30, 1116–1129. [Google Scholar] [CrossRef]
- Wang, Y.; Li, B.; Zhang, G.; Liu, Q.; Gao, T.; Dai, Y. Lrru: Long-short range recurrent updating networks for depth completion. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 9422–9432. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1397–1409. [Google Scholar] [CrossRef]
- Li, Y.; Huang, J.B.; Ahuja, N.; Yang, M.H. Deep joint image filtering. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 154–169. [Google Scholar]
- Hu, M.; Wang, S.; Li, B.; Ning, S.; Fan, L.; Gong, X. PENet: Towards Precise and Efficient Image Guided Depth Completion. arXiv 2021, arXiv:2103.00783. [Google Scholar] [CrossRef]
- Lin, Y.; Cheng, T.; Zhong, Q.; Zhou, W.; Yang, H. Dynamic spatial propagation network for depth completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; Volume 36, pp. 1638–1646. [Google Scholar]
- Zhang, Y.; Guo, X.; Poggi, M.; Zhu, Z.; Huang, G.; Mattoccia, S. Completionformer: Depth completion with convolutions and vision transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 18527–18536. [Google Scholar]
- Liu, S.; De Mello, S.; Gu, J.; Zhong, G.; Yang, M.H.; Kautz, J. Learning affinity via spatial propagation networks. Adv. Neural Inf. Process. Syst. 2017, 30, 1519–1529. [Google Scholar]
- Cheng, X.; Wang, P.; Guan, C.; Yang, R.C. Learning Context and Resource Aware Convolutional Spatial Propagation Networks for Depth Completion. arXiv 2019, arXiv:1911.05377. [Google Scholar] [CrossRef]
- Liu, X.; Shao, X.; Wang, B.; Li, Y.; Wang, S. Graphcspn: Geometry-aware depth completion via dynamic gcns. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 90–107. [Google Scholar]
- Park, J.; Joo, K.; Hu, Z.; Liu, C.K.; So Kweon, I. Non-local spatial propagation network for depth completion. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 120–136. [Google Scholar]
- Xu, Z.; Yin, H.; Yao, J. Deformable spatial propagation networks for depth completion. In Proceedings of the 2020 IEEE International Conference on Image, Processing (ICIP), Online, 25–28 October 2020; IEEE: New York, NY, USA, 2020; pp. 913–917. [Google Scholar]
- Cheng, X.; Wang, P.; Yang, R. Learning depth with convolutional spatial propagation network. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2361–2379. [Google Scholar] [CrossRef]
- Cheng, X.; Wang, P.; Guan, C.; Yang, R. Cspn++: Learning context and resource aware convolutional spatial propagation networks for depth completion. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 10615–10622. [Google Scholar]
- Kim, B.; Ponce, J.; Ham, B. Deformable kernel networks for joint image filtering. Int. J. Comput. Vis. 2021, 129, 579–600. [Google Scholar] [CrossRef]
- Tolan, J.; Yang, H.I.; Nosarzewski, B.; Couairon, G.; Vo, H.V.; Brandt, J.; Spore, J.; Majumdar, S.; Haziza, D.; Vamaraju, J.; et al. Very high resolution canopy height maps from RGB imagery using self-supervised vision transformer and convolutional decoder trained on aerial lidar. Remote Sens. Environ. 2024, 300, 113888. [Google Scholar] [CrossRef]
- Hänsch, R.; Persello, C.; Vivone, G.; Navarro, J.C.; Boulch, A.; Lefevre, S.; Saux, B.L. Data Fusion Contest 2022 (DFC2022); IEEE DataPrt: New York, NY, USA, 2022. [Google Scholar] [CrossRef]
- Huber, M.; Osterkamp, N.; Marschalk, U.; Tubbesing, R.; Wendleder, A.; Wessel, B.; Roth, A. Shaping the global high-resolution TanDEM-X digital elevation model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7198–7212. [Google Scholar] [CrossRef]
- Castillo-Navarro, J.; Le Saux, B.; Boulch, A.; Audebert, N.; Lefèvre, S. Semi-Supervised Semantic Segmentation in Earth Observation: The MiniFrance suite, dataset analysis and multi-task network study. Mach. Learn. 2022, 111, 3125–3160. [Google Scholar] [CrossRef]
- French National Institute of Geographical and Forest Information (IGN). BD ORTHO Database. 2019. Available online: https://geoservices.ign.fr/bdortho (accessed on 10 August 2024).
- Agency, E.E.; Agency, E.E. Urban Atlas Land Cover/Land Use 2012 (Vector), Europe, 6-Yearly, Jan. 2021; European Environment Agency (EEA): Copenhagen, Denmark, 2016. [Google Scholar] [CrossRef]
- French National Institute of Geographical and Forest Information (IGN). RGE ALTI Database. 2012. Available online: https://geoservices.ign.fr/rgealti (accessed on 10 August 2024).
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning requires rethinking generalization. arXiv 2016, arXiv:1611.03530. [Google Scholar] [CrossRef]
- Lahat, D.; Adali, T.; Jutten, C. Multimodal data fusion: An overview of methods, challenges, and prospects. Proc. IEEE 2015, 103, 1449–1477. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R. NTIRE 2017 Challenge on Single Image Super-Resolution: Dataset and Study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 1122–1131. [Google Scholar]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Vision meets Robotics: The KITTI Dataset. Int. J. Robot. Res. IJRR 2013, 32, 231–1237. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. Adv. Neural Inf. Process. Syst. 2019, 32, 721. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Gesch, D.B. Best practices for elevation-based assessments of sea-level rise and coastal flooding exposure. Front. Earth Sci. 2018, 6, 230. [Google Scholar] [CrossRef]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- Hawker, L.; Neal, J.; Bates, P. Accuracy assessment of the TanDEM-X 90 Digital Elevation Model for selected floodplain sites. Remote Sens. Environ. 2019, 232, 111319. [Google Scholar] [CrossRef]
- Loshchilov, I. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Yan, Z.; Wang, K.; Li, X.; Zhang, Z.; Li, J.; Yang, J. RigNet: Repetitive image guided network for depth completion. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 214–230. [Google Scholar]
- GDAL/OGR Contributors. GDAL/OGR Geospatial Data Abstraction Software Library; Open Source Geospatial Foundation: Beaverton, OR, USA, 2024. [Google Scholar] [CrossRef]
- Bernardi, G.; Brisebarre, G.; Roman, S.; Ardabilian, M.; Dellandrea, E. A comprehensive survey on image fusion: Which approach fits which need. Inf. Fusion 2025, 126, 103594. [Google Scholar] [CrossRef]
- Deng, Y.; Wilson, J.P.; Bauer, B. DEM resolution dependencies of terrain attributes across a landscape. Int. J. Geogr. Inf. Sci. 2007, 21, 187–213. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Ward, P.J.; Gayton, I.; ten Veldhuis, M.C.; Meijer, D.H.; Iliffe, M. Commentary: The Need for a High-Accuracy, Open-Access Global DEM. Front. Earth Sci. 2019, 7, 33. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Jongman, B.; Veldkamp, T.I.; Hallegatte, S.; Bangalore, M.; Ward, P.J. Disaster risk, climate change, and poverty: Assessing the global exposure of poor people to floods and droughts. Environ. Dev. Econ. 2018, 23, 328–348. [Google Scholar] [CrossRef]
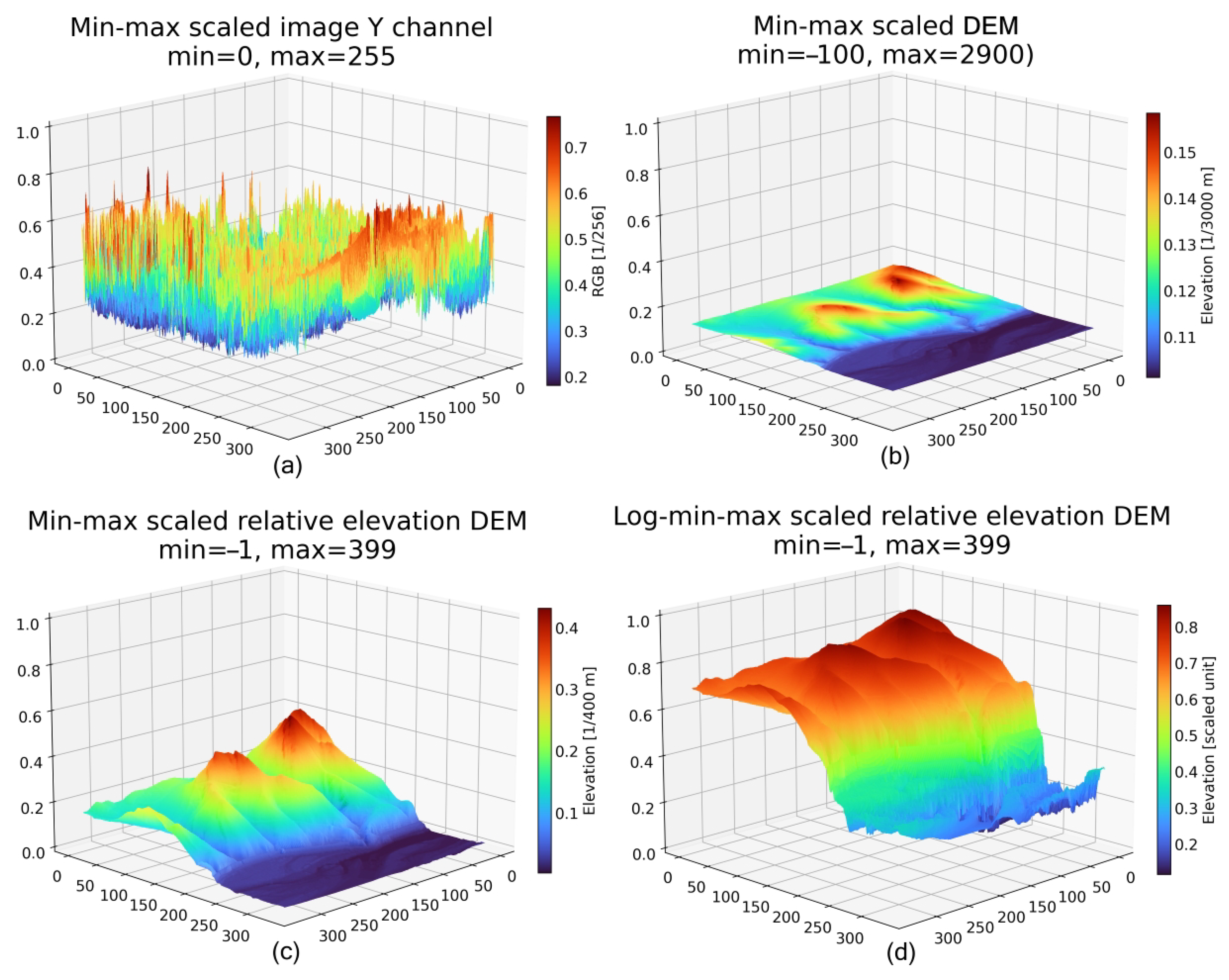




| Component | Type | Format | Pixel Size | Year | CRS | Role |
|---|---|---|---|---|---|---|
| DFC2022 | Image | Raster | 0.5 m | 2012–2014 | EPSG:2154 | Guidance data |
| DFC2022 | Mask | Vector | 0.25 ha | 2012 | EPSG:2154 | Auxilary guidance |
| DFC2022 | DTM | Raster | 1 m | 2019–2020 | EPSG:2154 | Ground truth |
| Copernicus GLO-30 | DSM | Raster | 30 m | 2011–2015 | EPSG:4326 | Target data |
| FABDEM | DTM | Raster | 30 m | 2014–2018 | EPSG:4326 | Comparison reference |
| FathomDEM | DTM | Raster | 30 m | 2014–2018 | EPSG:4326 | Comparison reference |
| HighResCanopyHeight | CHM | Raster | 1 m | 2017–2020 | EPSG:3857 | Auxilary guidance |
| Method | Aim | Basic Unit | Basic Channel | Backbone Architecture | Encoder Branch | Fusion Mode | Refinement Approach | Parameter (MB) | Mult-Adds (G) |
|---|---|---|---|---|---|---|---|---|---|
| EDSR | SISR | CNN | 256 | ResNet | 1 | Early fusion | 56.6 | 1260 | |
| ComplitionFormer | Depth Completion | Transformer | 64 | U-Net | 1 | Early fusion | Iterative SPN | 83.7 | 44.8 |
| LRRU | Depth Completion | CNN | 16 | U-Net | 2 | Late fusion | Pyramid SPN | 20.8 | 68.8 |
| JSPSR2b | DEM SR | CNN | 32 | U-Net | 2 | Late fusion | One-shot SPN | 29.2 | 66.8 |
| JSPSR3b | DEM SR | CNN | 32 | U-Net | 3 | Late fusion | One-shot SPN | 43.9 | 89.4 |
| Method | Input Data | 30 m to 8 m | 30 m to 3 m | |||||
|---|---|---|---|---|---|---|---|---|
| DEM | Image | Mask | CHM | RMSE | RMSE | |||
| BaseCOP30 | 3.7492 | 3.7547 | ||||||
| BaseFABDEM | 1.8443 | 1.8487 | ||||||
| BaseFathomDEM | 1.2952 | 1.2976 | ||||||
| EDSR | 2.4101 | ↓ 35.72 | 2.496 | ↓ 33.52 | ||||
| ✓ | ↑ 30.68 | ↑ 35.01 | ||||||
| ↑ 86.08 | ↑ 92.36 | |||||||
| CompletionFormer | 1.9886 | ↓ 46.96 | 1.334 | ↓ 64.47 | ||||
| ✓ | ✓ | ↑ 7.82 | ↓ 27.84 | |||||
| ↑ 53.54 | ↑ 2.805 | |||||||
| CompletionFormer | 1.2775 | ↓ 65.93 | 1.4696 | ↓ 60.8597 | ||||
| ✓ | ✓ | ✓ | ↓ 30.73 | ↓ 20.51 | ||||
| ↑ 1.367 | ↑ 13.26 | |||||||
| CompletionFormer | 1.1643 | ↓ 68.95 | 1.2967 | ↓ 65.46 | ||||
| ✓ | ✓ | ✓ | ↓ 36.87 | ↓ 29.86 | ||||
| ↓ 10.11 | ↓ 6.94 | |||||||
| LRRU | 1.1406 | ↓ 69.58 | 1.1256 | ↓ 70.02 | ||||
| ✓ | ✓ | ↓ 38.16 | ↓ 39.11 | |||||
| ↓ 11.94 | ↓ 13.26 | |||||||
| JSPSR2b | 1.0983 | ↓ 70.71 | 1.1314 | ↓ 69.87 | ||||
| ✓ | ✓ | ↓ 40.45 | ↓ 38.8 | |||||
| ↓ 15.2 | ↓ 12.81 | |||||||
| JSPSR3b | 1.0596 | ↓ 71.74 | 1.0851 | ↓ 71.1 | ||||
| ✓ | ✓ | ✓ | ↓ 42.55 | ↓ 41.3 | ||||
| ↓ 18.19 | ↓ 16.38 | |||||||
| JSPSR3b | 1.0644 | ↓ 71.61 | 1.104 | ↓ 70.6 | ||||
| ✓ | ✓ | ✓ | ↓ 42.29 | ↓ 40.28 | ||||
| ↓ 17.82 | ↓ 14.92 | |||||||
| Task | Method | Input Data | Metric | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DEM | Image | Mask | CHM | RMSE ↓ | Median | NMAD ↓ | LE95 ↓ | PSNR↑ | ||
| 30 m to 8 m | BaseCOP30 | 3.7492 | −0.587 | 0.8703 | 9.0313 | 47.8815 | ||||
| BaseFABDEM | 1.8443 | −0.723 | 0.7232 | 3.2182 | 54.0436 | |||||
| BaseFathomDEM | 1.2952 | −0.8614 | 0.4617 | 2.131 | 57.1138 | |||||
| EDSR | ✓ | 2.4101 | −0.0903 | 0.6661 | 4.6267 | 51.7197 | ||||
| CompletionFormer | ✓ | ✓ | 1.9886 | −0.3672 | 0.5926 | 2.8239 | 53.6744 | |||
| CompletionFormer | ✓ | ✓ | ✓ | 1.2775 | −0.0818 | 0.5637 | 2.2473 | 57.5184 | ||
| CompletionFormer | ✓ | ✓ | ✓ | 1.1643 | −0.053 | 0.5164 | 1.8621 | 58.0388 | ||
| LRRU | ✓ | ✓ | 1.1406 | −0.1391 | 0.5093 | 1.926 | 58.2175 | |||
| JSPSR2b | ✓ | ✓ | 1.0983 | −0.0714 | 0.5094 | 1.8641 | 58.5463 | |||
| JSPSR3b | ✓ | ✓ | ✓ | 1.0596 | −0.057 | 0.4931 | 1.7929 | 58.8572 | ||
| JSPSR3b | ✓ | ✓ | ✓ | 1.0644 | −0.0414 | 0.4761 | 1.7939 | 58.8182 | ||
| 30 m to 3 m | BaseCOP30 | 3.7547 | −0.587 | 0.8704 | 9.0496 | 47.9062 | ||||
| BaseFABDEM | 1.8487 | −0.7235 | 0.7256 | 3.2316 | 54.0605 | |||||
| BaseFathomDEM | 1.2976 | −0.8612 | 0.4644 | 2.1396 | 57.1345 | |||||
| EDSR | ✓ | 2.496 | −0.1246 | 0.5945 | 4.7755 | 51.4528 | ||||
| CompletionFormer | ✓ | ✓ | 1.334 | −0.1522 | 0.5058 | 2.1605 | 56.9594 | |||
| CompletionFormer | ✓ | ✓ | ✓ | 1.4696 | −0.1149 | 0.5241 | 2.3354 | 56.3014 | ||
| CompletionFormer | ✓ | ✓ | ✓ | 1.2967 | −0.0895 | 0.5375 | 2.0565 | 57.141 | ||
| LRRU | ✓ | ✓ | 1.1256 | −0.1039 | 0.5494 | 1.825 | 58.3698 | |||
| JSPSR2b | ✓ | ✓ | 1.1314 | −0.1481 | 0.4989 | 1.8444 | 58.3255 | |||
| JSPSR3b | ✓ | ✓ | ✓ | 1.0851 | −0.0163 | 0.5235 | 1.7975 | 58.6884 | ||
| JSPSR3b | ✓ | ✓ | ✓ | 1.104 | −0.0883 | 0.5094 | 1.8271 | 58.5379 | ||
| Method | Parameter (MB) | Mult-Adds (G) | GPU Time (ms) | GPU Memory (MB) |
|---|---|---|---|---|
| EDSR | 56.6 | 1260 | 18.3691 | 228.6 |
| ComplitionFormer | 83.7 | 44.8 | 13.9568 | 371.6 |
| LRRU | 20.8 | 68.8 | 5.7059 | 164 |
| JCDSR2b | 29.2 | 66.8 | 3.9759 | 235.2 |
| JCDSR3b | 43.9 | 89.4 | 5.1521 | 320.5 |
| Method | Guidance Data | Relative Elevation | Log-min–max Scale | RMSE ↓ | |
|---|---|---|---|---|---|
| Image | Mask | ||||
| JSPSR | ✓ | 1.29 | |||
| ✓ | ✓ | 1.1787 | |||
| ✓ | ✓ | ✓ | 1.0983 | ||
| ✓ | ✓ | 1.2136 | |||
| ✓ | ✓ | ✓ | 1.1482 | ||
| ✓ | ✓ | ✓ | ✓ | 1.0596 | |
| Method | Guidance Data | RMSE ↓ | ||||
|---|---|---|---|---|---|---|
| DEM | Image | Mask | CHM | 30 m to 8 m | 30 m to 3 m | |
| EDSR | ✓ | 2.4101 | 2.496 | |||
| EDSR | ✓ | ✓ | 1.5816 | 1.6258 | ||
| JSPSR | ✓ | ✓ | 1.0983 | 1.1314 | ||
| JSPSR | ✓ | ✓ | 1.1984 | 1.2231 | ||
| JSPSR | ✓ | ✓ | 1.0986 | 1.1506 | ||
| JSPSR | ✓ | ✓ | ✓ | 1.0596 | 1.0851 | |
| JSPSR | ✓ | ✓ | ✓ | 1.0644 | 1.104 | |
| Method | Guidance Data | Operation | RMSE ↓ | |||
|---|---|---|---|---|---|---|
| Image | Mask | Addition | Concatenation | Filtering | ||
| JSPSR | ✓ | ✓ | 1.2649 | |||
| ✓ | ✓ | 1.0983 | ||||
| ✓ | ✓ | 1.1527 | ||||
| ✓ | ✓ | ✓ | 1.22 | |||
| ✓ | ✓ | ✓ | 1.0596 | |||
| ✓ | ✓ | ✓ | 1.1592 | |||
| Method | Guidance Data | Refinement | RMSE ↓ | |
|---|---|---|---|---|
| Image | Mask | |||
| EDSR | 2.4101 | |||
| EDSR | ✓ | 1.5816 | ||
| EDSR | ✓ | ✓ | 1.2518 | |
| JSPSR | ✓ | 1.4034 | ||
| JSPSR | ✓ | ✓ | 1.0983 | |
| JSPSR | ✓ | ✓ | 2.0497 | |
| JSPSR | ✓ | ✓ | ✓ | 1.0596 |
| Region | Pixel % | Slope° | RMSE | COP. | FAB. | Fat. | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | Std. | COP. | FAB. | Fat. | JSPSR. | |||||
| Angers | 6.18 | 2.25 | 3.47 | 3.8748 | 2.0467 | 1.3129 | 1.0421 | ↓ 73.11 | ↓ 49.08 | ↓ 20.63 |
| Brest | 4.32 | 3.43 | 5.05 | 2.9449 | 2.0794 | 1.4164 | 1.0825 | ↓ 63.24 | ↓ 47.94 | ↓ 23.57 |
| Caen | 6.30 | 3.14 | 4.23 | 3.5006 | 2.0156 | 1.2933 | 0.9893 | ↓ 71.74 | ↓50.92 | ↓ 23.51 |
| Calais Dunkerque | 6.43 | 2.83 | 4.17 | 2.9356 | 1.6401 | 1.1805 | 1.2083 | ↓ 58.84 | ↓ 26.33 | ↑ 2.35 |
| Cherbourg | 2.84 | 3.63 | 4.50 | 2.8535 | 1.6931 | 1.5612 | 0.9416 | ↓ 67 | ↓ 44.39 | ↓39.69 |
| Clermont–Ferrand | 7.54 | 7.53 | 7.52 | 6.0747 | 3.1155 | 1.9411 | 2.2093 | ↓ 63.63 | ↓ 29.09 | ↑ 13.81 |
| LeMans | 5.38 | 2.64 | 3.48 | 5.7566 | 2.5362 | 1.2973 | 1.4077 | ↓75.55 | ↓ 44.5 | ↑ 8.51 |
| Lille Arras Lens Douai Henin | 10.22 | 2.00 | 3.12 | 3.4944 | 1.6858 | 1.2455 | 1.1283 | ↓ 67.71 | ↓ 33.07 | ↓ 9.41 |
| Lorient | 3.01 | 4.55 | 5.73 | 4.9893 | 2.8006 | 2.2847 | 2.1124 | ↓ 57.66 | ↓ 24.57 | ↓ 7.54 |
| Marseille Martigues | 7.76 | 8.66 | 10.48 | 3.0760 | 2.8171 | 2.2974 | 2.2606 | ↓ 26.51 | ↓ 19.75 | ↓ 1.6 |
| Nantes Saint-Nazaire | 10.88 | 2.06 | 3.01 | 2.7932 | 1.3676 | 1.1422 | 0.7918 | ↓ 71.65 | ↓ 42.1 | ↓ 30.68 |
| Nice | 8.36 | 23.52 | 13.10 | 7.0960 | 5.8516 | 4.9287 | 5.6147 | ↓20.88 | ↓4.05 | ↑13.92 |
| Quimper | 3.87 | 3.89 | 4.54 | 3.1250 | 1.8856 | 1.3329 | 0.9765 | ↓ 68.75 | ↓ 48.21 | ↓ 26.74 |
| Rennes | 9.82 | 2.82 | 3.34 | 3.7086 | 1.8336 | 1.4373 | 1.1217 | ↓ 69.75 | ↓ 38.83 | ↓ 21.96 |
| Saint-Brieuc | 3.42 | 3.73 | 4.84 | 4.3080 | 2.3262 | 1.2925 | 1.2245 | ↓ 71.57 | ↓ 47.36 | ↓ 5.26 |
| Vannes | 3.67 | 3.08 | 4.03 | 4.1938 | 1.9065 | 1.3968 | 1.1261 | ↓ 73.15 | ↓ 40.93 | ↓ 19.38 |
| Task | Method | Guidance Data | Overall | Slope 0–5° | Slope 5–10° | Slope 10–25° | Slope > 25° | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Image | Mask | RMSE | RMSE | RMSE | RMSE | RMSE | |||||||
| 30 m to 8 m | BaseCOP30 | 3.7492 | 3.5789 | 5.1544 | 6.611 | 7.1176 | |||||||
| BaseFABDEM | 1.8443 | 1.7021 | 2.7953 | 4.017 | 6.0347 | ||||||||
| BaseFathomDEM | 1.2952 | 1.1656 | 2.0447 | 3.1646 | 5.5909 | ||||||||
| JSPSR | 1.0983 | ↓ 70.71 | 0.9591 | ↓ 73.2 | 1.8072 | ↓ 64.94 | 3.0084 | ↓ 54.49 | 5.566 | ↓ 21.8 | |||
| ✓ | ↓ 40.45 | ↓ 43.65 | ↓ 35.35 | ↓ 25.11 | ↓ 7.77 | ||||||||
| ↓ 15.2 | ↓ 17.72 | ↓ 11.62 | ↓ 4.94 | ↓ 0.45 | |||||||||
| 1.0596 | ↓ 71.74 | 0.9174 | ↓ 74.37 | 1.7888 | ↓ 65.3 | 2.8803 | ↓ 56.43 | 5.9622 | ↓ 16.23 | ||||
| ✓ | ✓ | ↓ 42.55 | ↓ 46.1 | ↓ 36 | ↓ 28.3 | ↓ 1.2 | |||||||
| ↓ 18.19 | ↓ 21.29 | ↓ 12.52 | ↓ 8.98 | ↑ 6.64 | |||||||||
| 30 m to 3 m | BaseCOP30 | 3.7547 | 3.569 | 5.077 | 6.067 | 5.81 | |||||||
| BaseFABDEM | 1.8487 | 1.7077 | 2.6284 | 3.5545 | 4.6316 | ||||||||
| BaseFathomDEM | 1.2976 | 1.17 | 1.9 | 2.765 | 4.1696 | ||||||||
| JSPSR | 1.1314 | ↓ 69.87 | 1.0079 | ↓ 71.76 | 1.6968 | ↓ 66.58 | 2.5133 | ↓ 58.57 | 3.8077 | ↓ 34.46 | |||
| ✓ | ↓ 38.8 | ↓ 40.98 | ↓ 35.44 | ↓ 29.29 | ↓ 17.79 | ||||||||
| ↓ 12.81 | ↓ 13.85 | ↓ 10.69 | ↓ 9.1 | ↓ 8.68 | |||||||||
| 1.0851 | ↓ 71.1 | 0.9648 | ↓ 72.97 | 1.6396 | ↓ 67.71 | 2.424 | ↓ 60.05 | 3.625 | ↓ 37.61 | ||||
| ✓ | ✓ | ↓ 41.3 | ↓ 43.5 | ↓ 37.62 | ↓ 31.8 | ↓ 21.73 | |||||||
| ↓ 16.38 | ↓ 17.54 | ↓ 13.71 | ↓ 12.33 | ↓ 13.06 | |||||||||
| Class | Pixel % | Slope° | RMSE | W/O. | W. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | Std. | COP. | FAB. | Fat. | W/O. | W. | COP. | FAB. | Fat. | COP. | FAB. | Fat. | W/O. | ||
| 0 | 24.42 | 1.92 | 2.52 | 4.15 | 1.8994 | 1.4645 | 1.3983 | 1.3318 | ↓ 66.3 | ↓ 26.38 | ↓ 4.52 | ↓ 67.91 | ↓ 29.88 | ↓ 9.06 | ↓ 4.76 |
| 1 | 8.93 | 1.92 | 2.07 | 1.8552 | 1.274 | 1.1689 | 0.67 | 0.66 | ↓ 63.89 | ↓ 47.41 | ↓ 42.68 | ↓ 64.42 | ↓ 48.19 | ↓ 43.54 | ↓ 1.49 |
| 2 | 7.27 | 2.22 | 2.89 | 2.1557 | 1.4947 | 1.3074 | 0.9651 | 0.9234 | ↓ 55.23 | ↓ 35.43 | ↓ 26.18 | ↓ 57.16 | ↓ 38.22 | ↓ 29.37 | ↓ 4.32 |
| 3 | 0.53 | 4.94 | 8.29 | 3.2909 | 3.2024 | 2.998 | 2.8292 | 3.0121 | ↓14.03 | ↓11.65 | ↓ 5.63 | ↓8.47 | ↓5.94 | ↑ 0.47 | ↑ 6.46 |
| 4 | 1.31 | 2.63 | 3.95 | 4.7996 | 2.9084 | 1.5242 | 1.5493 | 1.578 | ↓ 67.72 | ↓ 46.73 | ↑ 1.65 | ↓ 67.12 | ↓ 45.74 | ↑ 3.53 | ↑ 1.85 |
| 5 | 35.19 | 1.64 | 1.78 | 1.4872 | 1.2024 | 0.9892 | 0.5649 | 0.5396 | ↓ 62.02 | ↓ 53.02 | ↓ 42.89 | ↓ 63.72 | ↓55.12 | ↓ 45.45 | ↓ 4.48 |
| 6 | 0.86 | 2.93 | 2.3 | 0.9703 | 0.9784 | 0.9569 | 0.5286 | 0.5856 | ↓ 45.52 | ↓ 45.97 | ↓ 44.76 | ↓ 39.65 | ↓ 40.15 | ↓ 38.8 | ↑10.78 |
| 7 | 18.94 | 2.07 | 2.36 | 2.0208 | 1.3587 | 1.1338 | 0.6276 | 0.6287 | ↓ 68.94 | ↓53.81 | ↓ 44.65 | ↓ 68.89 | ↓ 53.73 | ↓ 44.55 | ↑ 0.17 |
| 10 | 7.81 | 3.05 | 4.12 | 9.8595 | 4.0118 | 1.7801 | 2.1412 | 2.0479 | ↓78.28 | ↓ 46.63 | ↑20.29 | ↓79.23 | ↓ 48.95 | ↑15.04 | ↓ 4.36 |
| 11 | 0.1 | 3.88 | 5.4 | 2.8077 | 1.7666 | 1.7443 | 1.3312 | 1.1125 | ↓ 52.59 | ↓ 24.65 | ↓ 23.68 | ↓ 60.38 | ↓ 37.03 | ↓ 36.22 | ↓16.43 |
| 12 | 0.07 | 1.77 | 3.1 | 3.0564 | 3.1069 | 2.8956 | 2.2358 | 1.958 | ↓ 26.85 | ↓ 28.04 | ↓ 22.79 | ↓ 35.94 | ↓ 36.98 | ↓ 32.38 | ↓ 12.43 |
| 13 | 0.39 | 1.3 | 2.55 | 1.5092 | 1.0942 | 1.1734 | 0.5971 | 0.5517 | ↓ 60.44 | ↓ 45.43 | ↓49.11 | ↓ 63.44 | ↓ 49.58 | ↓52.98 | ↓ 7.6 |
| 14 | 1.38 | 1.44 | 3.1 | 2.7732 | 2.6266 | 2.5293 | 1.8475 | 1.8838 | ↓ 33.38 | ↓ 29.66 | ↓ 26.96 | ↓ 32.07 | ↓ 28.28 | ↓ 25.52 | ↑ 1.96 |
| Class Name | |||||||||||||||
| 1 | Urban fabric | 2 | Industrial, commercial, public, military, private and transport units | ||||||||||||
| 3 | Mine, dump and construction sites | 4 | Artifical non-agricultural vegetated areas | 5 | Arable land (annual crops) | ||||||||||
| 6 | Permanent crops | 7 | Pastures | 10 | Forests | ||||||||||
| 11 | Herbaceous vegetation associations | 12 | Open spaces with little or no vegetation | 13 | Wetlands | ||||||||||
| 14 | Water | 0 | No information | ||||||||||||
| Type | DEM | 8 m to 30 m | 3 m to 30 m | ||
|---|---|---|---|---|---|
| RMSE | RMSE | ||||
| DSM | COP302154 | 3.7482 | 3.7393 | ||
| DTM | FABDEM2154 | 1.8312 | 1.8274 | ||
| DTM | FathomDEM2154 | 1.2737 | 1.2721 | ||
| DTM | JSPSR | 1.0488 | ↓ 72.02 | 1.0558 | ↓ 71.76 |
| ↓ 42.73 | ↓ 42.22 | ||||
| ↓ 17.66 | ↓ 17 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, X.; Wilson, M.D. JSPSR: Joint Spatial Propagation Super-Resolution Networks for Enhancement of Bare-Earth Digital Elevation Models from Global Data. Remote Sens. 2025, 17, 3591. https://doi.org/10.3390/rs17213591
Cai X, Wilson MD. JSPSR: Joint Spatial Propagation Super-Resolution Networks for Enhancement of Bare-Earth Digital Elevation Models from Global Data. Remote Sensing. 2025; 17(21):3591. https://doi.org/10.3390/rs17213591
Chicago/Turabian StyleCai, Xiandong, and Matthew D. Wilson. 2025. "JSPSR: Joint Spatial Propagation Super-Resolution Networks for Enhancement of Bare-Earth Digital Elevation Models from Global Data" Remote Sensing 17, no. 21: 3591. https://doi.org/10.3390/rs17213591
APA StyleCai, X., & Wilson, M. D. (2025). JSPSR: Joint Spatial Propagation Super-Resolution Networks for Enhancement of Bare-Earth Digital Elevation Models from Global Data. Remote Sensing, 17(21), 3591. https://doi.org/10.3390/rs17213591







