A Hybrid-Weight TOPSIS and Clustering Approach for Optimal GNSS Station Selection in Multi-GNSS Precise Orbit Determination

Highlights

What are the main findings?

• A novel framework integrating hybrid-weight TOPSIS and k-means clustering effectively balances station data quality and spatial distribution. This method constructs highly efficient networks, where an optimized 60-station selection achieves POD accuracy comparable to a 90-station network.
• A uniform global distribution is identified as the most critical factor for multi-GNSS POD. A sparse 30-station network with optimal geometry achieves centimeter-level accuracy, proving far superior to a dense 90-station network of high-quality but geographically clustered stations.

What are the implications of the main findings?

• The proposed framework offers an objective, quantitative methodology for designing optimized GNSS networks, ensuring that solutions for POD (also for clock estimation, Earth Rotation Parameters (ERPs), etc.) remain at the highest accuracy while minimizing the size of the network.
• Using a controlled-variable approach, this study quantitatively reveals the impacts of station data quality and spatial distribution on POD. It demonstrates that while a uniform network geometry is the essential foundation, data quality is equally critical in sparse networks, providing key guidelines for future GNSS applications (e.g., integrity monitoring with custom networks, Low-Earth-Orbit (LEO) augmentation).

Abstract

The accuracy of Precise Orbit Determination (POD) for Global Navigation Satellite Systems (GNSS) critically depends on optimal tracking station selection. This study proposed and validates a novel framework that integrates a hybrid-weight Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) model with spherical k-means clustering, effectively resolving the challenge of balancing station data quality with uniform spatial distribution. The framework generates by first a comprehensive quality score for each station based on 40 indicators and then selects the top-scoring station from distinct geographical clusters to construct a well-distributed, high-quality network. To validate the methodology, we performed multi-GNSS POD using networks of 30, 60, and 90 stations selected by the proposed framework. The accuracy was assessed via two independent methods: orbit comparisons (Root Mean Square, RMS) against final Analysis Center (AC) orbits and Satellite Laser Ranging (SLR) validation. The results demonstrate that the optimized 60-station network (e.g., RMS of ~2.5, 5.3, 2.1, and 5.4 cm for GPS, GLONASS, Galileo, and BDS, respectively) achieves an accuracy comparable to that of a 90-station network. Moreover, a 30-station globally uniform network outperforms a 90-station network of high-quality but spatially clustered stations. This study provides an objective and quantitative solution for establishing efficient and reliable GNSS tracking networks, directly benefiting ACs and other high-precision applications.

1. Introduction

The International GNSS Service (IGS) and its Multi-GNSS EXperiment (MGEX) maintain a global network of over 500 continuously operating stations, providing the primary data for high-precision spatio-temporal reference products [1]. Comprehensive analysis of Global Navigation Satellite System (GNSS) observation data from this network yields products with millimeter-to-centimeter-level accuracy, including precise orbits, clock corrections, Earth rotation parameters, and station coordinates. These products are essential for a wide range of applications, such as global surveying, meteorological monitoring, and crustal deformation studies. However, processing data from the entire network is often impractical due to computational constraints. Therefore, a balance must be struck between solution accuracy and processing efficiency. A common strategy is to select a subset of stations based on criteria like data quality and uniform global geometry.

Several studies have proposed methods for optimal station selection based on geometric parameters to enhance the estimation of GNSS-based global parameters. Zhang et al. [2] investigated the impact of ground station geometry on precise orbit determination (POD) and proposed an optimization method based on discrete probability distribution. Wang et al. [3] introduced a method based on a minimum Orbit and ERP Dilution of Precision (OEDOP) criterion to rapidly select optimal station locations for orbit and Earth Rotation Parameter (ERP) determination. This approach was implemented using a combination of map grid zooming and heuristic techniques.

Recognizing the limitations of purely geometric approaches, other studies integrated data quality metrics. Lee et al. [4] developed a GNSS monitoring station selection method integrating both data quality and station distribution criteria. Data quality was assessed using four core index features of GNSS observations, including the number of IOnospheric Delay (IOD) cycle slips, the number of outliers, the percentage of observations, and the Root Mean Square (RMS) of multipath on L1 code (MP1). To ensure a well-distributed sub-network, the selection algorithm incorporated a two-dimensional iterative maximum sensitivity ratio search combined with the Voronoi method. Yang et al. [5] proposed a random optimization algorithm for GNSS station selection based on grid control probabilities in ultra-rapid POD and real-time satellite clock offset estimation applications. The core of this algorithm was the introduction of a Weighted Station Dilution of Precision (WSDOP) metric, designed to balance network geometry with observation quality. The WSDOP values were subsequently converted into station selection probabilities that guided a Monte Carlo sampling process to identify the optimal station subset.

More recent studies have targeted specific applications. Wang et al. [6] proposed an iterative method based on the information content to select stations for Global Ionosphere Map (GIM) reconstruction. Li et al. [7] focused on classifying GNSS data quality using machine learning algorithms. Gałdyn et al. [8] developed open-source software for network optimization based on RINEX file analysis; however, this software lacked application-level validation to assess the effectiveness of the station selection.

Overall, previous research in this area exhibits two primary limitations. First, in methods that integrate multiple data quality indices, the weights assigned to each metric are often selected empirically, lacking a systematic approach to balance their relative importance. Second, the validation of proposed algorithms is often confined to a single constellation (typically GPS), limiting Multi-GNSS applicability. This highlights the need for an adaptive, multi-GNSS station selection methodology that systematically integrates both network geometry and dynamically weighted data quality, forming the primary motivation for this study.

This study proposes and validates a novel framework that integrates a hybrid-weight Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) model with the k-means clustering algorithm to systematically optimize the selection of ground tracking stations for Multi-GNSS POD. We first develop a TOPSIS model, which integrates the Analytic Hierarchy Process (AHP) and the Entropy Weight Method, to generate a composite quality score for global IGS/MGEX stations based on 40 distinct quality indicators. Subsequently, a spherical k-means clustering algorithm is employed to partition the stations into a predefined number of clusters. From each cluster, the station with the highest score is selected, thereby constructing an optimized network that balances high data quality with uniform spatial coverage. The core source code for this methodology has been made publicly available in a GitHub repository (https://github.com/wtjin/gnss_station_selector; Version 1.0; accessed on 1 October 2025).

The rest of this paper is organized as follows. Section 2 introduces the key GNSS data quality indicators, the principles of the TOPSIS and k-means algorithms, and the detailed pipeline of our proposed methodology. Section 3 presents the station quality scores and clustering results derived from our selection algorithm, along with an accuracy analysis of the POD performed using the selected network. Section 4 employs a controlled variable approach to discuss the relative importance of the two core factors: data quality and spatial distribution. Finally, Section 5 concludes the paper and outlines directions for future research and potential applications.

2. Materials and Methods

2.1. Typical Index Features of GNSS Observations and Software for Quality Check

The evaluation of GNSS data quality relies on a range of metrics, including data integrity, pseudorange multipath, and cycle slip rates. This section focuses on the primary metrics selected as the basis for our station quality assessment, specifically in the context of POD.

(1) Carrier-to-Noise Ratio (cnr1, cnr2). These metrics represent the mean carrier-to-noise density ratio (C/N₀) for all signals on the first and second frequency bands, respectively. C/N₀ is defined as the ratio of the carrier power to the noise power in a 1 Hz bandwidth [9]. This indicator directly reflects the signal quality, which is influenced by a combination of factors including the observation environment, receiver hardware, and antenna characteristics.

(2) Number of Observations (nObs). This denotes the total number of available observations above a predefined elevation cut-off angle. For POD applications, the cut-off angle is typically set to 7°.

(3) Cycle Slips and Interruptions (csAll, nSlp). A cycle slip is defined as an instantaneous jump of an integer number of cycles in a carrier phase observation. The csAll metrics refers to the total count of phase cycle slips and data interruptions, the latter of which necessitates the re-initialization of a phase ambiguity. In contrast, nSlp represents only the number of detected cycle slips within a continuous tracking arc for a specific satellite and signal. The csAll is a superset of nSlp, as it also accounts for interruptions caused by missing epochs or the loss of signal lock. Therefore, the nSlp value is highly dependent on the performance of the cycle slip detection algorithm employed during data processing.

(4) Receiver Clock Jumps (nJmp). A clock jump is a sudden, discrete offset in a receiver’s internal clock that can occur when the clock bias of a low-cost quartz oscillator drifts significantly from the reference system time. This metric denotes the number of identified receiver clock jumps. As the data utilized for POD are exclusively collected from geodetic-grade receivers, clock jumps are generally infrequent.

(5) Data Gaps and Segments (nGap, nPcs). nGap represents the total number of data gaps, while nPcs indicates the number of small, fragmented data segments.

(6) Pseudorange Multipath (mp1, mp2). These metrics quantify the code pseudorange multipath effect, expressed as its moving average RMS in centimeters (cm). The suffixes ‘1’ and ‘2’ correspond to the average multipath values across all signals on the first and second frequency bands of a GNSS constellation, respectively.

Among these metrics, nObs is the most fundamental, as a sufficient number of observations is crucial for the robust estimation of orbit and clock parameters. The metrics csAll, nSlp, nJmp, nGap, and nPcs pertain to data integrity and continuity, which primarily influence the geometric strength of the solution. The C/N₀ indicators, cnr1 and cnr2, directly reflect the quality of the raw received signal. The multipath metrics, mp1 and mp2, primarily relate to pseudorange observations and are indicative of the station’s observation environment. These ten metrics collectively offer a comprehensive assessment of the factors that most significantly impact POD accuracy.

A variety of open-source software packages [10,11,12,13,14] are available for GNSS data preprocessing, capable of calculating some or all of the aforementioned indicators from either real-time streams or observation data in RINEX format. In this study, the Anubis-Free software(version 3.10 in Linux) [11] was selected to compute the index features of the GNSS observations. The primary reason for this choice was its capability to generate highly detailed output. Specifically, Anubis allows users to define a verbosity level (from 0 to 9) either in a configuration file or as a command-line parameter to control the level of detail in the output information.

2.2. The TOPSIS Algorithm

The TOPSIS [15] is a widely used multi-criteria decision-making (MCDM) method that effectively utilizes information from the original data, and its results accurately reflect the relative performance of each alternative. The fundamental principle of TOPSIS is to evaluate each alternative based on its simultaneous distance from an ideal solution and a negative-ideal solution.

Consider a system with n alternatives evaluated against m criteria. The TOPSIS score, $S_i$, for the i-th alternative is expressed as:

$$S_i={\displaystyle \frac{\sqrt{{\sum }_{j=1}^m{\left(z_j^{+}-z_{ij}\right)}^2}}{\sqrt{{\sum }_{j=1}^m{\left(z_j^{+}-z_{ij}\right)}^2}+\sqrt{{\sum }_{j=1}^m{\left(z_j^{-}-z_{ij}\right)}^2}}},$$

(1)

where $z_{ij}$ is an element of the weighted normalized decision matrix Z, which is constructed as follows:

$$Z=\left[\begin{array}{cccc}{z}_{11}& z_{12}& \dots & z_{1m}\\ z_{21}& z_{22}& \dots & z_{2m}\\ \dots & \dots & \dots & \dots \\ z_{n1}& z_{n2}& \dots & z_{nm}\end{array}\right].$$

(2)

Here, $z_j^{+}$ and $z_j^{-}$ represent the ideal solution (best-case) and the negative-ideal solution (worst-case) for each criterion, respectively, defined as $z_j^{+}=\left[\max \right\{z_{1j},z_{2j},\dots ,z_{nj}\left\}\right]$ and $z_j^{-}=\left[\min \right\{z_{1j},z_{2j},\dots ,z_{nj}\left\}\right]$.

The initial data processing step, termed “benefit-type conversion,” transforms all criteria into benefit-type indicators, for which higher values are preferable. For instance, the number of GNSS observations is inherently a benefit-type criterion. In contrast, the multipath effect is a cost-type criterion, as lower values are better; it can be converted into a benefit-type criterion by taking its reciprocal. Subsequently, a normalization procedure is applied to eliminate the influence of different scales and units among the criteria, which is achieved by dividing each element by the Euclidean norm of its corresponding criterion vector.

2.3. The K-Means Clustering Algorithm

The fundamental objective of clustering is to partition a dataset into distinct groups, or clusters, based on a specific criterion such as distance. This partitioning aims to maximize the similarity among data objects within the same cluster (intra-cluster similarity) while minimizing the similarity between objects in different clusters (inter-cluster similarity). For the k-means algorithm [16], given a set of clusters C = {C₁, C₂, …, C_k}, the objective is to minimize the sum of squared errors (SSE), also known as within-cluster sum of squares (WCSS), denoted by E:

$$\mathrm{E}={\sum }_{\mathrm{i}=1}^{\mathrm{k}}{\sum }_{\mathrm{x}\in {\mathrm{C}}_{\mathrm{i}}}{‖x-{\mu }_i‖}^2,$$

(3)

where x represents a data object in cluster ${\mathrm{C}}_{\mathrm{i}}$, and ${\mu }_i$ is the mean vector, or centroid, of that cluster. The centroid ${\mu }_i$ is calculated as:

$${\mu }_i={\displaystyle \frac{1}{\left|C_i\right|}}{\sum }_{x\in C_i}x.$$

(4)

Finding the optimal solution to this problem is NP-hard; therefore, heuristic and iterative methods are employed to find a locally optimal solution.

2.4. The Proposed Station Selection Algorithm

The station selection algorithm proposed in this paper is illustrated in Figure 1. It consists of three primary modules: (1) Data Preparation, (2) TOPSIS-based Quality Assessment, and (3) spherical k-means Clustering for Station Selection.

2.4.1. Data Preparation

The data preparation module begins by specifying a target date in the format of year and day of year (DOY). First, the official IGS station list and the corresponding IGS weekly solution file are downloaded. An initial candidate station set, S0, is compiled by filtering for stations that support four-constellation GNSS (GPS, GLONASS, Galileo, and BDS) observations and have precise coordinates available in the weekly solution file. For each station in S0, the daily broadcast navigation messages and observation data, both in RINEX format, are retrieved. Finally, any stations in S0 lacking available observation data for the target date is removed, yielding in the refined candidate list, S1.

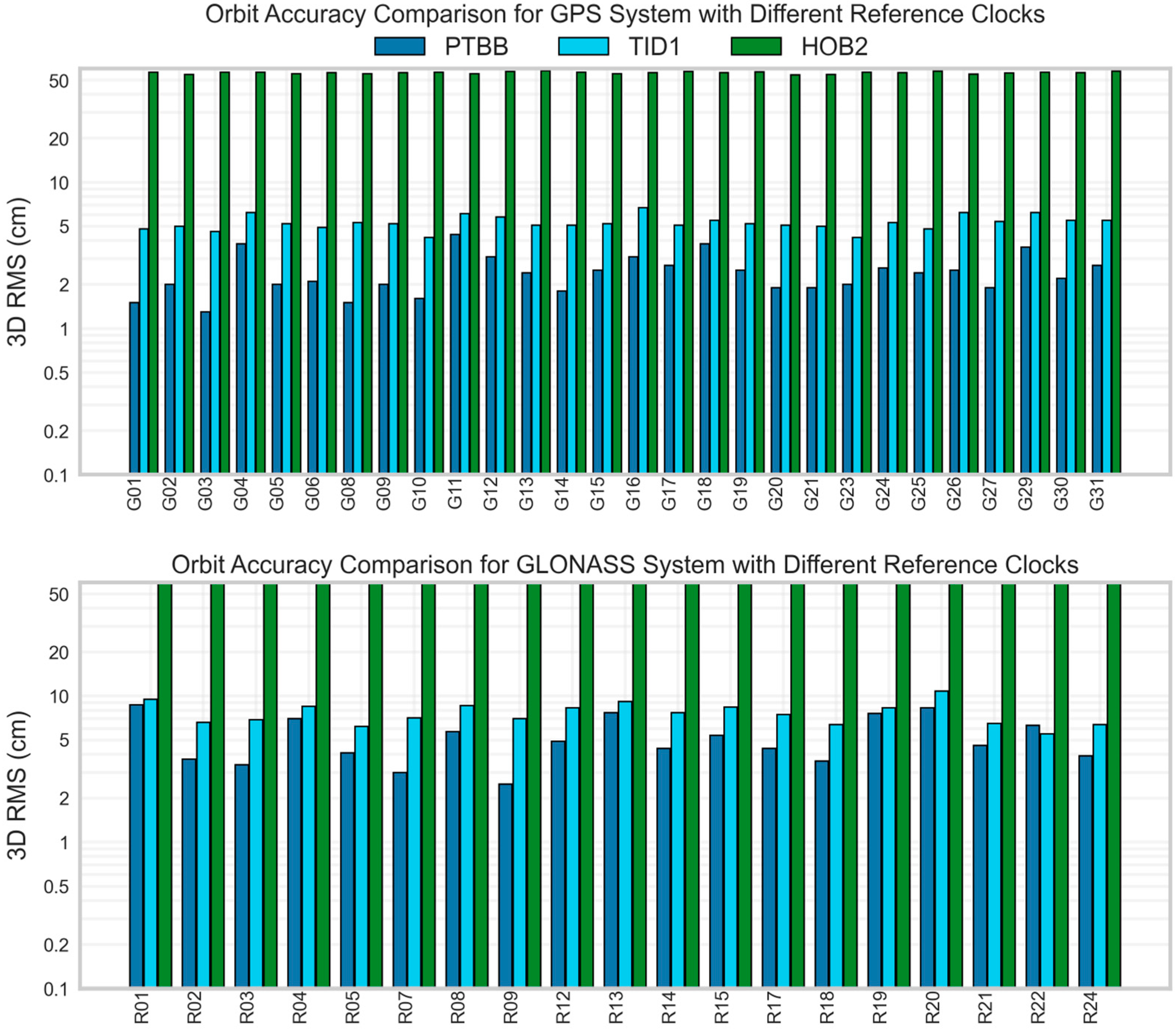
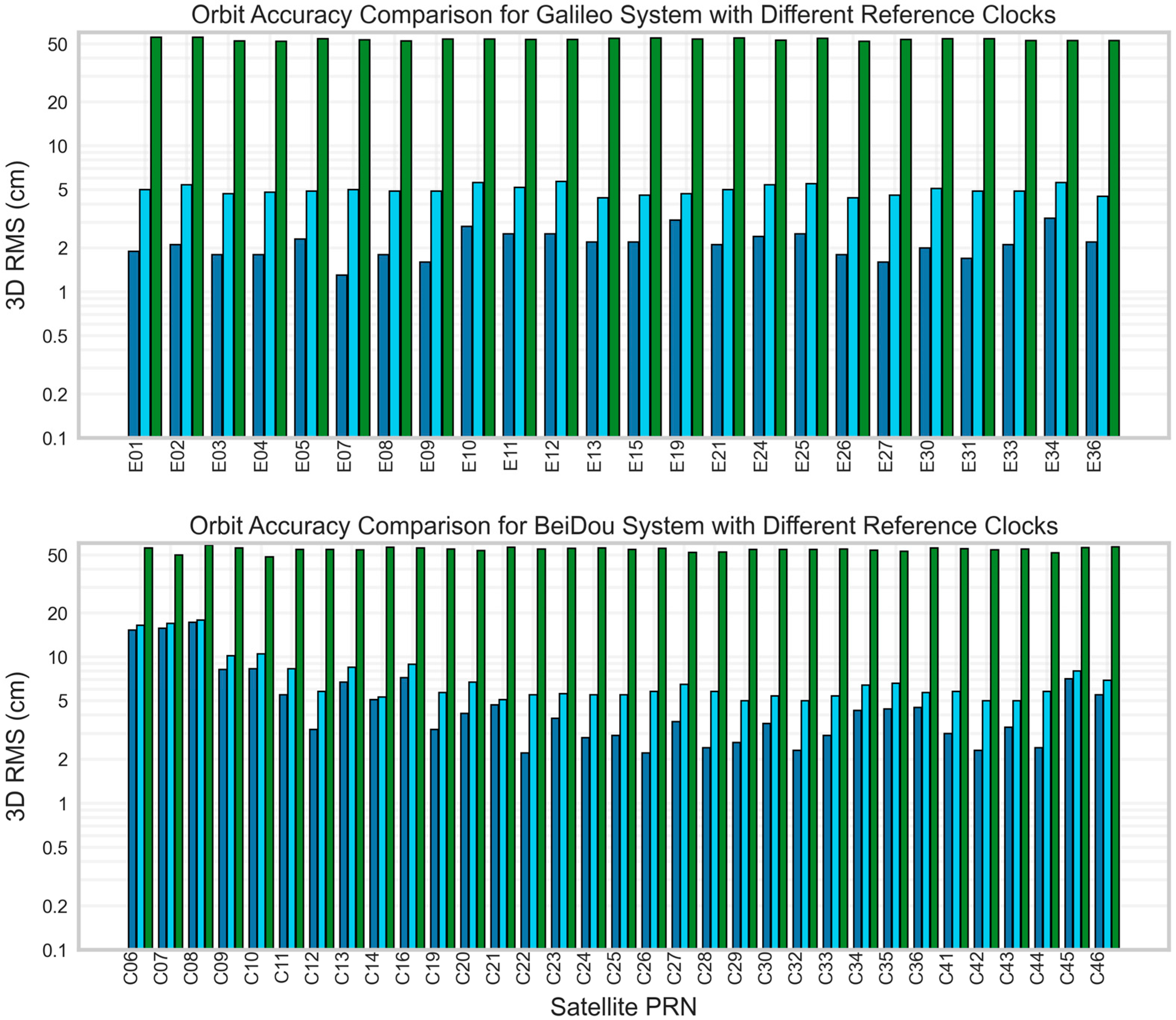
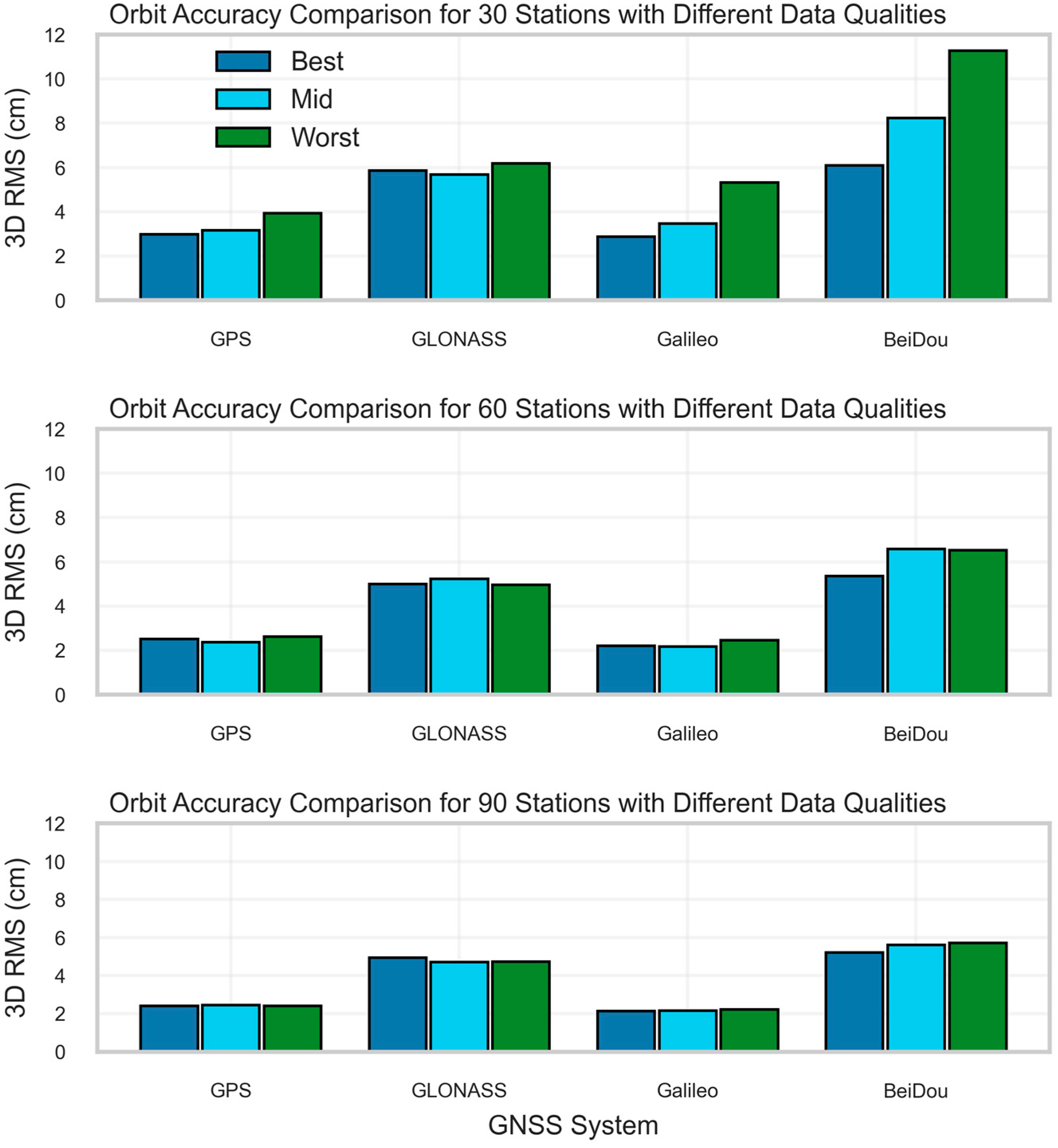
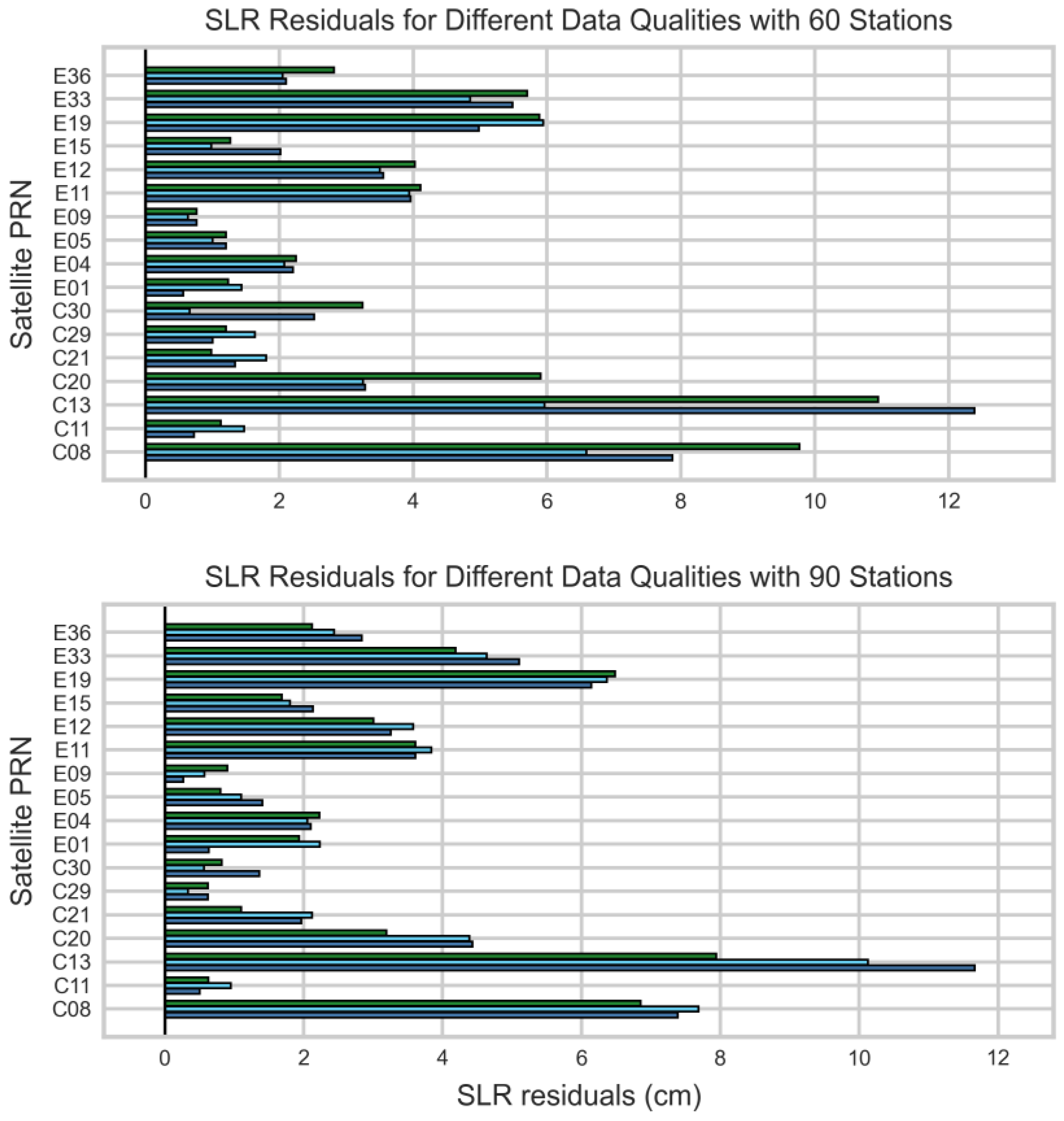
2.4.2. Quality TOPSIS Scoring

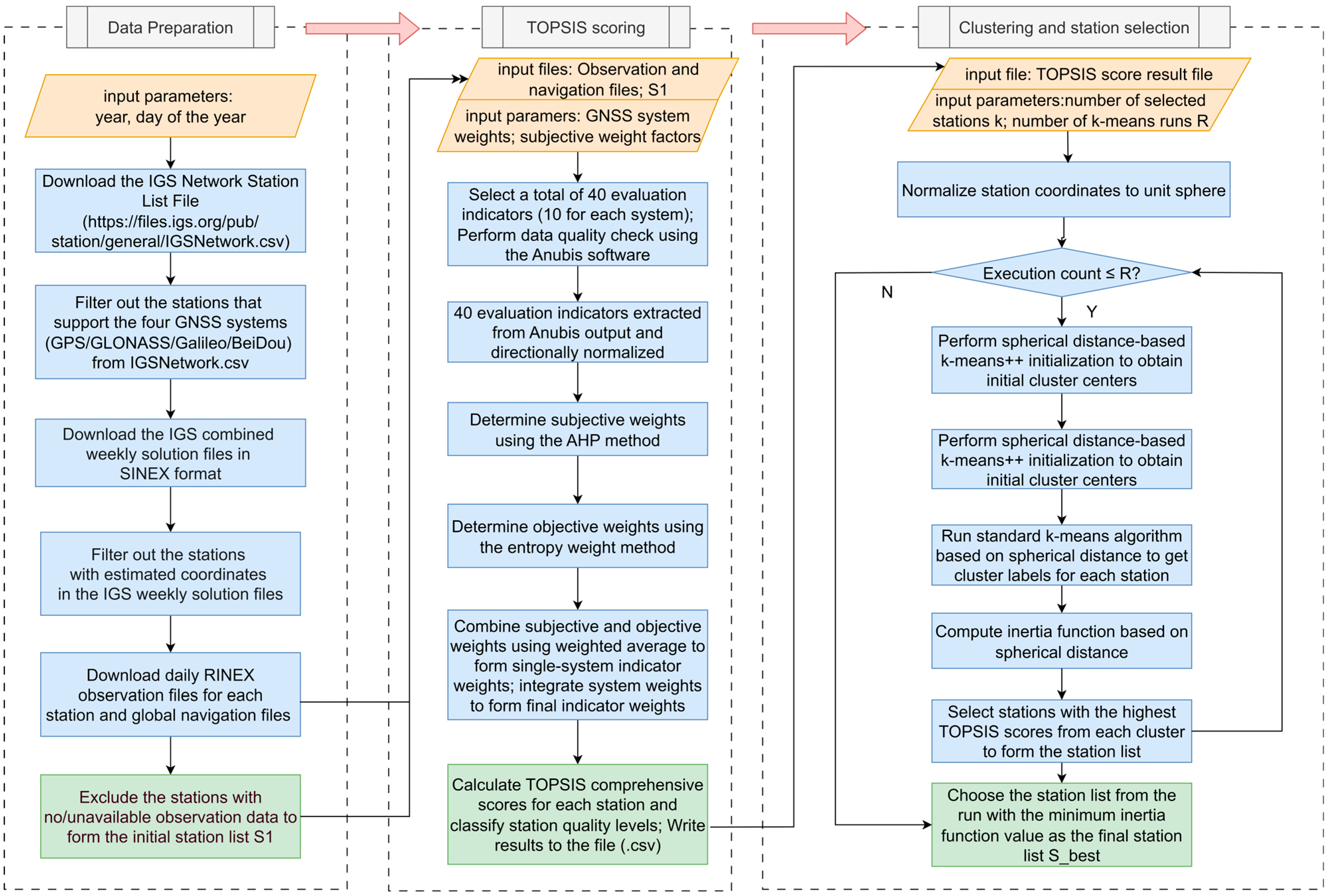
This module executes an eight-step process to generate a comprehensive quality score for each station in S1.

(1) Construction of the Quality Metric System. The quality assessment process begins by processing the observation data for all stations in S1 using the Anubis software. A comprehensive metric system is established, comprising 40 indicators—10 for each of the four GNSS constellations. For any constellation Q, where Q ∈ {G, R, E, C} (representing GPS, GLONASS, Galileo, and BDS, respectively), the 10-element metric vector is defined as:

Q_qc = [Q_nobs, Q_csAll, Q_nSlp, Q_nJmp, Q_nGap, Q_nPcs, Q_mp1, Q_mp2, Q_cnr1, Q_cnr2].

(5)

The definitions of these metrics correspond to those in Section 2.1. The processing parameters were configured with a 7° elevation cut-off angle, a 600 s data gap threshold, and a 1800 s minimum continuous observation segment. Stations with less than 0.5 h of data are consequently excluded. If a station lacks data for an entire constellation, a default penalty value is assigned to its corresponding metrics.

(2) Directional Normalization. To create a standardized decision matrix, all 40 metrics are normalized to a common scale using min-max scaling. The metrics Q_nobs, Q_cnr1, and Q_cnr2 are benefit-type indicators, whereas the remaining seven are cost-type indicators. For benefit-type indicators, the normalization is performed as follows:

$${\mathit{x}}_{\mathit{norm}\mathit{,}\mathit{ij}}={\displaystyle \frac{{\mathit{x}}_{\mathit{ij}}^{+}}{\max \left(x_j^{+}\right)}},$$

(6)

where ${\mathit{x}}_{\mathit{ij}}^{+}$ is the original value of the j-th benefit-type metric for the i-th station, $\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j^{+}\right)$ is the maximum value of that metric across all stations, and x_norm,ij is the resulting normalized value. For cost-type indicators, the normalization formula is:

$$x_{norm,ij}={\displaystyle \frac{\max \left(x_j^{-}\right)-x_{ij}^{-}}{\max \left(x_j^{-}\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j^{-}\right)}},$$

(7)

where the superscript “− denotes a cost-type indicator, and $\min (x_j^{-})$ is the minimum value of the j-th cost-type metric across all stations.

(3) Subjective Weighting via AHP. As a multi-criteria decision-making method, the AHP provides a formal structure for quantifying subjective assessments by transforming them into numerical values through a series of pairwise comparisons [17]. First, a 10 × 10 pairwise comparison matrix, A_h, is constructed based on expert knowledge.

$${\mathbf{A}}_{\mathbf{h}}=\left[\begin{array}{cccccccccc}1.0& 3.0& 3.0& 5.0& 7.0& 7.0& 3.0& 3.0& 1.0& 1.0\\ 1/3& 1.0& 1.0& 3.0& 5.0& 5.0& 1/3& 1/3& 1/3& 1/3\\ 1/3& 1.0& 1.0& 3.0& 5.0& 5.0& 1/3& 1/3& 1/3& 1/3\\ 1/5& 1/3& 1/3& 1.0& 3.0& 3.0& 1/5& 1/5& 1/5& 1/5\\ 1/7& 1/5& 1/5& 1/3& 1.0& 1.0& 1/7& 1/7& 1/7& 1/7\\ 1/7& 1/5& 1/5& 1/3& 1.0& 1.0& 1/7& 1/7& 1/7& 1/7\\ 1/3& 3.0& 3.0& 5.0& 7.0& 7.0& 1.0& 1.0& 1/3& 1/3\\ 1/3& 3.0& 3.0& 5.0& 7.0& 7.0& 1.0& 1.0& 1/3& 1/3\\ 1.0& 3.0& 3.0& 5.0& 7.0& 7.0& 3.0& 3.0& 1.0& 1.0\\ 1.0& 3.0& 3.0& 5.0& 7.0& 7.0& 3.0& 3.0& 1.0& 1.0\end{array}\right],$$

(8)

The core principle of this AHP matrix is to quantify the relative impact of the degradation of any two quality metrics on the ultimate goal: GNSS four-constellation POD. The matrix is populated using the fundamental 1–9 scale (

Table 1. The Fundamental Scale for Pairwise Comparisons in AHP [17].

Scale of Importance	Definition	Explanation
1	A and B are equally important.	The two elements contribute equally to the objective.
3	A is slightly more important than B.	Experience and judgment slightly favor one element over another.
5	A is obviously more important than B.	Experience and judgment strongly favor one element over another.
7	A is significantly more important than B.	One element is favored very strongly over another; its dominance is demonstrated in practice.
9	A is extremely more important than B.	The evidence favoring one element over another is of the highest possible order of affirmation.
2, 4, 6, 8	Intermediate values	Used when a compromise is needed between two adjacent judgments.
Reciprocals	If element B is more important than element A	If the importance of A to B is 3, then the importance of B to A is 1/3.

).

The order of the metrics in the matrix corresponds to their sequence in the Q_qc vector. For example, the element A_h[0][6] = 3 indicates that the number of observations is considered slightly more important than the multipath error. The rationale is that a sufficient quantity of observations is a prerequisite for reliable POD, rendering low multipath values meaningless in its absence. Similarly, A_h[6][7] = 1 implies that multipath effects on the first and second frequencies are of equal importance, as the quality of observations on both frequencies is equally critical for the dual-frequency ionosphere-free combination. Conversely, A_h[3][8] = 1/5 signifies that receiver clock jumps are considered significantly less important than the carrier-to-noise ratio. This judgment is based on the fact that clock jumps are typically detectable and correctable during data preprocessing, whereas a low C/N0 ratio indicates poor signal quality that systematically increases the noise level of all observations. The consistency of the matrix was validated, yielding a Consistency Ratio (CR) of 0.06, which falls below the standard threshold of 0.1. The subjective weight vector is derived by normalizing the columns of A_h and then averaging the elements in each row:

$$w_{\mathit{subj},i}={\displaystyle \frac{1}{10}}{\sum }_{j=1}^{10}{\stackrel{\mathrm{-}}{a}}_{\mathit{ij}},$$

(9)

where $w_{\mathit{subj},i}$ is the subjective weight of the i-th metric, and ${\stackrel{-}{a}}_{\mathit{ij}}={\displaystyle \frac{a_{\mathit{ij}}}{{\sum }_{\mathrm{k}=1}^{10}{a}_{\mathit{kj}}}}$ is the element of the column-normalized matrix A_h. In this equation, $a_{\mathit{ij}}$ denotes the element in the i-th row and j-th column of matrix A_h. The denominator ${\sum }_{\mathrm{k}=1}^{10}{a}_{kj}$ represents the sum of the first 10 elements of the j-th column of matrix A_h.

(4) Objective Weighting via the Entropy Weight Method. The fundamental principle of the Entropy Weight Method is to determine objective weights based on the amount of information conveyed by each indicator. An indicator with greater variation in its values across different alternatives is considered to contain more information and thus exerts a greater influence on the evaluation, assigning a higher weight. Conversely, an indicator with less variation is assigned a lower weight [18].

We first calculate the information entropy for each indicator according to the following equation:

$$e_j=-{\displaystyle \frac{1}{\ln \left(\mathrm{m}\right)}}{\sum }_{\mathrm{i}=1}^{\mathrm{m}}{p}_{\mathit{ij}}\ln (p_{\mathit{ij}}+\mathsf{ϵ}).$$

(10)

In this equation, $e_j$ denotes the information entropy of the j-th indicator, m represents the total number of stations, and $ϵ={10}^{-10}$ is a smoothing parameter introduced to prevent numerical instability. The term $p_{ij}$, representing the probability of the j-th indicator for the i-th station, is calculated as follows:

$$p_{\mathit{ij}}={\displaystyle \frac{x_{\mathit{norm},\mathit{ij}}+ϵ}{{\sum }_{k=1}^m(x_{\mathit{norm}\mathit{,}\mathit{ij}}+ϵ)}}.$$

(11)

Finally, the objective weight for the j-th indicator, $w_{\mathit{obj},j}$, is computed using the subsequent formula:

$$w_{\mathit{obj},j}={\displaystyle \frac{1-e_j}{{\sum }_{\mathrm{k}=1}^{10}(1-e_k)}}.$$

(12)

(5) Fusion of Subjective and Objective Weights. The subjective and objective weights are combined using a weighted average to form a single-system metric weight:

$$w_{\mathit{comb},\mathit{j}}=\alpha .w_{\mathit{subj},j}+\left(1-\alpha \right).w_{\mathit{obj},j},$$

(13)

where α is a coefficient representing the preference for subjective weights, set to 0.7 in this study to emphasize the importance of expert knowledge.

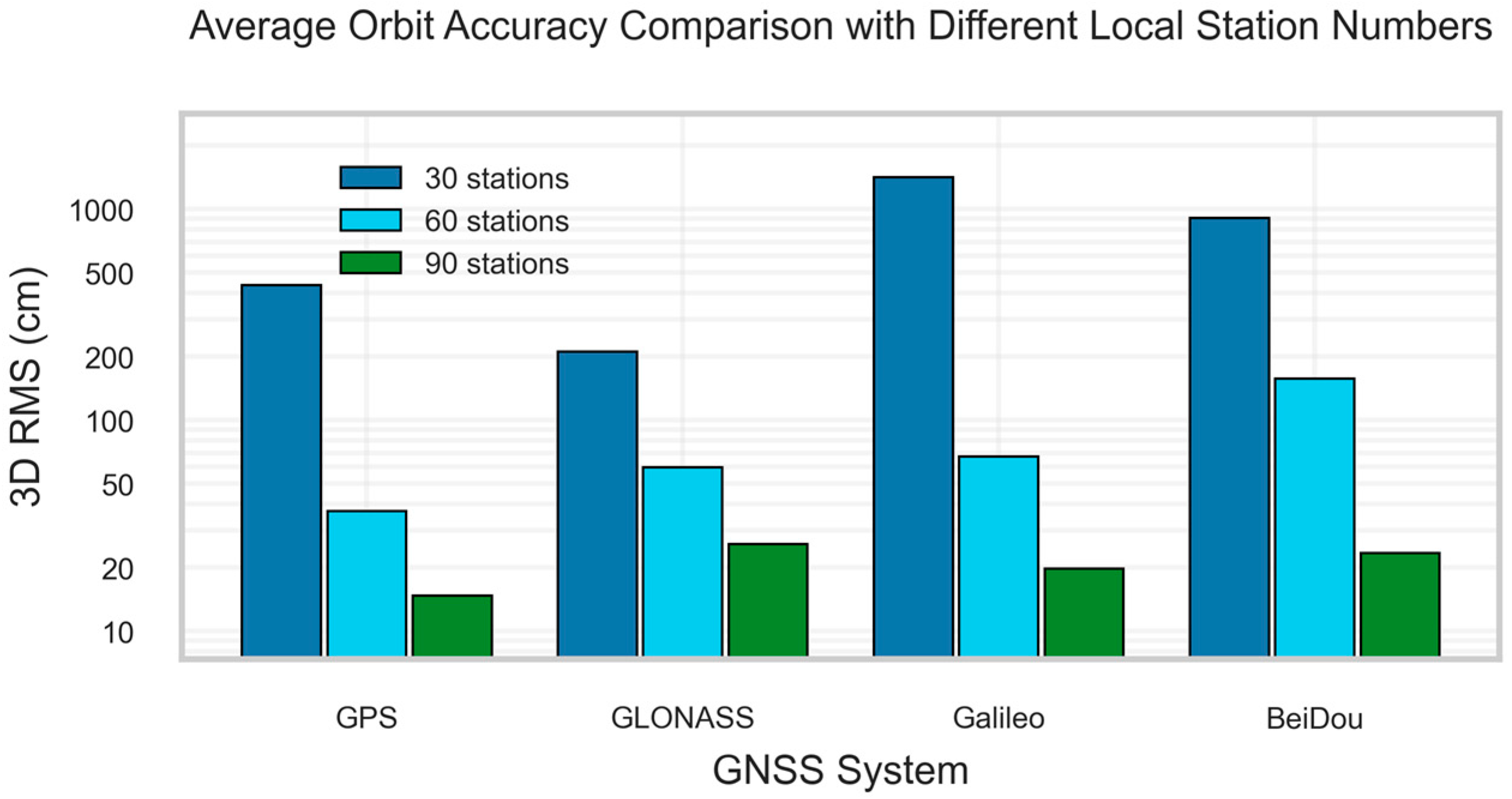
(6) Application of Constellation-Specific Weights. We use a three-thread parallel processing strategy (Thread 1: GPS + GLONASS; Thread 2: GPS + Galileo; Thread 3: GPS + BDS) in this study. Since GLONASS, Galileo, and BDS are all processed in conjunction with GPS, a higher weight is assigned to the GPS-related metrics. The final weight for each metric is thus defined as:

$$w_{\mathit{comb},Q, j} = w_Q.w_{\mathit{comb},j},$$

(14)

where w_Q is the constellation-specific weight: w_G = 0.4, w_R = 0.2, w_E = 0.2 and w_C = 0.2.

(7) Calculation of the Final TOPSIS Score. A weighted normalized decision matrix Z is constructed using the final metric weights, that is, $z_{\mathit{ij}} = x_{\mathit{norm},\mathit{ij}}\times w_{\mathit{comb},Q,j}$, where z_ij represents the weighted value of the j-th indicator for the i-th station. The ideal and negative-ideal solutions are then determined as described in Section 2.2, and the final TOPSIS score ${\mathrm{C}}_i$ for the i-th station, where ${\mathrm{C}}_i$ ∈ [0, 1], is calculated.

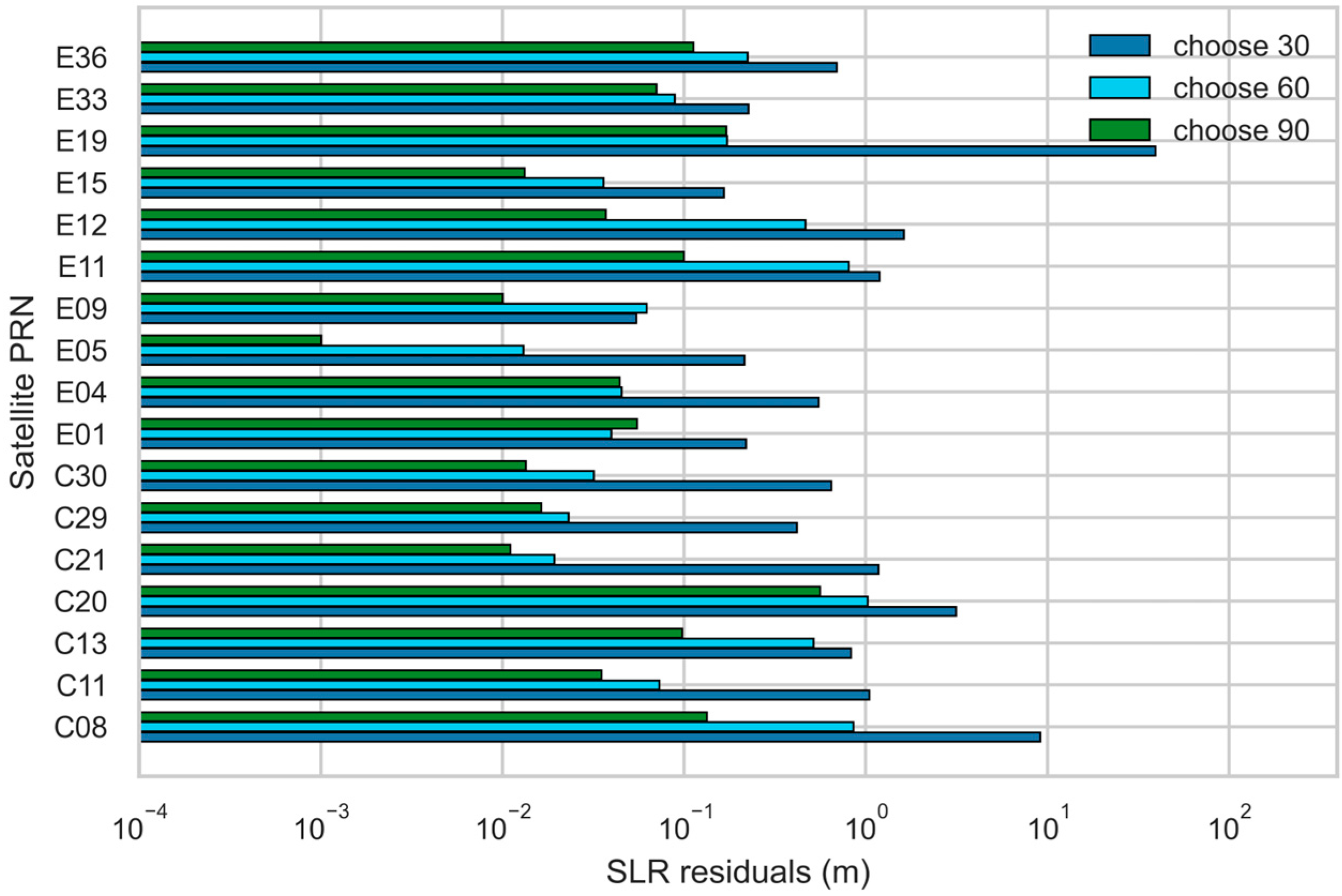
(8) Station Quality Classification. Finally, stations are classified into four quality levels based on their TOPSIS scores: Excellent (C ≥ 0.8), Good (0.6 ≤ C < 0.8), Fair (0.4 ≤ C < 0.6), and Poor (C < 0.4). The thresholds were derived empirically from the statistical distribution of the scores. Our analysis indicated that stations with scores above 0.8 generally exhibit high data integrity, whereas scores between 0.6 and 0.8 often signify missing data for a specific GNSS system or for a particular frequency within a system. This indicates that the TOPSIS score can serve as a preliminary diagnostic tool to identify potential issues in a station’s data.

The entire quality scoring procedure is summarized in Algorithm 1.

Algorithm 1: TOPSIS_SCORE

Input:

Station metric matrix X (dimensions: n stations × 40 metrics); Set of constellation identifiers Q = {G, R, E, C}; Metric directionality vector dir (benefit-type/cost-type); Constellation weights wsys; Subjective weight coefficient α = 0.7

Output:

A CSV file containing station names, coordinates, TOPSIS scores, and quality levels

Procedure:

X^ ← directional_normalize(X, dir)

for s in Q:

sub ← columns of X^ in system s (10 cols)

wobj ← entropy_weight(sub)

wcomb ← normalize(α·wsub + (1 − α)·wobj)

apply column weights wsys[s]*wcomb to sub → Ys

Y ← concats(Ys) by columns

v+ ← colwise max(Y); v− ← colwise min(Y)

for each station i: ${\mathrm{C}}_i\leftarrow \left|\right|{\mathrm{Y}}_i-{\mathrm{v}}^{-}\left|\right|/\left(\right||{\mathrm{Y}}_i-{\mathrm{v}}^{+}||+||{\mathrm{Y}}_i-{\mathrm{v}}^{-}|\left|\right)$

Rank stations based on Ci and assign quality levels based on predefined thresholds

Write results to a CSV file

2.4.3. Clustering and Station Selection

(1) Normalization to the Unit Sphere. Acknowledging that the station distribution is on a sphere rather than a plane, the k-means algorithm is adapted to use spherical distance. This requires first normalizing the three-dimensional Earth-Centered, Earth-Fixed (ECEF) coordinates of each station onto a unit sphere:

$${\mathbf{P}}_i^{\mathrm{norm}} ={\mathbf{P}}_i/{‖{\mathrm{P}}_i‖}_2,$$

(15)

where ${\mathbf{P}}_i = {\left({\mathrm{x}}_i, {\mathrm{y}}_i, {\mathrm{z}}_i\right)}^{\mathrm{T}}$ represents the ECEF coordinates of the i-th station, and ${\mathbf{P}}_i^{\mathrm{norm}}$ denotes its corresponding coordinates on the unit sphere.

(2) Initialization via Spherical k-means++. To mitigate the sensitivity of k-means to initial conditions, the k-means++ algorithm [19] is used to determine an intelligent initial set of k cluster centroids. The procedure (summarized in Algorithm 2) begins by selecting the first centroid uniformly at random. The next centroid is then chosen from the remaining stations with a probability proportional to the squared spherical distance to the nearest existing centroid. This is repeated until all k centroids are selected. For the selection of the j-th cluster centroid, the spherical distance from each point to its nearest previously selected centroid is calculated as follows:

$${\mathrm{d}}_i^{j-1}=\underset{a=1,\dots ,j-1}{\min }\arccos ({\mathbf{P}}_i^{\mathrm{norm}}.{\mathbf{c}}_a),$$

(16)

where ${\mathrm{d}}_i^{j-1}$ denotes the minimum spherical distance from the i-th point to the set of the first j − 1 selected centroids. The probability of selecting a point as the next centroid is then calculated using the following formula:

$${\mathrm{p}}_i={\displaystyle \frac{{\left({\mathrm{d}}_i^{j-1}\right)}^2}{{\sum }_{a=1}^n{\left(d_a^{j-1}\right)}^2}},$$

(17)

The entire procedure for the spherical distance-based k-means++ initialization is summarized in Algorithm 2.

Algorithm 2: Spherical K-Means Plus Plus

Input:

Normalized station coordinates ${\mathbf{P}}_i^{\mathrm{norm}}$ (dimensions: n stations × 3); the number of clusters k.

Output:

A set of k centroids {c1 … ck}

Procedure:

pick first center c1 uniformly at random

for t = 2…k:

Di ← mincarccos(clip(dot(${\mathbf{P}}_i^{\mathrm{norm}}$, c), −1, 1))

pi ← Di2/(${\sum }_j$ Dj2)

sample ct ~ Categorical(p)

return centers {c1…ck}

(3) Spherical k-means Iteration and Final Selection. The final selection stage involves three key aspects:

(a) Assignment Step: each station is assigned to the nearest centroid using spherical distance as the metric:

$${\mathrm{label}}_i=\arg \underset{j=1\dots ,k}{\min }\arccos ({\mathbf{P}}_i^{\mathrm{norm}}.{\mathrm{c}}_j),$$

(18)

where ${\mathrm{label}}_i$ denotes the cluster assignment for the i-th station, and k is the desired number of clusters (equivalent to the number of selected stations).

(b) Update Step: the new centroid for each cluster is calculated as the vector mean of all station coordinates within that cluster, which is then re-normalized to the unit sphere:

$${\mathrm{c}}_j^{\mathrm{new}}=1/\left|{\mathrm{S}}_j\right|\sum i\in {\mathrm{S}}_j{\mathbf{P}}_i^{\mathrm{norm}},$$

(19)

where ${\mathbf{c}}_{\mathit{j}}^{\mathbf{new}}$ is the updated centroid of the j-th cluster, ${\mathrm{S}}_j$ represents the set of stations belonging to cluster j, and $\left|{\mathrm{S}}_j\right|$ denotes the number of stations in that cluster.

(c) Optimality Criterion: the standard k-means procedure is iterated until convergence. To ensure a robust result, this entire process, from initialization to convergence, is repeated independently R times. The optimal clustering result is identified by minimizing the inertia J, defined as the sum of squared spherical distances of stations to their respective cluster centroids:

$$\mathrm{J}={\sum }_{i=1}^n\left(\arccos \right({\mathbf{P}}_i^{\mathrm{norm}}·{\mathrm{c}}_{\mathrm{labe}{\mathrm{l}}_i}){)}^2,$$

(20)

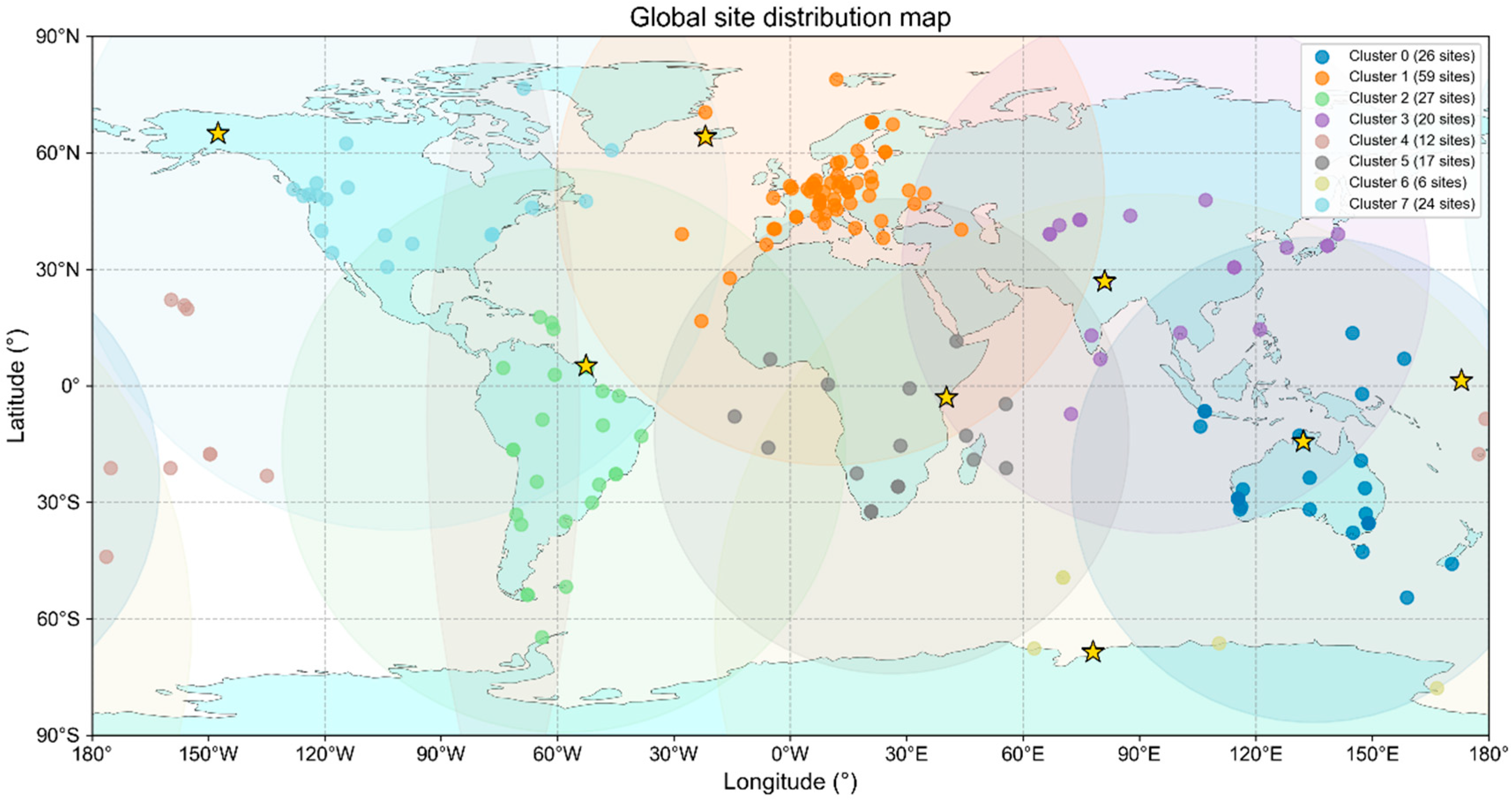
where ${\mathrm{c}}_{\mathrm{labe}{\mathrm{l}}_i}$ is the centroid of the cluster to which the i-th station belongs. The final station list, ${\mathrm{S}}_{\mathrm{best}} = \arg \underset{r=1,\dots ,\mathrm{R}}{\min }{\mathrm{J}}_r$, is composed of the highest-scoring stations from the clusters of the run that yields the minimum inertia value.

The complete algorithm for clustering-based station selection is summarized in Algorithm 3.

Algorithm 3: K-Means Based Station Selection

Input:

DataFrame df containing station coordinates, TOPSIS scores, etc.; Desired number of stations k; Number of independent runs R

Output:

The final optimal station list Sbest.

Procedure:

coords ← df.xyz; q ← df.topsis_score

x^ ← row_normalize(coords)

for r in 1…R:

c0 ← SphericalKMeansPlusPlus(x^, k) (Algorithm 2)

labels, centers ← KMeans(x^, init = c0)

Jr ← ∑iarccos(clip(dot(x^i, normalize(centers[labelsi])), −1,1))2

Sr ← argma xiqi within each cluster

r* ← argminrJr

Sbest ← Sr*

3. Results

3.1. Station Quality Scoring

This section presents a comprehensive evaluation of the data quality for IGS/MGEX stations, conducted for the period from DOY 91 to 97, 2022. The assessment utilized the TOPSIS composite scoring algorithm detailed in Section 2.4.2. As an illustrative example, the 10 highest-ranked stations from DOY 91, 2022, determined by their composite quality scores, are presented in

Table 2. Top 10 IGS/MGEX stations ranked by TOPSIS composite quality score on DOY 91, 2022.

Site Name	Longitude (°)	Latitude (°)	TOPSIS Score	Quality Level
REYK	−21.9	64.1	0.89693	Excellent
LCK3	80.9	26.9	0.89298	Excellent
LCK4	80.9	26.9	0.89069	Excellent
DAV1	77.9	−68.5	0.88795	Excellent
CAS1	110.5	−66.2	0.88546	Excellent
SOFI	23.3	42.5	0.88399	Excellent
SGOC	79.8	6.8	0.88372	Excellent
KAT1	132.1	−14.3	0.88247	Excellent
MET3	24.3	60.2	0.88215	Excellent
POL2	74.6	42.6	0.88140	Excellent

.

According to Table 2, station REYK ranked first on DOY 91 with a score of 0.89693, while station POL2 ranked tenth with a score of 0.88140. All top-10 stations achieved scores exceeding 0.88 and were classified in the “Excellent” quality grade. The score differential between the first and tenth stations was less than 0.02, indicating that these stations all exhibited outstanding performance on key metrics—including data integrity, multipath suppression, and signal-to-noise ratio (SNR)—for that specific day.

Figure 2 illustrates the ranking fluctuations among top-performing stations over the seven-day period (DOY 91–97, 2022). The analysis reveals that six stations—REYK, LCK3, LCK4, DAV1, CAS1, and SOFI—consistently remained within the top 10. Notably, REYK, LCK3, LCK4, and DAV1 persistently occupied the top four positions, suggesting these stations maintained better data quality and stability throughout this seven-day period. In contrast, the rankings of several other stations exhibited significant volatility. For instance, station CAS1, which ranked 5th on DOY 91, dropped to 11th by DOY 97. Similarly, station SGOC fell from 7th on DOY 91 to 14th on the following day. Other stations, such as POL2, KAT1, CIBG, and KRGG, fluctuated in and out of the top 10 during this period. This volatility highlights the limitation of relying on long-term or static rankings, as they may fail to capture short-term variations in data quality.

3.2. Station Selection Results

Following the comprehensive quality assessment of all available stations from DOY 91 to 97, 2022, the proposed station selection algorithm was applied. The resulting clustering for a selection of 8 stations, using data from DOY 91, 2022, as a case study, is illustrated in Figure 3. Here a network of 8 stations was selected primarily for visualization purposes, as a larger number would hinder the effective illustration of the clustering partitions. It should be noted that a network of this size is insufficient for practical POD applications.

Figure 3 reveals a significant imbalance in both the number of stations per cluster and their geographical distribution. The current IGS/MGEX network has the highest station density over continental Europe, which is consistent with the fact that Cluster 1 contains the largest number of stations. Clusters 2, 0, 7, and 3 contain a relatively balanced number of stations, ranging from 20 to 30, and collectively form a substantial portion of the IGS/MGEX network. The remaining clusters contain fewer stations, highlighting the sparsely covered regions of the global GNSS reference network, particularly over ocean areas and in environments of the polar regions where high-quality observation data are relatively scarce.

3.3. Performance Analysis of GNSS POD Based on the Selected Networks

3.3.1. Configuration for GNSS POD

In this study, precise orbits for GNSS satellites were determined using daily data from a network of ground stations. The processing was performed using an independently developed POD software package, which is described in detail in [20]. The detailed models and processing strategies are summarized in

Table 3. Models and Strategies for multi-GNSS POD.

Items	Relevant Settings
Force Models	Earth gravity field: EIGEN6S4 [21] (12 × 12); N-body Perturbations: JPL DE405 ephemeris [22]; Tidal Perturbations: Solid Earth tides [23], pole tides [23], ocean tides [24]; Solar Radiation Pressure: ECOM model [25] for GPS/GLONASS; a hybrid a priori box-wing and ECOM model for Galileo/BDS [26]; Relativistic Effects [23]
Observation Models	dual-frequency ionosphere-free combination of pseudorange and phase (GPS: L1/L2; GLONASS: G1/G2; Galileo: E1/E5a; BDS: B1I/B3I); Sampling interval: 300 s; Observation arc: 24 h; Elevation cut-off angle: 7°; Elevation-dependent weighting: 1 for elevations > 30°; 4 sin2E otherwise; PCO/PCV for satellite and receiver antennas based on igs14.atx, Phase wind-up [27]; Tropospheric delay (GMF mapping function [28] and Saastamoinen model [29])
Estimated Parameters	Estimation Method: Post-processing batch least-squares; parameters: Initial satellite state vectors (position and velocity), SRP parameters, satellite and receiver clock offsets (white noise), inter-system biases (constants), zenith wet delay (piecewise constant, 2 h intervals), tropospheric gradients (piecewise constant, 24 h intervals), station Coordinates: tightly constrained to IGS weekly solutions, ERPs: X-pole, Y-pole, their rates, and UT1-UTC (constants with tight constraints), ambiguities: integer ambiguities resolved using a double-differenced approach [30]

.

The optical parameters for the Galileo and BDS satellite panels were sourced from the European GNSS Agency [31] and BDS official website [32], respectively. A ground station receiver clock connected to a high-precision external atomic clock was selected as the reference clock.

As a case study, networks of 30, 60, and 90 IGS/MGEX stations were selected using the proposed algorithm based on data from DOY 91, 2022. The resulting geographical distributions are shown in Figure 4. The figure demonstrates that the algorithm achieves a high degree of spatial uniformity in the selected networks. A significant overlap is observed among the 30-, 60-, and 90-station networks, with most stations from the smaller networks being retained in the larger ones, which demonstrates the consistency of the selection algorithm across different network sizes.

3.3.2. Accuracy Assessment of Multi-GNSS POD

In this section, the accuracy of the orbit determination results for DOY 91, 2022, was assessed using two independent methods: comparison with external reference orbits and Satellite Laser Ranging (SLR) validation. The former involves comparing our computed orbits against the final precise orbit products from an external Analysis Center; for this study, we use the final orbits provided by the Center for Orbit Determination in Europe (CODE). The latter method consists of holding the computed orbits fixed, calculating the expected SLR ranges based on these orbits, and comparing them with the actual SLR measurements by analyzing the residuals [33,34]. Currently, numerous satellites across the BDS, GLONASS, and Galileo constellations, along with specific GPS satellites, are equipped with SLR retroreflectors, thereby enabling this validation method for their respective orbit products [35].

Figure 5 presents the results of the orbit comparison against the CODE final orbits for networks of 30, 60, and 90 stations selected using our proposed algorithm. The labels “30 stations,” “60 stations,” and “90 stations” correspond to the results derived from these three respective network configurations.

Overall, centimeter-level POD accuracy was achieved for all four GNSS constellations. Under the optimal 90-station configuration, the Galileo and GPS constellations reached average orbit RMS values of 2.1 cm and 2.46 cm, respectively, demonstrating a consistent 2–3 cm precision level. Under the same network configuration, the POD accuracy for GLONASS and BDS was slightly lower, with average orbit RMS values of 5.12 cm and 5.64 cm, respectively. The lower accuracy for BDS was primarily attributed to its Inclined GeoSynchronous Orbit (IGSO) satellites (e.g., C06, C07, C08), which have a weaker observation geometry compared to the Medium-Earth-Orbit (MEO) satellites. When considering only the MEO satellites, the accuracy of the BDS constellation become comparable to that of GPS and Galileo.

Regarding the effectiveness of the station selection, using just 30 stations selected by our method, the average orbit RMS for GPS and Galileo already reached 3.03 cm and 3.00 cm, respectively, while for GLONASS and BDS, the average RMS was 6.18 cm and 6.23 cm. These results demonstrate that even a minimal network selected by our approach can meet the basic requirements for POD. Increasing the network size from 30 to 60 stations yielded a significant improvement in POD accuracy. The average RMS values improved by 14.6%, 19.3%, 24.1%, and 9.5% for GPS, GLONASS, Galileo, and BDS, respectively. However, when the network was further expanded from 60 to 90 stations, the magnitude of the improvement diminished considerably, with the average RMS improving by only 4.3%, 1.9%, 4.5%, and 2.8% for the respective constellations. This trend validates that our proposed selection method can efficiently identify a core set of high-contributing stations, thereby balancing high POD accuracy with computational costs and complexity.

Furthermore, SLR data from the International Laser Ranging Service (ILRS) were used to validate the orbits of Galileo and BDS satellites equipped with retroreflectors, with the results presented in Figure 6. The labels “choose 30,” “choose 60,” and “choose 90” correspond to the SLR validation results for orbits determined using the 30-, 60-, and 90-station networks, respectively.

The SLR residuals for Galileo and BDS MEO satellites (e.g., C11, C20, C21, C29, C30) are generally small, mostly within the 1–4 cm range. The BDS IGSO satellites exhibit significantly larger SLR residuals, on the order of 8–12 cm, which is consistent with the larger RMS values observed in the comparison with CODE products in Section 3.3.2. Regarding the impact of network size, the SLR residuals for some satellites did not consistently decrease as the number of stations increased. This phenomenon suggests that while adding more stations generally enhances the overall stability and internal consistency of the orbit solution (reflected by the reduced RMS), the absolute radial accuracy of an individual satellite may be influenced by more complex factors, such as the geometric distribution of the tracking network relative to the SLR sites. Nevertheless, the absolute SLR residuals for all configurations remain at a low level, further confirming that the proposed station selection method yields high-quality precise orbit products, the accuracy of which is reliably validated by the independent SLR technique.

4. Discussion

The proposed station selection algorithm integrates two key factors: data quality and spatial distribution. A central objective of this section is thus to quantitatively analyze the respective impacts of these two factors on the accuracy of POD. However, the choice of the reference clock station is a critical factor known to significantly influence POD accuracy. To ensure that the performance evaluation of our algorithm is unbiased, the influence of this choice must be investigated and isolated first.

4.1. Impact of Reference Clock Selection on Multi-GNSS POD

The stability and data quality of the reference clock directly influence the datum for the parameter estimation and are key determinants of the final accuracy of the precise orbit and clock products. To ensure that the performance assessment of our proposed station selection algorithm is not biased by this choice, we first investigated the impact of different reference clock stations on POD accuracy.

We selected three IGS stations known for their high-precision atomic clocks as candidates for the reference clock: PTBB (Physikalisch-Technische Bundesanstalt, Braunschweig, Germany), TID1 (Tidbinbilla, Australia), and HOB2 (Hobart, Australia). Using the 90-station network selected by our algorithm, three separate POD solutions were computed, each using one of these stations as the reference. The resulting orbit accuracy was evaluated by computing the RMS of the differences relative to the CODE final products (Figure 7).

As shown in Figure 7, POD accuracy for all constellations achieved optimal levels when PTBB was selected as the reference clock. In contrast, switching the reference clock to TID1 resulted in a noticeable degradation of orbit accuracy across all systems. The average RMS for GPS and Galileo degraded to approximately 5 cm, effectively halving their precision. GLONASS and BDS also exhibited a similar degradation trend, indicating that the clock performance of TID1 station was inferior to that of PTBB during this processing period. A severe deterioration in POD results was observed when HOB2 was used as the reference clock, with the orbit RMS values for all systems increasing to over 50 cm.

The SLR residual validation results, shown in Figure 8, also underscore a similar issue. When HOB2 was selected as the reference clock, all satellites showed significantly larger SLR residuals, generally exceeding 10 cm, which is consistent with the results from the orbit RMS comparisons. It is noteworthy that the radial accuracy achieved with PTBB and TID1 as reference clocks is comparable. Although the 3D orbit RMS for TID1 as the reference clock was poorer than for PTBB, their respective SLR residuals remained at a similar level. For most Galileo and BDS MEO satellites, the SLR residuals in both scenarios were within the 1–4 cm range, showing minimal differences. This indicates that while the orbits derived from the two scenarios might exhibit systematic biases in their reference frames (leading to differences in 3D RMS), their absolute radial accuracies are in fact comparable. Despite TID1 also achieving orbits with high radial accuracy, the results obtained using PTBB as the reference clock showed superior consistency with the CODE final orbits in terms of reference frame. This consistency explains our choice of PTBB as the reference clock for all orbit determination solutions presented in Section 3.

In summary, a random selection of the reference clock could entirely mask or distort the true performance of the station selection algorithm itself. The discussions in this section ensure that the evaluation of different station network configurations is conducted under a stable, reliable, and consistent time datum, allowing the conclusions to more accurately reflect the intrinsic contributions of station spatial distribution and data quality to POD accuracy.

4.2. Impact of Data Quality

To isolate and quantify the intrinsic contribution of data quality to POD accuracy, a comparative experiment was designed as follows. For each of the 30-, 60-, and 90-station scenarios, the clustering partitions were held constant. Three distinct networks were then constructed by selecting the station with the highest (best), median (mid), and lowest (worst) TOPSIS composite score from each cluster, respectively. POD was then performed for each network.

The results of these comparisons against the CODE final orbits and the corresponding SLR validation results are presented in Figure 9 and Figure 10. The impact of data quality on POD accuracy is particularly pronounced in the 30-station configuration. For the Galileo and BDS constellations, the orbit accuracy achieved using the highest-scoring stations (‘best’ network) was 2.87 cm and 6.10 cm, respectively. This was better than the accuracy from the lowest-scoring stations (‘worst’ network), which was 5.33 cm and 11.28 cm, representing a precision degradation of 85% and 86%, respectively. A similar clear trend was observed for the GPS constellation, with the accuracy degrading from 2.99 cm for the ‘best’ network to 3.94 cm for the ‘worst’.

The results from the SLR validation are consistent with the orbit RMS comparisons. For the more challenging IGSO satellites (e.g., C08, C13), the SLR residuals from the ‘worst’-quality network were in the range of 17–18 cm, compared to 9–12 cm for the ‘best’ network. Similarly, for certain Galileo satellites like E04, the SLR residuals deteriorated from 2.2 cm to 6.0 cm. This demonstrates that when observational redundancy is low, the data quality of individual stations has a pronounced effect on the overall solution. In this context, the TOPSIS-based quality assessment and selection strategy employed in this study is a critical component for ensuring high POD accuracy.

As the number of stations increases to 60 and especially to 90, the discrepancy in POD accuracy among networks composed of different quality-grade stations diminishes significantly. In the 90-station configuration, the POD accuracy for the GPS and Galileo constellations becomes virtually identical, regardless of whether the ‘best’- or ‘worst’-quality stations are used, with their RMS values being nearly the same. For the BDS constellation, although the ‘best’ network (5.23 cm) still outperforms the ‘worst’ (5.74 cm), the performance gap is substantially smaller than that observed in the 30-station case. The accuracies of the three network types for the GLONASS constellation also converge as the network size increases to 60 and 90 stations.

Similarly, under the 90-station configuration, the SLR residuals for the ‘best,’ ‘mid,’ and ‘worst’ networks are highly comparable, with variations typically within a few millimeters. For satellite C20, for instance, their respective SLR residuals of 4.4 cm, 4.3 cm, and 3.2 cm all indicate a similar level of accuracy. This clearly demonstrates that a dense and highly redundant observation network can effectively suppress the observational noise introduced by lower-quality stations. This redundancy acts to “dilute” the impact of data quality deficiencies and “smooth” the overall solution during the estimation process. However, this does not imply that data quality becomes irrelevant; rather, its impact is masked by the high degree of redundancy. Therefore, for constructing cost-effective sparse networks, prioritizing stations with high-quality scores is a prerequisite for achieving high-precision POD results. In large-scale dense networks, redundancy can compensate for deficiencies in data quality to a certain extent.

4.3. Impact of Spatial Distribution

Another core principle of the station selection algorithm proposed in this study is to ensure a uniform spatial distribution of stations on a global scale. To independently validate the critical role of spatial distribution, the following comparative experiment was designed. We deliberately constructed spatially biased networks by selecting the top 30, 60, and 90 highest-scoring stations from within a single, geographically concentrated cluster. These networks were then used for POD. The resulting orbit accuracies, assessed through RMS comparisons against the CODE final orbits and through SLR validation, are presented in Figure 11 and Figure 12.

Here, a comparison against a random selection strategy is omitted. This is because the outcome of random selection is inherently unpredictable; it could by chance result in a spatially clustered network similar to the one in our experiment, or it could coincidentally obtain a well-distributed, high-quality network. The objective of our proposed strategy is to deterministically guarantee an optimal selection by systematically integrating both spatial distribution (via k-means) and data quality (via TOPSIS) in a single, holistic process.

The results demonstrate that using the 30-station spatially clustered network leads to a complete failure of the POD solution. The orbit RMS for all constellations soared to several meters, with some satellites for which a converged POD solution could not even be obtained. The SLR residuals for most satellites exceeded the meter level, with the residual for satellite E19 reaching nearly 40 m. This indicates that a sparse regional network cannot provide the continuous geometric constraints required for robust orbit modeling, leading to a severe divergence of the dynamical model and rendering the solution entirely unusable for any practical application. Even when expanding the regional network to 60 stations, the POD accuracy remained at an entirely unusable decimeter-to-meter level. When the geometric configuration is fundamentally flawed, merely densifying observations within a limited region is ineffective for improving the accuracy of global orbit determination.

Even when the regional network was expanded to 90 stations, the POD accuracy (with most satellites still exceeding 10 cm RMS) remained markedly inferior to the accuracy achieved with just 30 globally uniform stations from Section 3 (generally better than 5 cm). It is further reinforced by the SLR validation results: for the 90-station regional network, SLR residuals were still at the decimeter level (e.g., 56.1 cm for C20 and 9.9 cm for E11). In contrast, the 30-station globally uniform network achieved centimeter-level SLR validation accuracy (e.g., 4.9 cm for C20 and 3.1 cm for E11). This leads to the clear conclusion that a small but globally uniform network vastly outperforms a large but poorly distributed one in terms of POD performance. Employing spherical k-means clustering is validated as a core component of our algorithm.

5. Conclusions

This paper has proposed and validated a novel GNSS station selection framework that integrates a hybrid-weight TOPSIS algorithm with spherical k-means clustering, aimed at optimizing ground tracking networks for Multi-GNSS POD. The core source code for this methodology has been made publicly available in a GitHub repository (https://github.com/wtjin/gnss_station_selector; Version 1.0; accessed on 1 October 2025). Based on a series of comprehensive POD experiments and analyses, the following main conclusions are drawn:

1. The proposed methodology is both efficient and robust. By simultaneously balancing the comprehensive ranking of station data quality with the uniformity of global distribution, the methodology effectively identifies a core set of stations that contribute most significantly to orbit determination. The experiments demonstrated that a network of 60 stations selected by our method achieves POD accuracy comparable to that of a 90-station network, thereby significantly reducing computational costs and complexity without compromising the quality of the final products.

2. Data quality and spatial distribution play distinct and non-interchangeable roles. This study elucidates the relative importance of these two core factors through a controlled-variable approach. Data quality is paramount for small-scale networks (e.g., 30 stations), where poor-quality stations can significantly degrade orbit accuracy. However, a uniform spatial distribution is the fundamental prerequisite for achieving high-precision orbits. The experiments conclusively showed that a network of 90 high-quality but spatially clustered stations is outperformed by a network of just 30 globally uniform stations selected by our method.

This study provides an objective, quantitative, and repeatable station selection framework for GNSS analysis centers, research institutions, and any application domain reliant on high-precision orbits. Future research could extend this framework to dynamic station selection in near-real-time processing scenarios or to broader applications such as the POD of Low-Earth-Orbit (LEO) satellites.