Explainable Shape Anomaly Detection of Space Targets from ISAR Image Sequences
Highlights
- An explainable shape anomaly detection model combining A Fully Convolutional Data Description(FCDD) network with an attention-based GRU ensures abnormal detection of ISAR image sequences.
- By highlighting abnormal distribution through the Fully Convolutional Data Description(FCDD) network and enhancing the ability of extracting temporal features via the attention-based GRU, the model’s detection performance is elevated.
- This approach enhances the abnormal detection performance under conditions of insufficient abnormal samples.
- It provides a robust solution to detect and locate the abnormal shape of spatial targets.
Abstract
1. Introduction
- (1)
- To the best of our knowledge, this is the first paper to suggest employing an ISAR image sequence to detect shape anomalies in space targets. On one hand, ISAR images have the advantage of high-resolution, all-day, all-weather, and long-distance monitoring of uncooperative targets over low-resolution micro-Doppler data and cooperative housekeeping data. The existing literature, on the other hand, primarily focus on overall operations with housekeeping data or dynamic state monitoring using ISAR and micro-Doppler data. Public research on satellite shape anomalies is notably lacking.
- (2)
- In this work, we introduce a novel framework that leverages spatial and temporal information to detect shape anomalies in image sequences for satellites. By constructing a joint structure of FCDD and attention-based GRU, we can considerably improve shape anomaly performance using both spatial and contextual information, thanks to the sequential imaging operation of space targets in long-term surveillance.
- (3)
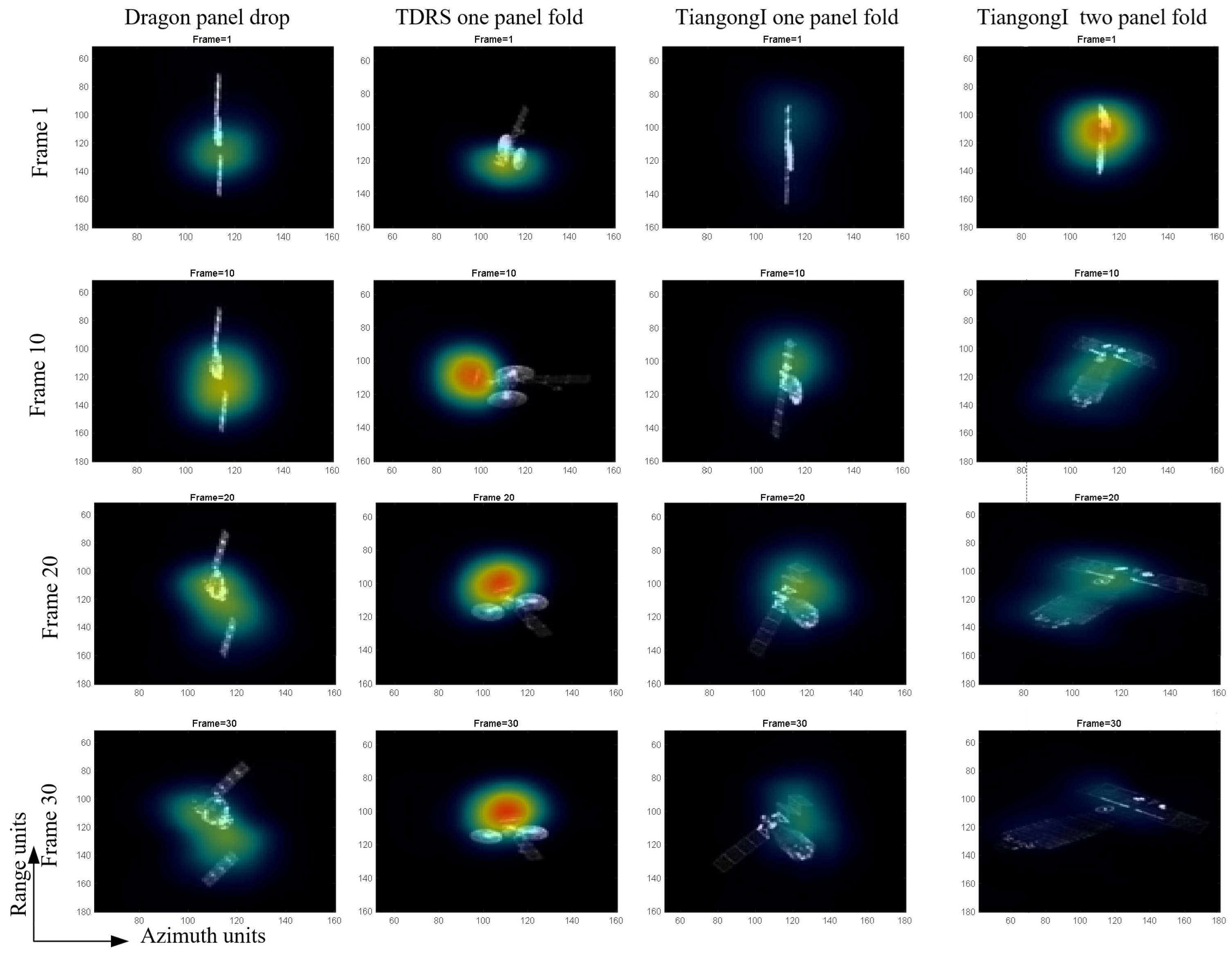
- We propose an interpretable architecture for shape anomaly detection in satellite ISAR image sequences. This architecture not only enables the detection of anomalous frames but also allows for the precise localization of the erroneous components inside the associated ISAR image frames. This architecture can aid in a better understanding of AD results and offer a robust result for human decision-making.
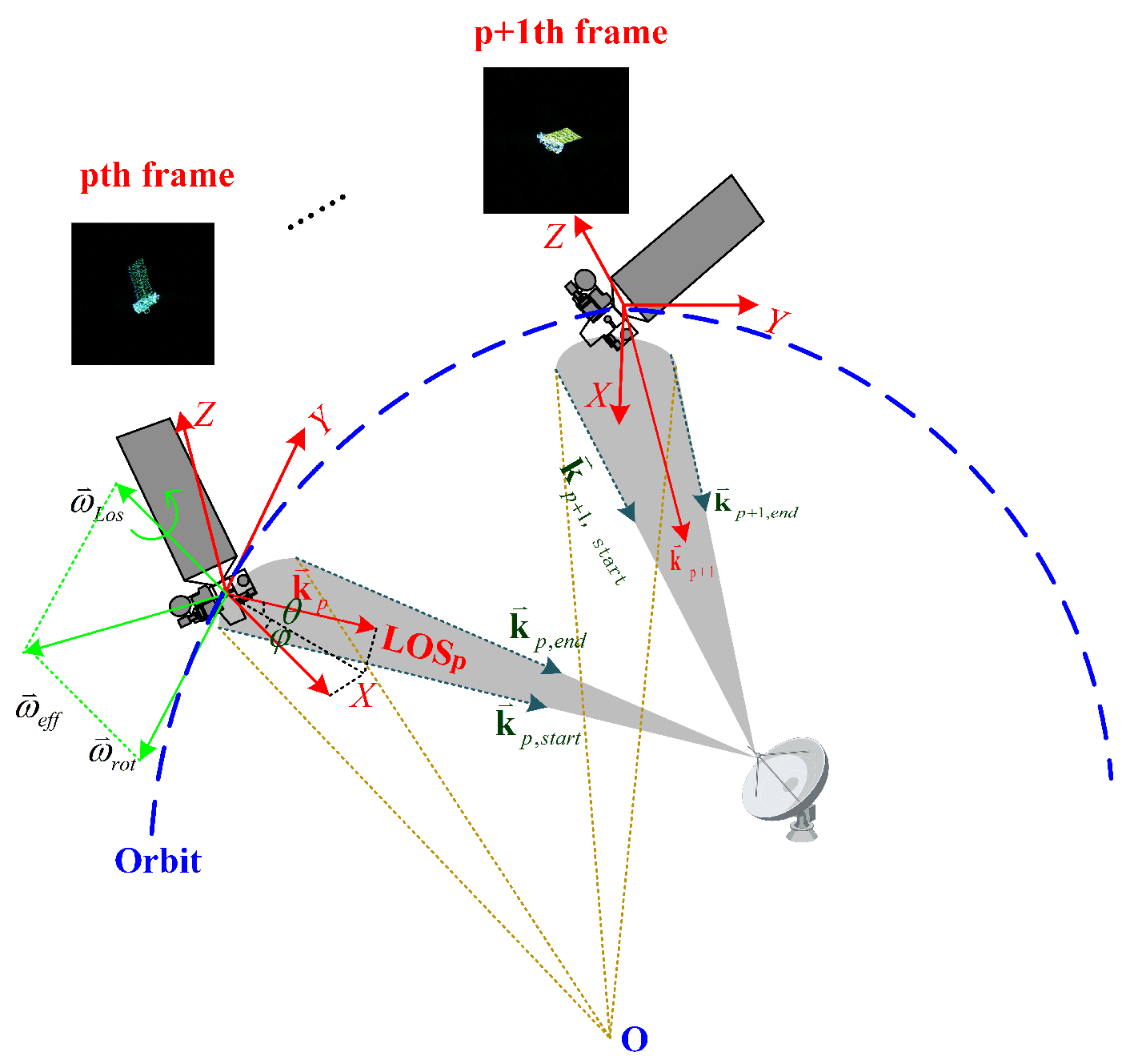
2. Sequential ISAR Imaging Geometry of Space Target
2.1. Sequential ISAR Imaging
2.2. Sequential ISAR Image of Satellite Shape Anomalies
3. Sequential Shape Anomaly Detection of Space Targets
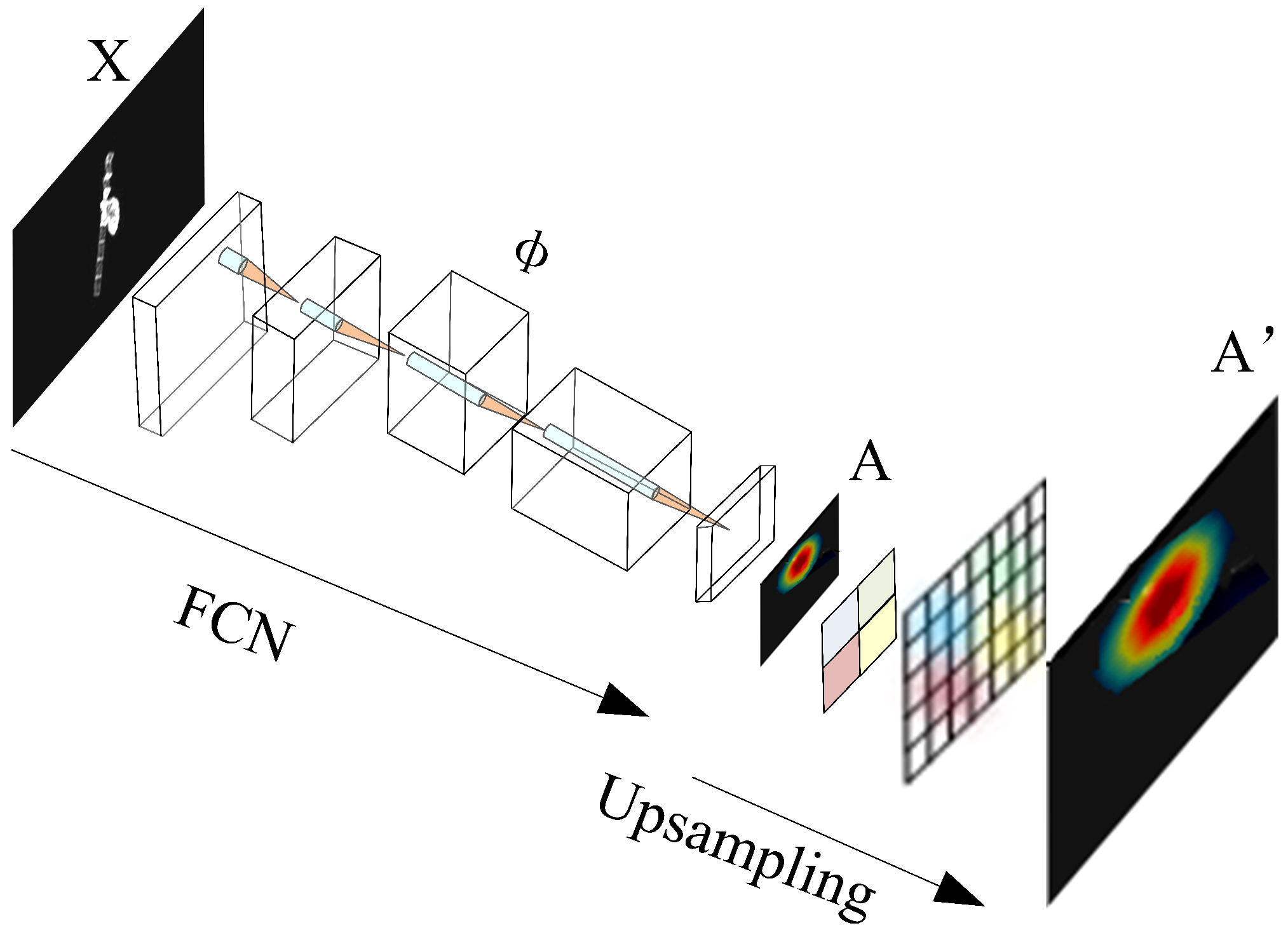
3.1. FCDD Network [33]
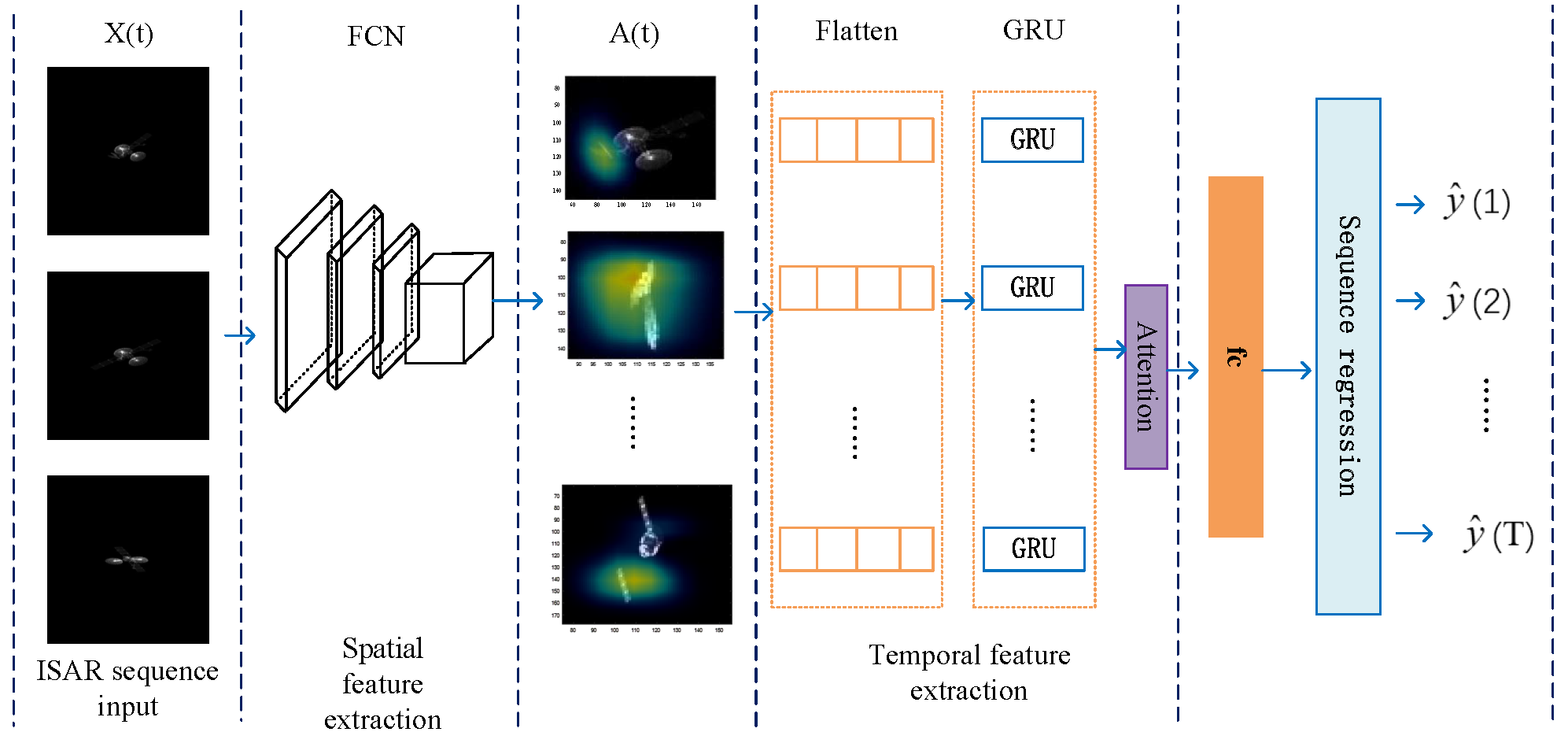
3.2. Sequential Shape Anomaly Detection Network
4. Experiments and Analysis
4.1. Introduction of Experimental Data
- (1)
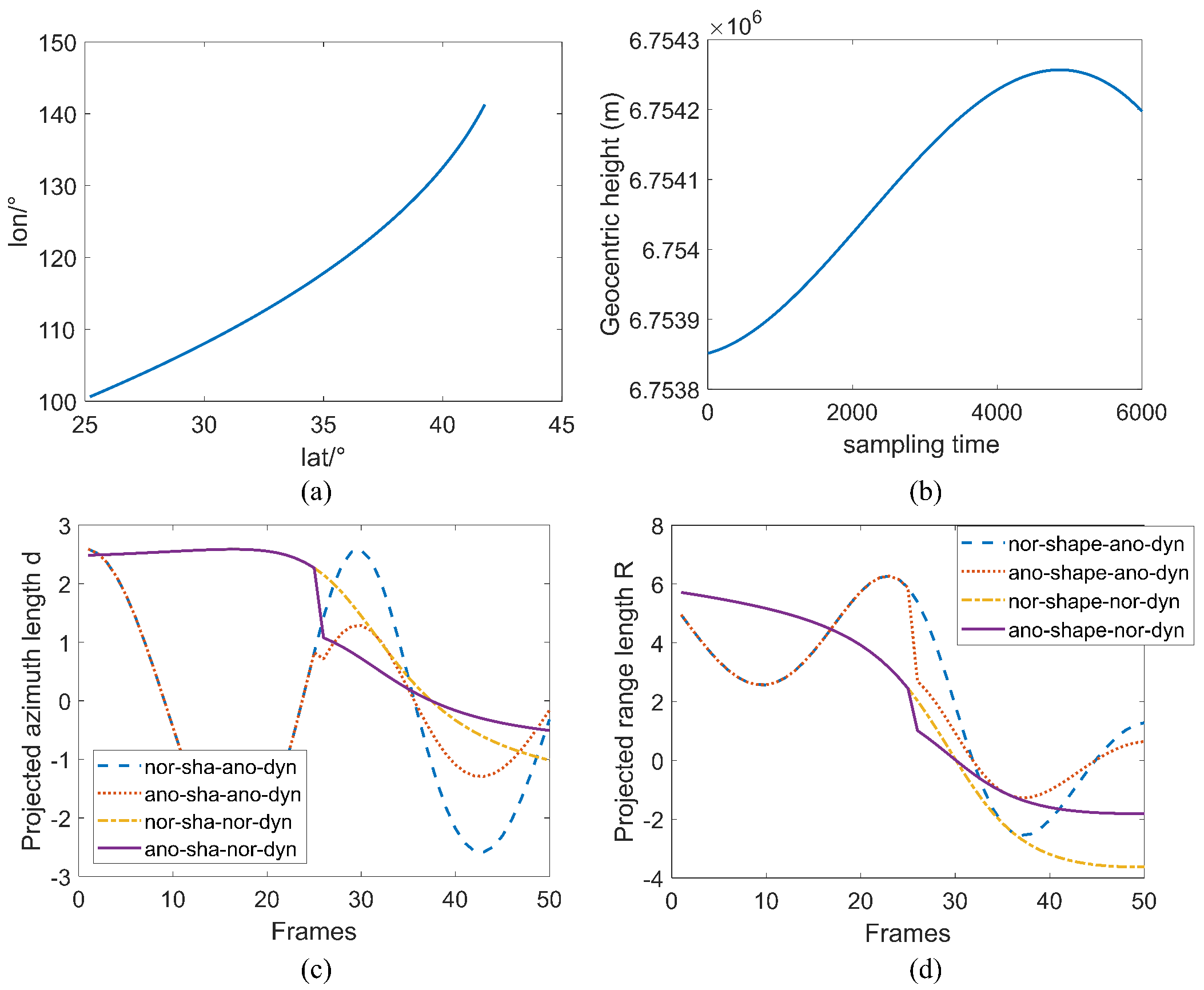
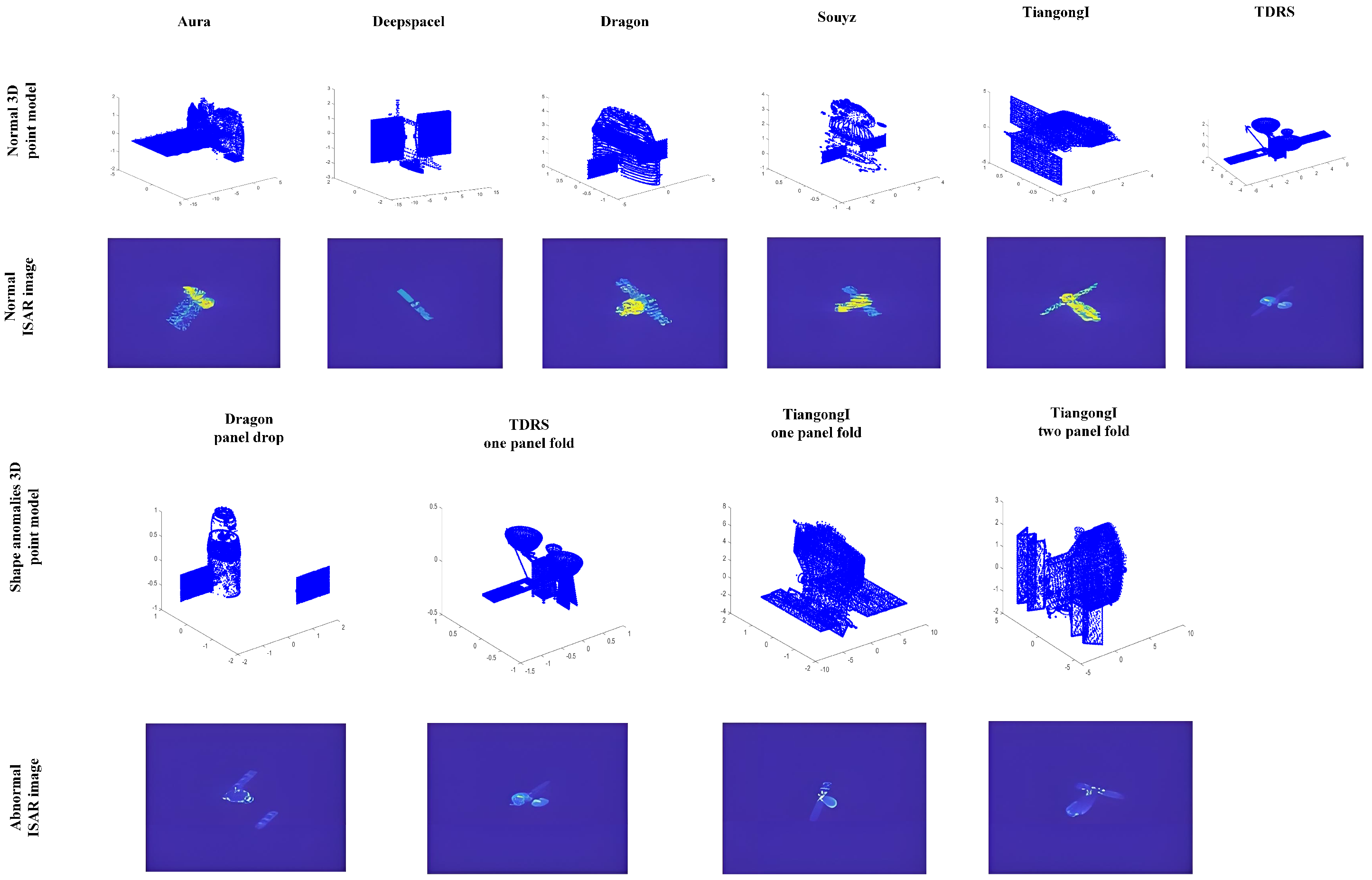
- ISAR image generation: Because of a paucity of real data, our experiments are conducted on simulated data of different satellites. Six distinct satellites are used, and the 3D point models are depicted in Figure 6. The improved physical optical (PO) algorithm is utilized for ISAR echo simulation, which has been proven to be effective for the majority of satellite echo generation [41]. Table 2 lists the simulated parameters of a Ku-band radar for clarity. For data diversity, two different ground stations are constructed for simulation, located in Beijing (39.9°N, 116.4°E) and Tianjin (39.1°N, 117.2°E). The real-measured TLEs are adopted for satellite orbit description. An example of TLE is shown in Figure 3a,b. The traditional RD imaging algorithm is used to generate ISAR images. Examples of simulated ISAR images for different targets are shown below their 3D point model.
- (2)
- Generation of different dynamic status: For the diversity of data, we also simulate satellites in a variety of dynamic statuses, including three-axis stability, self-rotation, and attitude adjustment within one frame. The rotation velocity is set as 0.1°/s and 1°/s for the last two statuses. For each orbiting circle, 30 frames of ISAR images with a 10 s interval are generated for sequential shape anomaly detection performance evaluation.
- (3)
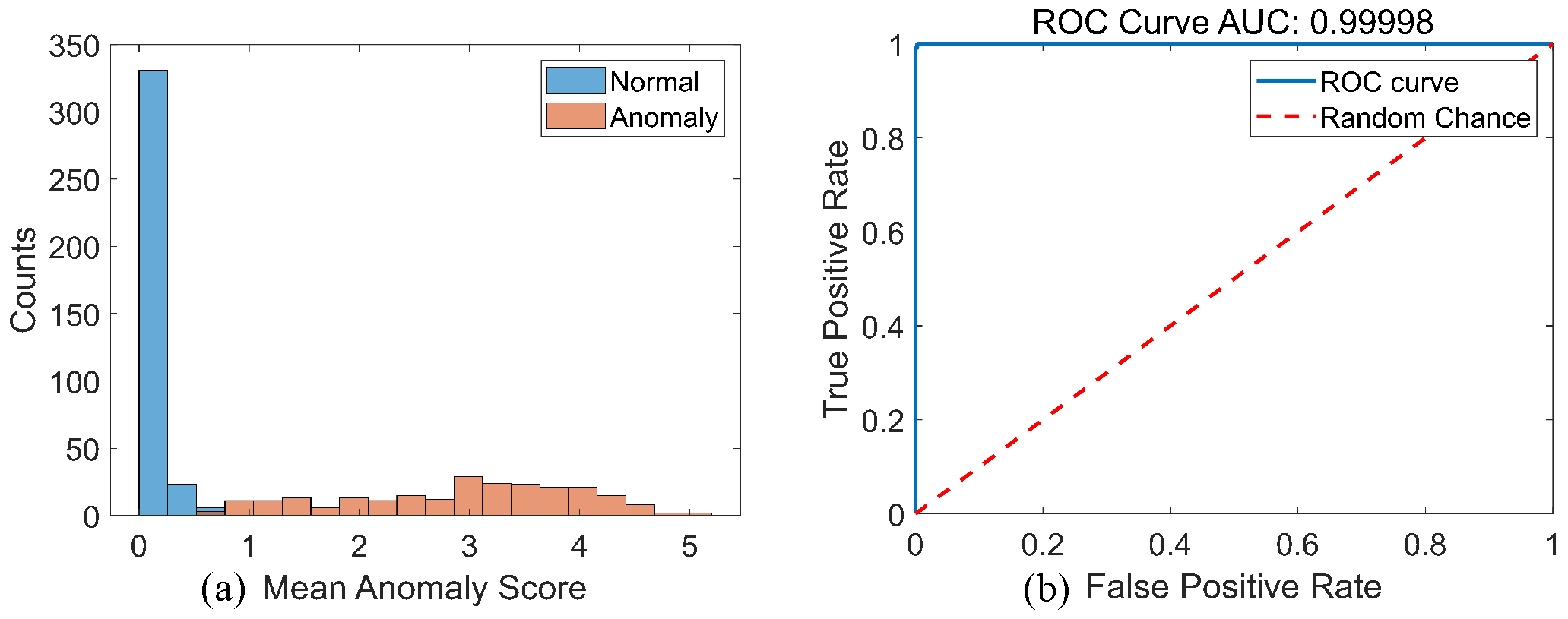
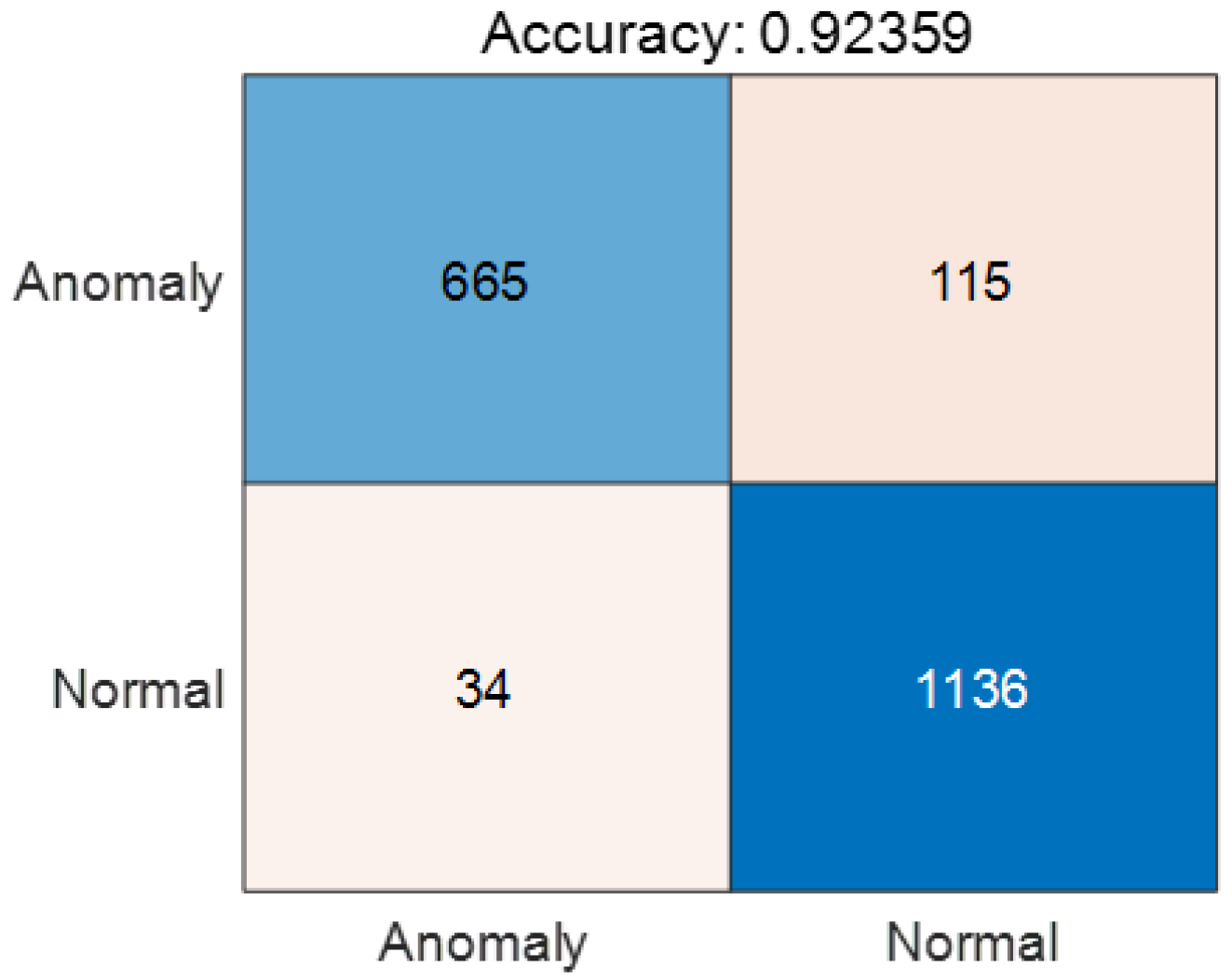
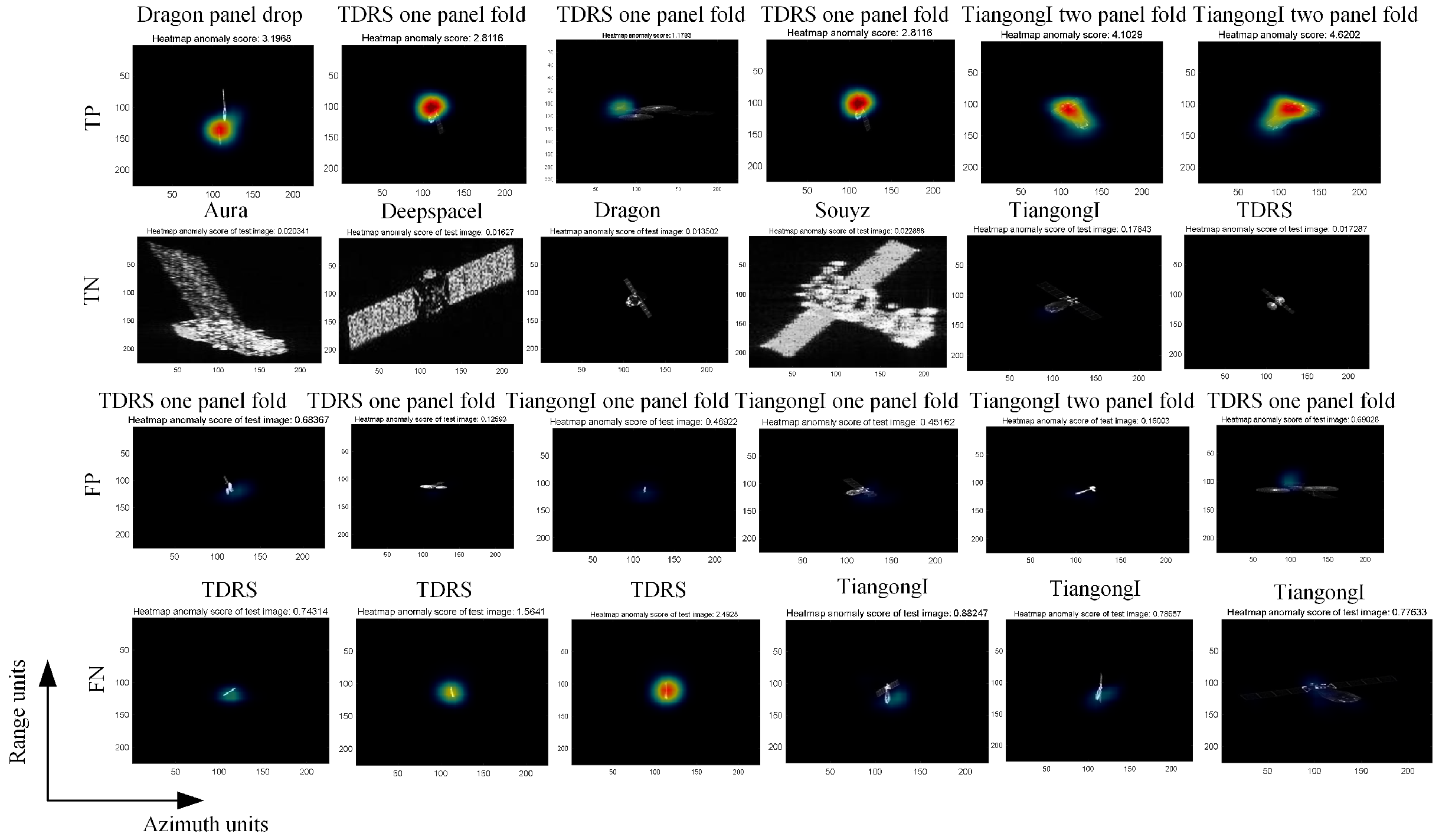
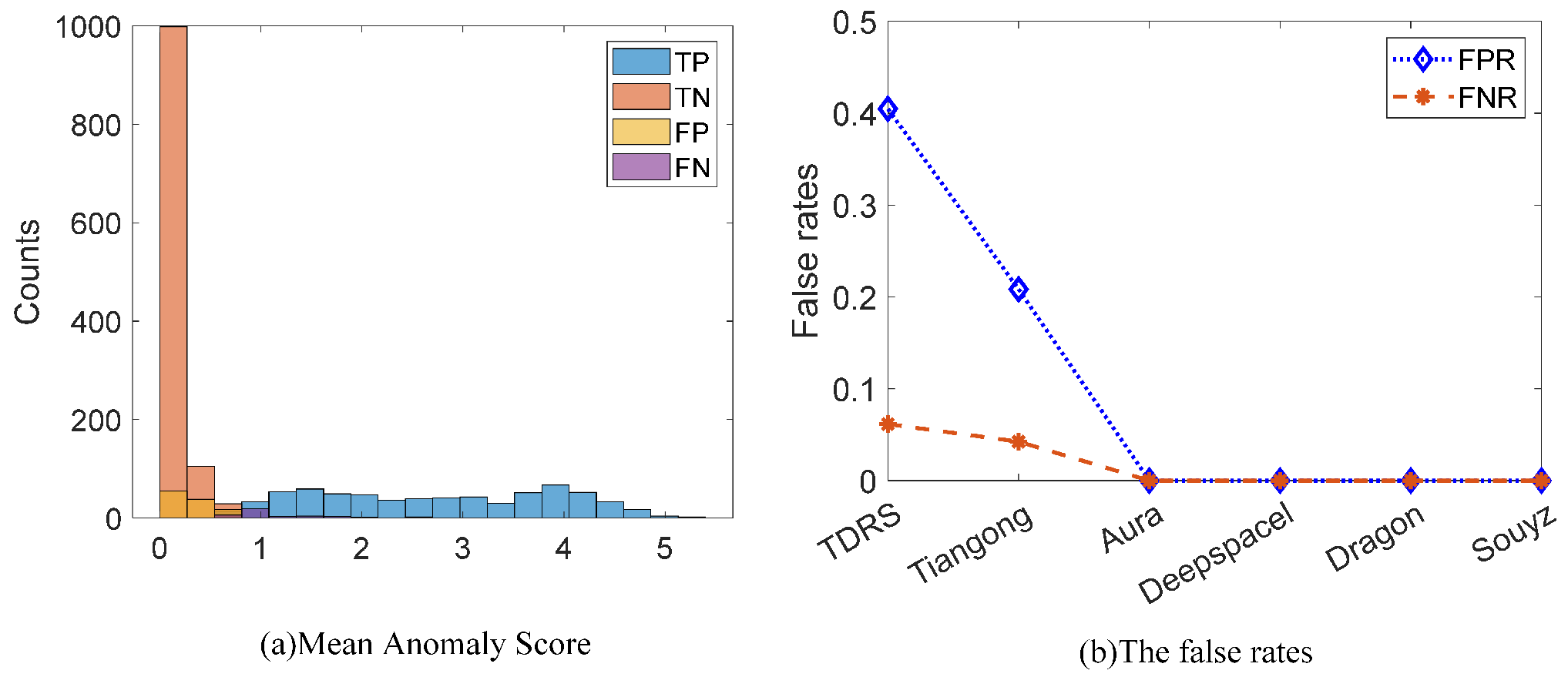
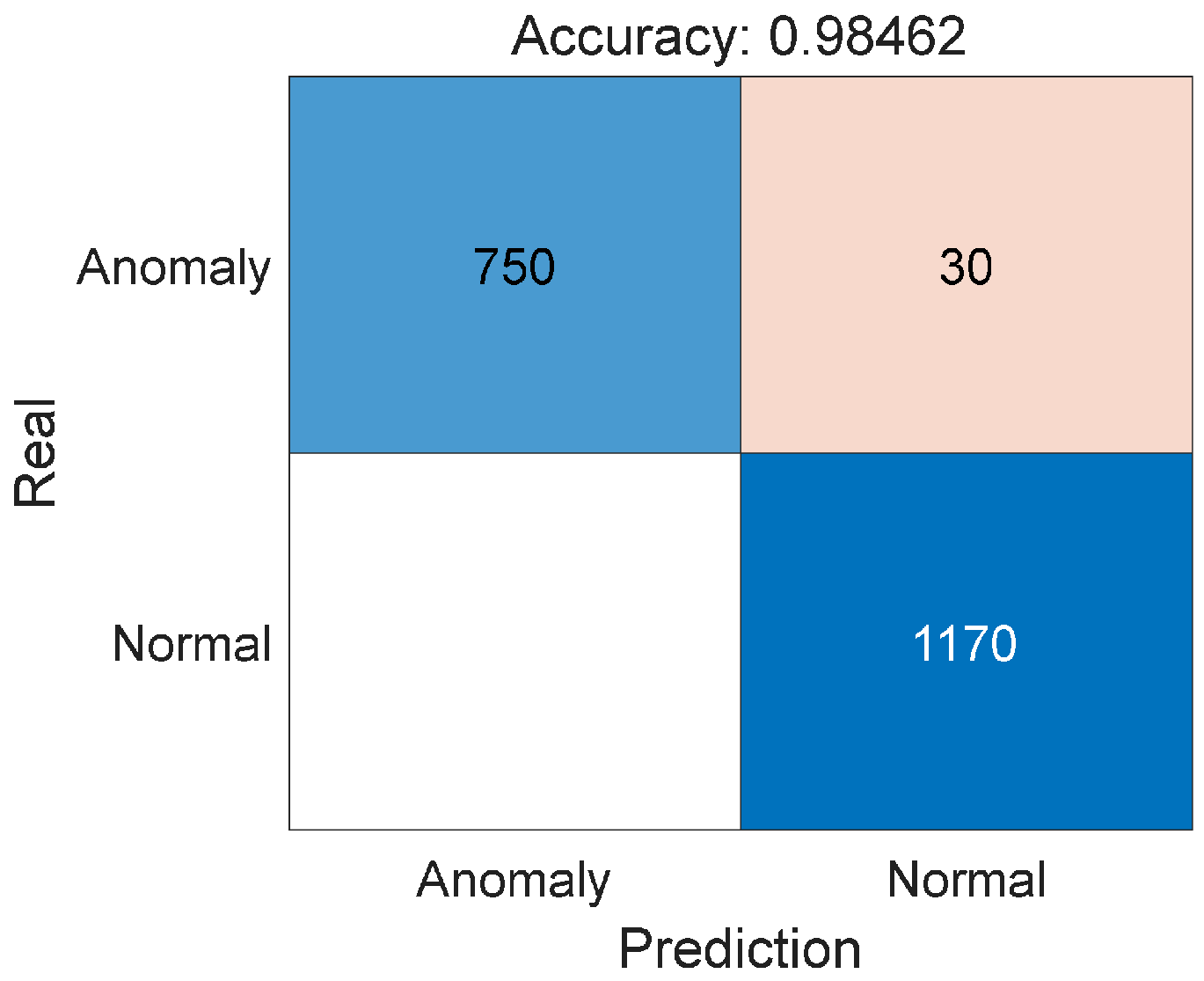
- Evaluate criterion: Same as detection problems, the fundamental criterion for anomaly detection that we care about is the detection capabilities under specific false alarm rates. As a result, overall precision (Prec), detection rates (Detec), and false alarm rates (FA) are computed for quantitative assessments, whose definitions are given asTrue anomalies are denoted as TP, true normal samples as TN, false detected anomalies as FP, and false detected normal samples as FN. For classification, they are the elements of a binary classification confusion matrix.
4.2. FCDD for One-Frame Shape Anomaly Detection
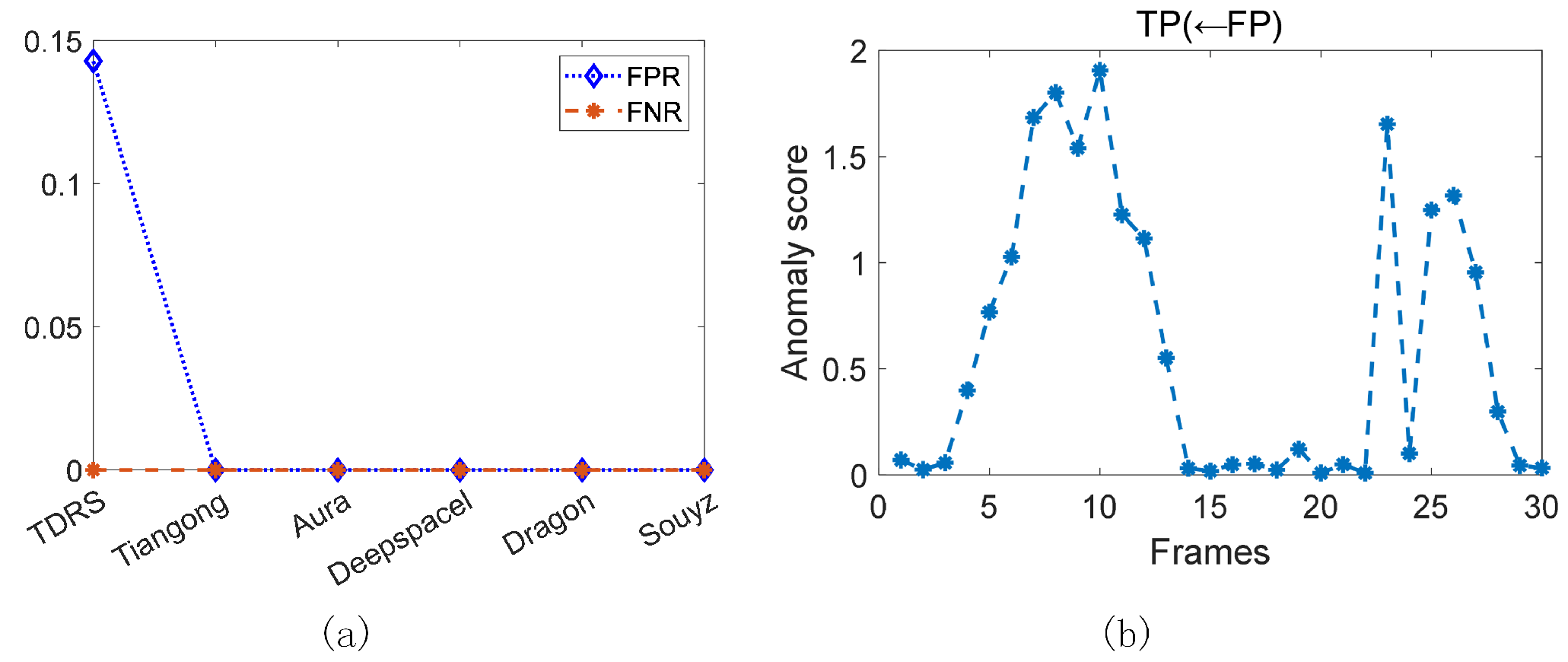
4.3. Sequential Shape Anomaly Detection for ISAR
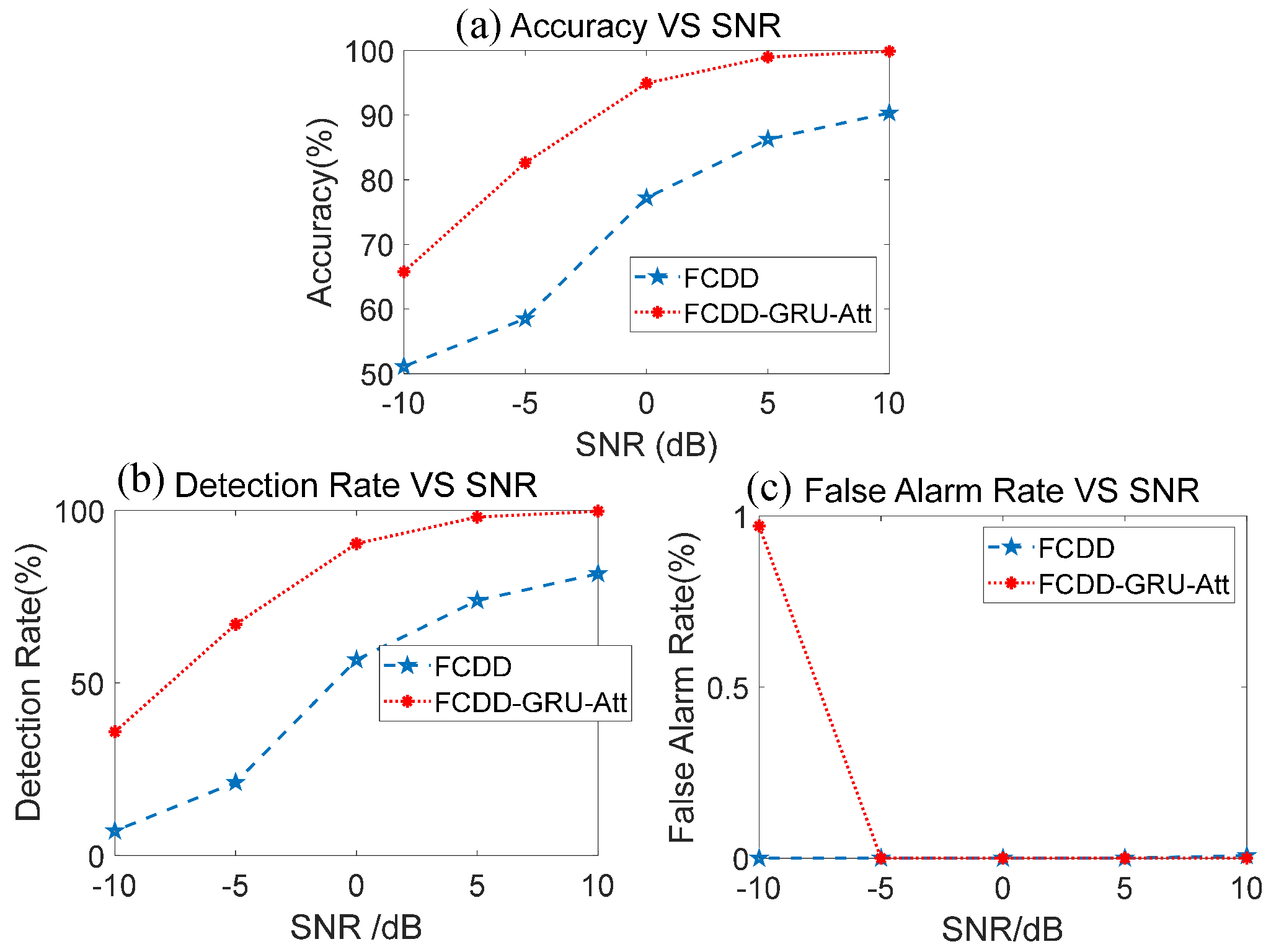
4.4. Performance Evaluation Under Different Conditions
4.5. Comparisons
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ISAR | Inverse Synthetic Aperture Radar |
| FCDD | Fully Convolutional Data Description |
| AD | Anomaly Detection |
| GMM | Gaussian Mixture Model |
| LOS | Light Of Sight |
| FCN | Fully Convolutional Description |
| HSC | Hypersphere Classifier |
References
- Rahimi, A.; Kumar, K.D.; Alighanbari, H. Fault isolation of reaction wheels for satellite attitude control. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 610–629. [Google Scholar] [CrossRef]
- Yuan, Z.; Song, N.; Pan, X.; Song, J.; Ma, F. Fault detection, isolation, and reconstruction for satellite attitude sensors using an adaptive hybrid method. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Patera Russell, P. Space Event Detection Method. J. Spacecr. Rocket. 2015, 45, 554–559. [Google Scholar] [CrossRef]
- Anz-Meador, P.D.; Johnson, N.L. A Decade of Growth. In Proceedings of the Third European Conference on Space Debris, ESOC, Darmstadt, Germany, 9–21 March 2001; pp. 753–758. [Google Scholar]
- Goff, G.M.; Black, J.T.; Beck, J.A. Tracking maneuvering spacecraft with filter-through approaches using interacting multiple models. Acta Astronaut. 2015, 114, 152–163. [Google Scholar] [CrossRef]
- Demars, K. Nonlinear Orbit Uncertainty Prediction and Rectification for Space Situational Awareness. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2010. [Google Scholar]
- Duan, J.; Ma, Y.; Zhang, L.; Xie, P. Abnormal Dynamic Recognition of Space Targets from ISAR Image Sequences with SSAE-LSTM Network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5102916. [Google Scholar] [CrossRef]
- Zhou, Y.; Wei, S.; Zhang, L.; Zhang, W.; Ma, Y. Dynamic estimation of spin satellite from the single-station ISAR image sequence with the hidden Markov model. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4626–4638. [Google Scholar] [CrossRef]
- Kelecy, T.; Jah, M. Detection and orbit determination of a satellite executing low thrust maneuvers. Acta Astronaut. 2010, 66, 798–809. [Google Scholar] [CrossRef]
- Lubey, D.P.; Scheeres, D.J.; Erwin, R.S. Maneuver detection and reconstruction of stationkeeping spacecraft at GEO using the optimal control-based estimator. Ifac. Pap. Online 2015, 48, 216–221. [Google Scholar] [CrossRef]
- Yong, Q. Failure Mechanism Analysis and Solution Research of a New Satellite Deployable Mechanism; Harbin Institute of Technology: Harbin, China, 2018. [Google Scholar]
- SinoSat-2 Unable to Deploy Solar Panels. 2006. Available online: https://www.tvtechnology.com/news/sinosat2-unable-to-deploy-solar-panels (accessed on 13 July 2025).
- Russian Satellite Breaks Up, Creating Debris in Low Earth Orbit. 2024. Available online: https://spacenews.com/russian-satellite-breaks-up-creating-debris-in-low-earth-orbit/ (accessed on 13 July 2025).
- Shao, S.; Zhang, L.; Wei, J.; Liu, H. Two-Dimension Joint Super-Resolution ISAR Imaging with Joint Motion Compensation and Azimuth Scaling. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1411–1415. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, B.; Yu, H.; Chen, J.; Xing, M.; Hong, W. Sparse Synthetic Aperture Radar Imaging from Compressed Sensing and Machine Learning: Theories, Applications and Trends. IEEE Geosci. Remote Sens. Mag. 2022, 10, 32–69. [Google Scholar] [CrossRef]
- Xu, G.; Xing, M.; Xia, X.G.; Zhang, L.; Chen, Q.; Bao, Z. 3D Geometry and Motion Estimations of Maneuvering Targets for Interferometric ISAR with Sparse Aperture. IEEE Trans. Image Process. 2016, 25, 2005–2020. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. Acm Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Aggarwal, C.C. Outlier Analysis; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978–3319475776. [Google Scholar]
- Bestagini, P.; Lombardi, F.; Lualdi, M.; Picetti, F.; Tubaro, S. Landmine detection using autoencoders on multipolarization GPR volumetric data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 182–195. [Google Scholar] [CrossRef]
- Shi, S.N.; Shui, P.L. Sea-surface floating small target detection by one-class classifier in time-frequency feature space. IEEE Geosci. Remote Sens. 2018, 56, 6395–6411. [Google Scholar] [CrossRef]
- Hendrycks, D.; Mazeika, M.; Dietterich, T.G. Deep anomaly detection with outlier exposure. arXiv 2019, arXiv:1812.04606. [Google Scholar] [CrossRef]
- Hendrycks, D.; Mazeika, M.; Kadavath, S.; Song, D. Using self-supervised learning can improve model robustness and uncertainty. Adv. Neural Inf. Process. Syst. 2019, 32, 15637–15648. [Google Scholar]
- Rasmus, A.; Berglund, M.; Honkala, M.; Valpola, H.; Raiko, T. Semi-supervised learning with ladder networks. Adv. Neural Inf. Process. Syst. 2015, 28, 3546–3554. [Google Scholar]
- Ruff, L.; Vermeulen, R.A.; Gornitz, N.; Binder, A.; Müller, E.; Müller, K.R.; Kloft, M. Deep semi-supervised anomaly detection. arXiv 2020, arXiv:1906.02694. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Huang, J.; Liu, S.; Long, H. An effective method for anomaly detection in industrial Internet of Things using XGBoost and LSTM. Sci. Rep. 2024, 14, 23969. [Google Scholar] [CrossRef]
- Abououf, M.; Singh, S.; Mizouni, R.; Otrok, H. Explainable AI for Event and Anomaly Detection and Classification in Healthcare Monitoring Systems. IEEE Internet Things J. 2024, 11, 3446–3457. [Google Scholar] [CrossRef]
- Yepmo, V.; Smits, G.; Pivert, O. Anomaly explanation: A review. Data Knowl. Eng. 2022, 137, 101946. [Google Scholar] [CrossRef]
- Du, M.; Liu, N.; Hu, X. Techniques for interpretable machine learning. Commun. ACM 2019, 1, 68–77. [Google Scholar] [CrossRef]
- Chen, Y.; Tian, Y.; Pang, G.; Carneiro, G. Unsupervised Anomaly Detection and Localisation with Multi-scale Interpolated Gaussian Descriptors. arXiv 2021, arXiv:2101.10043.2021. [Google Scholar]
- Venkataramanan, S.; Peng, K.C.; Singh, R.V.; Mahalanobis, A. Attention Guided Anomaly Localization in Images. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; pp. 485–503. [Google Scholar]
- Salehi, M.; Sadjadi, N.; Baselizadeh, S.; Rohban, M.H.; Rabiee, H.R. Multiresolution Knowledge Distillation for Anomaly Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14902–14912. [Google Scholar]
- Liznerski, P.; Ruff, L.; Vandermeulen, R.A.; Franks, B.J.; Kloft, M.; Müller, K.R. Explainable Deep One-Class Classification. arXiv 2021, arXiv:2007.01760. [Google Scholar]
- Zeng, Z.; Jin, G.; Xu, C.; Chen, S.; Zeng, Z.; Zhang, L. Satellite telemetry data anomaly detection using causal network and featureattention-based LSTM. IEEE Trans. Instrum. Meas. 2022, 71, 1–21. [Google Scholar]
- Yairi, T.; Takeishi, N.; Oda, T.; Nakajima, Y.; Nishimura, N.; Takata, N. A data-driven health monitoring method for satellite housekeeping data based on probabilistic clustering and dimensionality reduction. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1384–1401. [Google Scholar] [CrossRef]
- Tariq, S.; Lee, S.; Shin, Y.; Lee, M.S.; Jung, O.; Chung, D.; Woo, S.S. Detecting Anomalies in Space Using Multivariate Convolutional LSTM with Mixtures of Probabilistic PCA. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2123–2133. [Google Scholar]
- Zhao, H.; Liu, M.; Qiu, S.; Cao, X. Satellite unsupervised anomaly detection based on Deconvolution-Reconstructed Temporal Convolutional Autoencoder. IEEE Trans. Consum. Electron. 2024, 70, 2989–2998. [Google Scholar] [CrossRef]
- Wang, J.; Li, G.; Zhao, Z.; Jiao, J.; Ding, S.; Wang, K.; Duan, M. Space target anomaly detection based on gaussian mixture model and micro-Doppler Features. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5118411. [Google Scholar] [CrossRef]
- Barron, J.T. A General and Adaptive Robust Loss Function. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019; pp. 4326–4334. [Google Scholar] [CrossRef]
- Tang, J.; Li, Y.; Ding, M.; Liu, H.; Yang, D.; Wu, X. An ionospheric TEC forecasting model based on a CNN-LSTM-attention mechanism neural network. Remote Sens. 2022, 14, 2433. [Google Scholar] [CrossRef]
- Angel, F.; Omar, A.; Jesus, G. Facet model of moving targets for ISAR imaging and radar back-scattering simulation. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1455–1467. [Google Scholar]
- Bilgin, G.; Erturk, S.; Yildirim, T. Segmentation of hyperspectral images via subtractive clustering and cluster validation using oneclass support vector machines. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2936–2944. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 words: Transformers for Image Recognition at Scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]


| Module | Layers | Layer Type | Parameters |
|---|---|---|---|
| FCN | 1–24th | Layerl-24 in VGG | |
| 25–30th | Convolutional layer × 2 | Filters = 512; Kernel size = 3; Stride = 1 | |
| Batch normalization layer × 2 | Filters = 512 | ||
| Activation layer × 2 | ReLU | ||
| 31st | Convolutional Layer | Filters = 512; Kernel size = 1; Stride = 1 | |
| Geometrical Enhancement | 32nd | ||
| Sequential feature extraction | 33rd | Flatten layer | — |
| 34th | GRU | 128 GRUs | |
| 35th | Self-attention | 4 Heads Q,K,V channel = 256 | |
| Classification | 36th | Fully connected | — |
| 37th | Classification |
| Parameter | Value |
|---|---|
| Center frequency | 15 GHz |
| Bandwidth | 1.5 GHz |
| Coherent Processing Time | 0.6 s |
| Imaging Time Interval | 10 s |
| Image size | |
| Frame rate | 30 Hz |
| Criteria | Prec | Detec | FA |
|---|---|---|---|
| Structures | (%) | (%) | (%) |
| Score-Lstm | 93.9 | 88.46 | 2.48 |
| Score-Att-Lstm | 96.92 | 96.15 | 2.56 |
| A-Att-Lstm | 96.92 | 93.23 | 0 |
| A-GRU | 91.80 | 81.28 | 1.2 |
| A-Att-GRU | 98.46 | 96.15 | 0 |
| Training Portion (Nor:Ano) | Training Anomalies Number | Prec(%) | Detec(%) | FA(%) | |||
|---|---|---|---|---|---|---|---|
| FCDD | FCDD-GRU -Att↑ | FCDD | FCDD-GRU -Att↑ | FCDD | FCDD-GRU -Att↓ | ||
| 1.96:1 | 840 (28 seq) | 92.36 | 98.46 (↑6.1) | 85.2 | 96.15 (↑10.9) | 2.91 | 0 (↓2.91) |
| 2.75:1 | 600 (20 seq) | 86.15 | 93.85 (↑7.7) | 71.41 | 88.46 (↑17.05) | 4.02 | 2.56 (↓1.46) |
| 3.43:1 | 480 (16 seq) | 87.18 | 90.77 (↑3.59) | 71.03 | 88.46 (↑17.43) | 2.05 | 7.69 (↓−5.64) |
| 4.58:1 | 360 (12 seq) | 86.26 | 87.69 (↑1.43) | 70.26 | 84.62 (↑14.36) | 6.16 | 10.26 (↓−4.1) |
| Criteria | Prec | Detec | FA |
|---|---|---|---|
| Structures | (%) | (%) | (%) |
| Isolation Forest | 66.930 | 46.27 | 10.11 |
| OCSVM | 79.649 | 68.48 | 0.33 |
| FCDD | 92.3 | 95.77 | 0.19 |
| Vit | 88.509 | 92.03 | 15.4 |
| FCDD-Att-GRU | 99.474 | 100 | 1.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Duan, J.; Zhang, L. Explainable Shape Anomaly Detection of Space Targets from ISAR Image Sequences. Remote Sens. 2025, 17, 3541. https://doi.org/10.3390/rs17213541
Wang Z, Duan J, Zhang L. Explainable Shape Anomaly Detection of Space Targets from ISAR Image Sequences. Remote Sensing. 2025; 17(21):3541. https://doi.org/10.3390/rs17213541
Chicago/Turabian StyleWang, Zi, Jia Duan, and Lei Zhang. 2025. "Explainable Shape Anomaly Detection of Space Targets from ISAR Image Sequences" Remote Sensing 17, no. 21: 3541. https://doi.org/10.3390/rs17213541
APA StyleWang, Z., Duan, J., & Zhang, L. (2025). Explainable Shape Anomaly Detection of Space Targets from ISAR Image Sequences. Remote Sensing, 17(21), 3541. https://doi.org/10.3390/rs17213541







