Highlights
What are the main findings?
- Enables instantaneous PPP-B2b convergence from over 15 min to the first epoch, achieving decimeter-to-centimeter-level positioning immediately by integrating regional atmospheric constraints.
- Achieves robust positioning accuracy of better than 0.1 m horizontally and 0.2 m vertically within 1 min for dual-system PPP-B2b, even under challenging high-elevation mask conditions.
What is the implication of the main finding?
- Effectively resolves the core bottleneck of standard PPP-B2b service, bridging the performance gap with NRTK and PPP-RTK by addressing the lack of high-precision atmospheric information.
- Establishes a foundational model and error-handling framework for next-generation satellite-based augmentation services, providing a proven approach to mitigate system-specific errors like CCB and ionospheric variability.
Abstract
Currently, the PPP-B2b service faces challenges such as long convergence times and re-convergence issues after signal interruptions due to the lack of high-precision atmospheric enhancement. To address this, this study develops a multi-frequency uncombined Precise Point Positioning (PPP) model that accounts for Clock Constant Bias (CCB) based on PPP-B2b products, extracting atmospheric delays from reference stations and performing regional modeling. Considering the spatiotemporal characteristics of the ionosphere, a stochastic model for enhancement information that varies with time and satellite elevation is established. The performance of atmospheric-enhanced PPP-B2b is validated on the user end. Results demonstrate that zenith wet delay (ZWD) and ionospheric modeling generally achieve centimeter-level accuracy. However, during certain periods, ionospheric modeling errors are significant. By adjusting the stochastic model, approximately 98% of modeling errors can be enveloped. With atmospheric constraints, both convergence speed and positioning accuracy of PPP-B2b are significantly improved. Using thresholds of 30 cm horizontally and 40 cm vertically, the convergence times for horizontal and vertical components are approximately (16.7, 21.3) min for single BDS-3 and (3.8, 5.0) min for the dual-system combination, respectively. In contrast, with atmospheric constraints applied, convergence thresholds are met almost at the first epoch. Within one minute, single BDS-3 and the dual-system combination achieve accuracies better than (0.15, 0.3) m and (0.1, 0.2) m horizontally and vertically, respectively. Furthermore, even under high-elevation cutoff conditions, stable and rapid high-precision positioning remains achievable through atmospheric enhancement.
1. Introduction
The Global Navigation Satellite System (GNSS) is critical infrastructure that plays a significant role in establishing and maintaining spatiotemporal reference frameworks, as well as enabling spatiotemporal service applications. The BeiDou-3 Global Satellite Navigation System (BDS-3) was officially commissioned on 31 July 2020. Its constellation consists of 30 satellites, including 24 medium Earth orbit (MEO) satellites, 3 geostationary Earth orbit (GEO) satellites, and 3 inclined geosynchronous orbit (IGSO) satellites. It provides global users with high-precision positioning, navigation, and timing (PNT) services [1]. Additionally, the PPP-B2b signal broadcast by GEO satellites disseminates corrections such as orbit, clock, and differential code bias (DCB) parameters, enabling satellite-based enhanced Precise Point Positioning (PPP) services. This capability eliminates reliance on ground communication networks and expands the application of PPP in constrained scenarios such as weak communication environments [2,3].
Currently, PPP-B2b provides combined enhancement services for BDS-3 and GPS systems in China and surrounding regions. Xu et al. systematically evaluated the accuracy, availability, and real-time performance of PPP-B2b corrections. The results indicated that the radial orbit accuracy reaches centimeter-level, with MEO satellites exhibiting better orbit accuracy than IGSO satellites. The clock bias accuracy is generally at the sub-nanosecond level, representing an 85.1% improvement compared to broadcast ephemeris [4]. Ren et al. assessed the performance of PPP-B2b using iGMAS monitoring stations. The convergence time for static and kinematic PPP was approximately 8–22 min and 8–10 min, respectively, achieving static centimeter-level and dynamic 20 cm positioning accuracy [5]. To further compensate for residual errors in orbit and clock corrections, Xu et al. proposed a PPP-B2b model that estimates spatial signal-in-space range errors, improving real-time vehicular PPP horizontal and vertical accuracy by 36.0% and 19.0%, respectively [6]. Addressing the issue that the current user rang accuracy index (URAI) parameter cannot objectively reflect the accuracy of PPP-B2b orbit corrections, Chen et al. proposed a phase URA estimation method based on reference stations and developed a corresponding stochastic model, enhancing both static and kinematic PPP-B2b performance. Additionally, they identified a reference jump issue in GPS clock bias corrections within PPP-B2b and proposed corresponding detection and compensation methods [7]. In response to accuracy degradation of corrections due to orbital maneuvers, Nie et al. conducted research on real-time detection and identification methods for signal-in-space (SIS) anomalies in PPP-B2b at the user end [8].
PPP-B2b services have been widely applied in multiple fields. Geng et al. utilized PPP-B2b services for high-precision marine GNSS positioning, achieving 20 cm accuracy [9]. Yu et al. also validated its performance in marine real-time precise positioning and noted that multipath effects caused by sea surface reflections may prolong PPP-B2b convergence time [10]. Shang et al. verified PPP-B2b performance in real vehicular dynamic applications, achieving continuous positioning [11]. Yang et al. also retrieved precipitable water vapor (PWV) based on PPP-B2b services, attaining millimeter-level accuracy [12]. Wang et al. systematically evaluated the accuracy of Zenith Total Delay (ZTD) estimation using PPP-B2b across different coverage areas. The results showed that PPP-B2b performs well in ZTD estimation over China and neighboring regions but significantly degrades in areas far from China (e.g., Australia). The ZTD error in China was 10–20 mm, while in Europe it was 15–30 mm [13]. Furthermore, sub-nanosecond time transfer accuracy can be achieved using PPP-B2b, and leveraging multi-frequency data can further enhance the accuracy and stability of time transfer [14,15,16]. Yang et al. systematically evaluated the performance of dual-frequency to five-frequency PPP-B2b, demonstrating that multi-frequency combinations significantly improve accuracy during the convergence stage [17]. Considering pseudorange multipath and carrier noise, Dai et al. refined the stochastic model for multi-frequency PPP-B2b and developed a five-frequency PPP-B2b model accounting for signal inconsistencies, reducing convergence time by approximately 10% [18]. Wang et al. also evaluated PPP-B2b performance based on multi-frequency smartphones, validating it in various typical scenarios including open and obstructed environments [19]. Tao et al. extracted multi-frequency phase bias products compatible with PPP-B2b services. By enabling ambiguity resolution, they improved positioning stability and reduced convergence time to approximately 3–4 min [20].
To further enhance PPP-B2b service performance, Yuan et al. proposed a single-difference clock constant bias (CCB) real-time extraction method based on a single reference station. The CCB corrections are transmitted to users via BeiDou short messages, improving PPP-B2b positioning accuracy and convergence performance through CCB compensation [21]. Meanwhile, Dai et al., in addition to parametrically compensating for CCB, also addressed the reference jump issue in GPS satellite clock corrections by introducing independent receiver clock bias parameters, reducing convergence time by over 40% [22].
Although PPP-B2b has been proven to provide reliable PNT services, it still faces challenges such as long convergence time and re-convergence issues after signal interruptions compared to Network Real-Time Kinematic (NRTK) and PPP-RTK. The core issue lies in the lack of high-precision atmospheric enhancement. Yuan et al. attempted a PPP-B2b positioning method that integrates ambiguity resolution and atmospheric augmentation, which enhanced positioning accuracy and convergence time by generating SSR corrections from a single reference station to augment PPP-B2b [23]. Effectively compensating for regional atmospheric errors to further improve PPP-B2b convergence speed and positioning accuracy is a topic worthy of research. Therefore, this paper preliminarily explores the feasibility of extracting and modeling regional atmospheric parameters based on PPP-B2b and enhancing positioning performance. By integrating regional atmospheric enhancement information with the PPP-B2b model, the performance of PPP-B2b can be improved.
The remainder of this paper is structured as follows. Section 2 introduces the BeiDou PPP-B2b service and its core characteristics. Section 3 details the methodology, including the multi-frequency uncombined PPP model accounting for CCB and the regional atmospheric extraction and modeling approach. Section 4 presents the experimental data and analyzes the results, covering CCB characterization, atmospheric modeling accuracy, and positioning performance with atmospheric augmentation. Section 5 discusses the implications of the findings, and Section 6 provides concluding remarks.
2. Principle of BeiDou PPP-B2b Services
The BDS-3 PPP service utilizes the PPP-B2b signal as a data broadcast channel. This signal is transmitted by the three BDS-3 GEO satellites (C59, C60, C61) over China and its surrounding regions, broadcasting correction information such as orbit, clock bias, and DCB parameters for the BDS-3 and other GNSSs (as shown in Table 1). It provides open and free high-precision services to users. The PPP-B2b signal is designed to be compatible with the four major GNSSs and their combinations. Currently, it offers enhancement services only for GPS and BDS-3. The PPP-B2b information can be used to correct the LNAV navigation messages of GPS and the CNAV1 navigation messages of BDS-3, respectively.

Table 1.
Detailed information of PPP-B2b service.
It can be observed that different types of corrections vary in their update intervals and validity periods. When applying these corrections, in addition to using the corrections closest to the current epoch, it is necessary to complete the version number matching between the broadcast ephemeris and the different types of corrections. First, a search is conducted for clock bias corrections received before the current epoch. Within the nominal validity period of the clock bias corrections (12 s), the clock bias correction with the shortest interval to the current epoch is selected. Then, using the IOD Corr mask of the clock correction as the reference, a matching orbit correction is sought within the nominal validity period of the orbit corrections (96 s). Finally, using the IODN from the orbit correction to match with the broadcast ephemeris. Given that the clock bias has the shortest update interval (6 s), the aforementioned matching strategy, which starts with the clock correction as the anchor point of the matching chain, ensures the optimal timeliness of the corrections.
The orbit corrections broadcast by PPP-B2b are projected in three directions: radial (R), along-track (A), and cross-track (C). During application, the unit vectors for these three directions (R, A, C) must first be calculated based on the broadcast ephemeris:
where and represent the satellite position vector and satellite velocity vector from the broadcast ephemeris, respectively; , , and denote the unit vectors of the satellite in the radial (R), along-track (A), and cross-track (C) directions, respectively.
By converting the corrections in the R, A, and C directions to the Earth-fixed coordinate system, the satellite position calculated from the broadcast ephemeris is then corrected [24]:
where represents the orbit correction provided by PPP-B2b; denotes the corresponding orbit correction in the Earth-fixed coordinate system; is the satellite position calculated from the broadcast ephemeris; refers to the precise satellite position after correction.
The clock bias calculated from the broadcast ephemeris is then corrected using the clock correction value [24]:
where represents the precise clock bias after correction; denotes the satellite clock bias calculated from the broadcast ephemeris; is the clock correction value provided by PPP-B2b; refers to the speed of light in vacuum.
Furthermore, to enhance the self-consistency of multi-frequency data processing, when the pseudorange observations used are inconsistent with the clock bias reference, the DCB between different pseudorange observations must also be considered [24]:
where represents the original pseudorange observation of the satellite; denotes the observation signal type; is the satellite DCB correction value broadcast by PPP-B2b; refers to the corrected pseudorange observation.
It is important to note that although the accuracy of orbit and clock is significantly improved after applying the above corrections, limitations in the regional distribution of PPP-B2b service monitoring stations prevent continuous global tracking of satellites. As a result, a noticeable systematic bias remains in the corrected clock bias, known as the Clock Constant Bias (CCB). The root cause is that when a satellite is re-tracked, the clock bias solution introduces a reference derived from pseudorange observations, and the substantial uncertainty of pseudorange leads to this bias. The magnitude of CCB typically ranges from several nanoseconds to tens of nanoseconds, which can significantly degrade PPP performance in terms of convergence and accuracy. Therefore, this bias must be properly addressed during data processing.
3. Methodology
3.1. Multi-Frequency Uncombined PPP Model Based on PPP-B2b
3.1.1. Multi-Frequency PPP Model Considering PPP-B2b CCB
Without loss of generality, the multi-frequency uncombined PPP model for GNSS can be expressed as follows [25]:
where superscripts and denote the satellite and constellation, respectively (Q = G for GPS, Q = C for BDS-3); subscripts and represent different satellites and frequencies, respectively; and denote the pseudorange and carrier-phase observations in units of length; represents the geometric distance between the receiver and satellite; and are the zenith wet delay (ZWD) and its corresponding mapping function; and are the re-parameterized receiver and satellite clock biases, both referenced to the dual-frequency ionosphere-free (IF) combination; is the re-parameterized ionospheric delay for the first frequency; is the ionospheric scaling factor for the i-th frequency (); and are the wavelength and float ambiguity for the i-th frequency, which absorb time-stable hardware delays; and are the receiver-side and satellite-side inter-frequency bias (IFB) parameters for multi-frequency pseudorange observations; and represent the observation noise for pseudorange and carrier-phase, respectively.
Furthermore, errors not explicitly listed above, such as dry tropospheric delay, tidal effects, and phase wind-up, can be accurately corrected using existing models [26,27]. For IFB parameters, receiver-side IFB can be estimated as constants, while satellite-side IFB can be corrected using DCB products, such as the DCB corrections broadcast by PPP-B2b or multi-system DCB products released by institutions like the Chinese Academy of Sciences (CAS) [28]. The re-parameterized ionospheric term is specifically defined as:
where is the true ionospheric delay; and are the receiver-side and satellite-side DCBs for frequency 1 and 2, respectively. For GPS, frequency 1 and 2 correspond to the L1 and L2 bands, while for BDS-3, they correspond to the B2I and B6I bands, respectively.
For the GPS system, the clock reference of its LNAV broadcast ephemeris is based on the L1/L2 dual-frequency IF combination. Therefore, after PPP-B2b correction, the clock bias incorporated CCB is:
where is the CCB for GPS satellites (in units of meters).
For the BDS-3 system, the clock reference of its CNAV1 broadcast ephemeris is based on the B6I frequency, rather than the B2I/B6I dual-frequency IF combination widely used by analysis centers like IGS for generating precise products. Thus, after applying PPP-B2b corrections, in addition to CCB, the consistency of the clock bias reference itself must be considered:
where is the CCB for BDS-3 satellites (in units of meters); is the clock bias reference transformation parameter.
Based on the relationships described in Equations (7) and (8), and further integrating them with the model in Equation (5), the multi-frequency uncombined PPP model incorporating CCB can be derived as follows:
where
The parameters to be estimated in the multi-frequency uncombined PPP model considering CCB include:
3.1.2. Compensation and Constraint Methods for CCB
It is evident that the introduction of satellite-dependent CCB parameters into the model results in effects that cannot be absorbed by common parameters such as receiver clock bias, leading to a rank deficiency issue in the model. To address this, it is necessary to incorporate prior information on CCB to constrain these parameters. The prior values of CCB are typically extracted based on a dual-frequency IF combination model. The model after applying PPP-B2b corrections can be expressed as:
where and represent the IF pseudorange and carrier-phase observations, respectively; and denote the IF float ambiguity and its corresponding wavelength; and are the observation noises of the IF observations.
For a reference station with precisely known coordinates, Equation (13) can be simplified as:
where and represent the corrected IF observations:
In the model described by Equation (14), correlation still exists between CCB and receiver clock bias. Typically, one satellite can be selected as a reference and constrained to zero:
At the initial epoch, tight constraints can be applied (e.g., setting the constraint variance to 10−8 m2). For subsequent epochs, the reference is propagated through Kalman filter, eliminating the need for constraints at every epoch. It should be noted that, by combining Equations (13) and (16), CCB for each satellite can theoretically be extracted based on a single reference station. However, to obtain more stable CCB estimates, multiple regional reference stations can be further utilized for weighted estimation.
After obtaining the CCB estimates, they can be used as pseudo-observations to constrain the CCB parameters in Equation (10):
where is the prior pseudo-observation value of CCB.
The constraint strength is related to the accuracy of the CCB estimate. Given that its accuracy is typically at the nanosecond level, the variance is set to 0.52 m2 in this study.
3.2. Regional Atmospheric Extraction and Modeling Methods
High-precision atmospheric delay extraction methods based on PPP typically involve two approaches: one is implementing undifferenced ambiguity resolution to enhance the estimation accuracy of other parameters through integer constraints, and another one is relying on long-term convergence of float PPP solutions to improve parameter estimation accuracy. The first method offers higher reliability but requires satellite phase bias products. Since such products are currently unavailable, this study preliminarily extracts ZWD and slant ionospheric delays based on float solutions.
To ensure the accuracy of atmospheric delay extraction, the theoretical precision of parameter estimates is evaluated. Only estimates meeting predefined thresholds are included in subsequent regional modeling. The thresholds for ZWD and ionospheric delays are set to 0.03 m and 0.1 m, respectively. Another important consideration is that while ZWD values extracted from reference stations can be directly used for modeling, the re-parameterized ionospheric delay described in Equation (6) absorbs receiver-dependent hardware biases. Therefore, single differencing between satellites must be applied to eliminate these biases before modeling, meaning that single-differenced ionospheric delays are used for modeling.
Based on atmospheric delays extracted from multiple regional reference stations, interpolation methods (e.g., LIM, DIM) or surface fitting techniques can be employed for regional atmospheric modeling [29,30]. Using a first-order polynomial as an example, the model can be expressed as:
where , , represent the model coefficients; denotes the Gaussian plane coordinates of the station (for ZWD) or the longitude and latitude of the ionospheric piercing point (for ionospheric delay); represents the ZWD or single-differenced ionospheric delay extracted from the reference station.
For a network consisting of reference stations, the following system of equations can be established:
where represents the modeling residual.
For simplicity, the model can be abbreviated as:
where
The model coefficients are then solved using the least squares method:
where is the weight matrix.
If is an identity matrix, the established model depends solely on the distribution of reference stations, not on user locations. In this study, to enhance the model’s adaptability to different users, a distance-dependent weighting method between the user and reference stations is adopted for constructing the weight matrix, enabling customized modeling for diverse users [31]:
where represents the distance (in kilometers) between the user and the i-th reference station.
3.3. Constraint Strategies for Atmospheric Pseudo-Observations
After obtaining the modeled ZWD and single-difference ionospheric values at the user’s location, constraints are applied to the corresponding parameters in the uncombined PPP model to accelerate parameter convergence:
where denotes the reference satellite; represents the between-satellite single-difference operator; and represent the modeled ZWD and single-difference ionospheric values, respectively; and are the corresponding variances, the values of which are related to the modeling accuracy.
For ZWD, given its relatively small magnitude and smooth variation, modeling accuracy can reach centimeter or even millimeter levels, allowing strong constraints to be applied. In contrast, the ionosphere exhibits complex time-varying characteristics that are difficult to represent with a fixed value. This study primarily considers the correlation of the ionosphere with time and satellite elevation, establishing the following stochastic model:
where is the satellite elevation angle; is the time-dependent prior variance, which can be assigned different values based on the magnitude of ionospheric modeling residuals during different time periods.
Finally, the multi-frequency uncombined PPP model comprehensively incorporating CCB and regional atmospheric constraints is as follows:
4. Data and Experimental Results
Experiments were conducted using a reference station network in China and its surrounding regions. The distribution of stations is shown in Figure 1, where blue and red markers represent reference stations and user stations, respectively. The wide-area reference stations in the left figure are primarily used for extracting high-performance CCB products, while the reference stations within the smaller area in the right figure are mainly used for high-precision atmospheric extraction and modeling. The data collection date was 2025 DOY202. The data sampling rate for the stations in the right figure is 5 s, and all stations support receiving multi-frequency observation data including GPS L1/L2/L5 and BDS-3 B1c/B2I/B2a/B6I.
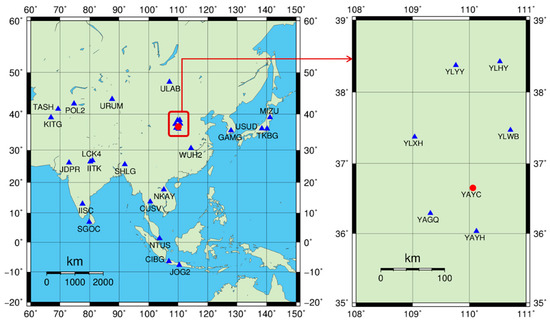
Figure 1.
Station distribution for CCB extraction and atmospheric-enhanced PPP validation.
During data processing, an elevation-dependent sine stochastic model was adopted, with zenith carrier-phase and pseudorange prior accuracies set to 3 mm and 0.3 m, respectively. A random walk process was employed to model and estimate the ionospheric delays, with a spectral density of 0.04 . Independent receiver clock parameters were established for GPS and BDS-3, respectively, to mitigate the impact of systematic jumps in PPP-B2b GPS clock corrections. For the satellite IFB introduced by multi-frequency pseudorange observations, BDS-3 corrections were applied using the Type 3 corrections broadcast by PPP-B2b. Since PPP-B2b does not currently broadcast DCB information for GPS, the DCB products provided by CAS were used for correction. Additionally, in multi-frequency data processing, the significant Inter-Frequency Clock Bias (IFCB) of GPS Block IIF satellites can also be extracted and corrected using regional reference stations [32,33,34].
In regional atmospheric modeling, a first-order polynomial model was employed. For single-difference ionospheric modeling, the satellite with the highest elevation angle was selected as the reference satellite. For terminal positioning validation, a kinematic mode was adopted. The variance of coordinates was reinitialized to 502 m2 at each epoch. To obtain more observation arcs, one day of data was segmented into 24 arcs at 1 h intervals, and each segment was processed individually.
4.1. Analysis of Clock Constant Bias (CCB) Results
Figure 2 and Figure 3 show the daily CCB sequences for GPS and BDS-3 satellites, respectively. Due to limitations in the availability of PPP-B2b corrections and the observational conditions of each station, the CCB sequences for a single day may contain interruptions. For the GPS system, significant overall offsets can also be observed in the CCB of the same satellite across different arcs, which is likely associated with the inherent systematic jumps in its clock corrections [7]. However, within a continuous arc, the CCB remains relatively stable. In terms of magnitude, BDS-3 CCB is slightly smaller than that of GPS. BDS-3 CCB generally does not exceed 10ns, while for some GPS satellites, it can approach 20 ns. Undoubtedly, this is a non-negligible error for achieving centimeter-level or higher precision positioning.
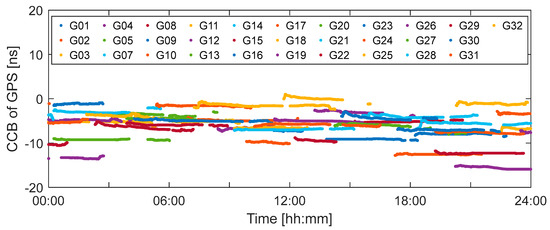
Figure 2.
CCB for each GPS satellite on 2025 DOY 202.
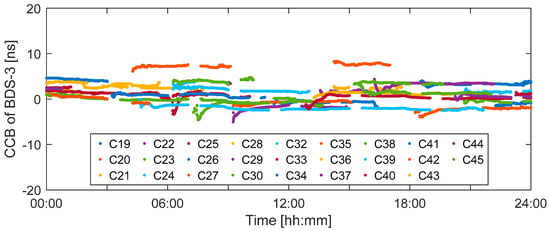
Figure 3.
CCB for each BDS-3 satellite on 2025 DOY 202.
By calculating the standard deviation (STD) of CCB across different arcs for each satellite, the temporal stability of CCB was analyzed, and the results are shown in Figure 4. It can be observed that the STD of CCB across different arcs generally does not exceed 0.5 ns. The maximum values are 0.52 ns for GPS G29 and 0.51 ns for BDS-3 C23. The average STDs of CCB for GPS and BDS-3 satellites are 0.18 ns and 0.23 ns, respectively, indicating that the stability of GPS CCB is slightly better than that of BDS-3. Overall, the CCB of both GPS and BDS-3 satellites exhibits high temporal stability.
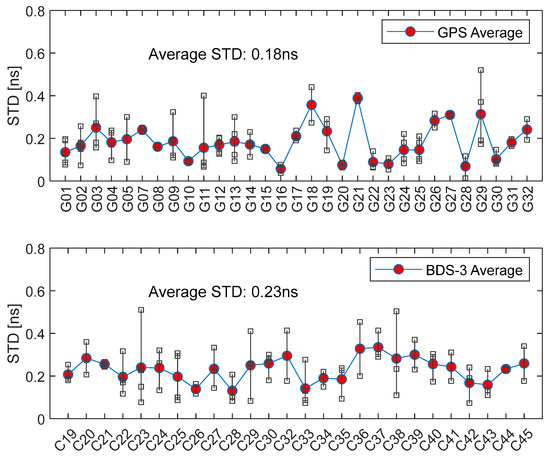
Figure 4.
STD of CCB for all arcs of GPS (top) and BDS-3 (bottom) satellites.
4.2. Accuracy Evaluation of Regional Atmospheric Modeling
Achieving high-precision regional atmospheric modeling is key to improving the performance of PPP-B2b services. To this end, the accuracy of ZWD and slant ionospheric modeling was evaluated separately. Figure 5 first presents the modeling results of ZWD at user stations. The interpolated values from the model generally align with the reference true values, with modeling errors mostly within the ±5 cm range. The RMS value of ZWD modeling for the entire day was 2.1 cm. Based on this, a constraint variance of 0.09 m2 was selected for ZWD in subsequent experiments.
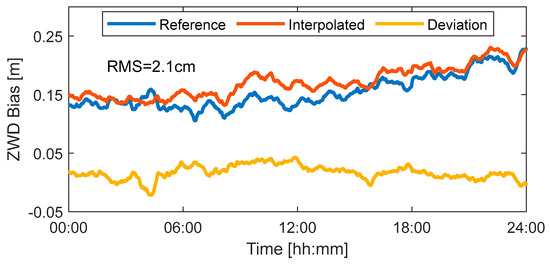
Figure 5.
Modeling results of ZWD.
Figure 6 shows the modeling biases of single-difference ionospheric delays for each satellite. It can be observed that the modeling biases for most periods do not exceed 20 cm, with an overall ionospheric modeling accuracy of 5.8 cm. However, it is noteworthy that during certain periods (e.g., 15:00–19:00), the ionospheric modeling biases exhibit significant fluctuations, even exceeding 40 cm. This is primarily related to the temporal variability and activity of the ionosphere.
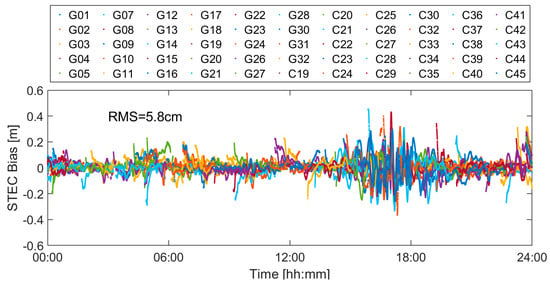
Figure 6.
Modeling biases of slant single-difference ionospheric delay for each satellite.
Figure 7 visually summarizes the ionospheric modeling accuracy statistics for different time periods (in 1 h intervals). It shows that the ionospheric modeling accuracy for most periods is better than 6 cm. However, during the 15:00–19:00 period and the final period (orange bars in the figure), the ionospheric modeling accuracy noticeably deteriorates, even exceeding 10 cm. Accurately characterizing the precision of ionospheric enhancement information is essential for achieving rapid and accurate parameter estimation at the user end. Therefore, it is necessary to adjust the stochastic model for ionospheric enhancement information based on different time periods. Additionally, ionospheric modeling accuracy is often strongly correlated with satellite elevation. As shown in Figure 7, satellites at low elevations tend to exhibit larger modeling errors.
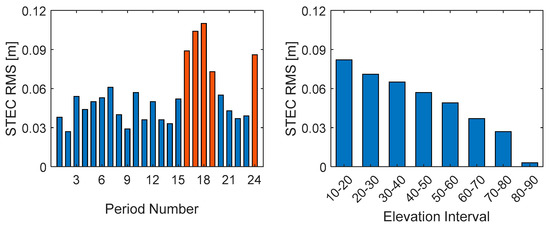
Figure 7.
Ionospheric modeling accuracy across different time periods (left) and elevation angle intervals (right). In the left figure, the orange and blue colors correspond to active and quiet ionospheric periods, respectively..
Based on the above analysis and the stochastic model described in Equation (25), different prior variances were set for different time periods: was used for normal periods, and was adopted for periods with poor modeling accuracy. Using the above stochastic model, Figure 8 illustrates the error envelope effects under two different threshold settings. It can be visually observed that, except for a very few satellites, the constructed stochastic model effectively envelopes the ionospheric modeling errors. The percentages of modeling errors falling within the envelope reached 98.87% and 98.78%, respectively. Overall, the model successfully characterizes the uncertainty of ionospheric enhancement information, providing a reliable reference for integrating enhancement information at the user end.
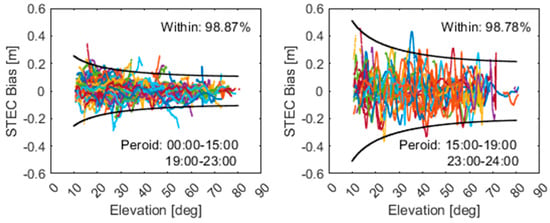
Figure 8.
Error envelope effect of the ionospheric prior stochastic model. The different colors represent different satellites.
4.3. Performance Assessment of Atmospheric-Enhanced PPP-B2b Positioning
Based on kinematic PPP mode, the positioning performance of BDS-3-only PPP-B2b was first analyzed. Corresponding to the two observation scenarios with high and low ionospheric modeling accuracy in Figure 7, two time periods (14:00–15:00 and 16:00–17:00) were selected as examples. Figure 9 shows the positioning results before and after applying atmospheric constraints. Atmospheric constraints significantly accelerated the convergence speed, achieving decimeter-level positioning from the first epoch. During the 14:00–15:00 period, the horizontal and vertical accuracy improved from (0.228, 0.249) m to (0.088, 0.091) m, representing improvements of 61.4% and 63.5%, respectively. During the 16:00–17:00 period, the horizontal and vertical accuracy improved from (0.225, 0.864) m to (0.093, 0.282) m, representing improvements of 58.7% and 67.4%, respectively. Furthermore, influenced by ionospheric activity, the vertical positioning accuracy during the 16:00–17:00 period was noticeably lower than the other period.
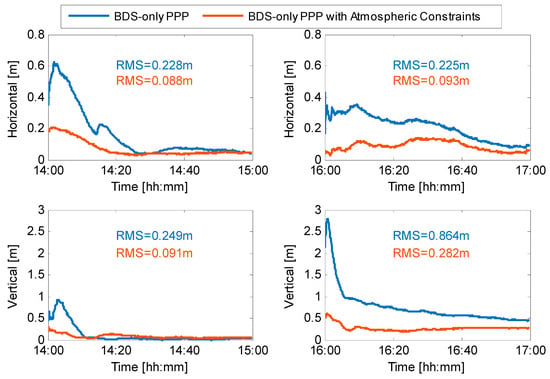
Figure 9.
BDS-3-only kinematic PPP results before and after applying atmospheric constraints (left: 14:00–15:00; right: 16:00–17:00).
By integrating the results from all 24 arcs of the day, the average positioning results are shown in Figure 10. A similar trend is observed: after applying atmospheric constraints, the convergence performance in both the horizontal and vertical directions was significantly improved. Using thresholds of 30 cm for horizontal and 40 cm for vertical accuracy [35,36], the standard single-system BDS-3 PPP-B2b required an average convergence time of approximately 16.7 min and 21.3 min, respectively. In contrast, with atmospheric constraints, the convergence thresholds were met from the first epoch, and subsequent epochs maintained continuous and stable positioning results. Within the 1 h arc, the horizontal and vertical positioning accuracy of single-system BDS-3 PPP-B2b improved from (0.282, 0.371) m to (0.087, 0.149) m, representing improvements of 69.3% and 59.9%, respectively.
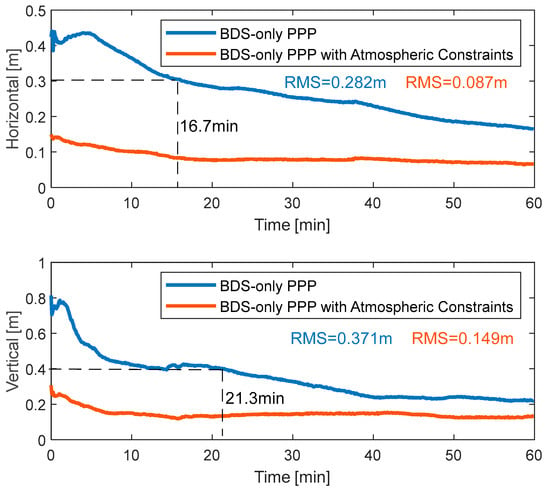
Figure 10.
Average positioning results of all 24 arcs for BDS-3-only kinematic PPP before and after applying atmospheric constraints.
Table 2 further provides statistics on positioning accuracy under different convergence durations. With atmospheric constraints, positioning accuracy better than 0.15 m horizontally and 0.3 m vertically was typically achieved within 1 min, with improvements of approximately 50–70% in both horizontal and vertical accuracy.

Table 2.
Positioning accuracy of single BDS-3 kinematic PPP under different convergence durations before and after applying atmospheric constraints.
Figure 11 illustrates the impact of atmospheric constraints on the positioning accuracy of the combined BDS-3/GPS dual-system PPP-B2b. It can be observed that the standard PPP-B2b exhibits a distinct convergence phase at the beginning of each arc. However, with atmospheric constraints aiding, the correlation among estimated parameters weakens rapidly, leading to significantly accelerated convergence speed. Figure 12 further presents the average positioning results across all arcs. Using the same convergence thresholds (30 cm horizontal and 40 cm vertical), the dual-system combination converged faster than the single BDS-3 system, requiring only 3.8 min and 5.0 min on average, which is 77.2% and 76.5% shorter, respectively. Similarly, atmospheric constraints markedly improved the convergence speed and positioning accuracy of the dual-system combination, achieving approximately 0.1 m horizontal and 0.2 m vertical accuracy from the first epoch. The statistical accuracy over the 1 h period improved from (0.167, 0.211) m to (0.069, 0.102) m on average horizontally and vertically, representing improvements of 58.7% and 51.7%, respectively.
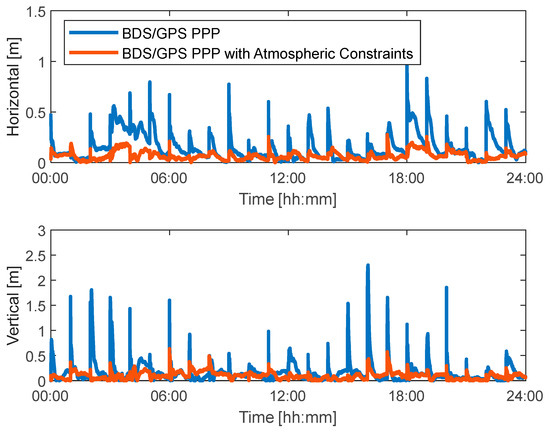
Figure 11.
Positioning results for each arc of BDS-3/GPS kinematic PPP before and after applying atmospheric constraints.
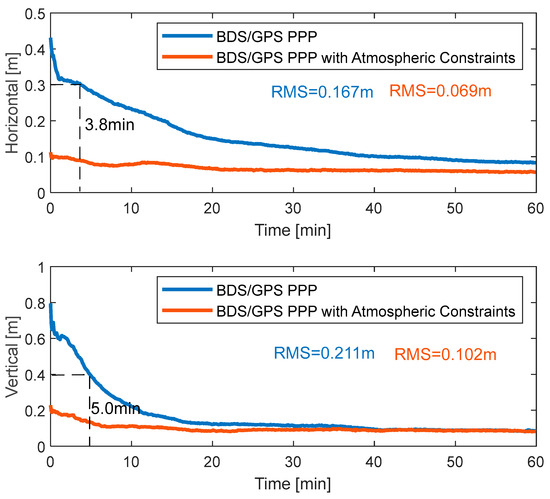
Figure 12.
Average positioning results of all 24 arcs for BDS-3/GPS kinematic PPP before and after applying atmospheric constraints.
Table 3 provides detailed positioning accuracy statistics. Under different convergence durations, the accuracy in both horizontal and vertical directions improved to varying degrees, with horizontal improvements ranging from approximately 50% to 70% and vertical improvements ranging from about 20% to 70%. Overall, with the assistance of high-precision atmospheric constraints, the dual-system combination achieved positioning accuracy better than 0.1 m horizontally and 0.2 m vertically within 1 min, significantly enhancing the service performance of standard PPP-B2b.

Table 3.
Positioning accuracy of BDS-3/GPS dual-system kinematic PPP under different convergence durations before and after applying atmospheric constraints.
To further explore the benefits of high-precision atmospheric constraints for standard PPP-B2b services under observation-constrained scenarios, Figure 13 shows the positioning results with a cutoff elevation of 30 degrees. Although the positioning performance degraded under high cutoff elevation conditions, similar conclusions can be drawn: regional atmospheric enhancement still enabled rapid high-precision positioning. The average accuracy from the first epoch was better than 0.2 m horizontally and 0.4 m vertically. Throughout the entire period, the average horizontal and vertical positioning accuracy improved from (0.249, 0.462) m to (0.081, 0.147) m, representing improvements of 67.5% and 68.2%, respectively.
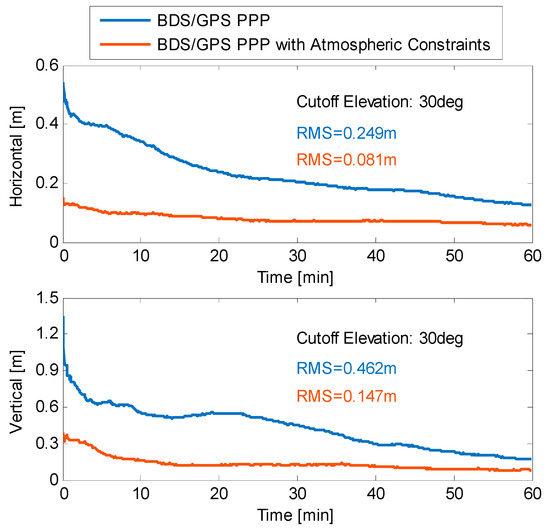
Figure 13.
Average positioning results of all 24 arcs for BDS-3/GPS kinematic PPP under a 30-degree cutoff elevation.
5. Discussion
The findings of this study demonstrate that the integration of regional atmospheric augmentation significantly enhances the performance of the standard PPP-B2b service, effectively addressing its primary limitations of prolonged convergence time and vulnerability to signal interruptions. By extracting high-precision atmospheric delay products from reference stations and incorporating them into a multi-frequency uncombined PPP model that explicitly accounts for Clock Constant Bias (CCB), the proposed method achieves near-instantaneous convergence and decimeter- to centimeter-level positioning accuracy. This breakthrough bridges a critical gap between the current PPP-B2b service and other advanced precise positioning technologies such as NRTK and PPP-RTK, highlighting the potential of atmospheric constraints in revolutionizing real-time high-precision positioning.
A particularly noteworthy achievement is the effective characterization and mitigation of CCB, a unique systematic error in PPP-B2b corrections. The high temporal stability of CCB—with standard deviations below 0.5 ns during continuous arcs—enables its precise modeling and compensation. This correction is essential, as unaddressed CCB can introduce significant biases in positioning results. Furthermore, the regionally derived zenith tropospheric delay (ZWD) and ionospheric models provide an additional layer of accuracy and reliability. The adaptive stochastic model, which accounts for temporal and elevation-dependent variations in ionospheric activity, offers a reliable strategy for integrating atmospheric enhancements into user-side positioning solutions.
In conclusion, this study validates the feasibility and effectiveness of enhancing PPP-B2b through regional atmospheric augmentation. The proposed framework significantly improves convergence speed, positioning accuracy, and reliability—particularly in demanding observation scenarios—paving the way for next-generation precise positioning services based on satellite-based augmentation systems.
It should be noted that the post-processing strategy employed in this study to evaluate ionospheric modeling accuracy has limitations for real-time applications, and this indeed represents a crucial direction for our future research. Accurately characterizing the precision of atmospheric enhancement information is both fundamental and challenging for PPP-RTK technology, especially in real-time operational scenarios. To address this challenge, our proposed approach involves introducing a crowdsourcing concept. This strategy leverages massive user terminals as mobile monitoring stations without requiring additional infrastructure investment. Through platform-user interaction, we aim to accurately capture the spatiotemporal irregularities of the ionosphere. Furthermore, we recognize that developing advanced AI models to characterize these ionospheric irregularities represents a promising future research trend. Another aspect worthy of investigation lies in conducting a theoretical analysis of the propagation of uncertainties in atmospheric extraction and modeling, rather than relying solely on post-processing empirical fitting models to characterize the modeling performance.
In addition, a broader statistical analysis involving multiple user stations distributed across different geographic regions and extended over longer time periods (e.g., weeks or seasons) would undoubtedly be valuable to further investigate the method’s robustness under a wider range of conditions. Therefore, conducting such a large-scale evaluation represents a key direction for future work.
6. Conclusions
The PPP-B2b service currently primarily broadcasts orbit, clock, and DCB corrections, enabling the provision of high-precision PNT services for China and its surrounding regions. However, compared to NRTK and PPP-RTK, the standard PPP-B2b still faces challenges such as long convergence time and re-convergence issues after signal interruptions due to the lack of enhancement from high-precision atmospheric products. To address this, a multi-frequency uncombined PPP model considering CCB was constructed to extract high-precision atmospheric information from a reference station network. By establishing a regional enhancement model and providing this enhanced information to users for fusion processing with raw PPP-B2b data, the feasibility of improving PPP-B2b performance through high-precision atmospheric enhancement was validated using real-tracked data.
Regarding the CCB characteristic of PPP-B2b, extraction results based on the reference station network indicate that the CCB for BDS-3 generally does not exceed 10 ns, slightly smaller in magnitude than that of GPS. Within continuous observation arcs, the STD of CCB is typically below 0.5 ns, with average daily STDs of 0.18 ns for BDS-3 and 0.23 ns for GPS. Overall, CCB demonstrates high temporal stability.
In terms of regional atmospheric modeling based on PPP-B2b, the accuracy of ZWD modeling is better than 3 cm, and the ionospheric modeling generally achieves accuracies of several centimeters. However, influenced by ionospheric activity, modeling errors can be significant during certain periods, even exceeding 40 cm. Therefore, a stochastic model tailored to different time periods was established while considering satellite elevation. The ionospheric modeling errors fell within the envelope with a probability of up to 98%, effectively characterizing the accuracy of the ionospheric enhancement information.
Regarding enhanced positioning at the user end, both single BDS-3 and BDS-3/GPS dual-system combined PPP-B2b showed significant improvements in convergence speed and positioning accuracy. Using thresholds of 30 cm horizontally and 40 cm vertically, the convergence times for horizontal and vertical components were approximately (16.7, 21.3) minutes for single BDS-3 and (3.8, 5.0) minutes for the dual-system combination, respectively. In contrast, with the application of atmospheric constraints, the convergence thresholds were achieved immediately at the first epoch. Within one minute, single BDS-3 achieved an accuracy better than 0.15 m horizontally and 0.3 m vertically, while the dual-system combination achieved an accuracy better than 0.1 m horizontally and 0.2 m vertically. Additionally, under high-elevation cutoff scenarios, stable and rapid high-precision positioning was still achievable with the assistance of high-precision atmospheric information, yielding horizontal and vertical accuracies of 0.081 m and 0.147 m, respectively, representing improvements of 67.5% and 68.2% compared to conventional PPP-B2b.
Author Contributions
Conceptualization, S.P. and W.G.; Methodology, Q.Z. and X.T.; Software, Q.Z. and Z.Z.; Supervision, S.P.; Validation, H.L., Z.Z. and Q.W.; Writing—original draft, Q.Z.; Writing—review & editing, X.T., Z.Z. and Q.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number 42204027), and the Foundation of Key Laboratory of Micro-Inertial Instrument and Advanced Navigation Technology, Ministry of Education, China (grant number SEU-MIAN-202401).
Data Availability Statement
The data from wide-area reference stations can be publicly accessed at the following URL: https://cddis.nasa.gov/archive/gnss/ (accessed on 22 October 2025). The regional observation data for atmosphere extraction and modeling are available upon request from the corresponding author considering it is not publicly available due to security issues.
Acknowledgments
The authors also sincerely acknowledge the IGS for providing multi-GNSS observation.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, L.; Li, J.; Yang, Y.; Zhang, T.; Mao, Y.; Sun, B.; Ren, X. Featured services and performance of BDS-3. Sci. Bull. 2021, 66, 2135–2143. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, Y.; Li, J. Performance evaluation of BDS-3 PPP-B2b precise point positioning service. GPs Solut. 2021, 25, 142. [Google Scholar] [CrossRef]
- Ren, Z.; Gong, H.; Peng, J.; Tang, C.; Huang, X.; Sun, G. Performance assessment of real-time precise point positioning using BDS PPP-B2b service signal. Adv. Space Res. 2021, 68, 3242–3254. [Google Scholar] [CrossRef]
- Xu, X.; Nie, Z.; Wang, Z.; Zhang, Y.; Dong, L. An improved BDS-3 PPP-B2b positioning approach by estimating signal in space range errors. GPS Solut. 2023, 27, 110. [Google Scholar] [CrossRef]
- Chen, J.; Song, Z.; Zhang, Y.; Ding, J.; Jiang, X.; Yang, S.; Hou, Y. Clock systematic jump estimation and URA refinement of BDS-3 B2b real-time precise point positioning service. GPS Solut. 2025, 29, 73. [Google Scholar] [CrossRef]
- Nie, Z.; Zhou, L.; Zhang, Y.; Wang, Z.; Xu, Y. Real-time detection and identification of BDS-3 PPP-B2b signal-in-space anomalies in the user-side. GPS Solut. 2025, 29, 97. [Google Scholar] [CrossRef]
- Geng, T.; Li, Z.; Xie, X.; Liu, W.; Li, Y.; Zhao, Q. Real-time ocean precise point positioning with BDS-3 service signal PPP-B2b. Measurement 2022, 203, 111911. [Google Scholar] [CrossRef]
- Yu, D.; Li, H.; Ji, B.; Chen, Y.; Huang, Y.; Li, X.; Wang, Z. Analysis of marine real-time PPP accuracy with the BDS-3 PPP-B2b service. Comput. Electr. Eng. 2025, 123, 110102. [Google Scholar] [CrossRef]
- Shang, R.; Xu, Z.; Gao, C.; Meng, X.; Gao, W.; Liu, Q. A Continuous B2b-PPP Model Considering Interruptions in BDS-3 B2b Orbits and Clock Corrections as Well as Signal-in-Space Range Error Residuals. Remote Sens. 2025, 17, 618. [Google Scholar] [CrossRef]
- Yang, H.; He, X.; Ferreira, V.; Ji, S.; Xu, Y.; Song, S. Assessment of precipitable water vapor retrieved from precise point positioning with PPP-B2b service. Earth Sci. Inform. 2023, 16, 315–328. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, K.; Zhang, J.; Li, H.; Liang, H.; Tu, M.; Chen, Y.; Qiu, C.; Li, L. An investigation of PPP-B2b coverage and its performance in ZTD estimation and positioning in different regions. Surv. Rev. 2025, 57, 258–272. [Google Scholar] [CrossRef]
- Tang, J.; Lyu, D.; Zeng, F.; Ge, Y.; Zhang, R. Comprehensive analysis of PPP-B2b service and its impact on BDS-3/GPS real-time PPP time transfer. Remote Sens. 2022, 14, 5366. [Google Scholar] [CrossRef]
- Ge, Y.; Cao, X.; Lyu, D.; He, Z.; Ye, F.; Xiao, G.; Shen, F. An investigation of PPP time transfer via BDS-3 PPP-B2b service. GPS Solut. 2023, 27, 61. [Google Scholar] [CrossRef]
- Zhang, R.; Li, L.; Li, X.; Ma, H.; Xiao, G.; Zhang, J. Research on quad-frequency PPP-B2b time transfer. IEEE Instrum. Meas. Mag. 2024, 27, 57–62. [Google Scholar] [CrossRef]
- Yang, H.; Ren, X.; Liu, M.; Zhang, X. Dual-frequency to five-frequency real-time precise point positioning using new BDS-3 PPP-B2b service. Earth Planets Space 2024, 76, 82. [Google Scholar] [CrossRef]
- Dai, W.; Qi, Q.; Pan, L.; Cai, C. Real-time uncombined PPP using BDS-3 PPP-B2b products with different multi-frequency integrations and refined stochastic model. Adv. Space Res. 2024, 74, 5569–5579. [Google Scholar] [CrossRef]
- Wang, J.; Shi, C.; Zheng, F.; Yang, C.; Liu, X.; Liu, S.; Xia, M.; Jing, G.; Li, T.; Chen, W.; et al. Multi-frequency smartphone positioning performance evaluation: Insights into A-GNSS PPP-B2b services and beyond. Satell. Navig. 2024, 5, 25. [Google Scholar] [CrossRef]
- Tao, J.; Zhang, G.; Chen, G.; Jiang, Y.; Zhao, Q. Real-time estimation of multi-frequency phase observable-specific bias for the BDS3 PPP-B2b service. GPS Solut. 2025, 29, 19. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, Z.; He, X.; Wang, H. Single-station-augmented PPP-B2b considering the satellite-specific clock bias via short-message communication. J. Geod. 2025, 99, 42. [Google Scholar] [CrossRef]
- Dai, W.; Liu, N.; Zhang, Z.; Tang, C.; Zhang, Z.; Yang, Y.; Pan, L. BDS-3/GPS uncombined real-time PPP with PPP-B2b precise products: Modeling and its long-term performance evaluation. Adv. Space Res. 2025, 75, 7212–7225. [Google Scholar] [CrossRef]
- Yuan, L.; Li, B.; Miao, W.; Ge, H.; Wu, Z. PPP-B2b-RTK: A PPP-B2b augmentation method by using the SSR corrections from a single reference station. GPS Solut. 2025, 29, 124. [Google Scholar] [CrossRef]
- CSNO BeiDou Navigation Satellite System Signal in Space Interface Control Document Precise Point Positioning Service Signal PPP-B2b. Version 1.0. Available online: http://www.beidou.gov.cn/xt/gfxz/202008/P020200803362062482940.pdf (accessed on 6 September 2025).
- Gao, W.; Zhao, Q.; Meng, X.; Pan, S. Performance of single-epoch EWL/WL/NL ambiguity-fixed precise point positioning with regional atmosphere modelling. Remote Sens. 2021, 13, 3758. [Google Scholar] [CrossRef]
- Wu, J.T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Manuscripta Geod. 1993, 18, 91–98. [Google Scholar] [CrossRef]
- Gerard, P.; Brian, L. IERS Conventions (2010); BIPM: Paris, France, 2010; p. 180. [Google Scholar]
- Guo, F.; Zhang, X.; Wang, J.; Ren, X. Modeling and assessment of triple-frequency BDS precise point positioning. J. Geod. 2016, 90, 1223–1235. [Google Scholar] [CrossRef]
- Wanninger, L. Improved ambiguity resolution by regional differential modelling of the ionosphere. In Proceedings of the 8th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1995), Palm Springs, CA, USA, 12–15 September 1995; pp. 55–62. [Google Scholar]
- Gao, Y.; Li, Z. Ionosphere effect and modeling for regional area differential GPS network. In Proceedings of the 11th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1998), Nashville, TN, USA, 15–18 September 1998; pp. 91–98. [Google Scholar]
- Zhao, Q.; Pan, S.; Gao, W.; Tao, X.; Liu, H.; Zhang, Z. Crowdsourcing User-Enhanced PPP-RTK with Weighted Ionospheric Modeling. Remote Sens. 2025, 17, 1099. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hugentobler, U.; Dach, R.; Steigenberger, P.; Hauschild, A. Apparent clock variations of the Block IIF-1 (SVN62) GPS satellite. GPS Solut. 2012, 16, 303–313. [Google Scholar] [CrossRef]
- Li, H.; Zhou, X.; Wu, B. Fast estimation and analysis of the inter-frequency clock bias for Block IIF satellites. GPS Solut. 2013, 17, 347–355. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, X.; Guo, F.; Liu, J. GPS inter-frequency clock bias estimation for both uncombined and ionospheric-free combined triple-frequency precise point positioning. J. Geod. 2019, 93, 473–487. [Google Scholar] [CrossRef]
- Gao, W.; Zhou, W.; Tang, C.; Li, X.; Yuan, Y.; Hu, X. High-precision services of BeiDou navigation satellite system (BDS): Current state, achievements, and future directions. Satell. Navig. 2024, 5, 20. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Y.; Yang, H.; Ren, X.; Lin, X.; Le, X.; Li, X. Performance of PPP and PPP-RTK with new-generation GNSS constellations and signals. Satell. Navig. 2025, 6, 17. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).