AI-Based Downscaling of MODIS LST Using SRDA-Net Model for High-Resolution Data Generation
Highlights
- SRDA-Net adopts an end-to-end deep learning architecture, overcoming the reliance of traditional methods on linear assumptions and multi-source high-temporal LST data, and achieving end-to-end nonlinear high-precision downscaling.
- Integrating the attention mechanism and multi-source feature fusion significantly enhances the ability to capture details of heterogeneous agricultural surfaces.
- With thermodynamic and spatial structure constraint loss function, it takes into account both reconstruction accuracy and physical interpret-ability.
- Producing LST data with a resolution of 500 and 250 m, serving agricultural, ecological and climate change research.
Abstract
1. Introduction
2. Materials and Methods
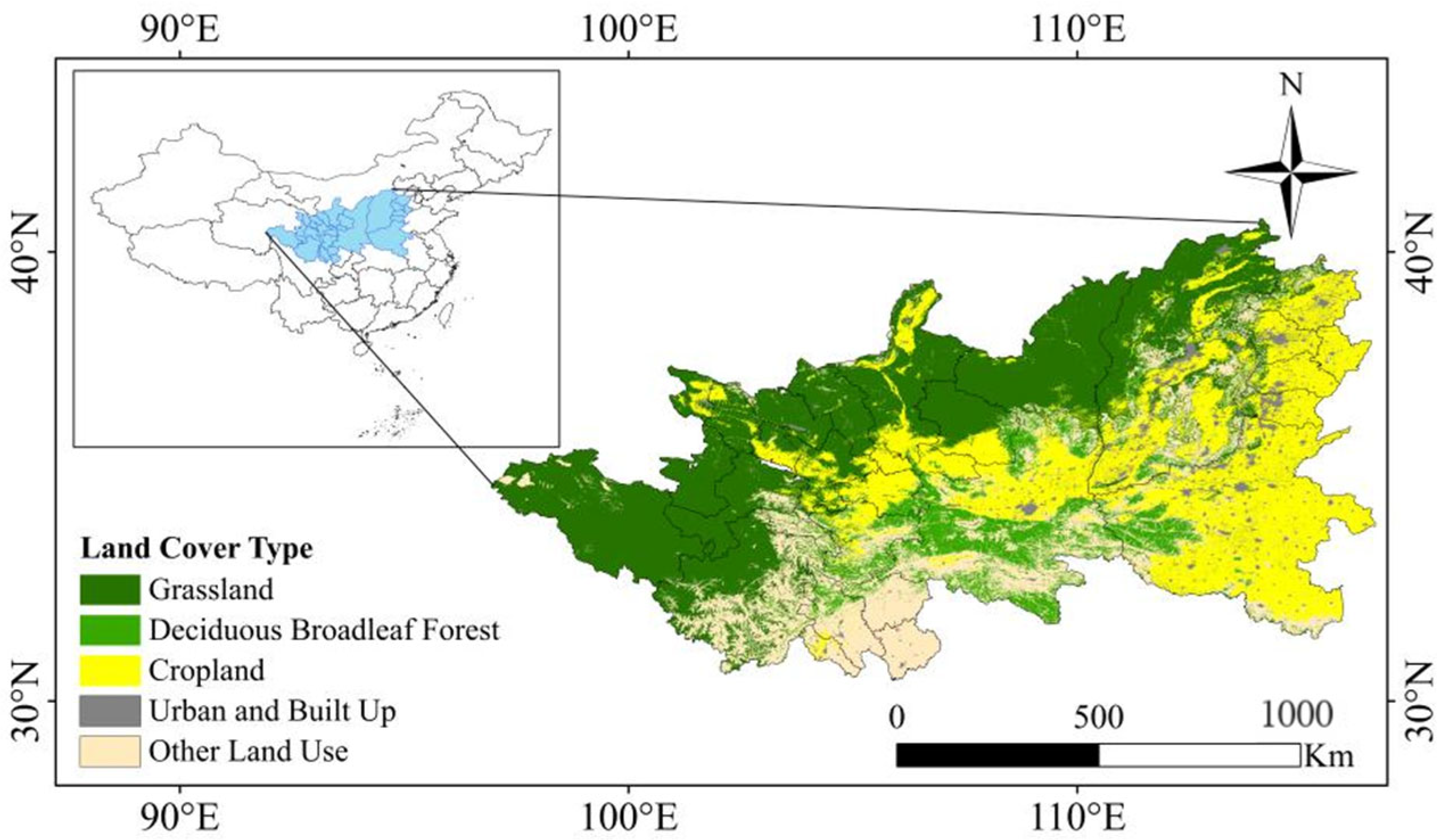
2.1. Study Area
2.2. Data Sources
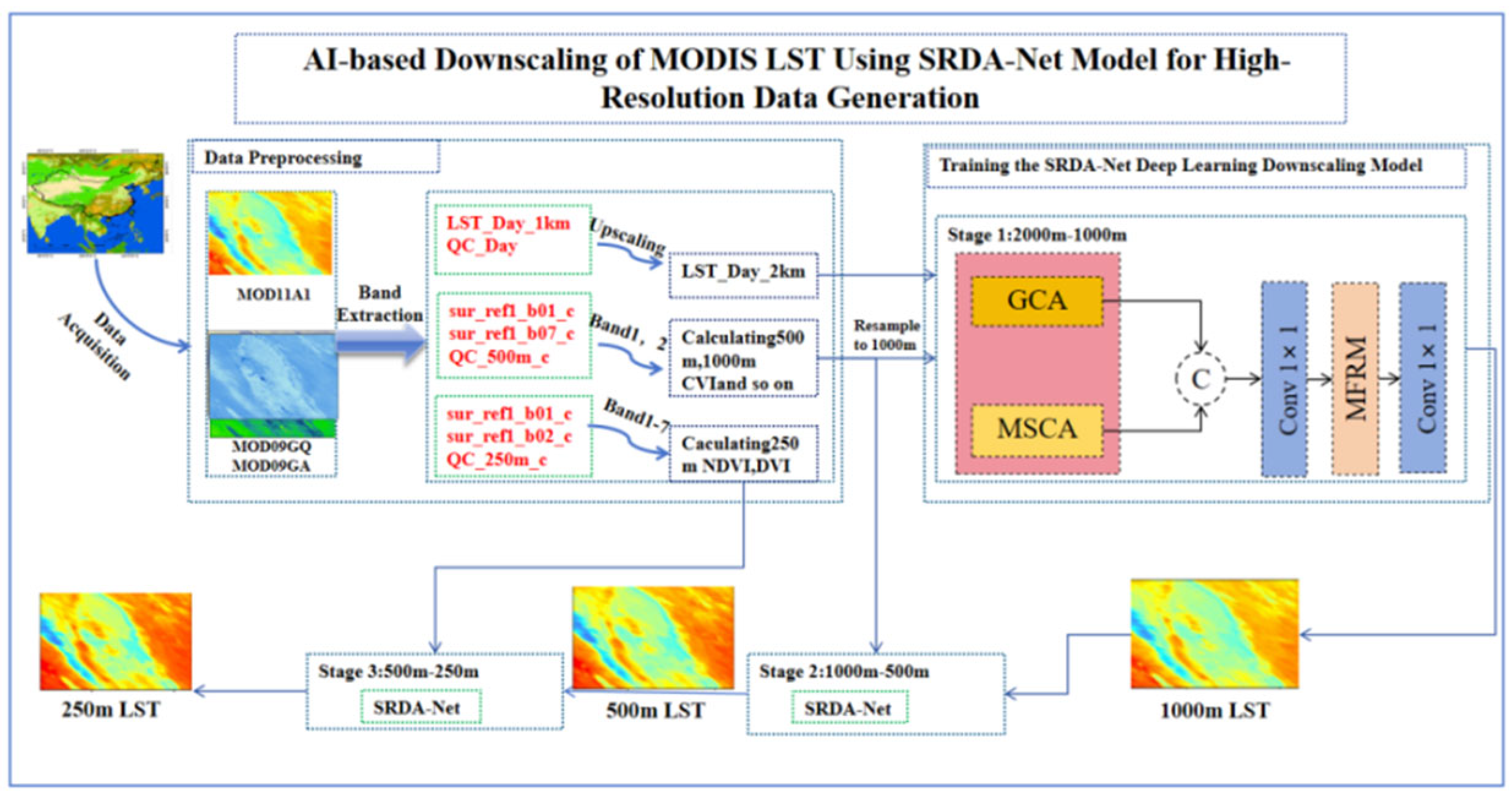
2.3. Stepwise Downscaling Framework of LST
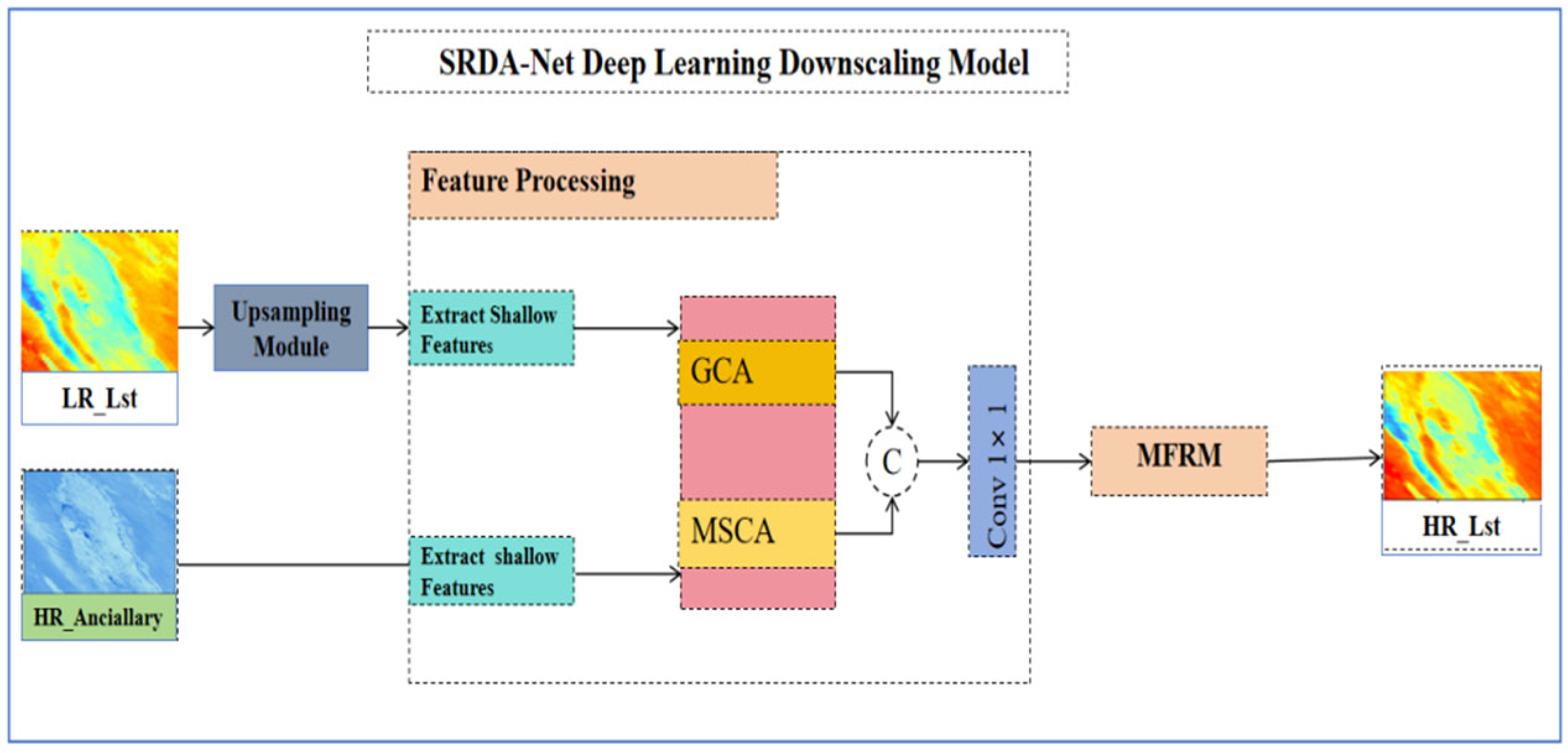
2.4. SRDA-Net Deep Learning Downscaling Model
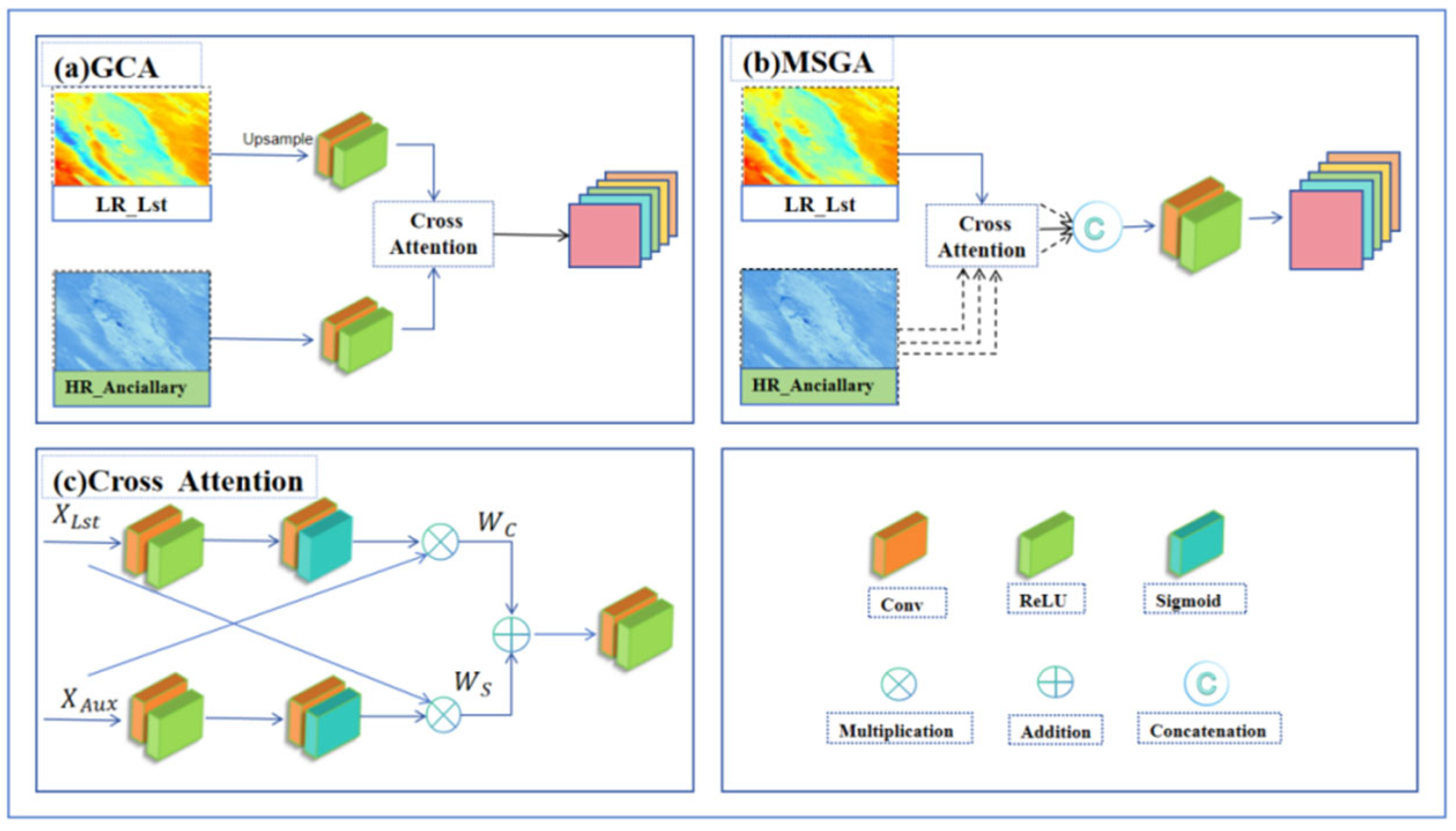
2.4.1. GCA and MSCA Modules
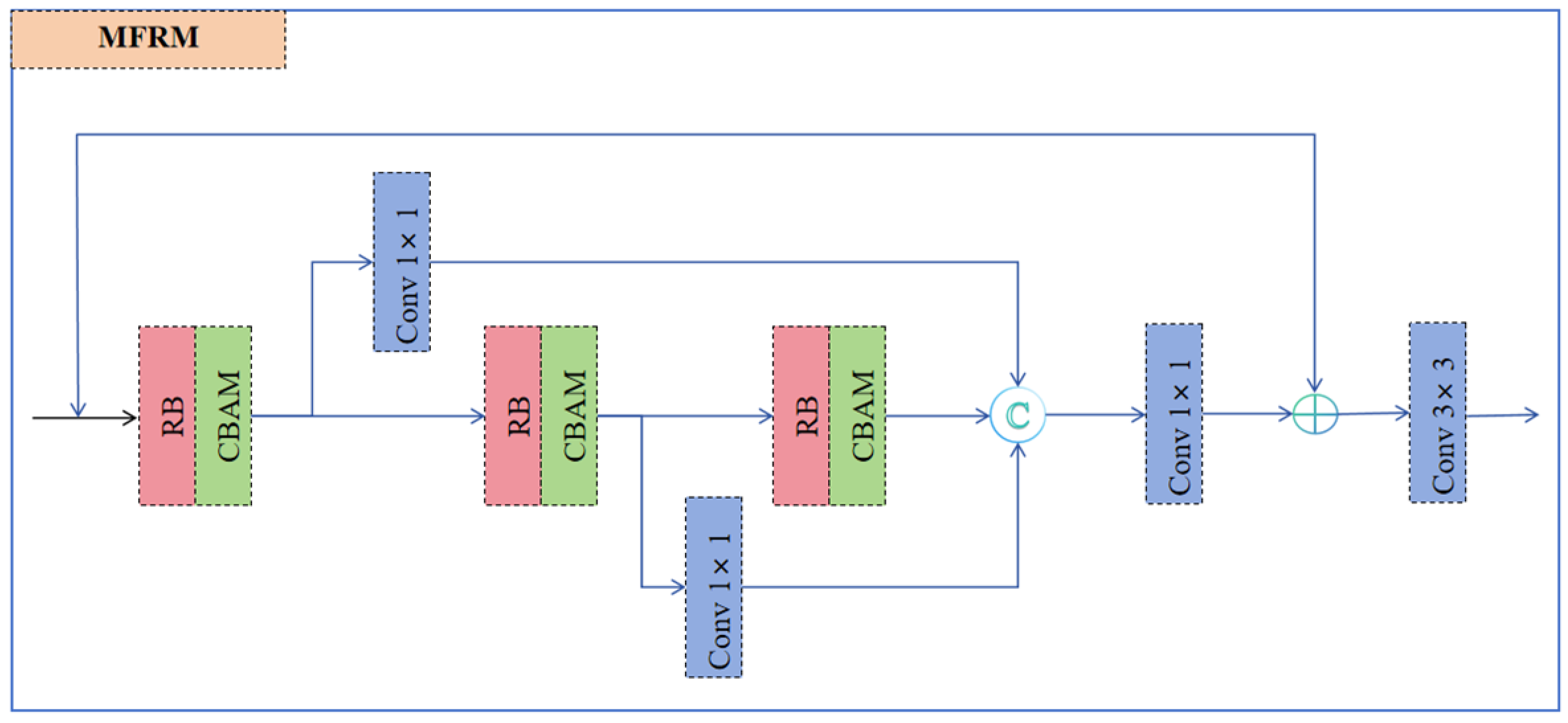
2.4.2. MFRM Module
2.4.3. Design of the Physical Constraint Loss Function
- (1)
- Degradation loss
- (2)
- Charbonnier Loss
- (3)
- Multi-scale SSIM Loss
- (4)
- Adaptive Fusion Mechanism
3. Results
3.1. Experimental Design
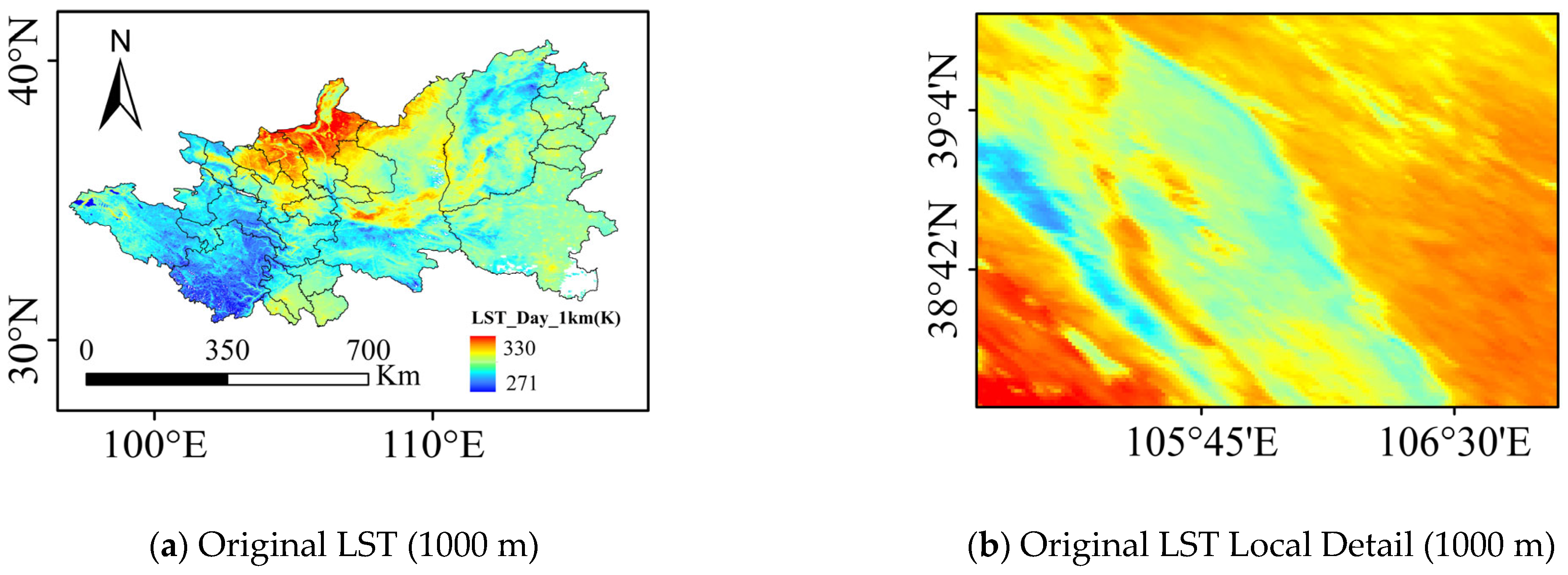
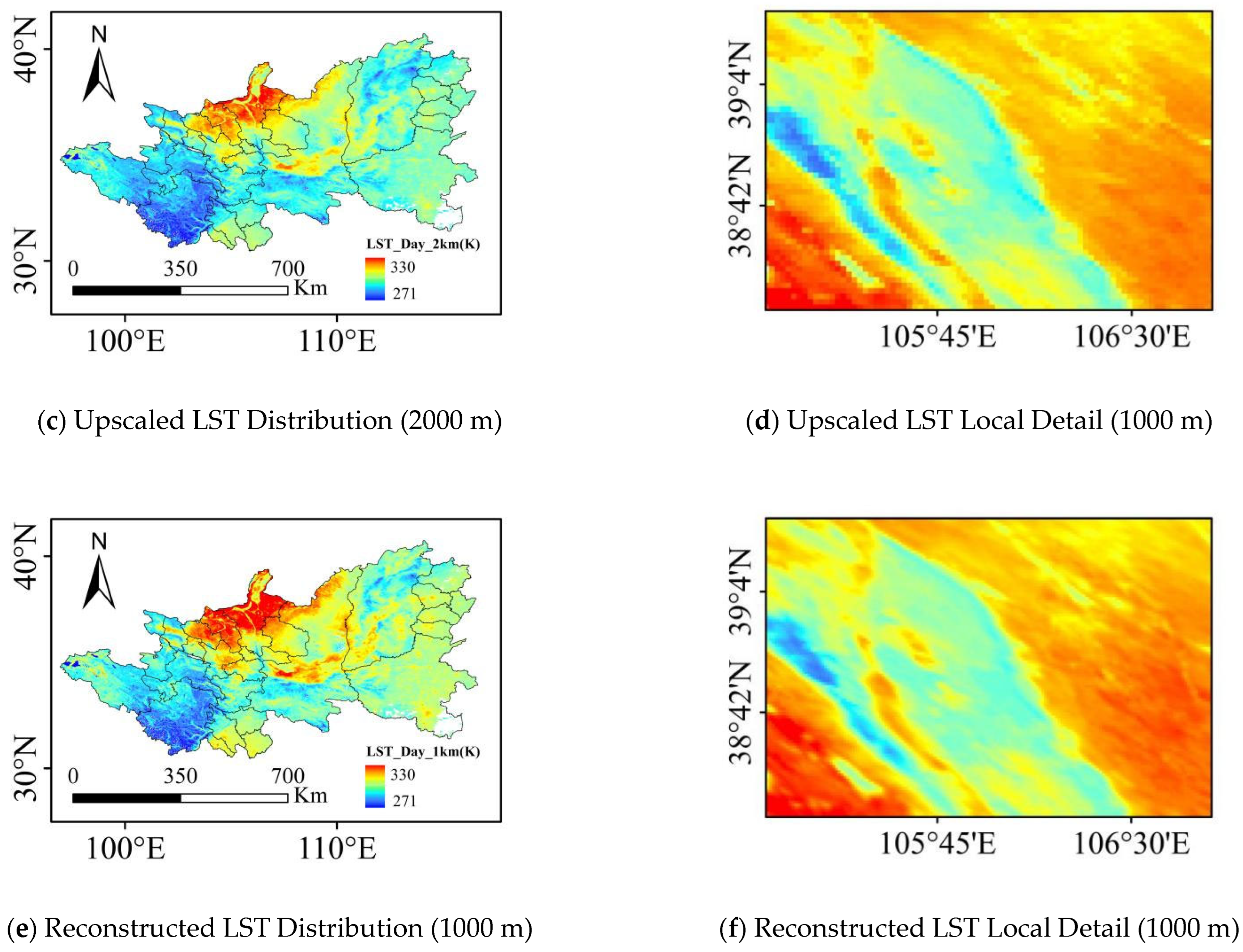
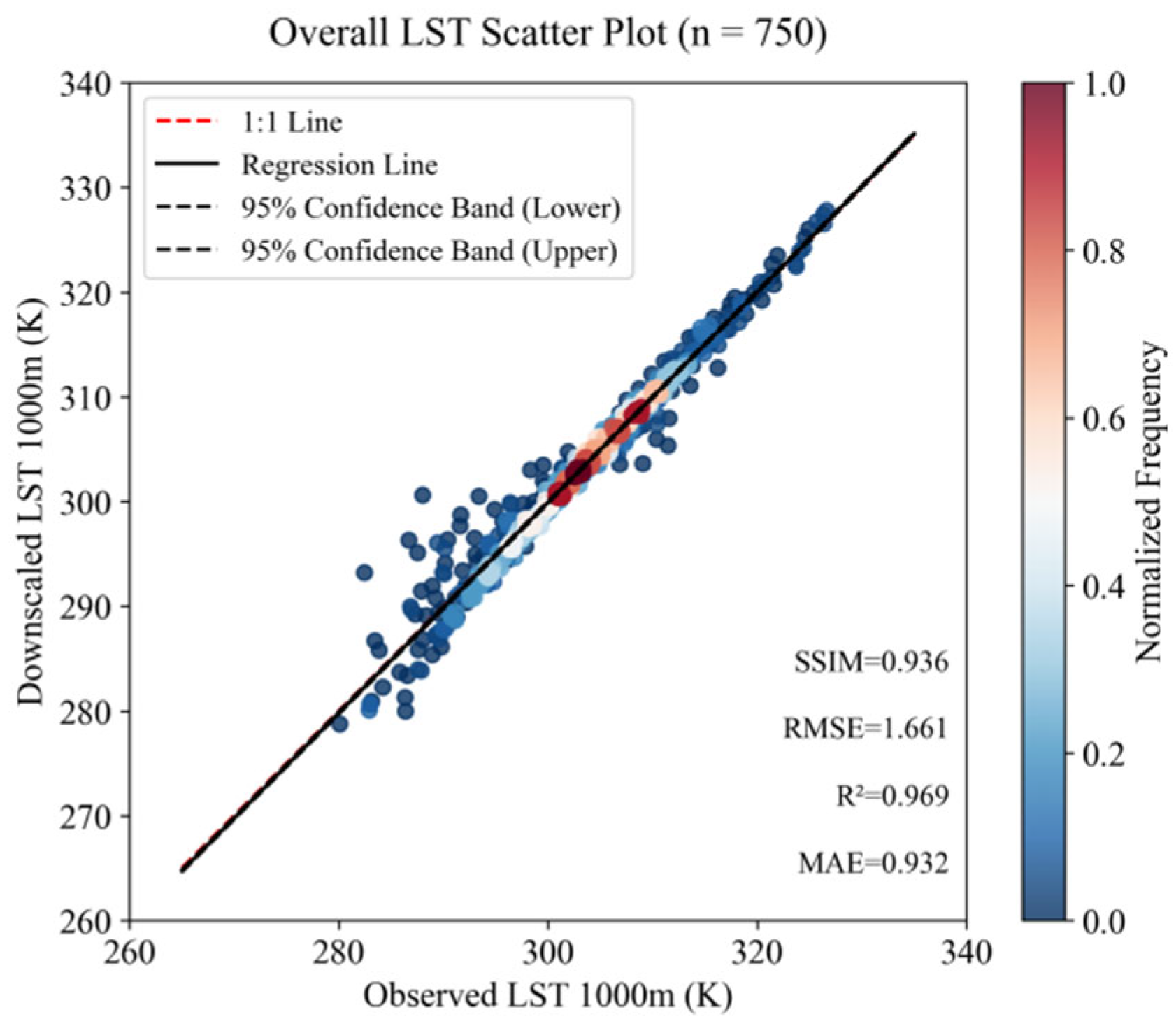
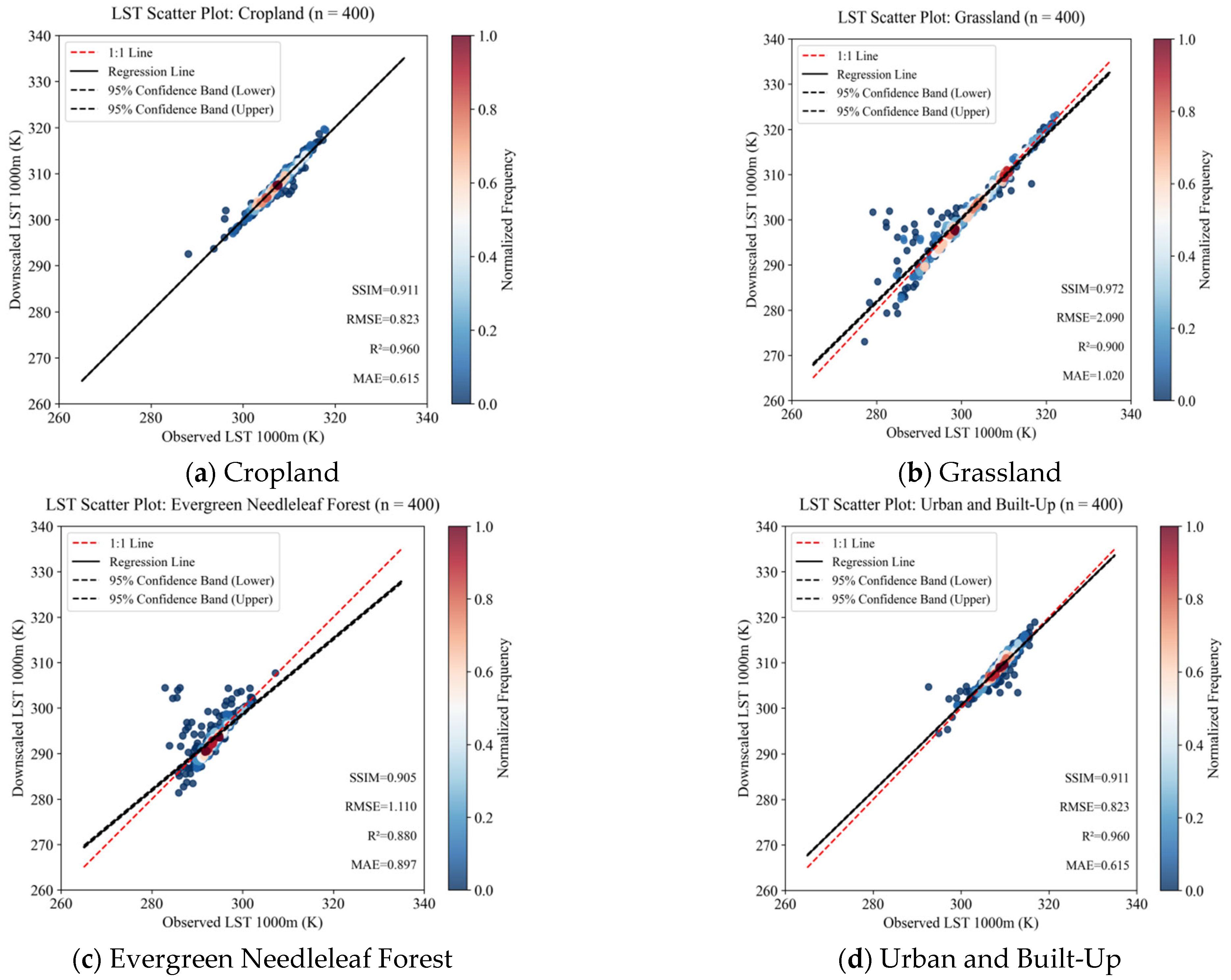
3.2. Simulation Experiment: Upscaling–Downscaling Closed-Loop Verification
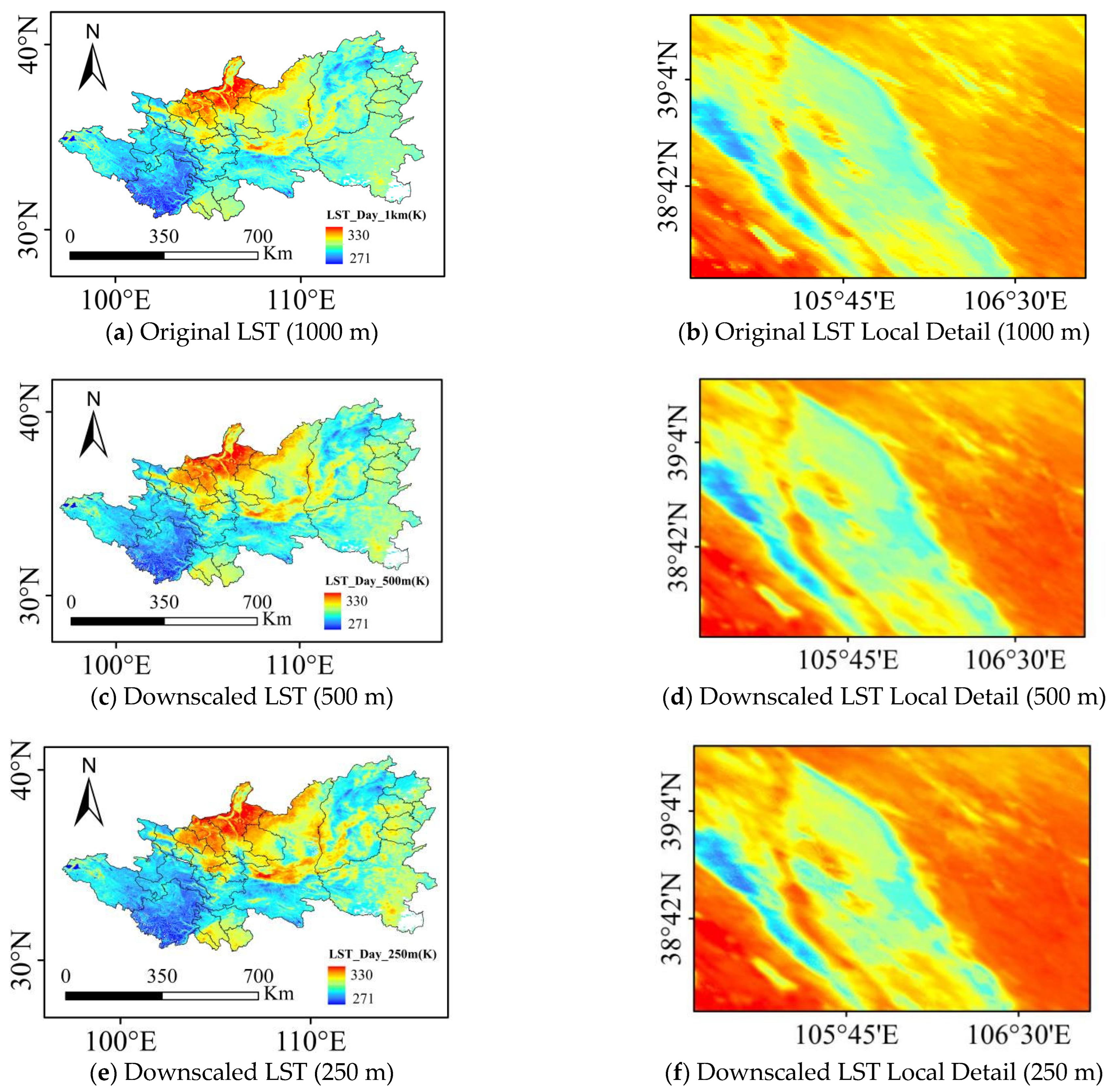
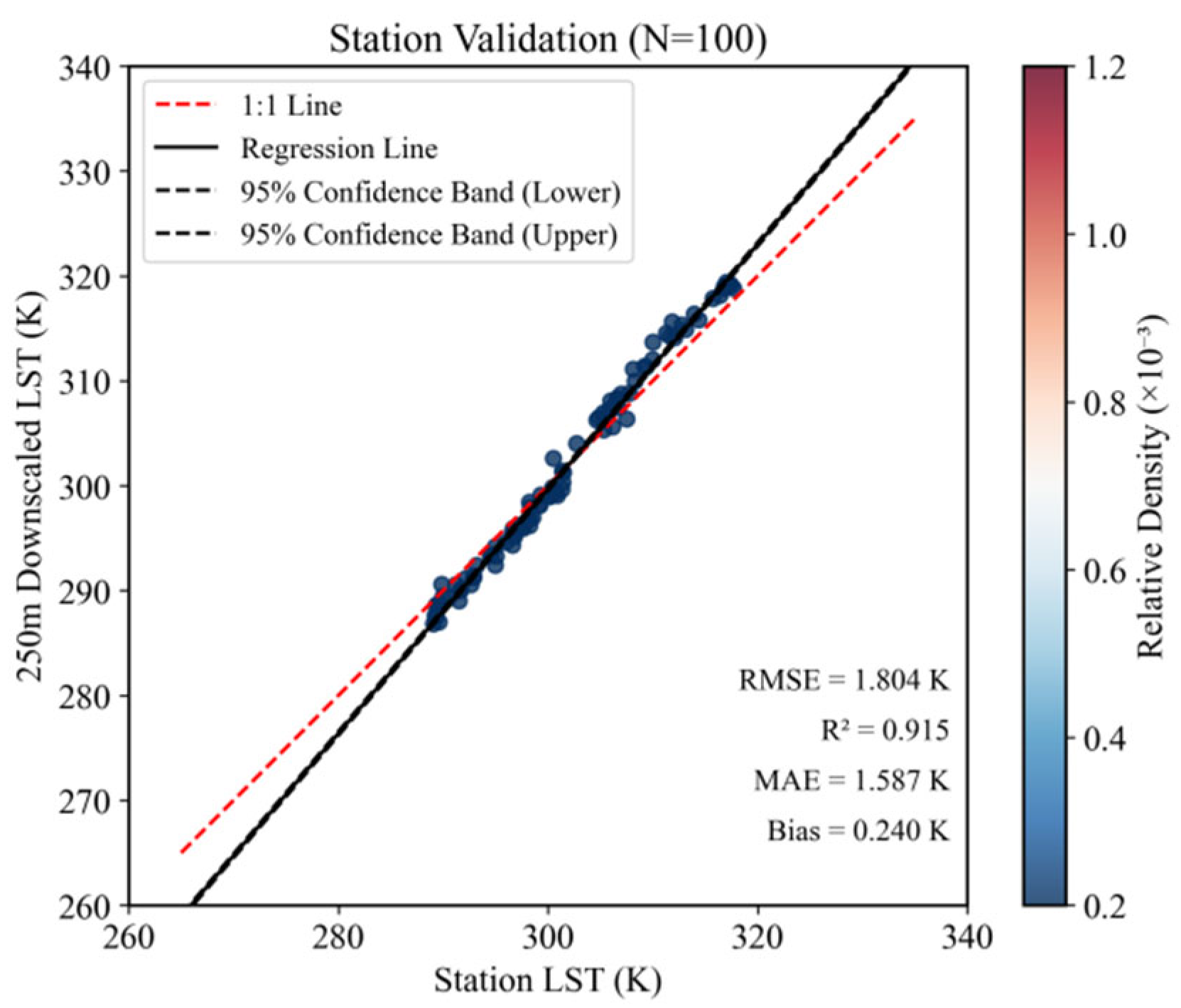
3.3. Target Experiment: Staged Multi-Scale Downscaling
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.L.; Tang, B.H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Bouaziz, S.; Hafiane, A.; Canals, R.; Nedjai, R. Deep learning for spatio-temporal fusion in land surface temperature estimation: A comprehensive survey, experimental analysis, and future trends. arXiv 2024, arXiv:2412.16631. [Google Scholar] [CrossRef]
- Wan, Z. New refinements and validation of the collection-6 MODIS land surface temperature/emissivity product. Remote Sens. Environ. 2014, 140, 36–45. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index–radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Norman, J.M. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ. 2007, 107, 545–558. [Google Scholar] [CrossRef]
- Hutengs, O.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Zhu, X.; Cai, F.; Tian, J.; Williams, T.K.A. Spatiotemporal Fusion of Multisource Remote Sensing Data: A Survey and Trends. Remote Sensing 2018, 10, 527. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J. Double ghost convolution attention mechanism network: A framework for hyperspectral reconstruction of a single RGB image. Sensors 2021, 21, 666. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Computer Vision—ECCV 2018; Springer: Cham, Switzerland, 2018; pp. 286–301. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Zhou, D.; Xiao, J.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.; Frolking, S.; Yao, R.; Qiao, Z.; Sobrino, J.A. Satellite remote sensing of surface urban heat islands: Progress, challenges, and perspectives. Remote Sens. 2019, 11, 48. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Daloye, A.M.; Erkbol, H.; Fritschi, F.B. Crop monitoring using satellite/UAV data fusion and machine learning. Remote Sens. 2020, 12, 1357. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, F. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
| Dataset Name | Dataset Code | Spatial Resolution | Temporal Resolution | Source URL |
|---|---|---|---|---|
| Land Surface Temperature | MOD11A1 | 1 km | Daily | https://ladsweb.modaps.eosdis.nasa.gov/ (accessed on 20 August 2024) |
| Surface Reflectance | MOD09GA | 500 m | Daily | https://ladsweb.modaps.eosdis.nasa.gov/ (accessed on 10 September 2024) |
| Surface Reflectance | MOD09GQ | 250 m | Daily | https://ladsweb.modaps.eosdis.nasa.gov/ (accessed on 10 September 2024) |
| DEM | SRTM | 30 m | Static | https://earthexplorer.usgs.gov/ (accessed on 10 September 2024) |
| Surface Albedo | MCD43A3 | 500 m | Daily | https://ladsweb.modaps.eosdis.nasa.gov/ (accessed on 10 September 2024) |
| Meteorological Data | ERA5/Station | 0.25°/Station | Hourly/Daily | https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5 or http://data.cma.cn/ (accessed on 25 September 2024) |
| Land Cover Classification | MCD12Q1 | 500 m | Annual | https://ladsweb.modaps.eosdis.nasa.gov (accessed on 10 September 2024) |
| Experiment/m | Resolution/m | ||
|---|---|---|---|
| Input(P,A) | Output(P) | ||
| Simulation Experiment | 2000–1000 | 2,000,500 | 1000 |
| Target Experiment | 1000–500 | 1,000,500 | 500 |
| 500–250 | 500,250 | 250 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Mao, K.; Yuan, Z.; Xu, L.; Shi, J.; Guo, Z.; Qin, Z. AI-Based Downscaling of MODIS LST Using SRDA-Net Model for High-Resolution Data Generation. Remote Sens. 2025, 17, 3510. https://doi.org/10.3390/rs17213510
Ma H, Mao K, Yuan Z, Xu L, Shi J, Guo Z, Qin Z. AI-Based Downscaling of MODIS LST Using SRDA-Net Model for High-Resolution Data Generation. Remote Sensing. 2025; 17(21):3510. https://doi.org/10.3390/rs17213510
Chicago/Turabian StyleMa, Hongxia, Kebiao Mao, Zijin Yuan, Longhao Xu, Jiancheng Shi, Zhonghua Guo, and Zhihao Qin. 2025. "AI-Based Downscaling of MODIS LST Using SRDA-Net Model for High-Resolution Data Generation" Remote Sensing 17, no. 21: 3510. https://doi.org/10.3390/rs17213510
APA StyleMa, H., Mao, K., Yuan, Z., Xu, L., Shi, J., Guo, Z., & Qin, Z. (2025). AI-Based Downscaling of MODIS LST Using SRDA-Net Model for High-Resolution Data Generation. Remote Sensing, 17(21), 3510. https://doi.org/10.3390/rs17213510






