Generating Accurate De-Noising Vectors for Sentinel-1: 10 Years of Continuous Improvements
Abstract
Highlights
- The noise vectors annotated in the S-1 L1 products have been optimized during the last 10 years to represent, with the highest accuracy, the effective thermal noise level in the data.
- The lessons learned from S-1A and S-1B allowed obtaining high-quality noise vectors for S-1C and S-1D from the beginning of the operational phase.
- The optimized noise vectors can be used by the users to de-noise the S-1 data, which is particularly useful in obtaining unbiased radiometric measures, especially over low-backscatter areas and cross-pol data.
- It will be possible to generate good-quality noise vectors for past S-1 products as well, exploiting dedicated open-source S-1 tools.
Abstract
1. Introduction
2. Methods
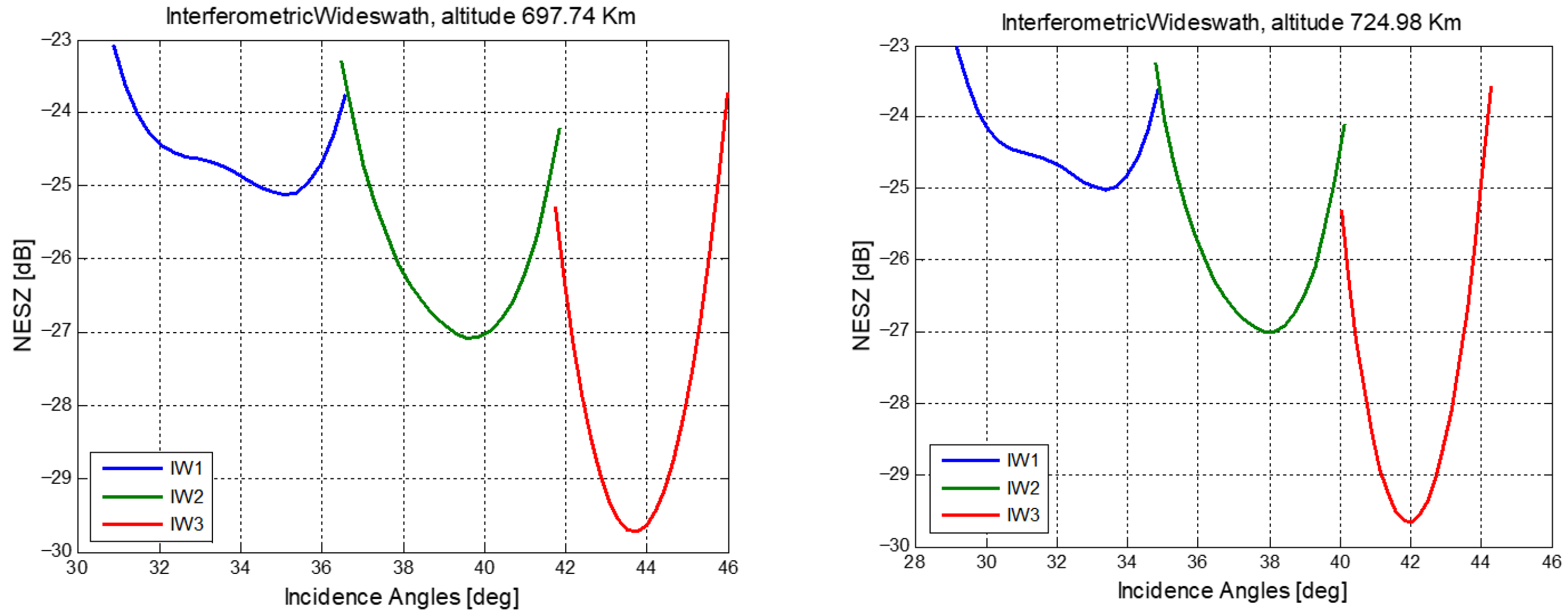
2.1. SAR Data and Thermal Noise
- is the slant range.
- is the Boltzmann constant.
- is the system temperature.
- is the range bandwidth of the transmitted pulse.
- is the noise figure of the system.
- is the satellite velocity.
- is the incidence angle.
- is the loss term that includes system losses, propagation losses, and processing losses.
- is the transmitted power.
- is the transmission duty cycle, i.e., the product of the Tx pulse length and of the Pulse Repetition Frequency (PRF).
- is the two-way antenna gain in the direction of the target.
- is the RADAR wavelength.
- is the speed of light.
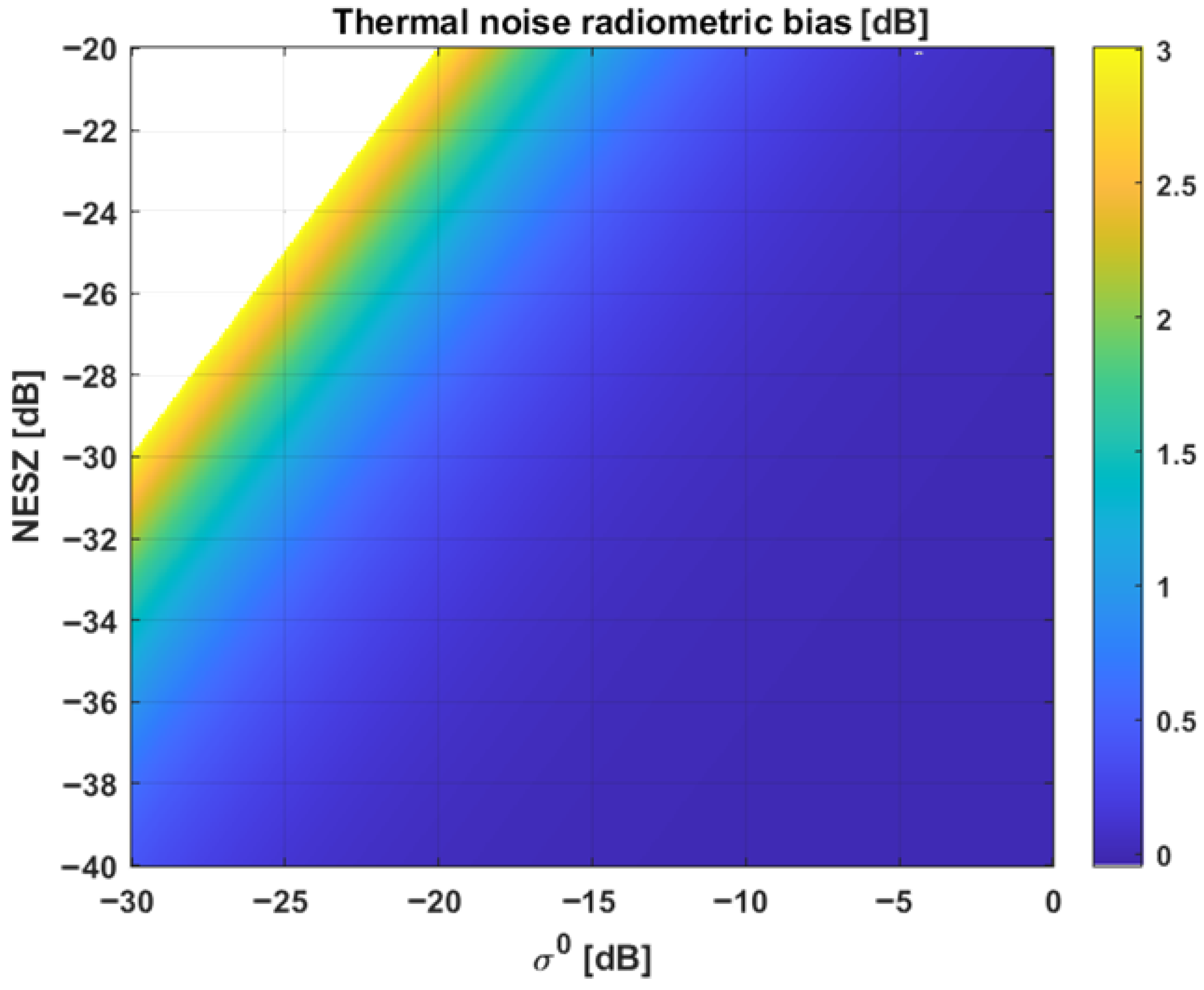
- it is paramount to know the SNR of a SAR image to be able to assess the accuracy of the geophysical parameters that will be measured from that image;
- the effect of thermal noise can be partially mitigated by increasing the number of looks used for the phase or amplitude estimation, at the cost of a proportional reduction in the geometric resolution.
- targets below the thermal noise level will not be discernible in the SAR image;
- the estimation of the reflectivity of targets close to the thermal noise level will be biased.
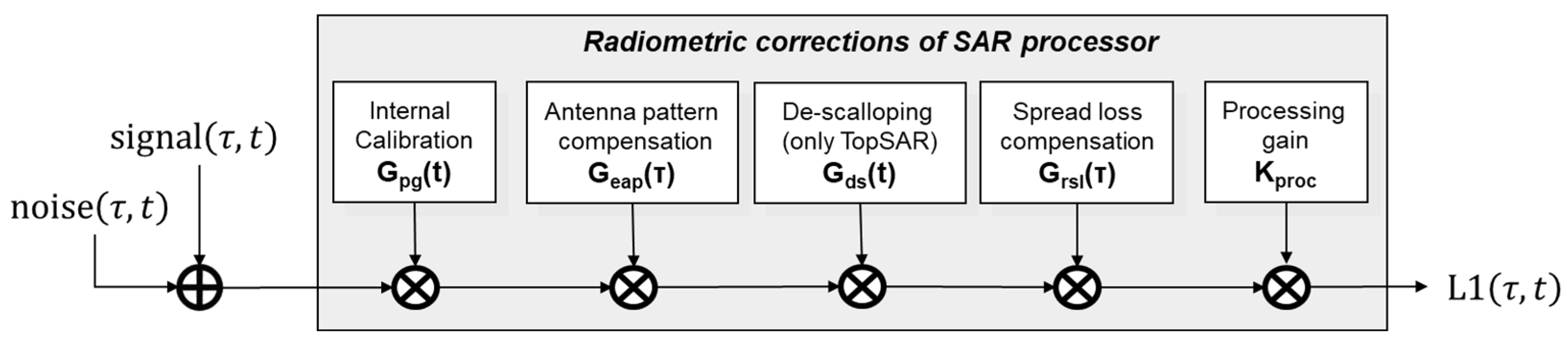
2.2. SAR Data Radiometric Corrections
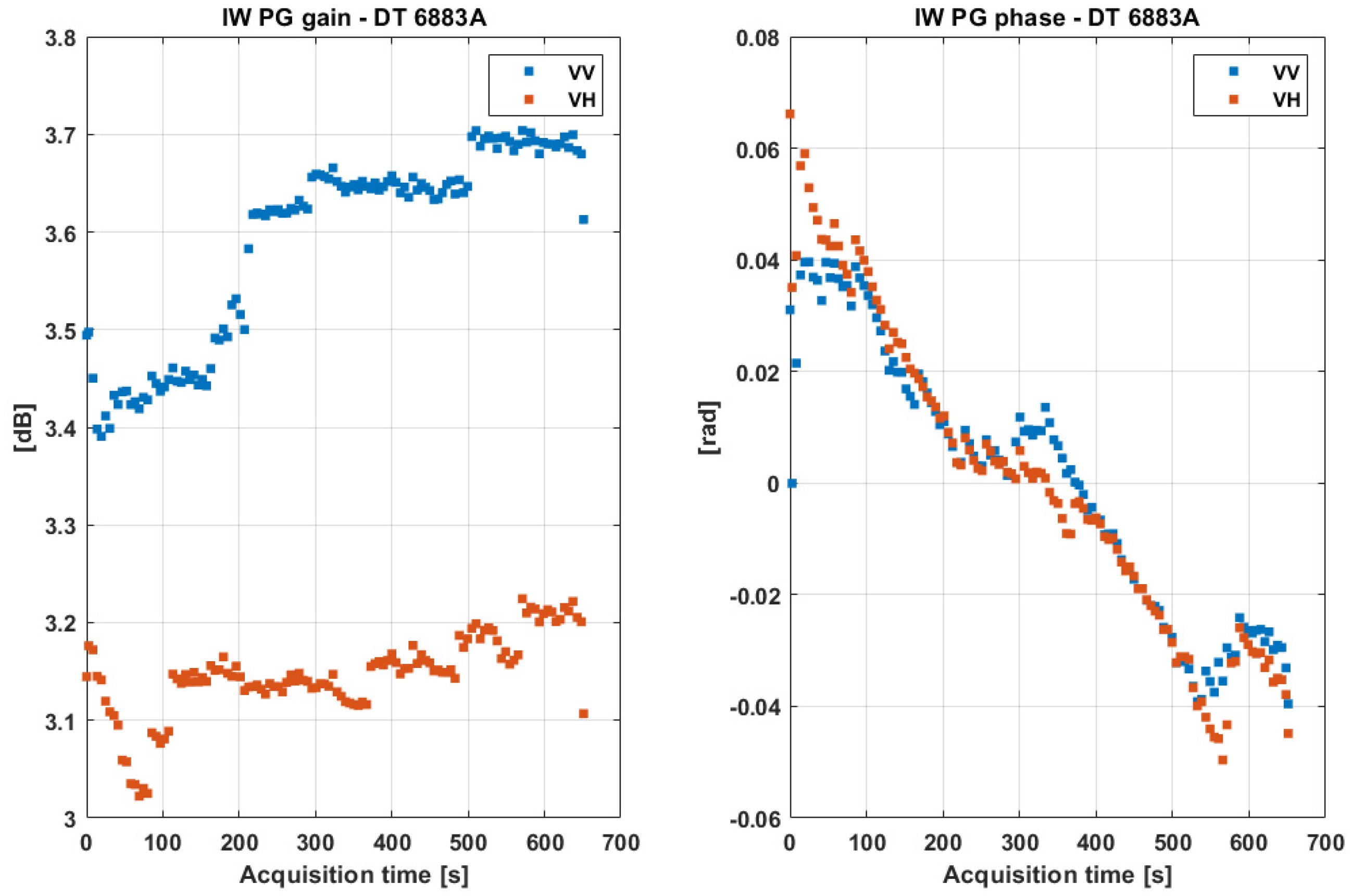
2.2.1. Internal Calibration
- The largest jump happened in September 2014 following the updating of the on-board Rx gain settings after the Commissioning Phase. This was needed to improve the efficiency of the flexible dynamic block adaptive quantization (FDBAQ) implemented on-board [14]
- A few jumps can be observed till mid 2015, due to intermittent failures in tile 5. This was fixed in 2015 by switching to a redundant configuration for tile 5.
- A small jump is observed in June 2016 due to an on-board issue affecting tile 11. Since then, the lower half of the tile 11 has been operated with reduced Tx power, resulting in the observed PG reduction.
- Finally, a very small decrease in time likely due to instrument aging can be observed.
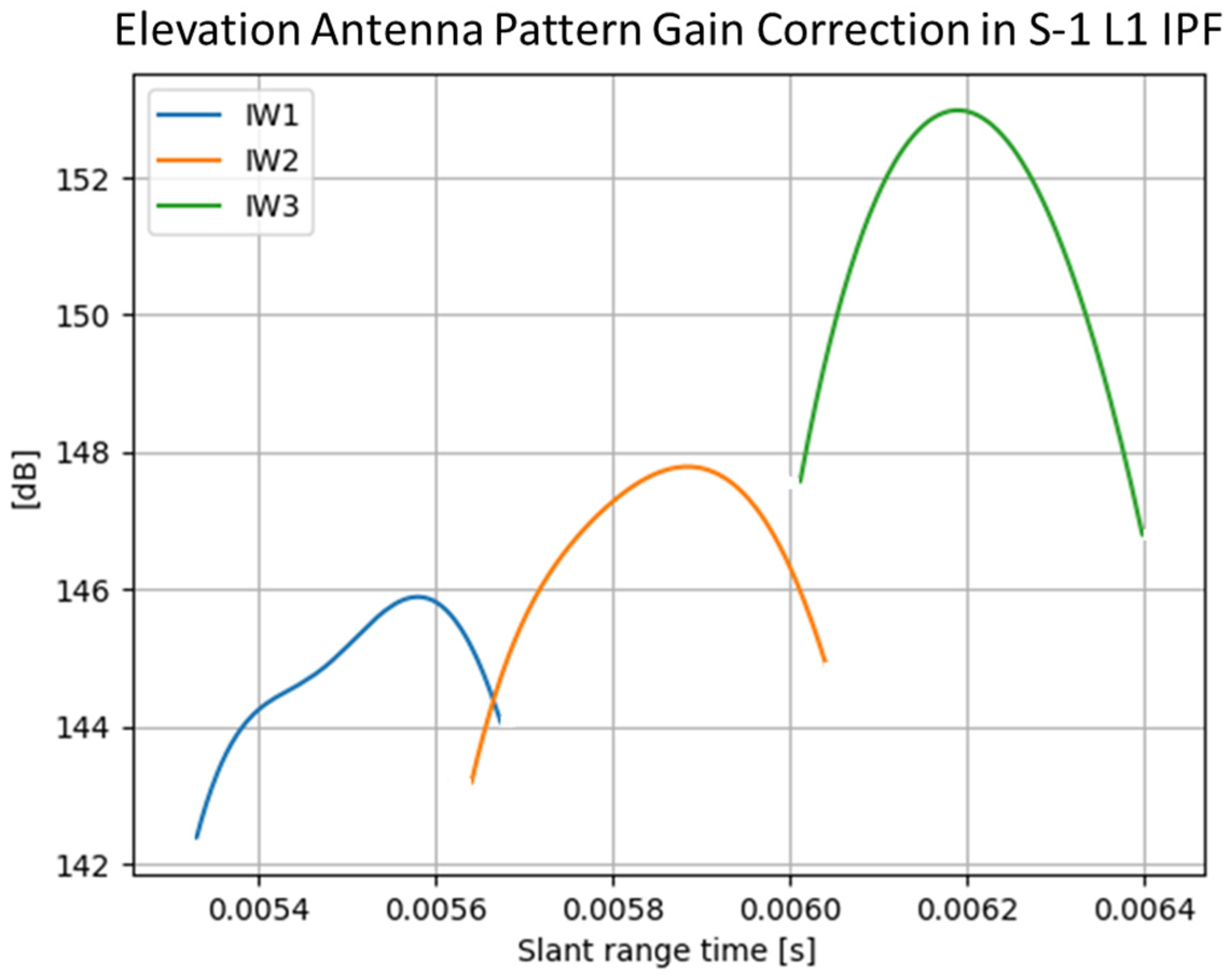
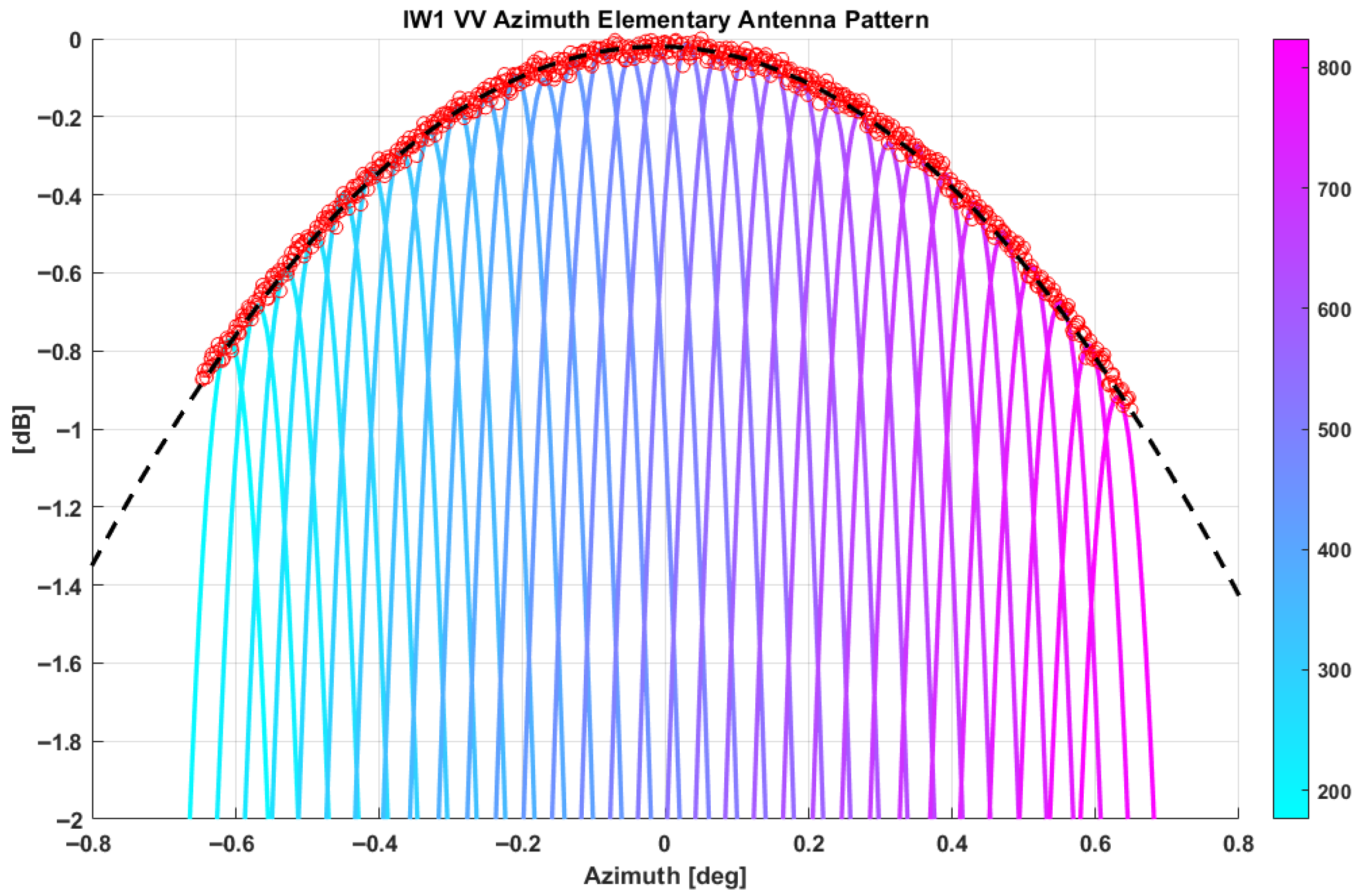
2.2.2. Antenna Patterns
2.2.3. De-Scalloping
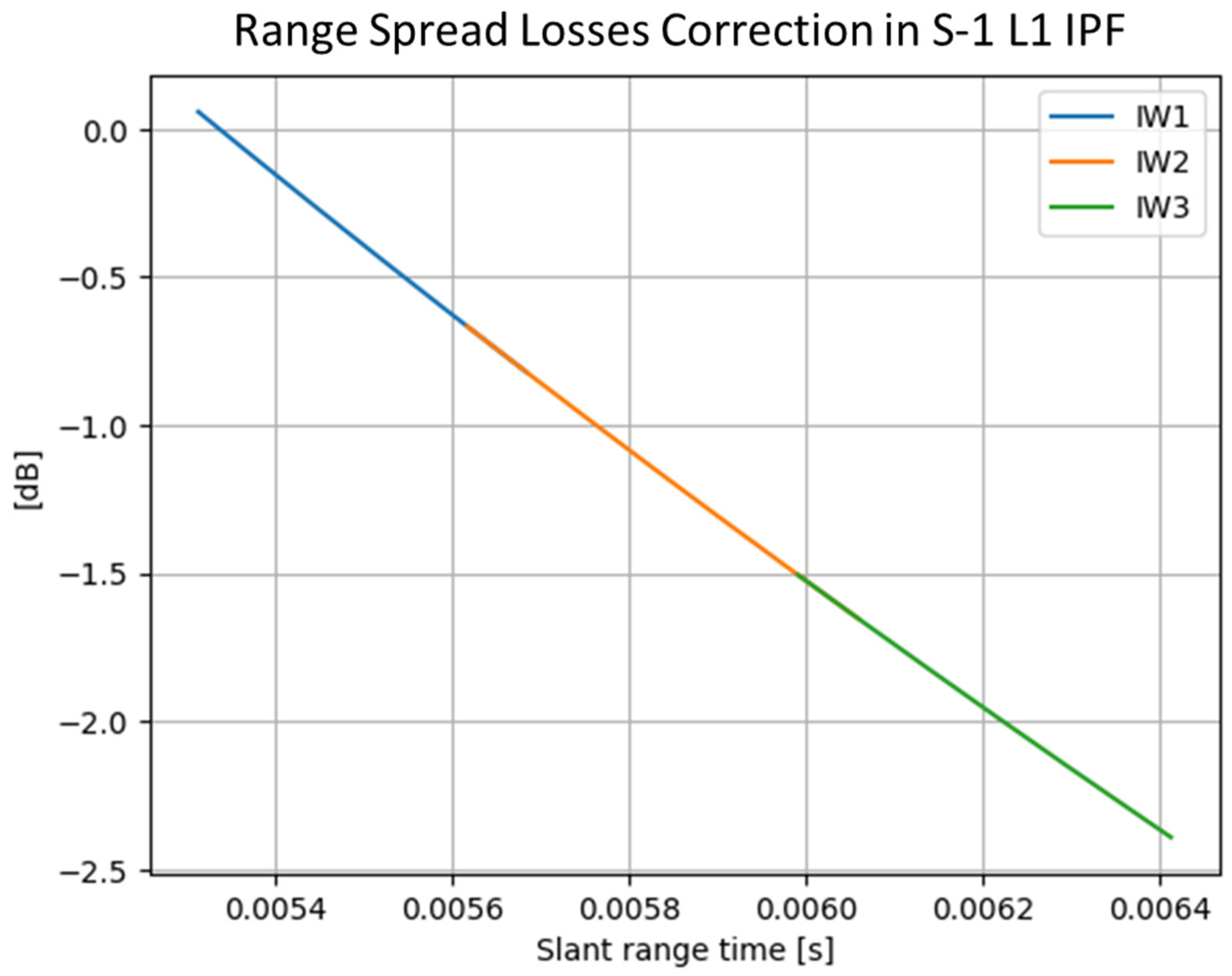
2.2.4. Spread Losses
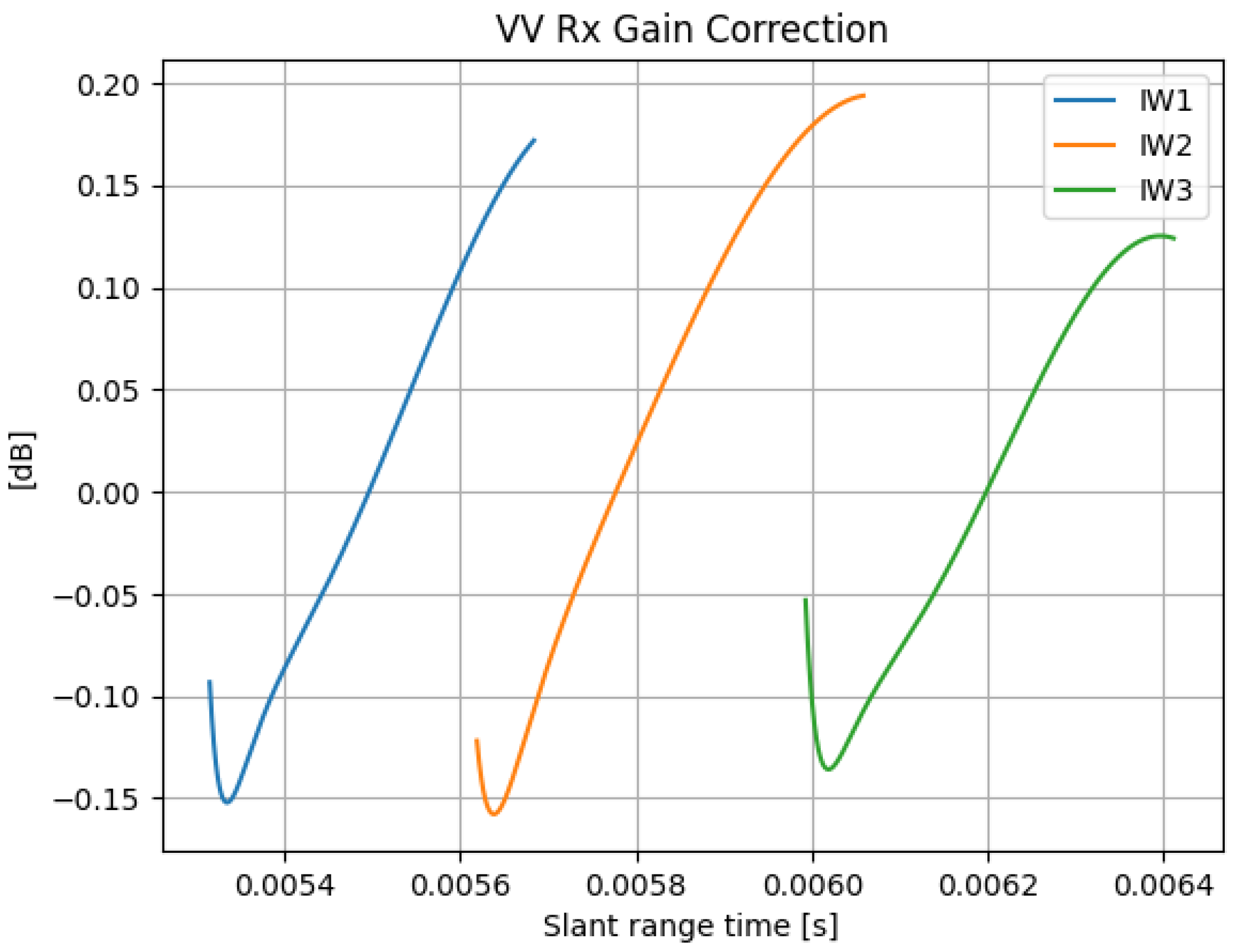
2.2.5. Processing Gain
2.2.6. Overall Processor Radiometric Corrections
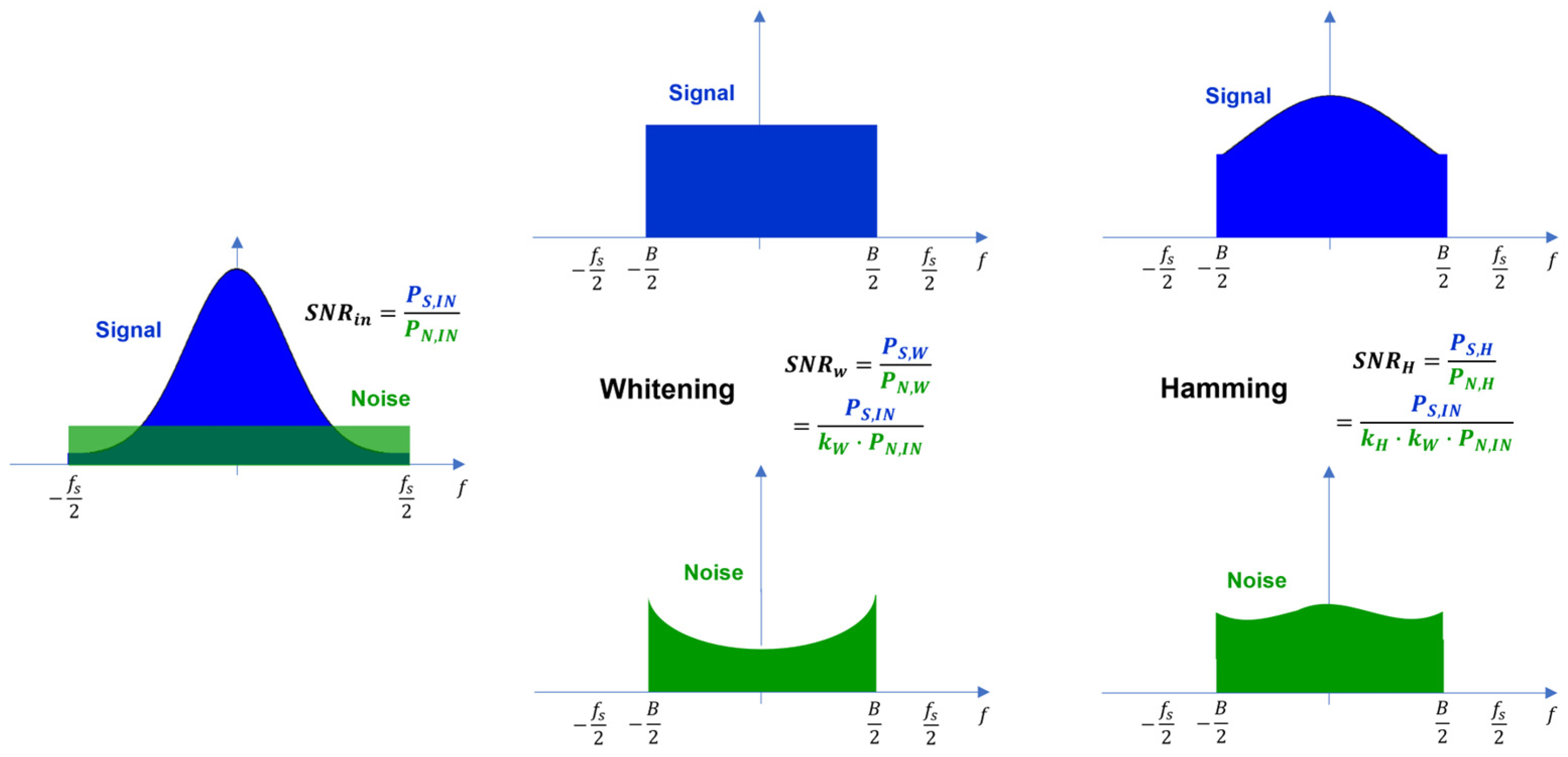
2.3. SAR Data De-Noising
2.3.1. De-Noising Vector Model
- Range compression.
- Azimuth compression.
- Range spectrum windowing.
- Doppler spectrum whitening and windowing.
- For TopSAR IW and EW modes with the deployment of IPF 2.82 on the 28 March 2017.
- For Stripmap and Wave modes with the deployment of IPF 2.90 on the 13 March 2018.
- is again the combination of all the radiometric corrections as reported in Equation (7).
- The factor is computed internally by the IPF and then applied to the de-noising vectors to ensure that they are correctly aligned to the noise level in the data for each L1 product (SLC and GRD with different resolution levels). This aspect is further discussed in Section 3.2.
- is the noise power measured from the noise pulses that are acquired at the begin (pre-amble) and at the end (post-amble) of each data acquisition process. Further details on this topic are provided in Section 2.3.2.
- is the noise calibration factor that is needed to align the de-noise vectors generated by IPF to the actual noise level measured in the data. for S-1 is empirically derived exploiting dedicated acquisitions over very low backscatter areas. The cross-polarization data of such acquisitions can be assumed to be signal-free; hence, they can be exploited for the derivation of the factor. The noise calibration procedure is discussed in Section 3.1.
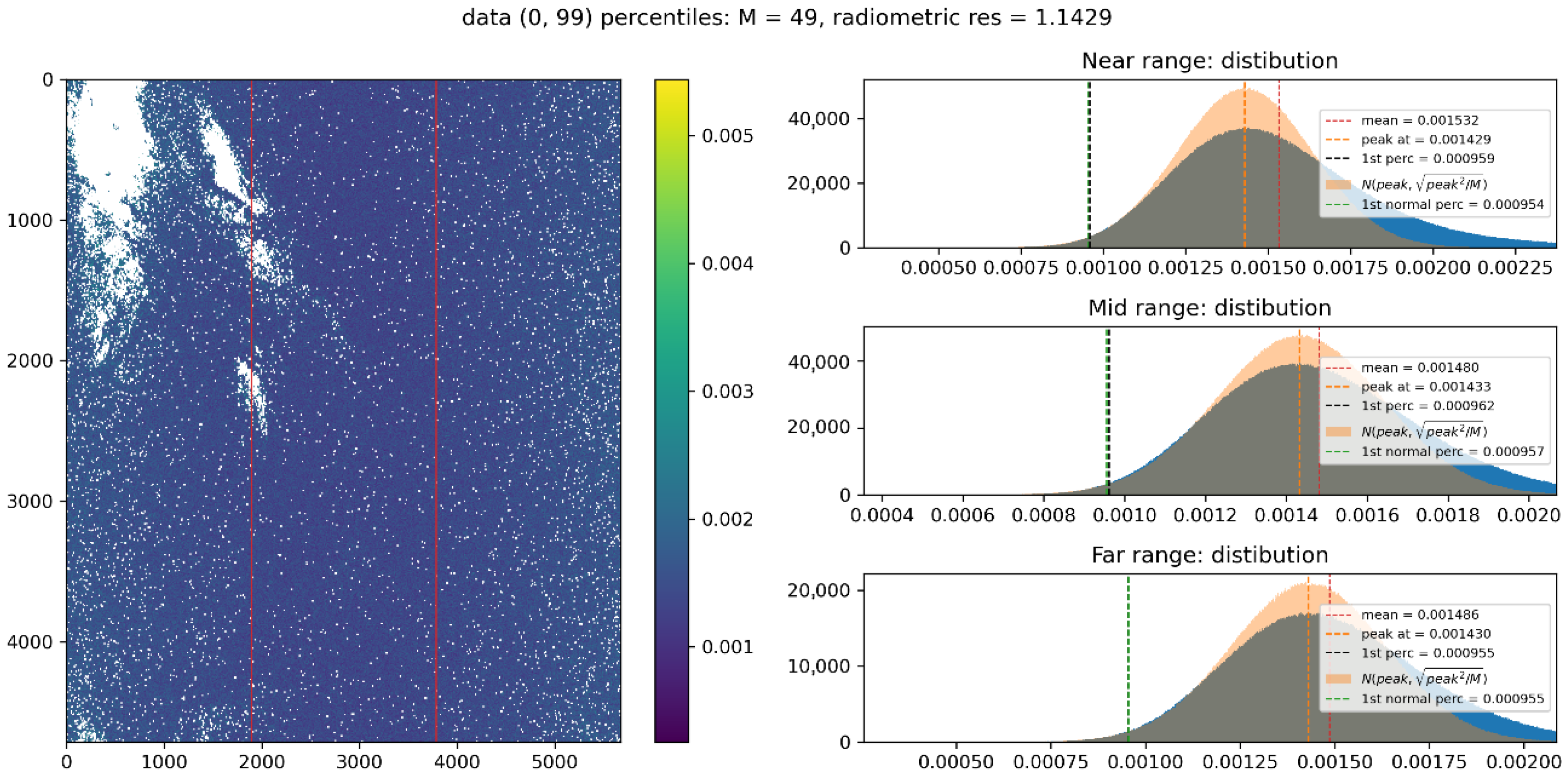
2.3.2. Noise Power from Noise Pulses
- Pre-amble: The initial part of the acquisition, including warmup echoes for instrument stabilization and noise and internal calibration pulses aimed at characterizing the instrument status.
- SAR imaging: The central part of the data acquisition, when SAR echoes are recorded according to the timeline of the current acquisition mode. Interleaved to the SAR echoes, calibration pulses are acquired for TopSAR, Wave and (optionally) for Stripmap modes. For S-1C and D, additional noise pulses for TopSAR and Wave modes will be acquired during the SAR imaging (see Section 3.1 for more details).
- Post-amble: The final part of the acquisition, including internal calibration and noise pulses.
- For the TopSAR IW mode, only rank echoes from even bursts (counting from the beginning of the data acquisition process) are kept, avoiding the noise-power fluctuations induced by the instrument.
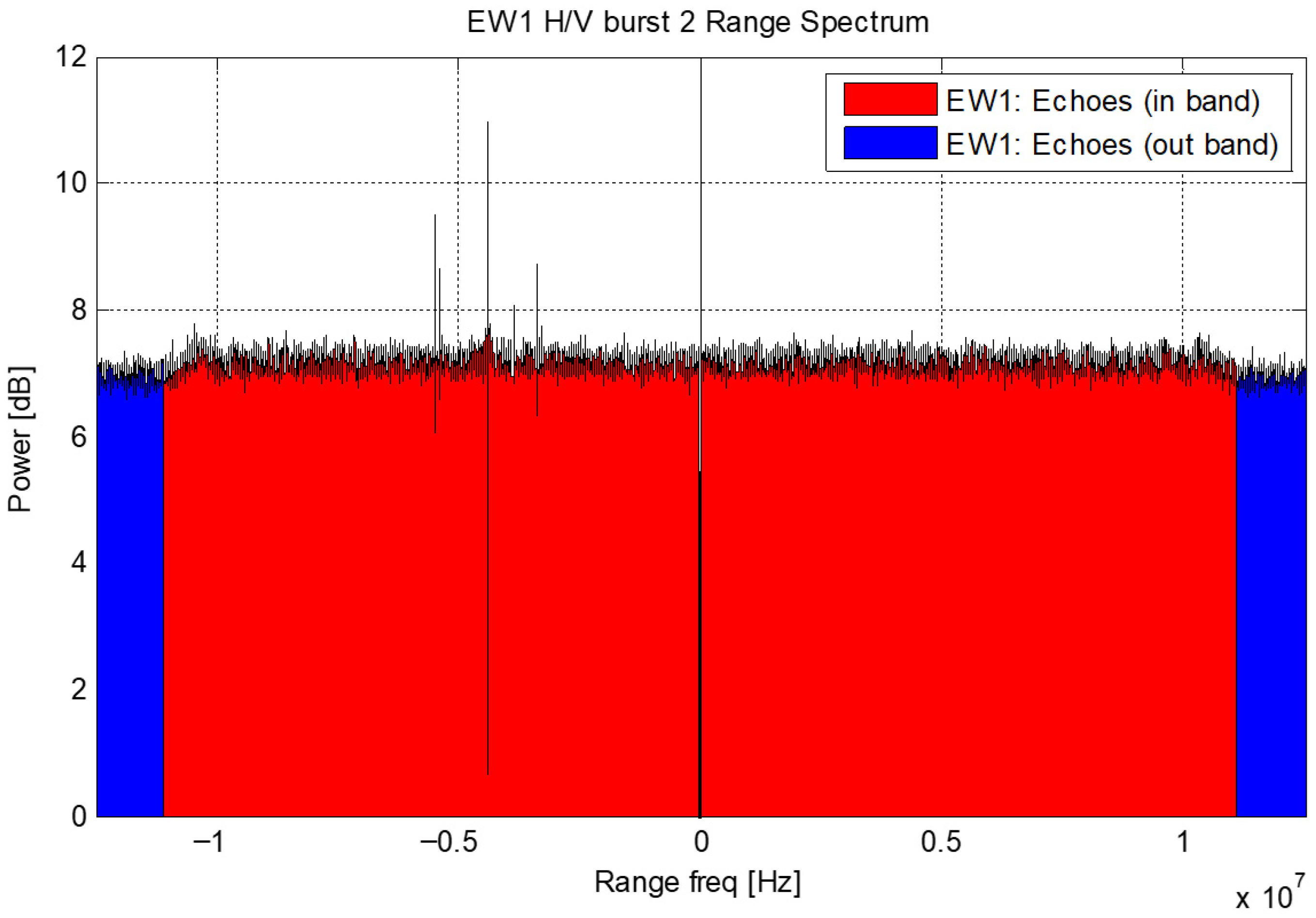
- For the TopSAR EW mode, the rank echoes from EW2 cannot be used since they contain the returns from Tx calibration pulses. The noise-power level is estimated from the rank echoes of EW3.
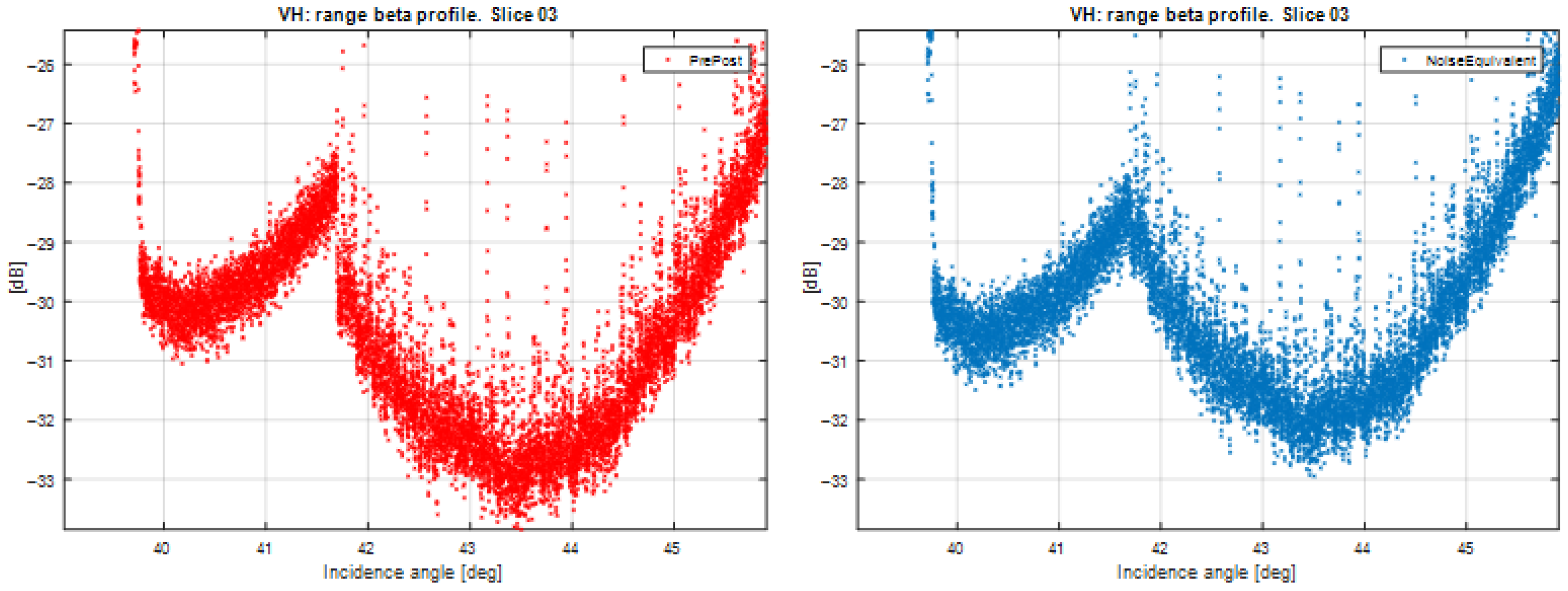
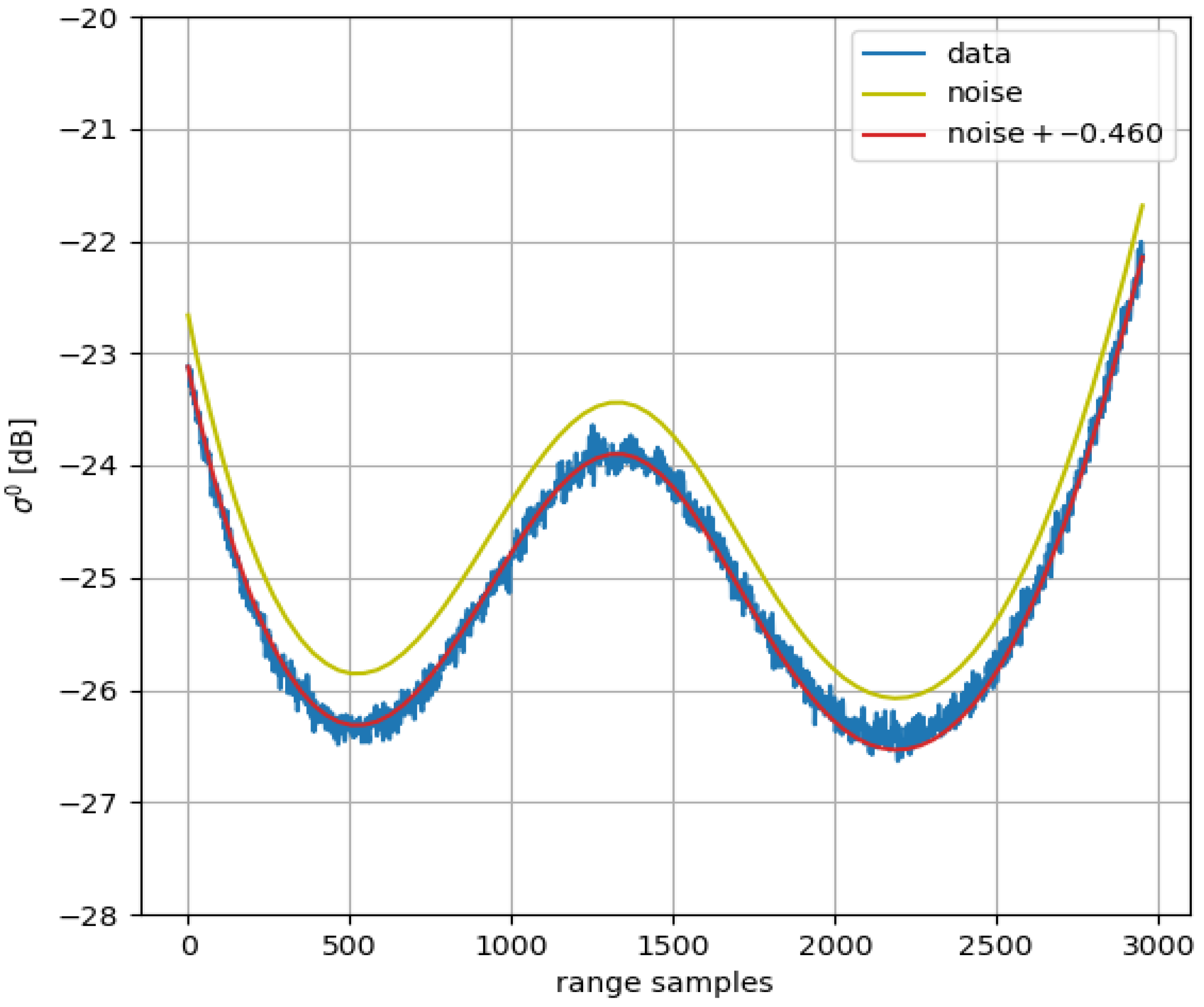
2.4. Calibration of Noise Vectors
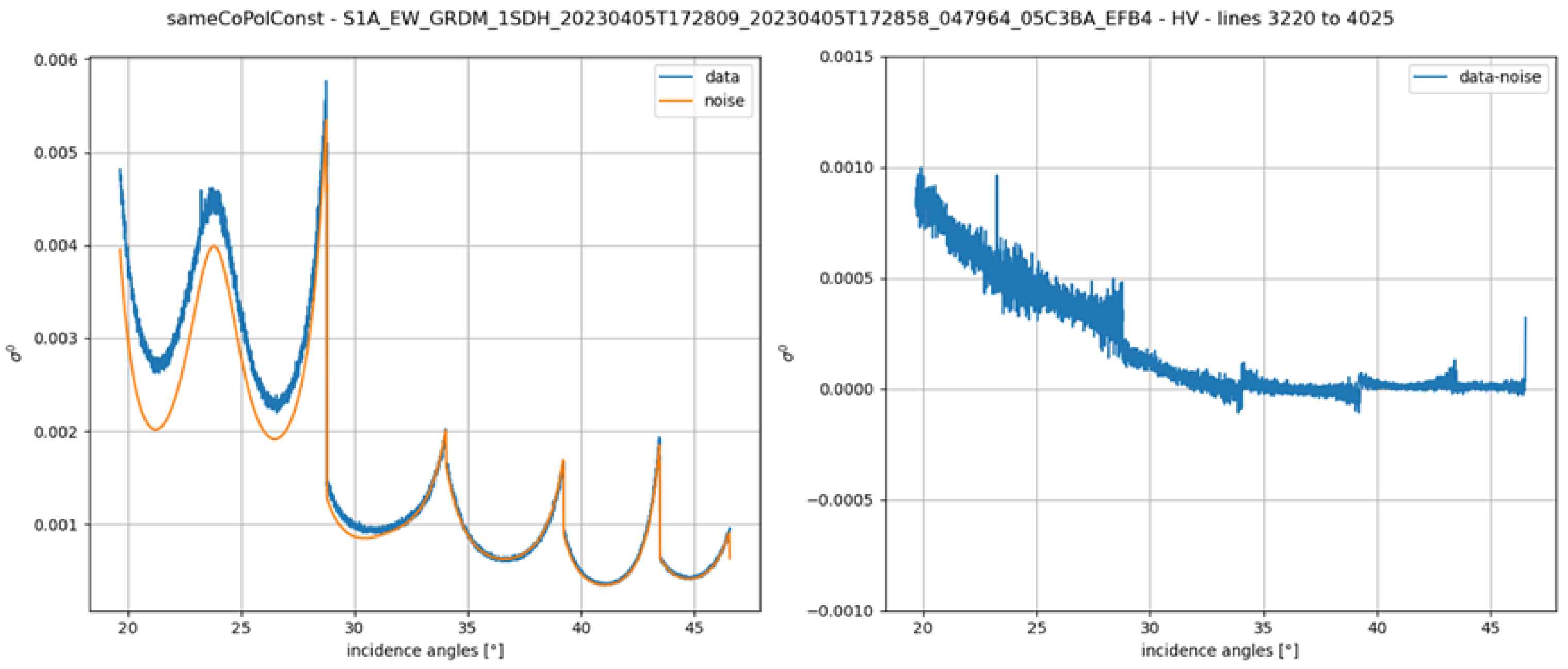
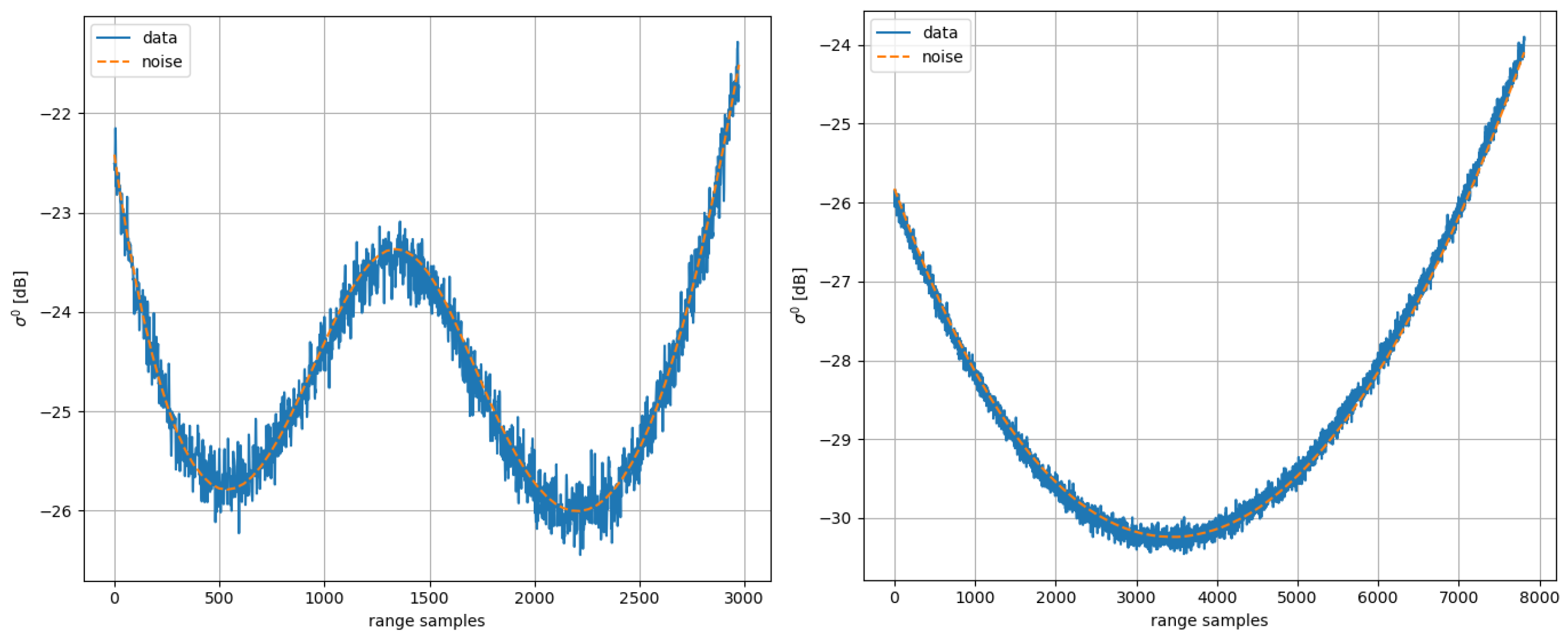
- The noise level is measured from each analyzed product.
- The noise calibration constant is computed by minimizing the distance between each noise profile and the corresponding noise vector annotated in the data.
3. Results
3.1. Validation of Noise-Vector Calibration Method
3.2. Noise-Vector Evolution in L1 IPF
- The azimuth variation in the noise vectors for TopSAR modes was introduced in March 2018 with IPF 2.9.0. This was introduced to account for the scalloping correction applied to the TopSAR bursts (see Section 2.2.3). The de-scalloping operation introduces an azimuth dependency of the noise level in TopSAR burst that was not captured by the original noise vectors, providing only the noise variation in the range direction.
- The usage of ranked echoes for noise-vector computation started with the deployment of IPF 2.9.1 on June 2018. As discussed in Section 2.3.2, this allowed for better tracking of the noise-power variation during the data acquisition.
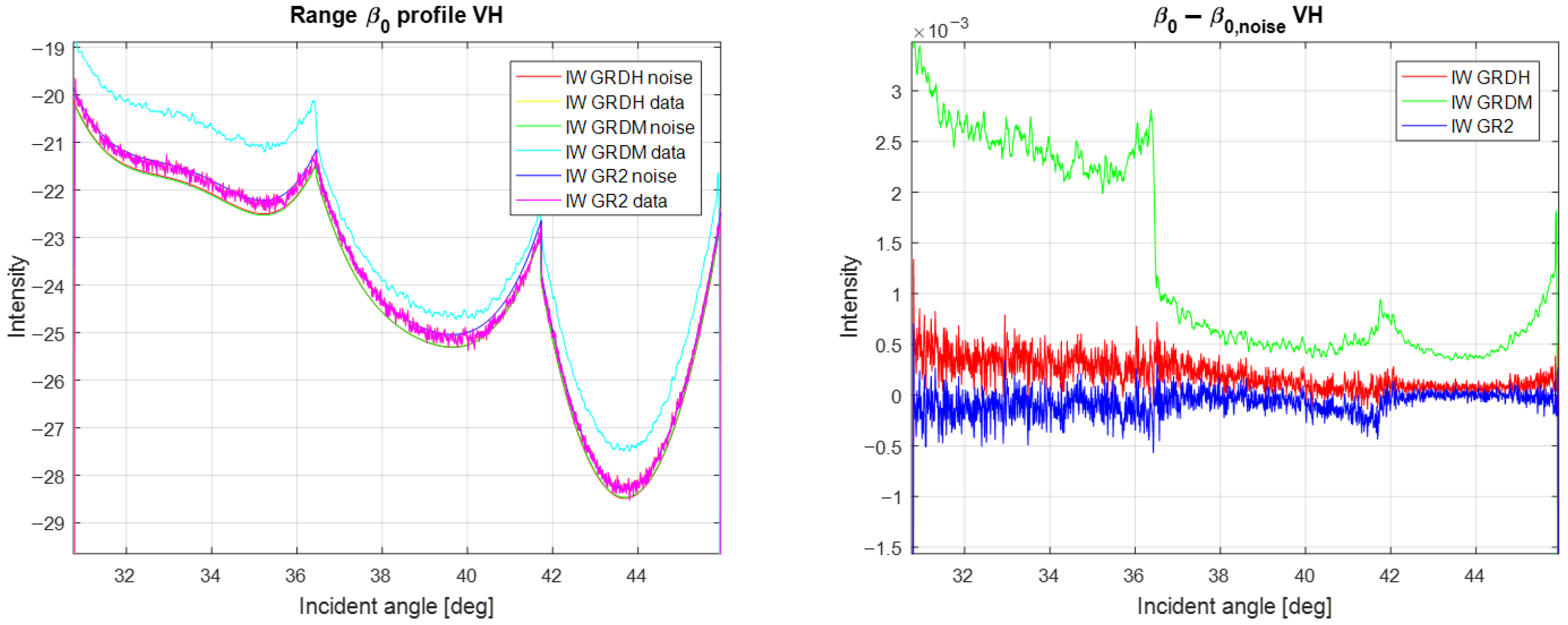
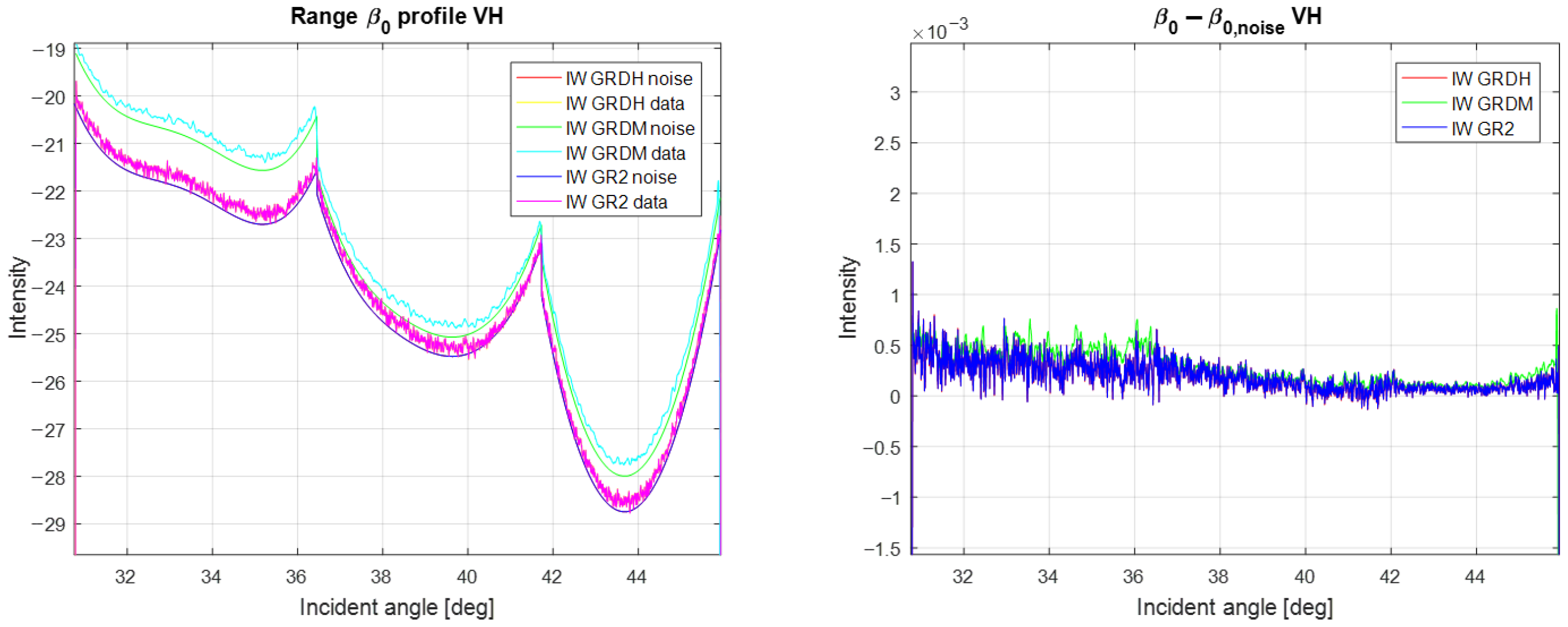
- The normalization of the noise vectors was introduced with IPF 3.1.0 in June 2019. Previously, the same noise vectors were annotated for all the product levels (SLC and GRD with different resolutions).
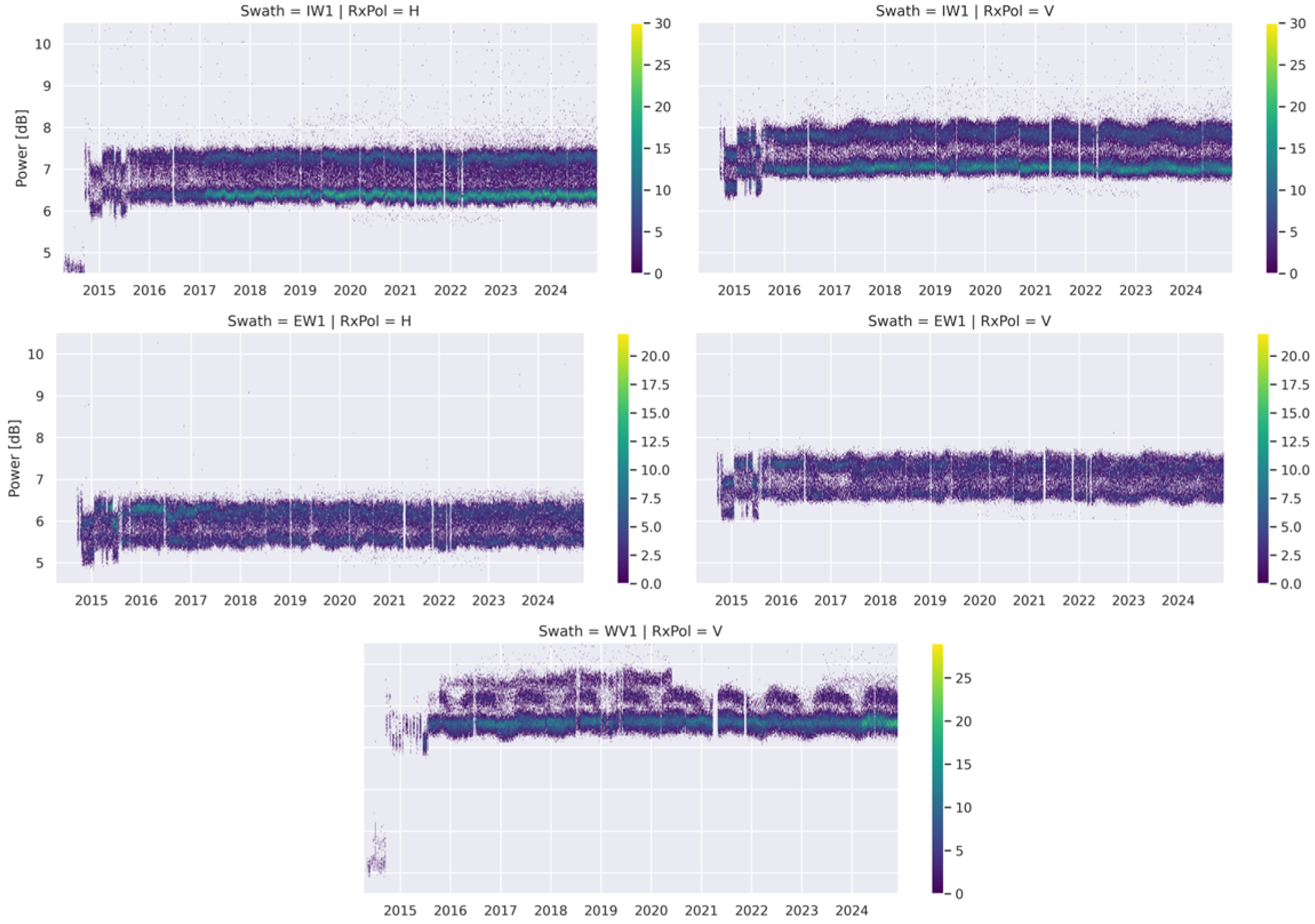
3.3. Re-Calibration of Noise Vectors
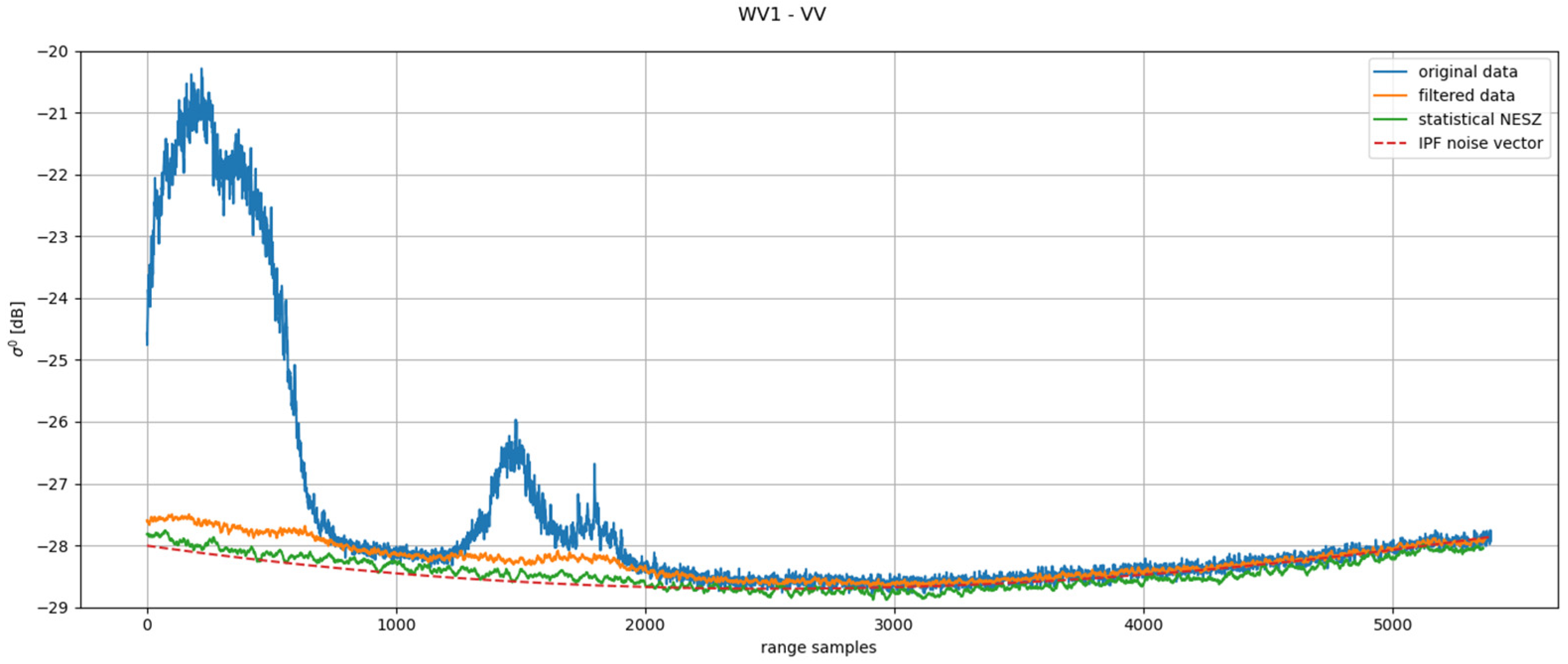
3.4. S-1 Data De-Noising Results
4. Discussion
4.1. Retro-Calibration of Noise Vectors
4.2. Auxiliary Noise Tools for S-1 Data Users
- A tool to generate the engineering products (L0N) that are needed to exploit ranked echoes for the de-noising of S-1A and S-1B products acquired before 2018.
- A tool to generate accurate de-noising vectors, starting from L1 product annotations and exploiting the updated algorithms and the latest calibration results reported in this paper. This second tool would allow for overcoming the limitations of the retro-calibration approach proposed in Section 4.2.
4.3. S-C/D Noise-Related Evolutions
- A slight modification to the instrument design that allowed for a reduction in the number of internal calibration pulses from 5 to 3 (see Section 2.2.1 for more details).
- The inclusion of an AIS receiver to enhance the ship detection capability of the mission. Please note that AIS functionality is independent from the SAR and does not have any impact on SAR data quality and on the thermal noise topic discussed in this paper.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Davidson, M.; Snoeij, P.; Attema, E.; Rommen, B.; Floury, N.; Levrini, G.; Duesmann, B. Sentinel-1 Mission Overview. In Proceedings of the 8th European Conference on Synthetic Aperture Radar (EUSAR), Aachen, Germany, 7–10 June 2010. [Google Scholar]
- Rostan, F.; Riegger, S.; Pitz, W.; Torre, A.; Torres, R. The C-SAR instrument for the GMES sentinel-1 mission. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007. [Google Scholar]
- De Zan, F.; Guarnieri, A.M. TOPSAR: Terrain Observation by Progressive Scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Miranda, N.; Rosich, B.; Putignano, C. The Sentinel-1 data processor and operational products. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 27 July 2012. [Google Scholar]
- Rosich, B.; Miranda, N.; Potin, P.; Putignano, C.; Sabella, G.; Geudtner, D. Sentinel-1 Ground Segment. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Hanssen, R.; Rocca, F. Sentinel 1: Interferometric applications. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Schmullius, C.; Cartus, O.; Riedel, T.; Santoro, M.; Thiel, C.; Christian, T. Thiel Sentinel-1 Land Applications based on Multi-temporal Data Acquisitions. In Proceedings of the 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June 2008. [Google Scholar]
- Loew, A.; Ludwig, R. Mauser Derivation of surface soil moisture from ENVISAT ASAR wide swath and image mode data in agricultural areas. IEEE Trans. Geosci. Remote. Sens. 2006, 44, 889–899. [Google Scholar] [CrossRef]
- Mouche, A.; Chapron, B.; Zhang, B. Husson Combined Co- and Cross-Polarized SAR Measurements Under Extreme Wind Conditions. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 6746–6755. [Google Scholar] [CrossRef]
- Snoeij, P.; Geudtner, D.; Østergaard, A.; Navas-Traver, I.; Brown, M.; Rommen, B.; Bibby, D.; Torres, R.; Schwerdt, M.; Zink, M.; et al. Sentinel-1 in-orbit calibration plan. In Proceedings of the 9th European Radar Conference, Amsterdam, The Netherlands, 31 October–2 November 2012. [Google Scholar]
- S1-PL-ASD-PL-0001; Sentinel 1 SAR Instrument Calibration and Characterisation Plan. Astrium: Friedrichshafen, Germany, 2014.
- Schmidt, K.; Schwerdt, M.; Miranda, N.; Reimann, J. Radiometric Comparison within the Sentinel-1 SAR Constellation over a Wide Backscatter Range. Remote Sens. 2020, 12, 854. [Google Scholar] [CrossRef]
- MPC-0307; Sentinel-1 Level 1 Detailed Algorithm Definition. SAR Mission Performance Center (MPC): Brest, France, 2022.
- Guccione, P.; Belotti, M.; Giudici, D.; Guarnieri, A.M.; Navas-Traver, I. Sentinel-1A: Analysis of FDBAQ Performance on Real Data. IEEE Trans. Geosci. Remote. Sens. 2015, 53, 6804–6812. [Google Scholar] [CrossRef]
- Recchia, A.; Giudici, D.; Piantanida, R.; Miranda, N.; Guarnieri, A.M. Sentinel-1 Radiometric Accuracy Enhancement Exploiting Antenna Model Refinement Technique. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6360–6363. [Google Scholar] [CrossRef]
- Schmidt, K.; Schwerdt, M.; Hajduch, G.; Vincent, P.; Recchia, A.; Pinheiro, M. Radiometric Re-Compensation of Sentinel-1 SAR Data Products for Artificial Biases due to Antenna Pattern Changes. Remote Sens. 2023, 15, 1377. [Google Scholar] [CrossRef]
- MPC-0677; Sentinel-1 Level-1 IPF Radiometric Corrections. SAR Mission Performance Center (MPC): Brest, France, 2024.
- MPC-0474; Sentinel-1 Level-0 Data Decoding Package. SAR Mission Performance Center (MPC): Brest, France, 2020.
- MPC-0392; Thermal Denoising of Products Generated by the S-1 IPF. SAR Mission Performance Center (MPC): Brest, France, 2017.
- SAR-MPC-0634; S-1 Annual Performance Report for 2023. SAR Mission Performance Center (MPC): Brest, France, 2024.
- Monti-Guarnieri, A.; Giudici, D.; Recchia, A. Identification of C-Band Radio Frequency Interferences from Sentinel-1 Data. Remote Sens. 2017, 9, 1183. [Google Scholar] [CrossRef]
- Korosov, A.; Demchev, D.; Miranda, N.; Franceschi, N.; Park, J.W. Thermal Denoising of Cross-Polarized Sentinel-1 Data in Interferometric and Extra Wide Swath Modes. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 5218411. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X.-M. Denoising Sentinel-1 Extra-Wide Mode Cross-Polarization Images Over Sea Ice. IEEE Trans. Geosci. Remote. Sens. 2021, 59, 2116–2131. [Google Scholar] [CrossRef]
- Lee, P.Q.; Xu, L.; Clausi, D.A. Sentinel-1 additive noise removal from cross-polarization extra-wide TOPSAR with dynamic least-squares. Remote. Sens. Environ. 2020, 248, 111982, ISSN 0034–4257. [Google Scholar] [CrossRef]
- Balss, U.; Breit, H.; Fritz, T. Noise-Related Radiometric Correction in the TerraSAR-X Multimode SAR Processor. IEEE Trans. Geosci. Remote. Sens. 2010, 48, 741–750. [Google Scholar] [CrossRef]








| Sub-Swath | Pol. | Proc. Gain [dB] | Pulse Length [μs] | Pulse Length [dB] | Total Gain [dB] |
|---|---|---|---|---|---|
| IW1 | VV | 120.01 | 52.41 | 0.00 | 120.01 |
| IW2 | VV | 119.63 | 62.00 | 0.73 | 120.36 |
| IW3 | VV | 119.73 | 53.39 | 0.08 | 119.81 |
| EW1 | HH | 121.58 | 30.34 | −2.37 | 119.21 |
| EW2 | HH | 122.95 | 25.78 | −3.07 | 119.88 |
| EW3 | HH | 122.42 | 30.34 | −2.37 | 120.05 |
| EW4 | HH | 122.97 | 26.34 | −2.98 | 119.99 |
| EW5 | HH | 121.94 | 30.66 | −2.32 | 119.62 |
| Unit | Calibration Constant |
|---|---|
| S-1A | 1.0 |
| S-1B | 1.393 |
| S-1C | 0.899 |
| S-1D | To be determined during the S1D Commissioning Phase |
| IPF Version | Start Operation Date | Updates |
|---|---|---|
| 2.8.2 | 28 March 2017 | Radiometric normalization of the TOPS processor. |
| 2.9.0 | 13 March 2018 | Radiometric normalization of the Stripmap and Wave processor. Update for noise-vector annotations to include azimuth antenna element patterns. |
| 2.9.1 | 26 June 2018 | Activation of the ranked-echo usage for noise-power estimation. |
| 3.1.0 | 26 June 2019 | Consistent noise-level annotation for all the L1 products (SLC, GRDM, GRDH, GR2). |
| 3.3.1 | 30 June 2020 | Fixed a failure in the NRT Slicing mode on EW products when pre-amble and/or post-amble are missing in L0N products. |
| 3.4.0 | 4 November 2021 | Discarded last EW ranked echo from noise-power estimation as it may be contaminated by nadir returns. Introduction of the in–out-band power ratio annotation. |
| 3.5.1 | 23 March 2022 | Correction of the misalignment between the elevation antenna pattern and the annotated thermal noise vector. |
| 3.6.1 | 30 March 2023 | Introduction of annotation in the manifest of L0 A/C/N products used during the processing. Avoid missing data in range de-noising vectors for TOPS GRD products on long data takes. |
| 3.7.1 | 19 October 2023 | Improvement of noise-vector quality when noise pulses are affected by RFI contamination. Fixing of a bug in the indexing of noise vectors in TOPS/SLC products. |
| Mode | Sub-Swath | Rx Polarization | Noise Calibration Constant Update [dB] |
|---|---|---|---|
| IW | IW1 | V | 0.095 |
| IW2 | −0.026 | ||
| IW3 | 0.323 | ||
| IW1 | H | 0.107 | |
| IW2 | 0.003 | ||
| IW3 | 0.208 | ||
| EW | EW1 | V | 0.035 |
| EW2 | −0.131 | ||
| EW3 | −0.038 | ||
| EW4 | 0.161 | ||
| EW5 | 0.035 | ||
| EW1 | H | −0.469 | |
| EW2 | −0.707 | ||
| EW3 | −0.730 | ||
| EW4 | −0.393 | ||
| EW5 | −0.421 |
| Mode | Sub-Swath | Rx Polarization | Noise Calibration Constant Update [dB] |
|---|---|---|---|
| IW | IW1 | V | −0.178 |
| IW2 | −0.352 | ||
| IW3 | −0.071 | ||
| IW1 | H | −0.040 | |
| IW2 | −0.024 | ||
| IW3 | 0.133 | ||
| EW | EW1 | V | −0.321 |
| EW2 | −0.677 | ||
| EW3 | −0.554 | ||
| EW4 | −0.344 | ||
| EW5 | −0.425 | ||
| EW1 | H | - | |
| EW2 | - | ||
| EW3 | - | ||
| EW4 | - | ||
| EW5 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Recchia, A.; Mai, B.; Fioretti, L.; Piantanida, R.; Steinisch, M.; Franceschi, N.; Hajduch, G.; Vincent, P.; Pinheiro, M.; Miranda, N.; et al. Generating Accurate De-Noising Vectors for Sentinel-1: 10 Years of Continuous Improvements. Remote Sens. 2025, 17, 3474. https://doi.org/10.3390/rs17203474
Recchia A, Mai B, Fioretti L, Piantanida R, Steinisch M, Franceschi N, Hajduch G, Vincent P, Pinheiro M, Miranda N, et al. Generating Accurate De-Noising Vectors for Sentinel-1: 10 Years of Continuous Improvements. Remote Sensing. 2025; 17(20):3474. https://doi.org/10.3390/rs17203474
Chicago/Turabian StyleRecchia, Andrea, Beatrice Mai, Laura Fioretti, Riccardo Piantanida, Martin Steinisch, Niccolò Franceschi, Guillaume Hajduch, Pauline Vincent, Muriel Pinheiro, Nuno Miranda, and et al. 2025. "Generating Accurate De-Noising Vectors for Sentinel-1: 10 Years of Continuous Improvements" Remote Sensing 17, no. 20: 3474. https://doi.org/10.3390/rs17203474
APA StyleRecchia, A., Mai, B., Fioretti, L., Piantanida, R., Steinisch, M., Franceschi, N., Hajduch, G., Vincent, P., Pinheiro, M., Miranda, N., & Valentino, A. (2025). Generating Accurate De-Noising Vectors for Sentinel-1: 10 Years of Continuous Improvements. Remote Sensing, 17(20), 3474. https://doi.org/10.3390/rs17203474







