Analysis of GNSS Precipitable Water Vapor and Its Gradients During a Rainstorm in North China in July 2023
Abstract
Highlights
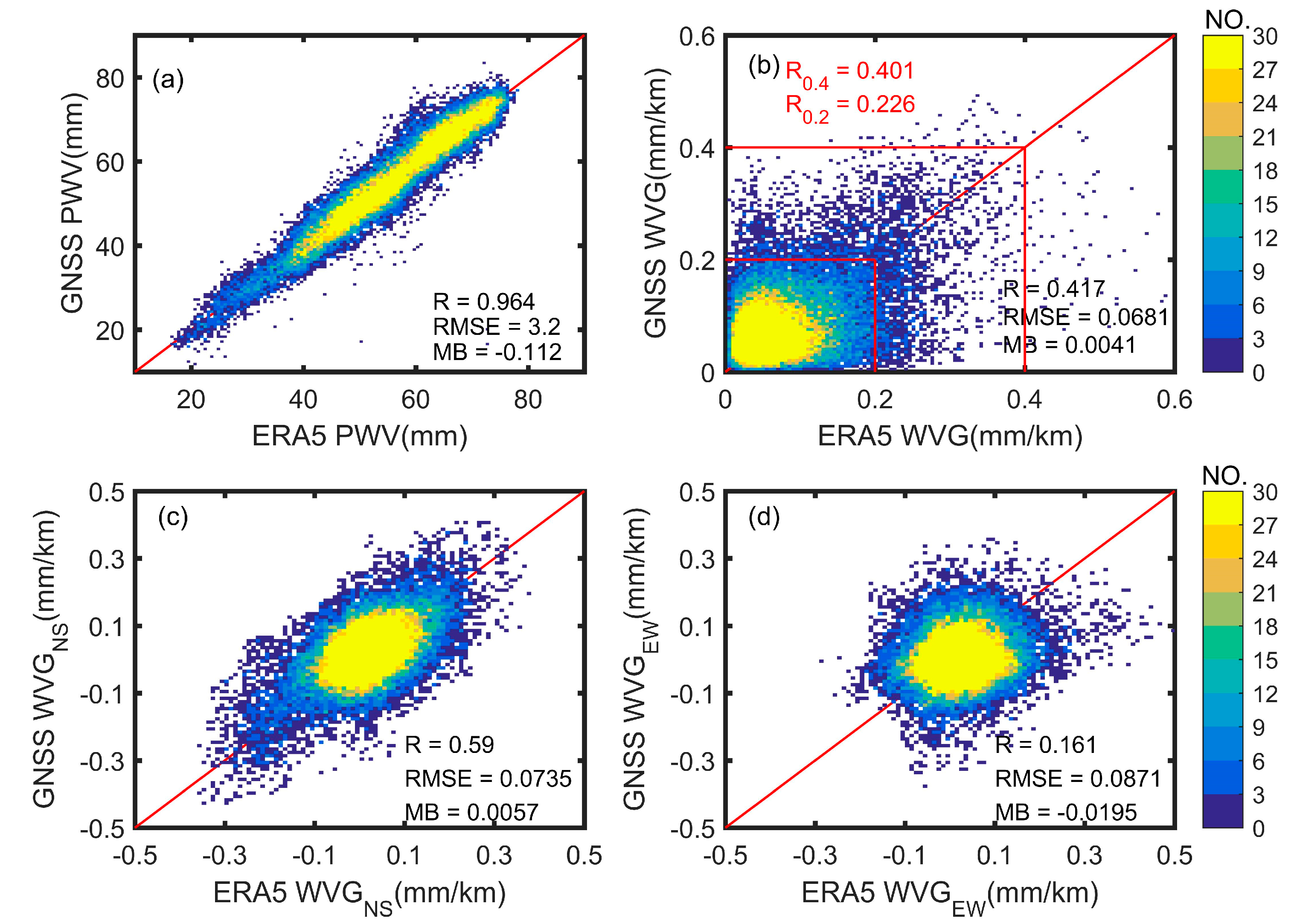
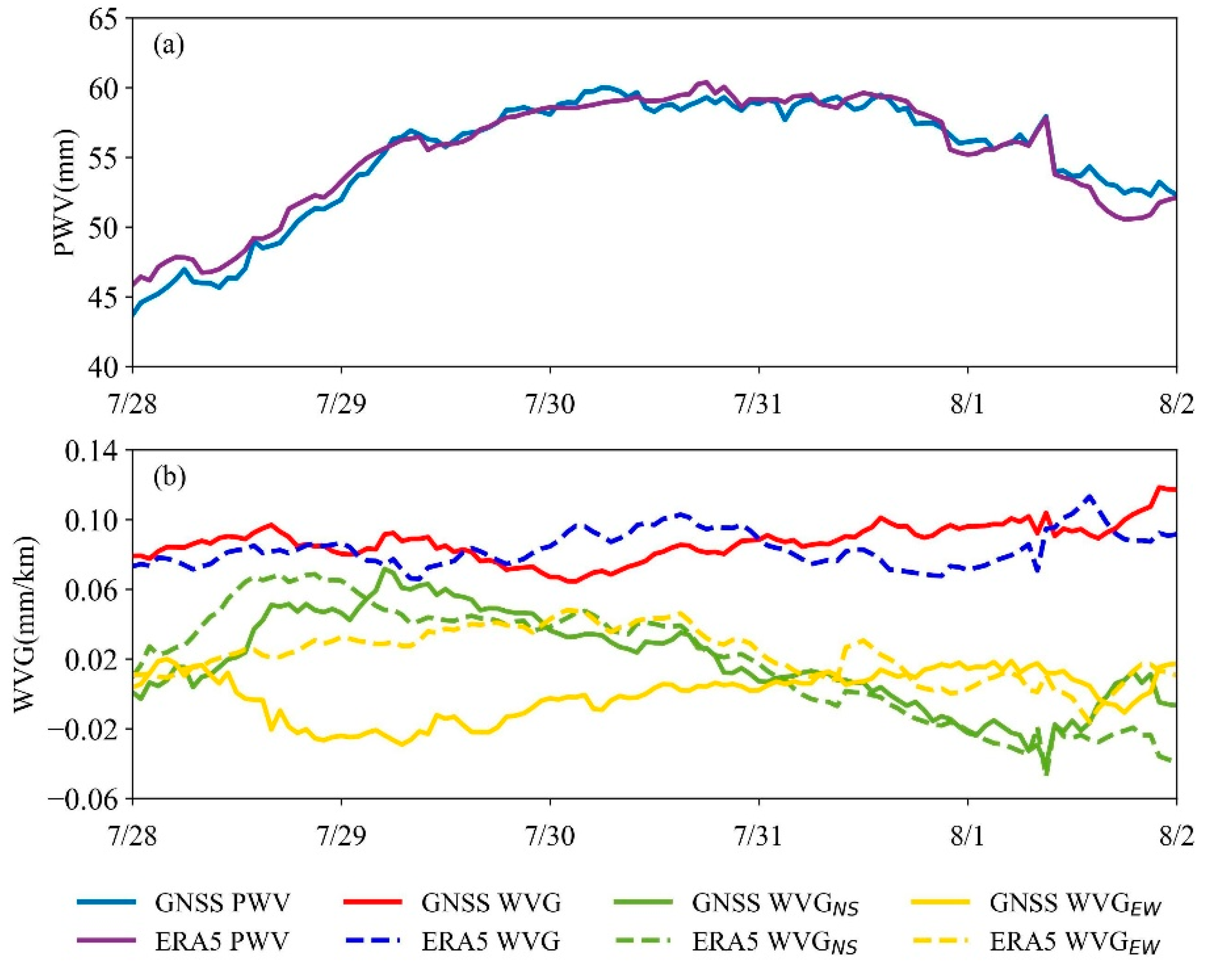
- Water vapor gradient (WVG) retrieval based on GNSS tropospheric parameters can effectively reflect the non-uniformity of water vapor per unit area at the station.
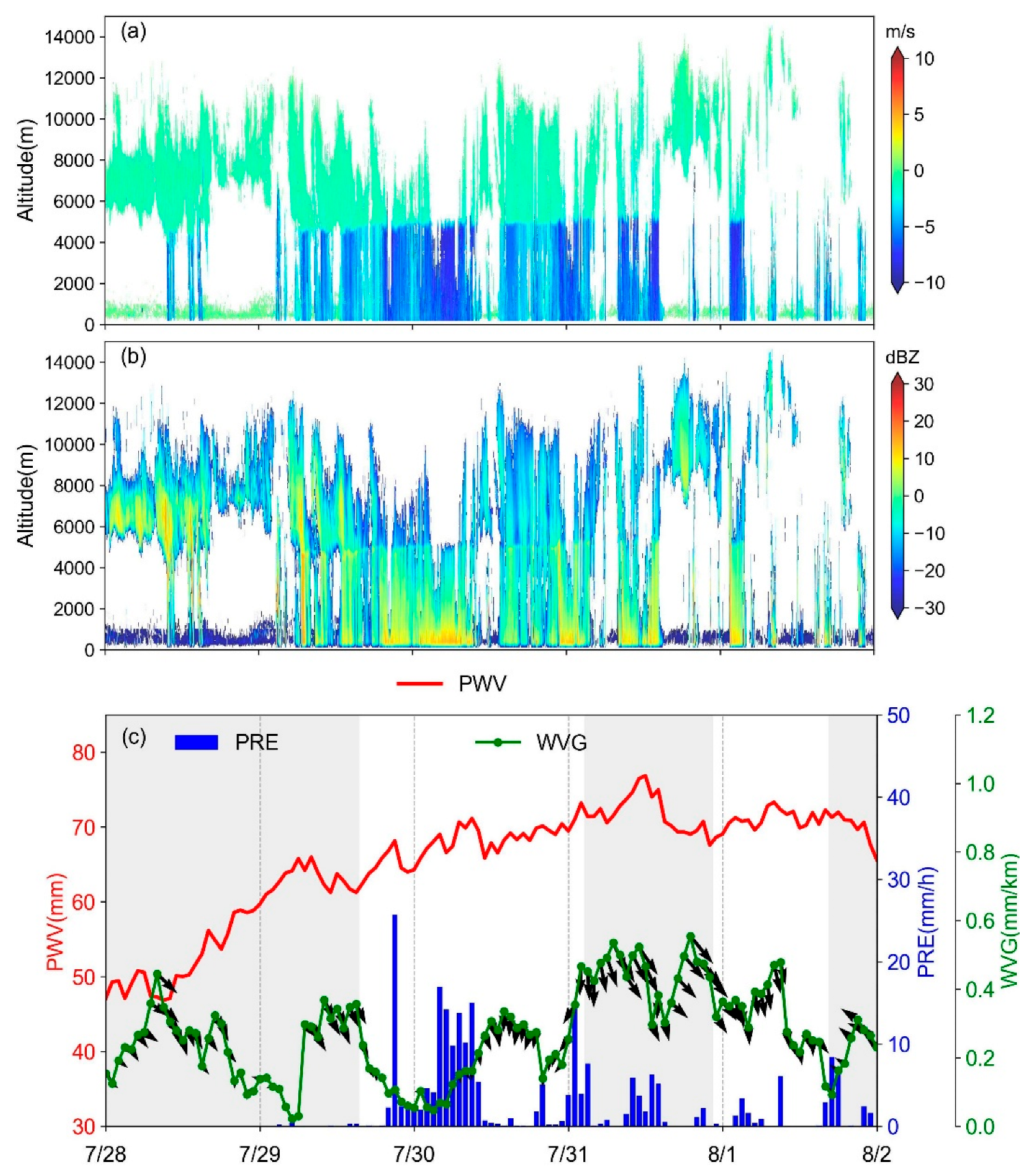
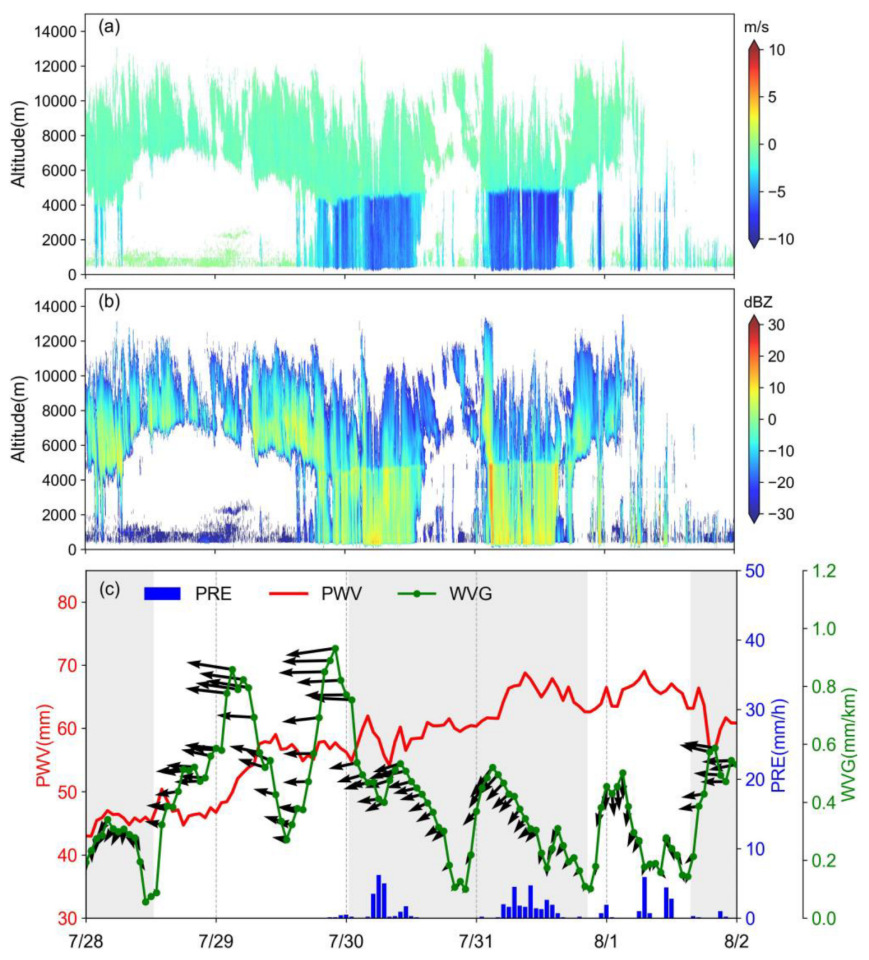
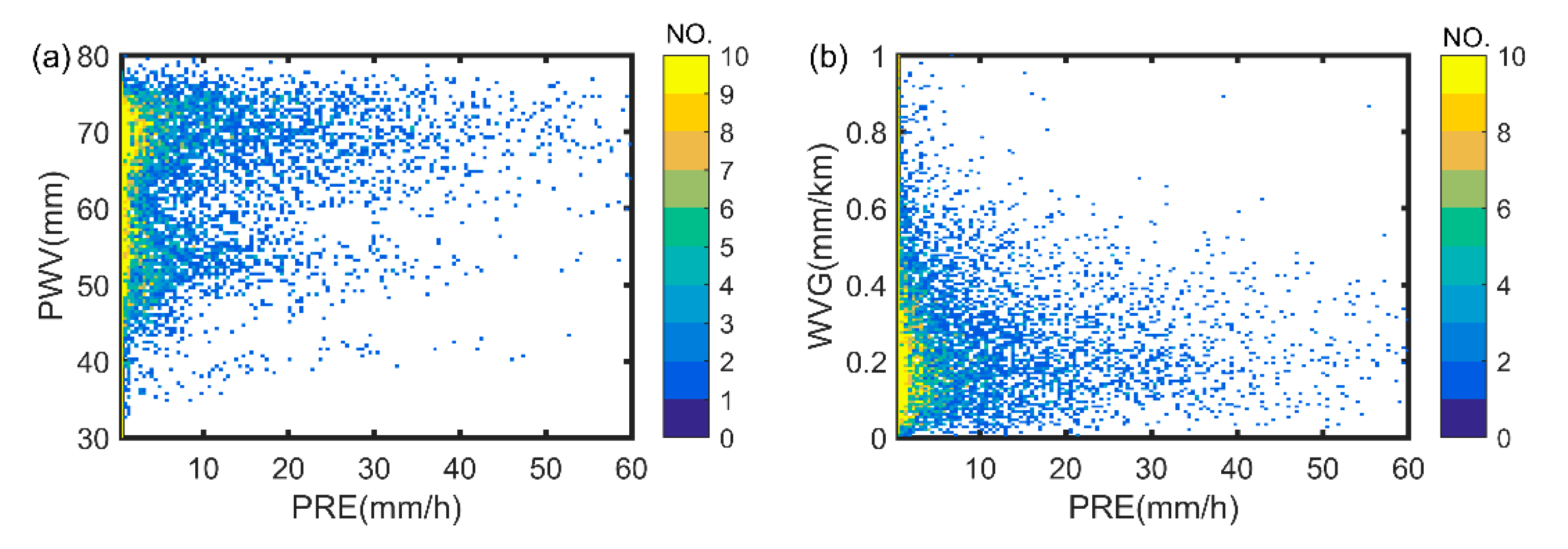
- When PWV is high (>60 mm) and WVG convergence is observed, radar reflectivity is significantly strong, and the precipitation occurs at the frontline of the big gradients and the convergence region.
- In case of a large PWV accompanied by plummeting WVG (down to 0.1–0.4 mm/km), large or persistent precipitation occurs.
- GNSS PWV and WVG can be key indicators for short-range weather forecasting of extreme rainstorm events.
Abstract
1. Introduction
2. Background
3. Data and Methods
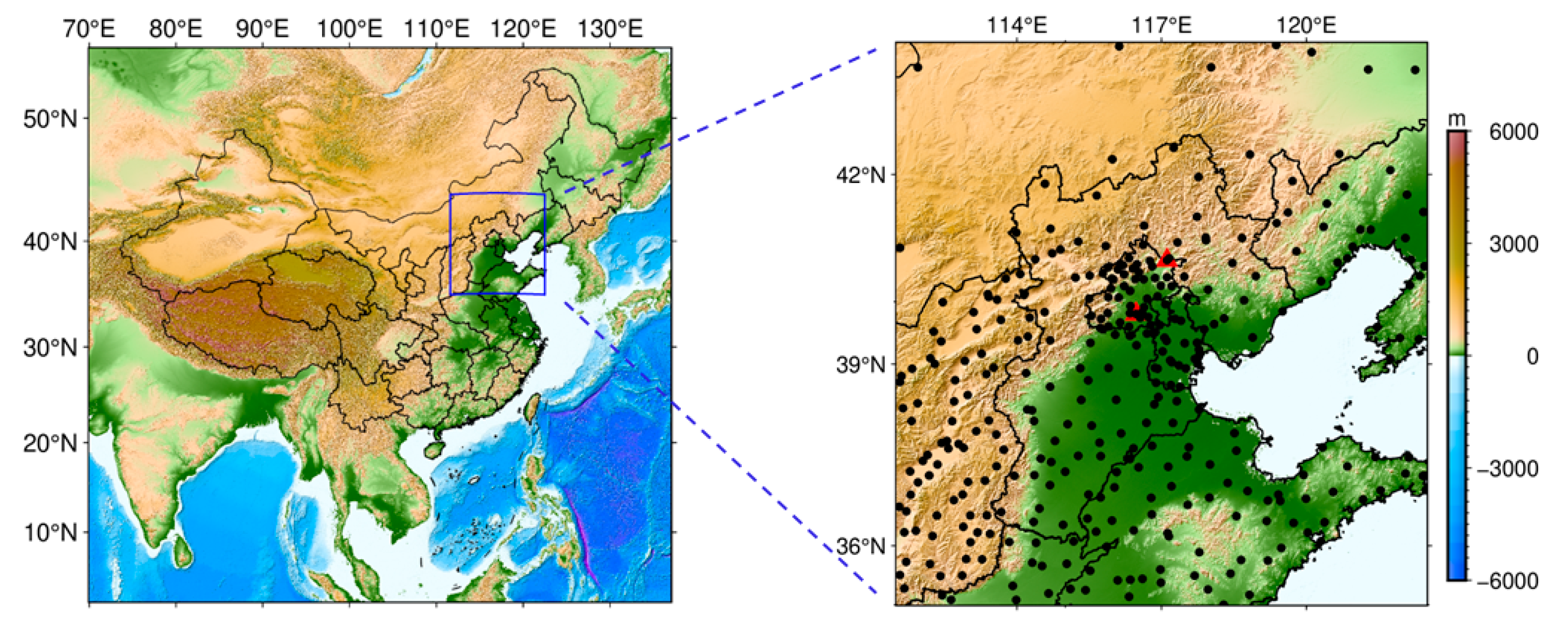
3.1. Data
3.2. Methods
3.2.1. Precipitable Water Vapor
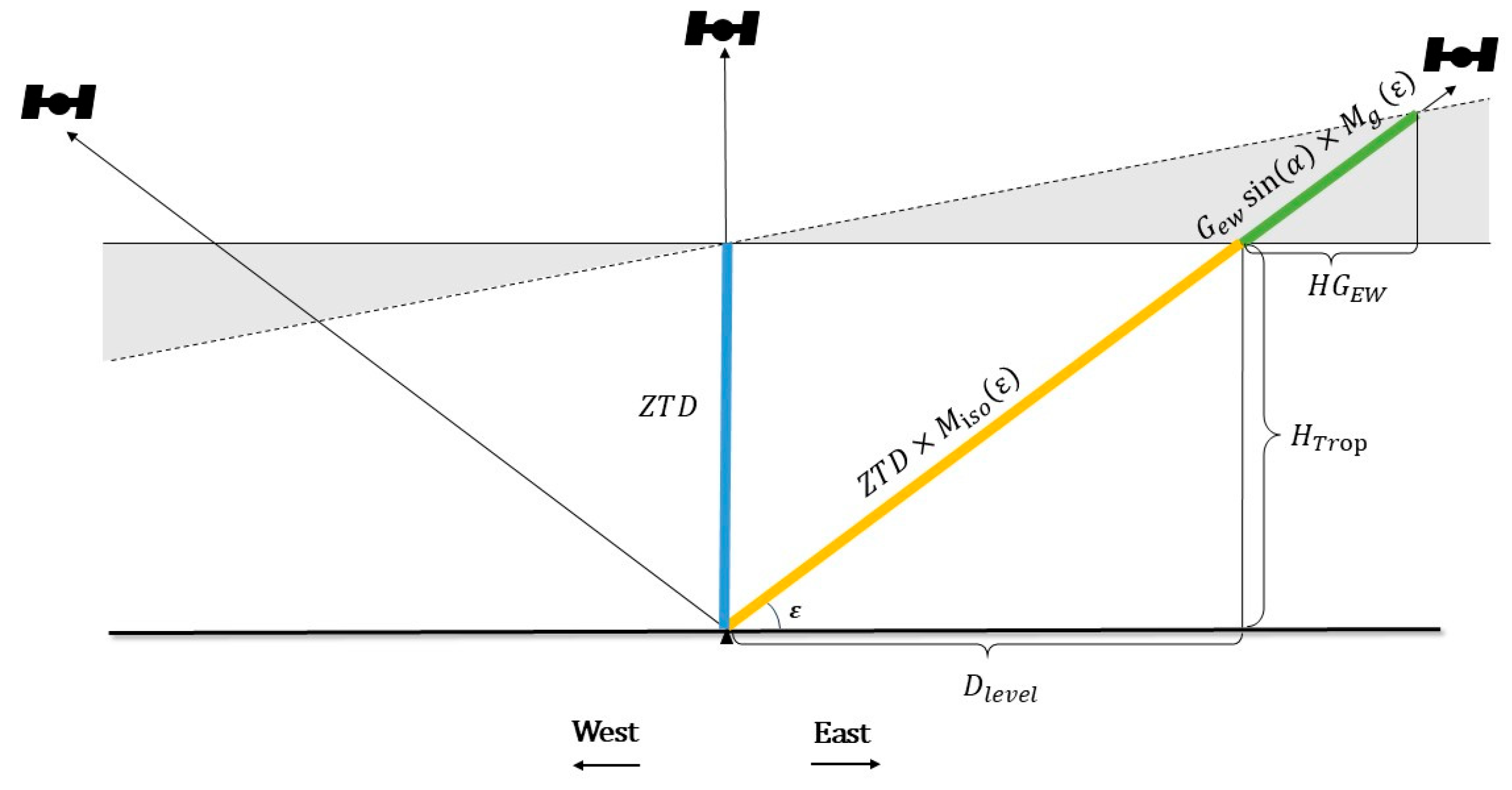
3.2.2. Water Vapor Gradients
4. Results and Discussion
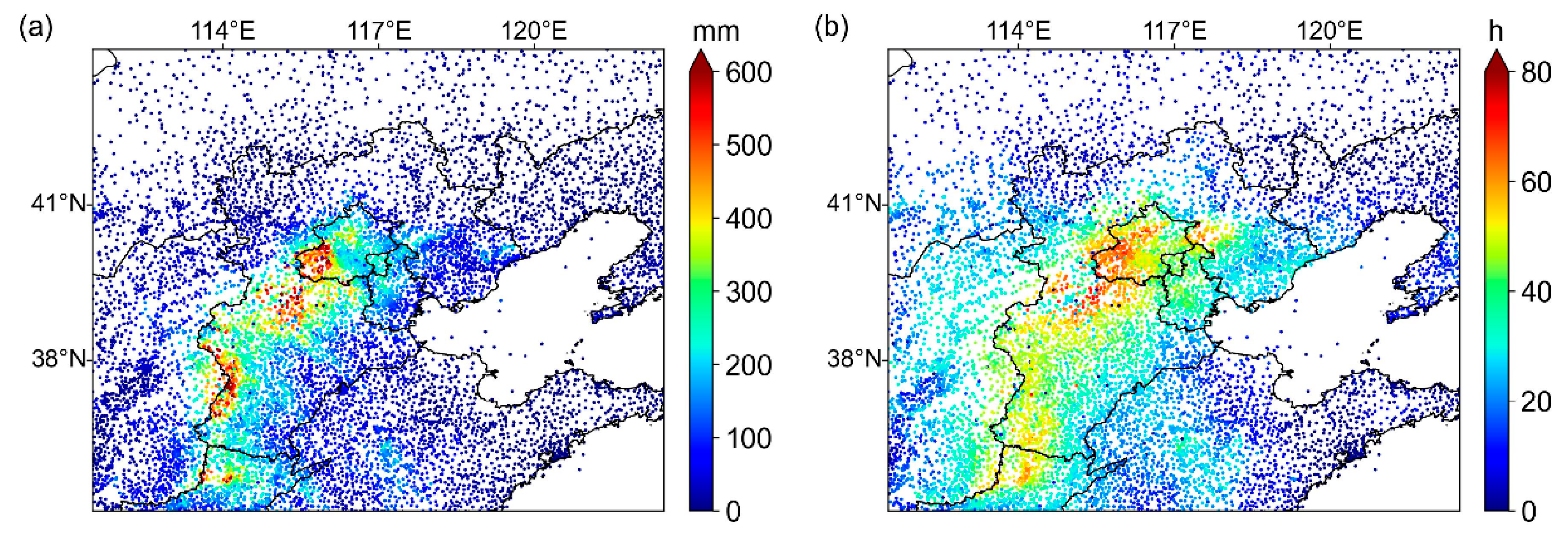
4.1. Data Validation
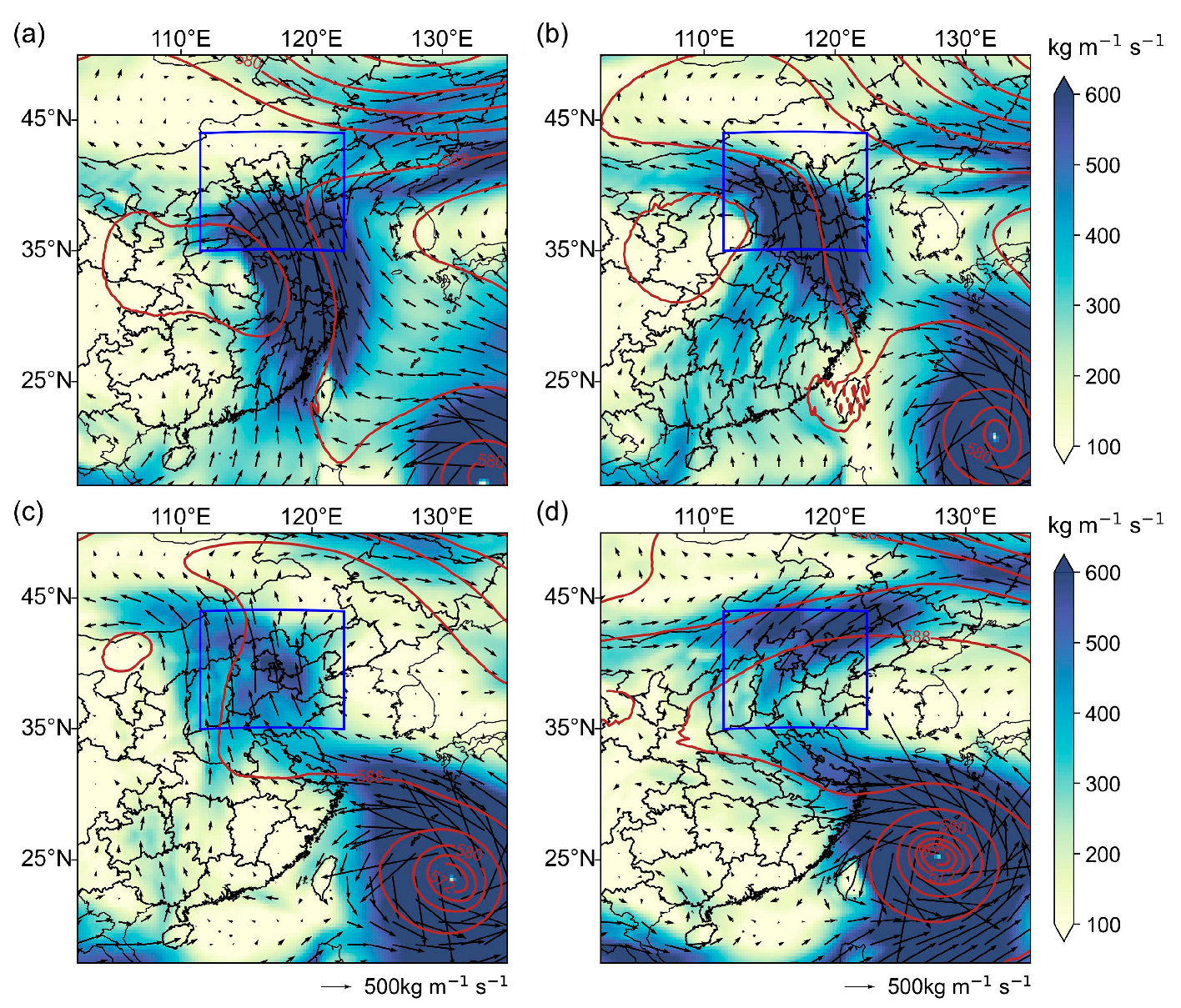
4.2. Spatial Distribution Analysis
4.3. Temporal Distribution Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, Z.; Wang, Z.; Peng, M. Impacts of climate trends on the heavy precipitation event associated with Typhoon Doksuri in Northern China. Atmospheric Res. 2025, 314, 107816. [Google Scholar] [CrossRef]
- Chen, S.; Kuo, Y.; Wang, W.; Tao, Z.; Cui, B. A Modeling Case Study of Heavy Rainstorms along the Mei-Yu Front. Mon. Weather. Rev. 1998, 126, 2330–2351. [Google Scholar] [CrossRef]
- Duan, J.; Bevis, M.; Fang, P.; Bock, Y.; Chiswell, S.; Businger, S.; Rocken, C.; Solheim, F.; van Hove, T.; Ware, R.; et al. Gps Meteorology: Direct Estimation of the Absolute Value of Precipitable Water. J. Appl. Meteorol. 1996, 35, 830–838. [Google Scholar] [CrossRef]
- Brettle, M.; Galvin, J. Back to Basics: Radiosondes: Part 1–The Instrument. Weather 2003, 58, 336–341. [Google Scholar] [CrossRef]
- Kaufman, Y.; Gao, B. Remote Sensing of Water Vapor in the near Ir from Eos/Modis. IEEE Trans Geosci. Remote Sens. 1992, 30, 871–884. [Google Scholar] [CrossRef]
- Zhou, L.; Fan, L.; Zhang, W.; Shi, C. Long-term correlation analysis between monthly precipitable water vapor and precipitation using GPS data over China. Adv. Space Res. 2022, 70, 56–69. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.; Rocken, C.; Anthes, R.; Ware, R. Gps Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Rocken, C.; Hove, T.; Johnson, J.; Solheim, F.; Ware, R.; Bevis, M.; Chiswell, S.; Businger, S. Gps/Storm—Gps Sensing of Atmospheric Water Vapor for Meteorology. J. Atmos. Ocean. Technol. 1995, 12, 468–478. [Google Scholar] [CrossRef]
- Seidel, D.; Berger, F.; Diamond, H.; Dykema, J.; Goodrich, D.; Immler, F.; Murray, W.; Peterson, T.; Sisterson, D.; Sommer, M.; et al. Reference Upper-Air Observations for Climate: Rationale, Progress, and Plans. Bull. Am. Meteorol. Soc. 2009, 90, 361–369. [Google Scholar] [CrossRef]
- Sosa, C. Evaluating Forecast Skills of Moisture from Convective-Permitting Wrf-Arw Model During 2017 North American Monsoon Season. Atmosphere 2019, 10, 694. [Google Scholar]
- Eriksson, D.; MacMillan, D.; Gipson, J. Tropospheric Delay Ray Tracing Applied in Vlbi Analysis. J. Geophys. Res. Solid Earth 2014, 119, 9156–9170. [Google Scholar] [CrossRef]
- Shoji, Y. Retrieval of Water Vapor Inhomogeneity Using the Japanese Nationwide Gps Array and Its Potential for Prediction of Convective Precipitation. J. Meteorol. Soc. Jpn. 2013, 91, 43–62. [Google Scholar] [CrossRef]
- Tu, M.; Zhang, W.; Bai, J.; Wu, D.; Liang, H.; Lou, Y. Spatio-Temporal Variations of Precipitable Water Vapor and Horizontal Tropospheric Gradients from Gps During Typhoon Lekima. Remote Sens. 2021, 13, 4082. [Google Scholar] [CrossRef]
- Nykiel, G.; Figurski, M.; Bałdysz, Z. Analysis of Gnss Sensed Precipitable Water Vapour and Tropospheric Gradients During the Derecho Event in Poland of 11th August 2017. J. Atmos. Solar-Terr. Phys. 2019, 193, 105082. [Google Scholar] [CrossRef]
- Zus, F.; Douša, J.; Kačmařík, M.; Václavovic, P.; Dick, G.; Wickert, J. Estimating the Impact of Global Navigation Satellite System Horizontal Delay Gradients in Variational Data Assimilation. Remote Sens. 2018, 11, 41. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, S.; Hu, Y.; Gong, Y.; Qing, H. Water vapor characteristics of the July 2023 severe torrential rain in North China. Meteorol. Mon. 2023, 49, 1421–1434. (In Chinese) [Google Scholar]
- Chen, T.; Chen, Y.; Fang, C.; Dong, L.; Fu, J.; Li, X.; Chen, S.; Shi, Y.; Shen, Y.; Xu, X.; et al. Fine characteristics of the July 2023 extreme rainfall in North China and associated synoptic weather patterns. Acta Meteorol. Sin. 2024, 82, 600–614. (In Chinese) [Google Scholar]
- Zhao, D.; Xu, H.; Li, Y.; Yu, Y.; Duan, Y.; Xu, X.; Chen, L. Locally Opposite Responses of the 2023 Beijing–Tianjin–Hebei Extreme Rainfall Event to Global Anthropogenic Warming. Npj Clim. Atmos. Sci. 2024, 7, 38. [Google Scholar] [CrossRef]
- Shi, C.; Guo, S.; Fan, L.; Gu, S.; Fang, X.; Zhou, L.; Zhang, T.; Li, Z.; Li, M.; Li, W.; et al. GSTAR: An innovative software platform for processing space geodetic data at the observation level. Satell. Navig. 2023, 4, 18. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Li, X.; Yuan, Y.; Zhang, K.; Zheng, H.; Zhang, W. GREAT: A scientific software platform for satellite geodesy and multi-source fusion navigation. Adv. Space Res. 2024, 74, 1751–1769. [Google Scholar] [CrossRef]
- Zhang, K.; Li, H.; Wang, X.; Zhu, D.; He, Q.; Zhang, W. Recent progresses and future prospectives of ground-based GNSS water vapor sounding. Acta Geod. Et Cartogr. Sin. 2022, 51, 1172–1191. [Google Scholar]
- Herring, T.; King, R.; Floyd, M.; McClusky, S. Introduction to Gamit/Globk; Department of Earth, Atmospheric, and Planetary Sciences Massachusetts Institute of Technology: Cambridge, MA, USA, 2018; Available online: https://www-gpsg.mit.edu/~simon/gtgk/docs.htm (accessed on 15 September 2025).
- Zhang, W.; Lou, Y.; Zhou, Y.; Liu, M.; Zhang, Z.; Ou, S.; Liu, J. GNSS meteorological ensemble tools (GMET): A free-access online service for GNSS meteorological applications. GPS Solut. 2024, 28, 202. [Google Scholar] [CrossRef]
- Zhou, Y.; Lou, Y.; Zhang, W.; Kuang, C.; Liu, W.; Bai, J. Improved performance of ERA5 in global tropospheric delay retrieval. J. Geod. 2020, 94, 103. [Google Scholar] [CrossRef]
- Pan, Y.; Gu, J.; Yu, J.; Shen, Y.; Shi, C.; Zhou, Z. Test of merging methods for multi-source observed precipitation products at high resolution over China. Acta. Meteorol. Sin. 2018, 76, 755–766. (In Chinese) [Google Scholar]
- Min, C.; Chen, S.; Gourley, J.; Chen, H.; Huang, C. Coverage of China New Generation Weather Radar Network. Adv. Meteorol. 2019, 2019, 5789358. [Google Scholar] [CrossRef]
- Ye, B.; Lee, G. Vertical Structure of Ice Clouds and Vertical Air Motion from Vertically Pointing Cloud Radar Measurements. Remote Sens. 2021, 13, 4349. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere Mapping Functions for Gps and Very Long Baseline Interferometry from European Centre for Medium-Range Weather Forecasts Operational Analysis Data. J. Geophys. Res. Solid Earth 2006, 111, B02406. [Google Scholar] [CrossRef]
- Chen, G.; Herring, T. Effects of Atmospheric Azimuthal Asymmetry on the Analysis of Space Geodetic Data. J. Geophys. Res. Solid Earth 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Graffigna, V.; Hernández-Pajares, M.; Gende, M.; Azpilicueta, F.; Antico, P. Interpretation of the Tropospheric Gradients Estimated with GPS During Hurricane Harvey. Earth Space Sci. 2019, 6, 1348–1365. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for the troposphere and stratosphere in radio ranging of satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Bar-Sever, Y.; Kroger, P.; Borjesson, J. Estimating Horizontal Gradients of Tropospheric Path Delay with a Single Gps Receiver. J. Geophys. Res. Solid Earth 1998, 103, 5019–5035. [Google Scholar] [CrossRef]
- Herring, T.; King, R.; Floyd, M.; McClusky, S. GAMITR Reference Manual; Department of Earth, Atmospheric, and Planetary Sciences Massachusetts Institute of Technology: Cambridge, MA, USA, 2018. [Google Scholar]
- Liu, Y.; Xu, T.; Liu, J. Characteristics of the seasonal variation of the global tropopause revealed by COSMIC/GPS data. Adv. Space Res. 2014, 54, 2274–2285. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, H.; Liang, H.; Lou, Y.; Cai, Y.; Cao, Y.; Zhou, Y.; Liu, W. On the suitability of ERA5 in hourly GPS precipitable water vapor retrieval over China. J. Geod. 2019, 93, 1897–1909. [Google Scholar] [CrossRef]
- Li, X.; Zus, F.; Lu, C.; Ning, T.; Dick, G.; Ge, M.; Wickert, J.; Schuh, H. Retrieving high-resolution tropospheric gradients from multiconstellation GNSS observations. Geophys. Res. Lett. 2015, 42, 4173–4181. [Google Scholar] [CrossRef]
- Kacmarik, M.; Douša, J.; Zus, F.; Vaclavovic, P.; Balidakis, K.; Dick, G.; Wickert, J. Sensitivity of GNSS tropospheric gradients to processing options. Ann. Geophys. 2019, 37, 429–446. [Google Scholar] [CrossRef]
- Shi, C.; Zhou, L.; Fan, L.; Zhang, W.; Cao, Y.; Wang, C.; Xiao, F.; Lü, G.; Liang, H. Analysis of “21.7” Extreme rainstorm process in Henan Province using BeiDou/GNSS observation. Chin. J. Geophys. 2022, 65, 186–196. (In Chinese) [Google Scholar]
- Zheng, F.; Lou, Y.; Gu, S.; Gong, X.; Shi, C. Modeling Tropospheric Wet Delays with National Gnss Reference Network in China for Beidou Precise Point Positioning. J. Geod. 2018, 92, 545–560. [Google Scholar] [CrossRef]
- Zhou, Y.; Cai, M.; Tan, C.; Mao, J.; Hu, Z. Quantifying the Cloud Water Resource: Basic Concepts and Characteristics. J. Meteorol. Res. 2020, 34, 1242. [Google Scholar] [CrossRef]
- Chen, D.; Pan, C.; Qiao, S.; Zhi, R.; Tang, S.; Yang, J.; Feng, G.; Dong, W. Evolution and Prediction of the Extreme Rainstorm Event in July 2021 in Henan Province, China. Atmos. Sci. Lett. 2023, 24, e1156. [Google Scholar] [CrossRef]
| Rainstorm Event | “96·8” Rainstorm | “12·7” Rainstorm | “16·7” Rainstorm | “23·7” Rainstorm |
|---|---|---|---|---|
| The onset and cessation times | 3–5 August 1996 | 21–22 July 2012 | 19–21 July 2016 | 29 July–2 August 2023 |
| Maximum cumulative rainfall (mm) | 231.3 | 541.0 | 453.7 | 744.8 |
| Maximum hourly rainfall (mm/h) | 45 | 100.3 | 56.8 | 111.8 |
| Maximum duration of rainfall (h) | 44 | 20 | 55 | 81 |
| The average rainfall in Beijing (mm) | 163.6 | 170 | 212.6 | 276.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.; Wang, Y.; Cao, Y.; Liang, H.; Zhou, L.; Mo, Z. Analysis of GNSS Precipitable Water Vapor and Its Gradients During a Rainstorm in North China in July 2023. Remote Sens. 2025, 17, 3247. https://doi.org/10.3390/rs17183247
Su H, Wang Y, Cao Y, Liang H, Zhou L, Mo Z. Analysis of GNSS Precipitable Water Vapor and Its Gradients During a Rainstorm in North China in July 2023. Remote Sensing. 2025; 17(18):3247. https://doi.org/10.3390/rs17183247
Chicago/Turabian StyleSu, Hualin, Yizhu Wang, Yunchang Cao, Hong Liang, Linghao Zhou, and Zusi Mo. 2025. "Analysis of GNSS Precipitable Water Vapor and Its Gradients During a Rainstorm in North China in July 2023" Remote Sensing 17, no. 18: 3247. https://doi.org/10.3390/rs17183247
APA StyleSu, H., Wang, Y., Cao, Y., Liang, H., Zhou, L., & Mo, Z. (2025). Analysis of GNSS Precipitable Water Vapor and Its Gradients During a Rainstorm in North China in July 2023. Remote Sensing, 17(18), 3247. https://doi.org/10.3390/rs17183247







