Extending SETSM Capability from Stereo to Multi-Pair Imagery
Abstract
Highlights
- Extended SETSM with multi-pair image matching for improved DSM generation.
- Object-based 3D KWHE algorithm for optimal height estimation across multiple heights.
- SETSM multiple-pair matching procedure effectively resolves occlusions and enhances DSM quality, while retaining the strengths of the stereopair SETSM algorithm.
- The developed 3D KWHE algorithm significantly reduces surface roughness and noise while preserving edge information in DSM.
Abstract
1. Introduction
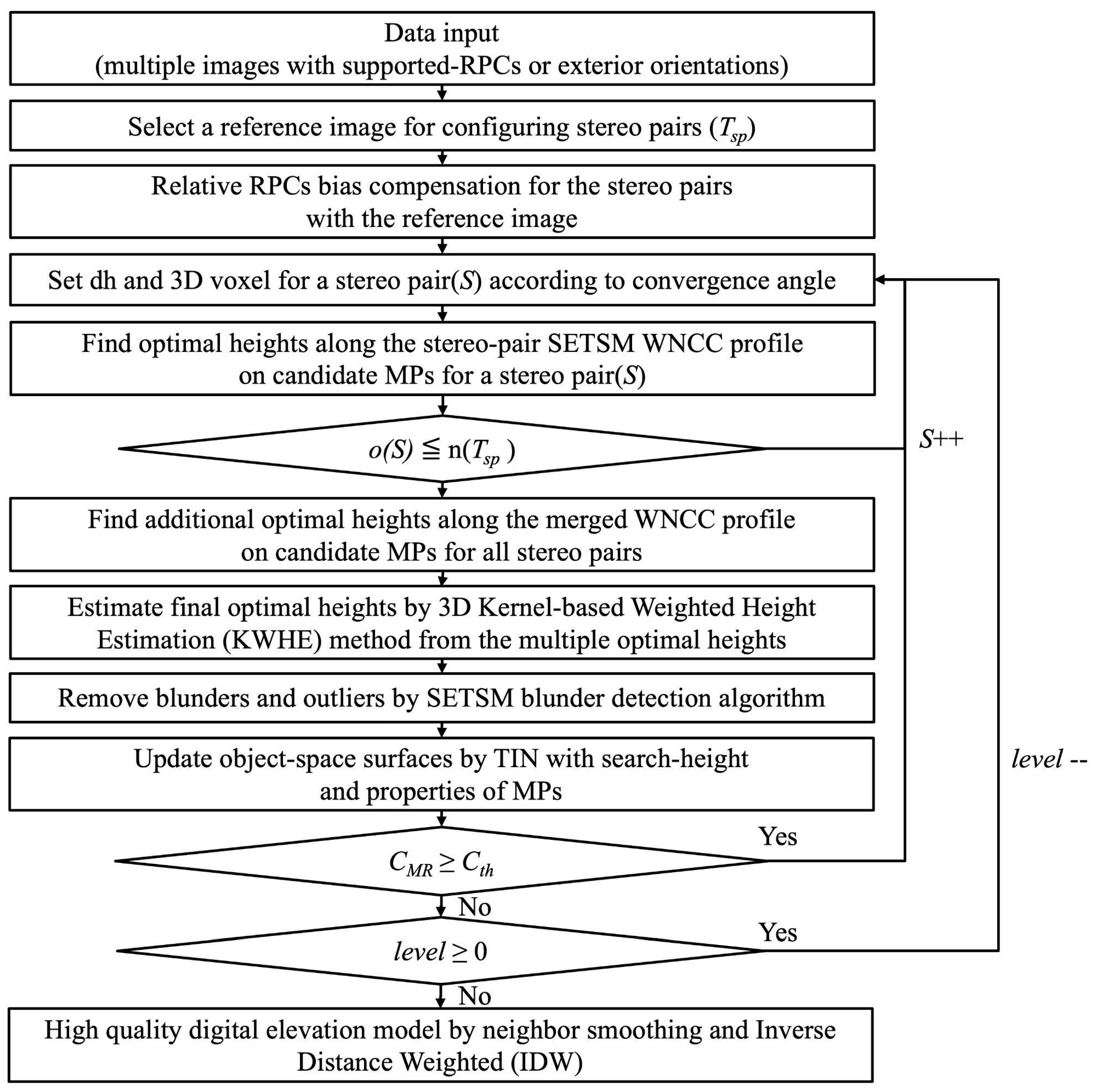
2. Methods
- The use of VLL to geometrically constrain matching features between images and apply object–space matching (no further update).
- Object–space matching to iteratively update the surface model and remove the dependency of the epipolar-resampled images on the VLL (no further update).
- Integrated similarity measurements through complimentary weighted normalized cross-correlation (WNCC) and uncorrected NCC (UNCC) from the original images and geometrically corrected NCC (GNCC) from geometrically corrected images (detailed in Section 2.2).
- Minimization of feature orientations by the modified keypoint descriptor of the Scale-Invariant Feature Transformation (SIFT) method (detailed in Section 2.2).
- Detection and removal of blunders and outliers with geometric constraints provided by the Triangulated Irregular Network (TIN) structure (detailed in Section 2.4).
- Search-space minimization is based on the TIN structure to minimize the matching ambiguity due to repetitive textures and low-contrast surfaces (detailed in Section 2.4).
2.1. Source Imagery and Preprocessing
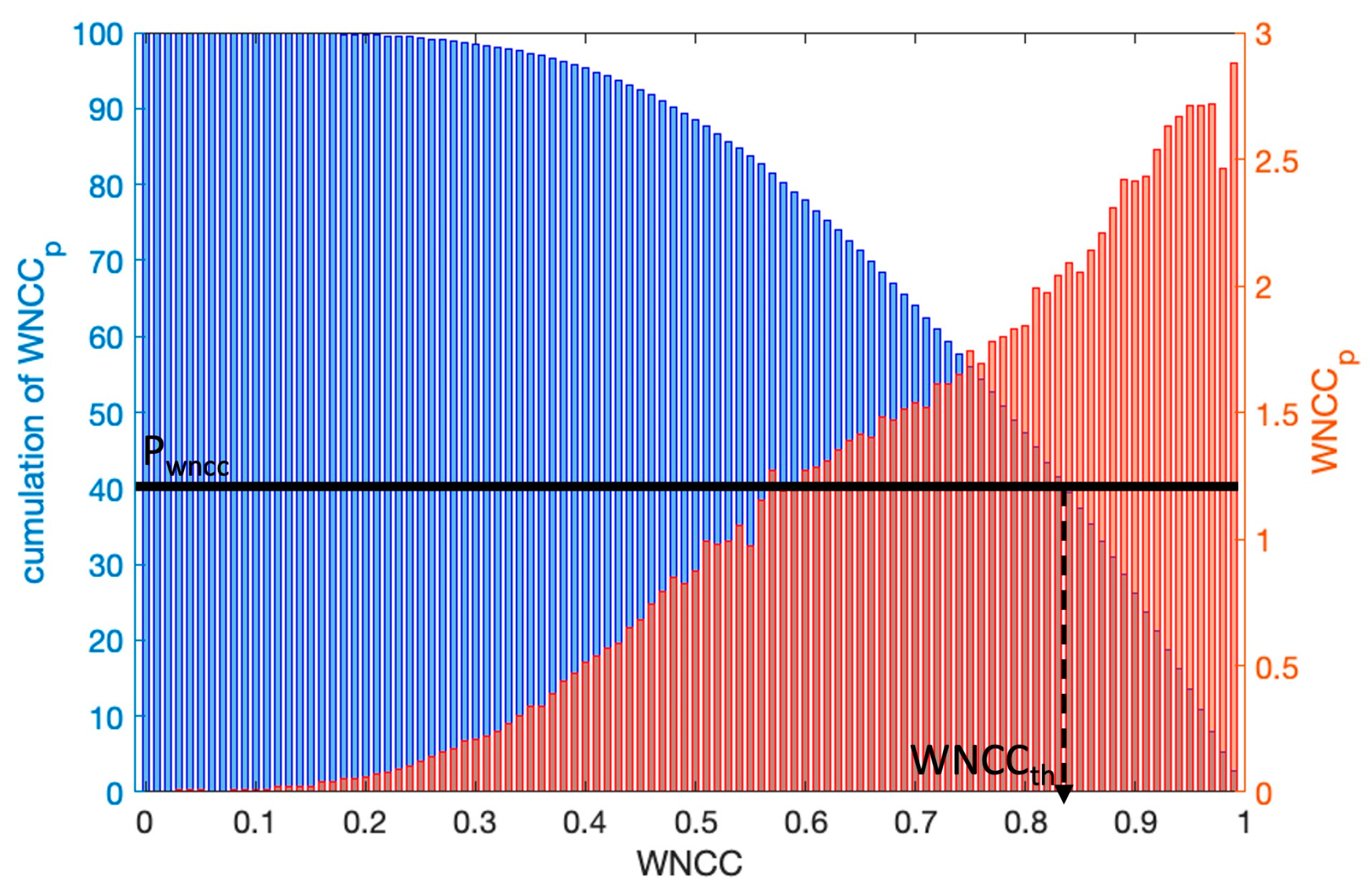
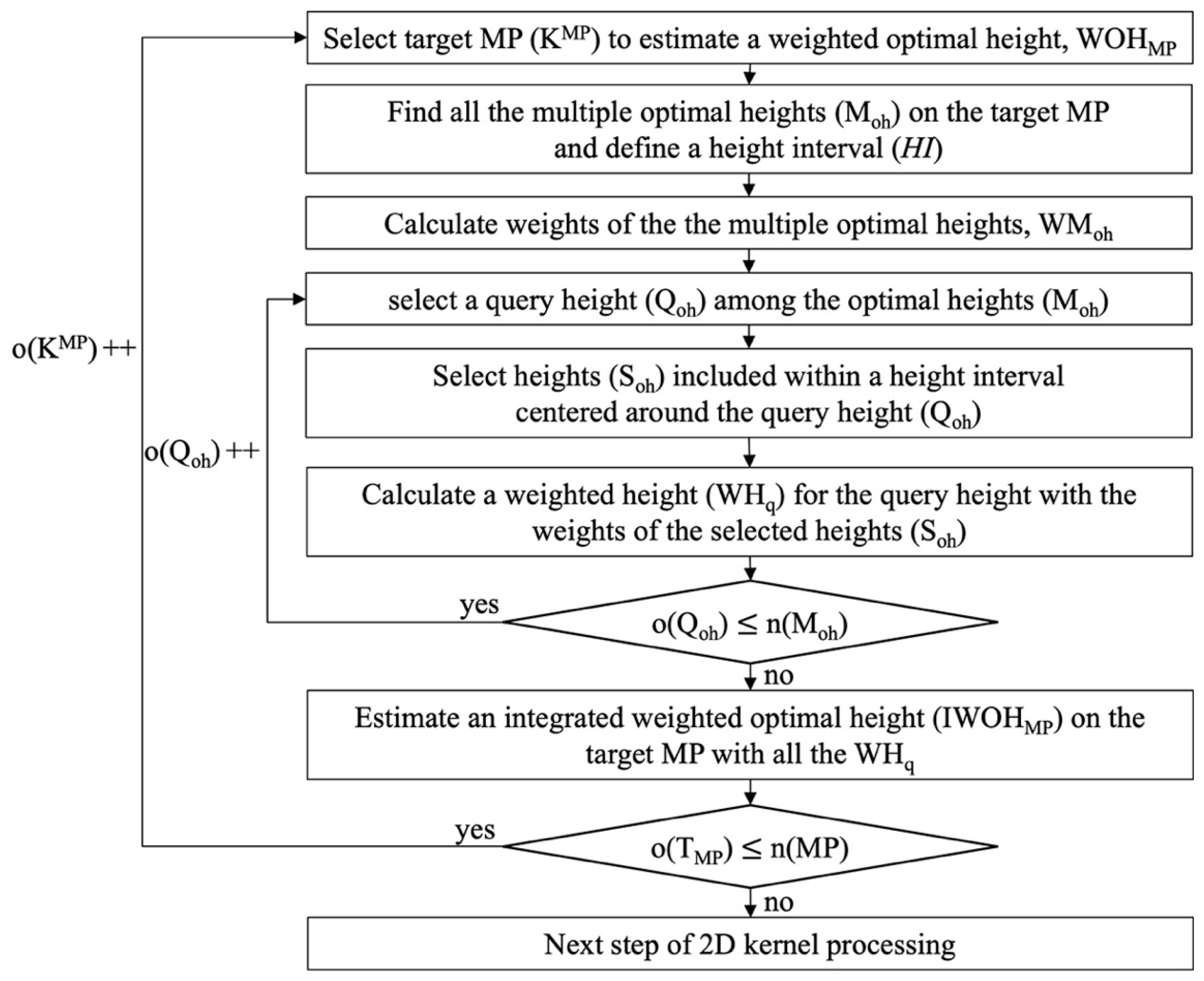
2.2. Estimation of Optimal Height at Each MP from Multiple Pairs
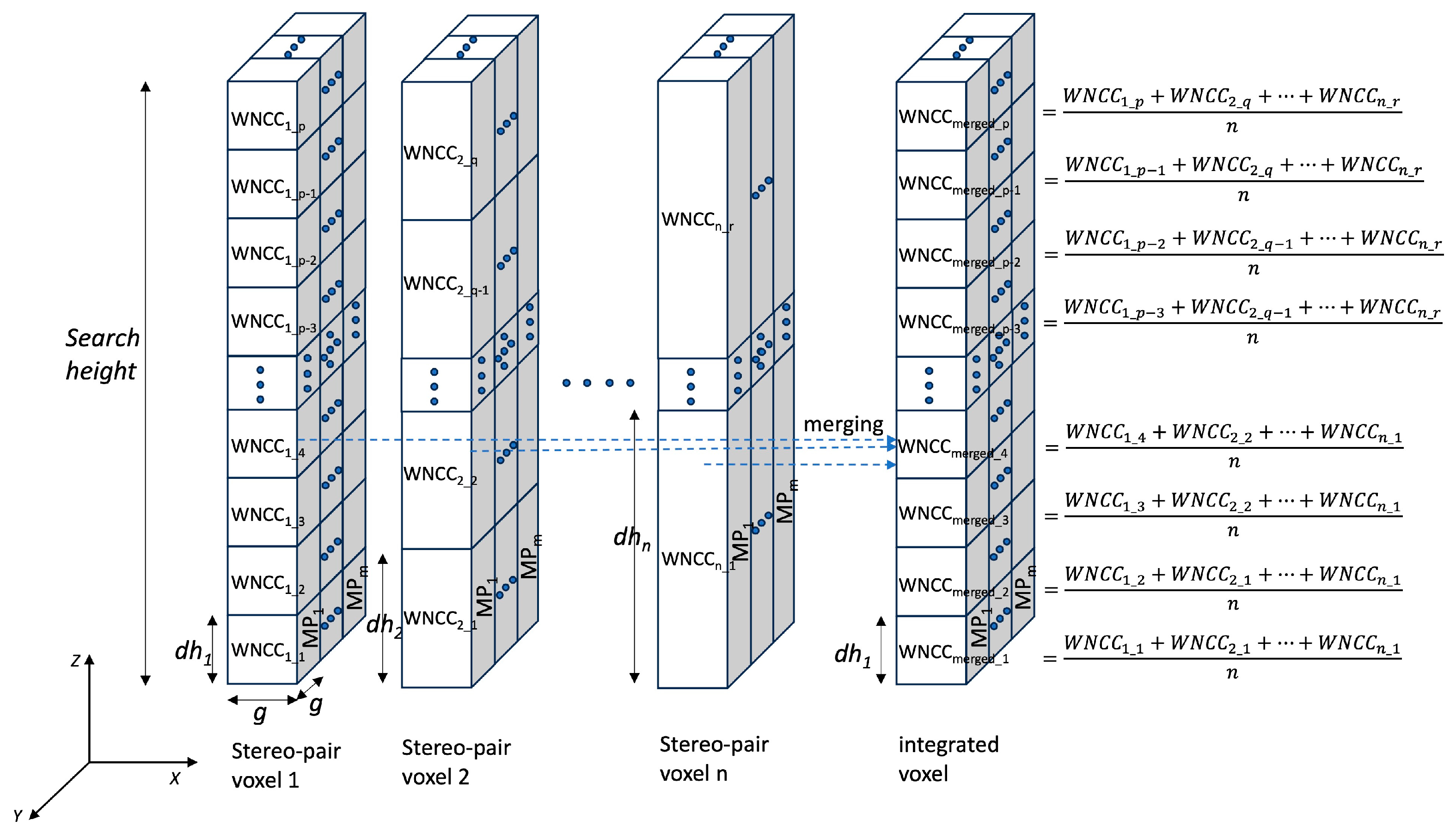
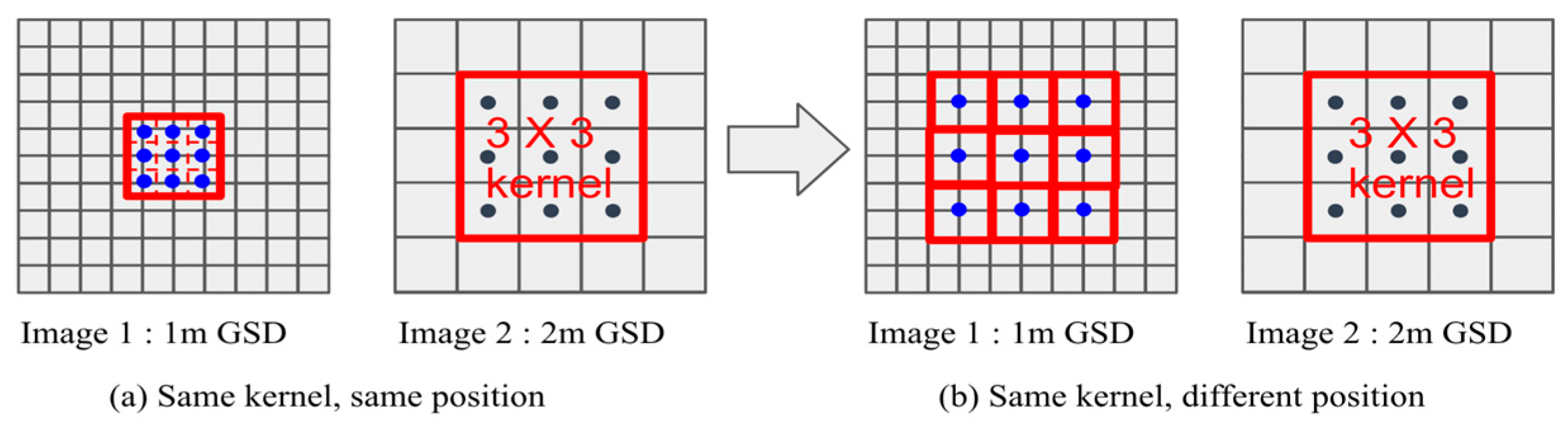
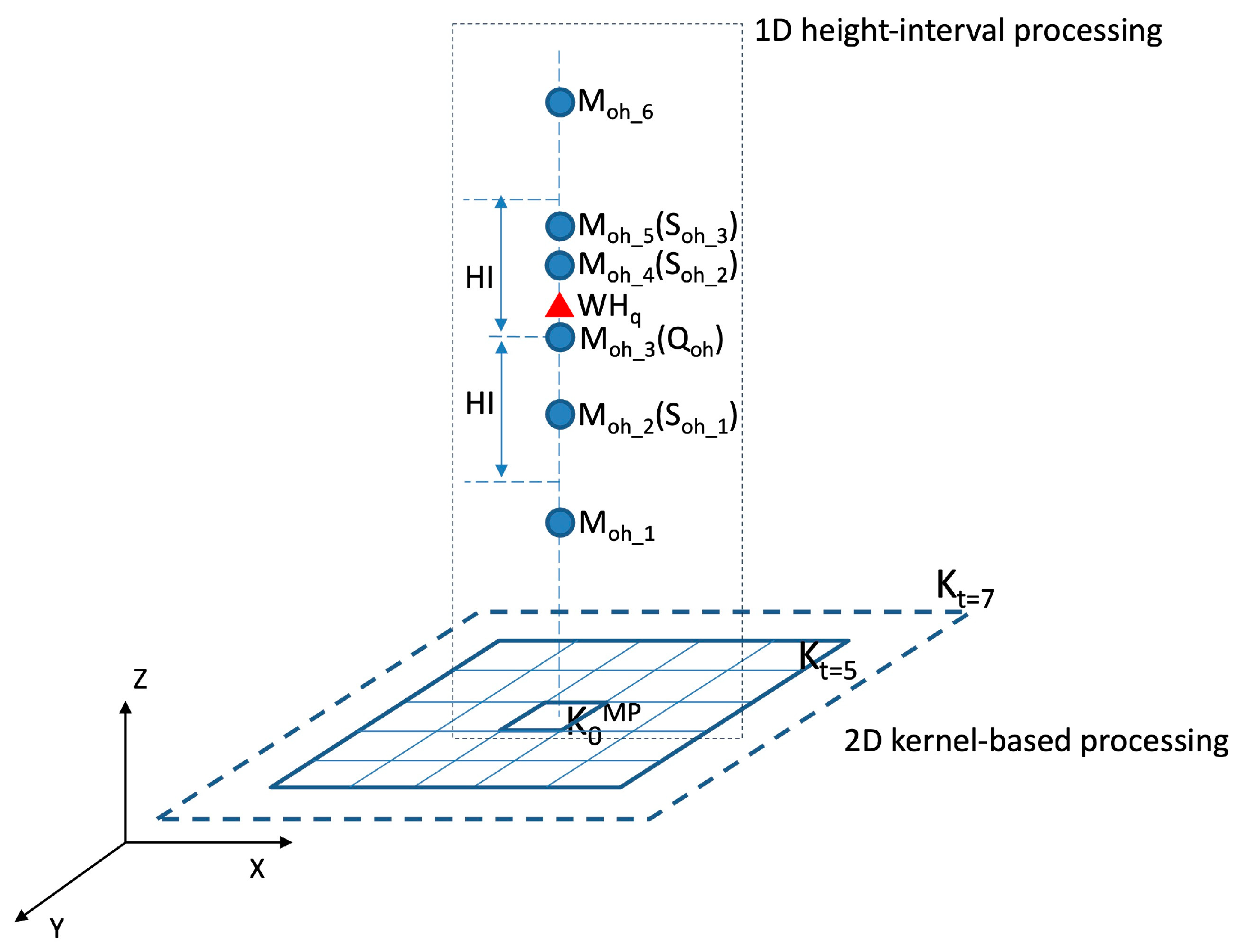
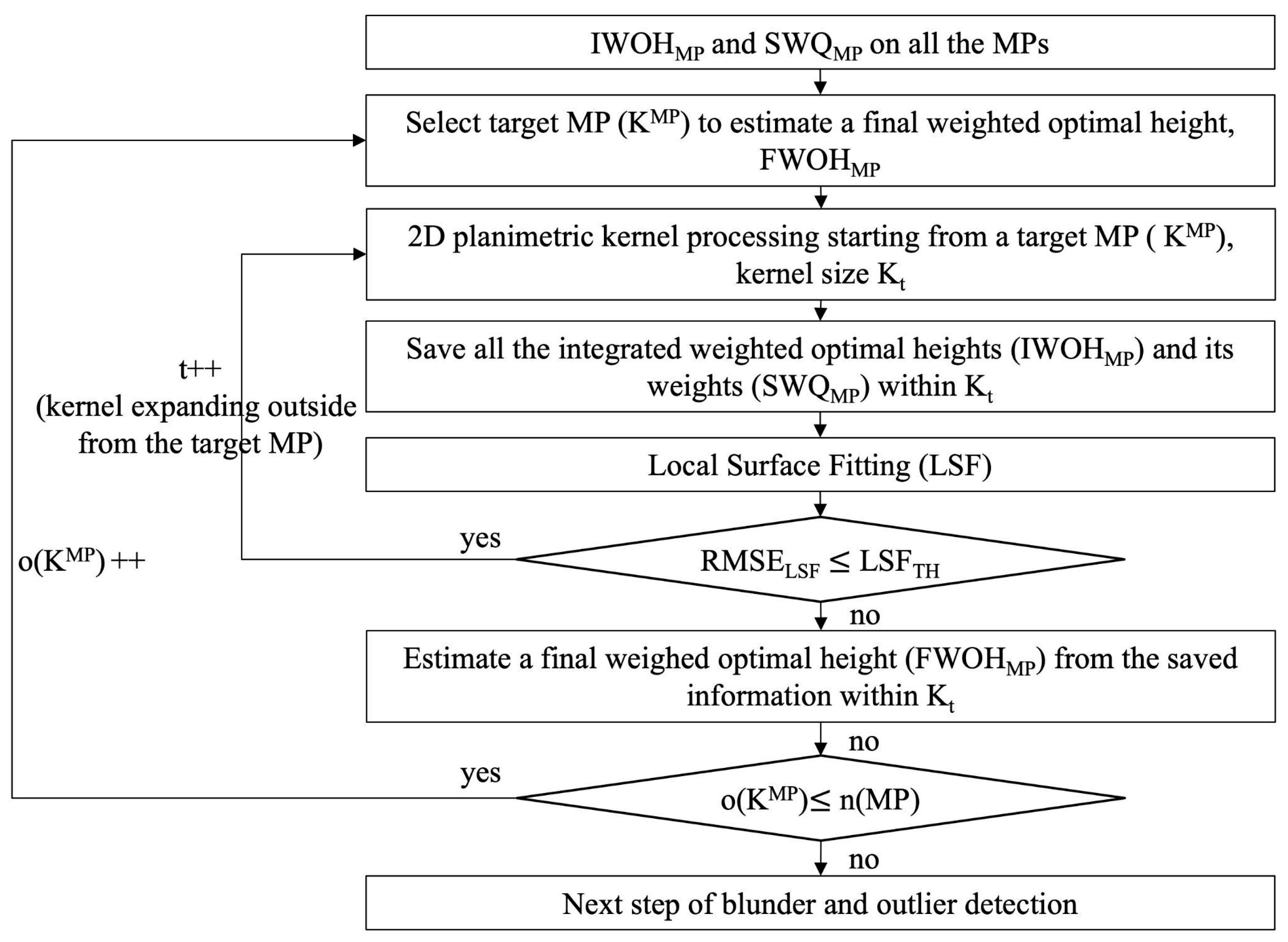
2.3. Three-Dimensional Kernel-Based Weighted Height Estimation
2.4. Blunder/Outlier Detection and Object–Space Surface Refinement
3. Materials
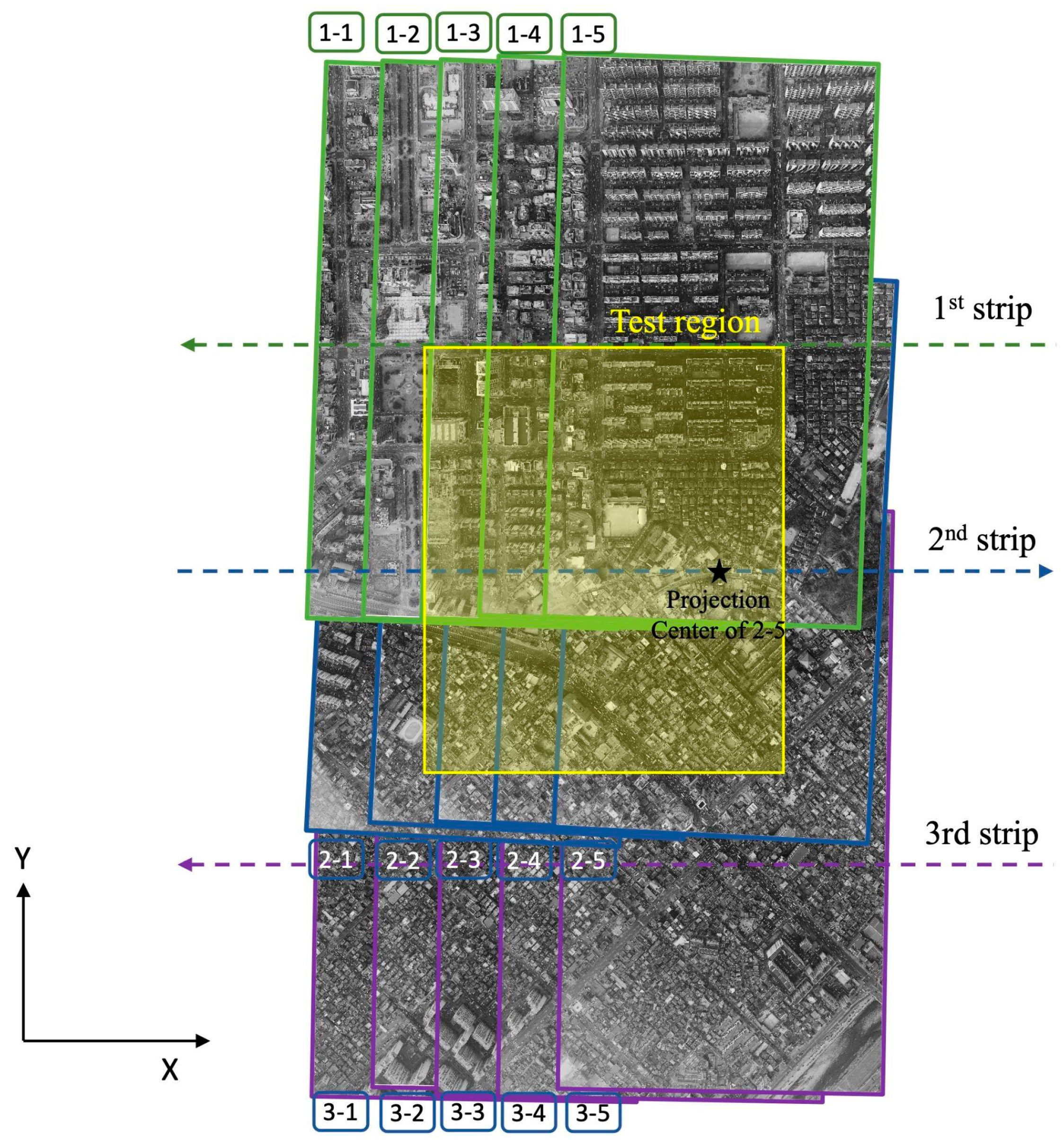
3.1. Experimental Dataset Descriptions
3.1.1. WorldView Images
3.1.2. Digital Mapping Camera Images
3.2. Description of Reference LiDAR Data for Validating DSMs Generated from WorldView Images
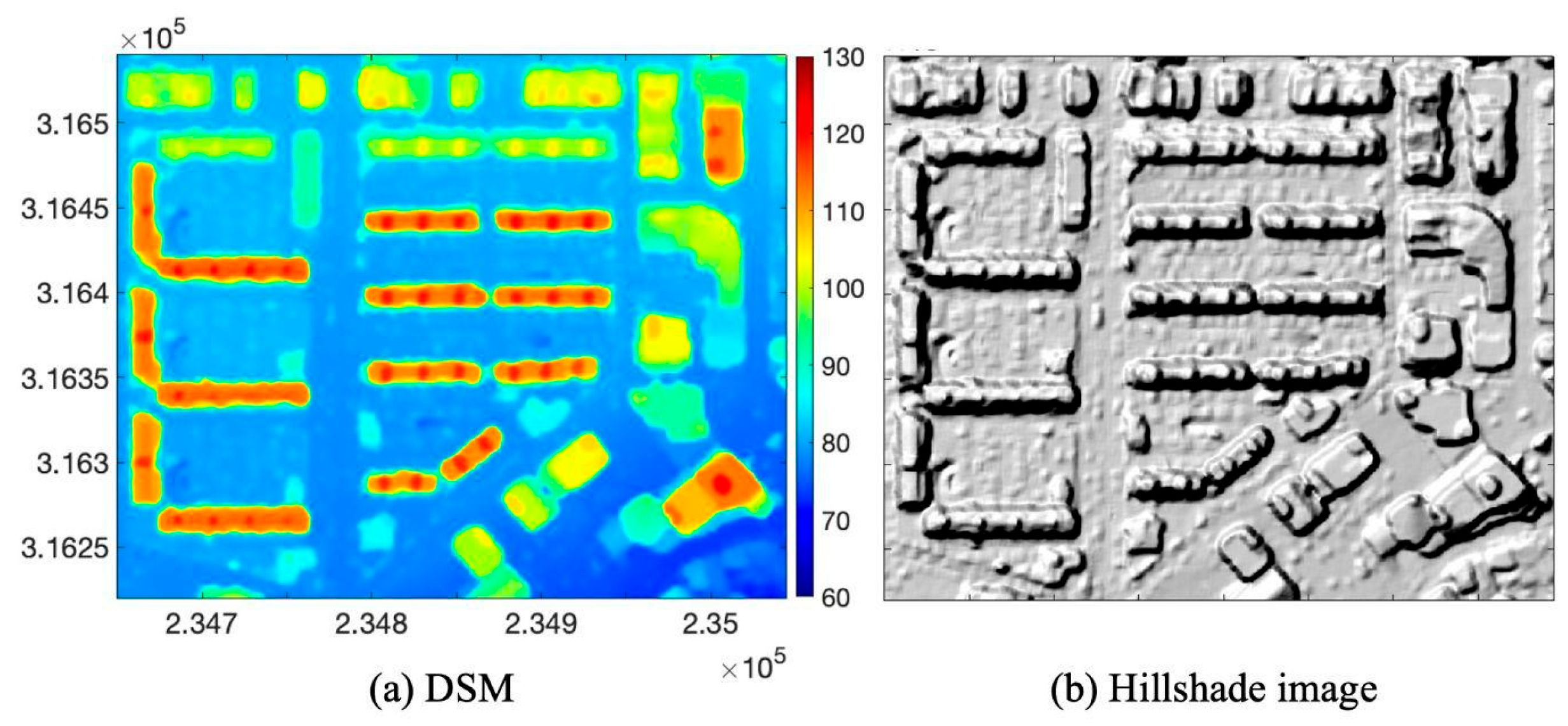
4. Results
4.1. SETSM DSMs with WorldView-2 Multiple Images
4.2. SETSM DSMs with DMC Multiple Images
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SETSM | Surface Extraction by TIN-based Search-space Minimization |
| MMP | multiple-pair matching procedure |
| DSM | Digital Surface Model |
| REMA | Reference Elevation Models for Antarctica |
| KWHE | Kernel-based Weighted Height Estimation |
| GSD | ground sample distance |
| DMC | digital modular camera |
| CNN | Convolutional Neural Network |
| PSM-Net | pyramid stereo-matching network |
| GCS-Net | group-wise correlation stereo network |
| CVA-Net | Cost Volume Analysis Network |
| VLL | Vertical Line Locus |
| NCC | Normalized Cross-Correlation |
| MDE | Matching Distance Error |
| WNCC | weighted normalized cross-correlation |
| UNCC | Uncorrected Normalized Cross-Correlation |
| GNCC | geometrically corrected normalized cross-correlation |
| SIFT | Scale-Invariant Feature Transformation |
| TIN | Triangulated Irregular Network |
| MP | Matching Position |
| RFM | Rational Function Model |
| RPC | Rational Polynomial Coefficient |
| RSM | Rigorous Sensor Model |
| GCP | Ground Control Point |
| LSF | Local Surface Fitting |
| USGS | United States Geological Survey |
| 3DEP | Three-dimensional Elevation Program |
References
- Noh, M.-J.; Howat, I.M. The Surface Extraction from TIN based Search-space Minimization (SETSM) algorithm. ISPRS J. Photogramm. Remote Sens. 2017, 129, 55–76. [Google Scholar] [CrossRef]
- Noh, M.-J.; Howat, I.M. Automated stereo-photogrammetric DEM generation at high latitudes: Surface Extraction with TIN-based Search-space Minimization (SETSM) validation and demonstration over glaciated regions. GISci. Remote Sens. 2015, 52, 198–217. [Google Scholar] [CrossRef]
- Howat, I.M.; Porter, C.; Smith, B.E.; Noh, M.-J.; Morin, P. The Reference Elevation Model of Antarctica. Cryosphere 2019, 13, 665–674. [Google Scholar] [CrossRef]
- Höhle, J. Automated mapping of buildings through classification of DSM-based ortho-images and cartographic enhancement. Int. J. Appl. Earth Obs. Geoinf. 2021, 95, 102237. [Google Scholar] [CrossRef]
- Du, S.; Liu, H.; Xing, J.; Du, S. Fusing multimodal data of nature-economy-society for large-scale urban building height estimation. Int. J. Appl. Earth Obs. Geoinf. 2024, 129, 103809. [Google Scholar] [CrossRef]
- Chang, J.-R.; Chen, Y.-S. Pyramid stereo matching network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Guo, X.; Yang, K.; Yang, W.; Wang, X.; Li, H. Group-wise correlation stereo network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Mehltretter, M.; Heipke, C. Aleatoric uncertainty estimation for dense stereo matching via CNN-based cost volume analysis. ISPRS J. Photogramm. Remote Sens. 2021, 171, 63–75. [Google Scholar] [CrossRef]
- Gao, J.; Liu, J.; Ji, S. A general deep learning based framework for 3D reconstruction from multi-view stereo satellite images. ISPRS J. Photogramm. Remote Sens. 2023, 195, 446–461. [Google Scholar] [CrossRef]
- He, S.; Li, S.; Jiang, S.; Jiang, W. HMSM-Net: Hierarchical multi-scale matching network for disparity estimation of high-resolution satellite stereo images. ISPRS J. Photogramm. Remote Sens. 2022, 188, 314–330. [Google Scholar] [CrossRef]
- Collins, R.T. Space-sweep approach to true multi-image matching. In Proceedings of the CVPR IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996. [Google Scholar]
- Guan, T.; Chang, S.; Deng, Y.; Xue, F.; Wang, C.; Jia, X. Oriented SAR ship detection based on edge deformable convolution and point set representation. Remote Sens. 2025, 17, 1612. [Google Scholar] [CrossRef]
- Tian, Z.; Wang, W.; Zhou, K.; Song, X.; Shen, Y.; Liu, S. Weighted pseudo-labels and bounding boxes for semisupervised SAR target detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 5193–5203. [Google Scholar] [CrossRef]
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef]
- Rupnik, E.; Pierrot-Deseilligny, M.; Delorme, A. 3D reconstruction from multi-view VHR-satellite images in MicMac. ISPRS J. Photogramm. Remote Sens. 2018, 139, 201–211. [Google Scholar] [CrossRef]
- Bulatov, D.; Wernerus, P.; Heipke, C. Multi-view dense matching supported by triangular meshes. ISPRS J. Photogramm. Remote Sens. 2011, 66, 907–918. [Google Scholar] [CrossRef]
- Lv, B.; Liu, J.; Wang, P.; Yasir, M. DSM generation from multi-view high-resolution satellite images based on the photometric mesh refinement method. Remote Sens. 2022, 14, 6259. [Google Scholar] [CrossRef]
- Stathopoulou, E.K.; Battisti, R.; Cernea, D.; Georgopoulos, A. Multiple view stereo with quadtree-guided priors. ISPRS J. Photogramm. Remote Sens. 2023, 196, 197–209. [Google Scholar] [CrossRef]
- Shen, S. Accurate multiple view 3D reconstruction using patch-based stereo for large-scale scenes. IEEE Trans. Image Process. 2013, 22, 1901–1914. [Google Scholar] [CrossRef]
- Schenk, T. Digital Photogrammetry, 3rd ed.; TerraScience: Laurelville, OH, USA, 1999. [Google Scholar]
- Zhang, L.; Gruen, A. Multi-image matching for DSM generation from IKONOS imagery. ISPRS J. Photogramm. Remote Sens. 2006, 60, 195–211. [Google Scholar] [CrossRef]
- Zhang, K.; Sheng, Y.; Wang, M.; Fu, S. An enhanced multi-view vertical line locus matching algorithm of object space ground primitives based on positioning consistency for aerial and space images. ISPRS J. Photogram. Remote Sens. 2018, 139, 241–254. [Google Scholar] [CrossRef]
- Kim, J.-I.; Hyen, C.-U.; Han, H.; Kim, H.-C. Digital surface model generation for drifting Arctic sea ice with low-textured surface based on drone images. ISPRS J. Photogramm. Remote Sens. 2021, 172, 147–159. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Mo, D.; Zhang, Y.; Li, X. Direct digital surface model generation by semi-global vertical line locus matching. Remote Sens. 2017, 9, 214. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Tseng, Y.-H.; Hsieh, C.-Y.; Wang, P.-C.; Tsai, P.-C. Object-space multi-image matching of mobile-mapping-system image sequences. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 465–470. [Google Scholar] [CrossRef]
- Li, R.; Zhou, F.; Niu, X.; Di, K. Integration of Ikonos and QuickBird Imagery for geopositioning accuracy analysis. Photogramm. Eng. Remote Sens. 2007, 73, 1067–1074. [Google Scholar]
- Noh, M.-J.; Howat, I.M. Applications of high-resolution, cross-track, pushbroom satellite images with the SETSM algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3885–3899. [Google Scholar] [CrossRef]
- Digital Mapping Camera System. Available online: https://aerial-survey-base.com/wp-content/uploads/2017/01/DMC-Brochure.pdf (accessed on 4 September 2025).



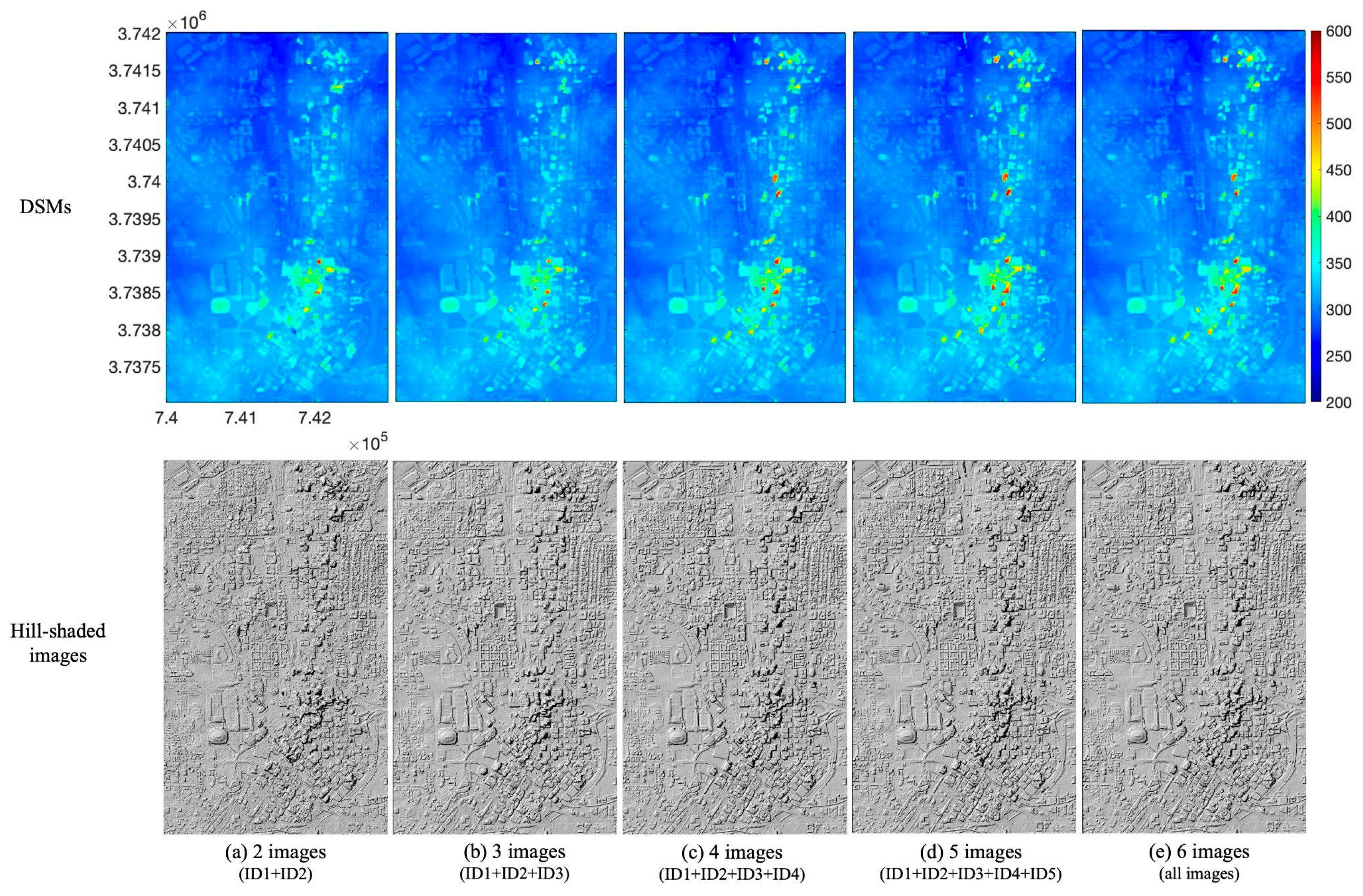

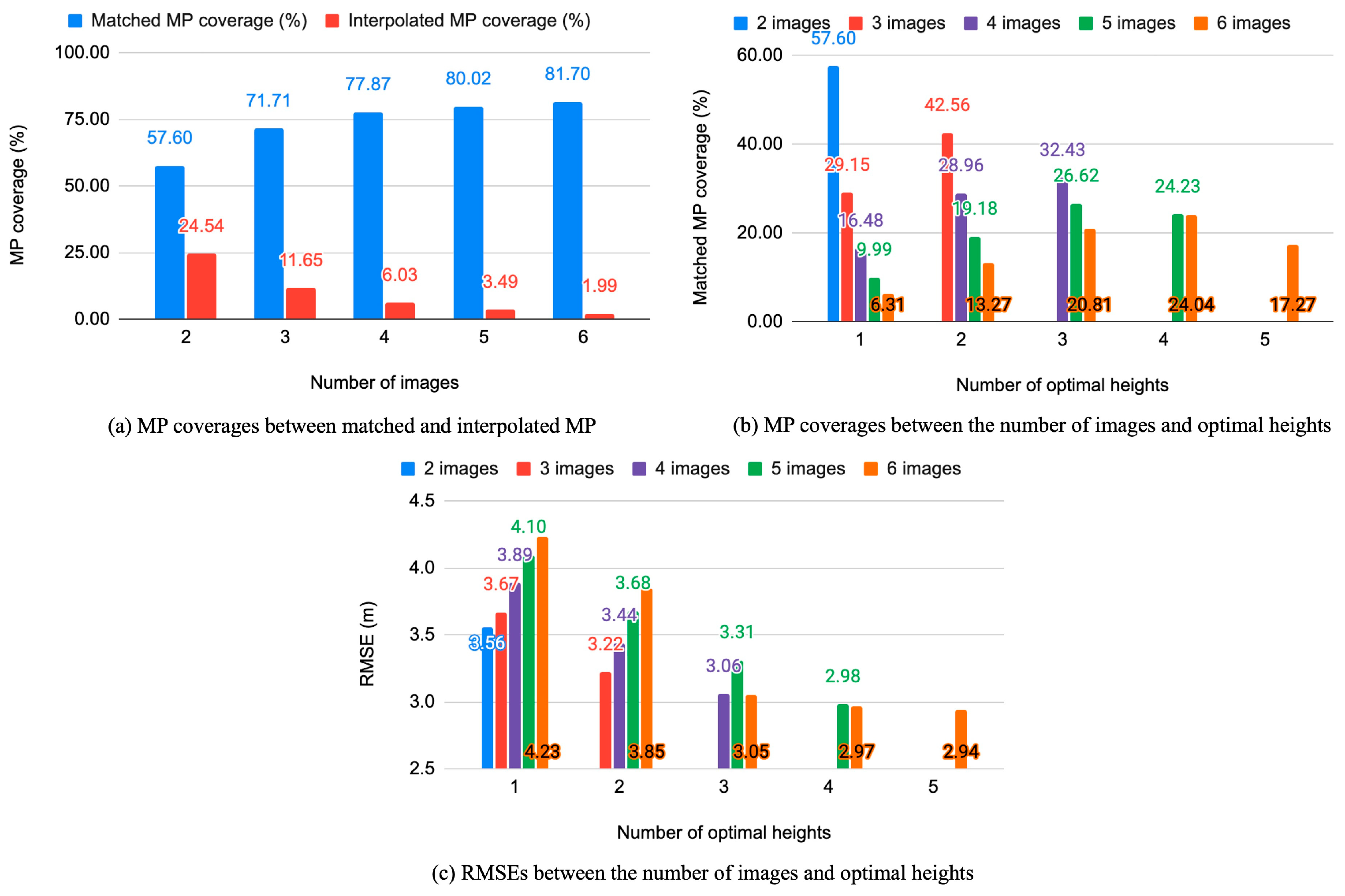
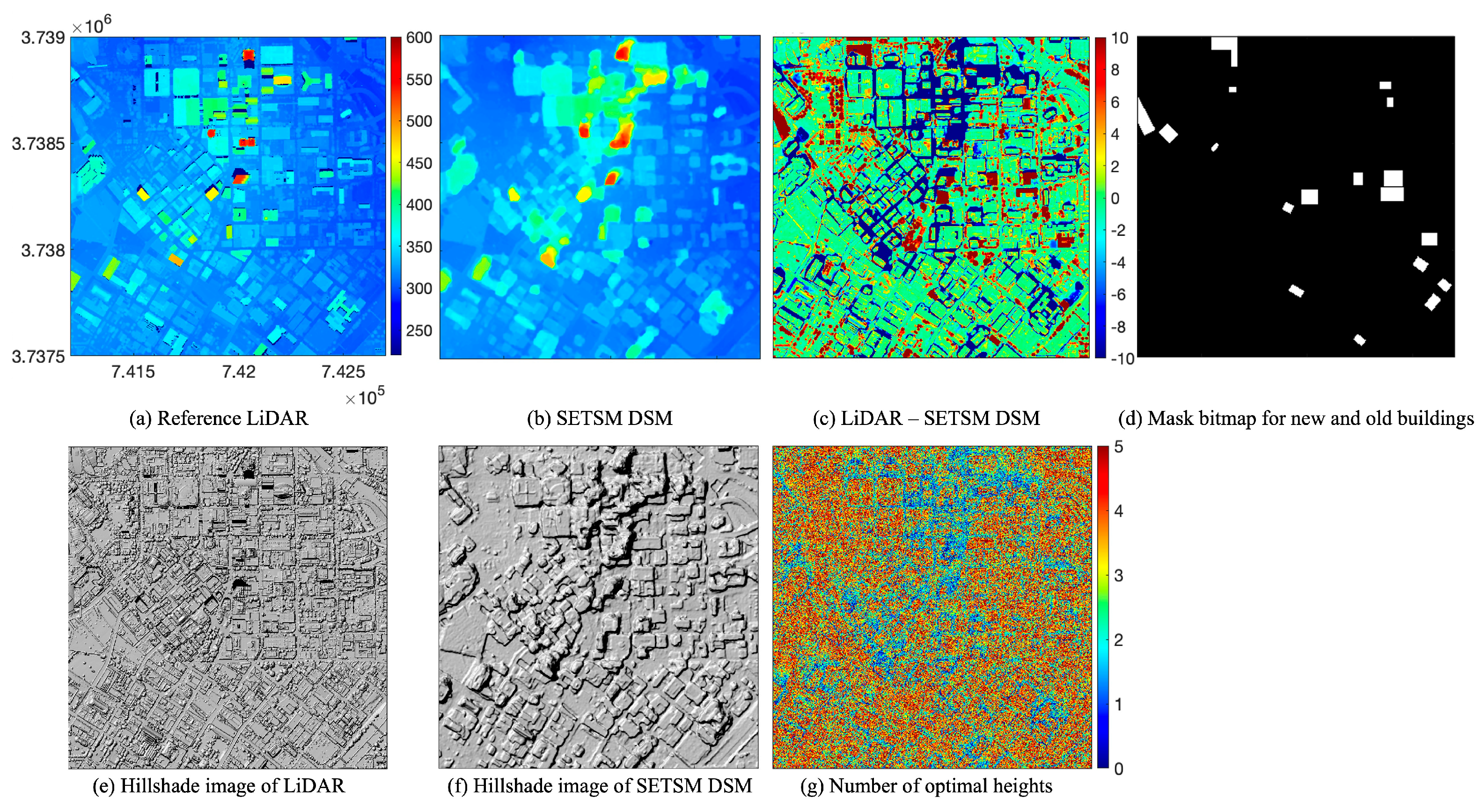
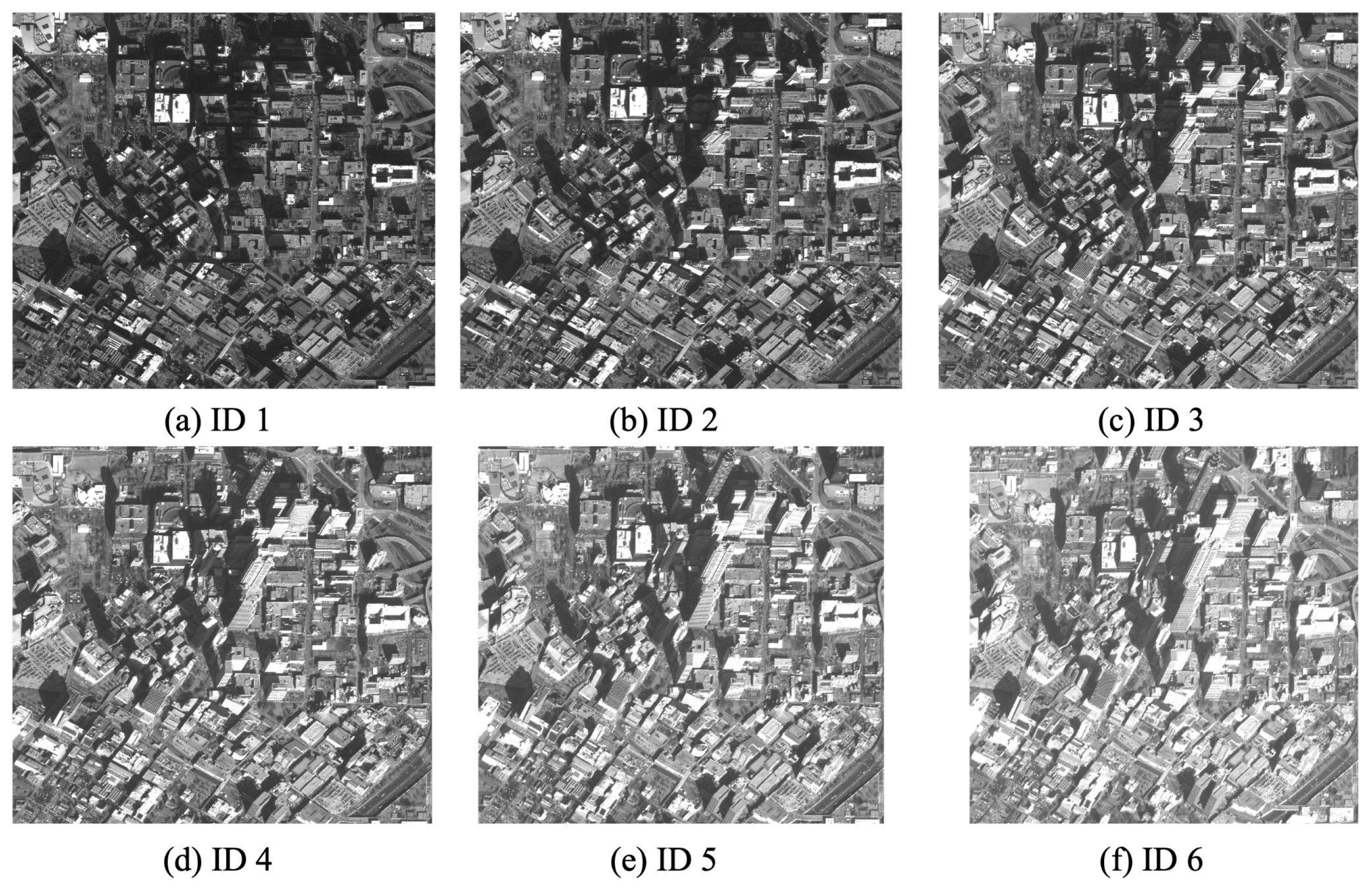



| ID | Image Name | Image Pixel Size (col by Row) | Col GSD (m) | Row GSD (m) | Product GSD (m) | Off Nadir (deg) | Intrack Angle (deg) |
|---|---|---|---|---|---|---|---|
| 1 | WV02_20091222_163622 (reference image) | 35,840 by 34,816 | 0.47 | 0.47 | 0.47 | 7.50 | 1.80 |
| 2 | WV02_20091222_163650 | 35,840 by 30,720 | 0.49 | 0.49 | 0.49 | 14.90 | −12.50 |
| 3 | WV02_20091222_163712 | 35,840 by 26,624 | 0.56 | 0.54 | 0.55 | 23.60 | −22.10 |
| 4 | WV02_20091222_163733 | 35,840 by 23,552 | 0.66 | 0.60 | 0.63 | 31.20 | −30.00 |
| 5 | WV02_20091222_163754 | 35,840 by 21,504 | 0.77 | 0.67 | 0.72 | 37.00 | −35.00 |
| 6 | WV02_20091222_163823 | 35,840 by 17,408 | 1.01 | 0.83 | 0.92 | 44.10 | −43.20 |
| Method | Quality Statistics | MPcov (%) Absolute Height Difference Ranging from 0 to 10 m | |||||
|---|---|---|---|---|---|---|---|
| RMSE (m) | MPcov (%) | 0–2 m | 2–4 m | 4–6 m | 6–8 m | 8–10 m | |
| a | 3.11 | 80.86 | 56.39 | 10.46 | 6.03 | 4.49 | 3.49 |
| b | 3.10 | 81.71 | 56.62 | 10.99 | 6.11 | 4.54 | 3.45 |
| c | 3.17 | 81.36 | 55.05 | 11.69 | 6.36 | 4.70 | 3.56 |
| d | 3.20 | 79.98 | 53.91 | 11.37 | 6.33 | 4.76 | 3.62 |
| e | 3.20 | 80.58 | 54.05 | 11.83 | 6.41 | 4.71 | 3.58 |
| f | 3.21 | 79.73 | 53.82 | 11.03 | 6.39 | 4.80 | 3.69 |
| g | 3.14 | 81.24 | 55.79 | 11.11 | 6.24 | 4.60 | 3.49 |
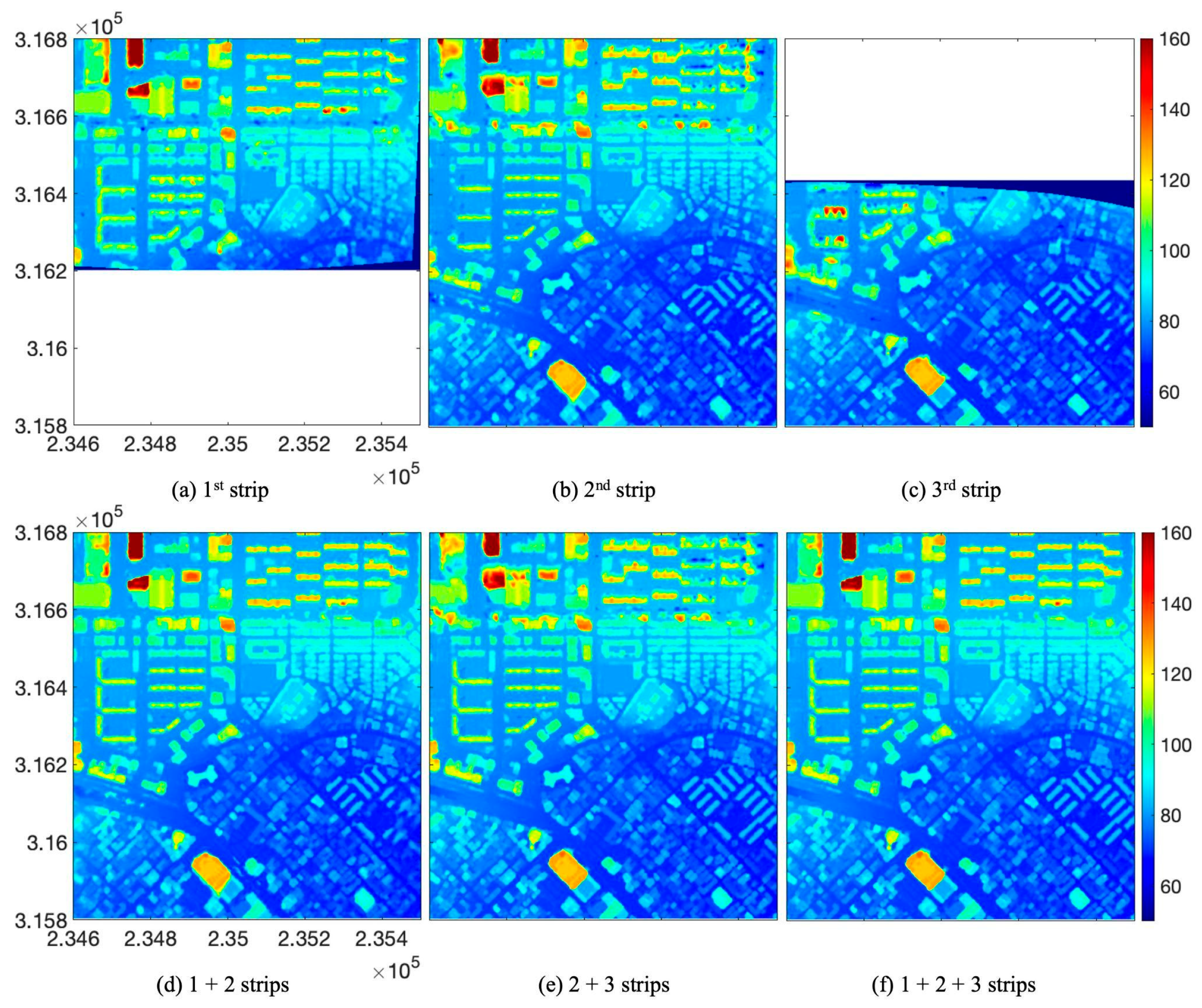
| Combined Strip | Recovered Occlusion (%) | ||
|---|---|---|---|
| Strip 1 | Strip 2 | Strip 3 | |
| 1 + 2 | 22.03 | 14.97 | - |
| 2 + 3 | 9.91 | 13.76 | |
| 1 + 2 + 3 | 22.40 | 17.36 | 14.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, M.-J.; Howat, I.M. Extending SETSM Capability from Stereo to Multi-Pair Imagery. Remote Sens. 2025, 17, 3206. https://doi.org/10.3390/rs17183206
Noh M-J, Howat IM. Extending SETSM Capability from Stereo to Multi-Pair Imagery. Remote Sensing. 2025; 17(18):3206. https://doi.org/10.3390/rs17183206
Chicago/Turabian StyleNoh, Myoung-Jong, and Ian M. Howat. 2025. "Extending SETSM Capability from Stereo to Multi-Pair Imagery" Remote Sensing 17, no. 18: 3206. https://doi.org/10.3390/rs17183206
APA StyleNoh, M.-J., & Howat, I. M. (2025). Extending SETSM Capability from Stereo to Multi-Pair Imagery. Remote Sensing, 17(18), 3206. https://doi.org/10.3390/rs17183206






